A Cost-Effective Approach for the Integrated Optimization of Line Planning and Timetabling in an Urban Rail Transit Line

Abstract

Line planning and timetabling play important roles in the design of urban rail transportation services. Due to the complexity of the integrated optimization of entire transportation plans, previous studies have generally considered line planning and timetabling design independently, which cannot ensure the global optimality of transportation services. In this study, the integrated design problem of line planning and timetabling was characterized as an equilibrium space–time network design problem and solved with a bi-objective nonlinear integer programming model. The model, in which train overtaking and passenger path choice behavior were considered, adjusted the network topology and link attributes (time and capacity) of the travel space–time network by optimizing the train service frequency, operation zone, stopping pattern, train formation, and train order to minimize the system life cycle cost and total passenger travel time perception. An algorithm was constructed using the non-dominated sorting genetic algorithm II combined with the self-adaptive gradient projection algorithm to solve the model. A real-world case was considered to evaluate the effectiveness of the proposed model and algorithm. The results showed that the model not only performed well in the trade-off between system cost and passenger travel efficiency, but it could also reduce the imbalance of train and station loads. Pareto front analysis of the model with different parameters showed that more types of trains did not correlate with a better performance, some line-planning strategies had a combination effect, and multi-strategy line planning was more suitable for scenarios with a high imbalance in the temporal and spatial distributions of passenger flow.

1. Introduction

Urban rail transit systems play an important role in the travel of residents in metropolises, especially commuters, owing to their low cost, large capacity, and punctuality. The diversity of passenger travel demands under the network operations of urban rail transit, such as travel efficiency and comfort, highlights the imbalance in the temporal and spatial distributions of passenger flow. The traditional stopping mode is difficult to adapt to such passenger flows due to non-differentiated services, and transport capacity will be wasted in sections with a low passenger flow because of providing a sufficient transport capacity in sections with a high passenger flow, which is not suitable for metro corporations.

To enhance the attractiveness and competitiveness of urban rail transit services, scholars have considered the needs of the service and served parties and have built different line-planning optimization models [1], including ones considering train service frequency (TSF), train operation zone (TOZ), train stopping pattern (TSP), and train formation (TF). Optimizing the service frequency and train formation are representative line-planning strategies for adapting the temporal imbalance of train loads, such as time-varying frequency [2] and variable train lengths [3] modes. Optimizing the train operation zone and stopping pattern are tactical strategies for adapting the spatial imbalance of passenger flow, such as multiple turn-backs [4] and express/local stopping [5] modes. Due to the extremely high complexity of the entire system, most existing studies have focused on quantitatively investigating a single specific issue.

Table 1. Effects of line-planning strategies (−/+ indicates decrease/increase).

Indicators	Time-Varying Frequency	Multiple Turn-Backs	Express/Local Stopping	Variable Train Lengths
Temporal imbalance of train load	−			−
Spatial imbalance of train load		−	−
Imbalance of station load		−	−
Operator cost	±	−	±	−
Total waiting time	−	±	+
Total passenger In-vehicle time			−
Total passenger Transfer time		+	+	−

summarizes the operational effects of four main line-planning strategies [6]. It can be seen that a single line-planning strategy cannot simultaneously deal with the imbalances in the temporal and spatial distributions of passenger flow. Rather, a combination of multiple strategies is required to provide diversified train services. These multi-strategy service modes have been widely applied in many metropolises, including London, Tokyo, Paris, and New York. Taking the Seibu-Shinjuku line in Japan as an example, Figure 1 shows the morning peak timetable on weekdays. There are five train operation zones: from Shinjuku to Kami-Shakujii, Tanashi, Kodaira (branch line to Haijima), Shi-Tokorozawa, and Hon-Kawagoe, respectively. Each operation zone has different stopping patterns, which include four types of trains: local, semi-express, express, and limited express Koedo-go. Although we can analyze the advantages and disadvantages of this complex line plan with diversified train services and all-stop modes by a quantitative calculation of operation indicators, such as cost and travel efficiency, it is difficult to determine whether the solution is optimal, because the theoretical research on strategy comparison and combination is behind the practical research. Optimal diversified train services must not only have a line plan with multiple line-planning strategies, but also a feasible timetable, which are two sequential processes of the train-planning process, including demand analysis, line planning, train scheduling (i.e., timetabling), rolling stock planning, crew scheduling, and crew rostering [7].

Considering the complexity of the integrated optimization of the entire train planning process, existing research generally optimizes these processes individually in stages by decomposing them into controllable subproblems and predefining the timetable structure information of other stages, such as the stopping pattern and train length in the line-planning stage and the departure time, train orders, and overtaking stations in the timetabling stage. Optimizing the entire problem sequentially is always inferior to integrated optimization, because the optimal output of a subtask will generally not result in an overall optimal solution [8]. With improvements in the performance of computer hardware and optimization methods, scholars have begun to deal with some sequential processes of the entire problem, such as the integrated optimization of line planning and timetabling [9,10]. These studies usually have a limited flexibility in the timetable structure (i.e., they have some predefined timetable structure information). The optimal results are theoretically different from the flexible timetable structure (i.e., without predefined timetable structure information) because this information directly affects the calculation of the detailed timetable solution described by the specific department and arrival times.

Passengers have a variety of travel paths under diversified train services because there are multiple paths between the same origin–destination (OD) pair in the passenger travel space–time network. Passengers will choose these paths differently because the travel times, which include waiting time, on-board time, transfer time, and train congestion, differ; thus, analyzing passenger path choice behavior is essential. The heterogeneity of passengers’ travel demands, such as travel congestion and fatigue, is an important reason for path choice behavior. Passengers will choose follow-up trains according to daily travel experiences and timetables to avoid discomfort caused by in-vehicle crowding [11] and fatigue caused by long journeys, especially for standing passengers [12]. However, in studies on the optimization of line planning for providing train services at different speeds [7,13], travel fatigue is rarely considered, which makes the original intention of designing fast trains (i.e., reducing travel time) unable to be fully reflected.

This study aimed to address the above research gap. The objective was to propose an integrated line-planning and timetabling optimization model, which can fully consider passenger path choice behavior to implement a new timetable, with multi-strategy line planning for an urban rail line. The remainder of this paper is organized as follows. Section 2 reviews the relevant state-of-the-art literature. The overall problem statement is presented in Section 3. In Section 4, a bi-objective equilibrium space–time network design model (ESTNDM) is formulated, and Section 5 describes the solution algorithms for the model. A real case study is reported in Section 6. Finally, conclusions and future work are discussed in Section 7.

2. Literature Review

Many technologies for urban rail transit operation come from the practice of bus [14] and railway operations [15]. Mathematical optimization methods for single line planning have been widely studied, including in terms of service frequency [16], operation zone [17], stopping pattern [18], and train formation [3,19]. Nowadays, the application of these line-planning strategies has become more common. However, with the expansion of the urban rail transit network and increases in travel demand, the diversity of passenger travel demands intensifies the imbalance in the temporal and spatial distributions of passenger flow, decreasing the applicability of a single line-planning strategy.

2.1. Multi-Strategy Line Planning

Scholars have begun to focus on multi-strategy line planning [20,21,22]. Cortés et al. [23] and Tirachini et al. [24] took the operator and passenger travel costs as their optimization objectives and the turn-back station and frequency of short-turn buses as their decision variables; then, they established an integrated short turning and deadheading model. Using the first-order conditions, they obtained analytical expressions for the optimal value of frequency. Chang et al. [25] presented an integrated optimization model to determine the optimal service frequency, stopping pattern, and train formation and to minimize the total passenger travel time loss and total operating costs, including the fixed overhead costs and variable operating costs of high-speed railways. A fuzzy mathematical programming method was used to solve the model.

Most studies predefine the line-planning strategies and remaining timetable structure information in the line-planning stage and timetabling stage, which presents two problems in their practical application.

The first problem is that there is insufficient research on the comparison and combination of line-planning strategies with the same (different) operational effects when improving the temporal and spatial imbalances of train or (and) station loads alone (simultaneously). For example, according to Table 1, when improving the spatial imbalance of train load (SIT), it is necessary to choose multiple turn-backs or express/local stopping modes. When improving the SIT and the temporal imbalance of train load (TIT) simultaneously, there are 11 possible combination strategies, which are obtained by combining time-varying frequency, multiple turn-backs, and variable train length modes with multiple turn-backs and express/local stopping modes. Only a few studies have compared the optimal solutions of different strategies, e.g., Nesheli et al. [26], but their research considered a bus system, so it is necessary to study a more comprehensive and general multi-strategy model for urban rail transit.

The second problem is that the coordination between the line plan and timetable is poor due to the predefined timetable structure information in the timetabling stage, which means that the line-plan- and timetable-designing processes are handled individually and sequentially. Although this top-down hierarchical approach can decompose the entire problem into subproblems of manageable size, it is not optimal, because the optimal output of a subtask, which serves as the input of a subsequent task, will generally not result in an overall optimal solution [7]. In addition, the predefined structure will not only lead to a limited efficiency, robustness [27], and flexibility of the output solutions (such as no overtaking), but it will also fail to fully consider the passenger path choice behavior, because a passenger’s alternative travel paths are affected by each train service level (such as train speed and service time, which depend on timetable structure) and cannot be ignored. This problem must be solved using the integrated optimization of line planning and timetabling.

2.2. Integrated Optimization of Line Planning and Timetabling

In recent years, the integrated optimization of line planning and timetabling has become popular [28,29,30,31]. Most research on the integrated optimization of frequency and timetabling assumes that the demand is evenly distributed in each period during the study period [2,32]. This strategy is easy to apply and performs well when the train capacity is sufficient under uncongested conditions [33]. To adapt to time-dependent passenger demands under congested conditions, Zhang, T. et al. [34] presented a nonlinear non-convex programming model to design timetables with the objective of minimizing the total passenger travel time (TTT) by considering variable numbers of trains, train running times, and train dwell times.

In research on the integrated optimization of operation zone and timetabling, Zhang, M. et al. [35] developed a mixed-integer nonlinear programming (MINLP) model for train scheduling with full-length and short-turn train services to minimize the headway deviation and number of trains. They solved the main decision variables, i.e., the types of train services, departure times, and arrival times, for each train at the origin and destination station based on the predefined headway obtained by passenger demand analysis using the CPLEX solver. The performance of the model, including its reduction in the utilization of trains, was evaluated through a case study on Beijing Subway Line 4.

Research on the integrated optimization of stopping patterns and timetabling is mainly conducted in the field of railways [36,37,38,39,40]. Yang et al. [9] developed a mixed-integer programming model to describe the problem of high-speed railways with the aim of minimizing the train dwell time at intermediate stations and delays in expected departure time. They used continuous variables to represent the train arrival and departure times and 0–1 variables to represent the train stop plan and indicator of train departure order. Meanwhile, in the field of urban rail transit, Wang et al. [41] described the integrated problem under a stop-skipping strategy as a bi-level MINLP model to reduce passenger travel time and energy consumption with penalties that ensured the service level of passengers on the last train. The high-level decision variable represented train stopping patterns, and the low-level variable represented the speed of the train speed holding phase and departure times. In the model, trains could only skip the stations that belonged to the predefined skipping set with no overtaking of other trains, and passengers could only take one train to arrive at their destination, i.e., transfer between different trains along the line was not allowed.

Most research on the integrated optimization of train formation and timetabling focuses on the field of public buses and railways and includes frequency optimization, because train formation is usually combined with frequency to determine the capacity distribution [42]. Sun et al. [10] proposed three flexible timetable optimization methods based on hybrid vehicle size, large vehicle size, and small vehicle size to minimize the vehicle operational costs and TTT by optimizing the vehicle size and scheduling interval (similar to headway in urban rail transit), which determine the frequency. The results of a case study indicated that the hybrid vehicle size model outperformed the other two models in both total time and total cost.

2.3. Optimization Algorithm Analysis

The integrated optimization of timetabling alongside other planning processes, with consideration for traffic equilibrium, can be regarded as a form of network design problem (NDP). This approach is predicated on the understanding that the timetable itself can be conceptualized as a space–time network. Karp et al. [43] first discussed the computational complexity of the NDP in theory and noted that general NDPs are NP-hard problems, and there is almost no possibility of an effective polynomial algorithm.

The NDP is commonly characterized as a multiobjective bilevel optimization (MOBO) problem. Popular solution approaches include exact methods, such as those based on Karush–Kuhn–Tucker (KKT) conditions, and approximate techniques such as metaheuristics [44]. The non-dominated sorting genetic algorithm II (NSGA-II) [45] is one of the most widely used and best solving algorithms in multi-objective programming evolutionary algorithms.

The essence of the traffic equilibrium problem (TEP) lies in a variational inequalities model. The Goldstein–Levitin–Polyak projection algorithm (GLP) is a classical algorithm for solving variational inequalities [46,47]. He et al. [48] originally proposed the self-adaptive scheme for GLP, which was extended through a new step size rule by Han et al. [49]. Chen et al. [50] applied this extended method to the nonadditive traffic equilibrium problem (NaTEP), and proposed a self-adaptive gradient projection algorithm (SAGP) in which the route-flow variables were rewritten in terms of the non-shortest route flows and the shortest path flow was used to ensure flow conservation.

2.4. Research Gaps

However, if these methods are applied directly, there may be some limitations. First, most of them do not allow for overtaking, which limits the express travel service of medium- and long-distance passengers, so they cannot fully reflect the advantages of multi-train services. Second, research that allows for overtaking aims at minimizing passenger travel time, such as [13,51], ignoring the cost of urban rail transit systems. Although this omission can ensure passenger service efficiency, it cannot account for the interests of the operator and may lead to some unrealistic decision schemes, such as an excessive train service frequency or overtaking stations. Third, although some studies have considered costs, they mainly focused on minimizing the operation costs and energy consumption, but such cost analysis is not comprehensive, because the decision schemes for providing multi-train services will have an impact on the cost of each stage of the system life cycle (LC), e.g., building overtaking stations in the construction or operation stage and maintaining vehicles in the operation stage. Fourth, research on optimizing the stopping pattern often assumes that the train sequence includes express trains and local trains, which means that the proportion of express trains and local trains is balanced, as in Li et al. [7]. This assumption is not easy to adapt to practical traffic flows with uneven temporal and spatial distributions, and it ignores the influence of the numbers and service times (or service orders) of trains of different service levels on passenger travel choices.

This study aimed to address the research gap described above. The objective was to propose the integrated optimization of multi-strategy line planning and periodic even-headway timetabling for an urban rail line, aiming to obtain a set of Pareto optimal solutions with the minimum system life cycle cost (LCC) and total passenger travel time perception (TTTP) under the given OD passenger flow. This study extends previous research in the following ways:

(1) In this paper, the integrated optimization of line planning and timetabling is described as a space–time network design problem of urban rail transit from a new perspective, which systematically describes timetable structure information and passenger path choice behavior. An equilibrium space–time network design model is proposed to solve this problem, which requires little predefined timetable structure information because it simultaneously optimizes the train service frequency, operation zone, stopping pattern, train formation, and train order, and allows for overtaking to ensure the efficiency and flexibility of the timetable.

(2) This study considers a more comprehensive heterogeneity of passengers, including not only the commonly used perception of in-vehicle time with congestion, but also the perception of travel fatigue related to path time. Using the user equilibrium model to describe passenger path choice behavior is more realistic than the assumption of first-in-first-out (FIFO) or prorate assignment, because this method allows passengers to freely choose their transfer station between different train services.

(3) This study considers a more comprehensive system cost by analyzing the cost impact of multi-train services at each stage of the LC of an urban rail transit system, such as the total costs of an overtaking station, train operation, maintenance, and staff, which is more in line with the actual management needs of operators.

3. Problem Description

The aim of this study was to determine a line plan and timetable by considering passenger path choice behavior to minimize TTTP and system LCC under a predefined number of train types and other operation parameters.

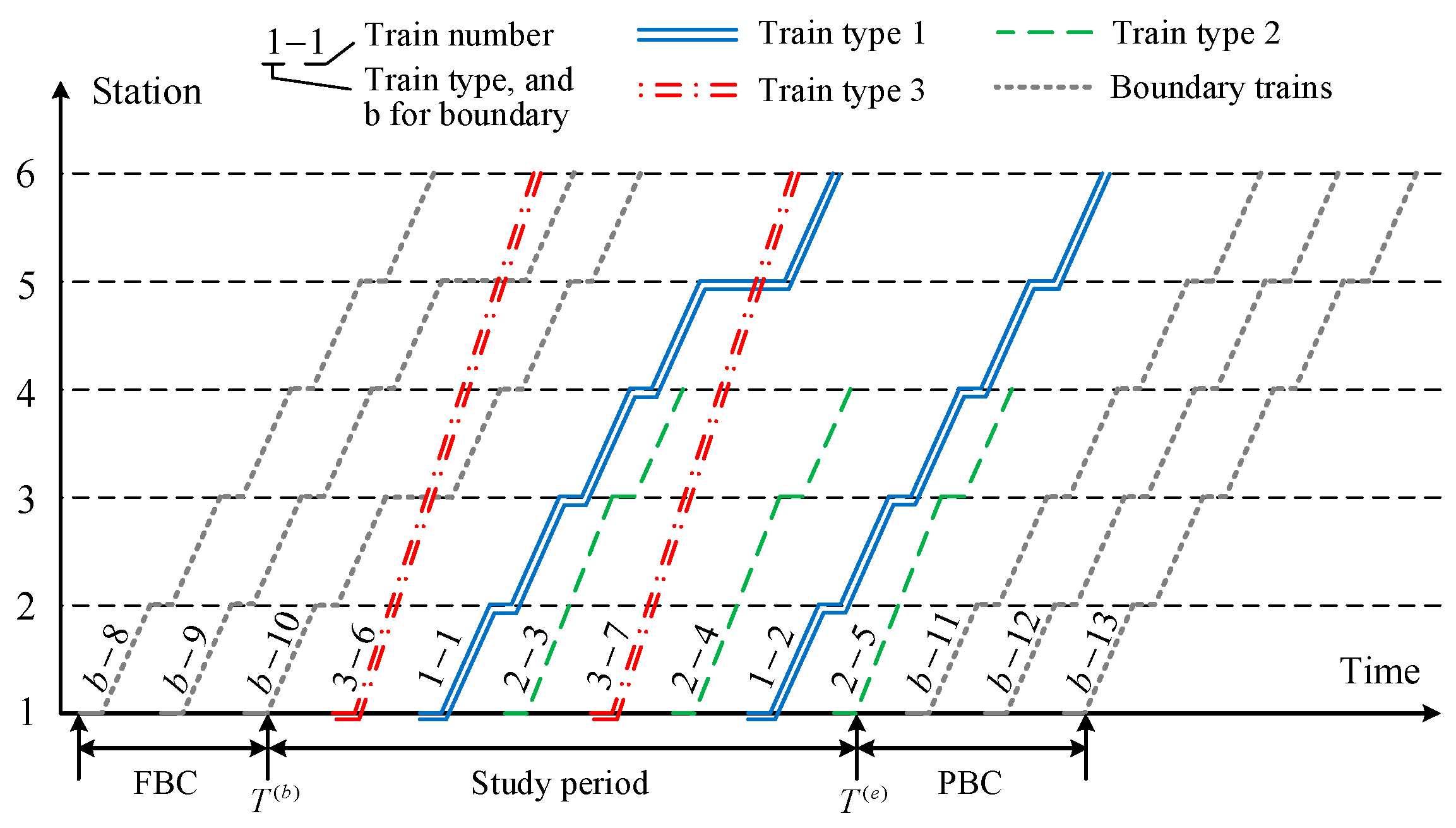
3.1. Line Plan and Timetable

An urban rail line has two directions, which can be treated as different lines or extended into a single line twice as long. An exemplary urban rail line with six stations and three train types is shown in Figure 2. Managers develop a line plan for each line to provide strategic guidance. These line plans describe the service frequencies, operation zones, stopping patterns, and train formation of each type of train. To facilitate management, such as scheduling and maintenance, and to improve the travel experience for passengers, managers typically design identical line plans for the two directions of urban rail lines. Figure 3 shows an exemplary line plan for the line in Figure 2 with three types of trains.

Different timetables can be designed for the same line plan. For example, Figure 4 shows the two timetables of the example line plan in Figure 2, where a single line represents four vehicles, a double line represents six vehicles per train, and the number next to the line is the train type and number. In timetable (a), train 7 overtakes train 1 at station 5 because its headway is less than the minimum departure–skipping headway. Timetable (a) is not a feasible solution because there are no overtaking facilities at station 5 (i.e., it is not an overtaking station). A feasible solution is timetable (b), which adjusts the sequences of trains 1 and 6 and trains 2, 4, and 7 at station 1 in timetable (a); this can be applied to the example line in Figure 2, because station 3 is an overtaking station. This problem can also be solved by adjusting the train departure time or headway, as enacted by Gao et al. [52].

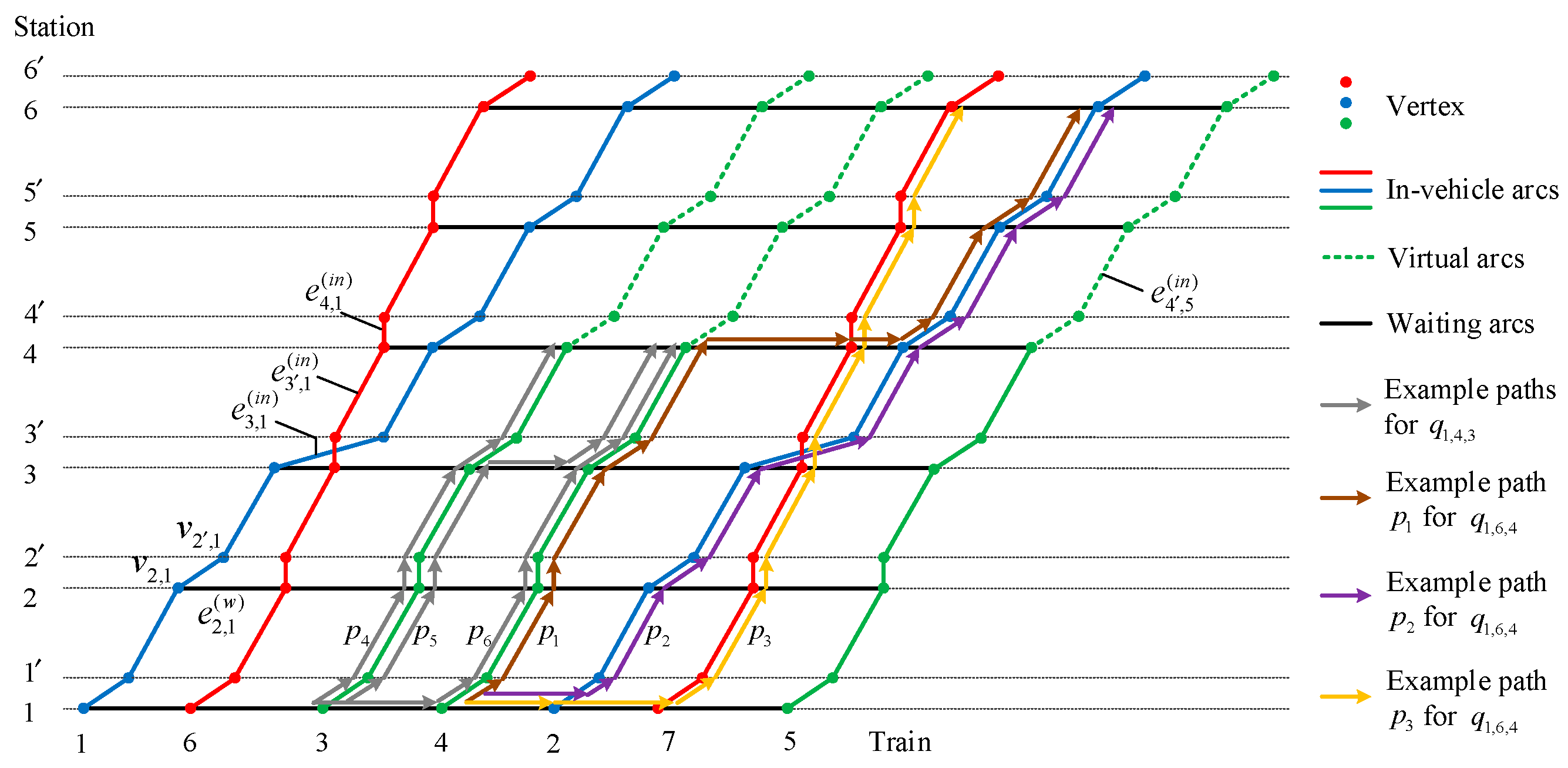
3.2. The Space–Time Network Design Problem

In fact, the timetable can be envisioned as a space-time network, wherein nodes signify the arrival and departure events of trains at each station, and arcs depict the passenger waiting process on platforms alongside the transit processes of trains between stations. Passengers board and alight trains within these arrival and departure windows, thereby navigating their travel demands through various segments that constitute a path. This network may also be delineated as a station-indexed and train-indexed network, with stations and trains distinguishing spatial positions and timestamps, respectively. Optimizing timetables is equivalent to identifying the optimal arc costs, which denote the durations of the events represented by these arcs. The process of the integrated optimization of line planning and timetabling seeks to determine the optimal network topology and arc costs. Consequently, these problems can be viewed as a network design problem (NDP) or a space–time network design problem (STNDP), as illustrated in Figure 5. When passengers’ boarding behaviors (also called travel path selection behaviors) satisfy the Wardrop’s first principle, it is termed an equilibrium space–time network design problem (ESTNDP).

3.3. Station-Indexed and Train-Indexed Network

One way to describe the travel space–time networks of passengers in rail transit systems is to incorporate temporal information into the timetable structure, such as in a time-expanded network [53]. Because the timetable in this study is a variable, the time-expanded network with the exact train arrival and departure times will change many times, and it is cumbersome to describe the OD path. Therefore, we use the station-indexed and train-indexed network (STN) to simplify the description, as shown in Figure 6, which corresponds to the timetable in Figure 4b. Each vertex in the STN contains time attributes that indicate the arrival or departure times of the train. The link with time and capacity attributes contains the waiting arc and in-vehicle arc. The link time is equal to 0 when the train skips. Link capacity refers to the capacity of trains or the platform capacity of stations. To unify the description form, we build virtual vertices and links at stations and sections outside the train operation zone, respectively. The timestamps of virtual vertices are the train arrival and departure times with virtual stopping at stations. The times of the virtual links are appended with a large positive number M and the capacities of the virtual links remain. Another advantage of this treatment is that the vertex set and in-vehicle arc structure of each train are stable and only affected by the number of trains, while the waiting arc structure can be determined only through the train order at each station.

3.4. Passenger Travel Path Selection

Passengers have multiple spatial–temporal paths in the STN, usually described by the link sequence, due to the diversified train services. Figure 6 shows three exemplary paths of passengers, marked $q_{1,6,4}$, who arrive at station 1 before the arrival of train 4 and go to station 6. The path $p_1$ contains 12 links and represents taking train 4 at station 1, transferring to train 2 at station 4, and going to station 6. Considering the characteristic of rail transit that passengers actually choose trains rather than links, these passengers’ choice elements are recorded as a path strategy. A path strategy comprises a set of train types that enable passengers to reach their destinations. If multiple train types are involved in a path strategy, passengers will transfer at the appropriate stations. Path $p_1$ is an instance of the path strategy defined by “boarding train type 2 and transferring to train type 1”.

A path strategy may have multiple path instances, but not all paths will be chosen when passengers are familiar with the timetable. For example, if passengers $q_{1,4,3}$ choose the path strategy “boarding train type 2”, they will choose path $p_4$ instead of $p_6$ because of the evident additional waiting time. Similarly, it is unreasonable to transfer to subsequent trains of the same type, such as $p_5$. Note that this is similar to some assumptions of timetabling optimization problems without considering passenger detention (i.e., only taking the current train).

In addition, path $p_1$ has the same travel time as path $p_2$, but a shorter in-vehicle time and longer transfer and waiting times. This means that the chosen probabilities of these two paths are not equal because of the different perceptions of waiting, transfer, and travel times [10]. Some comfort indicators have similar phenomena, such as vehicle congestion [33]. Therefore, we use non-dominated paths to describe the partial-order relationship. The definitions of the related concepts are provided below.

Definition 1 (Domination). 

Let vectors $f_1,f_2\in R^n$, $f_1={(f_{11},f_{12},\dots ,f_{1n})}^T$, $f_2=(f_{21},f_{22},$ $\dots ,f_{2n}{)}^T$. $f_1$ dominates $f_2$ if and only if $\forall i:f_{1i}\le f_{2i},\exists j:f_{1j}<f_{2j}$, written as $f_1\prec f_2$.

Definition 2 (Pareto front). 

Let vectors $f_1,f_2,\dots ,f_m\in R^n$, where $f_i={(f_{i1},f_{i2},\dots ,f_{in})}^T$, $i\in I\subseteq M$, and $M=\{1,2,\dots ,m\}$. $f_i$ is called the Pareto front if and only if $\cancel{\exists } j\in M-I:$ $f_{jk}\le f_{ik} ,\forall k\le n$

Definition 3 (Path domination). 

Let $P$ denote the set of all paths of an OD pair with path cost function $c(\cdot ):R_{+}^n\to R_{+}^m$. Path $p_1\in P$ dominates $p_2\in P$ if and only if $c(p_1)\prec c(p_2)$, written as $p_1\prec p_2$

Definition 4 (Non-dominated path). 

Let set $\mathcal{W}$ denote all OD pairs and $P_w$ denote the set of all paths between $w\in \mathcal{W}$ in a STN. Path $p_1\in P_w$ is called a non-dominated path if and only if $\cancel{\exists }{p}_2\in P_w:p_2\prec p_1$. The set of all non-dominated paths $p_i\in P_w$ is called the non-dominated path set ${\mathcal{P}}_w$ of OD pair $w\in \mathcal{W}$, and $\mathcal{P}={\cup }_{w\in \mathcal{W}}{\mathcal{P}}_w$ is called the non-dominated path set of the STN.

To simplify the description, the waiting time at station r and transfer time at the intermediate station $r^{\prime }$ of passengers $q_{rsi}$ are collectively called the passenger waiting time in this paper. The path of $q_{1,4,3}$ shown in Figure 6 has the following relationship when evaluating the passenger waiting time and in-vehicle time: $p_4\prec p_5$, $p_5$ and $p_6$ are not dominated by each other, and $p_4$ is a non-dominated path because there is no path that dominates it.

This study assumes that passenger travel path selection behavior, in accordance with Wardrop’s user-equilibrium principle, involves passengers freely choosing non-dominated paths within a path strategy that incorporates no more than two types of trains, with the objective of minimizing the perceived travel time. Some simple conclusions can be obtained: (a) Passengers $q_{rsi}$ do not choose train i at station r and wait for other trains because the new paths are non-dominated paths, rather than them being unable board train i as it is full, which is different from previous studies. (b) The timetable is infeasible when some passengers cannot board any trains in any non-dominated paths because all these trains are full, i.e., their loading-rates are all greater than or equal to the maximum loading rate ${\mu }_{\max }$. (c) Passengers will choose the first train in the same type of train set. (d) Passengers will take the first arriving train when there is only one type of train in the line plan.

3.5. Boundary Conditions

In the study of the urban rail transit timetable problem (TTP) in the optimization period $[T^{(b)},T^{(e)}]$, it is generally assumed that the line plan will have an all-stopping pattern, i.e., there is no overtaking between two successive trains. Thus, the head train in the study period will not affect the timetable of the previous period, and the tail train in the study period can clear passengers without affecting the passenger flow in the timetable of the posterior period. In other words, the study period is independent.

However, in the integrated optimization of the line-planning and timetabling problem, the first few trains in the study period may overtake the last train in the previous period because there are fewer stops, as with train 6 and trains 9 and 10 in Figure 7, which will also change the number of OD flows, because some passengers in the previous period are retained along with their boarding choice. The impact of this is the greatest when the first train only stops at the start and return terminals. Let n denote the maximum number of affected trains in this situation, which can be calculated using (1), where $h^{(FB)}$ is the headway of the previous period, $\lceil \cdot \rceil$ is the ceiling function, $t_s^{(s*)}$ is the minimum dwell time of any train at station s, and $t^{(0)}$ and $t^{(1)}$ are the accelerating time and decelerating time, respectively. In this study, these n trains were included in the research scope and set as the front boundary condition (FBC) of the ESTNDP. Similarly, some passengers will be retained and must board the trains in the posterior period, with the last few trains not stopping in the study period. We also consider these trains (n of them for convenience) and set them as the posterior boundary conditions (PBC). This treatment can ensure a fixed study period and fixed passenger flow at each station for variable line plans and timetables considering the stopping pattern; otherwise, it is not comparable.

$$n=\lceil {\displaystyle \frac{1}{h^{(FB)}}}{\displaystyle \sum _{s\in [2,S-1]}(t^{(0)}+t_s^{(s*)}+t^{(1)})}\rceil$$

(1)

3.6. Assumptions and Notations

The following assumptions are made throughout the paper:

(A.1) All passengers are assumed to be regular passengers who are familiar with the timetable and will adjust their travel path based on the timetable and their daily travel experiences. Passengers can freely choose non-dominated paths within a path strategy that incorporates no more than two types of trains, with the objective of minimizing the perceived travel time.

(A.2) The train dwell time at stations is same as that on the real timetable, and passengers board and alight at the train arrival time.

(A.3) All trains have the same kinematic characteristics, i.e., power, mass and resistance coefficients, acceleration and deceleration, and technical speed.

(A.4) To facilitate management and to improve the travel experience for passengers, each type of train adheres to the principle of even-headway at their origin station within a short period. For example, the short-turning train i starting from station s has the same headway as its adjacent stopping trains. Trains are only allowed to overtake a maximum of one train at a station. Vehicles in each type of train are used independently.

(A.5) The cost and degradation laws of the same type of infrastructure are the same. Turn-back stations are set as station-end double turn-backs, overtaking stations are set as double platforms with four tracks (two main tracks and two passing tracks), and other stations are island platforms. The effective length is the same for all stations, satisfying the stopping requirements of the longest train.

(A.6) The number of cycles in the periodic timetable that we considered in this study is equal to the greatest common divisor of the service frequency of each type of train, and the train type order is the same in different cycles.

A glossary of the symbols used in this paper is given in Appendix A.

4. Mathematical Formulation

The variables in the integrated optimization model of line planning and timetabling are categorized into three types, corresponding to the line plan, timetable, and passenger flow. The first two types of variables are coupled via the incidence ${\pi }_{ik},\forall i\in \mathcal{I},k\in \mathcal{K}$ as (2). Subsequently, they are jointly coupled with the passenger-flow-related variables via the structural parameters of the STN.

$${\pi }_{ik}=\{\begin{array}{l}1, if k>1,{\displaystyle {\sum }_{j\in [1,k-1]}{I}_j}<i\le {\displaystyle {\sum }_{j\in [1,k]}{I}_j}\\ 1, if k=1,i\le I_1\\ 0, otherwise\end{array},\forall i\in \mathcal{I},k\in \mathcal{K}$$

(2)

4.1. Constraints

4.1.1. Train Arrival and Departure Times

The arrival time of the boundary train at the origin station is a given constant $a_{1i},\forall i=I-2n+1,\dots ,I$. Other trains have the same headway as their adjacent stopping trains at their origin station $s_{J_{si}}^o$, as shown in Figure 8. For trains starting at station 1, the headways and arrival times are calculated using (3) and (4), as shown in Figure 8. Other short-turning trains are calculated using (5) and (6), where $J_{s\overline{i}}$ and $J_{s\overline{\overline{i}}}$ are the adjacent stopping trains with different train types. The arrival and departure times of the trains at other stations, i.e., not the origin station, are calculated using (7) and (8).

$$h_{si}={\displaystyle \frac{a_{s,I+n+1}-a_{s,I+n}}{1+{\displaystyle {\sum }_{j\le I}{\tau }_{s,J_{1j}}}}},\forall i\le I,s=1$$

(3)

$$a_{s,J_{si}}=a_{s,J_{si-1}}+{\tau }_{s,J_{si}}{h}_{si},\forall i\le I,s=1$$

(4)

$$h_{si}={\displaystyle \frac{a_{s,J_{s\overline{i}}}-a_{s,J_{s\overline{\overline{i}}}}}{1+{\displaystyle {\sum }_{\overline{i}<j<\overline{\overline{i}}}{\tau }_{s,J_{sj}}{x}_{s,J_{sj}}}}},\forall i\le I,s=s_{J_{si}}^o\ne 1$$

(5)

$$a_{s,J_{si}}=a_{s,J_{s\overline{i}}}+{\displaystyle {\sum }_{\overline{i}<j\le i}{\tau }_{s,J_{sj}}}{x}_{s,J_{sj}}{h}_{si},\forall i\le I,s=s_{J_{si}}^o\ne 1$$

(6)

$$d_{s,J_{si}}=a_{s,J_{si}}+t_{s,J_{si}}^{(s)},\forall s\in \mathcal{S},i\le I+2n$$

(7)

$$t_{s,J_{si}}^{(s)}=x_{s,J_{si}}\left(t_{s,J_{si}}^{(s*)}+t_{s,J_{si}}^{(e)}\right),\forall s\in \mathcal{S},i\le I+2n$$

(8)

$$a_{s+1,J_{si}}=d_{s,J_{si}}+t_{s,J_{si}}^{(r)},\forall s\in \mathcal{S}\backslash \left\{s_{J_{si}}^o\right\},i\le I+2n$$

(9)

$$t_{s,J_{si}}^{(r)}=t_{s,J_{si}}^{(r*)}+x_{s,J_{si}}{t}^{(0)}+x_{s+1,J_{si}}{t}^{(1)},\forall s\in \mathcal{S},i\le I+2n$$

(10)

4.1.2. Operation Zone and Overtaking Station

Due to the different commercial speeds of trains, the headway time between consecutive trains may not ensure operational safety. At this time, if overtaking is allowed at a station, the conflict can be solved by overtaking. This is the key to solving the even-headway periodic timetable, i.e., calculating $t_{s,J_{si}}^{(e)}$ in (8).

The necessary and sufficient conditions for train $J_{si}$ not to be overtaken by train $J_{si+1}$ at station s are (i) satisfying the minimum departure headway at station s, (ii) satisfying the minimum running interval in section [s, s + 1], and (iii) satisfying the minimum arrival headway at station s + 1. Suppose that the planned departure time $d_{s,J_{si}}^{(0)}$ of train $J_{si}$ at station s is given by (11), and use (12) to determine the departure headway constraint at station s and the arrival headway constraint at station s + 1.

$$d_{s,J_{si}}^{(0)}=a_{s,J_{si}}+x_{s,J_{si}}{t}_{s,J_{si}}^{(s*)},\forall s\in \mathcal{S},i\le I+2n$$

(11)

$$\Delta d_{s,J_{si}}^{(0)}=d_{s,J_{si+1}}^{(0)}-d_{s,J_{si}}^{(0)},\forall s\in \mathcal{S},i<I+2n$$

(12)

The advantage of this method is that, when conditions (i) and (iii) are satisfied, condition (ii) can be ensured because it is assumed that overtaking is only allowed at a station. At any station, the positional relationship of two consecutive trains can be categorized into forty-nine cases, considering whether they stop at, start from, or end at station s and station s + 1, and only five reasonable overtaking situations are considered in this paper, as shown in Figure 9.

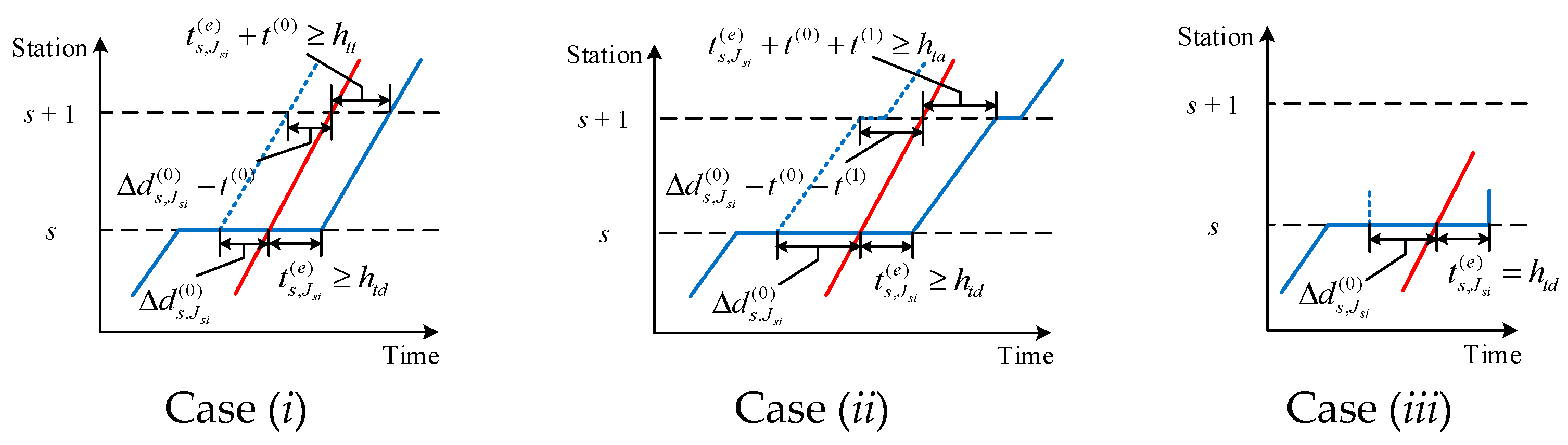
• Case (i): train $J_{si}$ and train $J_{si+1}$ both operate at station s and s + 1, i.e., ${\tau }_{s,J_{si}}{\tau }_{s+1,J_{si}}$${\tau }_{s,J_{s,i+1}}{\tau }_{s+1,J_{s,i+1}}=1$, and only train $J_{si}$ stops at station s, i.e., $x_{s,J_{si}}(1-x_{s+1,J_{si}})(1-x_{s,J_{s,i+1}})(1-$$x_{s+1,J_{s,i+1}})=1$. Train $J_{si}$ will be overtaken by train $J_{si+1}$ with an extra dwell time $t_{si}^{(e)}=\max \left(h_{td},h_{tt}-t^{(0)}\right)$ when $\Delta d_{s,J_{si}}^{(0)}<\max (h_{dt},h_{tt}+t^{(0)})$.
• Case (ii): train $J_{si}$ and train $J_{si+1}$ both operate at stations s and s + 1, and only train $J_{si}$ stops at stations s and s + 1, i.e., $x_{s,J_{si}}{x}_{s+1,J_{si}}(1-x_{s,J_{s,i+1}})(1-x_{s+1,J_{s,i+1}})=1$. Train $J_{si}$ will be overtaken by train $J_{si+1}$ with an extra dwell time $t_{si}^{(e)}=\max \left(h_{td},h_{ta}-t^{(0)}-t^{(1)}\right)$ when $\Delta d_{s,J_{si}}^{(0)}<\max (h_{dt},h_{at}+t^{(0)}+t^{(1)})$.
• Case (iii): train $J_{si}$ ends at station s and train $J_{si+1}$ operates at stations s and s + 1, i.e., ${\tau }_{s,J_{si}}(1-{\tau }_{s+1,J_{si}}){\tau }_{s,J_{s,i+1}}{\tau }_{s+1,J_{s,i+1}}=1$, and train $J_{si+1}$ skips station s, i.e., $x_{s,J_{si}}(1-x_{s,J_{s,i+1}})=1$. Train $J_{si}$ will be overtaken by train $J_{si+1}$ with an extra dwell time $t_{si}^{(e)}=h_{td}$ when $\Delta d_{s,J_{si}}^{(0)}<h_{dt}$.
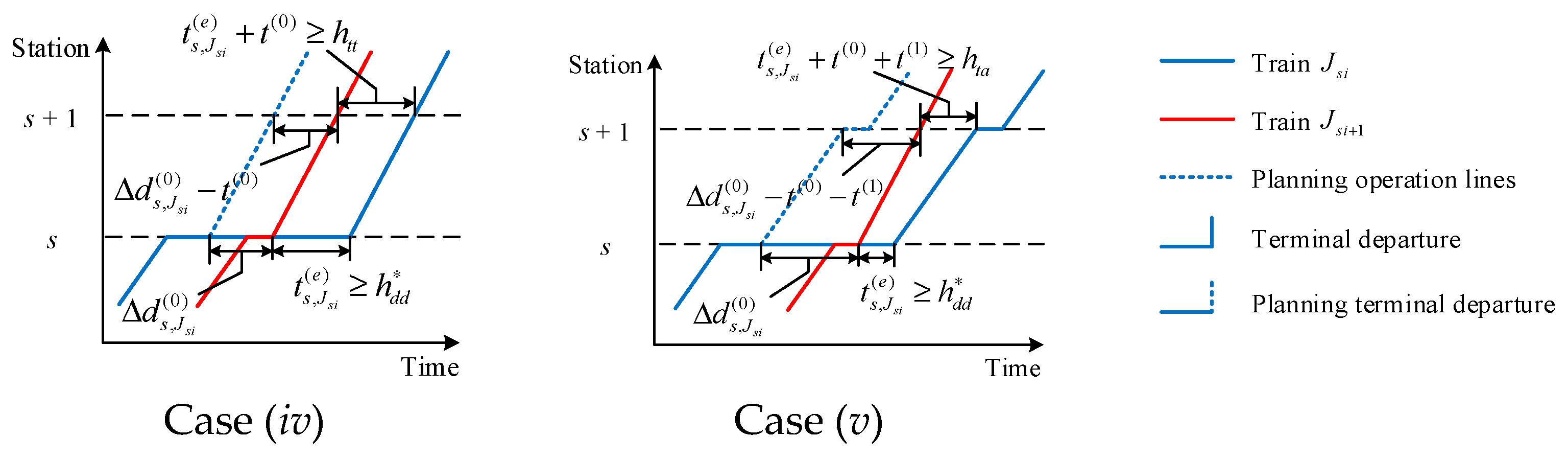
• Case (iv): train $J_{si}$ and train $J_{si+1}$ both operate at stations s and s + 1, and both stop at only station s, i.e., $x_{s,J_{si}}(1-x_{s+1,J_{si}})x_{s,J_{s,i+1}}(1-x_{s+1,J_{s,i+1}})=1$. Train $J_{si}$ will be overtaken by train $J_{si+1}$ with an extra dwell time $t_{si}^{(e)}=\max \left(h_{dd}^{*},h_{tt}-t^0\right)$ when $\Delta d_{s,J_{si}}^{(0)}<\max (h_{dd},h_{tt}+t^{(0)})$.
• Case (v): train $J_{si}$ and train $J_{si+1}$ both operate at stations s and s + 1, and only train $J_{si+1}$ skips station s + 1, i.e., $x_{s,J_{si}}{x}_{s,J_{s,i+1}}{x}_{s+1,J_{si}}(1-x_{s+1,J_{s,i+1}})=1$. Train $J_{si}$ will be overtaken by train $J_{si+1}$ with an extra dwell time $t_{si}^{(e)}=\max \left(h_{dd}^{*},h_{ta}-t^{(0)}-t^{(1)}\right)$ when $\Delta d_{s,J_{si}}^{(0)}<\max (h_{dd},$$h_{at}+t^{(0)}+t^{(1)})$.

There is, at most, one overtaking for each train, so we only need to calculate the planned interval $\Delta d_{s,J_{si}}^{(0)}$ once to obtain $t_{s,J_{si}}^{(e)}$ for conflict resolution. This process may change the departure order at station s, i.e., the arrival order at station s + 1, as shown in (13), where the 0–1 variable $T_{s,J_{si},J_{s,i+1}}$ denotes the overtaking state between train $J_{si}$ and $J_{si+1}$, and equals 1 if one of the above five cases occurs and 0 otherwise. Equation (13) also includes a situation that changes the train order, that is, where at least one train is in a virtual operation zone and their planned departure interval $\Delta d_{s,J_{si}}^{(0)}<0$. In this case, there is no actual overtaking between these two consecutive trains, so the departure time will not change, i.e., $t_{s,J_{si}}^{(e)}=0$.

$$\{\begin{array}{l}{J}_{s+1,i}=J_{s,i+1},J_{s+1,i+1}=J_{si},\\ \hspace{1em}\hspace{1em} \mathrm{if} T_{s,J_{si},J_{s,i+1}}=1, or \Delta d_{s,J_{si}}^{(0)}<0,{\tau }_{s,J_{si}}{\tau }_{s,J_{s,i+1}}=0\\ J_{s+1,i}=J_{si},J_{s+1,i+1}=J_{s,i+1}, \mathrm{otherwise}\end{array},\forall s\in \mathcal{S},i<I+2n$$

(13)

If the operator allows n trains (n > 1) to overtake or be overtaken, such as n = 2 in Figure 1, it is necessary to repeatedly calculate the p planned intervals $\Delta d_{s,J_{si}}^{(p-1)}$ and exchange train orders if necessary, where the n-th planned departure time $d_{s,J_{si}}^{(n-1)}$ is the sum of the (n − 1)-th planned departure time and additional dwell time. Thus, in the STN, the waiting arc can be described as $e_{si}^{(w)}=(v_{s{J}_{sj}},v_{s{J}_{s,j+1}}),\forall i=J_{sj}\in \mathcal{I},s\in \mathcal{S}$.

After n times of conflict resolutions, we must also ensure that consecutive trains satisfy the safety headway according to (14), because the interval between the overtaken train $J_{si}$ and other follow-up trains, such as train $J_{si+2}$, may decrease. The safety headway ${\tilde{h}}_{s,J_{s+1,i},J_{s+1,i+1}}$ of trains $J_{s+1,i}$ and $J_{s+1,i+1}$ at station s is taken from $h_{dd},h_{dd}^{*},h_{dt},h_{tt}$, and $h_{td}$ according to their stopping conditions and overtaking status.

$${\tau }_{s,J_{s+1,i}}{\tau }_{s,J_{s+1,i+1}}(d_{s,J_{s+1,i+1}}-d_{s,J_{s+1,i}})\ge {\tau }_{s,J_{s+1,i}}{\tau }_{s,J_{s+1,i+1}}{\tilde{h}}_{s,J_{s+1,i},J_{s+1,i+1}},\forall s\in \mathcal{S},i\le I+2n$$

(14)

4.1.3. Train Capacity

The equilibrium passenger flow of the in-vehicle arc $\tilde{a}\in \mathcal{B}$ shall not exceed its maximum capacity, which is equal to the product of the train capacity $ca{p}_{\tilde{a}}$ and maximum loading rate ${\mu }_{\max }$. This constraint is also called the loading rate constraint, as in (15) and (16).

$$ca{p}_{\tilde{a}}={\displaystyle \sum _{k\in \mathcal{K}}{\pi }_{ik}[2z_1+(m_k-2)z_2]},\forall i\in \mathcal{I},\tilde{a}=e_{·,i}^{(in)}\in \mathcal{B}$$

(15)

$$f_{\tilde{a}}^{*}\le {\mu }_{\max }ca{p}_{\tilde{a}},\forall \tilde{a}\in \mathcal{B}$$

(16)

4.1.4. Station Service

The station service constraint refers to the maximum service headway constraint (17) to ensure the passenger service level requirements, i.e., avoid an excessively long waiting time, and the minimum turn-back interval constraint (18) of the train at the turn-back station, where $\overline{\overline{i}}$ denotes the first stopping train after train $i\in \mathcal{I}$.

$$x_{si}(a_{s\overline{\overline{i}}}-a_{si})\le h_{\max },\forall s\in \mathcal{S},i\in \mathcal{I}$$

(17)

$${\pi }_{J_{si}k}{\pi }_{J_{sj}k}(a_{s,J_{sj}}-a_{s,J_{si}})\ge {\pi }_{J_{si}k}{\pi }_{J_{sj}k}{h}_r,\forall k\in \mathcal{K},s=s_{J_{si}}^{(o)},s_{J_{si}}^{(d)},i<j\le I+2n$$

(18)

4.1.5. Vehicle Configuration

The proposed model allows for overtaking, which may lead to an unequal turnover time and departure headway for the same train type. It is impossible to obtain an accurate value of the vehicle number by using the ratio of the average turnover time to the average departure headway. Therefore, we propose a new method for calculating the vehicle number, as shown in (19)–(23). When the train $i\in {\mathcal{I}}_k$ belonging to type $k\in \mathcal{K}$ starts operation at the origin station $s_i^{(o)}$, the number of remaining available vehicles belonging to type $k\in \mathcal{K}$ shall not be less than 0, i.e., (20)–(22), where $N_k^{(d)}(t)$ and $N_k^{(a)}(t)$ are the cumulative used and cumulative returned vehicles of type $k\in \mathcal{K}$ at time $t\ge T^{(b)}$, respectively. The turnover time $r_i$ of train $i\in \mathcal{I}$ is given by (23). Note that, when $r_i$ is too large, only calculating the trains in the planned period $[T^{(b)},T^{(e)}]$ may not ensure train turnover in the previous and posterior periods. Therefore, we take the planned period $[T^{(b)},T^{(e)}]$ as the cycle and consider the situation of M cycles, where M equals the ratio of the operation duration to the plan duration.

$$N^{(veh)}=\arg \min {\displaystyle \sum _{k\in \mathcal{K}}{N}_k^{(veh)}}$$

(19)

$$N_k^{(veh)}-m_k|N_k^{(d)}(t)|+m_k|N_k^{(a)}(t)|\ge 0,\forall k\in \mathcal{K},t\ge T^{(b)}$$

(20)

$$N_k^{(d)}(t)=\{i_j|a_{s_{i_j}^{(o)},i_j}+j(T^{(e)}-T^{(b)})\le t,\forall i_j\in {\mathcal{I}}_k,j\le M\},\forall k\in \mathcal{K},t\ge T^{(b)}$$

(21)

$$N_k^{(a)}(t)=\{i_j|a_{s_{i_j}^{(o)},i_j}+r_{i_j}+j(T^{(e)}-T^{(b)})\le t,\forall i_j\in {\mathcal{I}}_k,j\le M\},\forall k\in \mathcal{K},t\ge T^{(b)}$$

(22)

$$r_i=2(d_{s_i^{(d)},i}-a_{s_i^{(o)},i}+h_r),\forall i\in \mathcal{I}$$

(23)

4.1.6. Other Constraints

Equation (24) denotes that the line plan ${\mathbf{\Psi }}_k$ of train $k\in \mathcal{K}$ is different from others, (25) denotes the minimum length of the operation zone, (26) denotes that trains do not overtake each other, and (27) denotes that train $J_{si}$ is overtaken by, at most, one train at station $s\in \mathcal{S}$.

$${\mathbf{\Psi }}_i\ne {\mathbf{\Psi }}_j,\forall i\ne j\in \mathcal{K}$$

(24)

$${\displaystyle \sum _{s\in \mathcal{S}}{\tau }_{sk}}\ge L_{\min },\forall k\in \mathcal{K}$$

(25)

$${\displaystyle \sum _{s\in \mathcal{S}}(T_{sij}+T_{sji})}\le 1,\forall i,j\in \mathcal{I},i\ne j$$

(26)

$${\displaystyle \sum _{j\in \mathcal{I}\backslash \left\{i\right\}}(T_{sij}+T_{sji})}\le 1,\forall i\in \mathcal{I},s\in \mathcal{S}$$

(27)

4.2. Objective

4.2.1. System Life Cycle Cost

The LCC of an urban rail transit system refers to the total cost of the entire system LC, including the design, construction, operation, maintenance, and scrap disposal. It can be divided into four components: infrastructure cost $LC{C}^{(inf)}$, vehicle cost $LC{C}^{(veh)}$, staff cost $LC{C}^{(staff)}$, and other costs $LC{C}^{(other)}$, as in (28). The calculation method for each component is detailed in Appendix B.

$$LCC=LC{C}^{(inf)}+LC{C}^{(veh)}+LC{C}^{(staff)}+LC{C}^{(other)}$$

(28)

The LCC in the planning period $[T^{(b)},T^{(e)}]$ is defined by (29), where ${\kappa }^{(·)}$ represents the average downtime ratio of the equipment and staff. This is because most rail transit is not a 24 h operation (excluding some special cases, such as the New York City subway). Trains will also temporarily withdraw from operation due to maintenance, and the maximum working hours of staff per week are also limited. Taking Beijing Subway as an example, the maintenance activities of infrastructure use non-operating periods, such that ${\kappa }^{(inf)}=1-t^{(ope)}/24$, where $t^{(ope)}$ denotes the daily operating hours. These situations make it so that (28) cannot well-reflect the LCC in the planning period $[T^{(b)},T^{(e)}]$; therefore, (29) assigns the same LCC weight to the operating and non-operating periods.

$$LCC{|}_{T^{(b)}}^{T^{(e)}}:={\displaystyle \frac{T^{(e)}-T^{(b)}}{T}}({\displaystyle \frac{LC{C}^{(inf)}+LC{C}^{(other)}}{1-{\kappa }^{(inf)}}}+{\displaystyle \frac{LC{C}^{(veh)}}{1-{\kappa }^{(veh)}}}+{\displaystyle \frac{LC{C}^{(staff)}}{1-{\kappa }^{(staff)}}})$$

(29)

4.2.2. Total Passenger Travel Time Perception

In the space–time network corresponding to the integrated variable ${({\mathbf{\Psi }}^T,{\mathcal{J}}_1|\mathbf{\Psi })}^T$, the TTTP is equal to the inner product of the path equilibrium flow $F^{*T}{|}_{{\mathcal{J}}_1|\Psi }$ and path time perception $C(F^{*}{|}_{{\mathcal{J}}_1|\Psi })$:

$$TTTP=F^{*T}{|}_{{\mathcal{J}}_1|\Psi }\cdot C(F^{*}{|}_{{\mathcal{J}}_1|\Psi })$$

(30)

One form of path time perception $C(F):R_{+}^{\left|\mathcal{P}\right|}\to R_{+}^{\left|\mathcal{P}\right|}$ is given by (31), which is composed of travel time ${\Delta }^{T}t$, in-vehicle congestion penalty time $g(\tilde{t},V):R_{+}^{\left|\mathcal{B}\right|}\to R_{+}^{\left|\mathcal{P}\right|}$, and in-vehicle fatigue penalty time $h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t}):R_{+}^{\left|\mathcal{B}\right|}\to R_{+}^{\left|\mathcal{P}\right|}$, where $\tilde{t}=\Gamma t$ is the in-vehicle arc time vector.

$$C(F)={\mathbf{\Delta }}^{T}t+g(\tilde{t},V)+h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$$

(31)

The path $p\in \mathcal{P}$ component of $g(\tilde{t},V)$ is given by (32), where the in-vehicle arc $\tilde{a}\in \mathcal{B}$ equilibrium flow and capacity are $V^{*}=\mathbf{\Gamma }\mathbf{\Delta }{F}^{*}={(\dots ,f_{\tilde{a}}^{*},\dots )}^T$ and $ca{p}_{\tilde{a}}$, respectively. Passengers will feel crowded if the ratio of $f_{\tilde{a}}^{*}$ to $ca{p}_{\tilde{a}}$ is greater than the congestion penalty threshold $\theta \in [0,1]$. We construct a vector $\theta :={(\dots ,{\theta }_{\tilde{a}},\dots )}^T\in R_{+}^{\left|\mathcal{B}\right|},{\theta }_{\tilde{a}}=\theta ,\forall \tilde{a}\in \mathcal{B}$, and define the congestion coefficient as $L:=V^{*}\oslash cap-\theta$; then, $g(\tilde{t},V)$ is expressed by the vector of (33). It is worth noting that the symbols $\circ$ and $\oslash$ represent the Hadamard product and quotient, respectively, and that the elements of the new vector after the operation are composed of the product and quotient of the corresponding elements of the two vectors. The symbol $P_{R_{+}^n}(•)$ denotes the projection operator of Euclidean n-dimensional space on the nonnegative orthant, that is, the elements of the new vector after the operation are the maximum values of 0 and the corresponding elements of the original vector.

$$g_p={\mu }^{(c)}{\displaystyle \sum _{a\in \mathcal{E}}{\displaystyle \sum _{\tilde{a}\in \mathcal{B}}{\delta }_{ap}{\gamma }_{\tilde{a}a}{t}_{\tilde{a}}\cdot \max (0,f_{\tilde{a}}^{*}/ca{p}_{\tilde{a}}-\theta )}},\forall p\in \mathcal{P}$$

(32)

$$g(\tilde{t},V)={\mu }^{(c)}{\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T{P}_{R_{+}^{\left|\mathcal{B}\right|}}(\tilde{t}\circ L)$$

(33)

The path $p\in \mathcal{P}$ component of $h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ is given by (34), where the in-vehicle time is ${\tilde{t}}_p={\displaystyle {\sum }_{a\in \mathcal{E}}{\displaystyle {\sum }_{\tilde{a}\in \mathcal{B}}{\delta }_{ap}{\gamma }_{\tilde{a}a}{t}_{\tilde{a}}}}$. Passengers will feel fatigue if ${\tilde{t}}_p>t_0$. We construct a vector $t_0:={(\dots ,t_p,\dots )}^T\in R_{+}^{\left|\mathcal{P}\right|},t_p=t_0,\forall p\in \mathcal{P}$, and $h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ is then expressed by the vector of (35).

$$h_p={\mu }^{(s)}\cdot \max (0,{\displaystyle \sum _{a\in \mathcal{E}}{\displaystyle \sum _{\tilde{a}\in \mathcal{B}}{\delta }_{ap}{\gamma }_{\tilde{a}a}{t}_{\tilde{a}}}}-t_0),\forall p\in \mathcal{P}$$

(34)

$$h({\mathbf{\Delta }}^{\top }{\mathbf{\Gamma }}^{\top }\tilde{t})={\mu }^{(s)}{P}_{R_{+}^{\left|\mathcal{P}\right|}}({\mathbf{\Delta }}^{\top }{\mathbf{\Gamma }}^{\top }\tilde{t}-t_0)$$

(35)

Note that $g(\tilde{t},V)$ and $h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ are continuous non-differentiable functions. The component $g_p$ is non-differentiable at point $f_{\tilde{a}}=\theta {cap}_{\tilde{a}},{\displaystyle {\sum }_{a\in \mathcal{E}}{\delta }_{ap}{\gamma }_{\tilde{a}a}}=1,\forall \tilde{a}\in \mathcal{B}$, which means that the train loading rate of the in-vehicle arc $\tilde{a}\in \mathcal{B}$ of path $p\in \mathcal{P}$ just reaches the congestion penalty threshold $\theta$. The component $h_p$ is non-differentiable at the point ${\displaystyle {\sum }_{a\in \mathcal{E}}{\delta }_{ap}{\gamma }_{\tilde{a}a}{t}_a}=t_0$, which means that the in-vehicle time is equal to the fatigue penalty threshold $t_0$. To facilitate the following calculations, $g(\tilde{t},V)$ and $h({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ are smoothed using a quadratic function to approximate the original function in the neighborhood $U(x,\mu >0)$ of non-smooth point x, such that $g_{\mu }(\tilde{t},V)$ and $h_{\mu }({\Delta }^T{\Gamma }^T\tilde{t})$ are monotonically differentiable.

4.3. Equilibrium Space–Time Network Design Model

Assuming that the passenger path choice behavior in the space–time network conforms to Wardrop’s first principle, the integrated optimization of the line-planning and timetabling problem can be described as the urban rail transit ESTNDP. Then, it can be expressed as a generalized bi-level optimization problem named an equilibrium space–time network problem design model (ESTNDM) as follows:

$${\min }_{\mathbf{\Psi },{\mathcal{J}}_1|\mathbf{\Psi }} LCC{|}_{T^{(b)}}^{T^{(e)}}$$

(36)

$${\min }_{{\mathcal{J}}_1|\mathbf{\Psi }}TTTP$$

(37)

$$s.t. Constraints(2)-(27)$$

$$C{(F^{*})}^T(F-F^{*})\ge 0$$

(38)

$${\Phi }^{\top }F=Q$$

(39)

$$F_p^w\ge 0,\forall w\in \mathcal{W},p\in {\mathcal{P}}_w$$

(40)

The equilibrium constraints (38)–(40) of the ESTNDM are used to describe the path choice behavior of passengers. We assume that the time when passengers arrive at the platform is the same as when they swipe their card, i.e., passenger walking time at the station is not considered. Passenger $q_w,\forall w\in \mathcal{W}$ faces the same path selection problem with the inherent attribute representing their total waiting time before train i arrives. Thus, the passenger routing choice problem under ${({\mathbf{\Psi }}^T,{\mathcal{J}}_1|\mathbf{\Psi })}^T$ can be considered as equivalent to a static traffic assignment problem with a fixed demand. Passengers $q_w,\forall w=(r,s,i)\in \mathcal{W}$, have a fixed origin point $v_{ri}$ in the STN shown in Figure 6 and can freely choose their destination point $v_{sj},\forall j\in \mathcal{I}$. With the virtual network, by adding a virtual destination point $D_i^{rs}$ and virtual links $(v_{sj},D_i^{rs})$, the problem can be transformed into a static assignment problem with a fixed OD flow. Assuming that the cost of the virtual links is 0, the virtual network is equivalent to the original problem [54].

Because the in-vehicle fatigue penalty time $h_{\mu }({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ is a non-additive function, the path time perception is not equal to the sum of the link time perception, i.e., $h_{p\mu }=$$h_{p\mu }(t_p-t_0)\ne {\displaystyle {\sum }_{a\in \mathcal{E}}{\delta }_{ap}{h}_{p\mu }(t_a-t_0)},\forall p\in \mathcal{P}$. Therefore, we must build a variational inequality model with path flow as a variable [55], as in (38)–(40). Next, we prove the existence and uniqueness of the equilibrium flow. First, we introduce the following theorem.

Lemma 1. 

Suppose that $t$ is differentiable and (strictly) monotone, ${g^{\prime }}_{\mu i}(v_i)\ge 0$ and ${h^{\prime }}_{\mu i}(v_i)\ge 0$ for all $i=1,\dots ,n_{\mathcal{P}}$. Then, the path cost function $C$ is both differentiable and (strictly) monotone.

Theorem 1. 

Suppose that $C(F)$ is continuous on the compact convex set $\Omega$. Then the variational inequality problem $\mathit{VI}\left(C,\Omega \right)$ admits at least one solution $F^{*}$

Theorem 2. 

Suppose that $C(F)$ is strictly monotone on the compact convex set $\Omega$. Then, the solution is unique if one exists.

Because the link time $t$ is differentiable and strictly monotone, functions $g_{\mu }$ and $h_{\mu }$ are differentiable and monotone, and $C={\mathbf{\Delta }}^{T}t+g_{\mu }(\tilde{t},V)+h_{\mu }({\mathbf{\Delta }}^T{\mathbf{\Gamma }}^T\tilde{t})$ is both differentiable and strictly monotone based on Lemma 1. Moreover, because the OD flow is fixed, which means that the feasible set $\Omega =\left\{f\right|(39) \mathrm{and} (40) \mathrm{are} \mathrm{hold}\}$ is a bounded closed convex set in finite dimensional space [56], i.e., compact convex, $\mathit{VI}\left(C,\Omega \right)$ admits at least one solution $F^{*}$, i.e., the equilibrium path flow, and the solution is unique based on Theorems 1 and 2. For the proof of Lemma 1, see [55], and for that of Theorems 1 and 2, see [54].

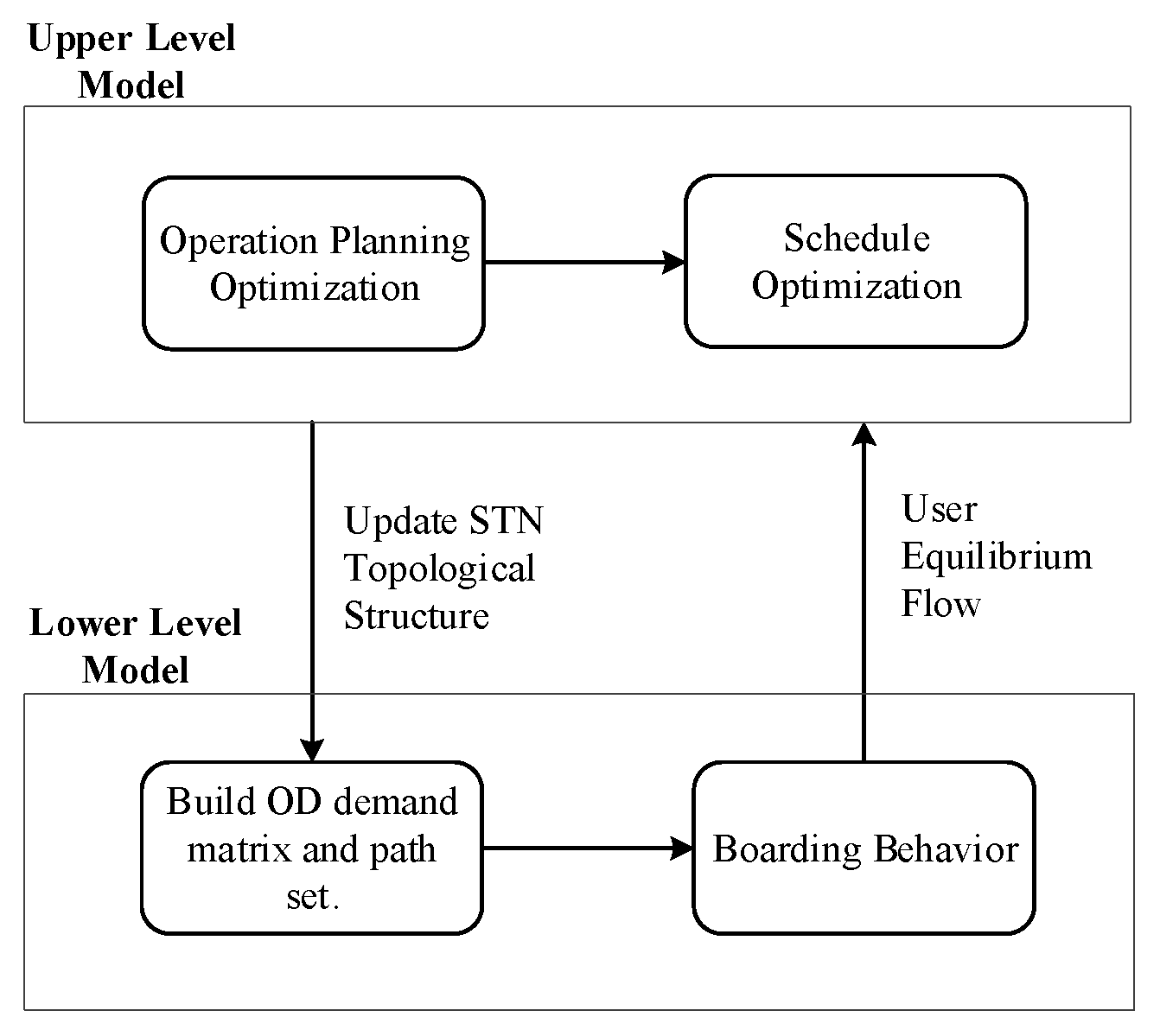
5. Solution Algorithm

Considering that the ESTNDM is a bi-objective programming model, this study constructed the algorithm framework using NSGA-II. The algorithm framework is structured into three modules: line-planning iterations, scheduling iterations, and equilibrium flow calculation, as illustrated in Figure 10. In the t-th iteration, scheduling iterations and equilibrium flow calculation are performed for each solution ${\mathbf{\Psi }}^{(n)}{|}_t$ of the offspring $Q_t$ to obtain the Pareto front $P_{tn}$, and then all $P_{tn}$ are combined with the Pareto front $P_t$ of parent $F_t$ to perform non-dominated sorting and congestion sorting to obtain the parent chromosome $F_{t+1}$ and Pareto front $P_{t+1}$ of the next generation. This loop continues until the algorithm terminates.

There are two reasons for the block iteration of line planning and timetabling. First, the feasible set of timetabling decision variables ${\mathcal{J}}_1$ is limited by the line-planning decision variable $\mathbf{\Psi }$, which makes the coding length and value range of decision variables ${({\mathbf{\Psi }}^T,{\mathcal{J}}_1|\mathbf{\Psi })}^T$ non-fixed, and cannot complete the crossover and mutation of NSGA-II. Second, $\mathbf{\Psi }$ is described by several integers focusing on the value, while ${\mathcal{J}}_1$ is described as an arrangement that focuses on the variable order. The block iteration can not only reduce the solution space of the two sub-processes, but also design the coding rule for chromosomes and select the crossover and mutation operators in a targeted manner.

The composition of chromosomes is shown in Figure 11. The gene of the n-th line plan offspring $Q_{tn}$ in the t-th iteration is a $K\times (S+2)$ matrix, in which each row corresponds to a type of train. Based on the train frequencies $I_k,k\in \mathcal{K}$ in the line plan, it can be deduced that the timetable consists of $N=\gcd (I_1,\dots ,I_K)$ cycles. The consistency of train orders across each cycle allows for the sequence of vehicle types within a single cycle to act as the chromosome ${\tilde{Q}}_{·}(Q_{tn})$ for scheduling iterations, thus effectively encapsulating the timetable. Taking frequencies $(I_1,I_2)=(2,4)$ as an example for detailed description, chromosome ${\tilde{Q}}_{·}(Q_{tn})$ is identified as one of the permutations of (1,2,2). In the process of calculating the objective function for chromosome ${\tilde{Q}}_{·}(Q_{tn})$, it becomes imperative to employ decoding using (2). For instance, decoding chromosome ${\tilde{Q}}_2(Q_{tn})=(2,1,2)$ results in timetable ${\mathcal{J}}_1=<3,1,4,5,2,6>$.

The crossover and mutation operators in the iterations of line planning are the same as in the original NSGA-II algorithm, which is a simulated binary crossover (SBX) and polynomial mutation (PM). The scheduling iterations employ the order crossover (OX) and displacement mutation (DM) as crossover and mutation operators, respectively. These operators effectively preserve neighborhood information, crucial for accurately depicting the overtaking relationships between consecutive trains.

The calculation of the equilibrium flow module is used to solve the variational inequalities of (38)–(40). In this study, the SAGP algorithm (see Section 4.2 of [50] for details) was used in the calculation of the equilibrium flow module to solve the equilibrium path flow, which is used to calculate the objective function, under a given STN and OD flow.

6. Case Study

The Beijing Subway Line L, a commuter line with 14 stations, as shown in Figure 12, is used to verify the effectiveness of the proposed model and algorithm. As of 2024, the line is 23.2 km in length, and a train adopts six type-B vehicles. This case study used real operation data on typical working days in the downstream direction during the morning peak hours from 6:52 to 8:36 at station 1 with four boundary trains.

6.1. Passenger Demand and Parameter Settings

The passenger demand data come from AFCSs, and the total number of passengers in the study period was 14,704. The OD flow and numbers of people entering and leaving at each station are shown in Figure 13. The scale of the outer circle of the chord graph is the number of passengers entering and leaving at each station, the second circle is the station indicator color, and the third circle is the cumulative number of passengers entering and leaving at each station. Taking station 5, YZQ, as an example, the gray histogram is the cumulative number of leaving passengers, the time axis is the center of the circle pointing in the circumferential direction, the red histogram is the cumulative number of entering passengers, and the time axis is the circumferential point to the center of the circle direction. The chord of the inner circle represents the OD flow, its color indicates the origin station, and its width indicates the flow. It can be seen that commuters from station SJZ in the central urban area of Beijing to WYJ, RJDJ, RCDJ, and TJNL in the Beijing Economic and Technological Development Regions represent the main flow. The actual timetable is shown in Figure 14. The solid lines denote the 12 optimized trains, and the dotted lines denote the front and posterior boundary trains, with two of each. The double line denotes that the train formation is four, the color denotes the train loading rate, and the number next to the line is the train type and number. The number of train types in this case is K = 3, and the boundary trains belong to type 4. The train formation is four, six, or eight, where the ratio of motor to trailer is 4:0 (e.g., Guangzhou Metro Line 4), 4:2 (e.g., Beijing Subway Line 4), or 6:2 (e.g., Beijing Subway Line 6). The other parameters of the model and algorithm are listed in Appendix C.

6.2. Computational Result Analyses

The case study was implemented in MATLAB R2020b at the Center for High Performance Computing at Beijing Jiaotong University with an Intel Xeon Gold 6240R @ 2.4 GHz CPU and 192 GB RAM. The solutions were obtained in 3260 min according to the maximum iteration number. The long solution time is due to energy consumption, STN construction, and equilibrium traffic assignment for each solution of the model, which is reflected in the multi-layer nesting of the algorithm. The optimization process of NSGA-II is shown in Figure 15, which shows that the Pareto front is convergent. The Pareto front and other feasible solutions are presented in Figure 16. The Pareto front presents nonlinear and non-convex relationships between two objects, indicating that the level of optimization of TTTP obtained by increasing the unit cost gradually decreased; that is, to further improve the service quality by a given amount, the additional costs increase.

Similarly, when enterprises reduce operating costs, the service quality decline will accelerate. Therefore, when implementing a line plan, enterprises should comprehensively consider their cost affordability, expected service quality, and line conditions to compare and select suitable Pareto front solutions. This ability is difficult to realize with other single-objective solution methods, such as the linear weighting method.

According to the relation of the objective function value size between feasible solutions and real timetable, we divided all feasible solutions into four categories: I, II, III, and IV, as shown in Figure 16. The solutions in region I are the inferior solutions dominated by the real timetable. The solutions in regions II and IV do not dominate the real timetable, so they can replace the real timetable if needed. The solutions in region III dominate the real timetable, which means that their cost and TTTP are both better than those of the real timetable. The obtained 72 Pareto front solutions (numbered in descending order of cost and marked with the superscript (n)) belong to regions II, III, and IV. The first solution, noted as ${\mathbf{\Psi }}^{(1)}$ in region II, has the optimal TTTP of 20,126,617 s, which is 19.2% better than the 24,901,940 s of the real timetable, saving 325 s per capita. Solution ${\mathbf{\Psi }}^{(2)}$ in region II has the optimal travel time of 16,069,045 s, which is 10.1% better than the 17,864,865 s of the real timetable, saving 122 s per capita. Solution ${\mathbf{\Psi }}^{(72)}$ in region IV has the optimal cost difference of CNY −7668.92, where the cost of variable items is CNY 18,525.41, which is 29.3% better than the CNY 26,194.33 of the real timetable.

Among the objective function values of the Pareto optimal solutions in region III, the TTTP of ${\mathbf{\Psi }}^{(39)}$, which is 23,062,247 s with 7.4% optimization, is the smallest. This is because the travel time, congestion penalty time, and fatigue penalty time are significantly reduced. Although the waiting time increases by 39.8%, passengers can still obtain fast and comfortable travel services due to the low weight of the waiting time in the TTTP. The total cost of variable items of ${\mathbf{\Psi }}^{(53)}$, which is CNY 22,427.17 with 14.4% optimization, is the smallest, realized by increasing turn-back stations (low weight of cost) and decreasing vehicle and staff costs (high weight of cost). In addition, this study uses three indexes to measure the TIT, SIT, and the imbalance of station load (IS), which are the standard deviation (SD) of the average train loading rate, section average loading rate, and station flow–service train capacity ratio. Higher values of these indexes reflect a greater imbalance, which is unexpected for managers, passengers, and this paper. The SIT and IS of ${\mathbf{\Psi }}^{(41)}$ are the best at 0.1471 and 0.1200, respectively, and the TIT of ${\mathbf{\Psi }}^{(42)}$ is the best at 0.1233. The TIT of most solutions is larger than that of the real timetable; this is because the planning period in this section is short, the fluctuation of passenger flow with time is not obvious (approximately linear in Figure 13), and the TIT in the real timetable is low.

When managers expect to obtain a higher service level than the real timetable, they can pay attention to the Pareto optimal solution in region II, for a smaller cost, they can look in region IV, and for trade-off solutions, they can see region III. Figure 17, Figure 18 and Figure 19 show the timetables of the representative Pareto optimal solutions ${\mathbf{\Psi }}^{(1)}$, ${\mathbf{\Psi }}^{(39)}$, and ${\mathbf{\Psi }}^{(65)}$ of regions II, III, and IV, respectively. The single line denotes four vehicles per train, while the double and triple lines denote six and eight, respectively. The color of the line denotes the train loading rate, and the number next to the line denotes the train type and number.

6.3. Performance of the Number of Train Types

The maximum number of train types K of the model in this study must be given by the manager, making it a super parameter. The upper limit of K is not easy to determine, and the decision space and solution time will increase if K is a decision variable. Therefore, this section analyzes the optimal line plan with K = 2, 3, and 4 and obtains the following conclusions.

First, the Pareto fronts of K = 2, 3, and 4 are shown in Figure 20, which are all in regions II, III, and IV, showing a nonlinear relationship between the two objective functions.

Second, K = 2 has the highest cost with the same service level in region II and a similar performance to K = 3 in regions III and IV. K = 3 performs better when the service level is low (TTTP is greater than 2.15 × 107), and K = 4 performs better when the service level is high. The sensitivity of the service level to the cost increases with an increasing K, which is reflected in the slope of the Pareto front curve. For example, the service level is significantly reduced and the cost is reduced slightly if K = 4; that is, by increasing the lower cost, the service level can be significantly improved.

In region III, K = 3 is better than K = 2, followed by K = 4 in general; in other words, a larger K is not necessarily better. The relationship between time and cost is approximately linear. The TTTP with K = 3 is sensitive when the cost difference is approximately 0. ${\mathbf{\Psi }}^{(39)}$ with K = 3 has the optimal TTTP, whose in-vehicle time, congestion penalty, and fatigue penalty are close to ${\mathbf{\Psi }}^{(27)}$ of K = 2, but with smaller waiting times. These two solutions have a higher TTTP optimization rate, owing to the better matching of the spatial imbalance of flow (i.e., low SIT and IS). ${\mathbf{\Psi }}^{(53)}$ with K = 3 is the optimal cost difference, followed by K = 4. This is because the costs of vehicles and staff, which account for the largest proportion of the cost difference, are improved significantly.

Finally, in region IV, K = 2 is better than K = 3, followed by K = 4 in general, while they all have lower costs and the curve difference is small.

6.4. Performance of Different Strategies

The ESTNDM is a general model, which considers multiple line-planning strategies and can be compatible with a single strategy (by setting non-optimized variables as constants). It provides convenience for us to compare the line plans of different strategies in one model with different parameters instead of developing different models. In this section, we compare the optimization results of different strategies to reflect the advantages of the multi-strategy line planning. We number the methods using the decimal number of the quaternion 0–1 array, which denotes whether the train service frequency, operation zone, stopping pattern, and train formation are optimized. For example, the model that optimizes train service frequency only is numbered 8, i.e., (1, 0, 0, 0), and the model proposed in Section 4 is numbered 15, i.e., (1, 1, 1, 1). The Pareto fronts of models 1, 8, and 9 are obtained by the enumeration method due to the small decision space, because the service frequency and train formation value range are small, while other models are solved by the algorithm in Section 5. All these models have the same parameters as model 15; unused strategies are taken according to the real timetable; and K = 3 (except K = 1 in model 8 because different types of trains cannot be distinguished by only optimizing the service frequency).

The Pareto fronts of all 15 models and the real timetable are shown in Figure 21. Theoretically, the Pareto front of model 15 is optimal, which is located at the lower left of the other curves, but the algorithm proposed in this paper obtains the approximate optimal solution in a limited time, so some solutions for model 6 (optimizing the operation zone and stopping pattern) are better than those of model 15. One possible reason for this is that the optimization of the operation zone and stopping pattern has a great impact on the quality of the solution, and a model with a fixed service frequency and train formation will have a small solution space to search for a better solution in the same generations. In region III, the ${\mathbf{\Psi }}^{(39)}$ for model 15 has the best TTTP with 7.4% optimization and the lowest SIT and IS. The ${\mathbf{\Psi }}^{(191)}$ for model 9 has the lowest TIT. The ${\mathbf{\Psi }}^{(24)}$ for model 6 has the lowest cost difference, and the cost of variable items is optimized by 14.9%.

The theoretical curve of the Pareto front of each model exhibits a good or bad relationship. For example, the Pareto front of model 8 is the Pareto front of the subspace composed of the special solutions, whose operation zone, stopping pattern, and train formation are the same as the real timetable of model 15. Therefore, all models can be divided into four categories (Classes A, B, C, and D) according to the number of line-planning strategies and rank, as shown in Figure 22, where the arrow points from good to bad models. There are no obvious advantages or disadvantages of the models in the same category or without continuous arrow connections, such as models 13 and 2. The distribution of the four categories in region III is shown in Figure 21.

Class A only contains model 15, and the Pareto front is optimal, i.e., at the bottom left. Models 7, 11, and 14 in Class B, models 3, 6, and 10 in Class C, and model 2 in Class D have obvious Pareto front aggregation, which is difficult to distinguish. Compared with other models, the biggest feature of these models is the optimization of the stopping pattern. This shows that strategies that contain stopping patterns are very effective. In particular, model 6 can achieve the performance of model 15 by only optimizing the operation zone and stopping pattern when the TTTP is greater than 2.42 × 107 s. The next aggregation area on the upper right contains models 12 and 13. Of the remaining models, only these two optimize the service frequency and operation zone simultaneously. Model 13 is better than model 12 in general as it also optimizes the train formation. This is consistent with our theoretical expectations. The next aggregation area on the upper right contains models 1, 5, and 9, which optimize the train formation in the remaining strategies.

The worst are model 4 with the strategy of optimizing the operation zone and model 8 with the strategy of optimizing the service frequency; they both have no Pareto front solutions in region III. The Pareto front of model 4 is in region IV, which shows that the strategy of optimizing the operation zone only, such as full-length and short-turn routing with a fixed service frequency, cannot obtain a better solution, but it has a lower cost with the same service level as model 8 by a smaller train service in the section with a low passenger flow. The Pareto front of model 8 is a curve passing through the real timetable, because the result is just the real timetable when the service frequency is 12.

In summary, the following conclusions are drawn:

(1) The optimization effect of model 15 is the best. We suggest conditional lines (overtaking stations and turn-back stations can be built, and vehicles can be purchased) or new lines adopting the line plan and timetable optimized by four strategies.

(2) For enterprises that have difficulty in changing the number of vehicles, we suggest using a model that simultaneously optimizes the operation zone and stopping pattern, including models 6, 7, 14, and 15, which is necessary to choose the solutions that satisfy the constraint of the vehicle number.

(3) When the line conditions do not support the construction of overtaking stations, we suggest using models that simultaneously optimize the service frequency and operation zone, including models 12, 13, 14, and 15, which is necessary to choose solutions without overtaking.

(4) When the line conditions do not support the construction of overtaking stations and turn-back stations, we propose adopting a line plan with multiple train formations, including models 1 and 9 and their dominating models (see Figure 22), which is necessary to choose the qualified solutions.

(5) When considering both system costs and passenger travel efficiency, it is not suggested to use model 4 with the strategy of optimizing the operation zone only or model 8 with the strategy of optimizing the service frequency only.

From these conclusions, some line-planning strategies can be said to have combinatorial effects. The first combination is all four strategies, because the optimization effect of model 15 is significantly better than that of all other models in general, i.e., the optimization effect will be significantly reduced if any strategy is not optimized, such as models in Class B. This may be because each strategy has advantages and disadvantages for improving the imbalance of trains and station loads, and it can only achieve good results when all four strategies are combined. The second combination optimizes the operation zone and stopping pattern. Because models 6, 7, 14, and 15 gather in the second aggregation area, the optimization effect is better than that of the other models. Although models 2, 3, 11, and 10 without an optimized operation zone are also in the second aggregation area, the performance of model 6, which can achieve the effect of model 15 under some service level, allows us to speculate that models 7, 14, and 15, which dominate model 6, will obtain better solutions with a sufficient solution time. This may be because express trains can provide efficient services for long-distance passengers, while local trains can satisfy the needs of short-distance passengers. Short-turn trains can improve the equipment utilization in sections with a small flow and leave more time windows for express trains to reduce overtaking times. The third combination optimizes the service frequency and operation zone. For the line plan that only allows an all-stopping pattern, the optimization effects of models 12 and 13 are close and significantly better than those of models 1, 4, 5, 8, and 9. Meanwhile, it can be seen that the effect of the third combination is not as strong as that of the second combination, because model 14 shows no obvious advantages over model 6.

6.5. Performance of Different Passenger Flow

In this section, we use the three scenarios of the morning, noon, and evening peaks of the Line L, where the total numbers of passengers are 14,704, 5753, and 16,074, respectively, to analyze the Pareto fronts under different passenger flow conditions. The morning and evening peaks are called the large passenger flow scenario, and the noon peak is called the small passenger flow scenario. For a fair comparison, we compare the unit cost, which is the ratio of the cost of variable items to the passenger kilometers, and average passenger travel time perception (ATTP) of each scenario.

The Pareto front of each scene is shown in Figure 23. The real timetable of the morning peak has the lowest unit cost, the noon peak has the highest unit cost, and the evening peak is in the middle. The ATTP decreases in the order of morning, noon, and evening.

The Pareto front presents a nonlinear relationship between two objects in each scenario, but the curves are straighter in the morning and evening peaks than in the noon peak, which indicates that the ATTP is more sensitive to the change in the unit cost in the morning and evening peaks. This is because, when the unit cost is reduced, the train congestion in the large passenger flow scenario changes significantly, while in the small passenger flow scenario, there are few sections exceeding the congestion penalty threshold, and the average congestion penalty time is only approximately 43 s. In addition, in the small passenger flow scenario, the average waiting time, which is the second-largest factor affecting the average travel time, is approximately 300 s, which affords a large unit cost when reducing the average waiting time by increasing the service frequency.

In region III, the maximum optimization rate of ATTP is 7.4% with a 126 s reduction in the morning peak, while it is 5.8% with a 92 s reduction in the noon peak and 2.3% with a 32 s reduction in the evening peak. The maximum optimization rate per unit cost is 14.4% with a 0.022 CNY/pkm reduction in the morning peak, while it is 3.7% with a 0.0125 CNY/pkm reduction in the noon peak and 6.8% with a 0.0125 CNY/pkm reduction in the evening peak.

It is interesting that the optimization rates of the morning and evening peaks are mostly higher than that of the noon peak. One potential reason for this is that the temporal and spatial imbalances of the passenger flow in the afternoon peak are lower, i.e., TIT, SIT, and IS are all less than those in the morning and evening peaks. This situation may reduce the applicability of line plans with multiple strategies, which is consistent with the original intention of using line plans with multiple strategies to deal with the imbalances in trains and station loads (see Section 1).

7. Conclusions

This study analyzed the integrated optimization problem of line planning and timetabling in urban rail transit and its essence, which showed that this problem can be described as an ESTNDP of urban rail transit from a new perspective, that is, adjusting the topology (the existence of vertices and links) and link attributes (time and capacity) of the passenger travel space–time network by line plan information (i.e., train service frequency, operation zone, stopping pattern, and train formation) and timetable information (e.g., train order and overtaking events at each station) to optimize the performance index of the system.

An instantiation of the bi-objective ESTNDM based on user equilibrium was proposed for the ESTNDP to solve the optimal line planning and train order to minimize the LCC of the urban rail transit system and the TTTP. To be more practical, the heterogeneity of passenger demands not only includes a congestion penalty, which is common, but also a travel fatigue penalty, which is important for commuters, especially long-distance ones. In this model, the timetable can provide multi-train services, which are allowed to overtake, and passenger path choice behavior conforms to Wardrop’s first principle and is described by a variational inequality model based on path flow.

An algorithm was constructed using the NSGA-II combined with the SAGP to solve the model. The algorithm included three modules, which were used to solve the equilibrium passenger flow under ${\mathcal{J}}_1{|\mathbf{\Psi }}^{(i)}$, the Pareto front $P_i$ of ${\mathbf{\Psi }}^{(i)}$, and the Pareto front $P$ of the original problem, respectively.

The feasibility of the model and algorithm proposed in this paper was tested for the case of the Beijing Subway Line L. This paper compared and analyzed the solution effects of the ESTNDM for different train types, line-planning strategies, and passenger flow scenarios. The results showed that more types of trains is not better, and the reasonable value must be calculated and compared according to the actual line. The line plan considering all strategies had the best optimization effect due to the least predefined timetable structure information. There are combination effects between some line-planning strategies, and the decision maker can adopt different combinations of strategies according to the specific conditions of the actual line. When it is difficult to change the number of vehicles, it is recommended to adopt the combination line planning strategy of optimizing the operation zone and stopping pattern, such as in models 6, 7, 14, and 15. When the line conditions do not support the construction of overtaking stations, the combination line-planning strategy of optimizing the service frequency and operation zone is acceptable, such as in models 12, 13, 14, and 15. When the line conditions do not support the construction of overtaking stations and turn-back stations, a line plan with multiple train formations can be considered, such as in models 1, 3, 5, 9, 7, 11, 13, and 15. In addition, multiple strategies are more suitable for the scenario of a high imbalance in trains and station loads, which also verifies the rationality of providing multi-train services in the morning peak in Japan.

There are some deficiencies in this study, and our future work will consider these deficiencies and focus on the following:

(1) The random arrival of passenger flow was not considered. This study assumed that all passengers are regular passengers, i.e., they often use the urban rail transit system, and that the OD flow is fixed. However, in the real world, there are still some irregular passengers who do not often use the urban rail transit system; these passengers generally do not pay much attention to the train timetable, and their arrival time is highly random. Additionally, multiple train services will also impact regular passengers, because medium- and long-distance passengers will purposefully take express trains and adjust their arrival times. Therefore, in future research, passenger flow prediction and control will be considered in the ESTNDM to build a more efficient and robust line plan and timetable.

(2) The ESTNDM solving algorithm took a long time and was not easy to apply to large-scale problems, such as all-day timetables and long lines. Although the actual application scenarios will not require the high solving efficiency for the model in this study, the computing efficiency for large-scale problems must be improved; otherwise, it will be difficult to ensure the optimality of the solution in a limited solving time. Therefore, in future research, algorithms, such as the column generation algorithm (CG), or software, such as the general algebraic modeling system (GAMS), which are suitable for solving large-scale problems, and linearization methods that approximate and simplify the nonlinear model in this paper will be considered.

(3) This study focused on a single urban rail line, which would not be very applicable to some cities where urban rail systems are operated as a network, because it ignores the interactions of passengers between lines. Under the network operation, the imbalance in the temporal and spatial distributions of passenger flow is obvious due to more demanding heterogeneity factors, such as the convenience of transfers. Therefore, our future research will consider transfer costs and passenger path choice behavior in urban rail transit networks and extend the model proposed in this paper to a three-dimensional space–time network design, which will be an integrated optimization model of line planning and timetabling under network operation to provide multi-train services adapting the imbalance in the temporal and spatial distributions of passenger flow.