Stress–Dilatancy Behavior of Alluvial Sands
Abstract
1. Introduction
2. Stress Ratio–Plastic Dilatancy Relationship
3. Material and Tests
- —the bulk density [Mg/m3];
- —Poisson’s ratio [-];
- —the velocity of the propagation of the shear wave in the ground medium [m/s];
- —the velocity of the propagation of the compression wave in the ground medium [m/s].
4. Methodology
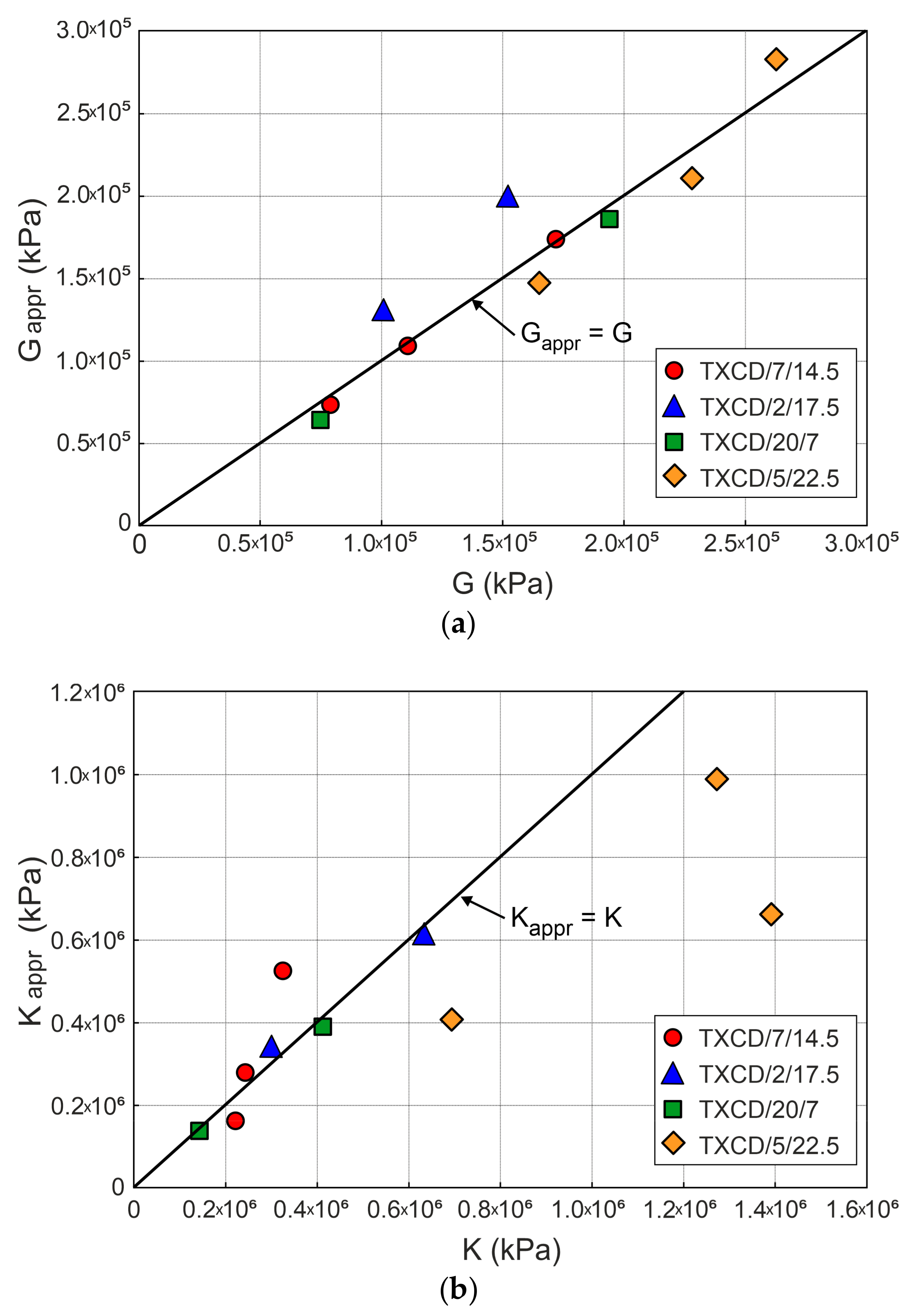
5. Elasticity Parameters
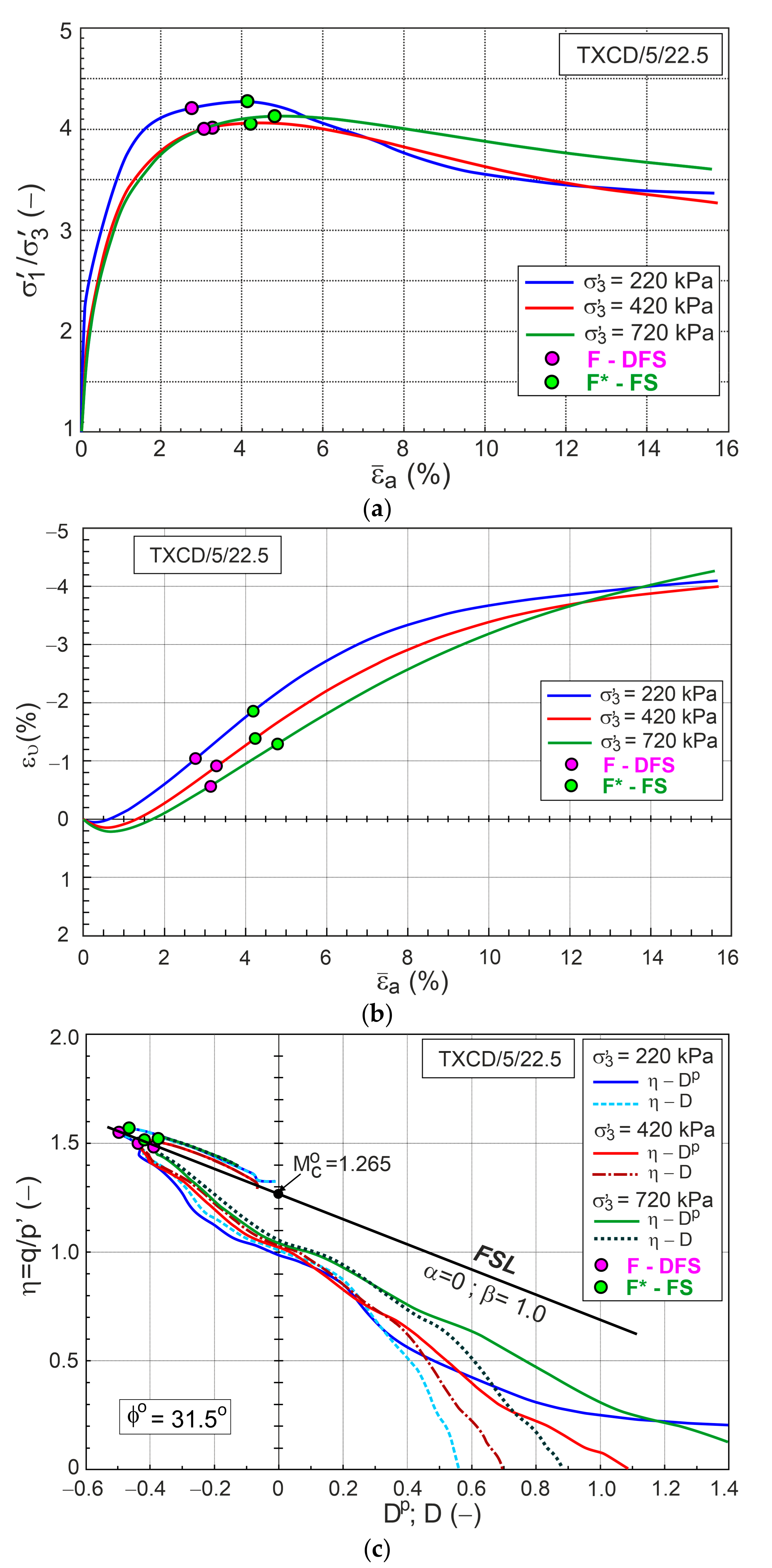
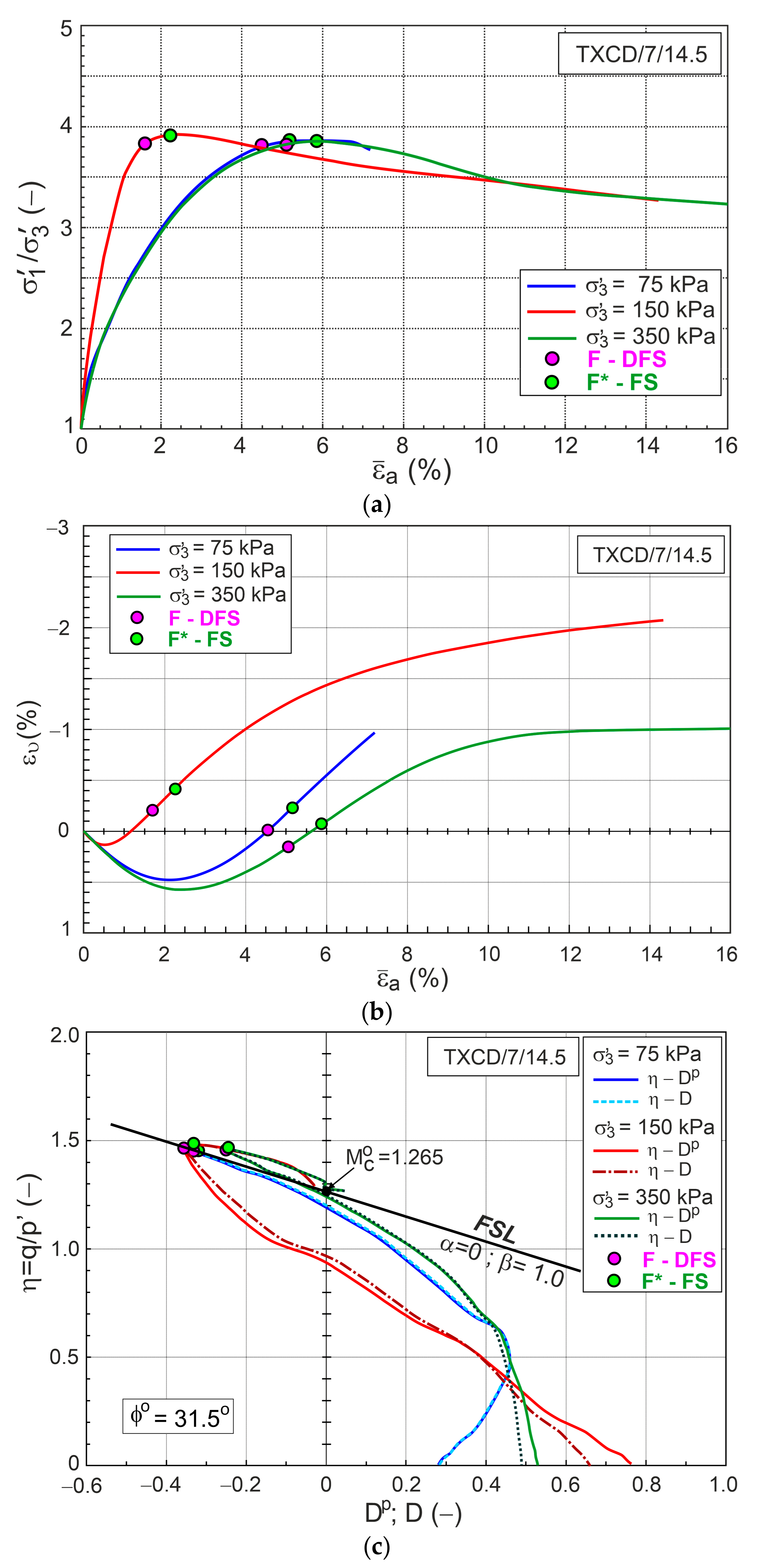
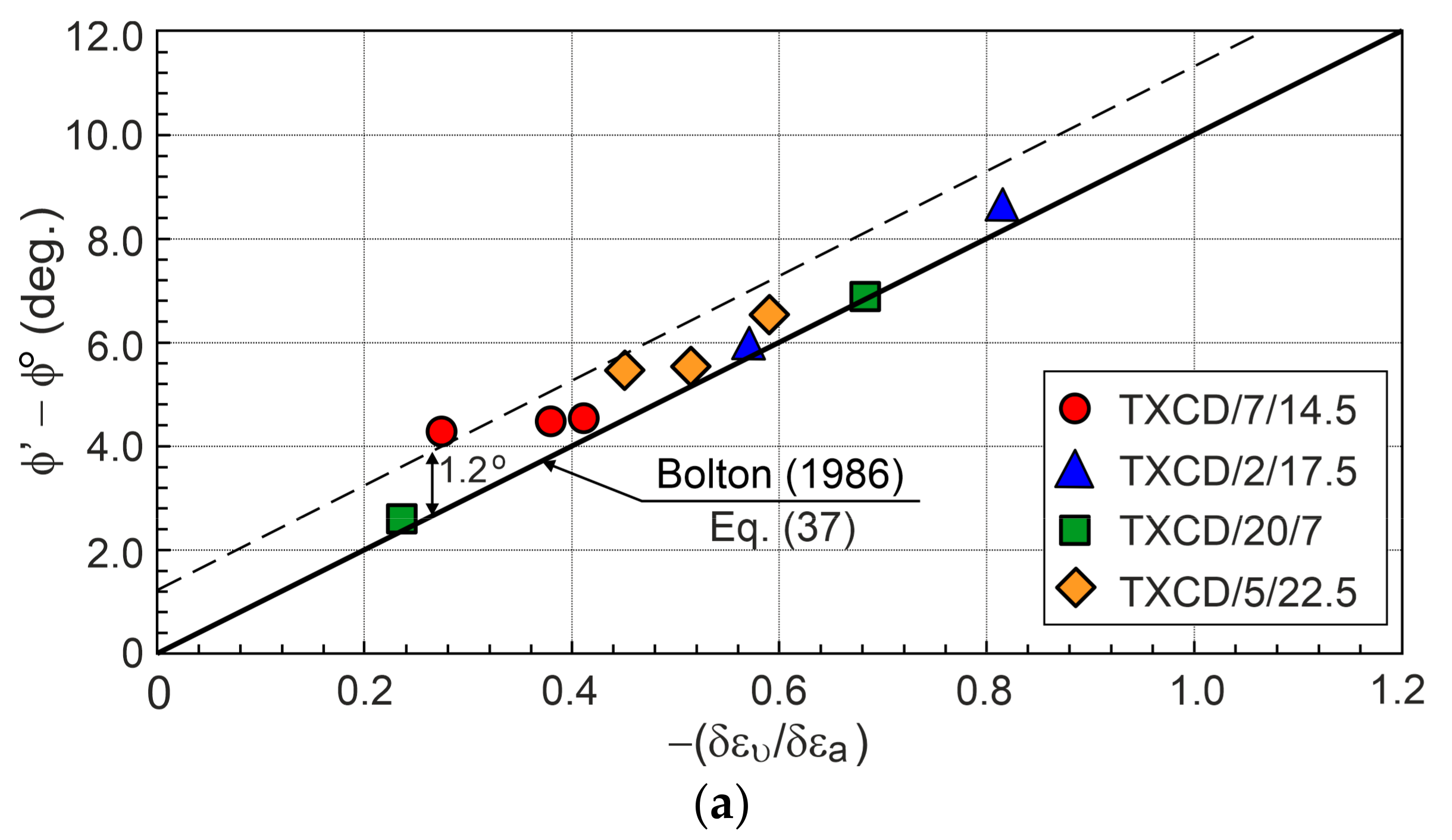
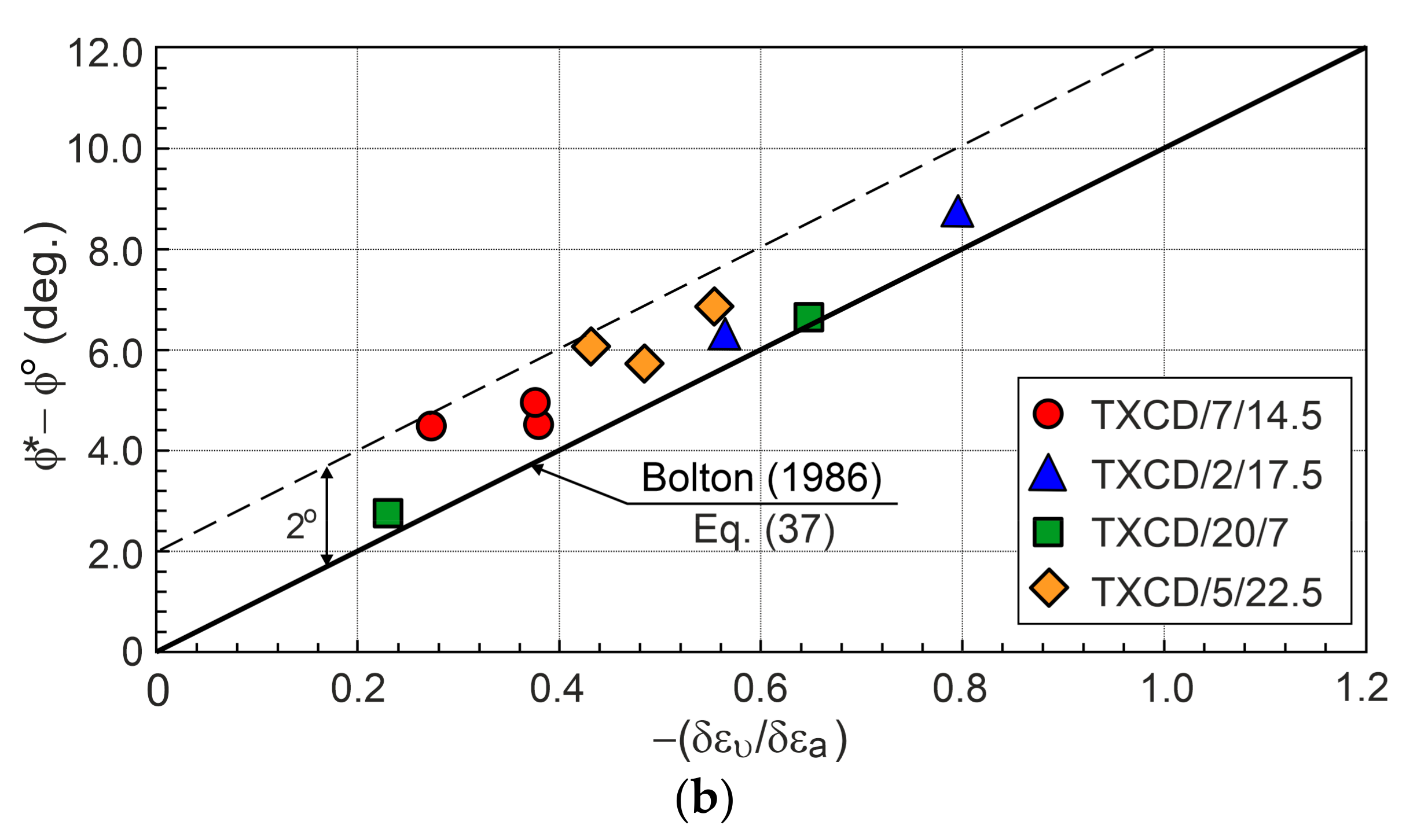
6. Stress Ratio–Plastic Dilatancy Relationship
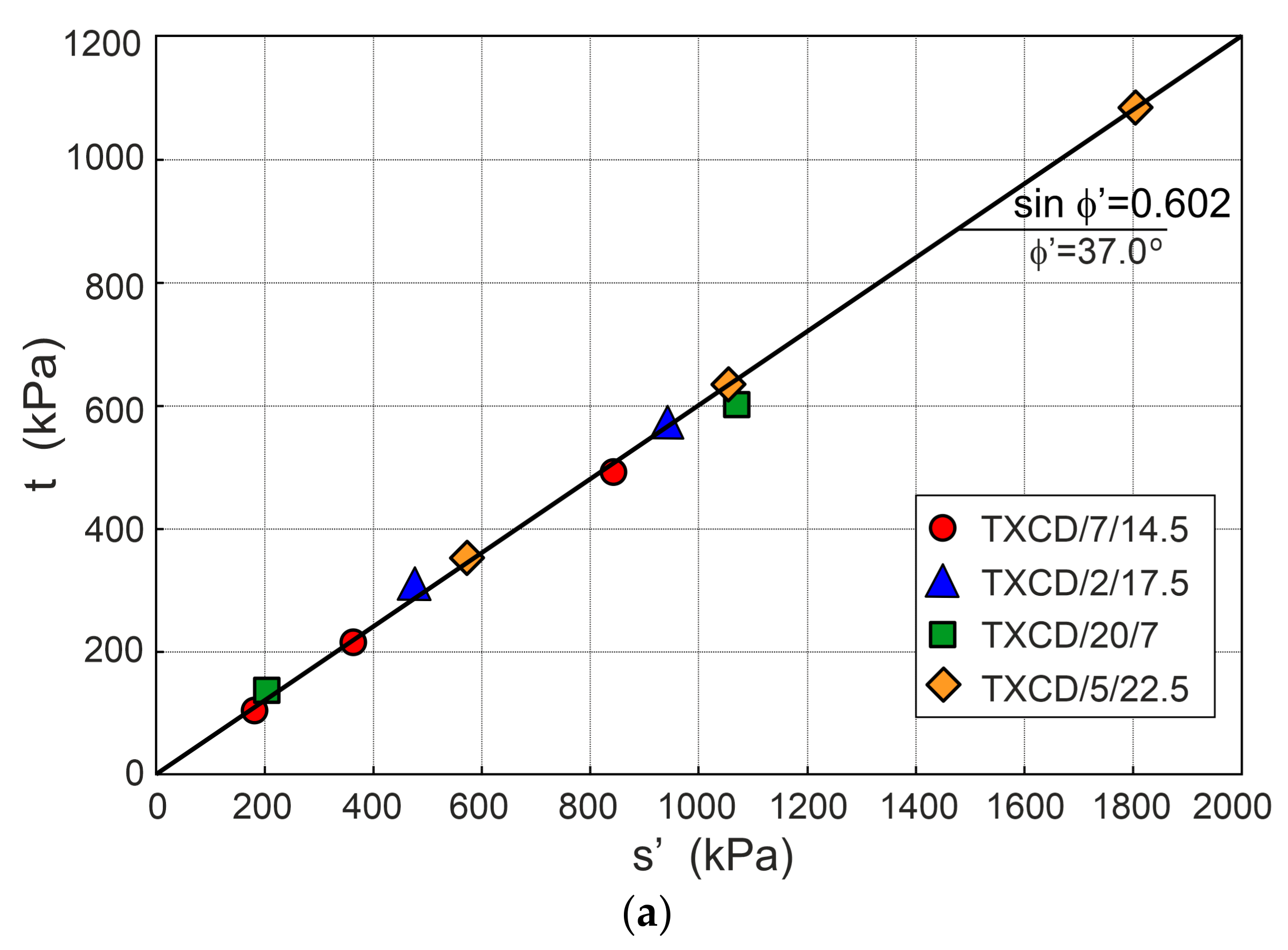
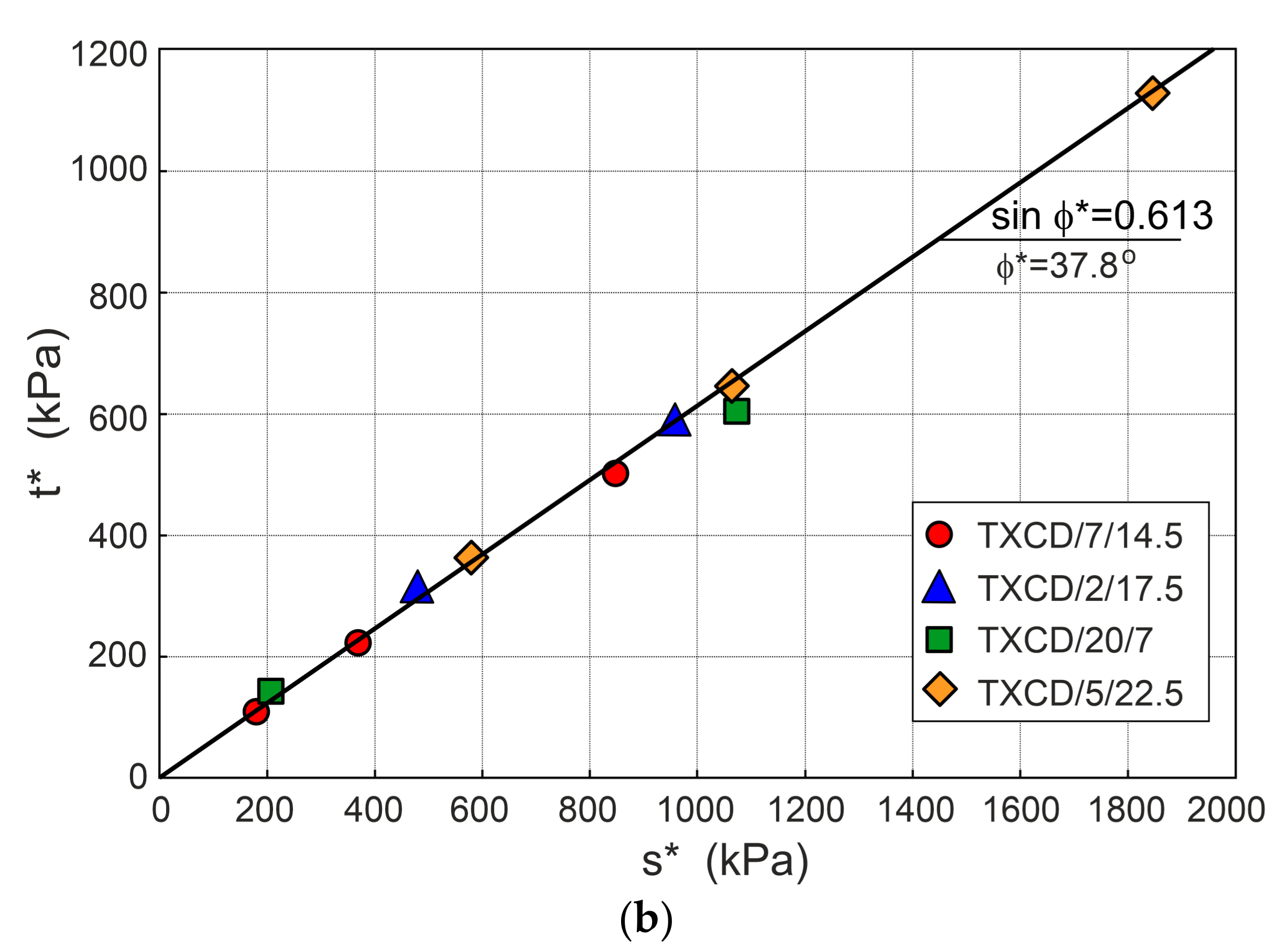
7. Friction Angle of Sand
8. Conclusions
- (1)
- The FSC offers new possibilities for describing the stress–dilatancy behavior of soils (sands).
- (2)
- The elastic parameters of sand identified from drained triaxial compression tests are lower than those obtained from wave propagation analysis.
- (3)
- The dilatant failure state and failure state are different for the tested sands. These states can be easily identified in the stress ratio–plastic dilatancy relationships.
- (4)
- The effective friction angles of the tested sands for the dilatant failure state and failure state are slightly greater than those obtained from Bolton’s formula.
- (5)
- The deviation in the experimental stress ratio–plastic dilatancy relations from the straight line representing dilatant failure states expresses the combined experimental errors of stress and strain measurements and verifies the quality of experiments.
- (6)
- The stress ratio–plastic dilatancy relationship obtained from the FSC is important for a complete description of the stress–strain behavior of soils and can be directly used to define the plastic potential function in the elastoplastic modeling of sands.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahimi, M. Review of proposed stress-dilatancy relationships and plastic potential functions for uncemented and cemented sands. J. Geol. Res. 2019, 1, 19–34. [Google Scholar] [CrossRef]
- Li, X.; Zhu, H.; Yuan, Q. Dilatancy equation based on the property-dependent plastic potential theory for geomaterials. Fractal Fract. 2023, 7, 824. [Google Scholar] [CrossRef]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Schofield, A.N.; Wroth, C.P. Critical State Soil Mechanics; Mc-Grow-Hill Book, Co.: London, UK, 1968. [Google Scholar]
- Le, L.A.; Nguyen, G.D.; Bui, H.H.; Andrade, J.E. Localised failure of geomaterials: How to extract localisation band behaviour from macro test data. Géotechnique 2022, 72, 569–609. [Google Scholar] [CrossRef]
- Li, L.; Li, P.; Cai, Y.; Lu, Y. Visualization of non-uniform soil deformation during triaxial testing. Acta Geotech. 2021, 16, 3439–3454. [Google Scholar] [CrossRef]
- Wan, R.G.; Guo, P.J. Stress dilatancy and fabric dependencies on sand behaviour. J. Eng. Mech. 2004, 130, 635–645. [Google Scholar] [CrossRef]
- Desrues, J.; Andò, E. Strain localization in granular media. C. R. Phys. 2015, 16, 26–36. [Google Scholar] [CrossRef]
- Dong, T.; Kong, L.; Zhe, M.; Zheng, Y. Anisotropic failure criterion for soils based on equivalent stress tensor. Soils Found. 2019, 59, 644–656. [Google Scholar] [CrossRef]
- Liang, J.; Ma, C.; Su, Y.; Lu, D.; Du, X. A failure criterion incorporating the effect of depositional angle for transversely isotropic soils. Comput. Geotech. 2022, 148, 104812. [Google Scholar] [CrossRef]
- Szypcio, Z. Stress-dilatancy behaviour of calcareous sand. In Proceedings of the 8th International Symposium on Deformation Characteristic of Geomaterials (ISDCG2023), Porto, Portugal, 3–6 September 2023; Available online: https://www.issmge.org/publications/publication/stress-dilatancy-behaviour-of-calcareous-sands (accessed on 4 February 2024).
- Lambe, W.T.; Whitman, R.V. Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Head, K.H.; Epps, R.J. Manual of Soil Laboratory Testing. Vol. III Effective Stress Tests, 3rd ed.; Whittles Publishing: London, UK, 2014. [Google Scholar]
- Liu, T.; Ferreira, P.M.V.; Vinck, K.; Coop, M.R.; Jardine, R.J.; Kontoe, S. The behaviour of a low- to medium-density chalk under a wide range of pressure conditions. Soils Found 2023, 63, 101268. [Google Scholar] [CrossRef]
- Gabryś, K.; Dołżyk-Szypcio, K.; Szypcio, Z.; Sas, W. Stress-strain behavior of crushed concrete as a special anthropogenic soil. Materials 2023, 16, 7381. [Google Scholar] [CrossRef] [PubMed]
- Hardin, B.O.; Richart, F.E. Elastic wave velocities in granular soils. J. Soil Mech. Found. Div. 1963, 89, 33–65. [Google Scholar] [CrossRef]
- Dołżyk-Szypcio, K. Stressv-dilatancy relationship of Erksak sand under drained triaxial compression. Geosciences 2020, 10, 353. [Google Scholar] [CrossRef]
- Bishop, A.W. Shear strength parameters for undisturbed and remoulded soil specimens. In Proceedings of the Roscoe Memorial Symposium on Stress-Strain Behaviour of Soils, Cambridge, UK, 29–31 March 1971; Parry, R.H.G., Rosco, K.H., Eds.; G.T. Foulis & Co.: Oxfordshire, UK; pp. 3–58. [Google Scholar]
- Aysen, A. Soil Mechanics: Basic Concepts and Engineering Applications; Taylor & Francis Group: London, UK, 2005. [Google Scholar]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–68. [Google Scholar] [CrossRef]
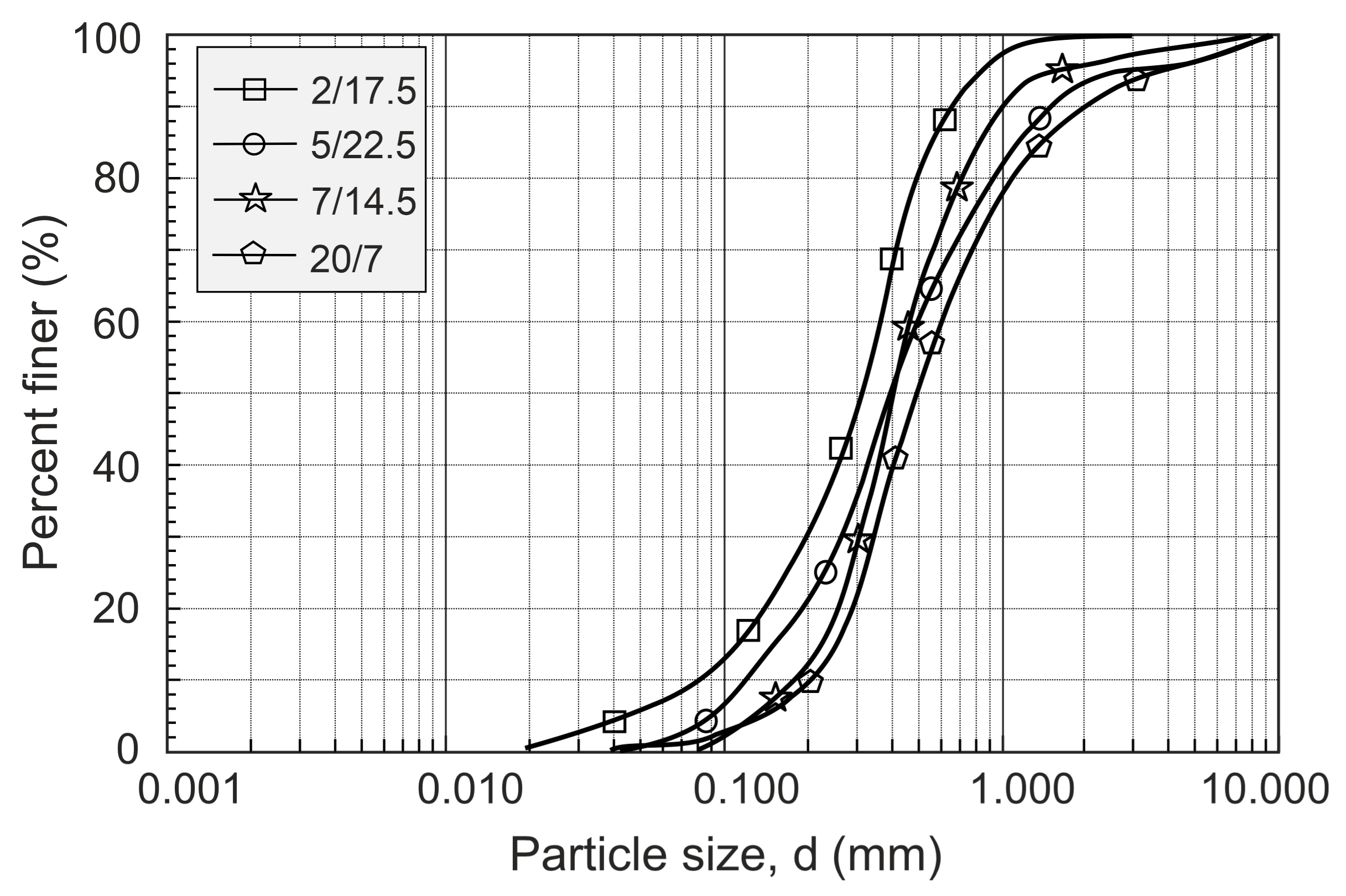




| Sample | D50 mm | Cu - | Cc - | Gs - | emax - | emin - | Dr % |
|---|---|---|---|---|---|---|---|
| TXCD 2/17.5 | 0.32 | 5.03 | 1.39 | 2.66 | 0.75 | 0.36 | 0.93 |
| TXCD 5/22.5 | 0.50 | 3.39 | 0.94 | 2.66 | 0.70 | 0.38 | 0.95 |
| TXCD 7/14.5 | 0.43 | 4.05 | 1.13 | 2.66 | 0.73 | 0.41 | 0.82 |
| TXCD 20/7 | 0.42 | 2.76 | 1.18 | 2.66 | 0.71 | 0.40 | 0.60 |
| Test | TXCD 2/17.5 | TXCD 5/22.5 | TXCD 7/14.5 | TXCD 20/7 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (kPa) | 170 | 370 | 220 | 420 | 720 | 75 | 150 | 350 | 70 | 470 |
| (%) | 0.095 | 0.384 | 0.209 | 0.003 | 0.222 | 0.002 | 0.808 | 0.529 | 0.001 | 0.007 |
| Test | TXCD 2/17.5 | TXCD 5/22.5 | TXCD 7/14.5 | TXCD 20/7 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (kPa) | 170 | 370 | 220 | 420 | 720 | 75 | 150 | 350 | 70 | 470 |
| (MPa) | 101.0 | 152.0 | 165.0 | 228.0 | 263.0 | 79.0 | 111.0 | 172.0 | 75.0 | 194.0 |
| (MPa) | 300.0 | 633.3 | 695.0 | 1393.0 | 1274.2 | 218.9 | 243.0 | 325.8 | 147.0 | 384.9 |
| (-) | 0.36 | 0.40 | 0.39 | 0.32 | 0.28 | 0.35 | 0.31 | 0.28 | 0.28 | 0.29 |
| (MPa) | 25.6 | 29.5 | 146.3 | 102.6 | 160.8 | 10.0 | 28.3 | 32.7 | 45.4 | 25.8 |
| (MPa) | 43.2 | 53.5 | 247.2 | 132.4 | 166.0 | 24.7 | 39.2 | 64.3 | 95.8 | 38.0 |
| (-) | 0.25 | 0.27 | 0.25 | 0.19 | 0.13 | 0.32 | 0.21 | 0.28 | 0.30 | 0.22 |
| (-) | 3.94 | 5.25 | 1.13 | 2.22 | 1.64 | 7.90 | 3.92 | 5.26 | 1.65 | 7.52 |
| (-) | 6.54 | 11.84 | 2.81 | 10.5 | 7.67 | 8.86 | 6.20 | 5.07 | 1.53 | 10.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dołżyk-Szypcio, K.; Szypcio, Z.; Godlewski, T.; Witowski, M. Stress–Dilatancy Behavior of Alluvial Sands. Appl. Sci. 2024, 14, 6228. https://doi.org/10.3390/app14146228
Dołżyk-Szypcio K, Szypcio Z, Godlewski T, Witowski M. Stress–Dilatancy Behavior of Alluvial Sands. Applied Sciences. 2024; 14(14):6228. https://doi.org/10.3390/app14146228
Chicago/Turabian StyleDołżyk-Szypcio, Katarzyna, Zenon Szypcio, Tomasz Godlewski, and Marcin Witowski. 2024. "Stress–Dilatancy Behavior of Alluvial Sands" Applied Sciences 14, no. 14: 6228. https://doi.org/10.3390/app14146228
APA StyleDołżyk-Szypcio, K., Szypcio, Z., Godlewski, T., & Witowski, M. (2024). Stress–Dilatancy Behavior of Alluvial Sands. Applied Sciences, 14(14), 6228. https://doi.org/10.3390/app14146228






