Advancing Crayfish Disease Detection: A Comparative Study of Deep Learning and Canonical Machine Learning Techniques

Abstract

This study evaluates the effectiveness of deep learning and canonical machine learning models for detecting diseases in crayfish from an imbalanced dataset. In this study, measurements such as weight, size, and gender of healthy and diseased crayfish individuals were taken, and at least five photographs of each individual were used. Deep learning models outperformed canonical models, but combining both approaches proved the most effective. Utilizing the ResNet50 model for automatic feature extraction and subsequent training of the RF algorithm with these extracted features led to a hybrid model, RF-ResNet50, which achieved the highest performance in diseased sample detection. This result underscores the value of integrating canonical machine learning algorithms with deep learning models. Additionally, the ConvNeXt-T model, optimized with AdamW, performed better than those using SGD, although its disease detection sensitivity was 1.3% lower than the hybrid model. McNemar’s test confirmed the statistical significance of the performance differences between the hybrid and the ConvNeXt-T model with AdamW. The ResNet50 model’s performance was improved by 3.2% when combined with the RF algorithm, demonstrating the potential of hybrid approaches in enhancing disease detection accuracy. Overall, this study highlights the advantages of leveraging both deep learning and canonical machine learning techniques for early and accurate detection of diseases in crayfish populations, which is crucial for maintaining ecosystem balance and preventing population declines.

1. Introduction

Freshwater crayfish play a significant role in assessing the health of aquatic ecosystems. These organisms occupy important positions in aquatic food webs and can reach high biomass levels [1]. Moreover, they can be utilized as effective bioindicators due to their sensitive responses to water quality and pollutants [2]. Despite having a wide distribution worldwide with nearly 540 species [3], they are predominantly found outside of Antarctica and the African continent [4].

The narrow-clawed crayfish, scientifically named Astacus leptodactylus Eschscholtz, 1823, holds the distinction of being Turkey’s sole noteworthy freshwater crayfish species. Additionally, it is recognized as one of Europe’s most esteemed and economically significant freshwater crustaceans [5,6]. In their comprehensive catalog of worldwide freshwater crayfish, Crandall and De Grave [7] have acknowledged Pontastacus leptodactylus Eschscholtz, 1823 as an equivalent term for A. leptodactylus Esch., 1823.

Every organism has responsibilities for sustainability, but human impact on the environment is pivotal, given our constant interaction with it [8]. Unfortunately, this often leads to environmental harm, with humans unknowingly threatening their habitats while benefiting from the environment. Fulfilling our responsibilities to protect the environment is crucial in addressing today’s environmental issues and pollution [9]. The preservation of underwater habitats is also crucial for the ecosystem balance of freshwater and inland waters [10,11].

Digital image processing is an extremely effective method used in fisheries for detecting diseases. This technique can analyze images of fisheries to identify signs of illness. For example, changes in skin color, lesions, or wounds on fish can be easily identified using digital image processing methods [12]. Additionally, image segmentation can be employed to examine specific regions of the fish’s body for signs of disease [13]. Digital image processing combined with machine learning and artificial intelligence techniques can facilitate automated and accurate diagnosis of diseases in fish. This makes it possible to quickly detect diseases in large-scale fish farming facilities and take preventive measures. Digital image processing provides speed and accuracy in detecting diseases in fisheries while helping to maintain the health of the fish and reduce losses for fish farmers [14,15,16].

Research on crayfish includes a variety of studies utilizing image processing and artificial intelligence techniques. One of these studies suggests that an improved version of the YOLOv5 model offers a lightweight method with high accuracy and generalization performance for automatic, contactless, quick, and accurate classifying of live freshwater crayfish [16]. Artificial intelligence-based machine learning methods have been employed to classify healthy and unhealthy individuals of the Astacus leptodactylus species, which is a good bioindicator [17]. Additionally, UDEEP (underwater deep learning edge computing platform) plays a crucial role in environmental monitoring and combating invasive species by detecting the presence and spread of signal crayfish and plastic waste using artificial intelligence, Internet of Things devices, and edge computing [18].

The main disease symptoms observed in crayfish include melanization, color lesions, and exoskeleton erosion [19]. These symptoms allow diseased individuals to quickly transmit the disease to healthy ones within the population, leading to significant declines in crayfish populations. The spread of disease in this way can result in rapid population decreases and disrupt the ecosystem balance [20]. Advances in image processing technology are expected to play a crucial role in detecting these diseases and preventing their spread in crayfish populations. These technologies can enable early diagnosis and isolation of diseased individuals, helping to control the disease and protect crayfish populations.

Detecting dark color changes on crayfish shells using artificial intelligence techniques and image processing methods is considered important for preventing the spread of disease in the ecosystem and identifying affected individuals. This study aims to detect changes in images of affected crayfish using canonical machine learning, deep learning, and vision transformer models. This approach can enable early intervention and control of the disease.

The contribution of our study can be presented in two main points. First, to the best of our knowledge, this is the first time that deep learning and vision transformer algorithms were utilized for disease detection in crayfish. Second, by combining the mechanisms of canonical machine learning and deep learning algorithms, disease detection with higher performance in terms of sensitivity than the models used in both learning categories was achieved.

The other sections of the study are as follows. Section 2 details the dataset used, the overarching framework, and the algorithms related to traditional machine learning, deep learning, and vision transformers. Section 3 discusses the metrics for evaluating the experiments, the statistical analyses performed, the configuration of the experiments, and the findings obtained. The paper culminates with Section 4, where the final assessments are articulated.

2. Materials and Methods

2.1. Data

During the fishing seasons of 2017 and 2018, specimens of Pontastacus leptodactylus Eschscholtz, 1823 were collected by local fishermen from the waters of the Eğirdir, Beyşehir, and Hirfanlı lakes. This study involved a comprehensive examination of 112 crayfish—comprising 62 females and 50 males. Once in the laboratory, various morphometric parameters were meticulously measured for each crayfish, including weight (W), carapace length (CL), carapace width (Cw), abdomen length (AL), abdomen width (Aw), chela leg length (ChlL), chela width (Chw), and chela length (ChL). The samples’ sexes were also identified, and at least five photographs were taken—both from the top and the underside after flipping the organism—according to standard measurement specifications. A total of 1277 photographs were used in the study. Based on the main disease symptoms observed in crayfish, including melanization, color lesions, and exoskeleton erosion [19], Pontastacus leptodactylus samples obtained from the field were physically examined. Crayfish showing signs of disease were classified as sick individuals. They were categorized into sick and healthy groups accordingly.

For the tabular data containing manually extracted features, there were a total of 112 samples, of which 47 were sick and 65 were healthy. Therefore, the imbalanced ratio is 0.723:1. To address missing values, they were replaced with 0. Additionally, to apply min-max normalization, missing values were replaced with the mean value of the respective feature.

Out of the 1277 crayfish photographs utilized for applying deep learning algorithms, 514 are classified as belonging to the sick class, while the remaining 763 are classified as belonging to the healthy class. For the deep learning tasks, the imbalanced ratio is 0.674:1 and is maintained for both the training and testing sets. The dataset comprising the photographs was partitioned into training and independent testing sets, with 70% allocated to the training set and 30% to the testing set. The training set contains a total of 894 photographs, with 535 belonging to the healthy class and 359 to the sick class. In the independent testing set, of the 383 photographs, 228 belong to the healthy class and the remaining 155 belong to the sick class.

2.2. General Framework

In this study, our aim is to predict whether crayfish are healthy or sick using canonical machine learning and deep learning models. Additionally, the results obtained by training canonical machine learning algorithms with features extracted from deep learning models have also been examined. For canonical machine learning algorithms, tabular data were used as features, while crayfish photographs were used for deep learning algorithms. While using deep learning algorithms, both transfer learning (TL) and training from scratch (FS) processes were performed. The general framework is given in Figure 1 and Figure 2.

2.3. Canonical Machine Learning Models

The support vector machine (SVM) is a method from the domain of statistical learning [21]. It is supervised and utilizes a kernel-based approach. The kernel-based learning technique involves an implicit transformation of the input data into a feature space of higher dimensions, which is defined by a kernel function [21]. There are numerous kernel functions that exist in literature [22]. The linear, polynomial, and radial basis function kernels are among the most commonly used.

To put it another way, kernel-based learning employs a linear hyperplane as a decision-making function for problems that are nonlinear, and then it applies a transformation back into the nonlinear space [21]. The SVM uses the Lagrange multiplier to calculate the partial differentiation of each feature in order to find the best solution. The objective of the training process is to optimize the margin of the hyperplane, which is defined as the distance between the hyperplane and the nearest support vectors from each class [23]. A broader margin implies that the hyperplane has a higher probability of effectively handling data that it has not encountered before. As a result, the model simplifies the training data to a significant subset known as support vectors, thereby reducing its complexity [21].

The naive Bayes (NB) method, a simple probability classifier, computes a series of probabilities by counting the occurrence and combinations of values within a certain dataset [24]. Taking into account the value of the class variable, the method employs Bayes’ theorem to determine the likelihood of a hypothesis based on the provided evidence, operating under the assumption that the input features are conditionally independent when the class label is given [25]. Despite the fact that this assumption of conditional independence is deemed naive due to its infrequent occurrence in real-world applications, the method is typically adept at rapidly learning in a wide range of controlled classification problems [24].

The strength of the naive Bayes classifier lies in its ability to estimate the necessary parameters (such as the means and variances of variables) for classification with only a minimal amount of training data. Due to the assumption of variable independence, it is only necessary to compute the variances of the variables for each class, rather than the entire covariance matrix [24].

K-nearest neighbor (KNN) is a supervised pattern recognition method that is both linear and non-parametric [26]. The core principle of this method is proximity-based: KNN forecasts the label of an unknown instance by identifying ‘k’ instances that are similar, determined by the computed Euclidean distances from instances in the training set. The classification is then determined by the group to which the majority of the ‘k’ objects belong, with any ties resolved by considering the sums of the relevant distances. The ‘k’ parameter plays a significant role in the classification model and is optimized by evaluating the prediction capability at various ‘k’ values [27].

The method presents a multitude of advantages. One of its primary attributes is its mathematical simplicity, which enables it to potentially yield classification results that may surpass those derived from more complex pattern recognition techniques. Moreover, its efficacy remains unaltered, irrespective of the spatial configuration of the classes [27].

A multilayer perceptron (MLP) is a type of neural network that consists of neuron layers linked by weighted connections [23]. These neural networks are designed to mimic the information-processing methods of the human brain. The multilayer perceptron begins with an input layer, which includes a neuron for each feature, and concludes with an output layer, which has a neuron for each potential class. In between these layers are hidden layers, which contain a varying number of neurons [28].

This classifier is trained using backpropagation techniques. A group of inputs traverses through the network of neurons layer by layer, moving from the input to the output direction. Each hidden layer possesses weight and bias parameters that govern the neurons. An activation function is employed to transition the data from the hidden layer to the output layer [23]. Learning algorithms are utilized to determine the weights within the neural network (NN) structure [28]. The selection of weights is based on minimizing performance metrics, such as the mean square error (MSE). Subsequently, the algorithm computes the error by contrasting the achieved outputs with the actual values. The algorithm continues to iterate through these steps for each group of inputs until a specified stopping criterion is met [23].

Random forest (RF) is a member of the decision tree family that utilizes a supervised ensemble learning method [29]. This ensemble technique is capable of mitigating the instability of the base trees, resulting in more reliable predictions. Unlike other decision tree algorithms that strive to identify the optimal variable, RF incorporates random variables. The main rationale behind this strategy is to diminish the correlation among these potential random trees [29]. This element of randomness is crucial in decision-making processes because the presence of highly correlated variables can influence the prediction stage and consequently degrade the prediction performance.

The model is usually executed through the following steps [30]: (i) bootstrapping is performed on the samples from the original dataset to produce several training datasets; (ii) the construction of unpruned decision trees involves the utilization of bootstrapped samples. At each decision point within the tree, a randomly chosen subset of variables is evaluated to ascertain the best possible division; and (iii) all predictions from the random trees are subjected to majority voting to obtain the final outcome.

2.4. Vision Transformer (ViT)

The vision transformer (ViT) model is an advanced deep learning model that has been explicitly engineered for computer vision tasks [31]. It employs a transformer-based architecture, originally intended for natural language processing, for performing tasks related to computer vision. The ViT model employs a decomposition method to segment the input image into separate patches. These patches are subsequently converted into a sequence of vectors through a linear embedding process. The patches are then processed through several transformer encoder layers to identify dependencies and obtain meaningful image representations. The model features a classification part that makes predictions based on the obtained embeddings [31]. ViT demonstrates superior efficacy across a diverse array of tasks pertaining to visual processing through pre-training and fine-tuning [31,32].

For this research, a variant of ViT known as MaxViT (multi-axis vision transformer) was chosen [33]. The architecture includes a powerful, all-purpose transformer backbone designed to encapsulate spatial interactions at both local and global scales throughout each layer of the network. It features an innovative, independent multi-axis attention module that merges blocked local attention with dilated global attention, thereby augmenting the network’s global comprehension while maintaining linear complexity [33].

2.5. Deep Learning Models

A convolutional neural network (CNN) is a sophisticated deep learning algorithm crafted for analyzing data with a grid-like topology, such as pixel data in images [34]. Distinct from standard neural networks, CNNs boast a unique structure that exploits the inherent spatial relationships within data. This is achieved through the deployment of convolutional filters across multiple layers, which are adept at autonomously identifying and learning from local patterns such as lines, textures, and contours. As one progresses through the layers of the network, these elementary features are synthesized into increasingly complex and significant conceptual depictions [34].

A key strength of these models lies in their innate capability to autonomously identify and learn salient features directly from raw data, eliminating the need for manual preprocessing steps [34]. As the training progresses, CNNs are designed to discern and prioritize the most promising features in a hierarchical manner. This intrinsic proficiency renders them exceptionally adept at a variety of computer vision applications [34,35,36].

Pre-trained CNN networks are models that have undergone training on extensive datasets such as ImageNet and are highly regarded within the deep learning domain [34,35]. These networks are adept at identifying a diverse array of visual elements, making them an excellent groundwork for further computer vision research. Utilizing these pre-trained models allows one to capitalize on the knowledge they have amassed, thereby conserving considerable time and resources that would otherwise be spent on training from the ground up and facilitating the achievement of high-quality outcomes with greater efficiency [36].

In this study, ConvNeXt-T [37], EfficientNet v2 [38], ResNet50 [39], VGG16 [40], and AlexNet [41] are utilized for classification tasks. EfficientNetV2 [38] represents an advancement over its predecessor, EfficientNetV1, and introduces a novel class of convolutional neural networks [42]. This upgraded version prioritizes two key objectives: accelerating the training process and boosting the efficiency of parameters. It uses a smart combination of neural architecture search that considers training needs and compound scaling methods [42] to achieve these goals.

ConvNeXt-T [37] represents a modernized convolutional network, evolving from traditional models such as Resnet through the integration of advanced methods akin to vision transformers. This evolution has established ConvNeXt-T as a favored instrument within the image-processing domain [43,44]. Distinguished from its counterparts, ConvNeXt-T is an architecture that stands out by employing convolution blocks organized into channel groups, which significantly enhances the network’s ability to learn [43]. The ConvNeXt-T framework is composed of an array of convolution blocks, each featuring channel grouping [37]. These are succeeded by pooling and fully connected layers. The channel grouping feature refines the traditional convolution layers by segmenting the input channels into distinct groups, which then connect to only a portion of the output channels [43]. This design trims the network’s parameter count and bolsters its ability to learn. ConvNeXt-T’s contribution lies in its convolution blocks with channel grouping, coupled with a residual convolution block structure, which collectively enhances learning efficiency and mitigates the risk of overfitting [44]. Additionally, the architecture’s multiple convolution blocks with channel grouping, followed by pooling and fully connected layers, contribute to its optimal performance in various computer vision applications [43,44].

As the CNN network deepens, there can be a decline in both performance and convergence speed [45]. ResNet50 [39], a type of residual network, addresses this issue by efficiently extracting features from input data through a series of stacked residual blocks. The ResNet-50 structure is organized into five stages, each containing a convolution and an identity block, followed by an average pooling layer, and culminating in a fully connected layer equipped with 1000 neurons [46]. Both the convolution and identity blocks consist of three convolution layers. Each convolution layer is succeeded by a batch normalization layer and a ReLU activation function. The batch normalization layers are responsible for normalizing the activations of the input volume by calculating and applying the mean and standard deviation of each convolutional filter’s response across mini-batches during each iteration, thus standardizing the activation of the current layer [46].

In 2014, VGGNet secured the runner-up position in the ImageNet image classification challenge, with its VGG16 model emerging as one of the top-performing classification networks [47]. The designation ‘VGG16’ [40] indicates the presence of 16 parameter-inclusive layers within the model. These layers are organized into five distinct blocks accompanied by a series of fully connected layers. The first two blocks each contain two convolutional layers, while the subsequent three blocks—block3, block4, and block5—each have three convolutional layers [48]. After each convolution, the ReLU activation function is applied. At the conclusion of every block, there is a max pooling layer. The VGG16 network’s concluding part is composed of three fully connected layers, with the softmax function being utilized to generate the final output [48].

AlexNet [41] is renowned as a highly influential CNN widely utilized for pattern recognition and various classification tasks [46,49]. Its structure is composed of five convolutional layers, interspersed with max-pooling layers, and followed by a trio of successive fully connected layers [46]. Initially, the input layer receives and processes the images. The resulting output is then relayed to the second convolutional layer. Subsequently, this output undergoes further processing through a pooling and normalization layer before advancing to the third and fourth convolutional layers. Finally, the output from the final convolutional layer is transformed into a one-dimensional array via a fully connected layer [46].

3. Results

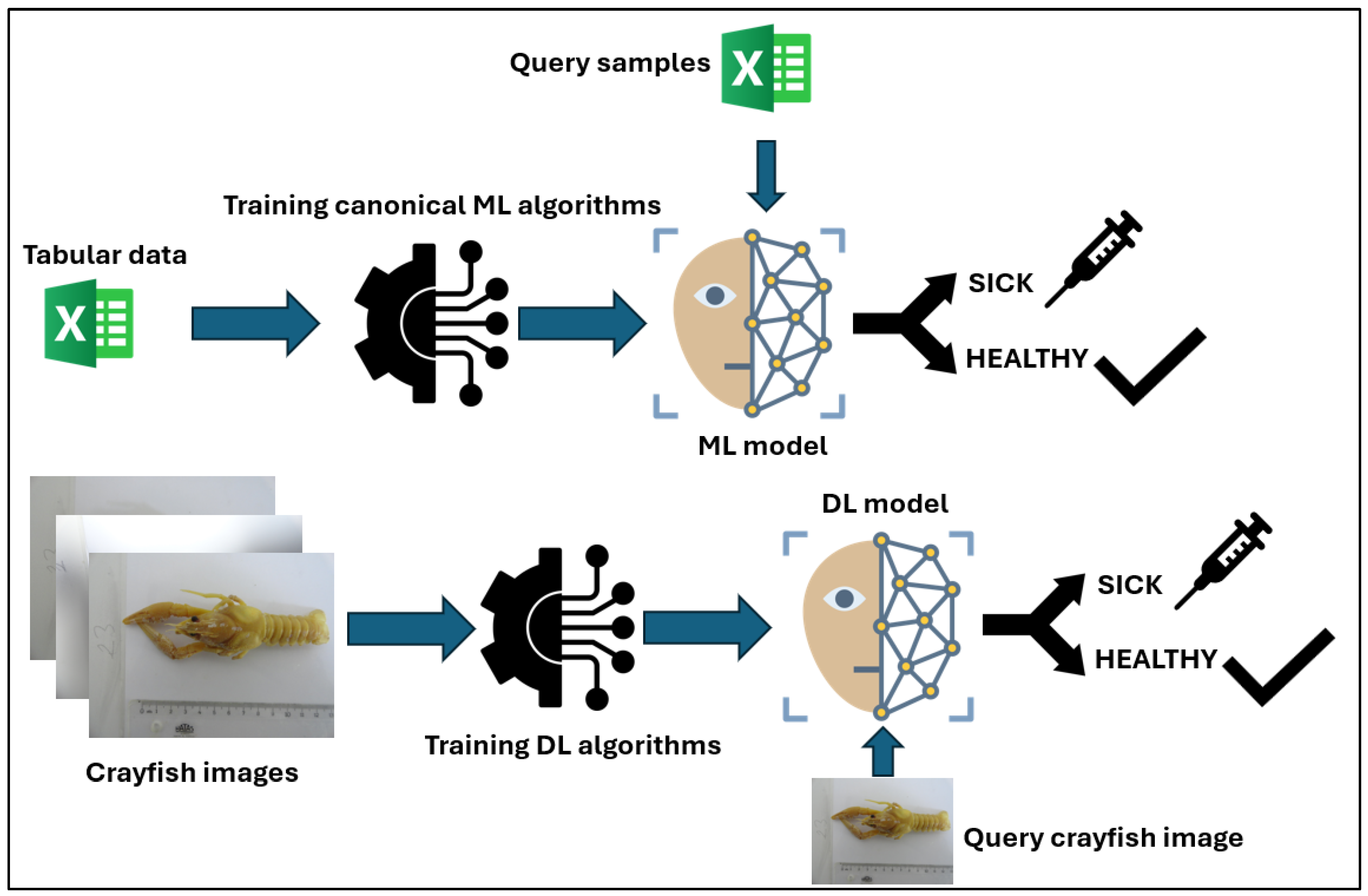
3.1. Evaluation Metrics

In our dataset, the terms true positives (TP) and true negatives (TN) denote the count of cases accurately identified as sick and healthy, respectively. Conversely, false positives (FP) refer to the instances wrongly labeled as sick, while false negatives (FN) pertain to the cases mistakenly classified as healthy.

Accuracy represents the proportion of correct predictions made by a classification model, compared to the overall number of predictions. It is calculated by dividing the count of accurate predictions by the dataset’s total number of predictions. Mathematically, accuracy can be expressed as:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+FP+TN+FN}}$$

(1)

Sensitivity, or recall, measures a classification model’s effectiveness in correctly identifying positive cases. It is calculated as the fraction of true positives out of the total positive instances, which includes both true positives and false negatives. It is particularly important in applications where identifying positive instances is critical, such as in medical diagnosis or fraud detection. Sensitivity can be expressed as:

$$Sensitivity={\displaystyle \frac{TP}{TP+FN}}$$

(2)

Specificity assesses a classification model’s accuracy in identifying negative cases. It is determined by the proportion of true negatives relative to the combined count of true negatives and false positives. Mathematically, specificity can be expressed as:

$$Specificity={\displaystyle \frac{TN}{TN+FP}}$$

(3)

Precision is a metric that gauges the accuracy of a model’s positive predictions in classification tasks. It is expressed as the ratio of true positive predictions to the overall number of positive predictions made:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(4)

The F1 score represents a balanced metric that combines precision and recall through their harmonic mean, offering a unified measure that equally weighs both aspects. It can be expressed as:

$$F1={\displaystyle \frac{2 \ast Precision \ast Recall}{Precision+Recall}}$$

(5)

The Matthews correlation coefficient (MCC) serves as an evaluative metric for the effectiveness of binary classification. It considers every quadrant of the confusion matrix. The MCC is mathematically formulated as follows:

$$MCC={\displaystyle \frac{TP\ast TN-FP\ast FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}}$$

(6)

The area under the curve (AUC) is a metric for assessing binary classification models’ performance. It quantifies the area beneath the receiver operating characteristic (ROC) curve—a plot that depicts a binary classifier’s diagnostic capacity as the discrimination threshold changes. The ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) across different thresholds. The AUC reflects the likelihood that the model will assign a higher score to a randomly selected positive instance over a negative one. AUC values range from 0 to 1, where 0.5 signifies no discriminative power—equivalent to random chance—and 1.0 signifies flawless discrimination, with all positive and negative instances correctly identified.

3.2. Statistical Tests

Two statistical tests were conducted to measure whether the results obtained with canonical machine learning and deep learning algorithms are statistically significant. The first is the Wilcoxon test, and the second is the McNemar’s test.

3.2.1. Wilcoxon Test

The Wilcoxon signed-rank test is a non-parametric statistical method used in binary classification to assess if two models differ significantly in their predictive accuracy. The formula is given in Equation (7):

$$W=\mathrm{m}\mathrm{i}\mathrm{n}({\sum }_{i:d_i>0}{R}_i, {\sum }_{i:d_i<0}{R}_i )$$

(7)

In this context, d_i represents the discrepancy between paired predictions, while R_i denotes the rank of the absolute discrepancies $\left|d_i\right|$. The test statistic W is subsequently evaluated against the critical value from the Wilcoxon signed-rank distribution table, or alternatively, the p-value is calculated to ascertain statistical significance.

3.2.2. McNemar’s Test

McNemar’s test, a non-parametric statistical method, is employed to evaluate and compare the error rates of two binary classification models applied to an identical dataset. It determines if the discrepancies in their performance are statistically significant. Given a binary classification task, let CM₁ and CM₂ be two classification models evaluated on the same set of n instances. Each instance is classified as either positive (1) or negative (0). McNemar’s test analyzes the disagreement between the two models’ predictions, focusing on instances where the models differ in their classification. The contingency table for McNemar’s test is as follows:

According to

Table 1. Contingency table.

	CM2 (1)	CM2 (0)
CM1 (1)	n11	n10
CM1 (0)	n01	n00

, n₁₁, n₁₀, n₀₁, and n₀₀ represent the number of instances correctly classified as positive by both models, classified as positive by CM₁ but negative by CM₂, classified as negative by CM₁ but positive by CM₂, and correctly classified as negative by both classification models, respectively. McNemar’s test statistic ${\chi }^2$ is based on the n₁₀ and n₀₁ and is calculated as follows:

$${\chi }^2={\displaystyle \frac{{\left(\left|n_{10}-n_{01}\right|-1\right)}^2}{n_{10}+n_{01}}}$$

(8)

The test statistic in question adheres to a chi-square distribution with one degree of freedom when the null hypothesis presumes identical error rates for the models. To evaluate the significance of the observed variance, the test statistic is adjoined with the critical value at a significance level α, as listed in chi-square distribution tables. Should the test statistic exceed the critical value, the null hypothesis is dismissed, signifying a statistically meaningful divergence in the error rates of the two classification models. Another approach to determining the statistical significance is to compute the p-value.

3.3. Experimental Setup

Given the dataset’s modest size and the structured nature of the data, the 10-fold cross-validation technique was employed. This resampling strategy is instrumental in assessing a model’s performance and its ability to generalize. It involves dividing the dataset into 10 equally sized segments, known as folds. The training occurs on 9 folds, while the 10th fold is used for testing. This cycle is conducted 10 times, ensuring each fold is used once as the test set. Such a method is effective in reducing overfitting and yields a more dependable performance metric for the model on new data. Additionally, the ratio of class imbalance was preserved across each fold.

Additionally, min-max normalization was applied to the tabular data to observe whether it would have an effect on the results. Min-max normalization, commonly referred to as feature scaling, is a method that adjusts the values of a feature to fall within a designated range, often between 0 and 1. The transformation is defined as follows:

$$x^{\prime }={\displaystyle \frac{x-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}{\max \left(x\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}}$$

(9)

where x is an original value, min (x) is the minimum value of the feature, max (x) is the maximum value of the feature, and x′ is the normalized new value. This normalization process ensures that the values of the feature are scaled proportionally within the specified range, preserving the relationships among the original data while enabling more effective comparison and processing by machine learning algorithms.

During the training phase of the deep learning algorithms, both transfer learning and training from scratch were applied. The stopping condition was set to 60 epochs or a training loss of less than 0.01. Stochastic gradient descent (SGD) [49] was utilized in all deep learning models. ConvNeXt-T was trained with adaptive moment estimation with weight decay regularization (AdamW) [50] because it is a newer model compared to the others. A batch size of 4 was used in all deep learning architectures.

In the hybrid model, the RF and ResNet50 models, which had the highest accuracy among canonical machine learning and deep learning models, were utilized. When selecting deep learning models, those utilizing SGD for optimization were considered. In the RF-ResNet50 hybrid model, features automatically extracted from crayfish images were utilized to feed the RF algorithm. The features were obtained from the average pooling layer immediately preceding the fully connected layer of the ResNet50 model. By providing these features as input to the RF algorithm, the class of the image was determined. The architecture of the hybrid model is given in Figure 3.

3.4. Experimental Results

The hyper-parameters for canonical machine learning algorithms without applying min-max normalization are given below. During the fine-tuning process, the accuracy evaluation metric was maximized, and the grid search method was utilized.

For MLP, the number of hidden layers was found as 3. The number of neurons was 50, 10, and 10 for the hidden layers, respectively. Since naive Bayes is a probabilistic classifier, it does not have any hyperparameters. For KNN, the number of the nearest neighbors was found as 17. For SVM, the cost and the gamma parameters were found as 1 × 10⁶ and 1 × 10⁻⁸, respectively. For RF, the maximum depth and the number of trees were found as 3 and 100, respectively.

The hyper-parameters for canonical machine learning algorithms with applying min-max normalization are given below. During the fine-tuning process, the accuracy evaluation metric was maximized, and the grid search method was utilized.

For MLP, the number of hidden layers was found as 1. The number of neurons was 100 in the hidden layer. For KNN, the number of the nearest neighbors was found as 25. For SVM, the cost and the gamma parameters were found as 1 × 10⁹ and 0.001, respectively. For RF, the maximum depth and the number of trees were found as 2 and 100, respectively.

The classification results for canonical machine learning algorithms without data normalization and with data normalization are given in

Table 2. The results for canonical machine learning algorithms without normalization.

Model	Accuracy	Sensitivity	Precision	Specificity	F1-Score	MCC
MLP	0.616	0.298	0.583	0.846	0.394	0.173
KNN	0.598	0.277	0.542	0.831	0.366	0.129
NB	0.616	0.277	0.591	0.862	0.377	0.172
RF	0.661	0.404	0.655	0.846	0.500	0.282
SVM	0.616	0.404	0.559	0.769	0.469	0.186

and

Table 3. The results for canonical machine learning algorithms with normalization.

Model	Accuracy	Sensitivity	Precision	Specificity	F1-Score	MCC
MLP	0.598	0.213	0.556	0.877	0.308	0.121
KNN	0.580	0.192	0.500	0.862	0.277	0.071
NB	0.580	0.021	0.500	0.985	0.041	0.022
RF	0.643	0.277	0.684	0.908	0.394	0.242
SVM	0.616	0.447	0.553	0.739	0.494	0.193

, respectively.

According to Table 2, the best accuracy, sensitivity, precision, F1-score, and MCC performances were obtained with 0.661, 0.404, 0.655, 0.5, and 0.282, respectively, by utilizing the RF model. On the other hand, the best specificity performance was obtained with 0.862 by utilizing the NB model. It can be said that the imbalanced data led to poor performance in detecting sick individuals.

According to Table 3, the best accuracy, precision, and MCC performances were obtained with 0.643, 0.684, and 0.242, respectively, by utilizing the RF model. The best results for sensitivity and F1-score were obtained with 0.447 and 0.494, respectively, by utilizing the SVM model. Finally, the best specificity performance was obtained with 0.985 by utilizing the NB model. All models, except SVM, experienced a performance loss in accuracy and sensitivity evaluation metrics. Therefore, it can be said that the data normalization had no influence on the performances of the canonical machine learning classifiers for the dataset. On the contrary, the data normalization resulted in a performance increase for detecting sick individuals with SVM, while it caused a performance decrease in identifying healthy individuals.

The classification results for deep learning algorithms and MaxViT vision transformer with TL and FS are given in

Table 4. The results for deep learning algorithms.

Model	Accuracy	Sensitivity	Precision	Specificity	F1-Score	MCC	Epoch
AlexNet (TL)	0.934	0.929	0.923	0.947	0.926	0.876	32
AlexNet (FS)	0.833	0.800	0.790	0.855	0.795	0.654	50
ResNet50 (TL)	0.945	0.929	0.935	0.956	0.932	0.886	16
ResNet50 (FS)	0.757	0.794	0.669	0.733	0.726	0.517	60
VGG (TL)	0.893	0.884	0.856	0.899	0.870	0.779	18
VGG (FS)	0.854	0.819	0.819	0.877	0.819	0.697	44
RF-ResNet (proposed hybrid model)	0.940	0.961	0.900	0.925	0.928	0.878	N/A
Effnetv2 (TL)	0.903	0.825	0.927	0.956	0.873	0.799	60
Effnetv2 (FS)	0.584	0.174	0.465	0.864	0.253	0.052	60
MaxVit (TL)	0.926	0.871	0.944	0.964	0.906	0.848	60
MaxVit (FS)	0.593	0.077	0.480	0.943	0.133	0.040	60
ConvNeXt-T (TL)	0.870	0.871	0.818	0.868	0.844	0.733	60
ConvNeXt-T (FS)	0.713	0.729	0.624	0.702	0.673	0.424	60
ConvNeXt-T AdamW	0.969	0.948	0.974	0.983	0.961	0.935	31

. The results were obtained by utilizing the independent test set.

According to Table 4, it can be seen that the models with transfer learning outperformed the same models trained from scratch. The best accuracy, precision, F1-score, and MCC performances were achieved with the ResNet50 model. For the specificity evaluation metric, the MaxVit model outperformed the other models. Additionally, the RF-ResNet50 hybrid model obtained the best sensitivity performance with 100 trees having a maximum depth of 3. Among the models evaluated, ResNet50 achieved the minimum number of epochs to complete the training process. The ConvNeXt-T model trained with the AdamW optimizer outperformed the other models in all metrics except for the sensitivity.

AUC scores for deep learning and vision transformer models are given in

Table 5. AUC Scores for deep learning models.

Model	AUC
AlexNet (TL)	0.987
AlexNet (FS)	0.891
ResNet50 (TL)	0.987
ResNet50 (FS)	0.842
VGG-16 (TL)	0.961
VGG-16 (FS)	0.922
EffNetv2 (TL)	0.973
EffNetv2 (FS)	0.614
MaxViT (TL)	0.982
MaxViT (FS)	0.519
ConvNeXt-T (TL)	0.957
ConvNeXt-T (FS)	0.535
RF-ResNet50 Hybrid	0.984
ConvNeXt-T AdamW	0.997

.

According to Table 5, the highest AUC score of 0.997 was obtained utilizing the ConvNeXt-T AdamW model. With an SGD optimizer, the highest AUC score of 0.987 was achieved by utilizing the AlexNet and ResNet50 models. The RF-ResNet50 hybrid model ranked third in terms of AUC. As can also be seen in the table, the models with transfer learning outperformed the same models trained from scratch.

In the tables presenting the Wilcoxon and McNemar’s test results for statistical significance, bold values indicate a significant difference between the two models at the 5% level. Arrows further indicate which model achieved higher accuracy. If both a left arrow and an upward arrow are present next to a value, it should be understood that the two models have the same accuracy value.

Wilcoxon test results for canonical machine learning algorithms without the data normalization and with the data normalization are given in

Table 6. Wilcoxon test results without normalization.

p < 0.05
Classifier	kNN	MLP	SVM	RF	NB
kNN		1	0.041 ↑	0.336	0.727
MLP			0.041 ↑←	0.297	0.617
SVM				0.251	0.014 ↑←
RF					0.144
NB

and

Table 7. Wilcoxon test results with normalization.

p < 0.05
Classifier	kNN	MLP	SVM	RF	NB
kNN		1	0.0009 ↑	0.819	0.0003 ↑←
MLP			0.0001 ↑	0.819	0.0002 ←
SVM				0.0009 ↑	0 ←
RF					0.0002 ←
NB

, respectively.

According to Table 6, there is a statistical significance between the results of the kNN and SVM, MLP and SVM, and SVM and NB models. The results show that the SVM model achieves statistically significant superiority in classification performance.

According to Table 7, there is a statistical significance between the results of the kNN and SVM, kNN and NB, MLP and SVM, MLP and NB, SVM and RF, SVM and NB, and RF and NB models. The results show that the SVM model achieves statistically significant superiority in classification performance.

McNemar’s test results for canonical machine learning algorithms without the data normalization and with the data normalization are given in

Table 8. McNemar’s test results without normalization.

p < 0.05
Classifier	kNN	MLP	SVM	RF	NB
kNN		0.637	0.683	0.177	0.479
MLP			1	0.297	1
SVM				0.251	1
RF					0.297
NB

and

Table 9. McNemar’s test results with normalization.

p < 0.05
Classifier	kNN	MLP	SVM	RF	NB
kNN		0.617	0.505	0.108	1
MLP			0.695	0.251	0.637
SVM				0.602	0.505
RF					0.127
NB

, respectively.

According to Table 8 and Table 9, there is no statistical significance among the canonical machine learning models. Data normalization also eliminated the statistically significant differences observed between the models in their unnormalized state.

Wilcoxon test results for deep learning algorithms are given in

Table 10. Wilcoxon test results for DL models.

p < 0.05
Model	AlexNet	ResNet50	VGG	EffNetv2	MaxViT	ConvNeXt-T	ConvNeXt-T AdamW	RF-ResNet50 Hybrid
AlexNet		0.002 ↑	0.041 ←	0.012 ←	0.67	0.059	0.001 ↑	0.542
ResNet50			0.0004 ←	0.154	0.193	0.001 ←	0.354	0.292
VGG				0.0001 ↑	0.311	0.877	0.001 ↑	0.892
EffNetv2					0.005 ↑	0.0004 ←	0.288	0.075
MaxViT						0.016 ←	0.175	0.393
ConvNeXt-T							0.006 ↑	0.877
ConvNext-T AdamW								0.151
RF-ResNet50 Hybrid

.

According to Table 10, Resnet50 and ConvNext-T with AdamW models have statistically significant superiority in classification performance. There is a statistical significance between the results of the AlexNet and ResNet50, VGG, EffNetv2, ConvNeXt-T with AdamW; ResNet50 and VGG, ConvNeXt-T; VGG and EffNetv2, ConvNeXt-T with AdamW; EffNetv2 and MaxViT, ConvNeXt-T; ConvNeXt-T and ConvNeXt-T with AdamW models.

McNemar’s test results for deep learning algorithms are given in

Table 11. McNemar’s test results for DL models.

p < 0.05
Model	AlexNet	ResNet50	VGG	EffNetv2	MaxVit	ConvNeXt-T	ConvNeXt-T AdamW	RF-ResNet50 Hybrid
AlexNet		0.715	0.013 ←	0.039 ←	0.423	0.0003 ←	0.028 ↑	2.51 × 10−29 ↑
ResNet50			0.0016 ←	0.016 ←	0.178	9.76 × 10−6 ←	0.039 ↑	1.01 × 10−30 ←
VGG				0.586	0.069	0.257	9.76 × 10−6 ↑	7.9 × 10−24 ↑
EffNetv2					0.216	0.107	0.0001 ↑	1.80 × 10−25 ↑
MaxVit						0.002 ←	0.003 ↑	2.92 × 10−28 ↑
ConvNeXt-T							4.14 × 10−8 ↑	1.52 × 10−19 ↑
ConvNeXt-T AdamW								4.47 × 10−34 ↑
RF-ResNet50 Hybrid

.

According to Table 11, ConvNext-T with AdamW and the RF-ResNet50 hybrid models have statistically significant superiority in classification performance. There is a statistical significance between the results of the AlexNet and VGG, EffNetv2, ConvNeXt-T, ConvNeXt-T with AdamW, RF-ResNet50 hybrid; ResNet50 and VGG, EffNetv2, ConvNeXt-T, ConvNeXt-T with AdamW, RF-ResNet50 hybrid; VGG and ConvNeXt-T with AdamW, RF-ResNet50 hybrid; EffNetv2 and ConvNeXt-T with AdamW, RF-ResNet50 hybrid; MaxViT and ConvNeXt-T, ConvNeXt-T with AdamW, RF-ResNet50 hybrid; ConvNeXt-T and ConvNeXt-T with AdamW, RF-ResNet50 hybrid; ConvNeXt-T with AdamW and RF-ResNet50 hybrid models.

4. Conclusions

In this study, on the existing imbalanced dataset, deep learning models demonstrated higher performance in terms of evaluation metrics compared to canonical machine learning models trained with manually extracted features. Although canonical models may yield poor results, they can be beneficial when combined with deep learning models. Utilizing the ResNet50 model for automatic feature extraction and subsequent training of the RF algorithm with these extracted features led to a hybrid model achieving the highest performance in diseased sample detection. Since deep learning algorithms automatically extract features, classifying these features with RF resulted in high accuracy. The boosting and bagging methods used in RF contribute to this effect because, in RF, features are randomly selected when constructing trees, which helps reduce the correlation between trees. This finding serves as evidence for the usefulness of the canonical machine learning algorithms. Utilizing AdamW as the optimizer in the ConvNeXt-T deep learning algorithm led to higher performance compared to the models obtained by utilizing SGD. However, the utilization of the AdamW optimizer resulted in a disease detection performance sensitivity that was 1.3% lower than that of the hybrid model. According to McNemar’s test results, the classification performances of the hybrid model and the ConvNeXt-T model trained with AdamW are also statistically significant. Another noteworthy result is that the performance of the ResNet50 model, which provided the highest performance among the models trained with SGD for detecting diseased samples, was enhanced by 3.2% when utilizing the RF canonical machine learning algorithm. This study focuses solely on classification; the detection of diseased areas in images will be conducted in the next phase of the research. Future work will involve developing advanced image processing techniques to accurately identify and localize affected regions. This will enhance the overall diagnostic process and provide a more comprehensive understanding of the disease progression.

Future research inspired by the findings of this study can focus on various directions. Firstly, enhancing the generalization capabilities of models by collecting larger and more balanced datasets is crucial. Investigating different organism species using similar models could expand biological monitoring capacity across ecosystems in terms of health and sustainability. Additionally, integrating the developed models with real-time data streams in field studies can facilitate rapid disease detection and control. Research efforts should prioritize optimizing deep learning models for more efficient operation. These endeavors could provide effective tools for monitoring and conserving the health of freshwater ecosystems, thereby contributing to environmental sustainability goals.