Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models
Abstract
1. Introduction
2. Background
2.1. Basic Methodology and Shortcomings of Existing Studies
2.2. Innovative Aspects of the Study
- Most of the existing methods are based on the meteorological features of numerical weather prediction as input features, and the input prediction model based on multiple correlation and target variables proposed in this study takes into account the historical patterns of correlation features and target variables, which can improve the accuracy of the model prediction.
- Aiming to address the shortcomings of the traditional DBO algorithm in the application of power load forecasting, such as its time-consuming nature, reduced search capability, ease of falling into local optimum and low convergence accuracy, the traditional DBO algorithm is improved by using the lens inverse-learning strategy, the spiral search strategy, the optimal value-guiding strategy, and the positional dynamic updating of weight coefficients strategy in order to form the MODBO-LSTM algorithm with multiple strategies, and the optimization outcomes of various optimization algorithms (FOA, SSA, GWO, etc.) are compared. The simulation findings indicate that the MODBO-LSTM algorithm outperforms the conventional DBO-LSTM approach, exhibiting superior prediction accuracy.
- A hybrid MODBO-VMD-MODBO-LSTM (MVMO-LSTM) model is proposed, whereas previous studies need to reset the number of decompositions when the center frequency domain is determined and seldom explore the penalty factor and decomposition layer values. This multi-strategy improved dung beetle algorithm not only optimizes the penalty factor and decomposition layer values of VMD but also optimizes the optimal number of hidden units, the optimal maximum training period and the optimal initial learning rate of LSTM. The combination of these two improvements can effectively help the LSTM learn and adapt to the complexity and seasonal changes of the power load data, thus improving the prediction accuracy and making the prediction results more reliable and practical.
3. Methodologies
3.1. Variational Modal Decomposition Algorithm (VMD)
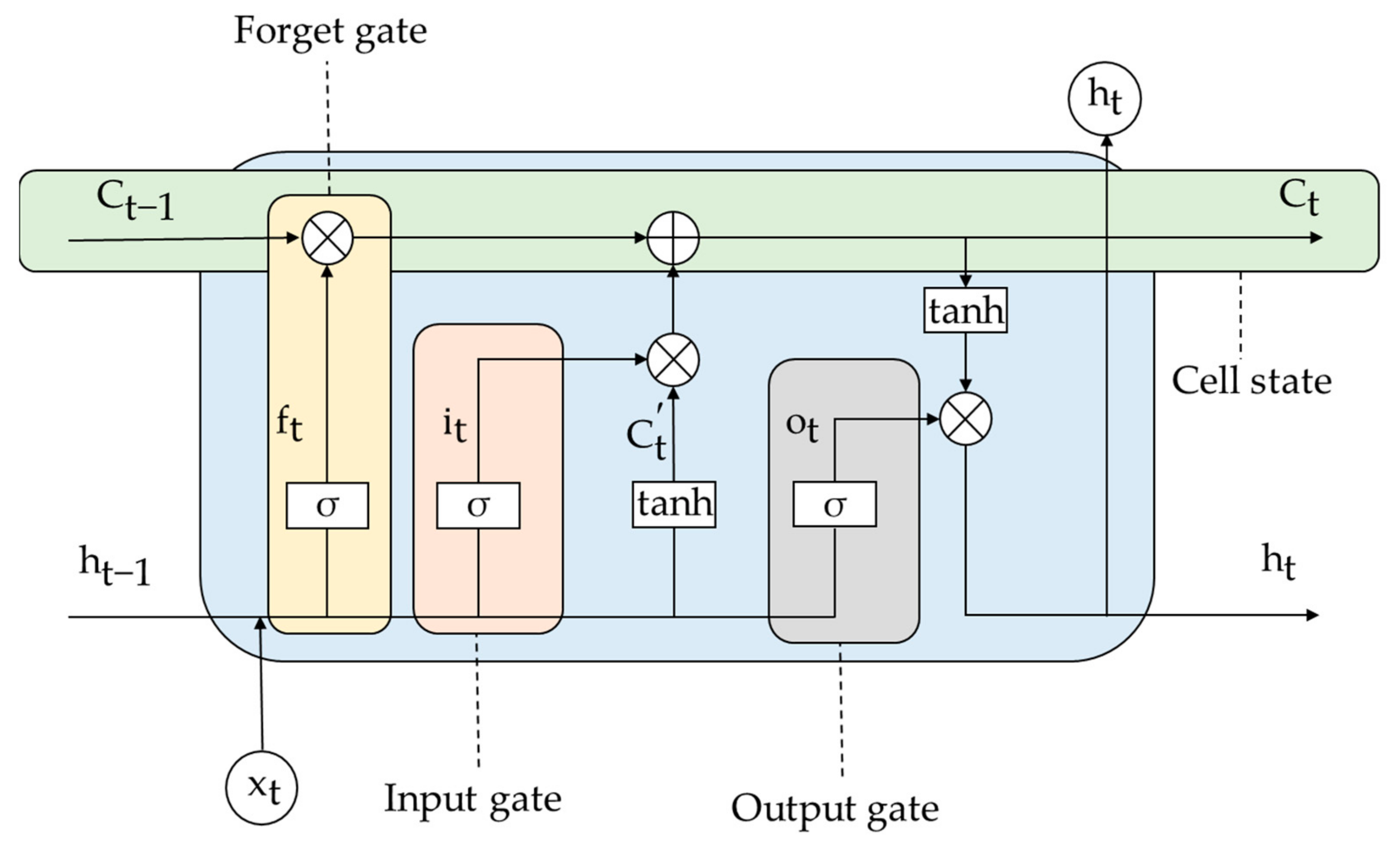
3.2. Long Short-Term Memory
3.3. Dung Beetle Algorithm for Multi-Strategy Optimization
3.3.1. Dung Beetle Optimizer
- Dung Beetle Rolling Balls
- Breeding Dung Beetles
- Foraging Dung Beetles
- Stealing Dung Beetles
3.3.2. Multi-Strategy Optimized Dung Beetle Algorithm
- (a)
- Lens-Imaging Inverse-Learning Strategist
- (b)
- Spiral Search Strategy
- (c)
- Optimal Value Guidance Strategy
- (d)
- Positional Update Dynamic-Weighting Coefficient Strategy
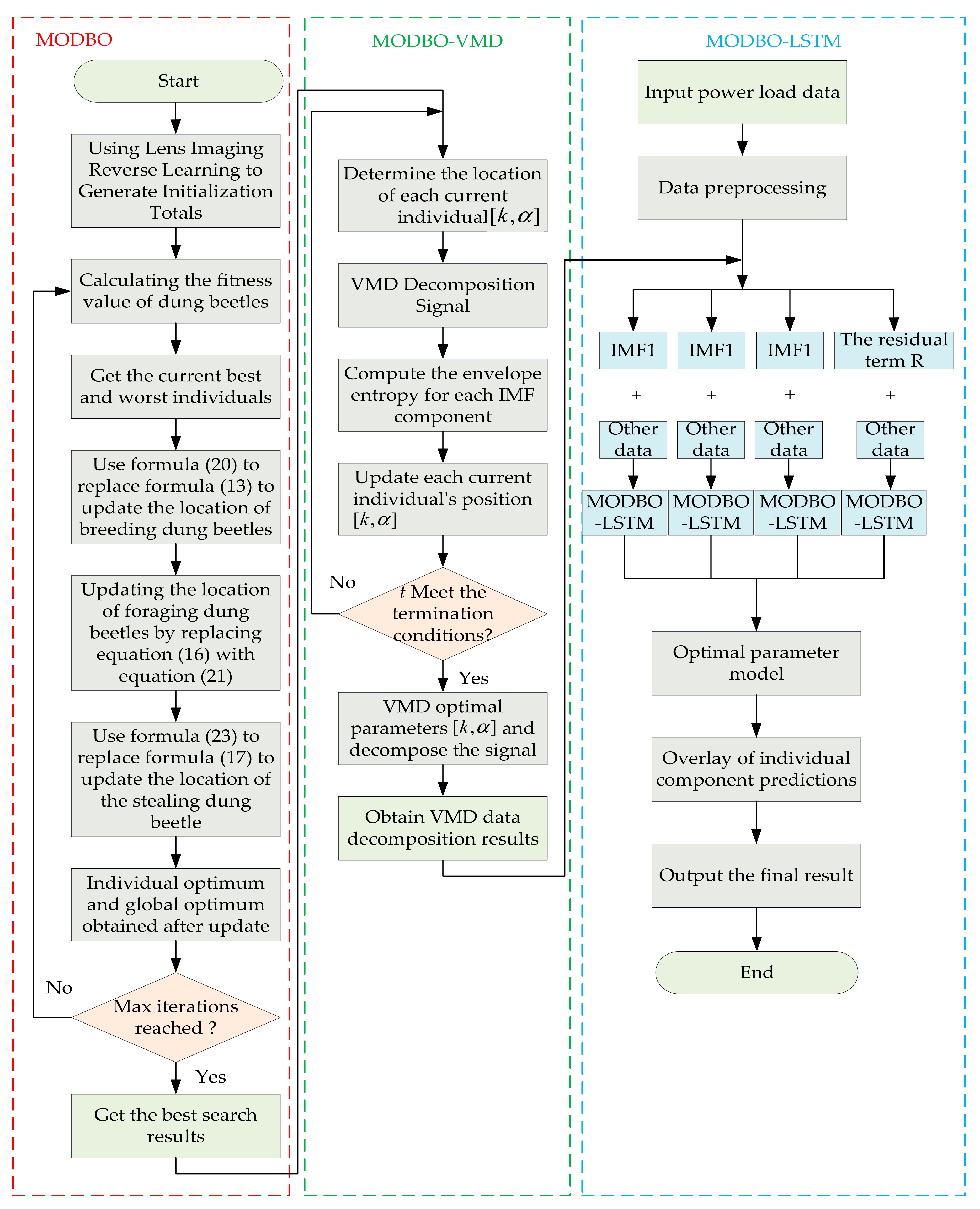
4. Electricity Load-Forecasting Model
The Algorithmic Flow of the Model
5. Experimentation and Analysis
5.1. Source of Data
5.2. Prediction Error Analysis
5.3. Experimental Environment
5.4. Analysis of Experimental Arithmetic
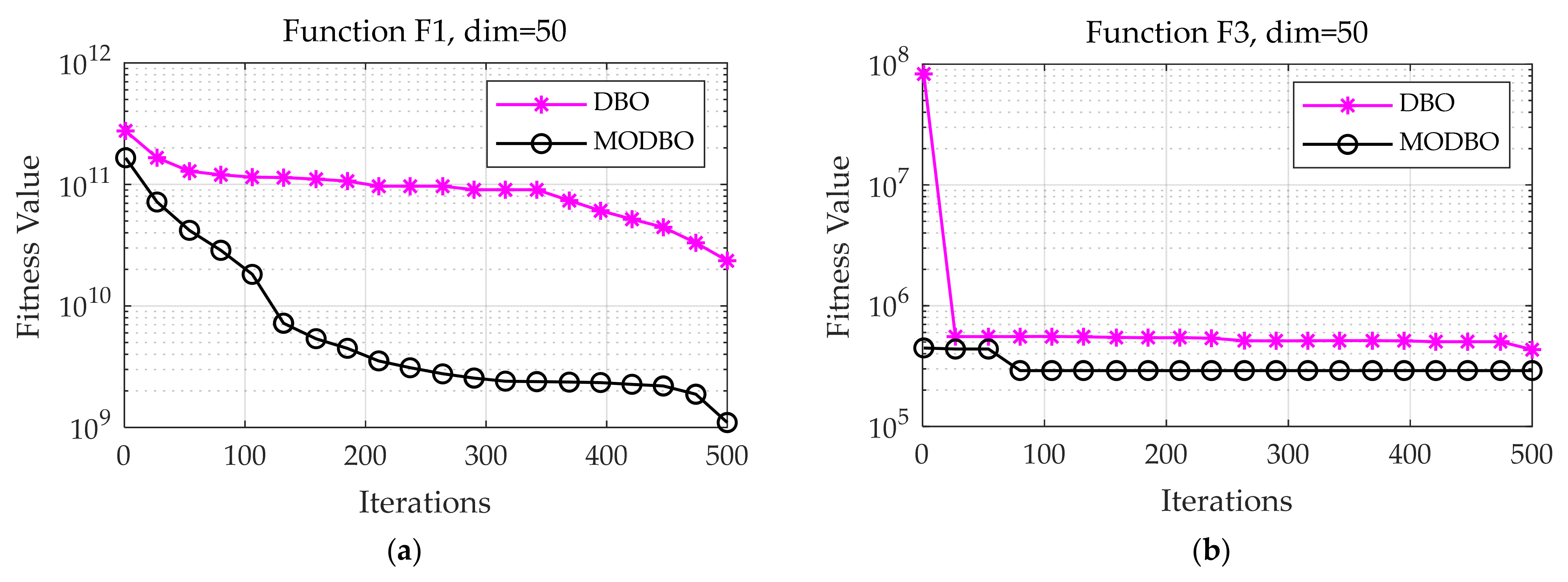
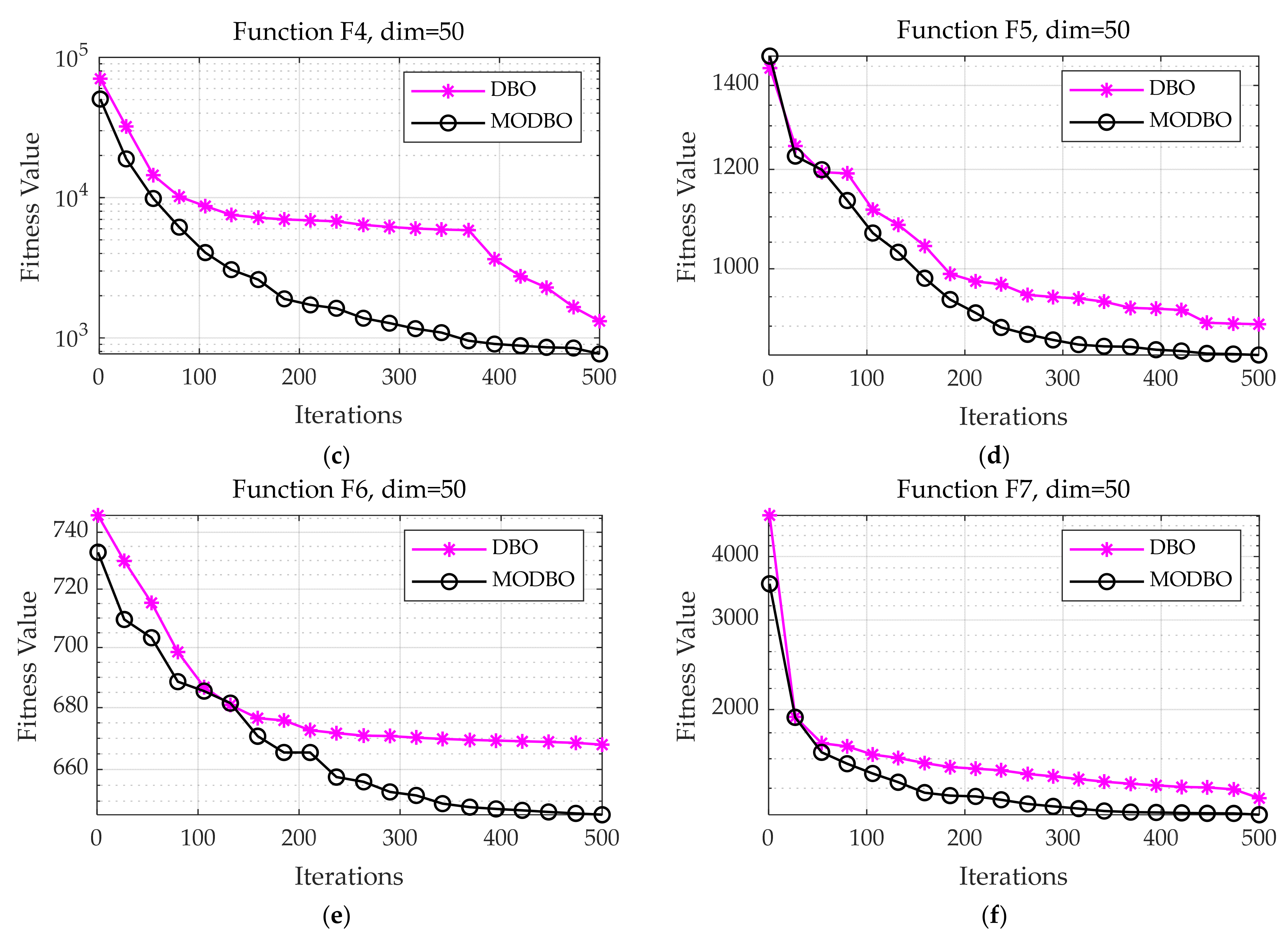
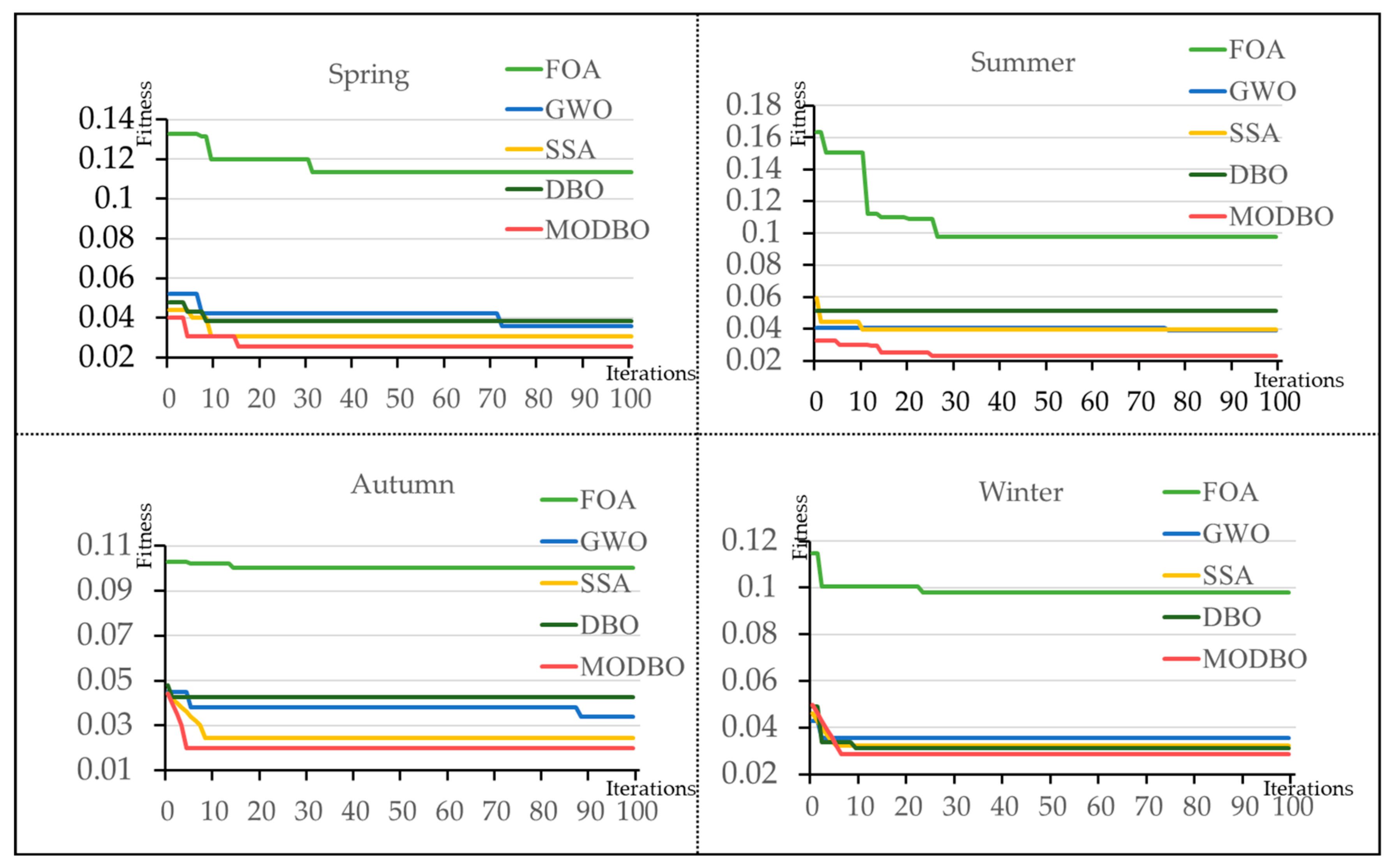
5.4.1. Comparison Results of the MODBO in Test Functions
5.4.2. Comparison Results of the MODBO in Load Data
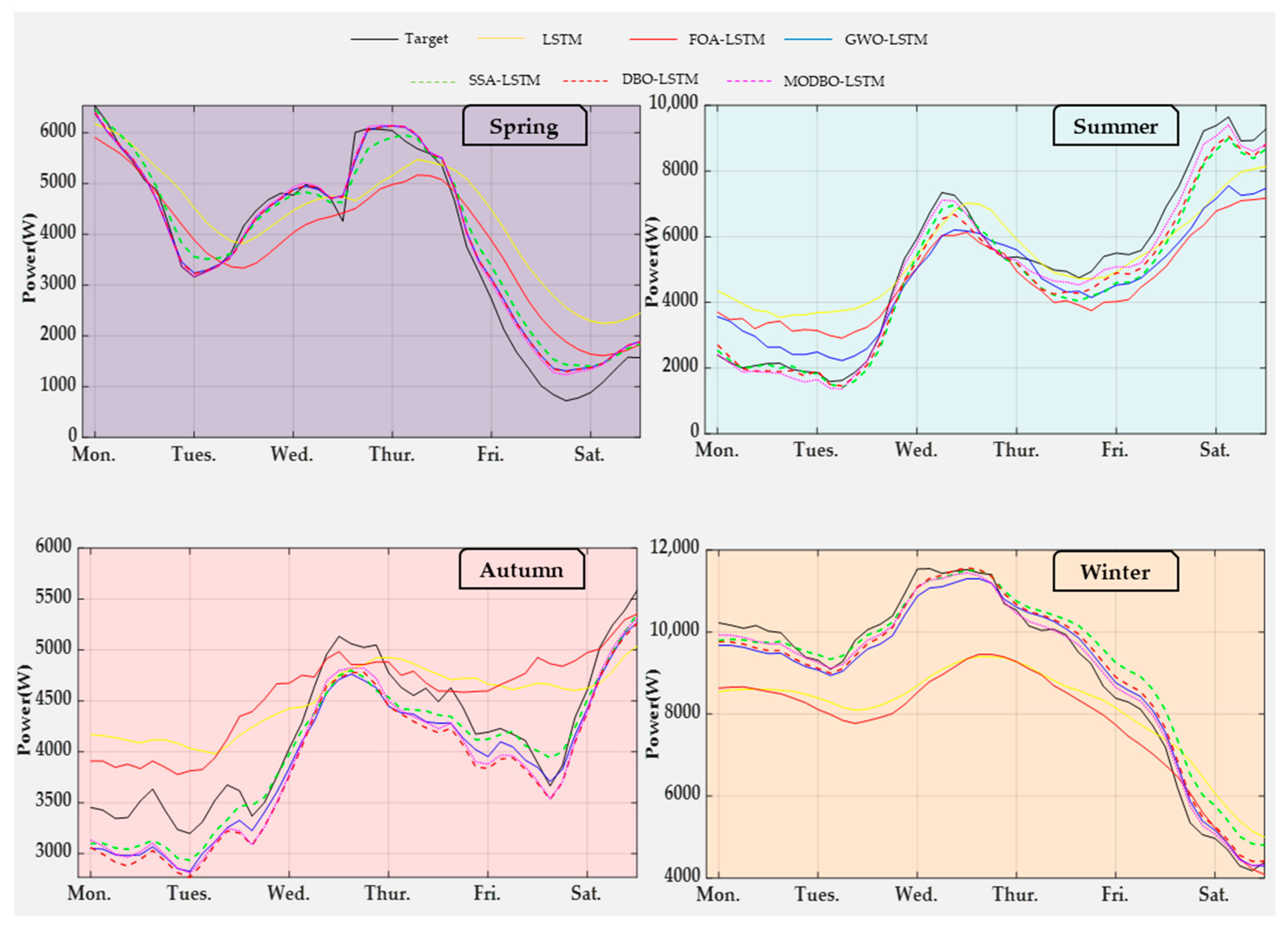
5.4.3. Comparison of Four-Season Load-Forecasting Models without Weather
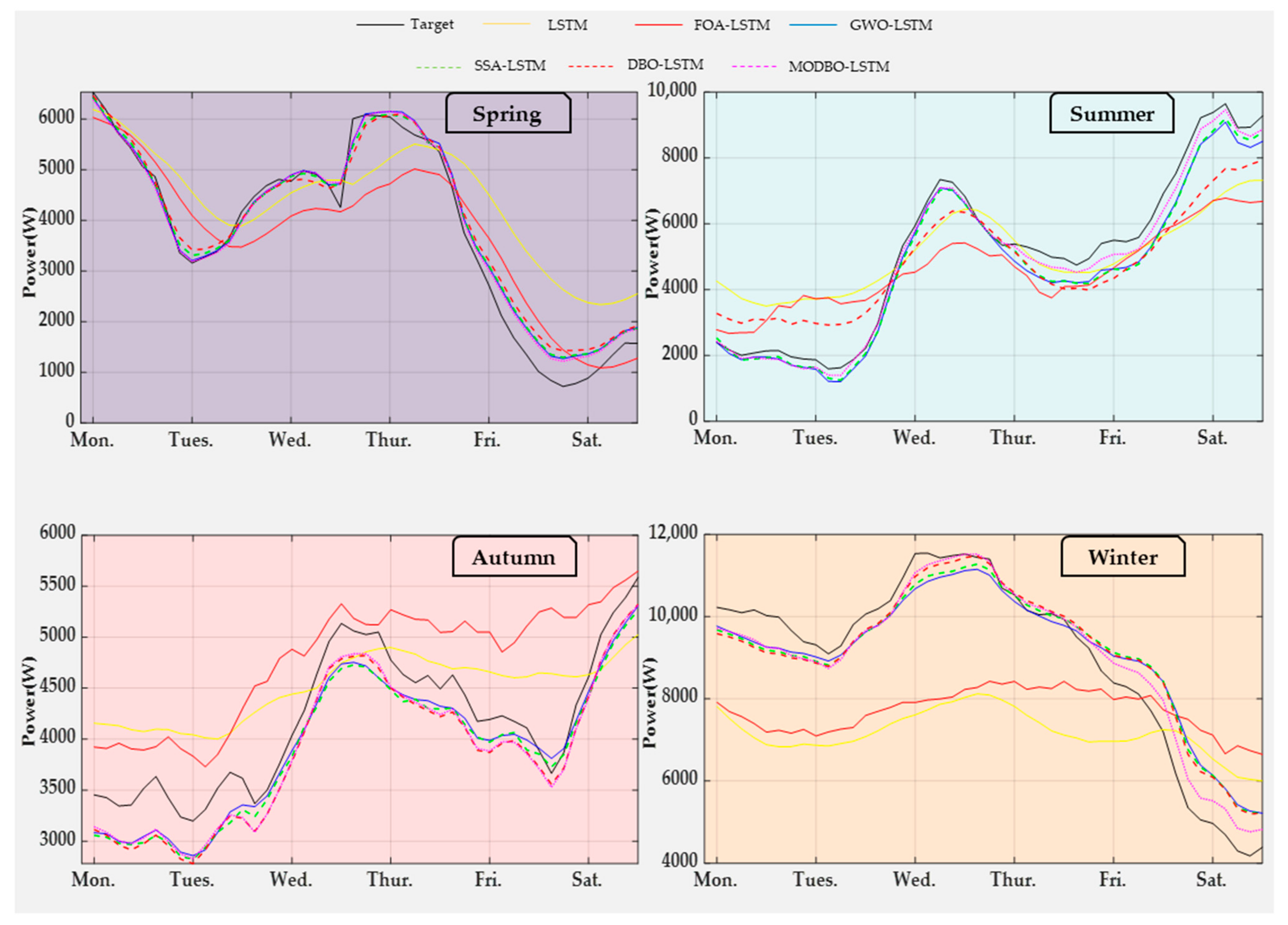
5.4.4. Comparison of Four-Season Load Forecasting Models with Weather
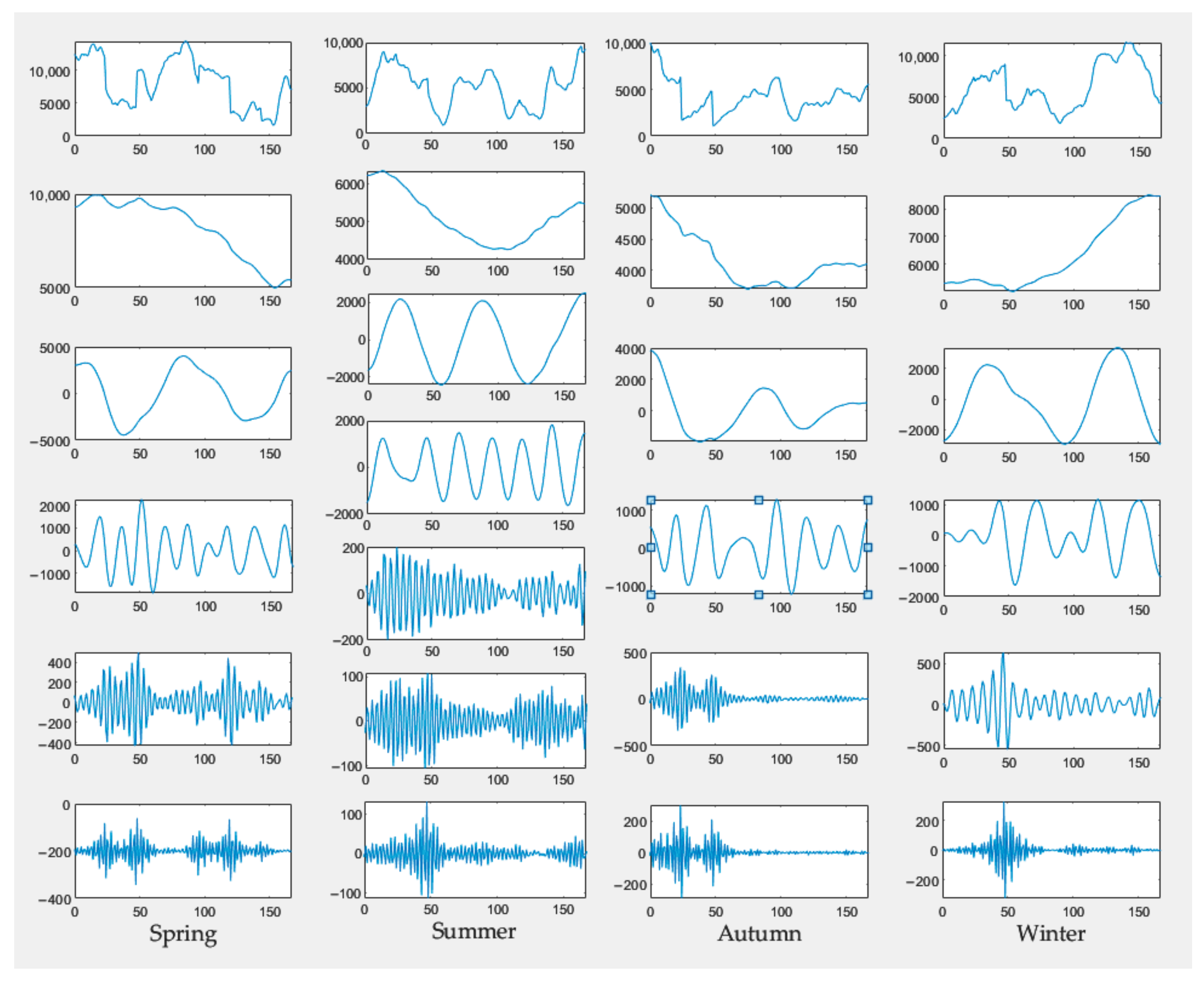
5.4.5. Comparison of Different Signal Decomposition Algorithms
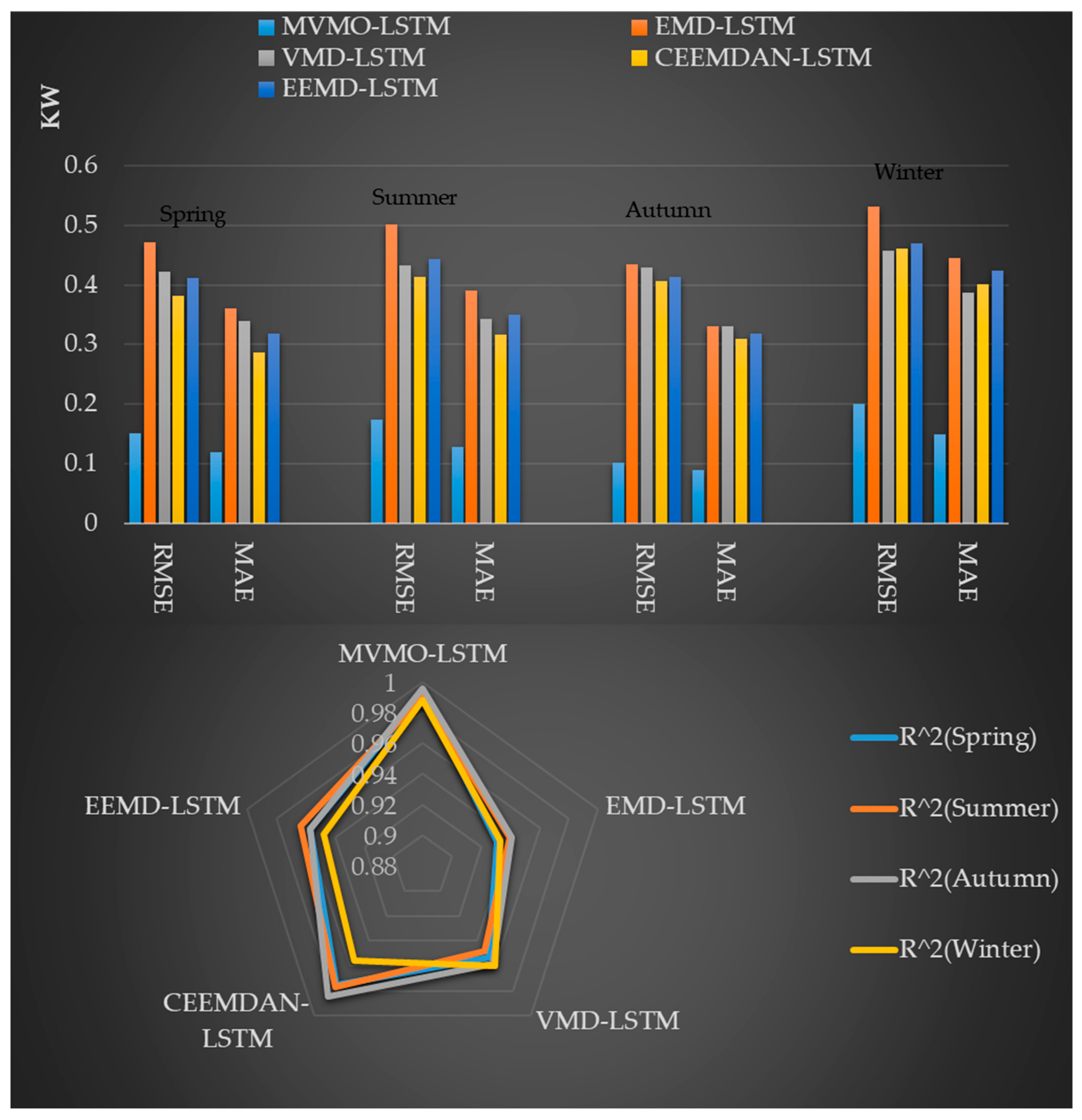
- (1)
- Based on Figure 9 and Table 4, it can be concluded that the efficiency of the proposed hybrid prediction system is better than the LSTM model based on signal decomposition such as VMD, and the mean values of the evaluation metrics are RMSE = 0.1564 KW, MAE = 0.1216 KW, and R2 = 99.20%, respectively. In addition, the model metrics with VMD were superior to the other four hybrid models as far as winter is concerned. The evaluation metrics were RMSE = 0.4572 KW, MAE = 0.3871 KW and R2 = 96.02%.
- (2)
- In addition, the CEEMDAN-LSTM outperforms the other three hybrid models in all three seasons: spring, summer and fall. The average RMSE of the three seasons = 0.4012 KW. MAE = 0.3045 KW. R2 = 97.89%. Due to the multi-strategy optimization of the dung beetle algorithm used in this study, the k-value of the VMD as well as the penalty factor were optimized. In addition to this, the parameters of LSTM are optimized. As for the MVMO-LSTM, this hybrid model is optimal in various experimental comparisons for various performance metrics. Thus, the proposed prediction model in this study provides better potential.
6. Conclusions
- (1)
- The model proposed in this study achieves significant accuracy in power load forecasting.
- (2)
- The predictions of this hybrid model are more robust and efficient than a single model or a model with only one fusion algorithm.
- (3)
- A hybrid MODBO-VMD-MODBO-LSTM model is proposed, and previous studies need to reset the decomposition number when the center frequency domain is determined, and they seldom explore the penalty factor and decomposition layer values. This multi-strategy improved dung beetle algorithm not only optimizes the penalty factor and decomposition layer values of VMD but also optimizes the optimal number of hidden units, the optimal maximum training period and the optimal initial learning rate of LSTM. The combination of these two improvements can effectively help LSTM learn and adapt to the complexity and seasonal changes of power load data, thus improving the prediction accuracy and making the prediction results more reliable and practical.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Yao, J.; Xue, G. Load prediction of integrated energy system based on MMoE multi-task learning and long short-term memory network. Electr. Power Autom. Equip. 2022, 42, 78–87. [Google Scholar]
- Eren, Y.; Küçükdemiral, İ. A comprehensive review on deep learning approaches for short-term load forecasting. Renew. Sustain. Energy Rev. 2024, 189, 114031. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, L.; Zhang, P.; Yan, Q.; Shi, H. Data Characteristics and Short-term Forecasting of Regional Power Load. Dianwang Jishu/Power Syst. Technol. 2022, 46, 1092–1099. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, N.; Chen, W.; Zhang, H.; Guo, B.; Shen, J.; Tian, Z. Multi-step ahead forecasting for electric power load using an ensemble model. Expert Syst. Appl. 2023, 211, 118649. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A power prediction method for photovoltaic power plant based on wavelet decomposition and artificial neural networks. Energies 2015, 9, 11. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Wang, Y.; Jiang, P. The study and application of a novel hybrid forecasting model—A case study of wind speed forecasting in China. Appl. Energy 2015, 143, 472–488. [Google Scholar] [CrossRef]
- Prasad, R.; Ali, M.; Kwan, P.; Khan, H. Designing a multi-stage multivariate empirical mode decomposition coupled with ant colony optimization and random forest model to forecast monthly solar radiation. Appl. Energy 2019, 236, 778–792. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A novel empirical mode decomposition with support vector regression for wind speed forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2014, 27, 1793–1798. [Google Scholar] [CrossRef]
- Lin, G.; Lin, A.; Cao, J. Multidimensional KNN algorithm based on EEMD and complexity measures in financial time series forecasting. Expert Syst. Appl. 2021, 168, 114443. [Google Scholar] [CrossRef]
- Ostertagova, E.; Ostertag, O. Forecasting using simple exponential smoothing method. Acta Electrotech. Et Inform. 2012, 12, 62. [Google Scholar] [CrossRef]
- Rizwan, M.; Alharbi, Y.R. Artificial Intelligence Based Approach for Short Term Load Forecasting for Selected Feeders at Madina Saudi Arabia. Int. J. Electr. Electron. Eng. Telecommun. 2021, 10, 300–306. [Google Scholar] [CrossRef]
- Xin, A.; Zhiyu, Z.; Yanping, W.; Hongzhi, Z. Bidding strategy for time-shiftable loads based on autoregressive integrated moving average model. Autom. Electr. Power Syst. 2017, 41, 26–31. [Google Scholar]
- Mahmud, A. Isolated area load forecasting using linear regression analysis: Practical approach. Energy Power Eng. 2011, 3, 547–550. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Y.; Chang, D.; Xie, J.; Ma, Z.; Sun, Q.; Yin, H.; Wennersten, R. Prediction of short-term PV power output and uncertainty analysis. Appl. Energy 2018, 228, 700–711. [Google Scholar] [CrossRef]
- Abumohsen, M.; Owda, A.Y.; Owda, M. Electrical Load Forecasting Based on Random Forest, XGBoost, and Linear Regression Algorithms. In Proceedings of the 2023 International Conference on Information Technology (ICIT), Orlando FL, USA, 4–6 April 2023; pp. 25–31. [Google Scholar]
- Kong, X.; Zheng, F.; Zhijun, E.; Cao, J.; Wang, X. Short-term load forecasting based on deep belief network. Autom. Electr. Power Syst. 2018, 42, 133–139. [Google Scholar]
- Dai, Y.; Zhao, P. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Naz, A.; Javaid, N.; Khalid, A.; Shoaib, M.; Imran, M. Electric Load Forecasting using EEMD and Machine Learning Techniques. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 2124–2127. [Google Scholar]
- Huang, Y.; Hasan, N.; Deng, C.; Bao, Y. Multivariate empirical mode decomposition based hybrid model for day-ahead peak load forecasting. Energy 2022, 239, 122245. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Elouaham, S.; Nassiri, B.; Dliou, A.; Zougagh, H.; El Kamoun, N.; El Khadiri, K.; Said, S. Combination time-frequency and empirical wavelet transform methods for removal of composite noise in EMG signals. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2023, 21, 1373–1381. [Google Scholar] [CrossRef]
- Cai, C.; Li, Y.; Su, Z.; Zhu, T.; He, Y. Short-Term Electrical Load Forecasting Based on VMD and GRU-TCN Hybrid Network. Appl. Sci. 2022, 12, 6647. [Google Scholar] [CrossRef]
- Ge, Q.; Jiang, H.; He, M.; Zhu, Y.; Zhang, J. Power load forecast based on fuzzy BP neural networks with dynamical estimation of weights. Int. J. Fuzzy Syst. 2020, 22, 956–969. [Google Scholar] [CrossRef]
- Yuan, C.; Niu, D.; Li, C.; Sun, L.; Xu, L. Electricity consumption prediction model based on Bayesian regularized bp neural network. In Cyber Security Intelligence and Analytics; Springer: Cham, Switzerland, 2020; pp. 528–535. [Google Scholar]
- Khashei, M.; Chahkoutahi, F. Electricity demand forecasting using fuzzy hybrid intelligence-based seasonal models. J. Model. Manag. 2022, 17, 154–176. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Ma, Q.; Zhang, C.; Li, R.; Li, F. A whole system assessment of novel deep learning approach on short-term load forecasting. Energy Procedia 2017, 142, 2791–2796. [Google Scholar] [CrossRef]
- Muzaffar, S.; Afshari, A. Short-term load forecasts using LSTM networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zheng, X.; Chen, Z.; Jin, T. A reliable short-term power load forecasting method based on VMD-IWOA-LSTM algorithm. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 1121–1132. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Li, W.; Quan, C.; Wang, X.; Zhang, S. Short-Term Power Load Forecasting Based on a Combination of VMD and ELM. Pol. J. Environ. Stud. 2018, 27, 2143–2154. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- ur Rehman, N.; Aftab, H. Multivariate variational mode decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Sheng, Z.; An, Z.; Wang, H.; Chen, G.; Tian, K. Residual LSTM based short-term load forecasting. Appl. Soft Comput. 2023, 144, 110461. [Google Scholar] [CrossRef]
- Liu, S.; Kong, Z.; Huang, T.; Du, Y.; Xiang, W. An ADMM-LSTM framework for short-term load forecasting. Neural Netw. 2024, 173, 106150. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Li, Y.; Sun, K.; Yao, Q.; Wang, L. A dual-optimization wind speed forecasting model based on deep learning and improved dung beetle optimization algorithm. Energy 2024, 286, 129604. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2024, 236, 121219. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.-B.; Tang, M.-Z.; Xu, M.; Cai, S.-H. Grey Wolf Optimizer Algorithm Based on Lens Imaging Learning Strategy. Zidonghua Xuebao/Acta Autom. Sin. 2020, 46, 2148–2164. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- El Khadiri, K.; Elouaham, S.; Nassiri, B.; El Melhaoui, O.; Said, S.; El Kamoun, N.; Zougagh, H. A Comparison of the Denoising Performance Using Capon Time-Frequency and Empirical Wavelet Transform Applied on Biomedical Signal. Int. J. Eng. Appl. 2023, 11, 358. [Google Scholar] [CrossRef]
- Liu, L.; Guo, K.; Chen, J.; Guo, L.; Ke, C.; Liang, J.; He, D. A Photovoltaic Power Prediction Approach Based on Data Decomposition and Stacked Deep Learning Model. Electronics 2023, 12, 2764. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]

| Season | K (MODBO) | (MODBO) | K | |
|---|---|---|---|---|
| Spring | 11 | 292 | 5 | 2000 |
| Summer | 10 | 100 | 6 | 2000 |
| Autumn | 8 | 223 | 5 | 2000 |
| Winter | 8 | 110 | 5 | 2000 |
| Model | Spring | Summer | Autumn | Winter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | |
| MVMO- LSTM | 0.2448 | 0.1899 | 0.991 | 0.2596 | 0.2238 | 0.996 | 0.2935 | 0.2832 | 0.991 | 0.2140 | 0.1810 | 0.993 |
| LSTM | 1.0860 | 0.8909 | 0.806 | 1.2886 | 1.0724 | 0.883 | 0.5294 | 0.4682 | 0.789 | 1.4795 | 1.3237 | 0.911 |
| FOA-LSTM | 0.7702 | 0.6614 | 0.847 | 1.3927 | 1.2455 | 0.895 | 0.5212 | 0.4222 | 0.797 | 1.5234 | 1.3238 | 0.910 |
| GWO-LSTM | 0.2696 | 0.2087 | 0.985 | 0.5308 | 0.4506 | 0.983 | 0.3013 | 0.2755 | 0.986 | 0.3688 | 0.3367 | 0.977 |
| SSA-LSTM | 0.2776 | 0.2159 | 0.981 | 0.5172 | 0.4299 | 0.986 | 0.2467 | 0.2156 | 0.988 | 0.5416 | 0.4342 | 0.971 |
| DBO-LSTM | 0.2819 | 0.2183 | 0.980 | 0.7232 | 0.4382 | 0.937 | 0.3126 | 0.2978 | 0.984 | 0.3545 | 0.3157 | 0.978 |
| Model | Spring | Summer | Autumn | Winter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | |
| MVMO- LSTM | 0.2582 | 0.2013 | 0.988 | 0.2785 | 0.2409 | 0.993 | 0.3026 | 0.2914 | 0.990 | 0.4607 | 0.3977 | 0.983 |
| LSTM | 1.1098 | 0.9024 | 0.794 | 1.2886 | 1.0724 | 0.883 | 0.5338 | 0.4738 | 0.775 | 2.5911 | 2.4433 | 0.637 |
| FOA-LSTM | 0.8111 | 0.6895 | 0.833 | 1.5098 | 1.3224 | 0.883 | 0.6940 | 0.6007 | 0.757 | 2.3165 | 2.1342 | 0.701 |
| GWO-LSTM | 0.2904 | 0.2250 | 0.979 | 1.0904 | 0.9146 | 0.943 | 0.3816 | 0.2546 | 0.979 | 0.7142 | 0.5931 | 0.956 |
| SSA-LSTM | 0.3927 | 0.3159 | 0.971 | 0.5899 | 0.4781 | 0.980 | 0.3194 | 0.2934 | 0.985 | 0.7074 | 0.5911 | 0.958 |
| DBO-LSTM | 0.3462 | 0.2738 | 0.975 | 0.5156 | 0.4382 | 0.989 | 0.3457 | 0.3323 | 0.981 | 0.6812 | 0.5638 | 0.961 |
| Model | Spring | Summer | Autumn | Winter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | |
| MVMO- LSTM | 0.1502 | 0.1192 | 0.9932 | 0.1732 | 0.1289 | 0.9907 | 0.1013 | 0.0893 | 0.9955 | 0.2008 | 0.1488 | 0.9879 |
| EMD- LSTM | 0.4724 | 0.3615 | 0.9311 | 0.5024 | 0.3915 | 0.9393 | 0.4354 | 0.3315 | 0.9406 | 0.5324 | 0.4447 | 0.9328 |
| VMD- LSTM | 0.4230 | 0.3393 | 0.9532 | 0.4328 | 0.3422 | 0.9482 | 0.4302 | 0.3306 | 0.9582 | 0.4572 | 0.3871 | 0.9602 |
| CEEMDAN-LSTM | 0.3827 | 0.2868 | 0.9752 | 0.4137 | 0.3163 | 0.9772 | 0.4073 | 0.3103 | 0.9843 | 0.4617 | 0.4016 | 0.9561 |
| EEMD-LSTM | 0.4109 | 0.3190 | 0.9572 | 0.4435 | 0.3493 | 0.9637 | 0.4144 | 0.3190 | 0.9573 | 0.4704 | 0.4245 | 0.9477 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Liu, L.; Guo, K.; Liu, S.; He, D. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Appl. Sci. 2024, 14, 5966. https://doi.org/10.3390/app14145966
Chen J, Liu L, Guo K, Liu S, He D. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Applied Sciences. 2024; 14(14):5966. https://doi.org/10.3390/app14145966
Chicago/Turabian StyleChen, Jiayu, Lisang Liu, Kaiqi Guo, Shurui Liu, and Dongwei He. 2024. "Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models" Applied Sciences 14, no. 14: 5966. https://doi.org/10.3390/app14145966
APA StyleChen, J., Liu, L., Guo, K., Liu, S., & He, D. (2024). Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Applied Sciences, 14(14), 5966. https://doi.org/10.3390/app14145966






