A Galerkin Finite Element Method for the Reconstruction of a Time-Dependent Convection Coefficient and Source in a 1D Model of Magnetohydrodynamics
Abstract
1. Introduction
2. The Direct and Inverse Problems
3. Reduction of the Inverse Problem to a Non-Classical Forward Problem
3.1. Reducing the Inverse Problem to a Direct One
3.2. Variational Formulation
4. Continuous Galerkin Approximation
5. Numerical Method
5.1. FEM Solution of the Direct Problem
5.2. Numerical Solution of the Inverse Problem
| Algorithm 1: Solving the inverse problem |
|
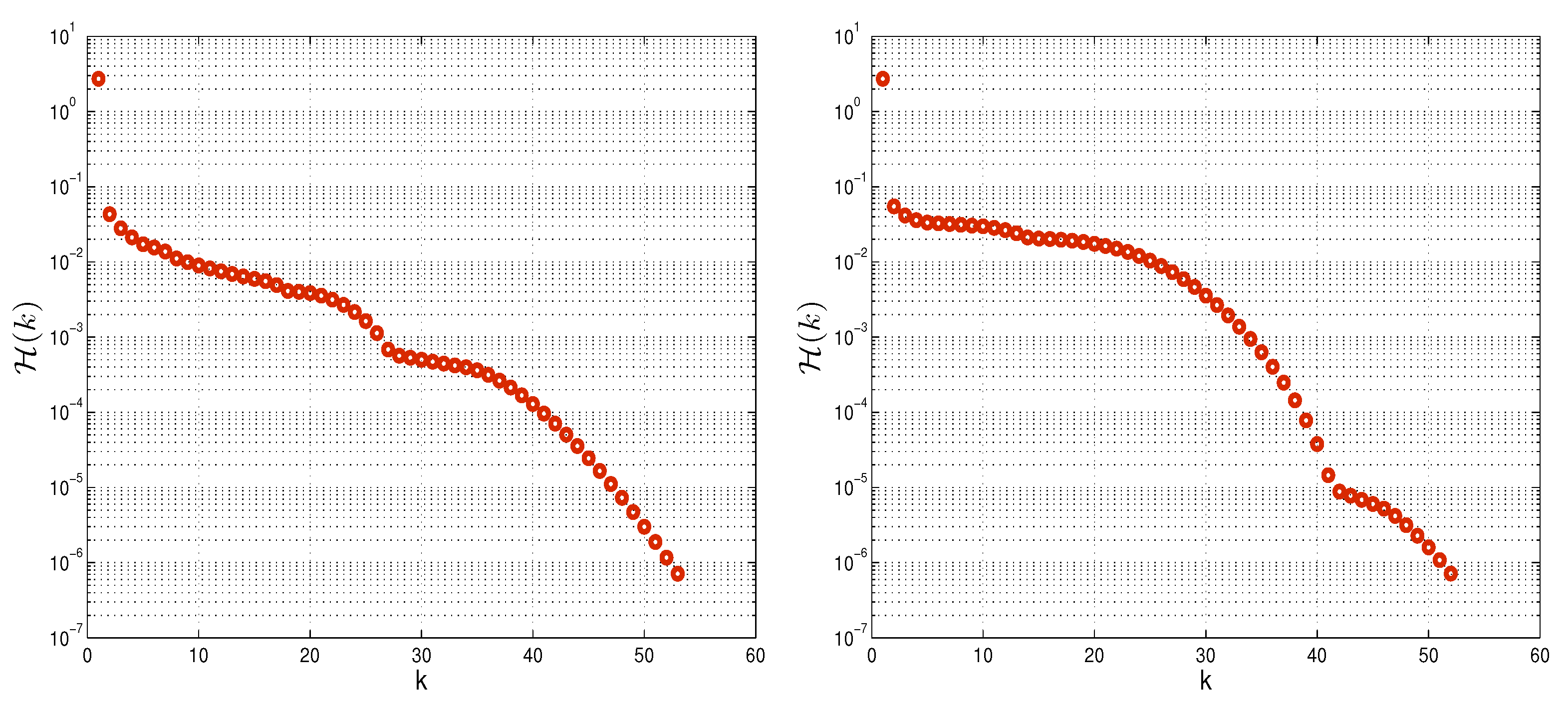
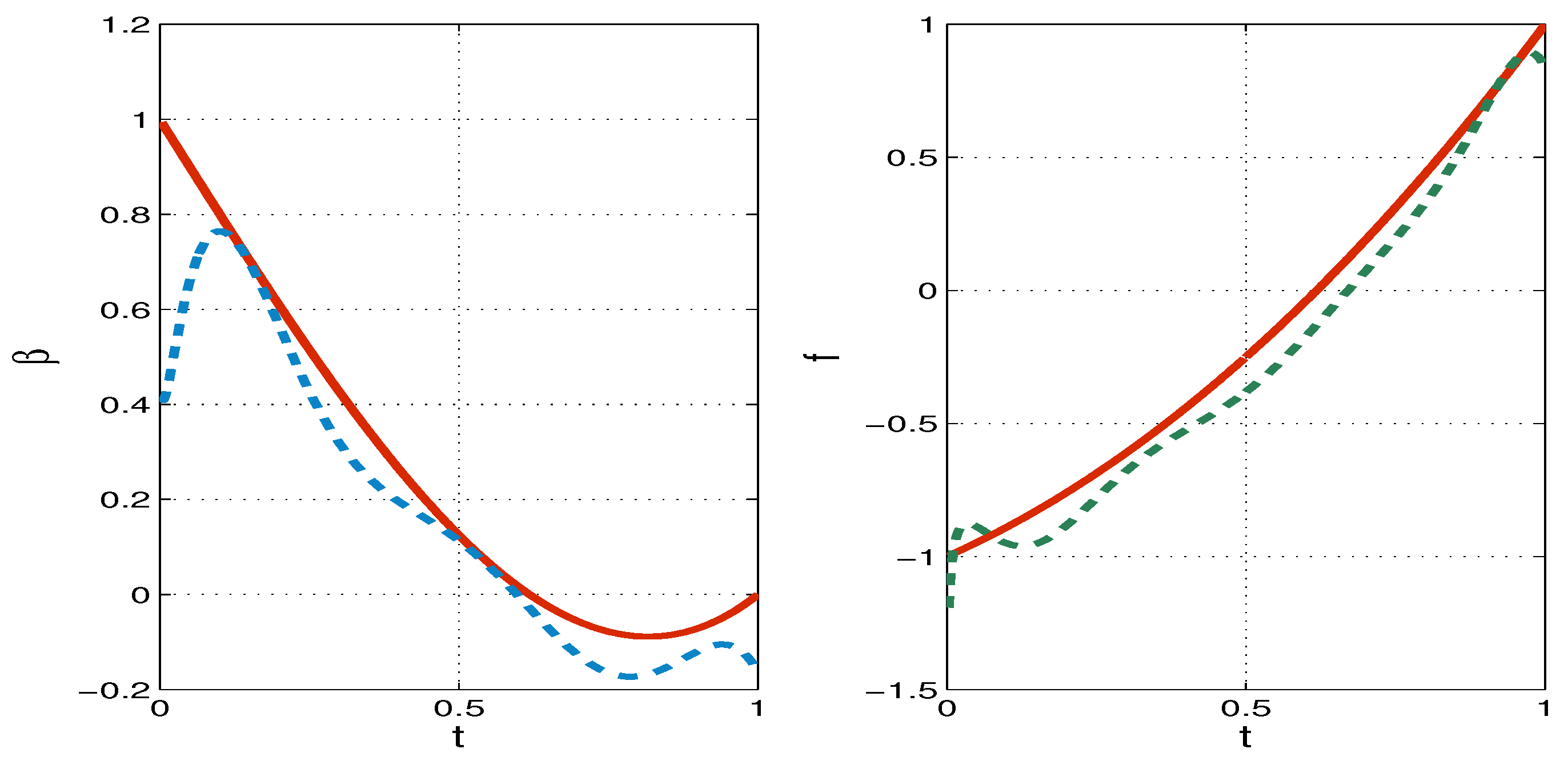
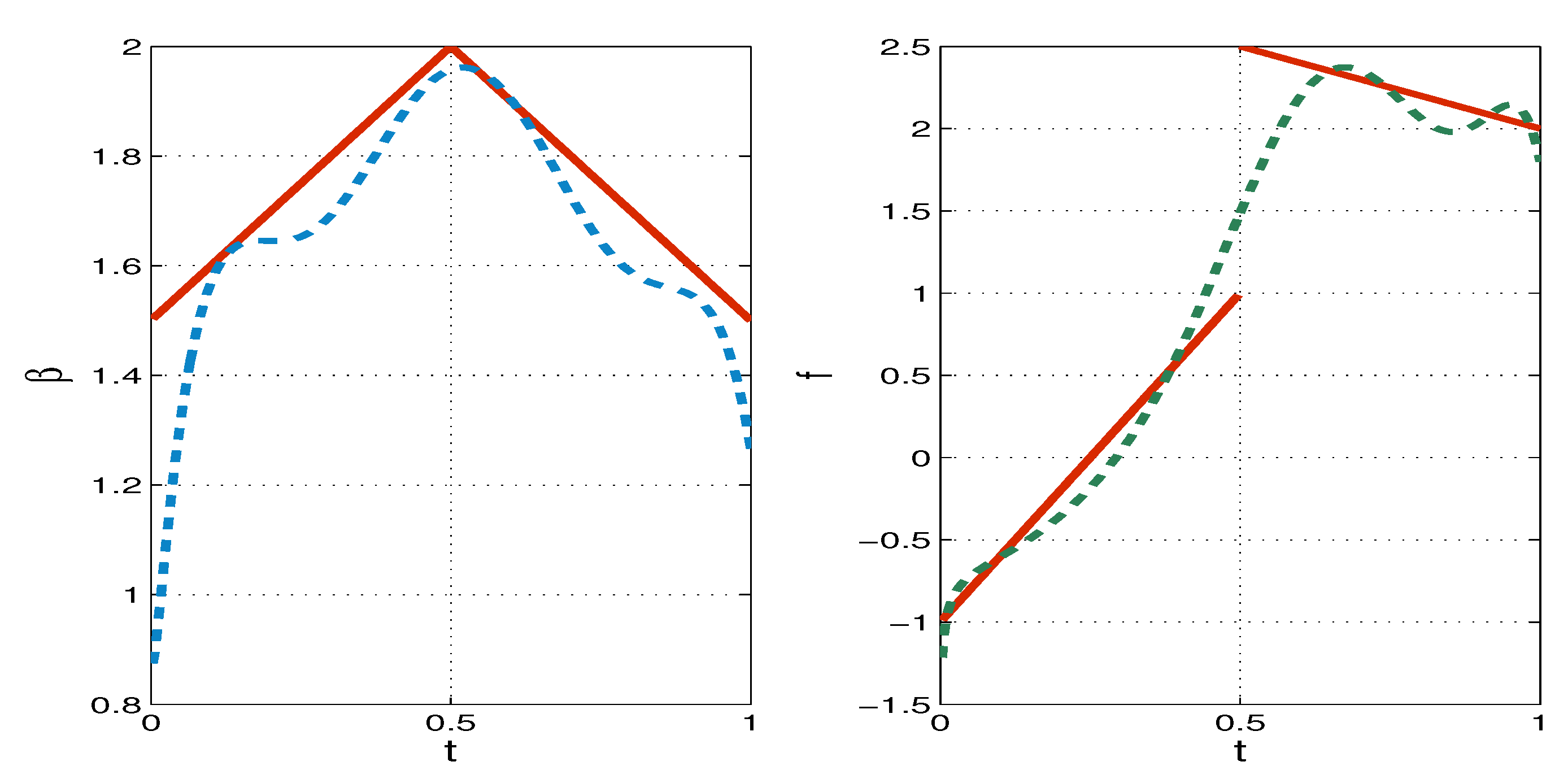
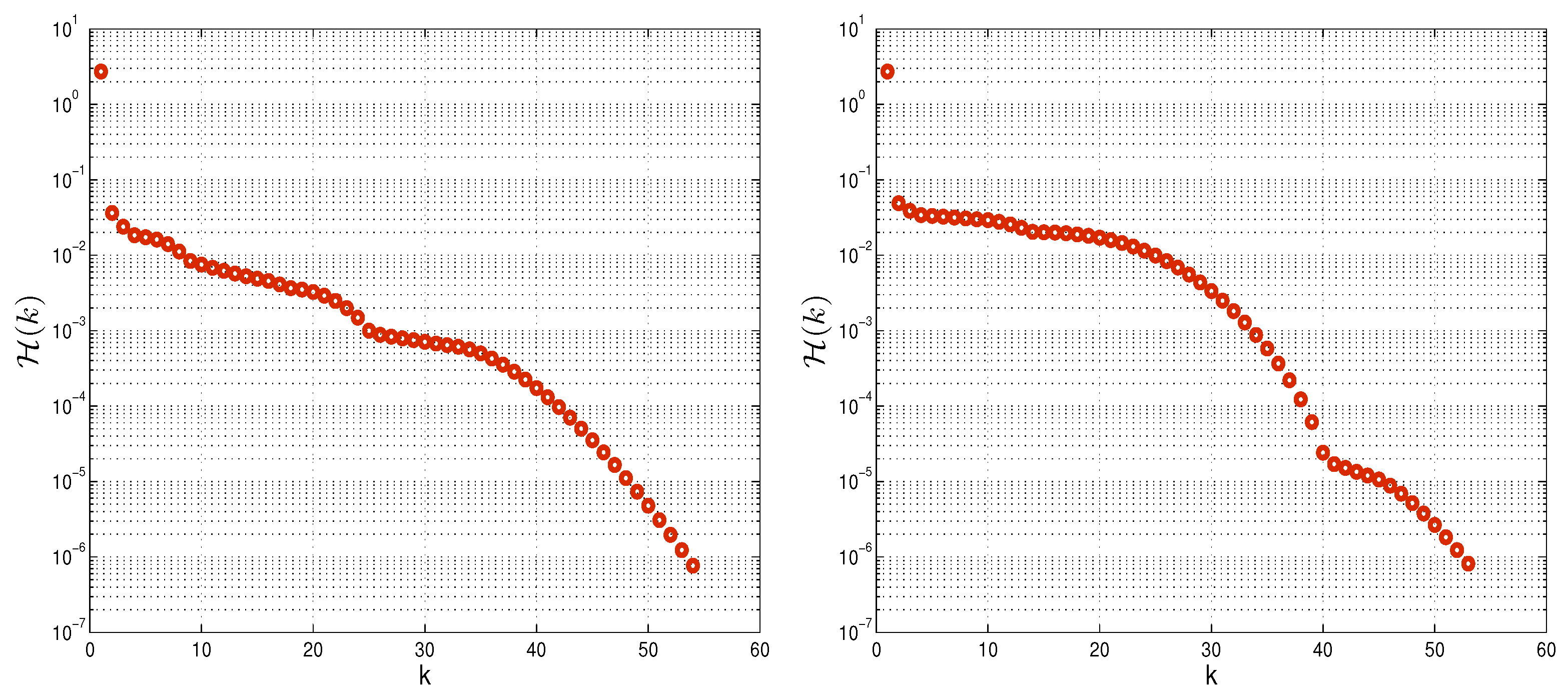
6. Numerical Tests
7. Conclusions
- We transform the inverse problem to a non-classical system of parabolic equations, which involve the boundary values of the solution in the differential operators.
- We show the equivalence of the obtained forward problem with the inverse problem.
- Applying the Galerkin approximation, we prove the well-posedness of the non-classical forward problem.
- An iteration algorithm, based on the FEM method, is developed for numerical solution of the inverse problems.
- The iteration process is convergent for a moderate number of iterations.
- The reconstruction of the source and convection coefficients is successful in the case when they are smooth functions, as well as for non-smooth and discontinuous functions.
- For noise-free data, the order of convergence of the numerical solution of the inverse problem is first in time and second in space.
- For the noisy measurements, the adjustment of the convection coefficient and source is accurate enough to obtain optimal precision of the numerical solutions U and b.
- The method is not limited with respect to the size of the convergence range of the initial data.
- The proposed numerical approach can also be applied in the case when the integral measurements are in the spatial subinterval.
- Galerkin approximation method, developed in this work, can be expanded to the case of the second and third kind of boundary conditions [34].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, Y. Unconditional convergence of the Euler semi-implicit scheme for the threedimensional incompressible MHD equations. IMA J. Numer. Anal. 2015, 33, 767–801. [Google Scholar] [CrossRef]
- Landav, L.D.; Bell, J.; Kearsley, M.; Pitaevski, L.; Lifshitz, E.; Sykes, J. Electrodynamics of Continuous Media; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ren, Z.; Guo, S.; Li, Z.; Wu, Z. Adjoint-based parameter and state estimation in 1-D magnetohydrodynamics (MHD) flow system. J. Optim. Manag. Optim. 2018, 14, 1579–1594. [Google Scholar] [CrossRef]
- Tsyba, V.; Chibatorev, A.Y. Optimal control asymptotics of a magnetohydrodynamic flow. Comp. Math. Math. Phys. 2009, 49, 466–473. [Google Scholar] [CrossRef]
- Yu, P.X.; Tian, Z.F. Comparison of the simplified and full MHD models for laminar incompressible flow past a circular cylinder. Appl. Math. Model. 2017, 41, 143–163. [Google Scholar] [CrossRef]
- Barnothy, M.F. Biological Effects of Magnetic Fields; Springer Science +Business Media, LLC: Berlin/Heidelberg, Germany, 1964. [Google Scholar]
- Yamagishi, A. Biological systems in high magnetic field. J. Magn. Arid. Magn. Mater. 1990, 90–91, 43–46. [Google Scholar] [CrossRef]
- Misra, J.; Sinha, A.; Shit, G. A numerical model for the magnetohydrodynamic flow of blood in a porous channel. J. Mech. Med. Biol. 2011, 11, 547–562. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.A.; Maskaniyan, M. Applications of magnetohydrodynamics in biological systems-a review on the numerical studies. J. Magn. Magn. Mater. 2017, 439, 358–372. [Google Scholar] [CrossRef]
- Ma, M.; Lin, B.-L.; Chen, C.; Horiguchi, F.; Eriguchi, T.; Li, Y.; Wang, X. A 3D-hydrodynamic model for predicting the environmental fate of chemical pollutants in Xiamen Bay, southeast China. Environ. Pollut. 2020, 256, 113000. [Google Scholar] [CrossRef] [PubMed]
- Bátkai, A.; Csomós, P.; Faragó, I.; Horányi, A.; Szépszé, G. Mathematical Problems in Meteorological Modelling, 1st ed.; Series Mathematics in Industry; Springer: Cham, Switzerland, 2016; 264p. [Google Scholar]
- Prusov, V.A.; Doroshenko, A.Y. Hydrodynamic modeling of industrial pollutants spreading in atmosphere. In Mathematical Problems in Meteorological Modelling Conference Proceedings; Bátkai, A., Csomós, P., Faragó, I., Horányi, A., Szépszó, G., Eds.; Springer: Cham, Switzerland, 2016; Volume 24, pp. 87–116. [Google Scholar]
- Mirparizi, M.; Zhang, C.; Amiri, M.J. One-dimensional electro-magneto-poro-thermoelastic wave propagation in a functionally graded medium with energy dissipation. Phys. Scr. 2022, 97, 045203. [Google Scholar] [CrossRef]
- Mirparizi, M.; Shariyat, M.; Fotuhi, A.R. A novel approach for generalized Green-Naghdi-type electro-magneto-thermo-hyperelasticity wave propagation and reflection investigations in near-incompressible layers under shock loads. J. Therm. Stress. 2024, 47, 743–765. [Google Scholar] [CrossRef]
- Kandilarov, J.; Vulkov, L. Simultaneous numerical reconstruction of time-dependent convection coefficient and source in magnetohydrodynamics flow system. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Khankishiyev, Z.F. Solution of one problem for linear loaded parabolic type differential equation with integral conditions. Adv. Math. Model. Appl. 2022, 7, 178–190. [Google Scholar]
- Ashyralyev, A.; Emharab, F. A note on the time identification nonlocal problem. Adv. Math. Model. Appl. 2022, 7, 105–120. [Google Scholar]
- Cai, K.; Lesnic, D. Determination of time-dependent effective ion collision frequency from an integral observation. J. Inverse Ill-Posed Probl. 2024. [Google Scholar] [CrossRef]
- Georgiev, S.G. Numerical and analytical computation of the implied volatility from option price measurementsunder regime-switching. AIP Proc. 2019, 2172, 070007. [Google Scholar]
- Ashyralyev, A.; Sazaklioglu, A.U. Integration of a time-dependent source identification inverse problem with integral overdetermination. Numer. Funct. Anal. Optim. 2017, 38, 1276–1294. [Google Scholar] [CrossRef]
- Glotov, D.; Hames, W.E.; Meir, A.J.; Ngoma, S. An inverse diffusion coefficient problem for aparabolic equation with integral constraint. Int. J. Numer. Anal. Model. 2018, 15, 552–563. [Google Scholar]
- Hasanov, A.H.; Romanov, V.G. Introduction to Inverse Problems for Differential Equations, 1st ed.; Springer: Cham, Switzerland, 2017; 261p. [Google Scholar]
- Isakov, V. Inverse Problems for Partial Differential Equations, 3rd ed.; Springer: Cham, Switzerland, 2017; p. 406. [Google Scholar]
- Kabanikhin, S.I. Inverse and Ill-Posed Problems; DeGruyer: Berlin, Germany, 2011. [Google Scholar]
- Lesnic, D. Inverse Problems with Applications in Science and Engineering; CRC Press: Abingdon, UK, 2021; p. 349. [Google Scholar]
- Prilepko, A.I.; Orlovsky, D.G.; Vasin, I.A. Methods for Solving Inverse Problems in Mathematical Physics; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Samarskii, A.A.; Vabishchevich, P.N. Numerical Methods for Solving Inverse Problems in Mathematical Physics; de Gruyter: Berlin, Germany, 2007; 438p. [Google Scholar]
- Vabishchevich, P.N.; Klibanov, M.V. Numerical identification of the leading coefficient of a parabolic equation. Diff. Equ. 2016, 52, 855–862. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations, 2nd ed.; Graduate Studies in Mathematics 19; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Ladyženskaja, O.A.; Solonnikov, V.A.; Ural’ceva, N.N. Linear and Quasi-Linear Equations of Parabolic Type; Translations of Mathematical Monographs 23; American Mathematical Society: Providence, RI, USA, 1988; 648p. [Google Scholar]
- Borzi, A. Modelling with Ordinarty Differential Equations, A Comprehensive Approach; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Larsson, S.; Thomée, V. Partial Differential Equations with Numerical Methods; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Thomée, V. Galerkin Finite Element Methods for Parabolic Problems, 2nd ed.; Ser. Comput. Math. 25; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Faragó, I.; Korotov, S.; Neittaanmäki, P. Galerkin approximations for the linear parabolic equation with the third boundary condition. Appl. Math. 2003, 48, 111–128. [Google Scholar] [CrossRef][Green Version]
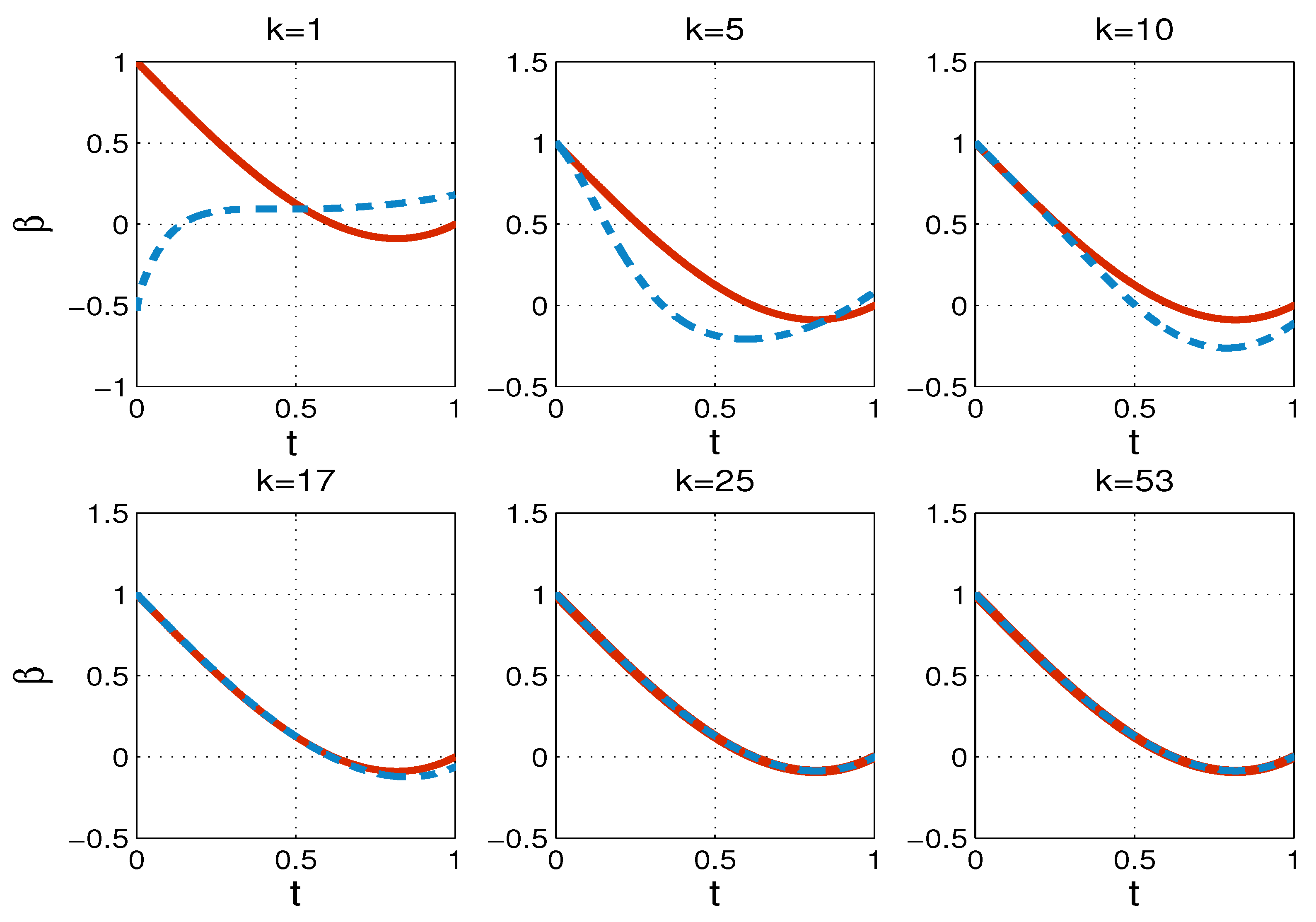
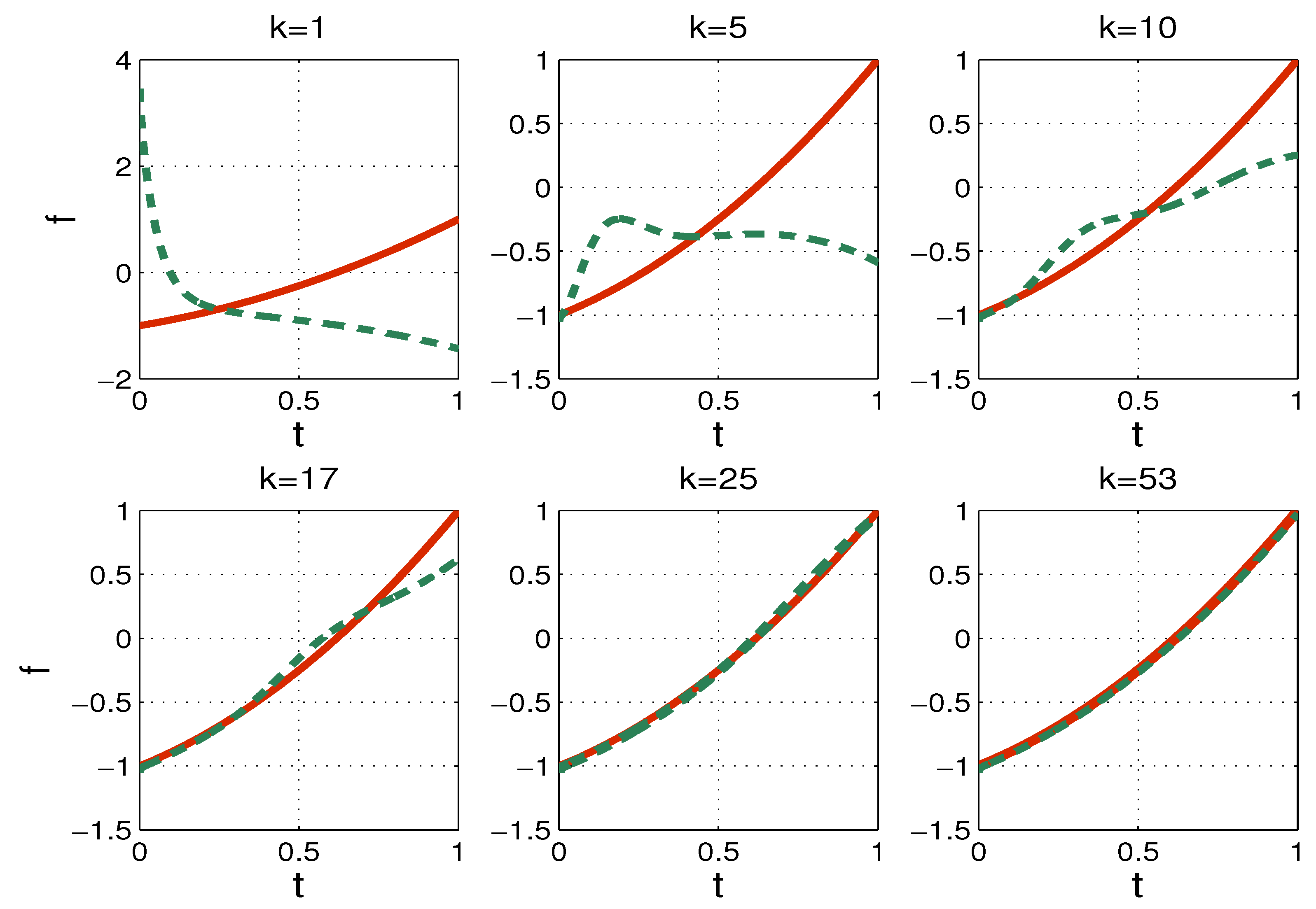
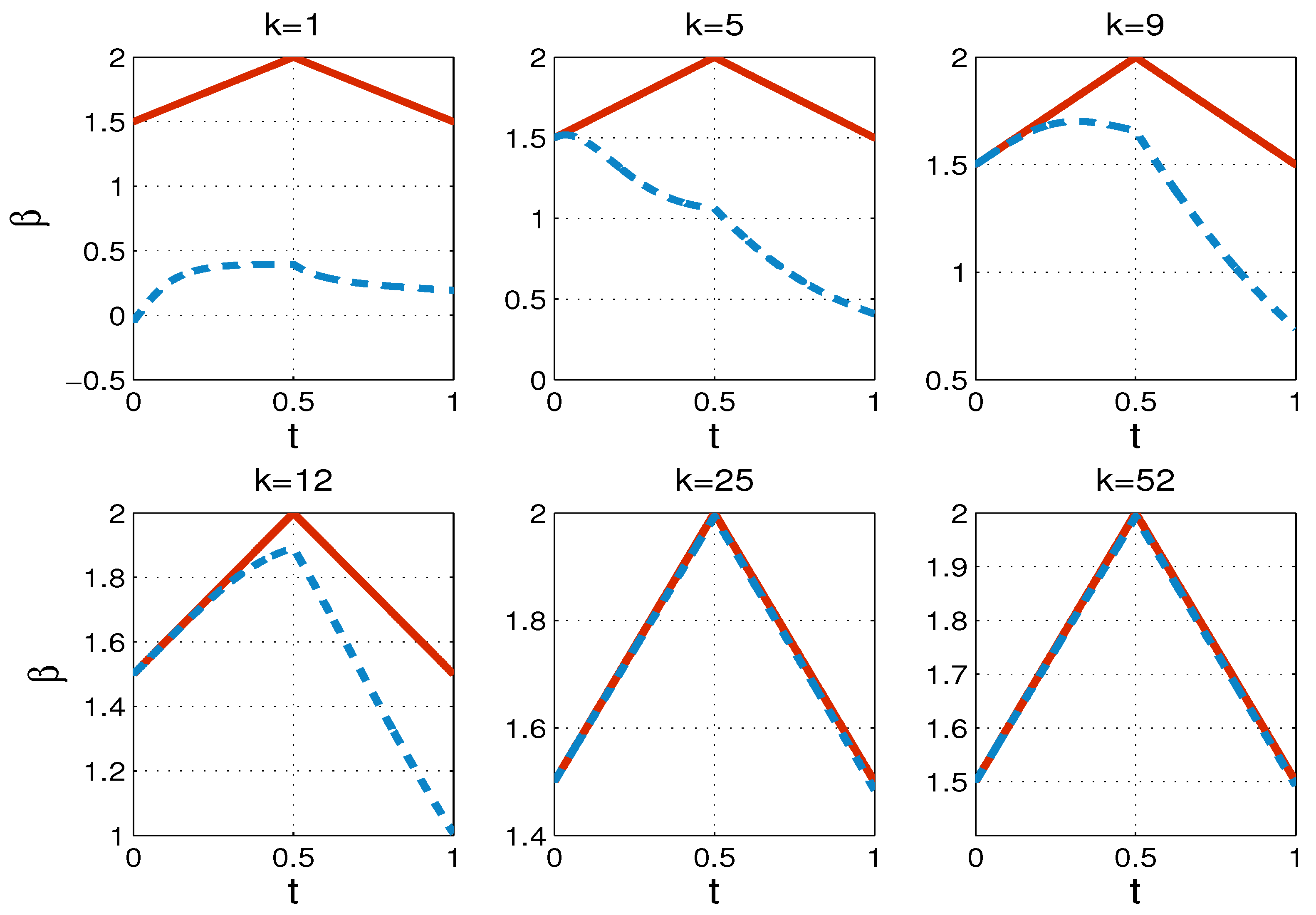
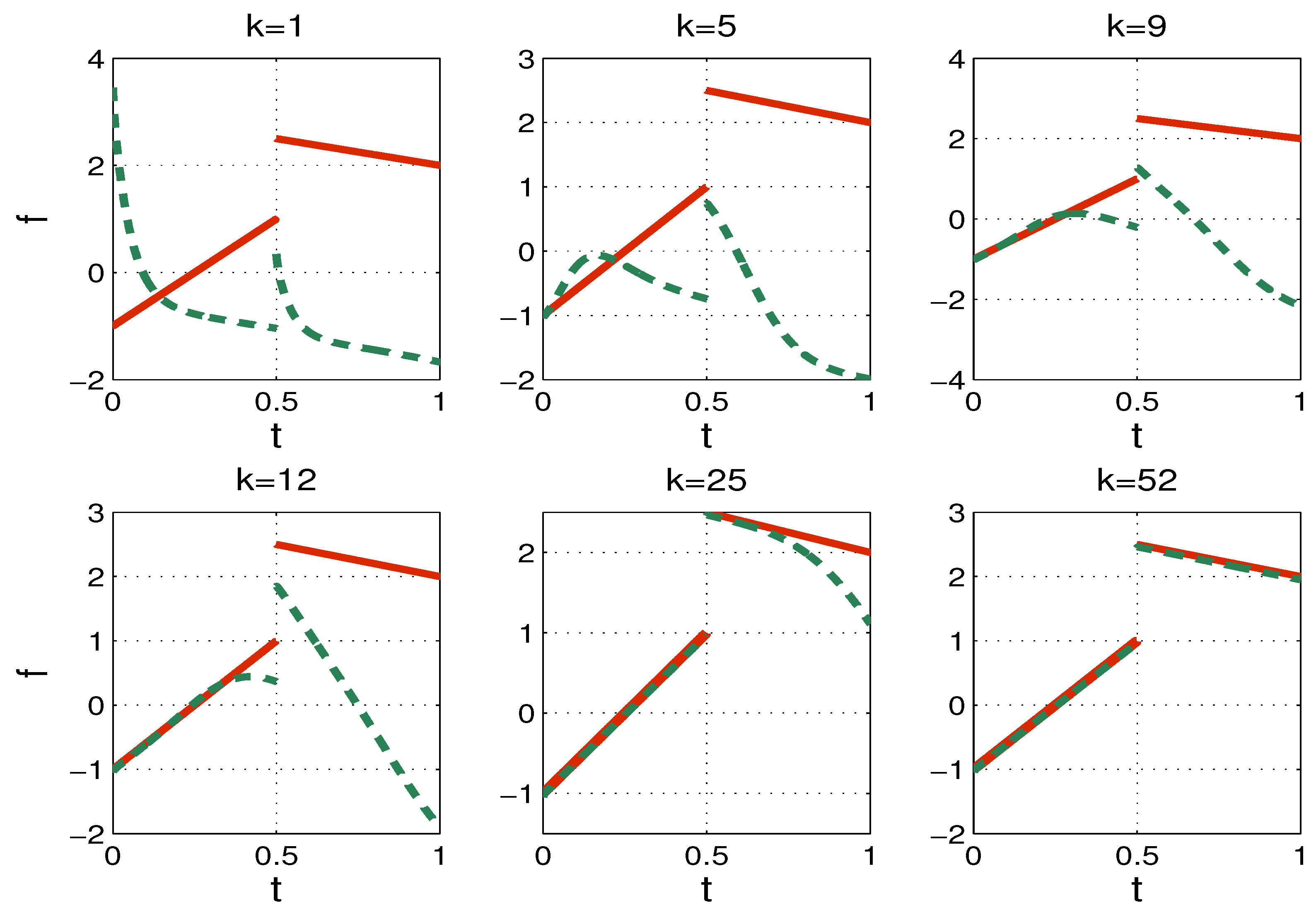
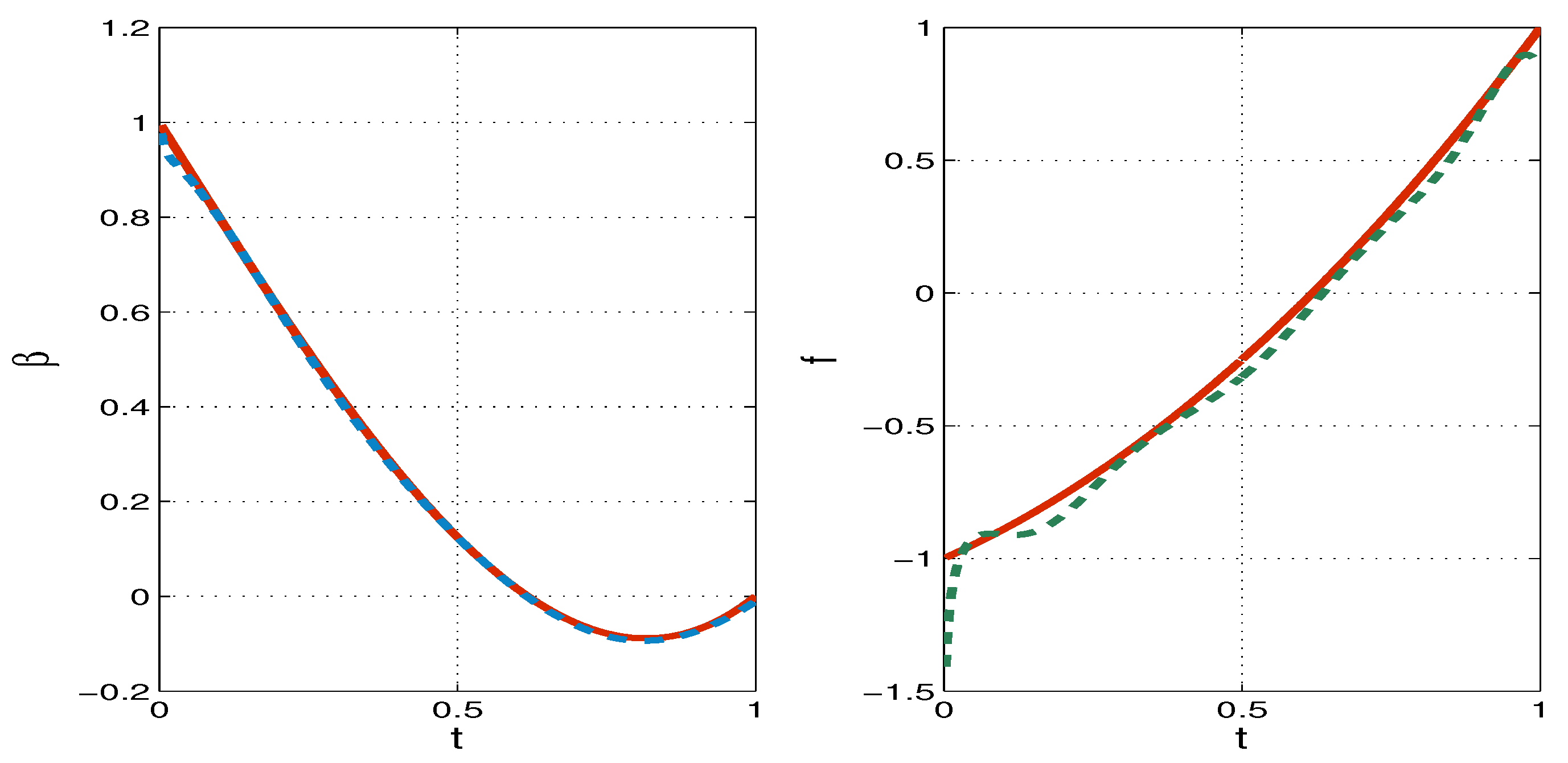

| TP1 | TP2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 20 | 3.4785 | |||||||
| 40 | 1.9470 | 1.9572 | 1.8988 | 1.8921 | ||||
| 80 | 1.9805 | 1.9829 | 1.9589 | 5.7206 | 1.9535 | |||
| 160 | 2.0040 | 1.9927 | 1.9871 | 1.4507 | 1.9794 | |||
| 320 | 2.0013 | 1.9994 | 2.0141 | 1.9916 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koleva, M.N.; Vulkov, L.G. A Galerkin Finite Element Method for the Reconstruction of a Time-Dependent Convection Coefficient and Source in a 1D Model of Magnetohydrodynamics. Appl. Sci. 2024, 14, 5949. https://doi.org/10.3390/app14135949
Koleva MN, Vulkov LG. A Galerkin Finite Element Method for the Reconstruction of a Time-Dependent Convection Coefficient and Source in a 1D Model of Magnetohydrodynamics. Applied Sciences. 2024; 14(13):5949. https://doi.org/10.3390/app14135949
Chicago/Turabian StyleKoleva, Miglena N., and Lubin G. Vulkov. 2024. "A Galerkin Finite Element Method for the Reconstruction of a Time-Dependent Convection Coefficient and Source in a 1D Model of Magnetohydrodynamics" Applied Sciences 14, no. 13: 5949. https://doi.org/10.3390/app14135949
APA StyleKoleva, M. N., & Vulkov, L. G. (2024). A Galerkin Finite Element Method for the Reconstruction of a Time-Dependent Convection Coefficient and Source in a 1D Model of Magnetohydrodynamics. Applied Sciences, 14(13), 5949. https://doi.org/10.3390/app14135949






