Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults
Abstract
1. Introduction
- (1)
- By creating a novel integral sliding mode surface, the fixed-time integral sliding mode controller naturally eliminates the singularity issue, overcoming a significant limitation of traditional fixed-time terminal sliding mode control.
- (2)
- By adopting the parameter adaptive control to estimate the square of the upper bound of the total uncertainty, the designed controller is smooth with no obvious chattering phenomenon and does not require any information on the upper bound of the total uncertainty.
- (3)
- The practical fixed-time stability of the closed-loop system is proven. The dynamic positioning errors under the designed controller can be reduced to about zero in the minor fields within a fixed time, even when subject to model uncertainties, external disturbances, and actuator faults.
2. Problem Formulation and Preliminaries
2.1. Mathematical Model
2.2. Lemmas and Assumptions
3. Main Results
3.1. Controller Design
3.2. Stability Analysis
- Step 1: Consider the following Lyapunov candidate function:where represents the estimation error.
- Step 2: When the system state reaches the sliding mode surface, there is the following:
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Yao, M.; Shan, Q.; Zhang, W. Observer-based asynchronous self-triggered control for a dynamic positioning ship with the hysteresis input. Sci. China Inf. Sci. 2022, 65, 212206. [Google Scholar] [CrossRef]
- Mu, D.; Feng, Y.; Wang, G.; Fan, Y.; Zhao, Y. Single-parameter-learning-based robust adaptive control of dynamic positioning ships considering thruster system dynamics in the input saturation state. Nonlinear Dyn. 2022, 110, 395–412. [Google Scholar] [CrossRef]
- Zheng, M.; Su, Y.; Yang, S.; Li, L. Reliable fuzzy dynamic positioning tracking controller for unmanned surface vehicles based on aperiodic measurement information. Int. J. Fuzzy Syst. 2023, 25, 358–368. [Google Scholar] [CrossRef]
- Zheng, M.; Su, Y.; Yan, C. Further Stability Criteria for Sampled-Data-Based Dynamic Positioning Ships Using Takagi–Sugeno Fuzzy Models. Symmetry 2024, 16, 108. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, Z.; Yuan, M.; Wang, S. Research on Multi-Sensor Data Fusion Positioning Method of Unmanned Ships Based on Threshold-and Hierarchical-Capacity Particle Filter. Appl. Sci. 2023, 13, 10390. [Google Scholar] [CrossRef]
- Bae, J.H.; Kim, J.Y. Position Tracking Control of 4-DOF Underwater Robot Leg Using Deep Learning. Appl. Sci. 2024, 14, 1031. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Liu, Y.; Liu, Z.; Ma, Z.; Zhang, W. Robust adaptive neural networks control for dynamic positioning of ships with unknown saturation and time-delay. Appl. Ocean Res. 2021, 110, 102609. [Google Scholar] [CrossRef]
- Li, H.; Lin, X. Robust fault-tolerant control for dynamic positioning of ships with prescribed performance. Ocean Eng. 2024, 298, 117314. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, X.; Liang, K. Robust tracking control for dynamic positioning ships subject to dynamic safety constraints. Ocean Eng. 2022, 266, 112710. [Google Scholar] [CrossRef]
- Gong, C.; Su, Y.; Zhang, D. Variable gain prescribed performance control for dynamic positioning of ships with positioning error constraints. J. Mar. Sci. Eng. 2022, 10, 74. [Google Scholar] [CrossRef]
- Cui, J.; Yang, R.; Pang, C.; Zhang, Q. Observer-based adaptive robust stabilization of dynamic positioning ship with delay via Hamiltonian method. Ocean Eng. 2021, 222, 108439. [Google Scholar] [CrossRef]
- Dong, D.; Li, J.; Yang, S.; Xiang, X. Dynamic Positioning of Ship Using Backstepping Controller with Nonlinear Disturbance Observer; NIScPR-CSIR: New Delhi, India, 2021. [Google Scholar]
- Zhang, Y.; Liu, C.; Zhang, N.; Ye, Q.; Su, W. Finite-Time Controller Design for the Dynamic Positioning of Ships Considering Disturbances and Actuator Constraints. J. Mar. Sci. Eng. 2022, 10, 1034. [Google Scholar] [CrossRef]
- Zhang, G.; Fu, M.; Xu, Y.; Li, J.; Zhang, W.; Fan, Z. Finite-time trajectory tracking control of dynamic positioning ship based on discrete-time sliding mode with decoupled sampling period. Ocean Eng. 2023, 284, 115030. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, M.; Zhang, W.; Zhang, W. Event-triggered distributed adaptive cooperative control for multiple dynamic positioning ships with actuator faults. Ocean Eng. 2021, 242, 110124. [Google Scholar] [CrossRef]
- Mu, D.; Feng, Y.; Wang, G.; Fan, Y.; Zhao, Y.; Sun, X. Ship dynamic positioning output feedback control with position constraint considering thruster system dynamics. J. Mar. Sci. Eng. 2023, 11, 94. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using Lyapunov methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- Wan, L.; Cao, Y.; Sun, Y.; Qin, H. Fault-tolerant trajectory tracking control for unmanned surface vehicle with actuator faults based on a fast fixed-time system. ISA Trans. 2022, 130, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Yao, Q.; Jahanshahi, H.; Golestani, M. Adaptive neural fault-tolerant control for output-constrained attitude tracking of unmanned space vehicles. Trans. Inst. Meas. Control. 2023, 45, 1229–1244. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Command-filtered fixed-time trajectory tracking control of surface vehicles based on a disturbance observer. Int. J. Robust Nonlinear Control 2019, 29, 4348–4365. [Google Scholar] [CrossRef]
- Cui, J.; Sun, H. Fixed-Time Trajectory Tracking Control of Autonomous Surface Vehicle with Model Uncertainties and Disturbances. Complexity 2020, 2020, 3281368. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yao, Q.; Alotaibi, N.D. Fixed-time nonsingular adaptive attitude control of spacecraft subject to actuator faults. Chaos Solitons Fractals 2024, 179, 114395. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y.; Zhang, X. Extended state observer-based fixed-time trajectory tracking control of autonomous surface vessels with uncertainties and output constraints. ISA Trans. 2022, 128, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Karimi, H.R.; Li, H.; Su, S.F. Accurate trajectory tracking of disturbed surface vehicles: A finite-time control approach. IEEE/ASME Trans. Mechatron. 2019, 24, 1064–1074. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Liu, H.; Weng, P.; Tian, X.; Mai, Q. Distributed adaptive fixed-time formation control for UAV-USV heterogeneous multi-agent systems. Ocean Eng. 2023, 267, 113240. [Google Scholar] [CrossRef]
- Piao, Z.; Guo, C.; Sun, S. Adaptive backstepping sliding mode dynamic positioning system for pod driven unmanned surface vessel based on cerebellar model articulation controller. IEEE Access 2020, 8, 48314–48324. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y. Adaptive neural network-based fault-tolerant trajectory-tracking control of unmanned surface vessels with input saturation and error constraints. IET Intell. Transp. Syst. 2020, 14, 356–363. [Google Scholar] [CrossRef]
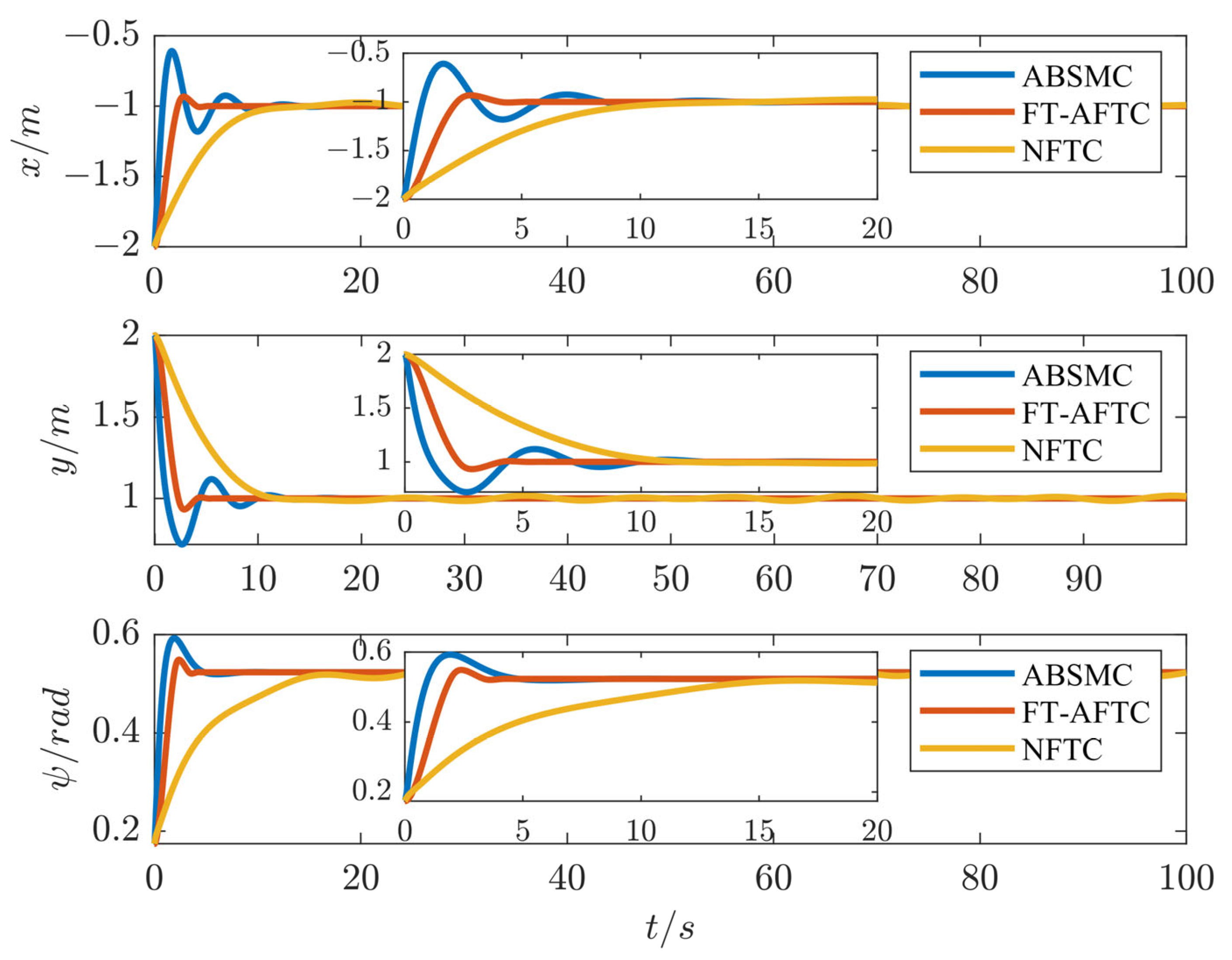
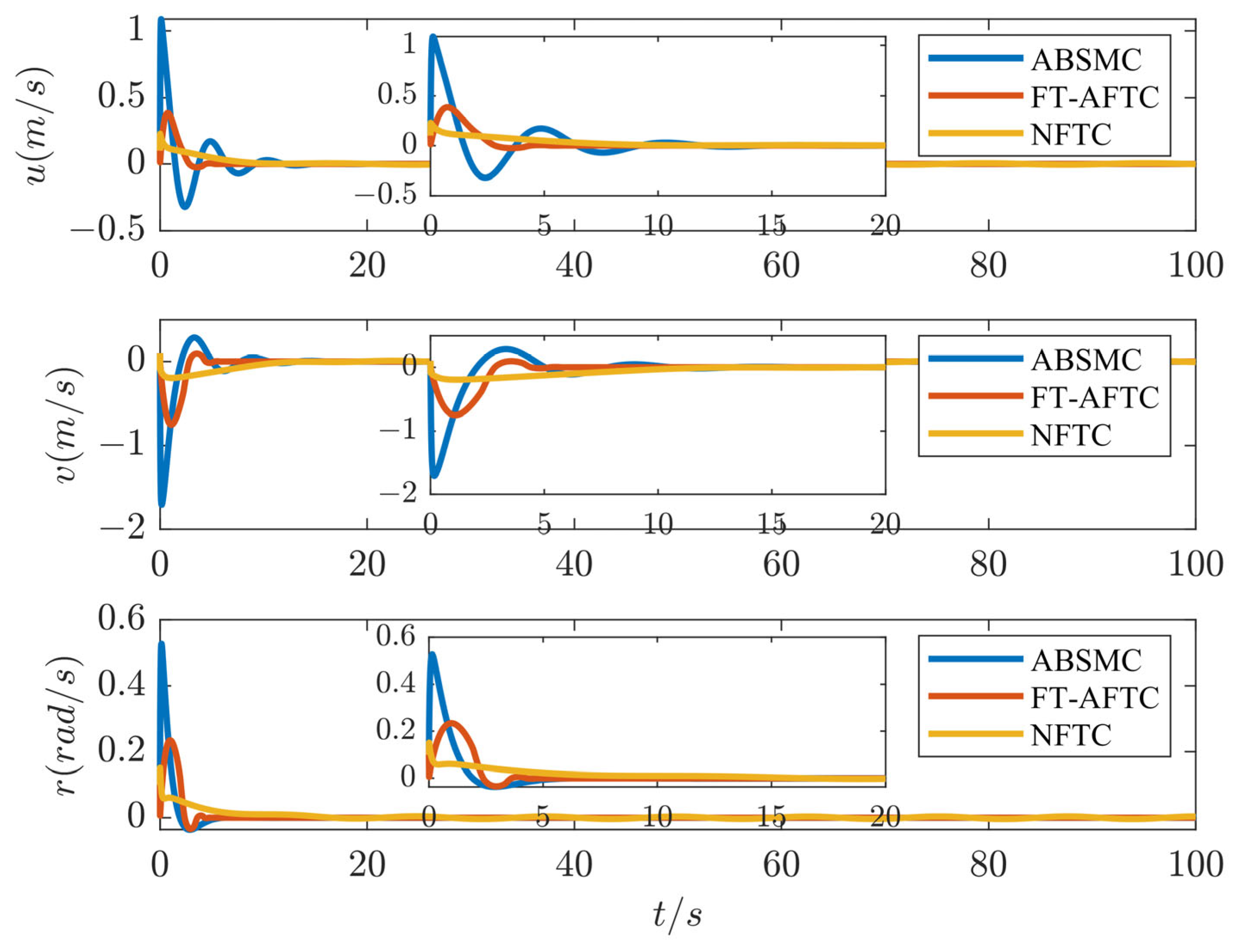
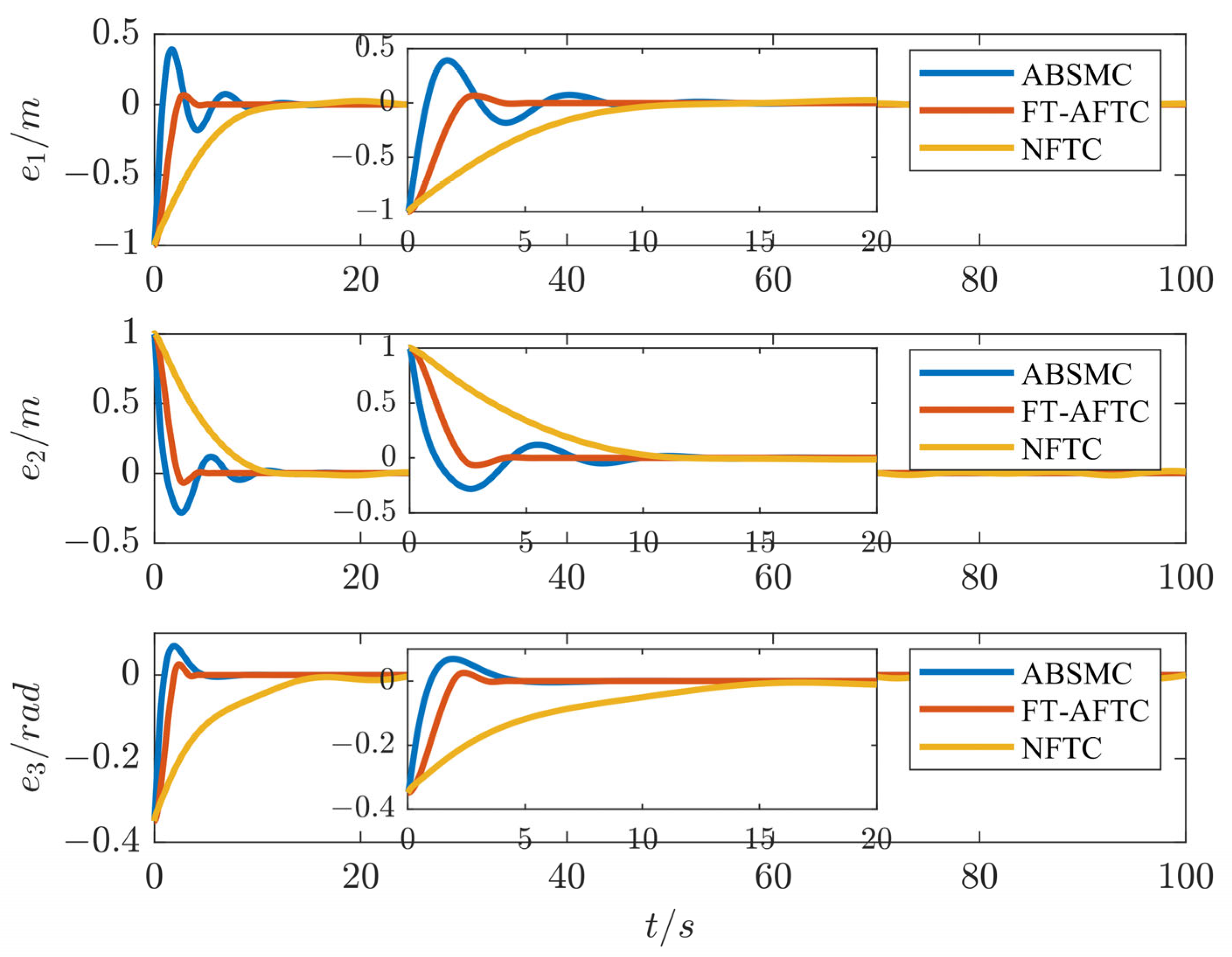
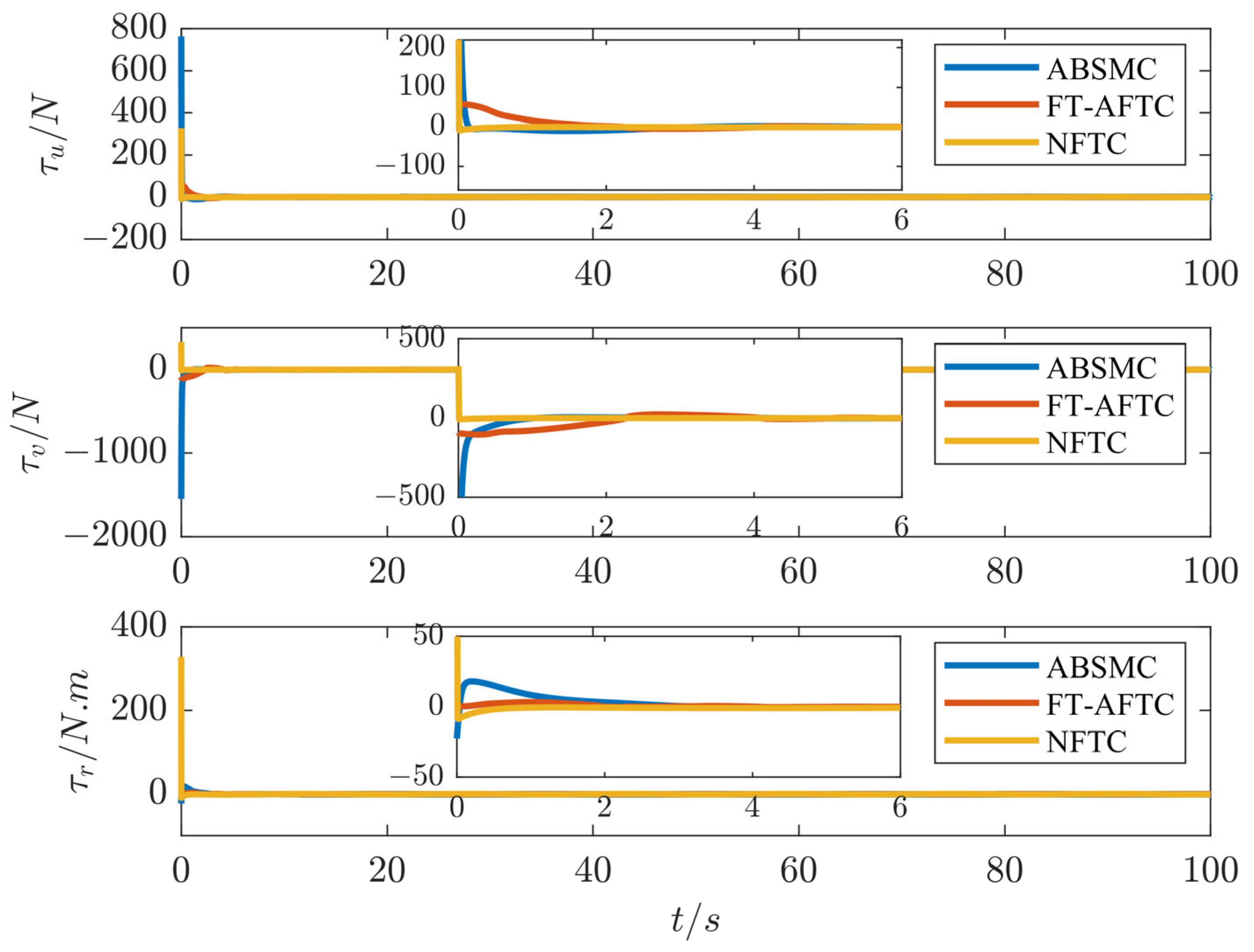
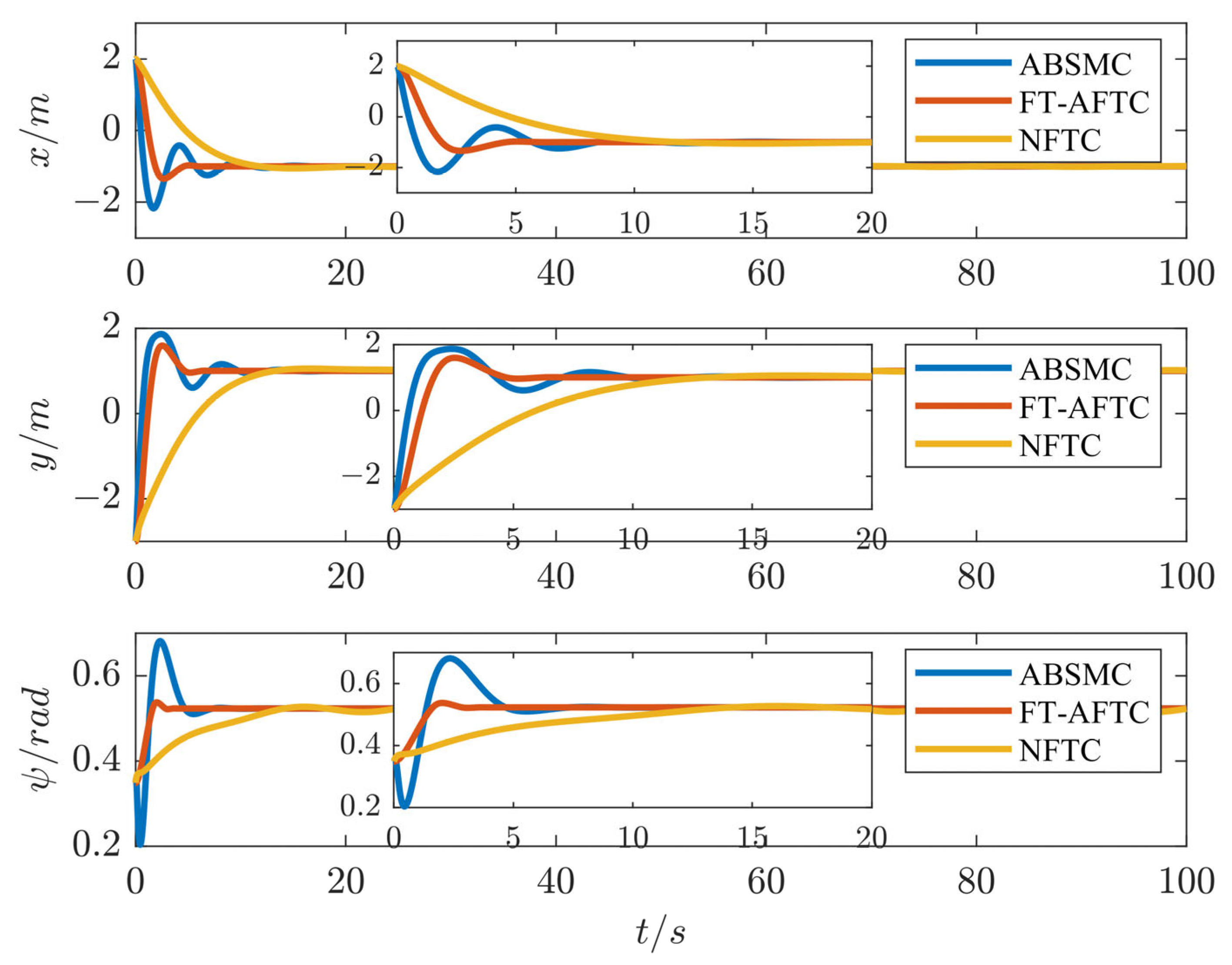
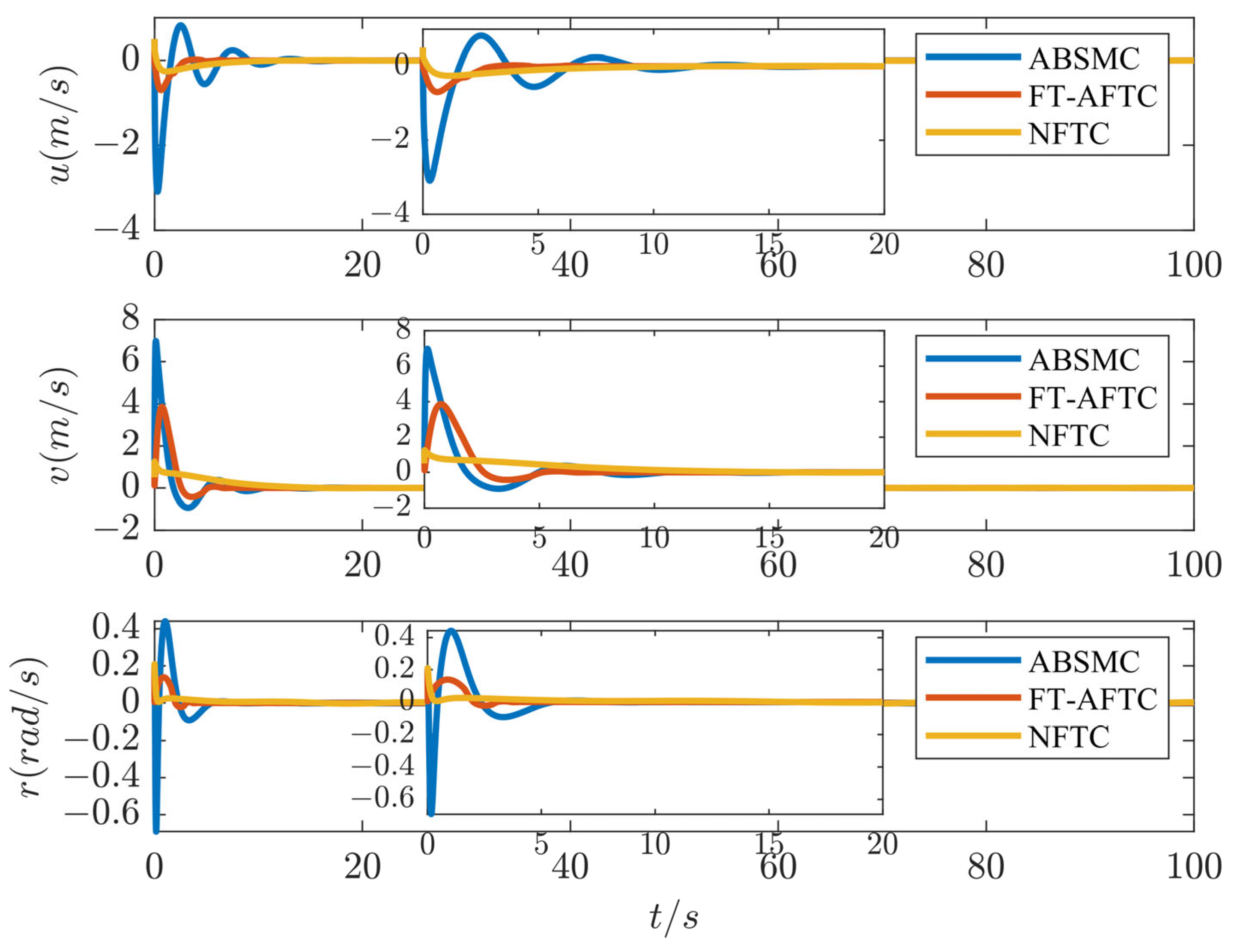
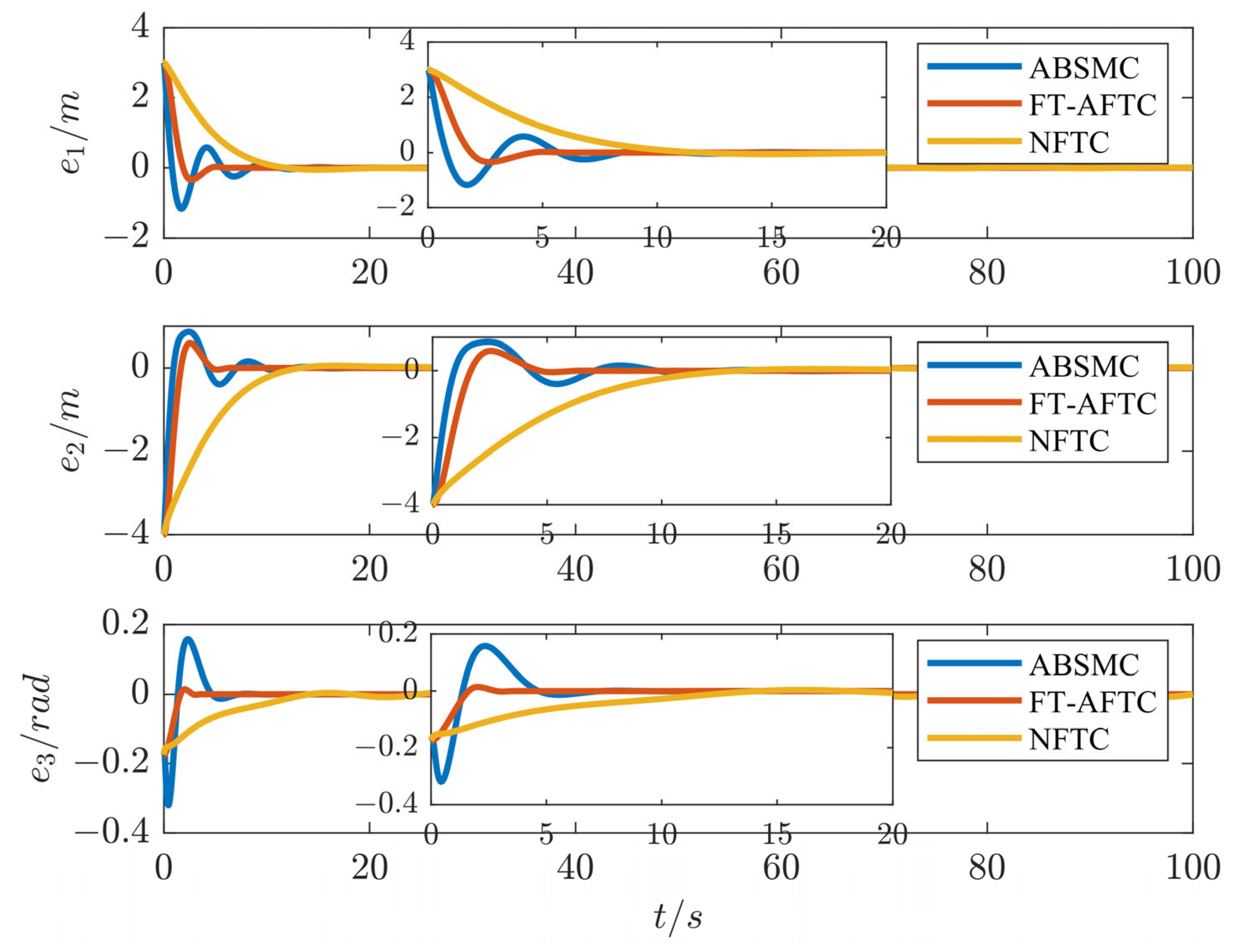

| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| 23.8 | 0.1079 | 2 | |||
| 1.76 | 0.1052 | 1 | |||
| 0.046 | 5.0437 | 3 | |||
| −0.7225 | −2 | 5 | |||
| −1.3274 | −10 | 4 | |||
| −5.8664 | 0 | 0.5 | |||
| -0.8612 | 0 | 0.8 | |||
| −36.2823 | −1 |
| FT-AFTC | 1.251 | 1.140 | 0.386 | 0.619 | 1.493 | 0.407 |
| ABSMC | 1.470 | 1.381 | 0.482 | 1.792 | 2.502 | 0.501 |
| NFTC | 4.518 | 4.757 | 2.030 | 0.883 | 1.664 | 0.545 |
| FT-AFTC | 1.087 | 1.099 | 0.289 | 0.750 | 2.190 | 1.173 |
| ABSMC | 4.298 | 4.189 | 0.437 | 5.128 | 5.711 | 5.790 |
| NFTC | 50.11 | 50.29 | 31.09 | 18.55 | 27.21 | 13.39 |
| FT-AFTC | 3.445 | 4.501 | 0.596 | 1.101 | 6.387 | 0.208 |
| ABSMC | 4.500 | 4.826 | 1.667 | 5.315 | 8.756 | 0.831 |
| NFTC | 12.695 | 17.041 | 12.324 | 1.459 | 5.349 | 0.382 |
| FT-AFTC | 3.451 | 4.995 | 0.108 | 1.367 | 8.786 | 0.232 |
| ABSMC | 13.722 | 13.839 | 10.846 | 15.490 | 18.413 | 16.242 |
| NFTC | 77.11 | 96.41 | 27.273 | 20.823 | 42.547 | 12.797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, J.; Sui, B. Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults. Appl. Sci. 2024, 14, 5738. https://doi.org/10.3390/app14135738
Zhang Y, Zhang J, Sui B. Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults. Applied Sciences. 2024; 14(13):5738. https://doi.org/10.3390/app14135738
Chicago/Turabian StyleZhang, Yuanyuan, Jianqiang Zhang, and Bowen Sui. 2024. "Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults" Applied Sciences 14, no. 13: 5738. https://doi.org/10.3390/app14135738
APA StyleZhang, Y., Zhang, J., & Sui, B. (2024). Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults. Applied Sciences, 14(13), 5738. https://doi.org/10.3390/app14135738





