A Low-Complexity Start–Stop True Random Number Generator for FPGAs

Abstract

This paper introduces a low-complexity start–stop true random number generator (TRNG) utilizing jitter in ring oscillators (ROs). Incorporating phase detectors enhances entropy extraction from the same number of ROs. The raw bits undergo online post-processing using the SHA-1 algorithm, which is widely supported by many programming languages. The output bit streams pass all NIST statistical tests (SP 800-22 and SP-90B). Bits are generated on demand, enhancing security by preventing eavesdropping during continuous bit production. The TRNG maintains its performance regardless of the FPGA manufacturer.

1. Introduction

Random number generators (RNGs) are widely used in many applications [1]. There are two types of RNGs: pseudo-random number generators (PRNGs), which can be described with a deterministic algorithm, and true random number generators (TRNGs), which produce non-deterministic sequences even if the generator’s structure is known. Currently, most systems are digital constructions. Therefore, true random number generators are anticipated to be fully digital and integrated into a single chip using a system that utilizes random numbers. This feature is essential for cryptographic systems because it makes it difficult for attackers to retrieve and manipulate the numbers or sequences produced by the TRNG.

The most popular fully digital TRNG solutions, easily implementable in FPGAs alongside cryptographic systems, rely on jitter or metastable states [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. However, the primary disadvantage of existing TRNGs is the need for the further processing of output bits due to biased output sequences and strong correlations between adjacent bits. Consequently, random sequences do not generally pass statistical tests from available packages like Statistical Test Suite described in SP 800-22 by NIST [43], TU01 [44], or DieHarder [45]. Such sequences need to be subjected to post-processing transformation(s), which improve the statistical properties but usually decrease the bit rate. Since statistical tests cannot differentiate between deterministic (PRNG) and non-deterministic (TRNG) generators, an additional mechanism is required to verify the source of the output bits. This determination is challenging, as TRNG signals contain both deterministic and non-deterministic components [11,12,46]. Thus, before a given solution is accepted as TRNG, we must assess the amount of true randomness. This assessment can be made directly by measuring, e.g., jitter in signals produced by entropy sources, or we can attempt to find another measure. Examples of the first approach are measurements made with an oscilloscope or a dedicated device. The second approach is represented by tests from NIST SP 800-90B [47]. The min-entropy can be estimated for sources with independent bits with an identical distribution IID, and for sources that fail to produce IID output [47]. Estimating the entropy of a noise source from a single, even long, output sequence may result in an overestimate. To address this, we performed a sequence of restarts and dedicated tests. These ensured that the distribution of samples in a restart sequence was independent of its position within the sequence. Knowledge of one restart sequence should not aid in predicting subsequent sequences [47]. During normal exploitation of a TRNG, health tests should be applied to detect deviations from the intended behavior of the entropy source as quickly as possible and with high probability [47]. General rules concerning the construction of random number generators can be found in SP 800-90C [48].

This paper proposes a novel method for producing random numbers with TRNG exploiting ring oscillators (ROs) implemented in an FPGA. The generator uses the concept introduced originally by Wold and Tan [8], described more widely in other publications [10,16]. Our proposition uses only two ROs and additional phase detectors to increase the true randomness harvested from these oscillators. To increase the security of the proposed TRNG, we postulate producing bits on demand, i.e., starting and stopping the work of a TRNG when random bits are needed by a digital system implemented in the same FPGA.

Section 2 contains a description of the proposed solution. The results of the tests are presented in Section 3. The paper ends with the conclusions in Section 4.

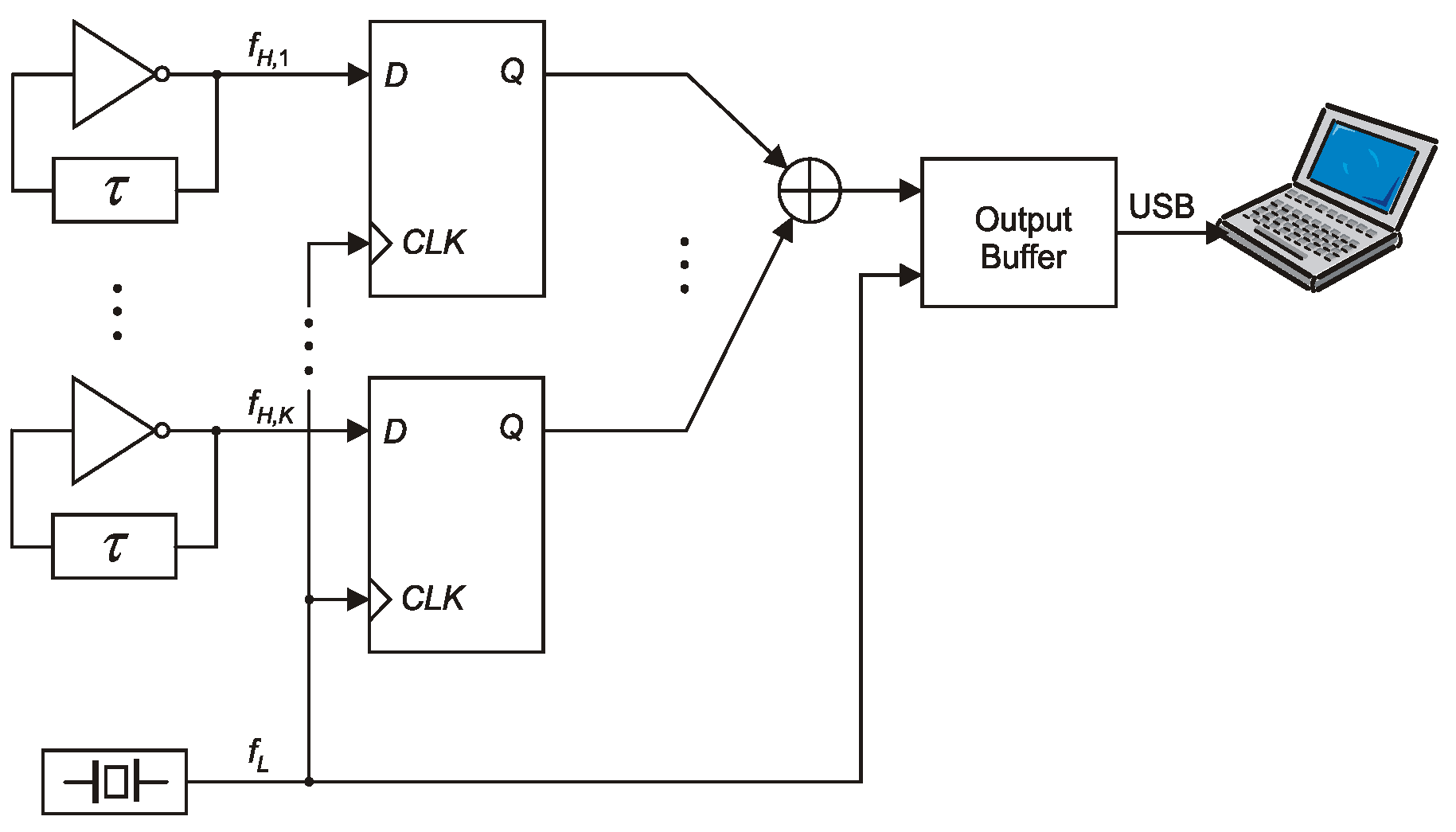
2. A Start–Stop TRNG with Two ROs and a Phase Detector

In an RO-based TRNG, the signal from RO is sampled in a flip-flop, using another signal with a lower frequency (Figure 1). Delay τ is usually implemented as a chain of even-number inverters, a chain of latches, or even a delay line [17].

Using only one ring oscillator does not output a bit string that meets all the statistical tests, even for small sampling frequencies and strong post-processing. To overcome this drawback, Sunar et al. proposed summing the XOR signals from multiple ROs and then sampling the resulting string using a signal with frequency f_L [7]. As shown in [7], the minimum number of ROs is 116. Then, Wold and Tan noticed that the number of ROs used can be significantly reduced if we combine XOR bit streams produced by many low-quality random bit generators called elementary generators (Figure 2) [8]. The TRNG obtained can be considered a combined generator with the XOR combining function, similar to combined PRNG generators.

In [9], N. Bochard et al. demonstrated, through simulation experiments, that Wold and Tan’s generators can produce sequences passing all statistical tests even when ring oscillators lack jitter. As a result, a fully deterministic source can achieve favorable statistical properties in the bit streams produced by the combined TRNG of Wold and Tan. Therefore, before accepting a solution as a TRNG, it is essential to evaluate the true randomness, especially when utilizing ROs. The structure of the RO-based start–stop TRNG proposed in this paper is shown in Figure 3.

The generator uses only two ROs and additional phase detectors. The outputs of the phase detectors are sampled with frequency $f_L$, with the sampling signal coming from a quartz oscillator. Next, two bitstreams are combined with the XOR function. The start–stop operation provides an external signal EN. For EN = “1”, ROs produce rectangular waves. For EN = “0”, the generator does not operate. When enabled, the TRNG can provide a specified number of bits on demand, controlled by the number of impulses from the quartz oscillator. The output bits are post-processed using the SHA-1 function.

The jittered signal from a single-ring oscillator can be written as a phase-modulated signal [49]:

$$s\left(t\right)=P\left[\omega t+\phi \left(t\right)\right],$$

(1)

where P denotes the sequence of periodic square pulses, t represents time, ω = 2πf signifies the pulsation of the periodic signal with frequency f, and φ denotes phase fluctuations (jitter). Utilizing Fourier series analysis of the s(t) signal reveals that the rectangular signal shares identical phase properties with its first harmonic [49]. This characteristic significantly simplifies the analysis of a signal affected by phase jitter. Consequently, a sinusoidal signal with jitter can be expressed as follows:

$$s\left(t\right)=\sin (\omega t+\phi \left(t\right)),$$

(2)

or,

$$s\left(t\right)=\sin \left(\omega t\right)\cos \left(\phi \left(t\right)\right)+\sin \left(\phi \left(t\right)\right)\cos \left(\omega t\right).$$

(3)

Due to the slight variations in phase, the cosine of small angles approximates to one, and the sine approximates to the angle value. Thus, Equation (3) can be approximated as follows:

$$s\left(t\right)=\sin \left(\omega t\right)+\phi \left(t\right)\cos \left(\omega t\right).$$

(4)

The signal from the kth ring oscillator is as follows:

$$s_k\left(t\right)=\sin \left({\omega }_{k}t\right)+{\phi }_k\left(t\right)\cos ({\omega }_{k}t).$$

(5)

As illustrated in Figure 3, the PD1 produces the signal outlined below:

$$s_1\left(t\right)=\sin \left({\omega }_{1}t\right)+({\phi }_1\left(t\right)+{\phi }_2\left(t\right))\cos ({\omega }_{1}t),$$

(6)

where ${\omega }_1$ is the pulsation of RO1. For PD2,

$$s_2\left(t\right)=\sin \left({\omega }_{2}t\right)+({\phi }_2\left(t\right)+{\phi }_1\left(t\right))\cos ({\omega }_{2}t),$$

(7)

where ${\omega }_2$ is the pulsation of RO2.

Subsequently, signals $s_1\left(t\right)$ and $s_2\left(t\right)$ undergo sampling. For simplicity, ideal sampling is assumed using Dirac pulses with a period $T_s$. The sampled signals are the following:

$$\begin{gathered} d_1\left(t\right)=\sum _{n=-\infty }^{\infty }\left[\sin \left({\omega }_{1}n{T}_s\right)+\left({\phi }_1\left(n{T}_s\right)+{\phi }_2\left(n{T}_s\right)\right)\cos \left({\omega }_{1}n{T}_s\right)\right]\delta (t-n{T}_s) \\ {d}_2\left(t\right)=\sum _{n=-\infty }^{\infty }\left[\sin \left({\omega }_{2}n{T}_s\right)+\left({\phi }_2\left(n{T}_s\right)+{\phi }_1\left(n{T}_s\right)\right)\cos \left({\omega }_{2}n{T}_s\right)\right]\delta (t-n{T}_s). \end{gathered}$$

(8)

After summing modulo 2 (both signals) and applying the Fourier transform, we obtain the following spectrum:

$$\begin{array}{ll}S\left(\omega \right)=\frac{1}{2T_s}{\displaystyle \sum _{n=-\infty }^{\infty }}& \frac{1}{j}\left(\delta \left(\omega -{\omega }_1-{n\omega }_s\right)-\delta \left(\omega +{\omega }_1-{n\omega }_s\right)\right)\\ & +{\mathsf{\Phi }}_1\left(\omega -{\omega }_1-{n\omega }_s\right)+{\mathsf{\Phi }}_1\left(\omega +{\omega }_1-{n\omega }_s\right)\\ & +{\mathsf{\Phi }}_2\left(\omega -{\omega }_1-{n\omega }_s\right)+{\mathsf{\Phi }}_2\left(\omega +{\omega }_1-{n\omega }_s\right)\\ & +\frac{1}{j}\left(\delta \left(\omega -{\omega }_2-{n\omega }_s\right)-\delta \left(\omega +{\omega }_2-{n\omega }_s\right)\right)\\ & +{\mathsf{\Phi }}_2\left(\omega -{\omega }_2-{n\omega }_s\right)+{\mathsf{\Phi }}_2\left(\omega +{\omega }_2-{n\omega }_s\right)\\ & +{\mathsf{\Phi }}_1\left(\omega -{\omega }_1-{n\omega }_s\right)+{\mathsf{\Phi }}_1\left(\omega +{\omega }_1-{n\omega }_s\right)-4\pi C\delta \left(0\right).\end{array}$$

(9)

The value of C is constant. In comparison, the signal spectrum from generator WT2 is as follows:

$$\begin{array}{ll}SW\left(\omega \right)=\frac{1}{2T_s}{\displaystyle \sum _{n=-\infty }^{\infty }}& \frac{1}{j}\left(\delta \left(\omega -{\omega }_1-{n\omega }_s\right)-\delta \left(\omega +{\omega }_1-{n\omega }_s\right)\right)\\ & +{\mathsf{\Phi }}_1\left(\omega -{\omega }_1-{n\omega }_s\right)+{\mathsf{\Phi }}_1\left(\omega +{\omega }_1-{n\omega }_s\right)\\ & +\frac{1}{j}\left(\delta \left(\omega -{\omega }_2-{n\omega }_s\right)-\delta \left(\omega +{\omega }_2-{n\omega }_s\right)\right)\\ & +{\mathsf{\Phi }}_2\left(\omega -{\omega }_2-{n\omega }_s\right)+{\mathsf{\Phi }}_2\left(\omega +{\omega }_2-{n\omega }_s\right)-4\pi C\delta \left(0\right).\end{array}$$

(10)

On examining Equations (9) and (10), it is evident that, within the proposed generator, the spectral elements associated with phase disturbances traverse to the output twice on two distinct subcarriers. This feature is advantageous as it enables more precise band coverage and makes the signal more like white noise, as depicted in Figure 4. The generators that were tested comprised two source ring oscillators. The sampling frequency was 10 MHz, and the bit rate was 10 Mbit/s.

Upon examining the spectra, it is evident that the WT2 generator’s spectrum is focused on a few frequencies only. In contrast, the spectrum of the WT2D generator, equipped with a phase detector, is more spread out and effectively covers the entire signal band. This observation aligns with the spectral flatness values calculated using Wiener entropy, as outlined in the following formula [50]:

$$F_l=\frac{\sqrt[N]{\prod _{n=0}^{N-1}x\left(n\right)}}{\frac{1}{N}\sum _{n=0}^{N-1}x\left(n\right)}=\frac{e^{\frac{1}{N}\sum _{n=0}^{N-1}\ln x\left(n\right)}}{\frac{1}{N}\sum _{n=0}^{N-1}x\left(n\right)}.$$

(11)

The spectrum samples in set N, denoted as x(n), have a spectrum flatness of one when dealing with white noise in the measured signal band. A spectrum flatness value of zero indicates a pure harmonic. When comparing WT2D to WT2, the value of F_l is 0.553671 for WT2 and 0.673340 for WT2D. Thus, better statistical properties of output sequences are expected to be produced by WTD2 than by WTD.

3. The Quality of Bit Streams Produced by the Proposed Generator

The statistical properties analysis was preceded by entropy calculations for output sequences from Wold and Tan’s generator using 2-, 3-, and 4-ring oscillators and the proposed generator with two oscillators and two phase detectors. Numerical values were obtained for five sampling frequencies with the TRNG implemented in Virtex 5 XC5VLX50T, as shown in

Table 1. The entropy of output sequences for five values of sampling frequency f_L.

fL [MHz]	25	15	10	5	1
WT2	0.228335	0.542281	0.654215	0.784981	0.894990
WT3	0.893081	0.970915	0.995306	0.995389	0.998268
WT4	0.994968	0.997237	0.999889	0.999311	0.998281
WT2D	0.999998	0.999999	0.999999	0.999999	0.999999

. The values differed by no more than 16% for other FPGA technologies. WTx represents a TRNG with the construction in Figure 2 using x ROs, while the generator in Figure 3 corresponds to the WT2D symbol.

Next, whether the generators produced IID strings and whether the received strings passed the restart tests described by NIST [47] were checked. The results are shown in

Table 2. The results of tests described by NIST in SP 800-90B for five sampling frequencies f_L.

fL [MHz]	25		15		10		5		1
Tests	IID	RES	IID	RES	IID	RES	IID	RES	IID	RES
WT2	—	—	—	—	—	Y	—	Y	—	Y
WT3	—	—	—	—	—	—	—	Y	—	Y
WT4	—	—	—	Y	—	Y	Y	Y	Y	Y
WT2D	—	—	—	Y	Y	Y	Y	Y	Y	Y

. Symbol Y denotes that the generator passed the tests.

In additional studies, only the sampling frequencies for which the WTD2 generator produced IID strings that passed the restart tests from NIST SP-90B across all dominant FPGA technologies were considered. These have successfully integrated true random number generators (TRNGs) into Virtex 5, Spartan-3, Spartan-6, Artix-7, Cyclone V, and Max-10. The maximum output bit rate is limited to 10 Mbit/s. Exceeding this threshold results in output sequences that do not pass at least one of the NIST statistical tests from SP 800-22 and SP 90B. Nonetheless, for most cryptographic applications such as key generation, authentication vector generation, and Initial Vector (IV) generation, a bit rate of several Mbit/s is adequate. Initially, the statistical tests described in SP 800-22 were performed on raw bits. Subsequently, the same bits were processed using the SHA-1 function from the Hashlib Python Library [51].

The SP 800-22 test suite comprises 15 statistical tests, some with multiple subtests. NIST proposed two testing approaches examining the proportion R_β of sequences that pass a statistical test and analyzing the distribution of p-values computed by the software, which examines the value of P_T [43]. A standard set of parameters proposed by NIST in version 2.1.1 was assumed during the tests. For the significance level β = 0.01 and 1000 tested sequences, each with a length of 10⁶ bits, the minimal passing value for the proportion was approximately R_β = 0.9805. If P_T ≥ 0.0001, then p-values can be considered uniformly distributed. The NIST tests were performed for sampling frequencies of f_L = 10 MHz, 5 MHz, and 1 MHz. The final results are included in

Table 3. The final results of statistical tests described in SP 800-22, f_L = 10 MHz.

Test	Raw Data				Raw Data + SHA1
	WT2	WT3	WT4	WT2D	WT2	WT3	WT4	WT2D
1. Frequency	—	—	—	Y	Y	Y	Y	Y
2. Block frequency	—	—	—	—	Y	Y	Y	Y
3. Cumulative sums	—	—	—	Y	Y	Y	Y	Y
4. Runs	—	—	—	—	—	—	Y	Y
5. Longest run	—	—	—	—	Y	Y	Y	Y
6. Rank	—	—	—	Y	Y	Y	Y	Y
7. DFT	—	—	—	—	Y	Y	Y	Y
8. Nonoverlapping template	—	—	—	—	—	Y	Y	Y
9. Overlapping template	—	—	—	—	Y	—	—	Y
10. Universal	—	—	—	—	Y	Y	Y	Y
11. Approximate entropy	—	—	—	Y	Y	Y	Y	Y
12. Random excursions	—	—	—	—	Y	Y	Y	Y
13. Random excursions variants	—	—	—	Y	Y	Y	—	Y
14. Serial	—	—	—	—	Y	Y	Y	Y
15. Linear complexity	Y	Y	Y	Y	Y	Y	Y	Y

,

Table 4. The final results of statistical tests described in SP 800-22, f_L = 5 MHz.

Test	Raw Data				Raw Data + SHA1
	WT2	WT3	WT4	WT2D	WT2	WT3	WT4	WT2D
1. Frequency	—	—	—	Y	Y	Y	Y	Y
2. Block frequency	—	—	—	—	Y	Y	Y	Y
3. Cumulative sums	—	—	—	Y	Y	Y	Y	Y
4. Runs	—	—	—	—	—	—	Y	Y
5. Longest run	—	—	—	—	Y	Y	Y	Y
6. Rank	—	Y	Y	Y	Y	Y	Y	Y
7. DFT	—	—	—	—	Y	Y	Y	Y
8. Nonoverlapping template	—	—	—	—	—	—	Y	Y
9. Overlapping template	—	—	—	—	Y	Y	—	Y
10. Universal	—	—	—	—	Y	Y	Y	Y
11. Approximate entropy	Y	—	—	Y	Y	Y	Y	Y
12. Random excursions	—	—	—	—	Y	Y	Y	Y
13. Random excursions variants	—	—	—	Y	Y	Y	—	Y
14. Serial	—	—	—	—	Y	Y	Y	Y
15. Linear complexity	Y	Y	Y	Y	Y	Y	Y	Y

and

Table 5. The final results of statistical tests described in SP 800-22, f_L = 1 MHz.

Test	Raw Data				Raw Data + SHA1
	WT2	WT3	WT4	WT2D	WT2	WT3	WT4	WT2D
1. Frequency	—	—	—	Y	Y	Y	Y	Y
2. Block frequency	—	—	—	—	Y	Y	Y	Y
3. Cumulative sums	—	—	—	Y	Y	Y	Y	Y
4. Runs	—	—	—	—	—	—	Y	Y
5. Longest run	—	—	—	—	Y	Y	Y	Y
6. Rank	—	Y	Y	Y	—	Y	Y	Y
7. DFT	—	—	—	—	Y	Y	Y	Y
8. Nonoverlapping template	—	—	—	—	—	—	—	Y
9. Overlapping template	—	—	—	—	Y	Y	—	Y
10. Universal	—	—	—	—	Y	Y	Y	Y
11. Approximate entropy	Y	Y	—	Y	Y	Y	Y	Y
12. Random excursions	—	—	—	—	Y	Y	Y	Y
13. Random excursions variants	—	—	—	Y	—	—	—	Y
14. Serial	—	—	—	—	Y	Y	Y	Y
15. Linear complexity	Y	Y	Y	Y	Y	Y	Y	Y

. Symbol Y denotes that the generator produces sequences that pass all tests, including subtests, and that the distribution of p-values is uniform.

The proposed generator yields IID bit sequences that pass the restart tests specified in NIST 800-90B and, following the application of SHA1, all tests outlined in SP800-22. For the generator depicted in Figure 2, achieving the same outcome requires combining at least seven-bit streams using the XOR function, each produced in the circuit shown in Figure 1. This conclusion holds under the condition that the sampling frequency f_L does not exceed 10 MHz and the outcome remains consistent across different FPGA technologies.

Table 6. The values of proportion R_β and the values of P_T for raw data and after their processing for WT2D and WT7, f_L = 10 MHz.

Test	Raw Data				Raw Data + SHA1
	WT7		WT2D		WT7		WT2D
	Rβ	PT	Rβ	PT	Rβ	PT	Rβ	PT
1. Frequency	0.958	0.000	0.918	0.000	0.986	0.196	0.987	0.745
2. Block frequency	0.428	0.000	0.910	0.000	0.989	0.169	0.989	0.326
3. Cumulative sums	0.949	0.000	0.991	0.534	0.987	0.081	0.991	0.721
4. Runs	0.993	0.435	0.980	0.114	0.992	0.426	0.989	0.982
5. Longest run	0.000	0.000	0.910	0.000	0.990	0.998	0.983	0.872
6. Rank	0.990	0.175	0.986	0.094	0.992	0.890	0.989	0.739
7. DFT	0.995	0.771	0.974	0.007	0.990	0.249	0.991	0.494
8. Non overlapping template	0.000	0.000	0.037	0.000	0.987	0.699	0.992	0.133
9. Overlapping template	0.983	0.046	0.004	0.000	0.988	0.473	0.993	0.220
10. Universal	0.000	0.000	0.808	0.000	0.991	0.152	0.991	0.173
11. Approximate entropy	0.000	0.000	0.991	0.004	0.989	0.684	0.991	0.957
12. Random excursions	0.938	0.000	0.955	0.000	0.988	0.188	0.986	0.012
13. Random excursions variants	0.961	0.000	0.998	0.012	0.993	0.000	0.996	0.077
14. Serial	0.000	0.000	0.007	0.000	0.992	0.465	0.992	0.159
15. Linear complexity	0.990	0.028	0.998	0.167	0.989	0.697	0.990	0.420

The worst cases were shown. Bold denotes the results that do not pass the test.

presents the proportion R_β and the values of P_T for raw data and after processing for WT7 and WT2D implemented in Virtex 5 XC5LVX50T.

Reliable comparison of existing proposals of TRNGs is very difficult, and the result depends strongly on the assumed criteria. For comparison, TRNGs that meet the following conditions were selected:

• The generator can be integrated into the same FPGA alongside a digital system that employs random sequences.
• The authors declare that the generator produces IID sequences and that the restart tests described in the SP800-90B are performed.
• The authors declare that the generator produces sequences that pass the randomness tests described in NIST 800-22, so that the proportion of R_β of strings that pass the test is within the limits set by NIST for all tests and subtests, and so that the distribution of p-values is uniform.
• The authors have specified the FPGA resources for the proposed TRNG.

The criteria selection reflects users’ current expectations regarding the methodology and quality of random number sequence generation for cryptographic purposes. The first criterion enhances security by eliminating the necessity to transmit random sequences to the FPGA from an external circuit, which could be more susceptible than the FPGA itself. The second criterion ensures that random sequences originate from phenomena for which non-deterministic processes prevail. The third criterion assures the high statistical integrity of the generated sequences. The fourth criterion excludes TRNGs that provide comparable security while demanding substantial resources or consuming excessive power.

However, the existing literature predominantly features proposals that do not adhere to the first two conditions, which stem from the characteristics and historical development of FPGAs, along with the relatively recent NIST recommendations on entropy sources for generating random sequences [47]. Consequently, the number of proposals validated using the comprehensive methodology outlined by NIST is relatively small [28,29,36,38,39,40,41,42,52]. We refrain from discussing the efficacy of alternative methods for assessing the randomness of generated sequences here. Alternatively, evaluations can employ AIS-31 tests [53,54], tests from the TU01 package [44], or DieHarder [45]. Some authors adopt a hybrid approach, evaluating the entropy source with NIST 800-90B tests while verifying statistical properties using methods such as AIS-31 [37]. This choice highlights the preference for NIST’s methodology despite its limited adoption in everyday research practices. Meanwhile, the proposed method by BSI remains in the draft stage [54].

Table 7. A comparison of TRNGs that meet conditions (I)–(IV).

TRNG Design Technique	Number		Throughput [Mbit/s]
	LUTs	Flip-Flops
Self-timed rings [28]	56	19	100
Fibonacci-Galois RO [29]	288	190	400
Metastability+jitter [36]	4	3	0.76
Metastability+jitter [38]	36	0	12.50
Multi-stage feedback ring oscillator [39]	24	2	290
RO with XOR gates [40]	13	4	500
Non-identical ROs [41]	15	13	3.50
Delay-Difference-Cell [42]	256	256	225
Metastability [52]	14	6	25
RO with XOR gates [8]	23	23	10
WTD2 (this work)	11	13	10

compares TRNGs that meet criteria (I)–(IV).

Notably, the proposed generator achieves a throughput of up to 10 Mbit/s consistently across various FPGA manufacturing technologies, belonging to the category of generators characterized by low complexity and resource requirements. The specific resource values depend on the layout type. What sets this proposal apart from other known designs meeting criteria (I)–(IV) are its complete scalability and portability across different chips and predominant FPGA technologies. In contrast, other authors’ designs (listed in Table 7) are tailored to specific chip types and may not function reliably when implemented on different FPGA technologies. The concept of scalability involves deploying multiple instances of the same TRNG within an FPGA without requiring further adjustments to their placement. For example, by integrating 32 instances of the TRNG shown in Figure 3 into a single FPGA, the bit generation rate can be substantially increased to 320 Mbit/s. However, it is crucial to consider that augmenting the number of instances also amplifies complexity, resource utilization, and power consumption due to the rapid switching of flip-flops. Therefore, while scalability offers enhanced throughput potential, the fundamental limitation remains the availability of FPGA resources required for building these TRNGs and power consumption, especially in devices such as IoT.

4. Conclusions

This paper introduces a novel approach to generating true random number sequences utilizing two-ring oscillators as primary sources of entropy. Phase detectors complement these oscillators by exploiting phase jitter from both sources, enhancing randomness extraction. The proposed TRNG operates on-demand, seamlessly integrating into a single FPGA alongside any digital system requiring random bits. Additionally, raw bit sequences undergo real-time post-processing using established software implementing the SHA-1 algorithm.

This study evaluates performance across various FPGA technologies, specifically Virtex 5, Spartan-3, Spartan-6, Artix-7, Cyclone V, and Max-10. As described, WT2D finds application across systems necessitating authentic random bit generation, with particular relevance to cryptographic contexts.

Enhancing resilience against attacks, particularly frequency injection attacks, is a promising area for exploration in the field of security. One method involves deploying multiple ring oscillators with significantly distinct nominal frequencies. Another approach entails integrating health tests within the FPGA structure to promptly detect deficiencies in randomness and potential interference in the random number generation process caused by attackers, thereby enhancing overall security. The implementation of multiple WTD2 generators, which includes the random selection of the current source of random bits within the same FPGA, appears to be another promising approach to bolster robustness against cryptographic attacks.

Significantly, the proposed TRNG demonstrates exceptional efficiency metrics. It utilizes less than 1% of resources in the smallest FPGA device and consumes under 260 mW for all sampling frequencies up to 10 MHz. These attributes underscore its suitability for resource-constrained environments and highlight its potential impact in cryptographic applications where robust random number generation is critical.