Abstract
For vibration signals, this paper proposes an ensemble classification method based on stochastic configuration networks (SCNs). Firstly, the time–frequency analysis methods are used to obtain the frequency spectrum signal and time–frequency images. The sample data in the frequency domain and the time–frequency domain can characterize fault information from different perspectives. The hybrid data that consist of the sample data from the two domains are used to build a SCN model. Moreover, a SCNs ensemble method is proposed to solve the fault classification problem, and the sub-classifiers are built to extract fault features from different training data. In the experiment, the bearing and gear fault datasets are used for performance comparison. The experimental results show that the proposed SCNs ensemble model obtains good classification results, and compared with the deep learning methods, the SCN modeling process is more simple and effective for industrial data classification.
1. Introduction
In the industry process, the bearing and gears are important parts of the rotating machinery, and the failure of them may cause production breakdown and economic losses. Therefore, detecting the anomaly and diagnosis fault severity is worth studying, and is of great significance to ensure the safe operation and economic maintenance of machinery equipment [1]. In the fault diagnosis, the analysis of vibration signals plays an important role. For the time-series monitor signals, several features such as peak, mean, variance and root mean square are extracted for fault analysis [2]. The time-series signals are also transformed to the frequency domain and time–frequency domain by time–frequency analysis methods to obtain various features and identify fault severity [3,4,5,6].
In recent years, due to the strong representation learning ability, deep learning methods have been widely used for fault diagnosis [7,8,9]. Lu et al. [10] split the vibration signal into a series of time sub-series samples by continuous interleved sampling, and fault feature maps were used to build a convolutional neural network (CNN) for fault diagnosis. Liu et al. [11] proposed an optimized network structure to describe the correlation between signals at different time intervals, and the diagnosis performance was improved under non-stationary conditions. Huang et al. [12] proposed a multi-scale cascade CNN to extract more distinguishable fault features. Xu et al. [13] proposed an online fault diagnosis method based on a deep transfer CNN framework, which was made up of an online CNN based on LeNet-5 and several offline CNNs with a shallow structure. Zhang et al. [14] designed an adaptive activation function with a slope and threshold of the tanh function and proposed a deep adaptive network based on ResNet and STAC-tanh for fault diagnosis. Guan et al. [15] proposed a multi-sensor and multi-scale model to bring a new perspective to accurate fault diagnosis. For time–frequency image data, Zhang et al. [16] utilized the SELU function and hierarchical regularization to build a CNN network. He et al. built [17] a large memory storage retrieval neural network on the spectrum matrix data obtained through short-time Fourier transform. Gltekin et al. [18] proposed a multi-sensory data fusion diagnosis method based on ResNets to deal with the time–frequency images. Wang et al. [19] proposed a multi-view feature selection with information complementarity and consensus to efficiently select relevant features for fault diagnosis. For fault diagnosis, deep learning-based methods can obtain good recognition performance. However, the learning process requires a large number of parameters and computing resource, and it is sensitive to parameters, such as initial weights, learning rate, etc.
To overcome the aforementioned issues above, random neural networks (RNNs) have been presented, in which the weight parameters are stochastically configured [20]. Schmidt et al. [21] proposed a feed-forward neural network with random weights (NNRW) based on the randomization technique. Pao et al. [22,23,24] proposed a random vector functional link (RVFL) neural network that uses a direct link to connect the input layer to the output layer, and the weights and biases from the input layer to the hidden layer are generated randomly from a certain range. Wang and Li [25] proposed the stochastic configuration networks (SCNs), where the stochastic configuration learning process was performed under a supervisory mechanism that ensures the resulting SCN models hold the universal approximation property. A 2-D stochastic configuration network (2DSCN) [26] was developed for matrix inputs, and the experimental results showed its good potential for image data analytics. Wang and Felicetti [27,28] proposed a framework of stochastic configuration machines (SCMs) by composing a mechanism and a DeepSCN model and implemented on FPGAs.
Due to the parameter randomness, RNN-based ensemble learning has been proposed in order to improve the accuracy and stability of the models. Alhamdoosh and Wang [29] employed the RVFL networks as base components and incorporated with the negative correlation learning strategy for building neural network ensembles. Wang and Cui [30] proposed a fast decorrelated neuro-ensemble with heterogeneous features for large-scale data analytics, where the SCNs are employed as base learner models and the negative correlation learning strategy is adopted for weights evaluation. Wang and Li [31] proposed a SCN model with a deep network structure, which realizes the layer-by-layer approximation of the objective function by stacking the hidden features freely. Huang et al. [32] proposed an ensemble model with the base models, selecting from a set of SCN-based learners, and it has been used for large-scale and/or online stream data modeling. Meanwhile, for the fault diagnosis problem, Liu et al. [33] built a SCN model to classify the types of fault by using the fault features extracted from the vibration signals. Li et al. [34] adopted a self-attention long short-term memory (LSTM) network and self-attention residual network to extract fault features, then a SCN-based method was built with these fault features for bearing fault classification. Although experimental results have demonstrated the advantages of SCN-based models for application in fault diagnosis, the recognition performance is strongly dependent on the early feature extraction methods.
This paper proposes a SCNs ensemble model, which aims to combine different fault characters extracted from multiple source signals for the classification task. The proposed model makes use of the fault vibration information in the frequency domain and the time–frequency domain; the extracted features are fused in different ways to improve the classification effect. The ensemble algorithm randomly initializes the hidden layers parameters in the base SCNs, and the global output weight is calculated by employing the least square method with the norm constraint, which is easy and simple to implement. The experimental results show that the proposed SCNs ensemble model outperforms the compared stochastic models and obtains better classification performance for vibration fault signal.
The remainder of this paper is organized as follows. Section 2 overviews the stochastic configuration networks, including the SCN framework and 2DSCN with image inputs. Section 3 details the classification model based on SCN with hybrid data and the proposed ensemble SCNs with algorithmic descriptions. Section 4 presents the experimental study on industry fault dataset. Finally, the conclusion is presented in Section 5.
2. Stochastic Configuration Networks
As a feedforward neural network, SCNs [25] introduce a supervision mechanism to configure the weights of new nodes in the hidden layer, and the stochastic configuration algorithm can ensure the universal approximation ability of the built model. The SCN with a single hidden layer is shown in Figure 1. Given the input data , then the modeling process of the SCN framework can be described as follows.

Figure 1.
The SCN structure with a single hidden layer.
Given a target function , it is assumed that we have already built a SCN model with hidden nodes. The output is
where is the weight parameter, is the bias, is the weight of the output layer, and g is the activation function. Then, the residual error is calculated
If the error does not reach the stop condition, a new node should be added, and the new weights are configured to calculate the hidden output
Denote a set of variables as follows:
where , is a real sequence with . Based on the the universal approximation property of SCNs in [25], the SCN model is built under the constraint condition
Besides, is calculated by
and the current output is
In the stochastic configure learning algorithm, the hidden layer weights are firstly taken from a certain distribution (e.g., uniform distribution or Gaussian distribution), and the bias can be calculated by
where is randomly taken from the training dataset [35]. Then, the supervision mechanism (5) is employed to select proper weight values and add new hidden nodes. The output weight can also be calculated by solving the following least square problem
Similarly, for the 2DSCN model, i.e., the input is matrix data , the target function is . The 2DSCN model is also built under the supervised mechanism (5) with the configured parameters, and the output of the hidden node is
where , are the hidden layer weights, is the bias, and is the output weight. Then, the model output is
3. Fault Diagnosis Based on Ensemble SCNs
In fault diagnosis, the monitor data are a time-series vibration signal. For different operating states, the collected signals have different characters for fault classification. In addition, the time-series signals can be transformed to frequency spectrum and time–frequency images. In this section, we firstly combine the frequency spectrum and time–frequency image via vectorization, and a SCN model is built on the hybrid data in Section 3.1. Then, the ensemble SCNs model is proposed to improve the recognition performance and described in Section 3.2.
3.1. SCN Model with Hybrid Data
As shown in Figure 2, the monitor vibration signal is sampled by a sliding window with a certain size, then the time–frequency analysis methods such as Fourier transform and short time Fourier transform (STFT) are employed to analyze the sample signal and obtain the frequency spectrum from the frequency domain and the time–frequency image from the time–frequency domain, respectively. Fault data in the frequency domain and the time–frequency domain describe the fault features from different perspectives. The hybrid data that consist of samples from these two domains are used to build a SCN model in order to achieve better classification results.
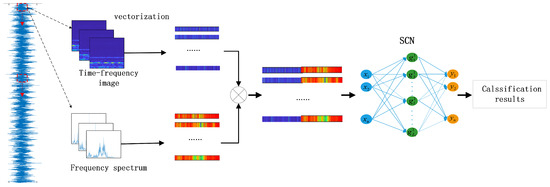
Figure 2.
The fault classification method based on the SCN model with hybrid data.
Given a dataset that consists of time–frequency image , the frequency spectrum signal is and the target label is . In order to combine the samples from these two domains, the 2D images in are vectorized to one-dimensional data denoted as , i.e.,
The hybrid data are obtained and will be used to build the SCN model. Because the hidden parameters are randomly configured under the constraint condition (5), the hidden layer output can be evaluated by
The output weight can be estimated by solving the following optimization problem:
where is a non-linearly transformed feature matrix, is the target label, and is the regularization parameter. The detailed modeling process of the SCN with hybrid data is described in Algorithm 1.
3.2. SCNs Ensemble
In order to improve the classification effect, we propose an ensemble method based on SCNs. The time–frequency image has been used to build the model, but the vectorization operation damages the image structure and cause a loss of information; the image data can be directly used via 2DSCN modeling. As shown in Figure 3, the frequency spectrum, time–frequency images and the hybrid data are used to build sub-learners based on SCNs, respectively. And the ensemble learning is applied to combine the SCN learners and obtain the final classification result.
| Algorithm 1: SCN with hybrid data |
 |

Figure 3.
The ensemble method based on SCNs for fault diagnosis.
The SCNs ensemble learning process is described as follows:
(1) Data pre-processing.
Given the dataset with N samples, where , , and target label , all sample data are normalized to .
(2) Select the base model.
Because the samples from the training dataset have different dimensions, i.e., , , and , then two 1D-SCN learners and a 2D-SCN learner will be built on the datasets , and , respectively.
(3) Building the SCN learners.
- SCN-D:
- SCN-X:
- SCN-H:
(4) Ensemble learning.
The hidden feature matrices of the model SCN-D, SCN-X and SCN-H are , and , respectively. Then, concatenate the hidden feature matrix , and the corresponding parameter is calculated by
The output is obtained .
(5) Calculate the classification error.
The residual error is calculated via , then it is used to configure the weights of new hidden nodes by the supervised constraint. The SCNs ensemble model is built incrementally until the tolerance error is reached or the number of hidden nodes L equals to . Finally, the output is normalized to to predict the sample classes and obtain the resultant classification labels for fault identification.
In the proposed ensemble method, the SCN learners (i.e., SCN-D, SCN-X and SCN-H) are built on different training datasets, including frequency spectrum data, time–frequency images, and their hybrid data, respectively. The pseudo code of the SCNs ensemble for fault recognition in this section is described in Algorithm 2. The goal of the ensemble learning is to combine the various features extracted from the sample data in different domains via the SCN based sub-learners for fault analysis. Because the stochastic configuration algorithm is incremental learning, the SCN model is built by adding new hidden nodes gradually. So in the ensemble learning process, the SCN learners are modeled synchronously and have the same number of hidden nodes with the weight , and the error is calculated with the configured parameters. In addition, the SCN model can also be built separately to obtain the optimal sub-learners, and then the global weight is calculated, and the classification results are output.
| Algorithm 2: SCNs ensemble |
 |
4. Performance Evaluation
4.1. Experimental Setup
In this section, the vibration data are used for experimental comparison. The original collected bearing data are time–series vibration signals, and they are sampled via a sliding window with a fixed size. In this experiment, the window size is set to 1024 and used to obtain learning samples, then the Fourier transform and STFT are carried out to obtain samples of the frequency domain and time–frequency domain. The size of the frequency spectrum is 512, and that of the time–frequency image is . As shown in Figure 4, the samples of different fault modes in multiple domains are displayed. We can find that the signal of the normal sample is low frequency, while the samples of different fault locations have more high–frequency signals, and there are differences among them.
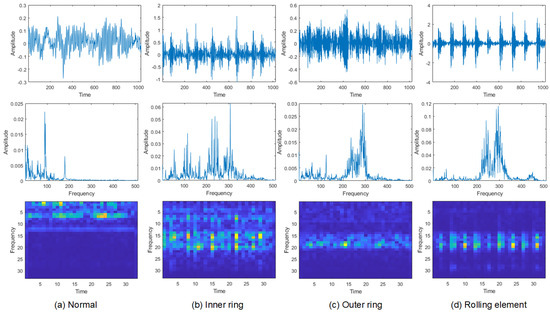
Figure 4.
Samples of different categories in multiple domains on the CWRU dataset.
We first evaluate the classification results with samples from different domains, and the dataset provided by the Bearing Data Center at Case Western Reserve University (CWRU) [36] is used for comparison. The bearing data are collected from the drive end of the electrical machining with 1797 r/min rotating speed and 12 KHz the sampling frequency. There are four modes in the CWRU dataset including normal, inner ring faults, outer ring faults, and rolling element faults. As shown in Table 1, because of the different bearing diameters, the dataset has ten different classes in total, including normal condition and nine different severity faults. In the learning process, the samples are randomly selected, with as the training dataset and the remaining as the testing dataset. For SCN and 2DSCN, we take constructive sequence , , training tolerance error , maximum number of candidate nodes , and g is the sigmoid activation function.

Table 1.
The description of the CWRU dataset.
For the CWRU dataset, the samples from the time domain, frequency domain, and time–frequency domain are used to build the SCN models, respectively. The recognition rates of the SCN models in each domain are shown in Figure 5. The results show that the recognition rate increases with the increase in the number of hidden nodes L; in particular, the SCN model built with the frequency-domain samples obtains high testing accuracy with fewer nodes, followed by the SCN model built with the time–frequency domain samples. However, the SCN model built with time-domain samples has a lower recognition rate at the same number of hidden nodes L. The result demonstrates that the SCN model built by using samples in the frequency domain and the time–frequency domain has advantages in the fault data classification task.

Figure 5.
Performance comparison of different samples on the CWRU dataset.
4.2. Results and Discussion
In the experiments, the vibration data provided by the Jiangnan University (JNU) [37], the Southeast University (SEU) [38] and the University of Connecticut (UoC) [39] are used for performance comparison. The JNU dataset is collected under different rotating speeds, and there are four operating modes for each speed. The JNU dataset has twelve categories with a total of 8790 samples. The SEU dataset is also collected under different rotating speeds and load conditions, and has twenty categories with a total of 2040 samples. Similarly, the UoC dataset has nine categories with a total of 3238 samples. Then, the corresponding frequency spectrum data and time–frequency images are obtained via Fourier transform and STFT.
For each dataset, the samples are randomly selected, with as the training dataset and the remaining as the testing dataset. In the algorithm implementation, the weights in NNRW and NNRW2D are randomly assigned from and , respectively, while the biases for them are randomly assigned from . For the SCNs, the parameters and r are the same as those set on the CWRU dataset.
In the stochastic configuration algorithm, the output weight parameter is calculated via the optimal model, i.e., Equation (16). For the regularization factor , first we take with other parameters fixed. The difference in the classification rate under different values is small. As shown in Figure 6, is reset to some smaller values . For the JNU dataset, the optimal model is insensitive to the factor and obtains close values, which indicates that the parameter itself calculated by the stochastic configuration algorithm is sparse and the regular term has a weak effect. For the SEU and UoC dataset, there is no obvious trend in the recognition rate with different regularization factor values. According to the comparison results, is set to 0.05 in the following discussion.
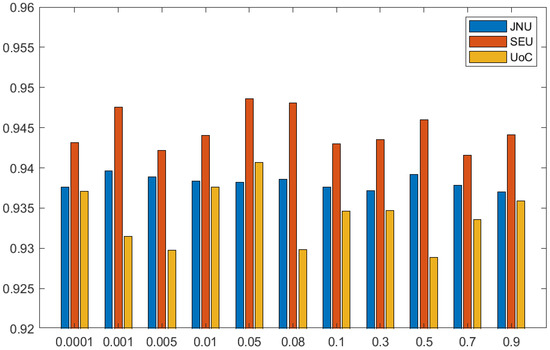
Figure 6.
Testing results of the SCNs on different factor .
To show the results of the visual comparison, set the maximum number of hidden modes for the JNU dataset and for the SEU dataset, and the other parameters are fixed. For the randomized algorithms, the SCN-D and NNRW are built with frequency spectrum signal , the SCN-X and NNRW2D are built with time–frequency image data , and the SCN-H is built with hybrid data . As shown in Figure 7 and Figure 8, the recognition rates of the comparison models increase with the increase in the number of hidden layer nodes L. The results show that the SCN-H model built with the hybrid data obtains the highest accuracy values. Meanwhile, the SCN-D and SCN-X methods obtain higher accuracy than the NNRW and NNRW2D methods under the same training data, respectively. Compared with SCN-X, the SCN-D can be built with fewer hidden nodes to obtain the same recognition rate, and more fault features can be extracted from the frequency spectrum data.
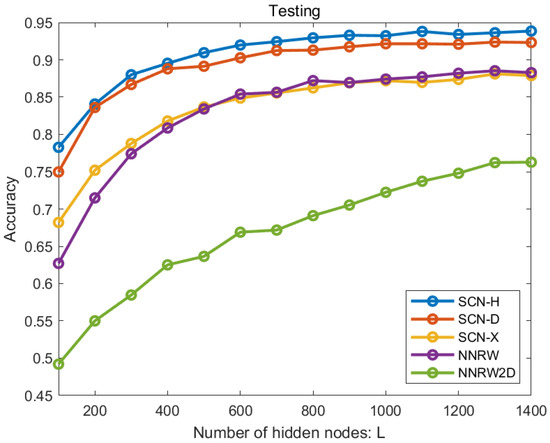
Figure 7.
Performance comparison on JNU dataset.
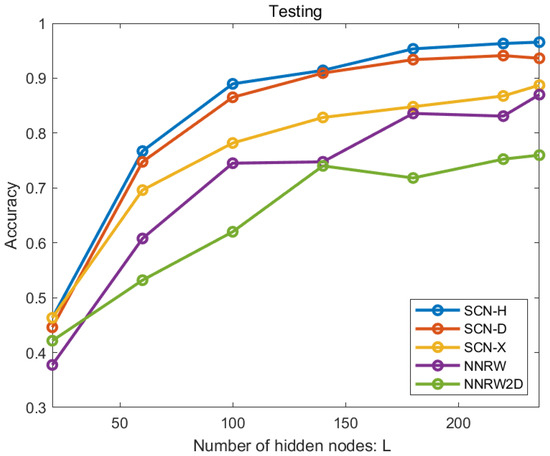
Figure 8.
Performance comparison on SEU dataset.
To demonstrate the effectiveness of the proposed model, for the SCN-based models, we set the parameter , , , , . For the NNRW and NNRW2D models, the weights and bias are randomly configured from . The comparison models are fully trained with the sigmoid activation function, and 30 independent trials are performed on each dataset. As shown in Table 2, the indexes accuracy, precision and recall score are calculated. The SCN-H model has the highest recognition rate, followed by the SCN-, NNRW- and SCN2D-based models, and the NNRW2D-based model obtains the lowest accuracy. The experimental results show the SCN-based models are superior to the NNRW-based models on the training samples with same data dimension. And the SCN model built with the hybrid data has learned better fault representation on each dataset.

Table 2.
Performance comparison with fault dataset.
We also evaluate the effectiveness and advantages of the proposed ensemble SCNs on the JNU, SEU and UoC datasets with the existing ensemble models: DNNE [29], SCNE [30], RNNE-RVFL and RNNE-SCN [32]. For the SCNs ensemble algorithm, the average, voting and negative correlation learning (NCL) [40] strategies are used for ensemble learning. As shown in Table 3, the SCN ensemble models with NCL strategy obtain higher values on JNU and SEU dataset, and are comparable on the UoC dataset. The evaluation results show that the SCNs ensemble model with sub-learners built on multiple source training data obtains comparable fault classification results. Moreover, for the SCN-ensemble methods, due to the proposed method only having three sub-learners, the average and NCL strategies obtain higher resulted values than the voting strategy.

Table 3.
Performance comparison on ensemble models.
4.3. Comparison with Deep Learning Models
In our experimental study, the proposed method is compared with some classic deep learning models, including multi-layer perceptron (MLP) [41], CNN [42], denoising auto-encoder (DAE) [43], AlexNet [44], ResNet18 [45] and long short-term memory network (LSTM) [46]. Table 4 shows the recognition results of the comparison methods. It can be seen that all the methods can achieve accuracy on the CWRU dataset because of its low data complexity. For the JNU and SEU datasets, the SCN-H and SCN-Ensemble methods obtain comparable recognition rates. In particular, the proposed SCNs-based method outperforms the compared methods on the UoC dataset.

Table 4.
Performance comparison with deep learning methods.
5. Conclusions
This paper proposes a classification method based on SCNs ensemble, and the sample data in different domains are analyzed and used to build SCNs-based classifiers. Due to the stochastic configuration mechanism for the random weights and bias in the modeling process, the SCN models obtain better classification results than the NNRW models. The experimental results show that the proposed SCNs ensemble method outperforms other randomized methods because of the application of multiple domain sample data, and obtains good classification results. Compared with deep learning methods, the proposed method has comparable recognition performance, and the algorithm implementation is simple and easy, which demonstrates great potential in the field of industrial informatics. For future works, the deep SCNs can be considered the base classifier, and various hybrid data are analyzed to characterize the fault information.
Author Contributions
Conceptualization, Q.W.; methodology, Q.W.; software, Q.W.; validation, Q.W.; formal analysis, Q.W.; investigation, Q.W., D.L., H.T., Y.Q. and D.Z.; resources, Q.W.; data curation, Q.W., D.L., H.T. and Y.Q.; writing—original draft preparation, Q.W.; writing—review and editing, Q.W. and D.Z.; visualization, Q.W. and D.Z.; supervision, Q.W.; project administration, Q.W.; funding acquisition, Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fundamental Research Funds for the Central Universities (2022QN1045).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Benbouzid, M. Bibliography on induction motors faults detection and diagnosis. IEEE Trans. Energy Convers. 1999, 14, 1065–1074. [Google Scholar] [CrossRef]
- Zarei, J.; Tajeddini, M.A.; Karimi, H.R. Vibration analysis for bearing fault detection and classification using an intelligent filter. Mechatronics 2014, 24, 151–157. [Google Scholar] [CrossRef]
- Peng, Z.; Chu, F. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mech. Syst. Signal Process. 2004, 18, 199–221. [Google Scholar] [CrossRef]
- Al-Badour, F.; Sunar, M.; Cheded, L. Vibration analysis of rotating machinery using time–frequency analysis and wavelet techniques. Mech. Syst. Signal Process. 2011, 25, 2083–2101. [Google Scholar] [CrossRef]
- He, Q.; Liu, Y.; Long, Q.; Wang, J. Time-Frequency Manifold as a Signature for Machine Health Diagnosis. IEEE Trans. Instrum. Meas. 2012, 61, 1218–1230. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to bearing defect diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, T.; Wu, J.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Deep Learning Algorithms for Rotating Machinery Intelligent Diagnosis: An Open Source Benchmark Study. ISA Trans. 2020, 107, 224–255. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar] [CrossRef]
- Liu, R.; Meng, G.; Yang, B.; Sun, C.; Chen, X. Dislocated Time Series Convolutional Neural Architecture: An Intelligent Fault Diagnosis Approach for Electric Machine. IEEE Trans. Ind. Inform. 2017, 13, 1310–1320. [Google Scholar] [CrossRef]
- Huang, W.; Cheng, J.; Yang, Y.; Guo, G. An improved deep convolutional neural network with multi-scale information for bearing fault diagnosis. Neurocomputing 2019, 359, 77–92. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Shen, W.; Huang, C. Online Fault Diagnosis Method Based on Transfer Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2020, 69, 509–520. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, S.; Wei, Y.; Zhang, H. A novel feature adaptive extraction method based on deep learning for bearing fault diagnosis. Measurement 2021, 185, 110030. [Google Scholar] [CrossRef]
- Guan, Y.; Meng, Z.; Sun, D.; Liu, J.; Fan, F. 2MNet: Multi-sensor and multi-scale model toward accurate fault diagnosis of rolling bearing. Reliab. Eng. Syst. Saf. 2021, 216, 108017. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image. Measurement 2020, 157, 107667. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Gültekin, Ö.; Cinar, E.; Özkan, K.; Yazıcı, A. A novel deep learning approach for intelligent fault diagnosis applications based on time-frequency images. Neural Comput. Appl. 2022, 34, 4803–4812. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, F.; Li, Z. Multiview Feature Selection With Information Complementarity and Consensus for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5058–5070. [Google Scholar] [CrossRef]
- Scardapane, S.; Wang, D. Randomness in neural networks: An overview. WIREs Data Min. Knowl. Discov. 2017, 7, e1200. [Google Scholar] [CrossRef]
- Schmidt, W.F.; Kraaijveld, M.A.; Duin, R.P.W. Feedforward neural networks with random weights. In Proceedings of the 11th IAPR International Conference on Pattern Recognition, Hague, The Netherlands, 30 August–3 September 1992; pp. 1–4. [Google Scholar]
- Pao, Y.H.; Takefuji, Y. Functional-link net computing: Theory, system architecture, and functionalities. Computer 1992, 25, 76–79. [Google Scholar] [CrossRef]
- Pao, Y.H.; Phillips, S.M.; Sobajic, D.J. Neural-net computing and the intelligent control of systems. Int. J. Control 1992, 56, 263–289. [Google Scholar] [CrossRef]
- Igelnik, B.; Pao, Y.H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net. IEEE Trans. Neural Netw. 1995, 6, 1320–1329. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, M. Stochastic Configuration Networks: Fundamentals and Algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, D. 2-D Stochastic Configuration Networks for Image Data Analytics. IEEE Trans. Cybern. 2019, 51, 359–372. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Felicetti, M.J. Stochastic Configuration Machines for Industrial Artificial Intelligence. arXiv 2023, arXiv:2308.13570. [Google Scholar]
- Felicetti, M.J.; Wang, D. Stochastic Configuration Machines: FPGA Implementation. arXiv 2023, arXiv:2310.19225. [Google Scholar]
- Alhamdoosh, M.; Wang, D. Fast decorrelated neural network ensembles with random weights. Inf. Sci. 2014, 264, 104–117. [Google Scholar] [CrossRef]
- Wang, D.; Cui, C. Stochastic configuration networks ensemble with heterogeneous features for large-scale data analytics. Inf. Sci. 2017, 417, 55–71. [Google Scholar] [CrossRef]
- Wang, D.; Li, M. Deep Stochastic Configuration Networks with Universal Approximation Property. In Proceedings of the 2018 International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Huang, C.; Li, M.; Wang, D. Stochastic configuration network ensembles with selective base models. Neural Netw. 2021, 137, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hao, R.; Zhang, T.; Wang, X. Vibration fault diagnosis based on stochastic configuration neural networks. Neurocomputing 2021, 434, 98–125. [Google Scholar] [CrossRef]
- Li, W.; Deng, Y.; Ding, M.; Wang, D.; Sun, W.; Li, Q. Industrial data classification using stochastic configuration networks with self-attention learning features. Neural Comput. Appl. 2022, 34, 22047–22069. [Google Scholar] [CrossRef]
- Dudek, G. Generating random weights and biases in feedforward neural networks with random hidden nodes. Inf. Sci. 2019, 481, 33–56. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Li, K.; Ping, X.; Wang, H.; Chen, P.; Cao, Y. Sequential Fuzzy Diagnosis Method for Motor Roller Bearing in Variable Operating Conditions Based on Vibration Analysis. Sensors 2013, 13, 8013–8041. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; McAleer, S.M.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, S.; Tang, J. Gear Fault Data. 2018. Available online: https://figshare.com/articles/dataset/Gear_Fault_Data/6127874/1 (accessed on 12 May 2023).
- Rosen, B.E. Ensemble Learning Using Decorrelated Neural Networks. Connect. Sci. 1996, 8, 373–384. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Volume 1: Foundations; MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1998; pp. 255–258. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).