Biophotons: A Hard Problem
Abstract
1. Introduction
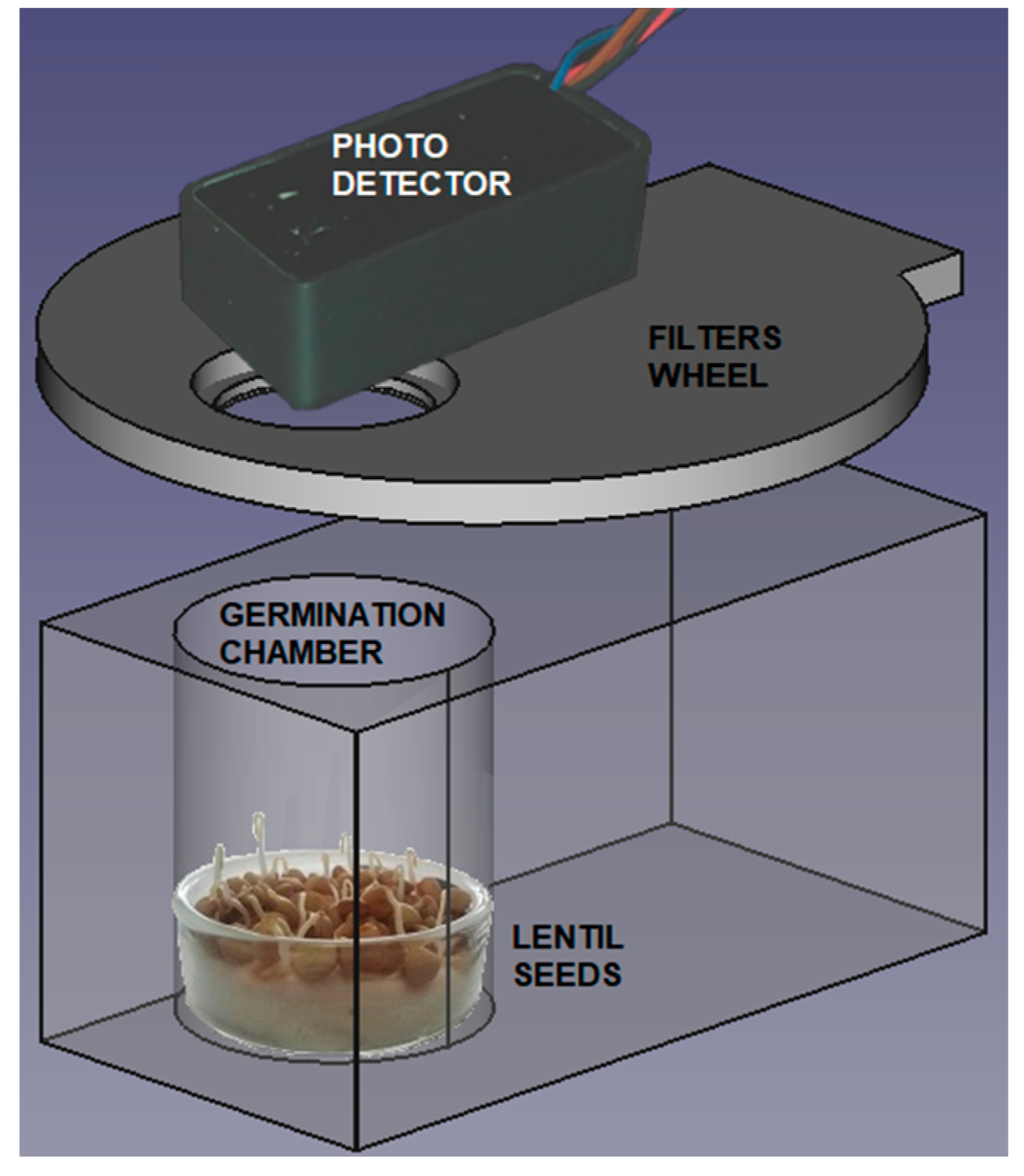
2. Methods and Experimental Data
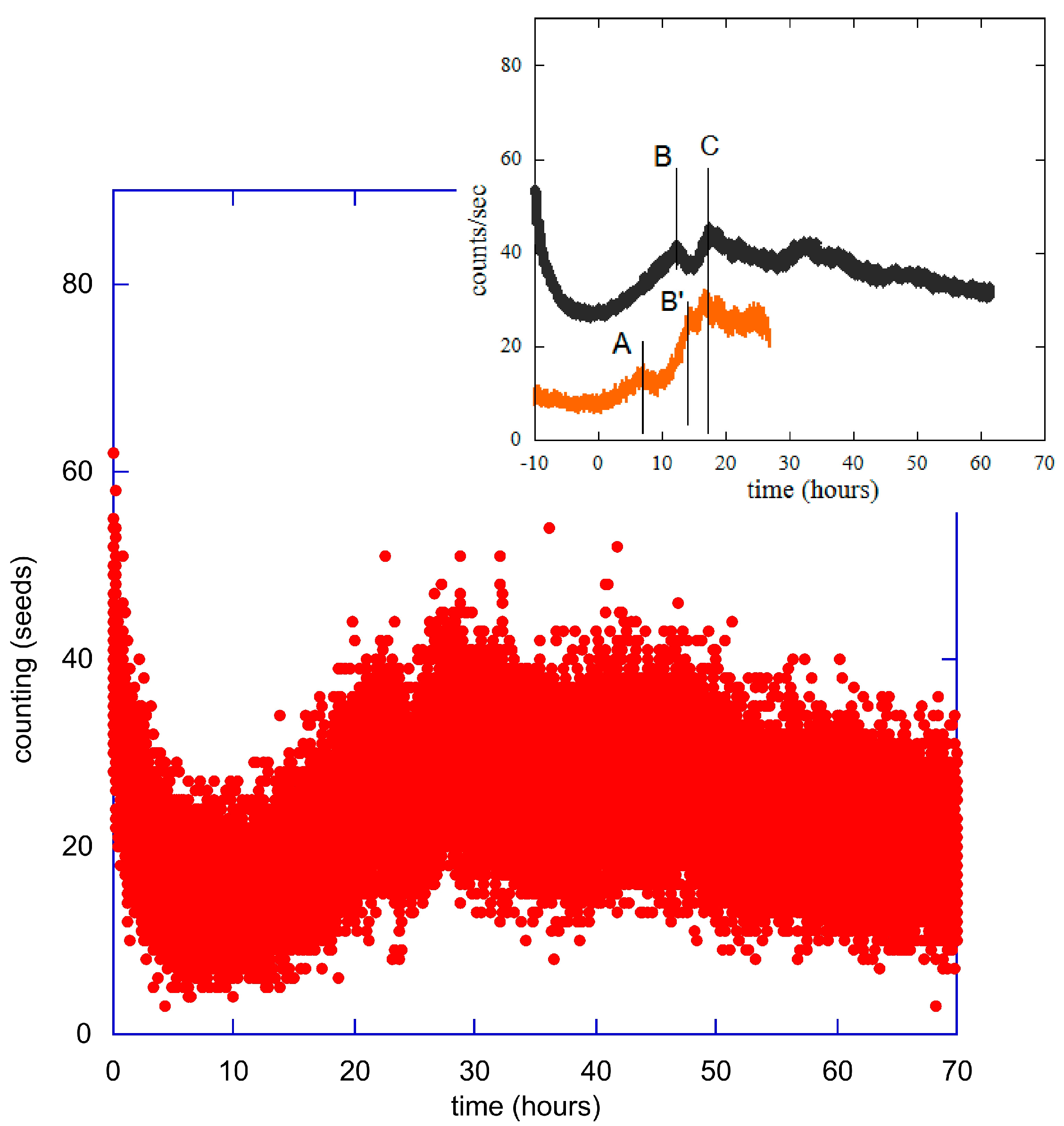
3. Statistical Analysis of the Experimental Data
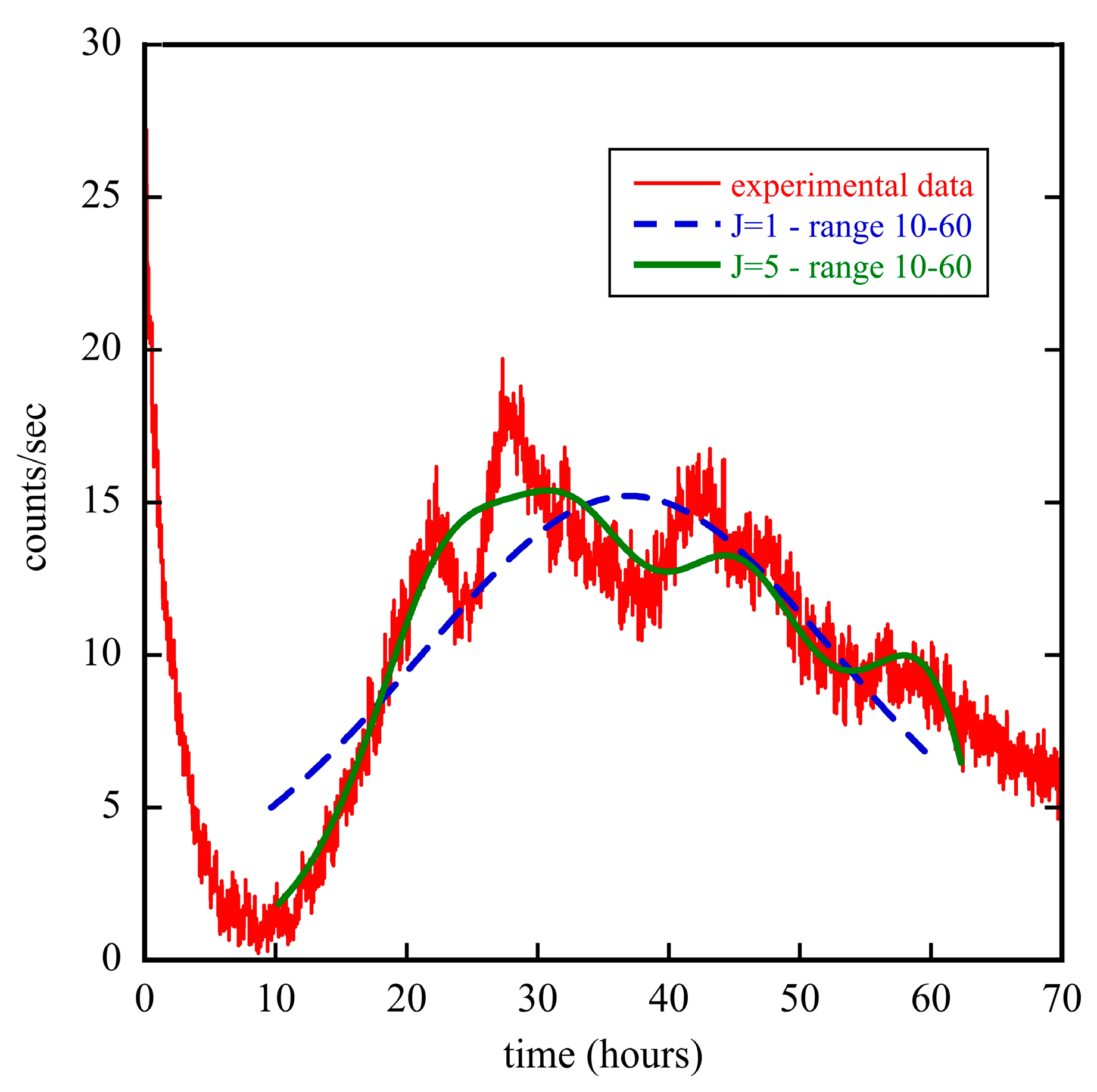
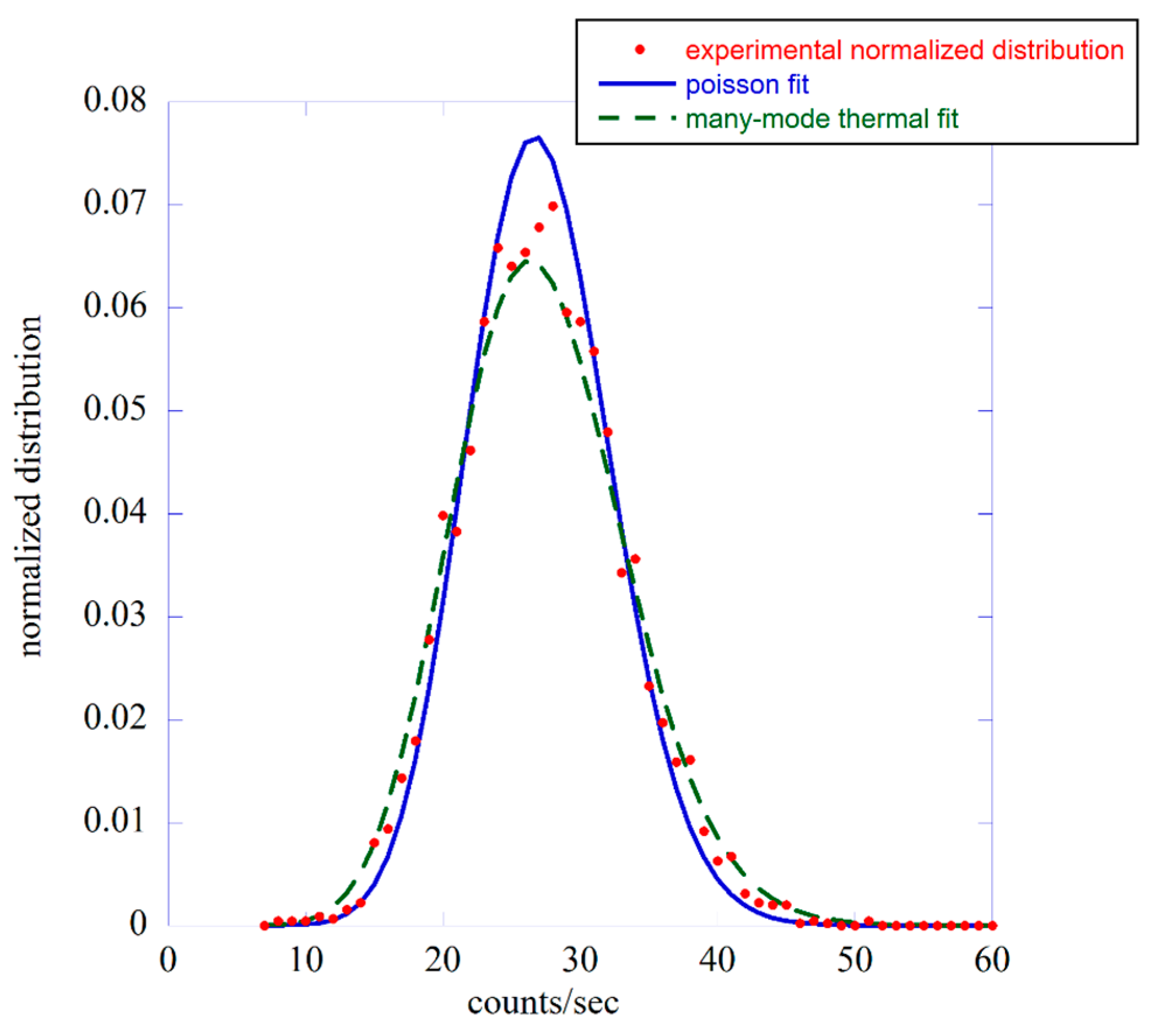
3.1. The Probability Distribution Function Approach
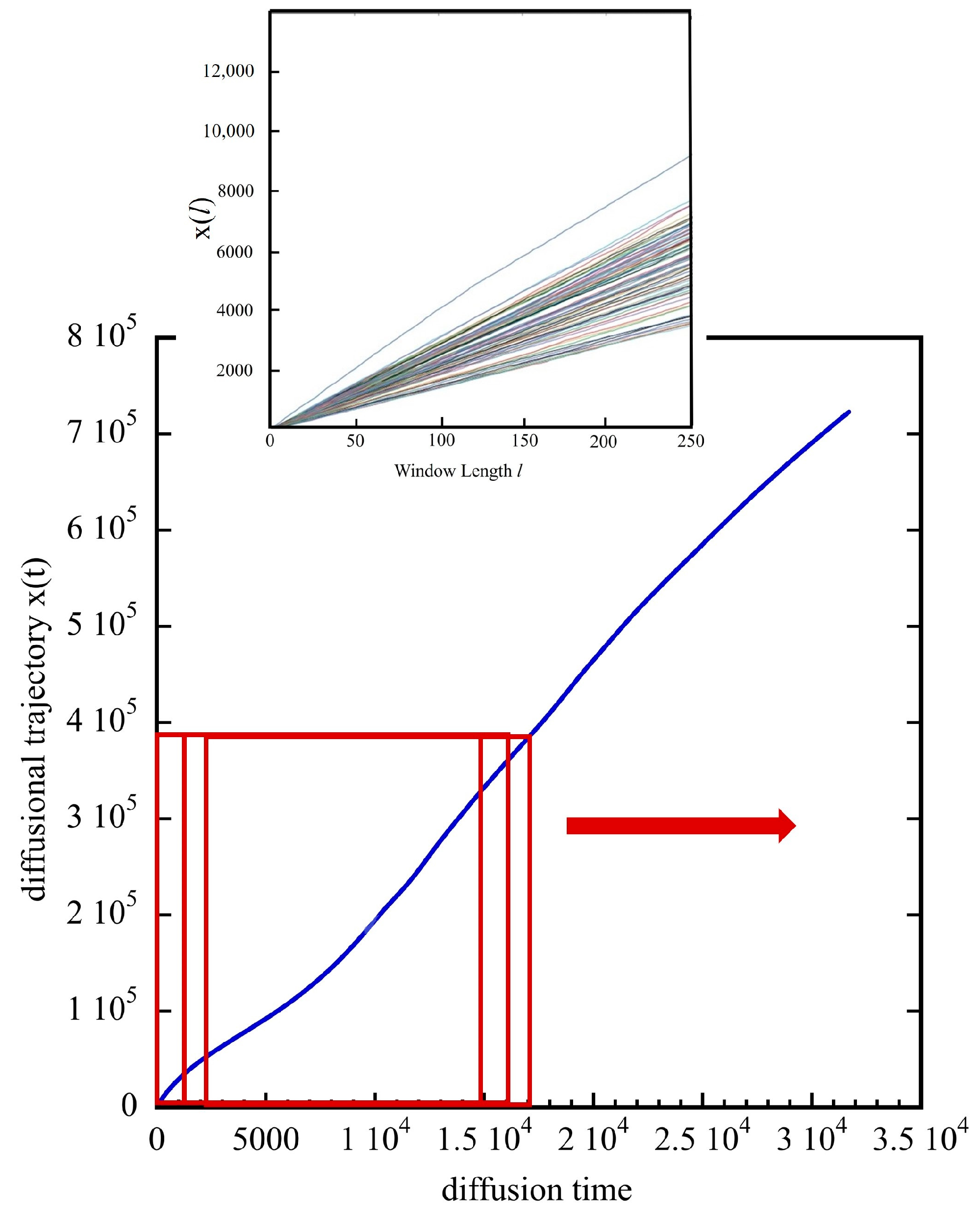
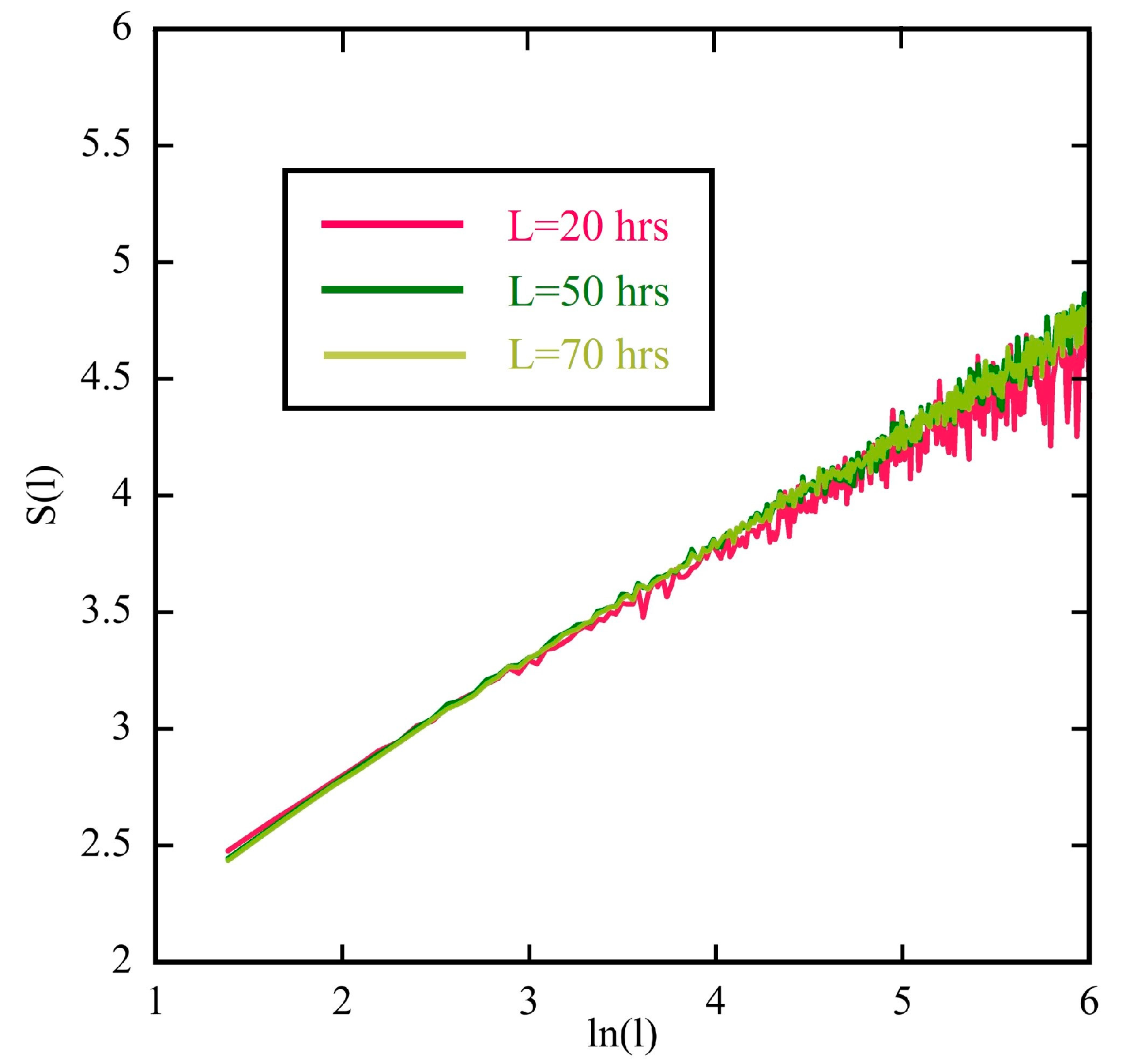
3.2. The Diffusion Entropy Method
4. External Excitation and Biophoton Emission
5. Biophotons in Living Materials
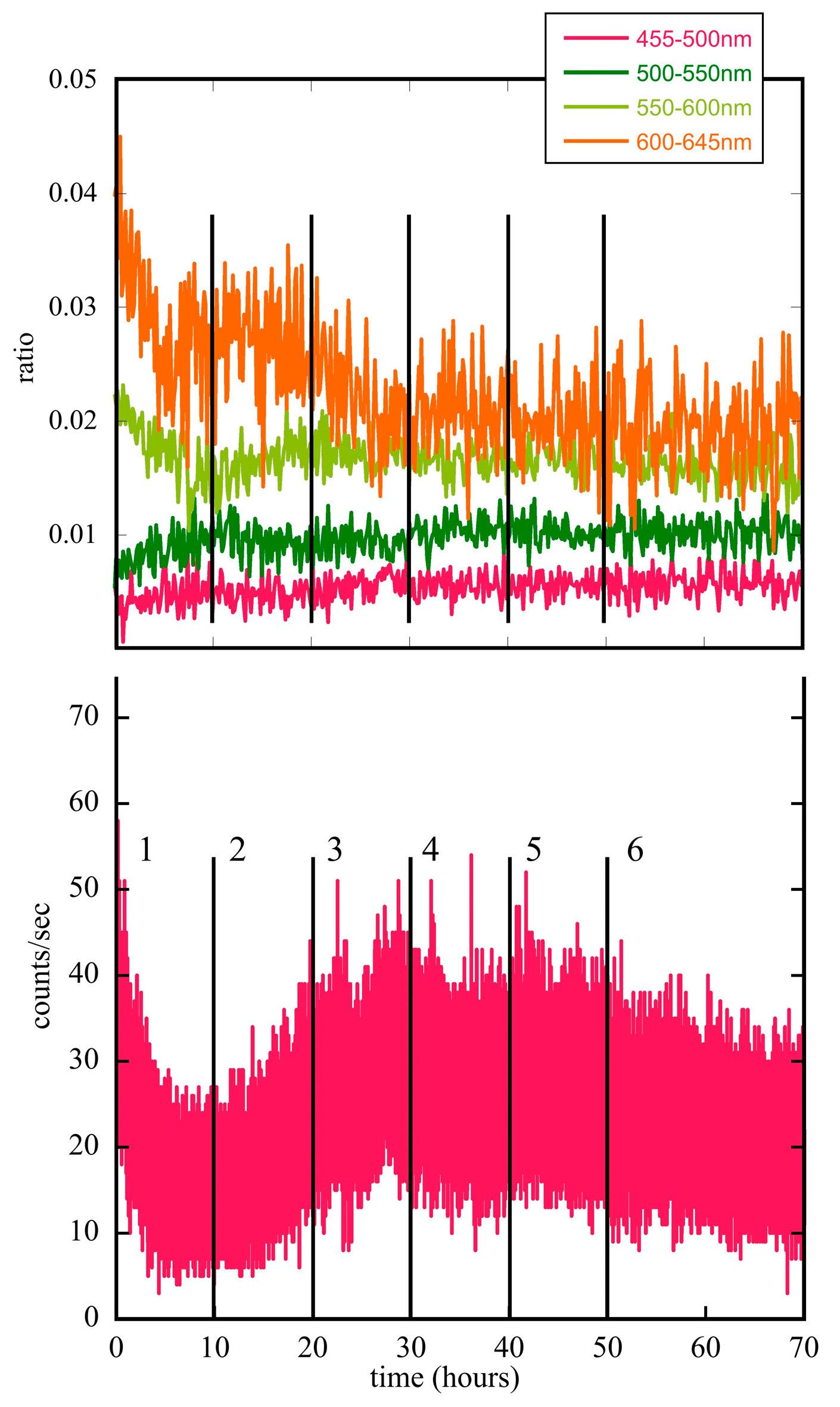
5.1. Seeds and Plants
5.2. Food Quality
5.3. Humans and Animals
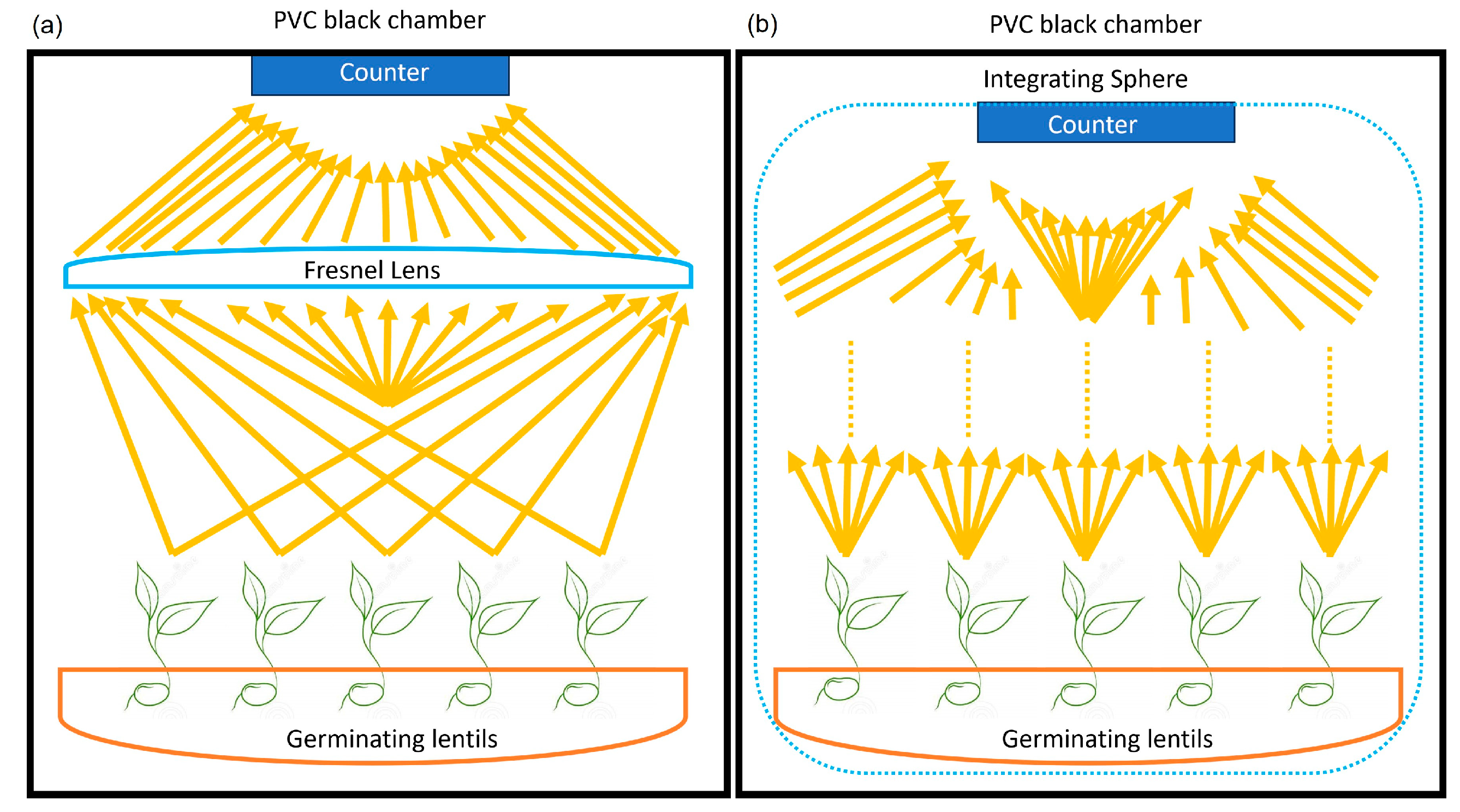
6. Future Experimental Upgrade and Perspective
7. Conclusions and Suggestions for Future
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popp, F.A.; Gu, Q.; Li, K.H. Biophoton Emission: Experimental Background and Theoretical Approaches. Mod. Phys. Lett. B 1994, 8, 1269–1296. [Google Scholar] [CrossRef]
- Van Wijk, R. Light in Shaping Life: Biophotons in Biology and Medicine; Boekenservice: Almere, The Netherlands, 2014. [Google Scholar]
- Mayburov, S.; Volodyaev, I. Photon production and communications in Biological Systems. In Proceedings of the Progress In Electromagnetics Research Symposium Proceedings, Moscow, Russia, 18–21 August 2009; pp. 1937–1941. [Google Scholar]
- Gurwitsch, A.G. Die Natur des spezifischen Erregers der Zellteilung. Arch. Entw. Mech. Org. 1923, 100, 11–40. [Google Scholar] [CrossRef]
- Reiter, T.; Gabor, D. Ultraviolette Strahlung und Zellteilung; Wiss. Verffentlichungen Aus Dem Siemens-Konzern; Springer: Berlin/Heidelberg, Germany, 1928; p. 184. [Google Scholar]
- Colli, L.; Facchini, U. Light Emission by Germinating Plants. Il Nuovo C. 1954, 12, 150–153. [Google Scholar] [CrossRef]
- Colli, L.; Facchini, U.; Guidotti, G.; Dugnani Lonati, R.; Orsenigo, M.; Sommariva, O. Further Measurements on the Bioluminescence of the Seedlings. Experientia 1955, 11, 479–481. [Google Scholar] [CrossRef]
- Fels, D. Cellular Communication through light. PLoS ONE 2009, 4, e5086. [Google Scholar] [CrossRef]
- Mayburov, S.N. Photonic Communications in Biological Systems. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2011, 15, 260–265. [Google Scholar]
- Kucera, O.; Cifra, M. Cell-to-cell signaling through light: Just a ghost of chance? Cell Commun. Signal. 2013, 11, 87. [Google Scholar] [CrossRef] [PubMed]
- Hunt von Herbing, I.; Tonello, L.; Benfatto, M.; Pease, A.; Grigolini, P. Crucial Development: Criticality Is Important to Cell-to-Cell Communication and Information Transfer in Living Systems. Entropy 2021, 23, 1141. [Google Scholar] [CrossRef]
- Beloussov, L.V.; Burlakov, A.B.; Louchinskaia, N.N. Biophotonic Pattern of optical interaction between fish eggs and embryos. Indian J. Exp. Biol. 2003, 41, 424–430. [Google Scholar]
- Volodyaev, I.; Beloussov, L.V. Revisiting the mitogenetic effect of ultra-weak photon emission. Front. Physiol. 2015, 6, 241. [Google Scholar] [CrossRef]
- Gallep, C.M.; Dos Santos, S.R. Photon-count during germination of wheat (Triticum aestivum) in waste water sediment solution correlated with seedling growth. Seed Sci. Technol. 2007, 35, 607–614. [Google Scholar] [CrossRef]
- Tessaro, L.W.E.; Dotta, B.T.; Persinger, M.A. Bacterial biophotons as non-local information carriers: Species-specific spectral characteristics of a stress response. Microbiol. Open 2019, 8, e761. [Google Scholar] [CrossRef]
- Popp, F.A. Cancer growth and its inhibition in terms of Coherence. Electromagn. Biol. Med. 2009, 28, 53–60. [Google Scholar] [CrossRef]
- Benfatto, M.; Pace, E.; Curceanu, C.; Scordo, A.; Clozza, A.; Davoli, I.; Lucci, M.; Francini, R.; De Matteis, F.; Grandi, M.; et al. Biophotons and Emergence of Quantum Coherence—A Diffusion Entropy Analysis. Entropy 2021, 23, 554. [Google Scholar] [CrossRef]
- Allegrini, P.; Grigolini, P.; Hamilton, P.; Palatella, L.; Raffaelli, G. Memory beyond memory in heart heating, a sign of a healthy physiological condition. Phys. Rev. E 2002, 65, 041926. [Google Scholar] [CrossRef]
- Allegrini, P.; Benci, V.; Grigolini, P.; Hamilton, P.; Ignaccolo, M.; Menconi, G.; Palatella, L.; Raffaelli, G.; Scafetta, N.; Virgilio, M.; et al. Compression and diffusion: A joint approach to detect complexity. Chaos Solitons Fractals 2003, 15, 517–535. [Google Scholar] [CrossRef]
- Falconi, M.; Loreto, V.; Vulpiani, A. Kolmogorov Legacy about Entropy; Springer: Berlin/Heidelberg, Germany, 2003; pp. 85–105. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph, and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Mancuso, S. The Revolutionary Genius of Plants: A New Understanding of Plant Intelligence and Behaviour; Simon and Shuster: New York, NY, USA, 2018. [Google Scholar]
- Mancuso, S.; Viola, A. Brilliant Green: The Surprising History and Science of Plant Intelligence; Island Press: Washington, DC, USA, 2015. [Google Scholar]
- Photon Counting Head H12386-210. Available online: https://www.hamamatsu.com/eu/en/product/optical-sensors/pmt/pmt-module/photon-counting-head/H12386-210.html (accessed on 12 June 2024).
- Test Sheet Hamamatsu for the Phototube H12386-210, Serial Number 30050260. (This Test Sheet Is Specific for the Phototube We Have Used). Available online: https://www.hamamatsu.com/resources/pdf/etd/H12386_TPMO1073E.pdf (accessed on 12 June 2024).
- Saeidfirozeh, H.; Shafiekhani, A.; Cifra, M.; Masoudi, A.A. Endogenous Chemiluminescence from Germinating Arabidopsis thaliana Seeds. Sci. Rep. 2018, 8, 16231. [Google Scholar] [CrossRef]
- Benfatto, M.; Pace, E.; Davoli, I.; Francini, R.; De Matteis, F.; Scordo, A.; Clozza, A.; De Paolis, L.; Curceanu, C.; Grigolini, P. Biophotons: New Experimental Data and Analysis. Entropy 2023, 25, 1431. [Google Scholar] [CrossRef]
- Verhulst, P.F. Recherches mathmatiques sur la loi d’accroissement de la population. Nouv. Mem. Acad. R. Sci. Brux. 1845, 18, 1–40. [Google Scholar]
- Alvermann, M.; Srivastava, Y.N.; Swain, J.; Widom, A. Biological electric fields and rate equations for biophotons. Eur. Biophys. J. 2015, 44, 165–170. [Google Scholar] [CrossRef]
- Mahmoodi, K.; West, B.J.; Grigolini, P. Self-organizing Complex Networks: Individual versus global rules. Front. Physiol. 2017, 8, 478. [Google Scholar] [CrossRef]
- Volodyaev, I.; van Wijk, E.; Cifra, M.; Vladimirov, Y.A. (Eds.) Ultra-Weak Photon Emission from Biological Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Cifra, M.; Brouder, C.; Nerudova, M.; Kucera, O. Biophotons, coherence and photo-count statistics: A critical review. J. Lumin. 2015, 164, 38–51. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Oxford University Press: Oxford, UK, 2000; ISBN 978-0-19-850176-3 (Pbk). [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Latora, V.; Baranger, M. Kolomogorov-Sinai Entropy Rate versus Physical Entropy. Phys. Rev. Lett. 1999, 82, 520. [Google Scholar] [CrossRef]
- Scafetta, N.; Hamilton, P.; Grigolini, P. The thermodynamics of social processes: The teen birth phenomenon. Fractals 2001, 9, 193–208. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion Entropy analysis. Phys. Rev. E 2002, 66, 036130. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Cakir, R.; Grigolini, P.; Krokhin, A.A. Dynamical origin of memory and renewal. Phys. Rev. E 2006, 74, 021108. [Google Scholar] [CrossRef] [PubMed]
- Grigolini, P.; Palatella, L.; Raffaelli, G. Anomalous Diffusion: An Efficient Way to Detect Memory in Time Series. Fractals 2001, 9, 439–449. [Google Scholar] [CrossRef]
- Grigolini, P. Emergence of biological complexity: Criticality, renewal and memory. Chaos Solitons Fractals 2015, 81, 575–588. [Google Scholar] [CrossRef]
- Vanni, F.; Lukovi’c, M.; Grigolini, P. Criticality and Transmission of Information in a Swarm of Cooperative Units. Phys. Rev. Lett. 2011, 107, 078103. [Google Scholar] [CrossRef]
- Attanasi, A.; Cavagna, A.; Del Castello, L.; Giardina, I.; Melillo, S.; Parisi, L.; Pohl, O.; Rossaro, B.; Shen, E.; Silvestri, E.; et al. Finite-Size Scaling as a Way to Probe Near-Criticality in Natural Swarms. Phys. Rev. Lett. 2014, 113, 238102. [Google Scholar] [CrossRef]
- Bohara, G.; Lambert, D.; West, B.J.; Grigolini, P. Crucial events, randomness and multifractality in heartbeat. Phys. Rev. E 2017, 96, 062216. [Google Scholar] [CrossRef]
- West, B.J.; Grigolini, P.; Bologna, M. Crucial Event Rehabilitation Therapy; Springer Briefs in Bioengineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Culbreth, G.; West, B.J.; Grigolini, P. Entropic Approach to the Detection of Crucial Events. Entropy 2019, 21, 178. [Google Scholar] [CrossRef]
- Allegrini, P.; Menicucci, D.; Bedini, R.; Fronzoni, L.; Gemignani, A.; Grigolini, P.; West, B.J.; Paradisi, P. Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E 2009, 80, 061914. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Tuladhar, R.; Culbreth, G.; Bohara, G.; Cornforth, D.; West, B.J.; Grigolini, P. Diffusion Entropy versus Multiscale and Renyi Entropy to detect progression of Autonomic Neuropathy. Front. Physiol. 2020, 11, 607324. [Google Scholar] [CrossRef]
- Popp, F.A. Electromagnetic Bio-Information, 2nd ed.; Popp, F.A., Becker, G., Konig, H.L., Peschka, W., Hershberger, W., Eds.; Urban & Schwarzenberg: Muchen, Germany, 1989; pp. 144–167. [Google Scholar]
- Slawinski, J.; Popp, F.A. Temperature Hysteresis of Low-Level Luminescence from Plants and its Thermodynamical Analysis. J. Plant Physiol. 1987, 130, 111–123. [Google Scholar] [CrossRef]
- Slawinski, J.; Ezzahir, A.; Godlewski, M.; Kwiecinska, T.; Rajfur, Z.; Sitko, D.; Wierzuchowska, D. Stress-induced photon emission from perturbed organisms. Experientia 1992, 48, 1041–1058. [Google Scholar] [CrossRef]
- Salin, M.L.; Bridges, S.M. Chemiluminescence in Wounded Root Tissue. Plant Physiol. 1981, 67, 43–46. [Google Scholar] [CrossRef]
- Winkler, R.; Guttenberger, H.; Klima, H. Ultraweak and Induced Photon Emission after Wounding of Plants. Photochem. Photobiol. 2009, 85, 962–965. [Google Scholar] [CrossRef]
- Tudisco, S.; Musumeci, F.; Scordino, A.; Privitera, G. Advanced research equipment for fast ultraweak luminescence analysis. Rev. Sci. Instrum. 2003, 74, 4485–4490. [Google Scholar] [CrossRef]
- Scordino, A.; Triglia, A.; Musumeci, F.; Grasso, F.; Rajfur, Z. Influence of the presence of atrazine in water on the in-vivo delayed luminescence of Acetabularia acetabulum. J. Photochem. Photobiol. B Biol. 1996, 32, 11–17. [Google Scholar] [CrossRef]
- Brizhik, L.; Scordino, A.; Triglia, A.; Musumeci, F. Delayed luminescence of biological systems arising from correlated many soliton states. Phys. Rev. E 2001, 64, 031902. [Google Scholar] [CrossRef]
- Scordino, A.; Grasso, R.; Gulino, M.; Lanzanò, L.; Musumeci, F.; Privitera, G.; Tedesco, M.; Triglia, A.; Brizhik, L. Delayed. luminescence from collagen as arising from soliton and small polaron states. Int. J. Quantum Chem. 2010, 110, 221–229. [Google Scholar] [CrossRef]
- Daqing, P. On the stress-induced photon emission from organism: II, how will the stress-transfer kinetics affect the photo-genesis? Appl. Sci. 2020, 2, 1556. [Google Scholar] [CrossRef]
- Sarmah, B.; Rajkhowa, R.; Chakraborty, I.; Govindaraju, I.; Dwivedi, S.K.; Mazumder, N.; Baruah, V.J. Precision opto-imaging techniques for seed quality assessment: Prospects and scope of recent advances. In Earth Observation, Remote Sensing in Precision Agriculture; Academic Press: Cambridge, MA, USA, 2024; Chapter 21. [Google Scholar]
- Jócsák, I.; Lukács, H.; Varga-Visi, É.; Somfalvi-Tóth, K.; Keszthelyi, S. Identification and investigation of barley powdery mildew (Blumeria graminis f. sp. tritici) infection in winter wheat with conventional stress reactions and non-invasive biophoton emission parameters. J. Biosci. 2024, 49, 6. [Google Scholar]
- Lukaács, H.; Joócsaák, I.; Somfalvi-Tóth, K.; Keszthelyi, S. Physiological Responses Manifested by Some Conventional Stress Parameters and Biophoton Emission in Winter Wheat as a Consequence of Cereal Leaf Beetle Infestation. Front. Plant Sci. 2022, 13, 839855. [Google Scholar] [CrossRef]
- Jócsák, I.; Malgwi, I.; Rabnecz, G.; Szegő, A.; Varga-Visi, É.; Végvári, G.; Pónya, Z. Effect of cadmium stress on certain physiological parameters, antioxidative enzyme activities and biophoton emission of leaves in barley (Hordeum vulgare L.) seedlings. PLoS ONE 2020, 15, e024470. [Google Scholar] [CrossRef]
- Cordeiro, A.C.; Henning, F.A.; Couto, G.H.; Kamikawachi, R.C. Optical analysis of the physiological quality of Triticum aestivum L. seeds with two vigor levels treated with Thiamethoxam. Concilium 2023, 23, 250–263. [Google Scholar] [CrossRef]
- Salieres, O.L.H.; Oussedik, S.A.D. Mesure de l’impact de l’eau hydrogéneée H2 sur la germination des graines de Luzerne (Medicago sativa L.). Int. J. Nat. Resour. Environ. 2023, 5, 31–57. [Google Scholar]
- Kobayashi, K.; Okabe, H.; Kawano, S.; Hidaka, Y.; Hara, K. Biophoton Emission Induced by Heat Shock. PLoS ONE 2014, 9, e105700. [Google Scholar] [CrossRef]
- Mackenzie, A.M.; Smith, H.E.; Mould, R.R.; Bell, J.D.; Nunn, A.V.W.; Botchway, S.W. Rooting out ultraweak photon emission a-mung bean sprouts. J. Photochem. Photobiol. 2024, 19, 100224. [Google Scholar] [CrossRef]
- Nematollahi, M.A.; Alinasab, Z.; Nassiri, S.M.; Khaneghah, A.M. Ultra-weak photon emission: A nondestructive detection tool for food quality and safety assessment. Qual. Assur. Saf. 2020, 12, 18–31. [Google Scholar] [CrossRef]
- Sekulska-Nalewajko, J.; Gocławski, J.; Korzeniewska, E.; Kiełbasa, P.; Dróżdż, T. The verification of hen egg types by the classification of ultra-weak photon emission data. Expert Syst. Appl. 2023, 238, 122130. [Google Scholar] [CrossRef]
- Salières, O. Mesurer le niveau d’émission de biophotons de vins issus de différentes pratiques viti-vinicoles. Laboratoire ENERLAB. 2021. Available online: https://www.chateau-de-la-vieille-chapelle.com/file/Measurements_of_the_level_of_biophoton_emission.pdf (accessed on 12 June 2024).
- Sipka, S.; Nagy, A.; Nagy, J.; Nokhoijav, E.; Csősz, É.; Baráth, S. Measurement of chemiluminescence induced by cytochrome c plus hydrogen peroxide to characterize the peroxidase activity of various wines and the Botrytis cinerea related quality of Aszú wines of Tokaj in Hungary. Eur. Food Res. Technol. 2024, 250, 111–118. [Google Scholar] [CrossRef]
- Jócsák, I.; Végvári, I.G.; Klász, K.; Andrássy-Baka, G.; Somfalvi-Tóth, K.; Varga-Visi, E. Analytical and bioluminescence-based non-invasive quality assessment of differentially grown strawberry (Fragaria x ananassa Duch. ‘Asia’) during household refrigeration storage. Heliyon 2023, 9, e18358. [Google Scholar] [CrossRef]
- Gong, Y.; Yu, L.; Liu, Y.; Zhao, W.; Peng, W.; Nie, X.; Ge, H. Non-destructive detection method for wheat freshness degree based on delayed luminescence. J. Cereal Sci. 2023, 113, 103748. [Google Scholar] [CrossRef]
- Vahalová, P.; Havelka, D.; Vaněčková, E.; Zakar, T.; Kolivoška, V.; Cifra, M. Biochemiluminescence sensing of protein oxidation by reactive oxygen species generated by pulsed electric field. Sens. Actuators B Chem. 2023, 385, 133676. [Google Scholar] [CrossRef]
- Zangari, A.; Micheli, D.; Galeazzi, R.; Tozzi, A.; Balzano, V.; Bellavia, G.; Caristo, M.E. Photons detected in the active nerve by photographic technique. Sci. Rep. 2021, 11, 3022. [Google Scholar] [CrossRef]
- Moro, C.; Valverde, A.; Dole, M.; Hoh Kam, J.; Hamilton, C.; Liebert, A.; Bicknell, B.; Benabid, A.-L.; Magistretti, P.; Mitrofanis, J. The effect of photobiomodulation on the brain during wakefulness and sleep. Front. Neurosci. 2022, 16, 942536. [Google Scholar] [CrossRef]
- Moro, C.; Liebert, A.; Hamilton, C.; Pasqual, N.; Jeffery, G.; Stone, J.; Mitrofanis, J. The code of light: Do neurons generate light to communicate and repair? Neural Regen. Res. 2022, 17, 1251–1252. [Google Scholar]
- Gillmore, B.; Chevalier, G.; Kasian, S. Resolving Specific Psychological Stressors Can Instantly Reduce or Relieve Chronic Neck Pain and Upper Back Pain: Case Reports. Health 2023, 15, 1116–1149. [Google Scholar] [CrossRef]
- Murugan, N.J.; Persinger, M.A.; Karbowski, L.M.; Dotta, B.T. Ultraweak biophoton photon emissions as a non-invasive, early- malignancy detection tool: An in vitro and in vivo study. Cancers 2020, 12, 1001. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Z.; Luo, Y.; Peng, S.; Song, H.; Li, T.; Zheng, J.; Liu, N.; Wu, S.; Zhang, J.; et al. Reduced biophotonic activities and spectral blueshift in Alzheimer’s disease and vascular dementia models with cognitive impairment. Front. Aging Neurosci. 2023, 15, 1208274. [Google Scholar] [CrossRef] [PubMed]
- Tsuchida, K.; Iwasa, T.; Kobayashi, M. Imaging of ultraweak photon emission for evaluating the oxidative stress of human skin. J. Photochem. Photobiol. B 2019, 198, 111562. [Google Scholar] [CrossRef]
- Tsuchida, K.; Sakiyama, N. Blue light-induced lipid oxidation and the antioxidant property of hypotaurine: Evaluation via measuring ultraweak photon emission. Photochem. Photobiol. Sci. 2023, 22, 345–356. [Google Scholar] [CrossRef]
- Tsuchida, K.; Sakiyama, N.; Ogura, Y.; Kobayashi, M. Skin lightness affects ultraviolet A induced oxidative stress: Evaluation using ultraweak photon emission measurement. Exp. Dermatol. 2023, 32, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, D.; Xu, R.; Chen, L.; Song, X.; Wang, Y. Research on the application of biological ultra-weak luminescence in the medical field. J. Laser Biol. 2022, 31, 289–294. [Google Scholar]
- Guo, L.; Guo, Y.; Zhang, G.X.; Zhao, X.W.; Fan, Z.J.; Zhi, M.J.; Li, T.; Wang, F.C. Biological Ultra-weak Luminescence and Its Application to Research of Acupuncture. Zhen Ci Yan Jiu 2018, 43, 384–387. [Google Scholar]
- Yang, M.; Zhang, Z.; Fu, J.; Liu, J.; Pang, J.; Fan, H.; Yang, Z.; Zhang, Y.; Han, J. Ultra-weak photon emission as a potential tool for evaluating the therapeutic effect of traditional Chinese medicine in patients with type 2 diabetes. Heliyon 2023, 9, e18055. [Google Scholar] [CrossRef]
- Zapata, F.; Pastor-Ruiz, V.; Ortega-Ojeda, F.; Montalvo, G.; García-Ruiz, C. Increment of spontaneous human biophoton emission caused by anger emotional states. Microchem. J. 2021, 169, 106558. [Google Scholar] [CrossRef]
- Nevoit, G.V.; Korpan, A.S.; Nastroga, T.V.; Kitura, O.E.; Sokolyuk, N.L.; Lyulka, N.A.; Potiazhenko, M.M. Assessment of the stress and metabolism levels by using electro-photonic emission analysis method in Ukrainian military personnel after frontline service. Актуальні прoблеми сучаснoї медицини: Вісник Українськoї медичнoї стoматoлoгічнoї академії 2023, 23, 46–51. [Google Scholar] [CrossRef]
- Murugana, N.M.; Rouleaub, N.; Karbowskic, L.M.; Persingerb, M.A. Biophotonic markers of malignancy: Discriminating cancers using wavelength-specific biophotons. Biochem. Biophys. Rep. 2018, 13, 7–11. [Google Scholar] [CrossRef]
- Takeda, M.; Kobayashi, M.; Takayama, M.; Suzuki, S.; Ishida, T.; Ohnuki, K.; Moriya, T.; Ohuchi, N. Biophoton detection as a novel technique for cancer imaging. Cancer Sci. 2004, 95, 656–661. [Google Scholar] [CrossRef]
- Takeda, M.; Tanno, Y.; Kobayashi, M.; Usa, M.; Ohuchi, N.; Satomi, S.; Inaba, H. A novel method of assessing carcinoma cell proliferation by biophoton emission. Cancer Lett. 1998, 127, 155–160. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paolis, L.D.; Francini, R.; Davoli, I.; De Matteis, F.; Scordo, A.; Clozza, A.; Grandi, M.; Pace, E.; Curceanu, C.; Grigolini, P.; et al. Biophotons: A Hard Problem. Appl. Sci. 2024, 14, 5496. https://doi.org/10.3390/app14135496
Paolis LD, Francini R, Davoli I, De Matteis F, Scordo A, Clozza A, Grandi M, Pace E, Curceanu C, Grigolini P, et al. Biophotons: A Hard Problem. Applied Sciences. 2024; 14(13):5496. https://doi.org/10.3390/app14135496
Chicago/Turabian StylePaolis, Luca De, Roberto Francini, Ivan Davoli, Fabio De Matteis, Alessandro Scordo, Alberto Clozza, Maurizio Grandi, Elisabetta Pace, Catalina Curceanu, Paolo Grigolini, and et al. 2024. "Biophotons: A Hard Problem" Applied Sciences 14, no. 13: 5496. https://doi.org/10.3390/app14135496
APA StylePaolis, L. D., Francini, R., Davoli, I., De Matteis, F., Scordo, A., Clozza, A., Grandi, M., Pace, E., Curceanu, C., Grigolini, P., & Benfatto, M. (2024). Biophotons: A Hard Problem. Applied Sciences, 14(13), 5496. https://doi.org/10.3390/app14135496








