Figure 1.
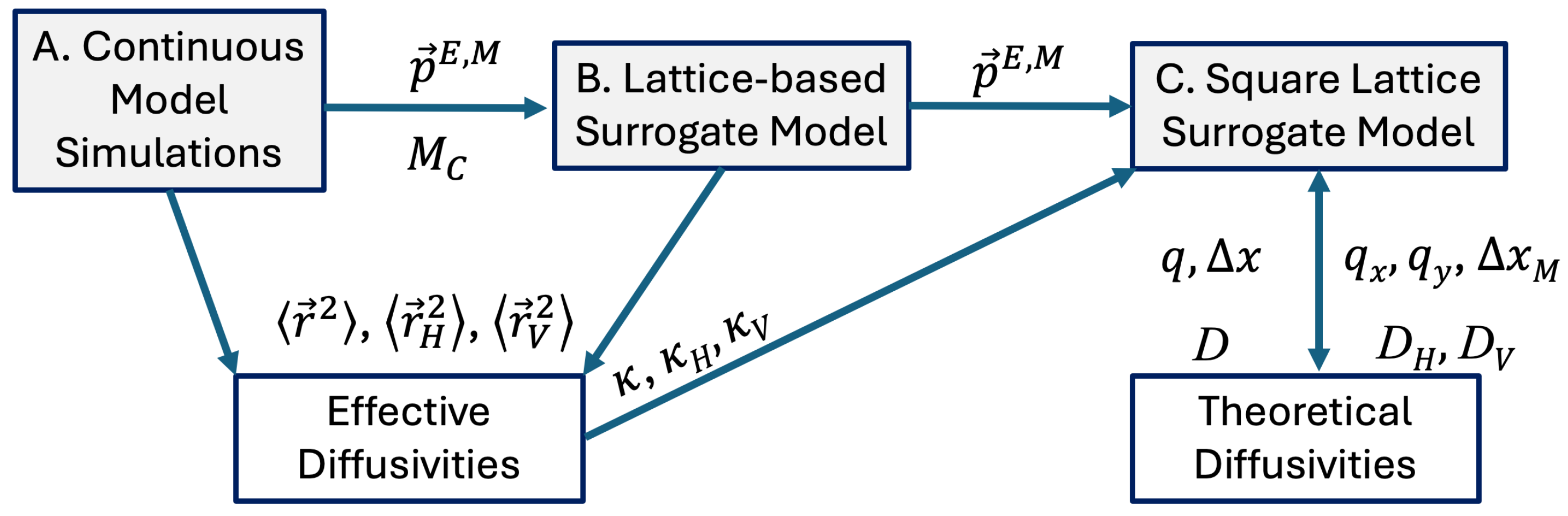
Illustration of the approach used for bridging continuous and lattice-based models in this study.
Figure 1.
Illustration of the approach used for bridging continuous and lattice-based models in this study.
Figure 2.
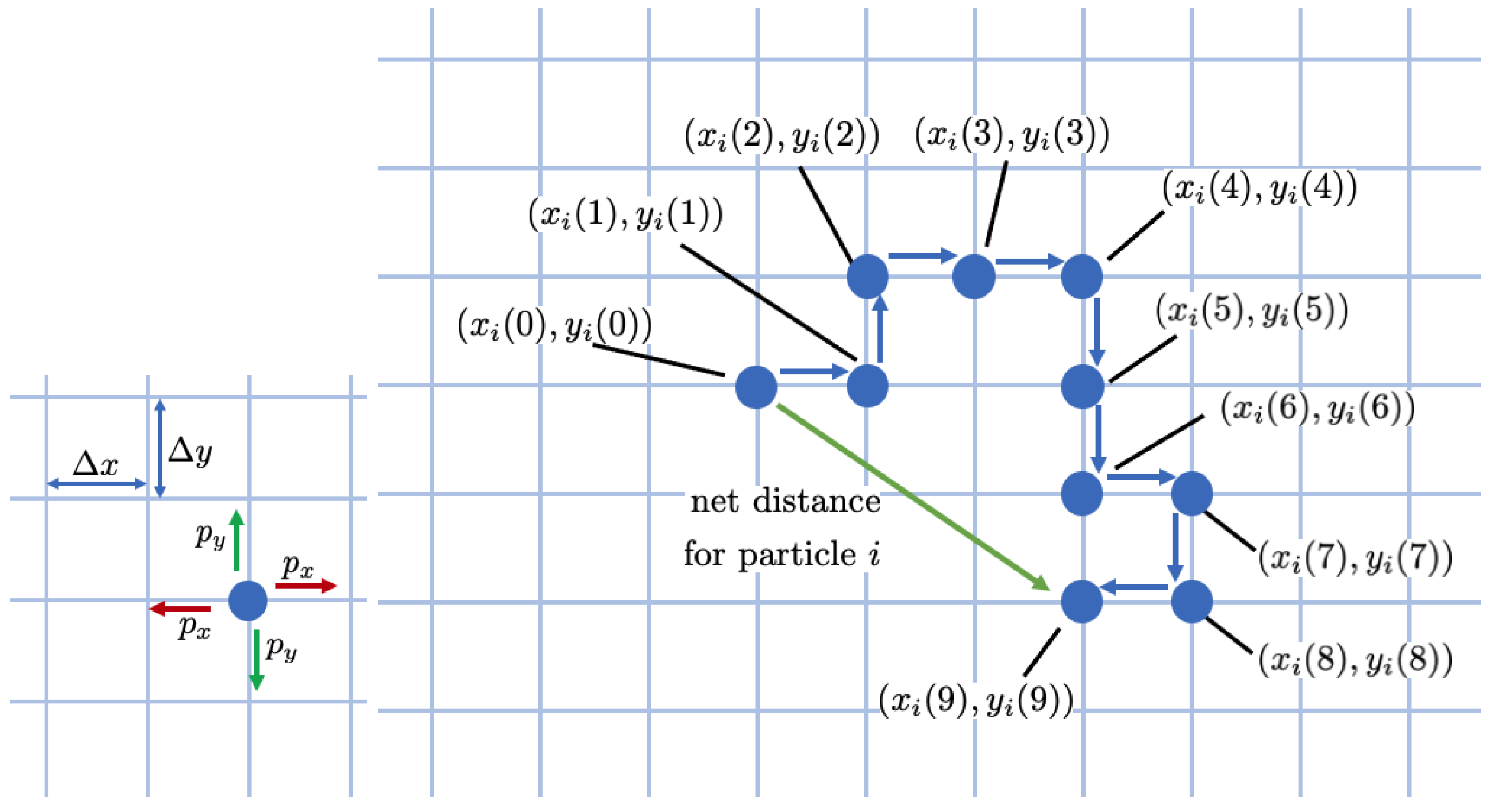
Illustration of a particle undergoing a random walk on a 2D lattice. The particle moves one step (size ) in the horizontal direction with probability (left) and one step (size ) in the vertical direction with probability (right). The probability of staying in place is .
Figure 2.
Illustration of a particle undergoing a random walk on a 2D lattice. The particle moves one step (size ) in the horizontal direction with probability (left) and one step (size ) in the vertical direction with probability (right). The probability of staying in place is .
Figure 3.
Sample domains (RVEs) for continuous model simulations (), with numbered subdomains: (a) equally spaced obstacles model (with ); (b) multisize obstacles model (with and ). Obstacles are shown as black circles and the particle undergoing random walks is shown as a red circle.
Figure 3.
Sample domains (RVEs) for continuous model simulations (), with numbered subdomains: (a) equally spaced obstacles model (with ); (b) multisize obstacles model (with and ). Obstacles are shown as black circles and the particle undergoing random walks is shown as a red circle.
Figure 4.
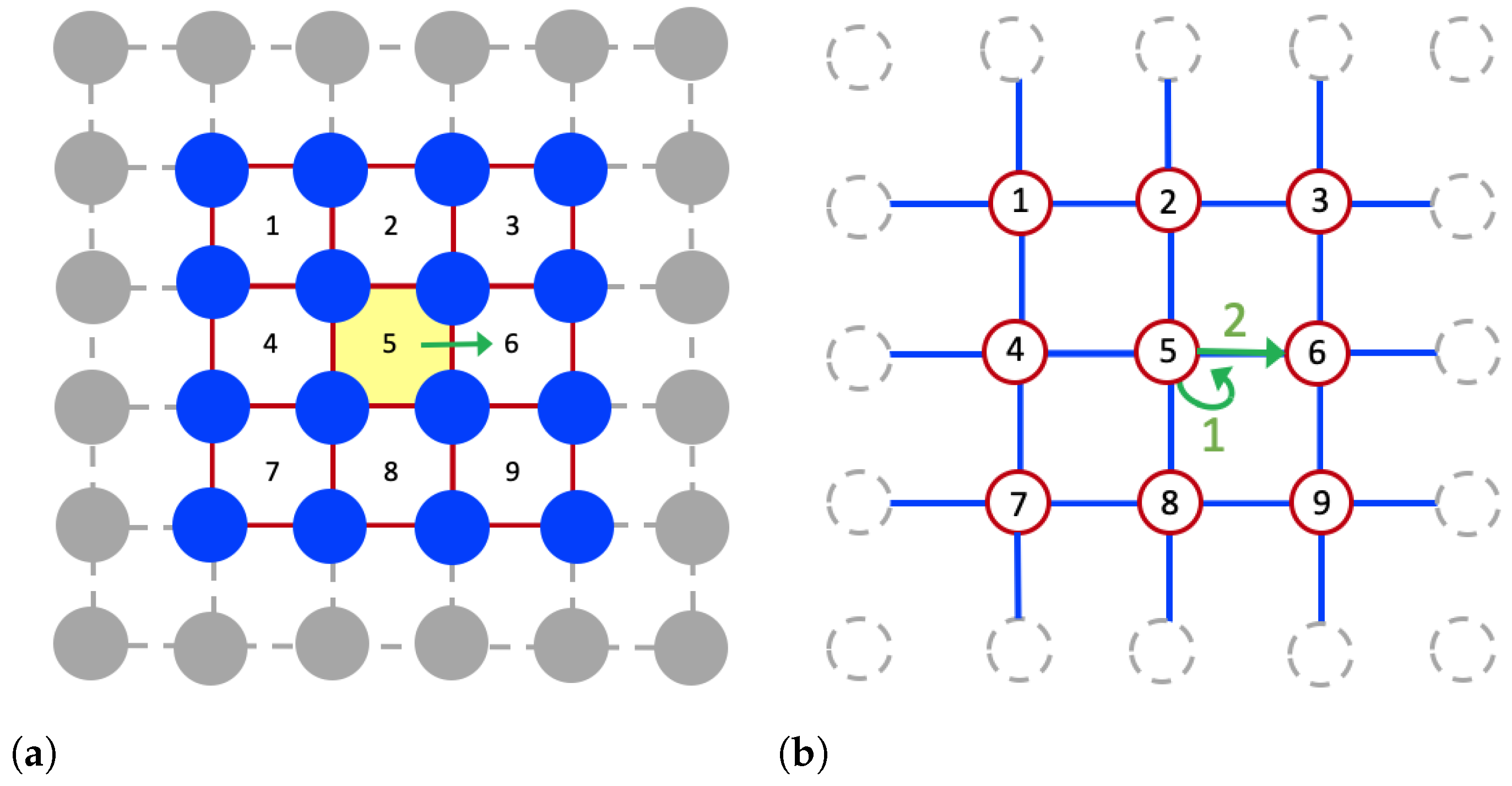
Building a lattice-based surrogate model for the continuous model in the equally spaced obstacles case: (a) nine subdomains are used to exploit symmetry of the obstacle arrangement. and transitions between subdomains are tracked. (b) Lattice-based surrogate representation is shown, with red circles denoting corresponding subdomains in the continuous model.
Figure 4.
Building a lattice-based surrogate model for the continuous model in the equally spaced obstacles case: (a) nine subdomains are used to exploit symmetry of the obstacle arrangement. and transitions between subdomains are tracked. (b) Lattice-based surrogate representation is shown, with red circles denoting corresponding subdomains in the continuous model.
Figure 5.
Building a lattice-based surrogate model for the continuous model in the multisize obstacles case: (a) four subdomains are used to exploit symmetries of the obstacle arrangement, and transitions between subdomains are tracked. Smaller green circles indicate obstacles of fixed radius , and larger blue circles indicate obstacles with varying obstacle radius ; (b) lattice-based surrogate representation with red circles denoting corresponding subdomains in the continuous model.
Figure 5.
Building a lattice-based surrogate model for the continuous model in the multisize obstacles case: (a) four subdomains are used to exploit symmetries of the obstacle arrangement, and transitions between subdomains are tracked. Smaller green circles indicate obstacles of fixed radius , and larger blue circles indicate obstacles with varying obstacle radius ; (b) lattice-based surrogate representation with red circles denoting corresponding subdomains in the continuous model.
Figure 6.
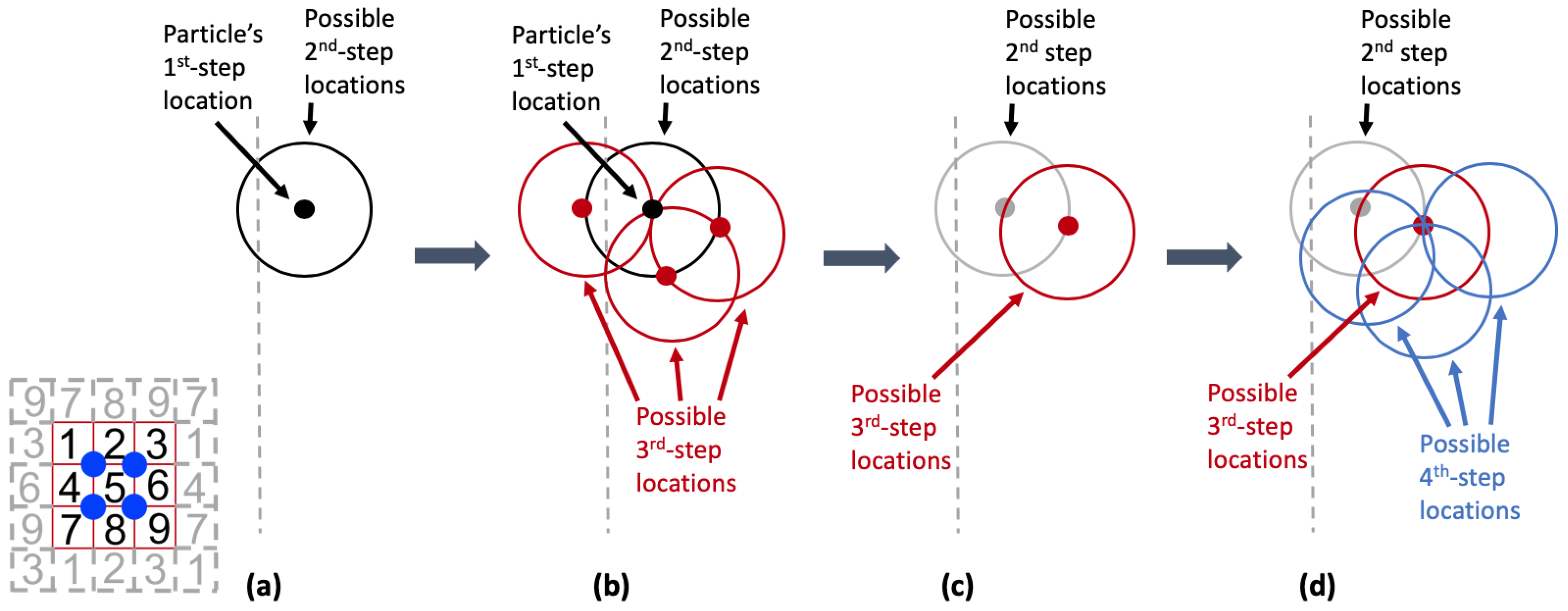
Illustration of the role of the commitment index (calibration) parameter : (a) The particle (solid black circle) has just crossed the boundary between subdomains (dashed gray line) to reach its 1st-step location. Possible 2nd-step locations are indicated by the solid black ring. (b) Three possible 2nd-step locations are indicated by solid red circles. Some possible next steps (3rd-step locations) are shown with red rings. (c) A red ring illustrates the particle’s remaining possible 3rd-step locations when it has remained in the current subdomain at the prior step. (d) Possible 4th-step locations are indicated with blue rings.
Figure 6.
Illustration of the role of the commitment index (calibration) parameter : (a) The particle (solid black circle) has just crossed the boundary between subdomains (dashed gray line) to reach its 1st-step location. Possible 2nd-step locations are indicated by the solid black ring. (b) Three possible 2nd-step locations are indicated by solid red circles. Some possible next steps (3rd-step locations) are shown with red rings. (c) A red ring illustrates the particle’s remaining possible 3rd-step locations when it has remained in the current subdomain at the prior step. (d) Possible 4th-step locations are indicated with blue rings.
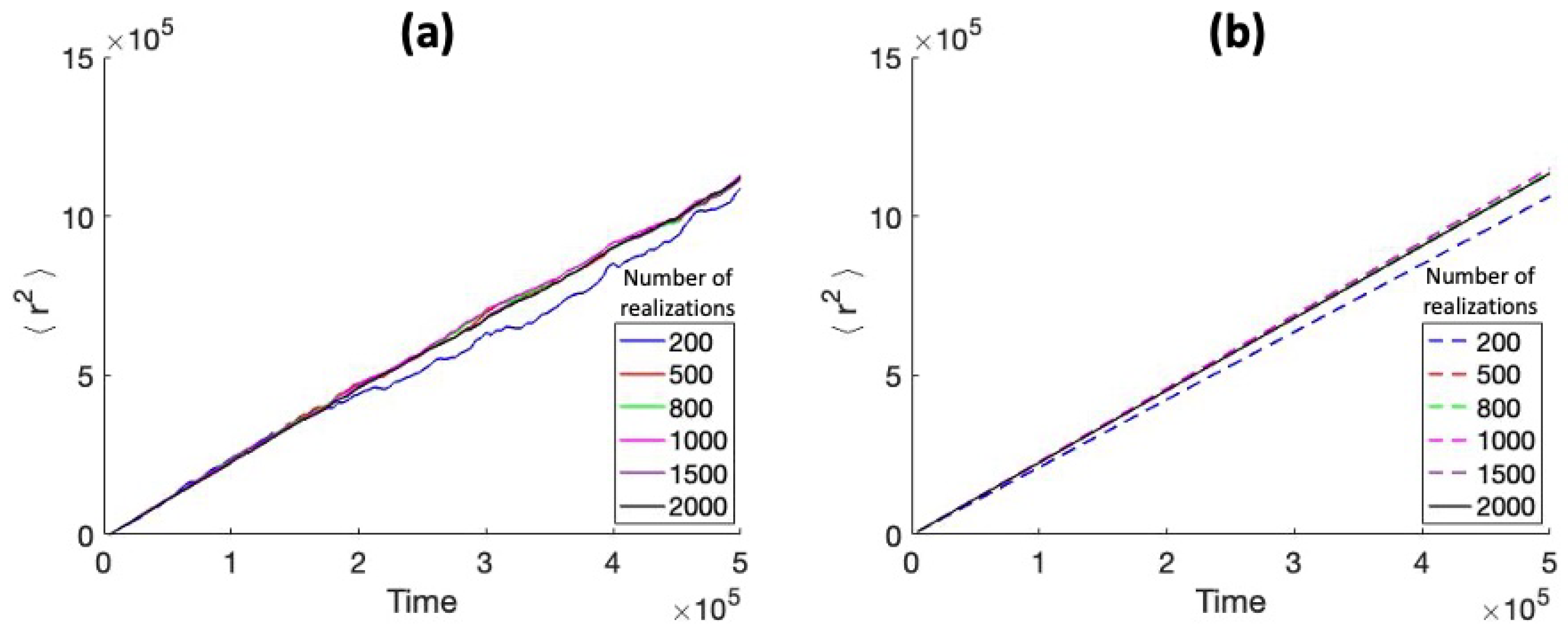
Figure 7.
Mean squared displacement versus time for the equally spaced obstacles model. Effects of an increasing number of realizations are shown for the case and : (a) curves; (b) linear fits to the curves.
Figure 7.
Mean squared displacement versus time for the equally spaced obstacles model. Effects of an increasing number of realizations are shown for the case and : (a) curves; (b) linear fits to the curves.
Figure 8.
Transition probabilities for building the lattice-based surrogate model from the equally spaced obstacles (continuous) model. Transitions from subdomain 6 are illustrated: (a) simulation domain showing the 9 subdomains; (b) plot of all transition probabilities (here, only the stay probability is discernible); (c) magnified plot to illustrate the stay probability; (d) magnified plot to illustrate the leave probabilities.
Figure 8.
Transition probabilities for building the lattice-based surrogate model from the equally spaced obstacles (continuous) model. Transitions from subdomain 6 are illustrated: (a) simulation domain showing the 9 subdomains; (b) plot of all transition probabilities (here, only the stay probability is discernible); (c) magnified plot to illustrate the stay probability; (d) magnified plot to illustrate the leave probabilities.
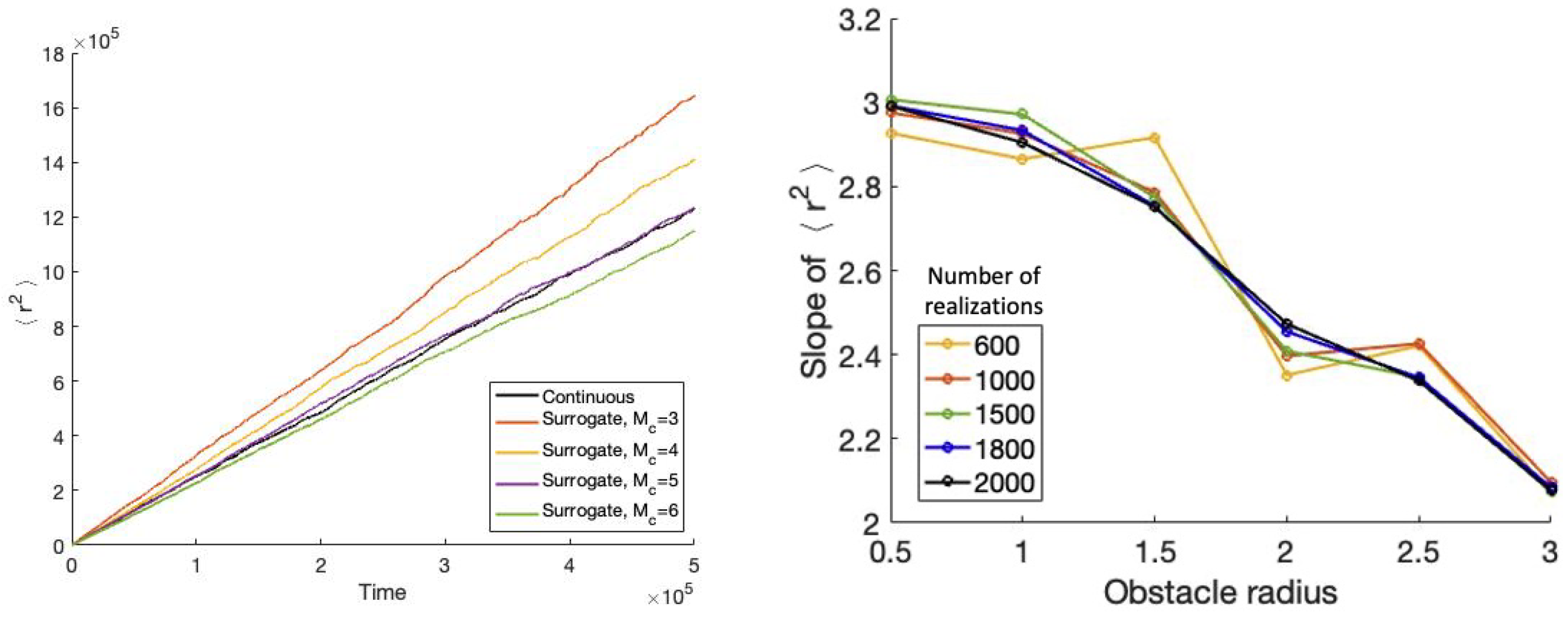
Figure 9.
Mean squared displacement and its slope for the equally spaced obstacles model. Results are shown for particle radius and obstacle radius : (left) versus time for continuous model and resulting surrogate model as the commitment index is varied; (right) slope as a function of obstacle radius for an increasing number of realizations.
Figure 9.
Mean squared displacement and its slope for the equally spaced obstacles model. Results are shown for particle radius and obstacle radius : (left) versus time for continuous model and resulting surrogate model as the commitment index is varied; (right) slope as a function of obstacle radius for an increasing number of realizations.
Figure 10.
Slope of versus time for equally spaced obstacles (continuous) model and the lattice-based surrogate model with best values. Results are shown for particle radius and varying obstacle radius .
Figure 10.
Slope of versus time for equally spaced obstacles (continuous) model and the lattice-based surrogate model with best values. Results are shown for particle radius and varying obstacle radius .
Figure 11.
Mean squared displacement versus time for the multisize obstacles model. Effects of an increasing number of realizations are shown for the case , and : (a) curves; (b) linear fits to the curves.
Figure 11.
Mean squared displacement versus time for the multisize obstacles model. Effects of an increasing number of realizations are shown for the case , and : (a) curves; (b) linear fits to the curves.
Figure 12.
Slope of the mean squared displacement for the multisize obstacles model: (left) variation with obstacle radius as the number of realizations is increased; (right) comparison of the continuous and lattice-based surrogate models for the best values.
Figure 12.
Slope of the mean squared displacement for the multisize obstacles model: (left) variation with obstacle radius as the number of realizations is increased; (right) comparison of the continuous and lattice-based surrogate models for the best values.
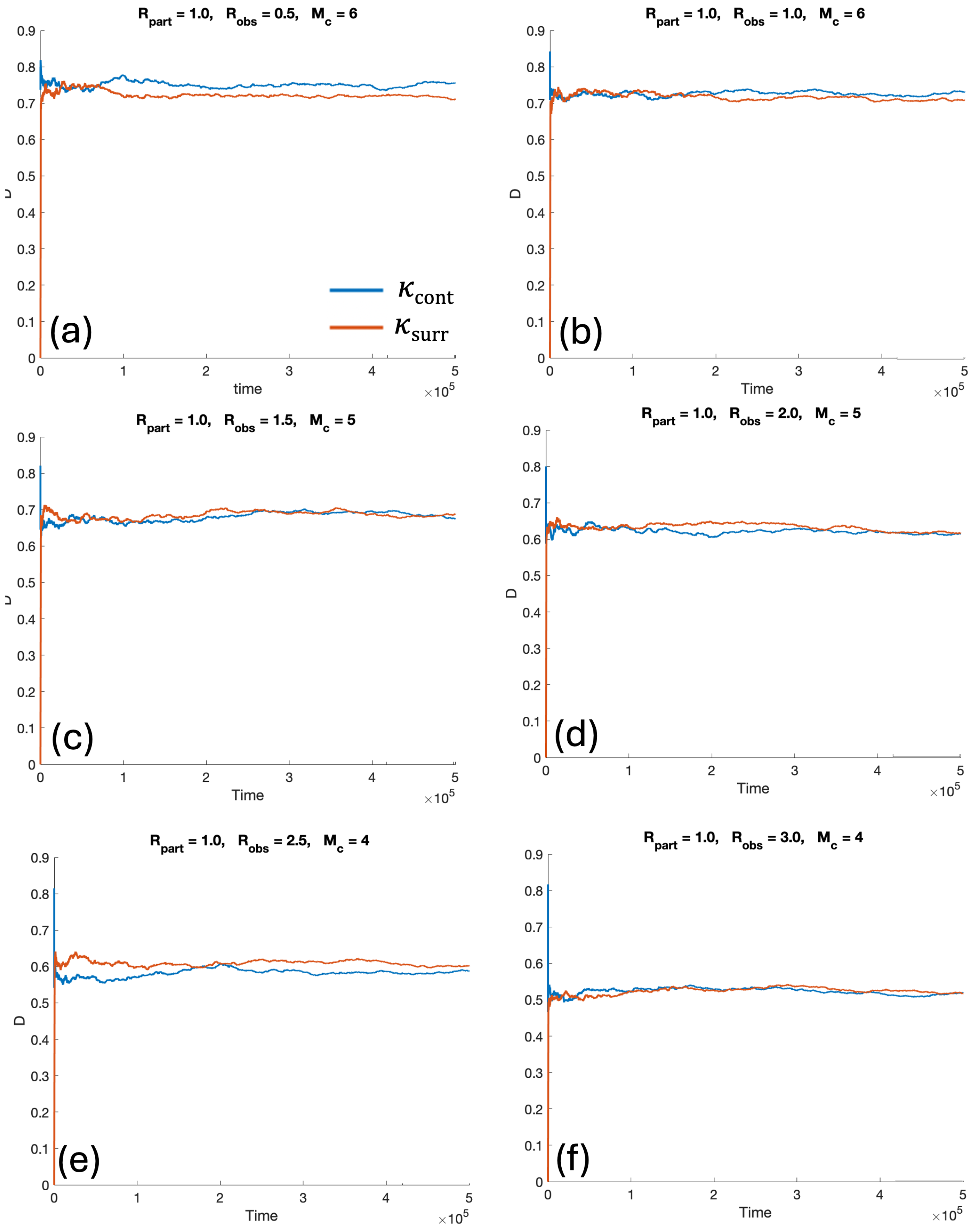
Figure 13.
Estimated effective diffusivities for the continuous and lattice-based surrogate models in the equally spaced obstacles case with : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Figure 13.
Estimated effective diffusivities for the continuous and lattice-based surrogate models in the equally spaced obstacles case with : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
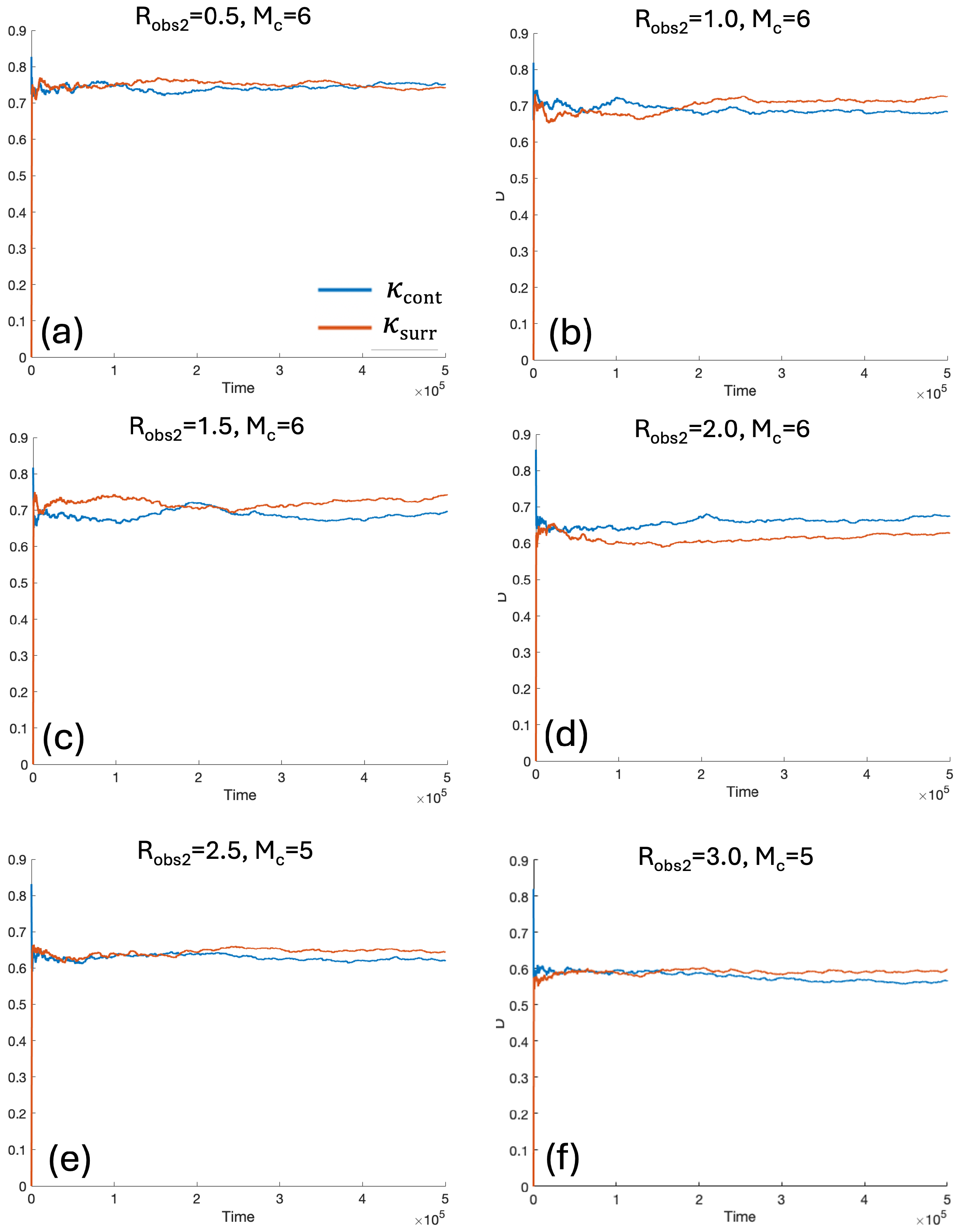
Figure 14.
Estimated effective diffusivities for the continuous and lattice-based surrogate models in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Figure 14.
Estimated effective diffusivities for the continuous and lattice-based surrogate models in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Figure 15.
Horizontal, vertical and (regular) mean squared displacements for the lattice-based surrogate model in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Figure 15.
Horizontal, vertical and (regular) mean squared displacements for the lattice-based surrogate model in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
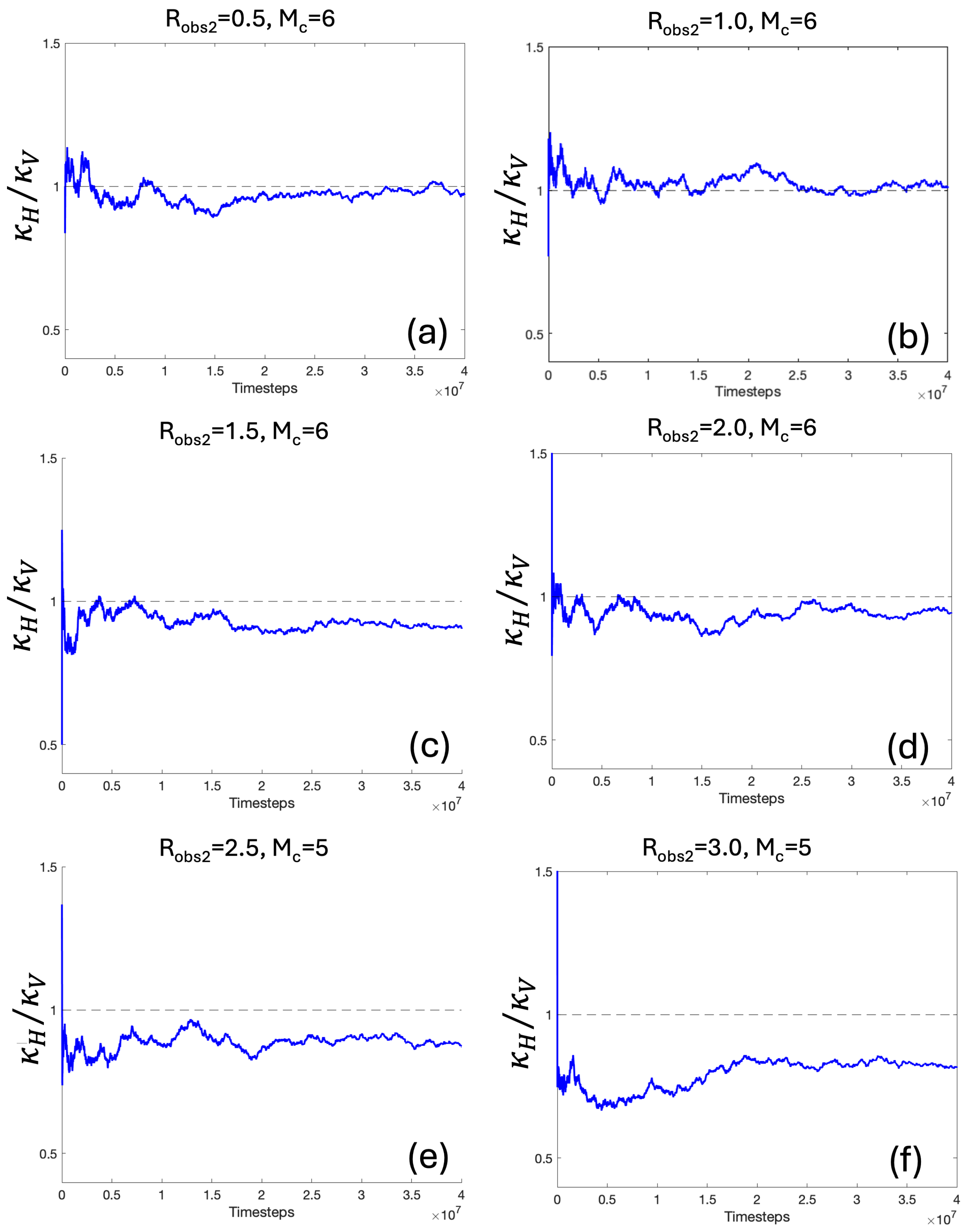
Figure 16.
Ratio of horizontal and vertical diffusivities for the lattice-based surrogate model in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Figure 16.
Ratio of horizontal and vertical diffusivities for the lattice-based surrogate model in the multisize obstacles case with , : (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .
Table 1.
Transition probabilities in the lattice-based surrogate model for the equally spaced obstacles (continuous) model for the best values of with particle radius .
Table 1.
Transition probabilities in the lattice-based surrogate model for the equally spaced obstacles (continuous) model for the best values of with particle radius .
| | | Probability by Transition Type |
|---|
| | | |
|---|
| 0.5 | 7 | | |
| 1.0 | 6 | | |
| 1.5 | 5 | | |
| 2.0 | 5 | | |
| 2.5 | 4 | | |
| 3.0 | 4 | | |
Table 2.
Slope values for vs. t in the equally spaced obstacles (continuous) model () and the lattice-based surrogate model. The best values of are also shown.
Table 2.
Slope values for vs. t in the equally spaced obstacles (continuous) model () and the lattice-based surrogate model. The best values of are also shown.
| | Slope (Continuous) | Slope (Surrogate) | Percent Difference |
|---|
| 0.5 | 7 | 2.9984 | 2.8770 | 4.049% |
| 1.0 | 6 | 2.9044 | 2.8468 | 1.983% |
| 1.5 | 5 | 2.7507 | 2.7506 | 0.004% |
| 2.0 | 5 | 2.4731 | 2.5094 | 1.468% |
| 2.5 | 4 | 2.3376 | 2.4310 | 3.996% |
| 3.0 | 4 | 2.0765 | 2.1016 | 1.209% |
Table 3.
Transition probabilities in the lattice-based surrogate model for the multisize obstacles (continuous) model for the best values of with particle radius and .
Table 3.
Transition probabilities in the lattice-based surrogate model for the multisize obstacles (continuous) model for the best values of with particle radius and .
| | | Probability by Transition Type |
|---|
| | | | | |
|---|
| 0.5 | 6 | | | | |
| 1.0 | 6 | | | | |
| 1.5 | 6 | | | | |
| 2.0 | 6 | | | | |
| 2.5 | 5 | | | | |
| 3.0 | 5 | | | | |
Table 4.
Slope values for vs. t in the multisize obstacles (continuous) model (, ) and the lattice-based surrogate model. The best values of are also shown.
Table 4.
Slope values for vs. t in the multisize obstacles (continuous) model (, ) and the lattice-based surrogate model. The best values of are also shown.
| | Slope (Continuous) | Slope (Surrogate) | Percent Difference |
|---|
| 0.5 | 6 | 2.9870 | 3.0059 | 0.632% |
| 1.0 | 6 | 2.7357 | 2.8531 | 4.291% |
| 1.5 | 6 | 2.7376 | 2.8939 | 5.709% |
| 2.0 | 6 | 2.6618 | 2.4751 | 7.014% |
| 2.5 | 5 | 2.4995 | 2.5904 | 3.637% |
| 3.0 | 5 | 2.2710 | 2.3651 | 4.144% |
Table 5.
Effective diffusivities in the equally spaced obstacles case for the continuous model () and the lattice-based surrogate model (). The stay probability (q) and best commitment index () are also shown for each obstacle radius ().
Table 5.
Effective diffusivities in the equally spaced obstacles case for the continuous model () and the lattice-based surrogate model (). The stay probability (q) and best commitment index () are also shown for each obstacle radius ().
| | q | | | Percent Difference |
|---|
| 0.5 | 7 | 0.99276 | 0.7550 | 0.7100 | 5.960% |
| 1.0 | 6 | 0.99291 | 0.7314 | 0.7084 | 3.145% |
| 1.5 | 5 | 0.99297 | 0.6759 | 0.6862 | 1.524% |
| 2.0 | 5 | 0.99371 | 0.6146 | 0.6165 | 0.309% |
| 2.5 | 4 | 0.99384 | 0.5885 | 0.6016 | 2.226% |
| 3.0 | 4 | 0.99493 | 0.5188 | 0.5187 | 0.019% |
Table 6.
Theoretical diffusivity (D) and grid size () in the equally spaced obstacles case. The stay probability (q), best commitment index () and theoretical diffusivity with () are also shown for each obstacle radius ().
Table 6.
Theoretical diffusivity (D) and grid size () in the equally spaced obstacles case. The stay probability (q), best commitment index () and theoretical diffusivity with () are also shown for each obstacle radius ().
| q | | | | | D | |
|---|
| 0.5 | 0.99276 | 5.1048 | 4.4260 | 0.7550 | 0.7100 | 0.7100 | 3.6243 |
| 1.0 | 0.99291 | 5.0027 | 4.4709 | 0.7314 | 0.7084 | 0.7084 | 3.5440 |
| 1.5 | 0.99297 | 5.1224 | 4.4184 | 0.6759 | 0.6862 | 0.6862 | 3.5149 |
| 2.0 | 0.99371 | 5.0907 | 4.4321 | 0.6146 | 0.6165 | 0.6165 | 3.1384 |
| 2.5 | 0.99384 | 5.0728 | 4.4399 | 0.5885 | 0.6016 | 0.6016 | 3.0517 |
| 3.0 | 0.99493 | 4.8863 | 4.5239 | 0.5188 | 0.5187 | 0.5187 | 2.5343 |
Table 7.
Effective diffusivities in the multisize obstacles case for the continuous model () and the lattice-based surrogate model (). The resulting stay probability () in the square lattice surrogate model and the best commitment index () are also shown for each obstacle radius ().
Table 7.
Effective diffusivities in the multisize obstacles case for the continuous model () and the lattice-based surrogate model (). The resulting stay probability () in the square lattice surrogate model and the best commitment index () are also shown for each obstacle radius ().
| | | | | Percent Difference |
|---|
| 0.5 | 6 | 0.9925 | 0.7509 | 0.7428 | 1.084% |
| 1.0 | 6 | 0.9929 | 0.6842 | 0.7261 | 6.133% |
| 1.5 | 6 | 0.9932 | 0.6943 | 0.7418 | 6.845% |
| 2.0 | 6 | 0.9935 | 0.6746 | 0.6290 | 6.755% |
| 2.5 | 5 | 0.9932 | 0.6205 | 0.6440 | 3.785% |
| 3.0 | 5 | 0.9939 | 0.5667 | 0.5942 | 4.859% |
Table 8.
Estimated values of grid size based on the lattice-based surrogate model simulation results for the multisize case using the effective horizontal diffusivity () and the effective vertical diffusivity (). The resulting transition (leave) probabilities in the square lattice surrogate model are also shown.
Table 8.
Estimated values of grid size based on the lattice-based surrogate model simulation results for the multisize case using the effective horizontal diffusivity () and the effective vertical diffusivity (). The resulting transition (leave) probabilities in the square lattice surrogate model are also shown.
| | | ( est.) | ( est.) |
|---|
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |