The Fractal Characteristics of Ground Subsidence Caused by Subway Excavation
Abstract
1. Introduction
2. Theoretical Foundation
2.1. Wavelet Transform
2.2. Fractal Interpolation
2.3. Fractal Dimension
3. Processes
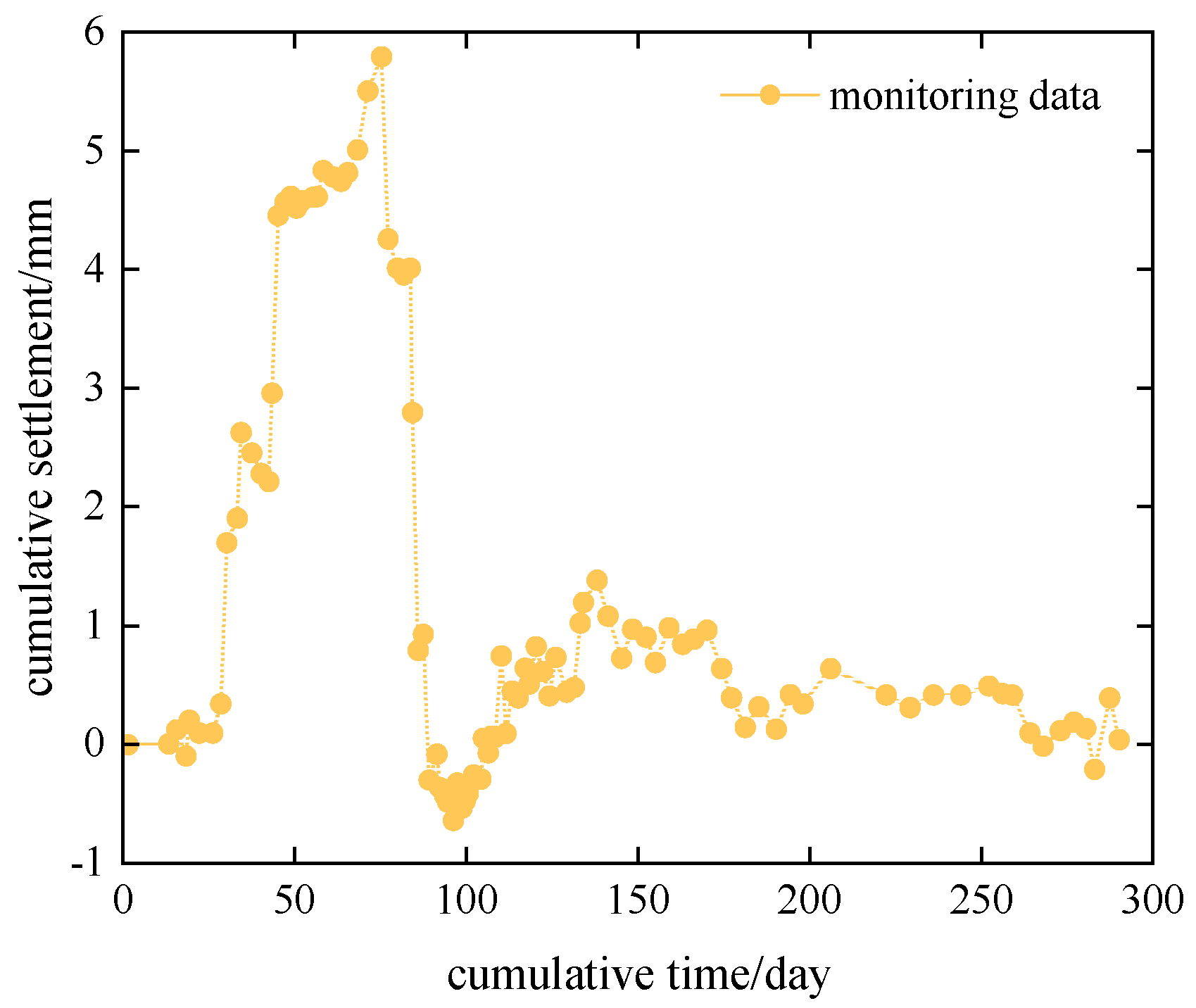
3.1. Project Overview
3.2. Evaluating Indicator
3.3. Wavelet Transform
3.3.1. The De-Noising Model
- A.
- Wavelet function
- B.
- Decomposition level
- C.
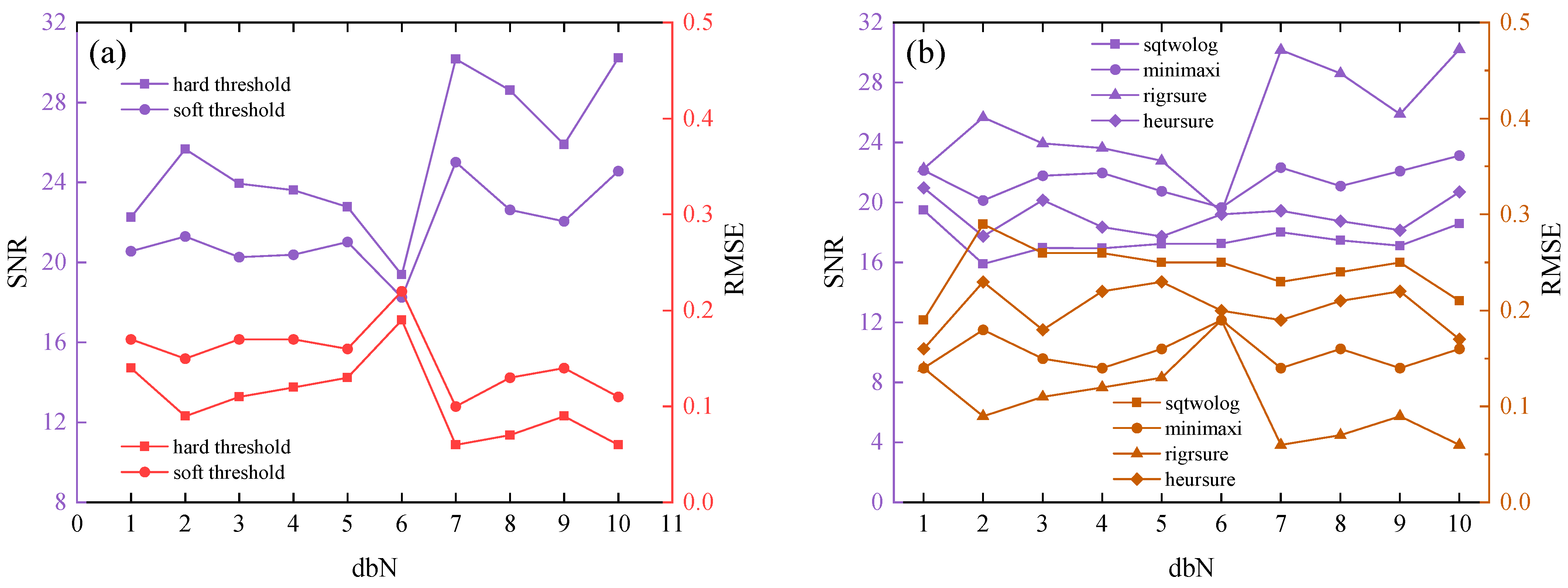
- Threshold
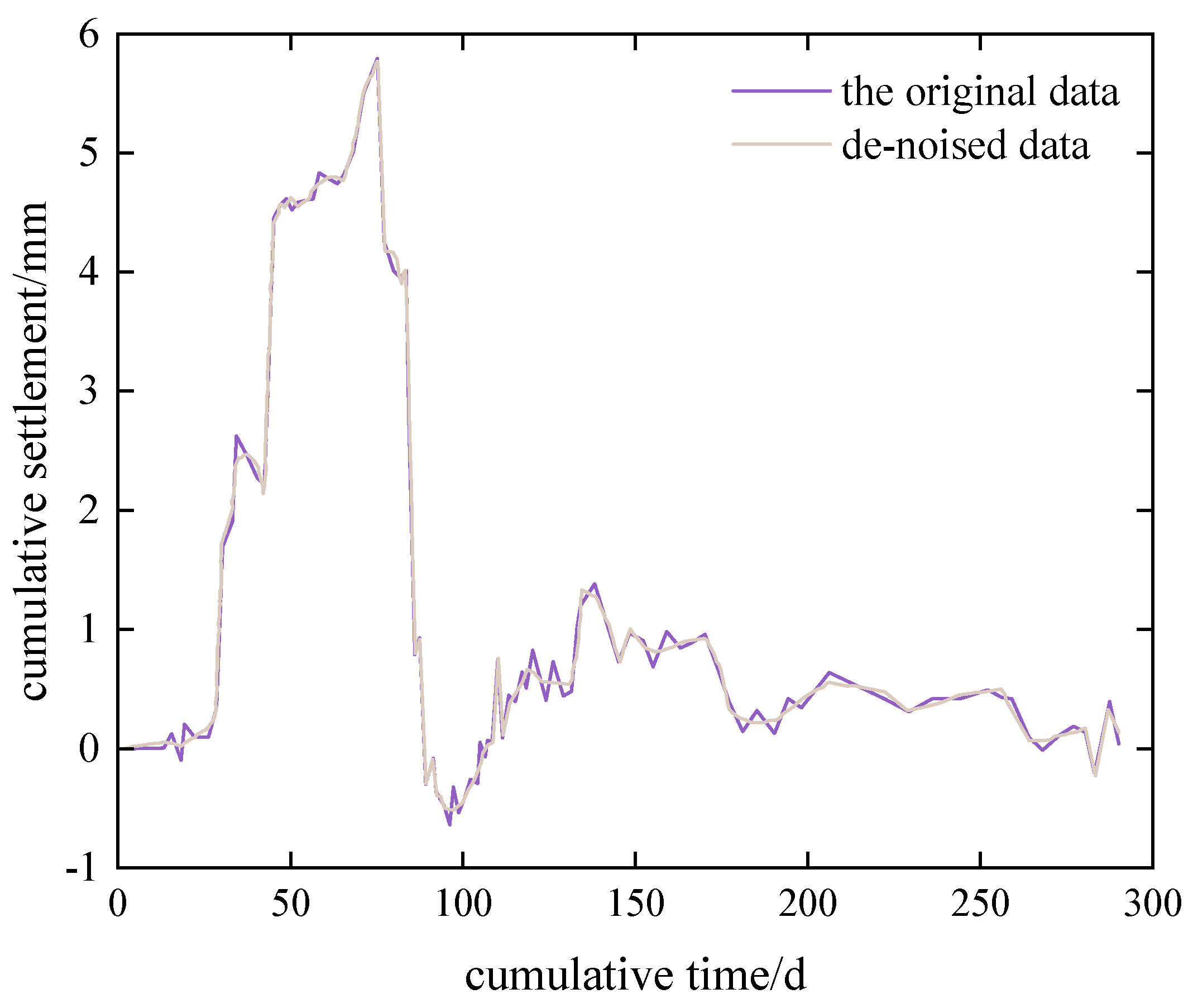
3.3.2. The De-Noising Effect
4. Fractal Interpolation Simulation
4.1. The Algorithm
- Choose the interpolation point (xi, yi), where i = 0, 1, …, n;
- Compute the contraction factor di by analytic [56]. In general, the factor di lies in the interval (−1, 1);
- Compute the map parameters with (4);
- Store the data set generated by the map, which is empty at the beginning;
- The fractal interpolation function of de-noised data has been searched.
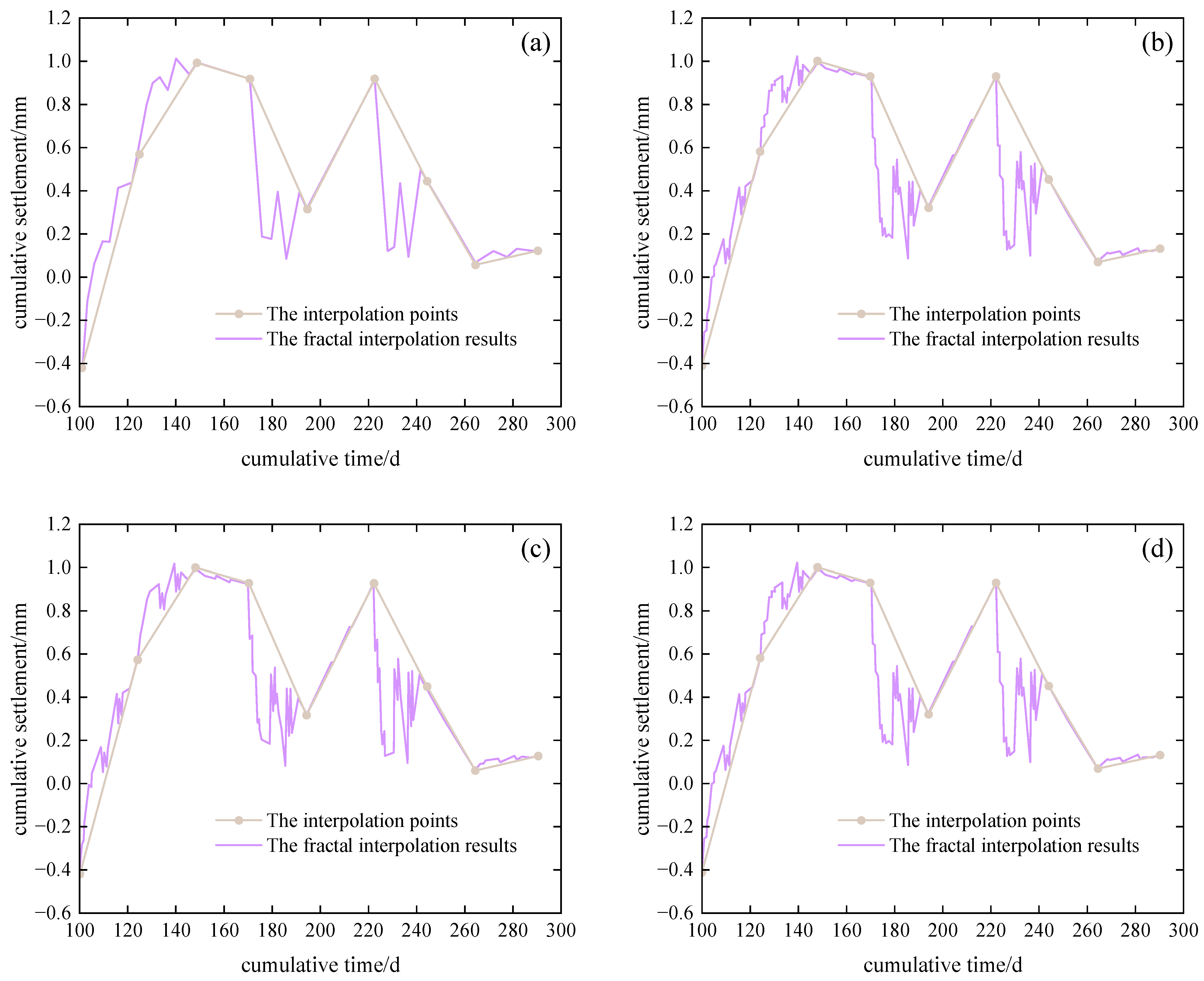
4.2. The Effect
5. Fractal Dimension Feature
5.1. The Algorithm
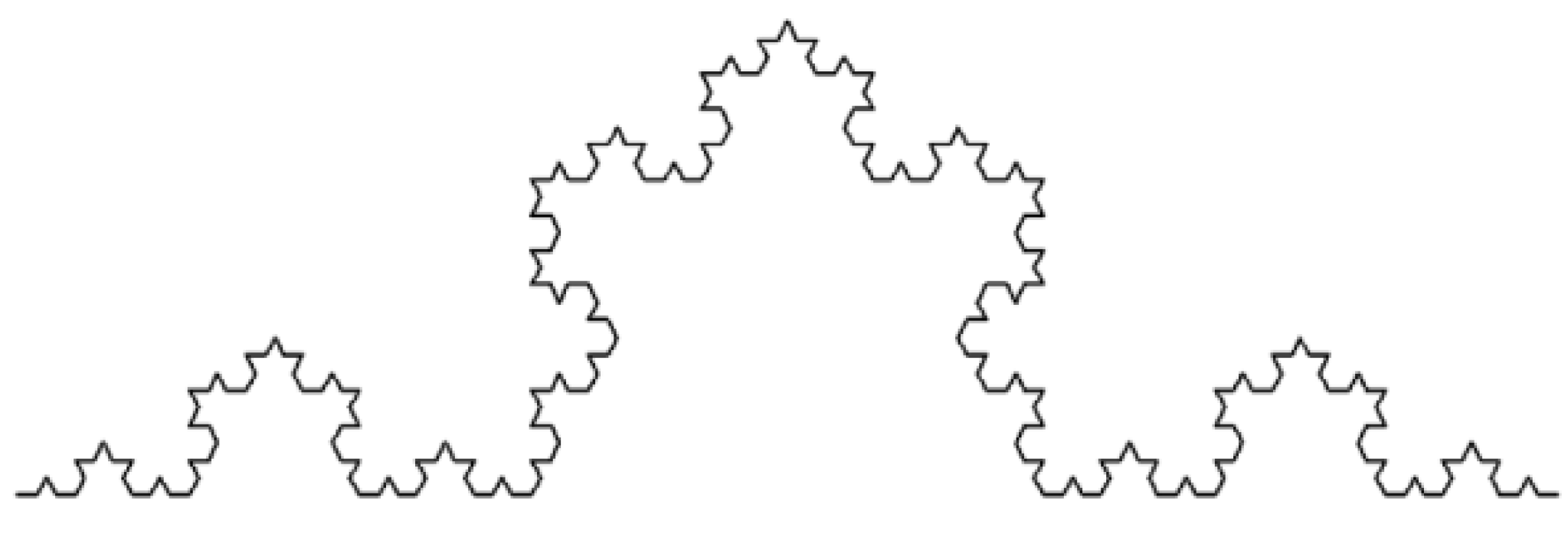
- Plot Von Koch curve, as shown in Figure 10;
- Gray processing of the target object, the result is as shown in Figure 11;
- By changing the scale r, we could obtain the total box counts needed to cover the target object;
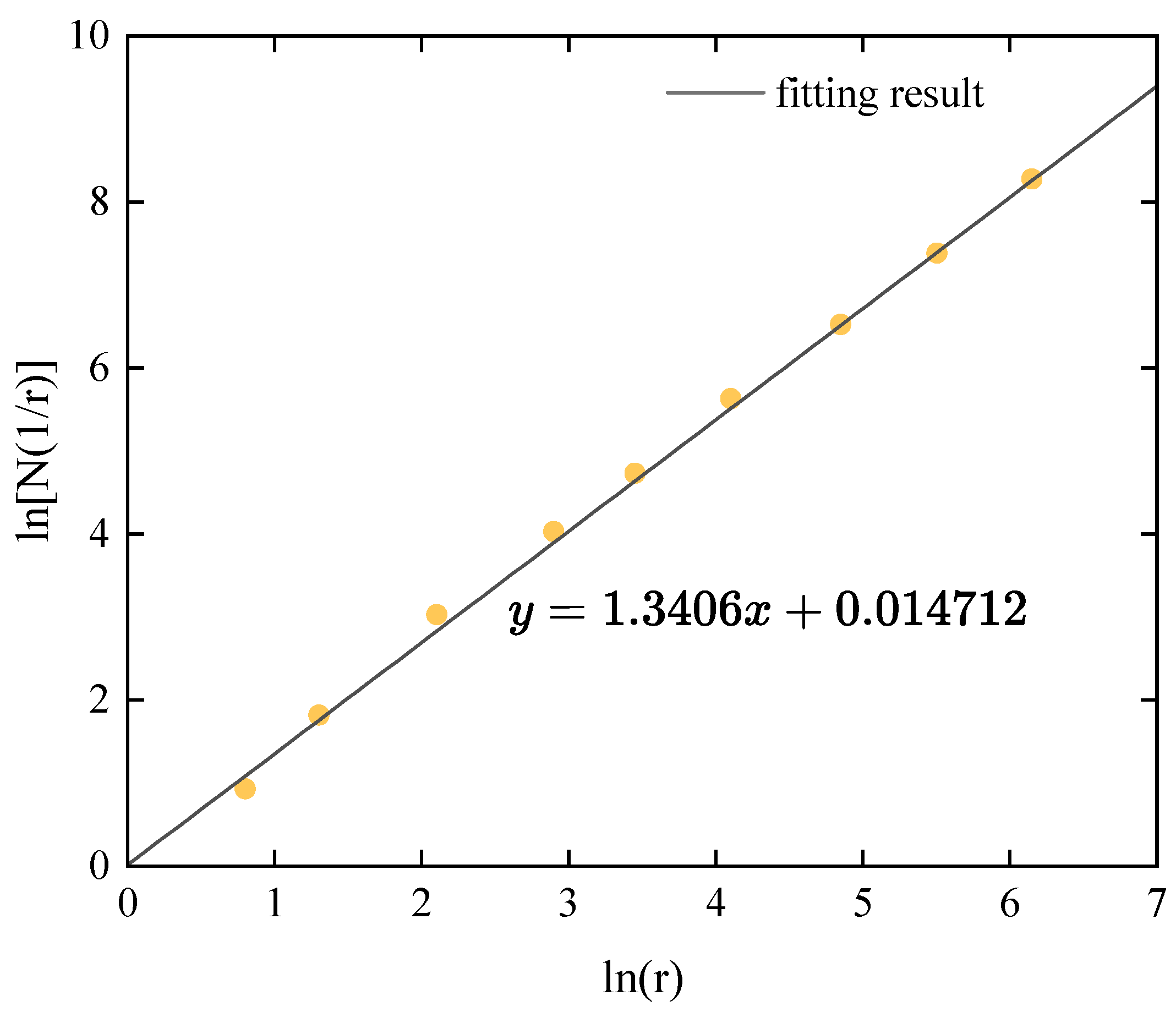
- Linearly fit ln(r)–ln(N(1/r)), as shown in Figure 12. The slope of ln(r) and ln(N(1/r)) is regarded as the fractal dimension.
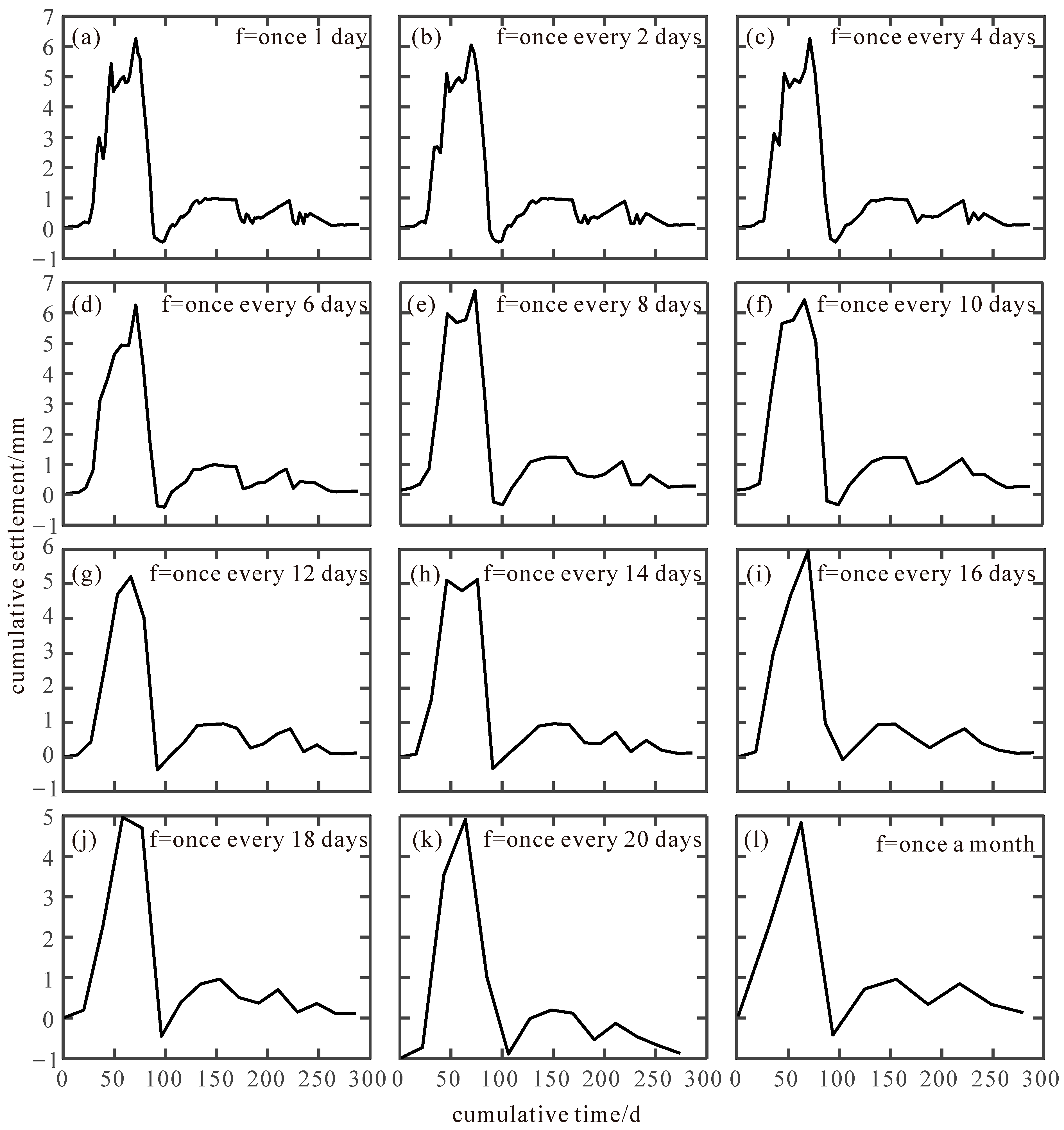
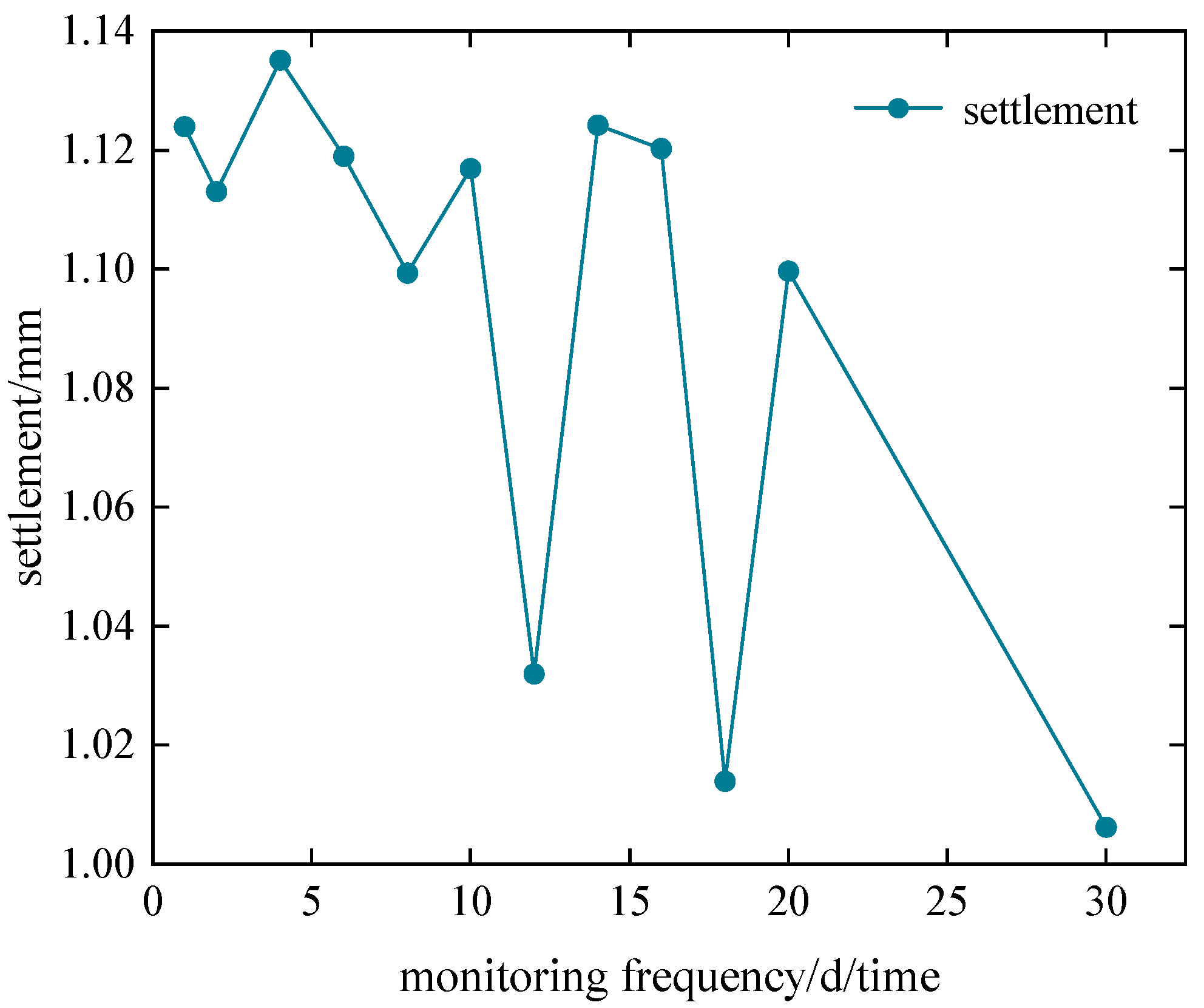
5.2. The Fractal Characteristics
6. Conclusions
- (1)
- When utilizing the dbN wavelet function, a decomposition level of 1, the hard threshold method, and the rigrsure threshold rule, the noise reduction model exhibited a high SNR and a low RMSE and exhibited the most effective noise reduction in this instance.
- (2)
- The daily surface deformation data were derived by fractal interpolation, and 291 data points were successfully extracted from 18 interpolated points, which compensated for the effects of missing data and outliers, to a certain extent. This method effectively captured the actual deformation information with an average relative error of only 13%.
- (3)
- The fractal dimension of the monitoring curves was consistently greater than 1, indicating that the surface deformation caused by the construction of the Urumqi subway was self-similar. Additionally, as the monitoring frequency decreased, the fractal dimension exhibited a declining trend, and the surface settlement and deformation curves tended to smooth, accompanied by a concurrent decrease in the actual information that could be captured.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Xie, Y.; Feng, H.; He, D.; Lei, B.; Wang, Y. China Urban Rail Transit TOD Policy Index Report, 1st ed.; Southwest Jiaotong University Press: Chengdu, China, 2022; p. 169. [Google Scholar]
- Liu, Q.; Zhang, Y.; Deng, M.; Wu, H.; Kang, Y.; Wei, J. Time series prediction method of large-scale surface subsidence based on deep learning. Acta Geod. Cartogr. Sin. 2021, 50, 396–404. [Google Scholar]
- Zhu, L.; Gong, H.; Li, X.; Zhou, C.; Ye, M.; Wang, H.; Zhang, K.; Han, M. Research progress and prospect of land subsidence. Hydrogeol. Eng. Geol. 2023, 50, 1–11. [Google Scholar] [CrossRef]
- Zhang, W.-S.; Yuan, Y.; Long, M.; Yao, R.-H.; Jia, L.; Liu, M. Prediction of surface settlement around subway foundation pits based on spatiotemporal characteristics and deep learning models. Comput. Geotech. 2024, 168, 106149. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.-Y.; Jin, Y.-F.; Chan, T.H.T. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest. Eng. Geol. 2020, 265, 105328. [Google Scholar] [CrossRef]
- Savvides, A.-A.; Papadopoulos, L. A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics 2022, 2, 1084–1108. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature/B.B. Mandelbrot. Am. J. Phys. 1983, 51, 286. [Google Scholar] [CrossRef]
- Scholz, C.H.; Mandelbrot, B.B. Fractals in Geophysics; Springer: Basel, Switzweland, 1989. [Google Scholar]
- Quadri, S. Centrifuge Studies on Rainfall Induced Slope Instability and Modelling of Mass Movement using Fractals and DEM. Ph. D. Thesis, Department of Civil Engineering, IIT Bombay, Mumbai, India, 2000. [Google Scholar]
- Venkatachalam, G.; Nagesha, M.S.; Dodagoudar, G.R. Landslide modelling using remote sensing and GIS. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- He, K.; Sun, L.; Wang, S. Displacement Fractal Parameter Hurst Index and its Application to Prediction of Debris Landslides. Chin. J. Rock Mech. Eng. 2009, 28, 1107–1115. [Google Scholar]
- Li, Y.; Yin, K.; Chen, W. Application of R/S method in forecast of landslide deformation trend. Chin. J. Geotech. Eng. 2010, 32, 1291–1296. [Google Scholar]
- Liu, Y.; Ren, T.; Wang, P. Study on inspection of slope safety with fractal theory based on Matlab. Water Resour. Hydropower Eng. 2010, 41, 17–19+23. [Google Scholar] [CrossRef]
- Gui, L.; Yin, K. Analysis of landslide surface monitoring displacement based on multi-fractal theory. J. Cent. S. Univ. (Sci. Technol.) 2014, 45, 3908–3914. [Google Scholar]
- Wang, H.; Xie, F. Research on Calculation of the Fractal of Tunnel after Excavation Settlement Deformation. Low Temp. Archit. Technol. 2012, 34, 118–120. [Google Scholar]
- Zhang, P.; Chen, J.; Zhang, L.; Xiao, Y. Relationship between Fractal Dimension of Section Profile and Joint Parameters of Tunnel Surrounding Rocks. Chin. J. Rock Mech. Eng. 2012, 31, 2745–2750. [Google Scholar]
- Xu, K.; Zhu, K.; Yu, Y. Fractal Structure Analysis for Surrounding Rock Deformation of Shallow-buried Soft Rock Tunnel. Railw. Eng. 2017, 7, 71–73. [Google Scholar]
- Hu, X.; Yan, E.; Zhou, Y.; Zhang, T. Fractal characteristics of landslide monitoring point movement trace and its application. Chin. J. Rock Mech. Eng. 2012, 31, 570–576. [Google Scholar]
- Gao, Y.; Cao, J.; Zhang, S.; Li, Z. Analysis of the Pore Structure and Fractal Characteristics of Coal and Gas Outburst Coal Seams Based on Matrix Compression Correction. Sustainability 2023, 15, 12670. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, J.; Sa, Z.; Wang, Z.; Lu, S.; Lv, Z. Fractal characteristics of acoustic emission of gas-bearing coal subjected to true triaxial loading. Measurement 2021, 169, 108349. [Google Scholar] [CrossRef]
- Li, Z.; Liu, D.; Cai, Y.; Wang, Y.; Si, G. Evaluation of coal petrophysics incorporating fractal characteristics by mercury intrusion porosimetry and low-field NMR. Fuel 2020, 263, 116802. [Google Scholar] [CrossRef]
- Song, W.; Wang, D.; Yao, J.; Li, Y.; Sun, H.; Yang, Y.; Zhang, L. Multiscale image-based fractal characteristic of shale pore structure with implication to accurate prediction of gas permeability. Fuel 2019, 241, 522–532. [Google Scholar] [CrossRef]
- Zuo, C.; Liu, D.; Ding, S.; Li, L. Analysis and Prediction of Tunnel Surface Subsidence Based on Fractal Theory. J. Yangtze River Sci. Res. Inst. 2016, 33, 51–56. [Google Scholar]
- Lai, S.M.; Wan, L.; Zeng, X.J. Comparative Analysis of Multi-fractal Data Missing Processing Methods. Appl. Comput. Math. 2019, 8, 44–49. [Google Scholar]
- Jiang, P.; Liu, F.; Wang, J.; Song, Y. Cuckoo search-designated fractal interpolation functions with winner combination for estimating missing values in time series. Appl. Math. Model. 2016, 40, 9692–9718. [Google Scholar] [CrossRef]
- Liu, H.; He, T.; Chen, Y.; Li, X. A new approach for high fidelity seismic data recovery by fractal interpolation. Earthq. Sci. 2012, 25, 339–346. [Google Scholar] [CrossRef][Green Version]
- Wei, L. Signal De-noising Research Based on Wavelet Transformation. Master’s Thesis, Hunan University, Changsha, China, 2008. [Google Scholar]
- Zhang, J.; Cheng, Z. Prediction of Surface Subsidence of Deep Foundation Pit Based on Wavelet Analysis. Processes 2023, 11, 107. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, T.; Zhang, P. GPS dynamic deformation monitoring on high-rise buildings. Sci. Surv. Mapp. 2012, 37, 47–50. [Google Scholar]
- Xie, B.; Shi, F.; Ma, S.; Li, F. Micro-Seismic Signal Denoising Method Based on EWT-Component Threshold and SVD. J. Geod. Geodyn. 2021, 41, 319–322. [Google Scholar]
- Li, Z.; Ke, S.; Yin, Y. Analysis on Noise Reduction Method for Deformation Monitoring Data. Northwest Hydropower 2017, 3, 98–101. [Google Scholar]
- Qin, Y.; Zhang, J.; Tan, S. Combined Forecast of Subway Settlement Based on Wavelet De-noising and BP Neural Network. Water Power 2020, 46, 42–46. [Google Scholar]
- Yang, Q.; Guo, J.; Xia, P.; Xue, F. Research on deep foundation settlement prediction based on wavelet-neural network. J. Wuhan Polytech. Univ. 2013, 32, 75–79. [Google Scholar]
- Li, M.; Chen, W.; Yang, J. An analysis method for the online monitoring data of tunnel structure. Rock Soil Mech. 2016, 37, 1208–1216. [Google Scholar]
- Kong, X. Analysis of Tunnel Monitoring Results Based on Modulus Maxima Method of Wavelet Transform. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016. [Google Scholar]
- Ghaderpour, E.; Pagiatakis, S.D. Least-Squares Wavelet Analysis of Unequally Spaced and Non-stationary Time Series and Its Applications. Math. Geosci. 2017, 49, 819–844. [Google Scholar] [CrossRef]
- Wang, D.; Ding, H.; Singh, V.P.; Shang, X.; Liu, D.; Wang, Y.; Zeng, X.; Wu, J.; Wang, L.; Zou, X. A hybrid wavelet analysis–cloud model data-extending approach for meteorologic and hydrologic time series. J. Geophys. Res. Atmos. 2015, 120, 4057–4071. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, L. Applications of wavelet analysis in differential propagation phase shift data de-noising. Adv. Atmos. Sci. 2014, 31, 825–835. [Google Scholar] [CrossRef]
- Baili, J.; Lahouar, S.; Hergli, M.; Al-Qadi, I.L.; Besbes, K. GPR signal de-noising by discrete wavelet transform. NDT E Int. 2009, 42, 696–703. [Google Scholar] [CrossRef]
- Beenamol, M.; Prabavathy, S.; Mohanalin, J. Wavelet based seismic signal de-noising using Shannon and Tsallis entropy. Comput. Math. Appl. 2012, 64, 3580–3593. [Google Scholar] [CrossRef]
- Ji, Y.; Li, D.; Yu, M.; Wang, Y.; Wu, Q.; Lin, J. A de-noising algorithm based on wavelet threshold-exponential adaptive window width-fitting for ground electrical source airborne transient electromagnetic signal. J. Appl. Geophys. 2016, 128, 1–7. [Google Scholar] [CrossRef]
- Yuan, M.; Wen, H.; Zhou, L.; Chen, G. Application of High-Speed Railway Deformation Analysis Based on Improved Wavelet Threshold Value. J. Guilin Univ. Technol. 2015, 35, 107–110. [Google Scholar]
- Zhang, Z. Theory of Wavelet Analysis and Its Application in Deformation Monitoring. Master’s Thesis, Central South University, Changsha, China, 2014. [Google Scholar]
- Zheng, J.; Xie, X.; Liu, S. Deformation prediction of high-speed rail based on wavelet analysis. Sci. Surv. Mapp. 2016, 41, 161–164. [Google Scholar]
- Barnsley, M.F. Fractal functions and interpolation. Constr. Approx. 1986, 2, 303–329. [Google Scholar] [CrossRef]
- Feng, Z.; Feng, Y.; Yuan, Z. Fractal interpolation surfaces with function vertical scaling factors. Appl. Math. Lett. 2012, 25, 1896–1900. [Google Scholar] [CrossRef]
- Marvasti, M.A.; Strahle, W.C. Fractal interpolation methods in spatial cross-correlation velocimetry. Exp. Fluids 1994, 18, 129–130. [Google Scholar] [CrossRef]
- Ri, S. New types of fractal interpolation surfaces. Chaos Solitons Fractals 2019, 119, 291–297. [Google Scholar] [CrossRef]
- Bruno, O.M.; de Oliveira Plotze, R.; Falvo, M.; de Castro, M. Fractal dimension applied to plant identification. Inf. Sci. 2008, 178, 2722–2733. [Google Scholar] [CrossRef]
- Chen, W.-S.; Yuan, S.-Y.; Hsieh, C.-M. Two algorithms to estimate fractal dimension of gray-level images. Opt. Eng. 2003, 42, 2452–2464. [Google Scholar] [CrossRef]
- Giorgilli, A.; Casati, D.; Sironi, L.; Galgani, L. An efficient procedure to compute fractal dimensions by box counting. Phys. Lett. A 1986, 115, 202–206. [Google Scholar] [CrossRef]
- Grassberger, P. On the fractal dimension of the Henon attractor. Phys. Lett. A 1983, 97, 224–226. [Google Scholar] [CrossRef]
- Liebovitch, L.S.; Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 1989, 141, 386–390. [Google Scholar] [CrossRef]
- Bouboulis, P.; Dalla, L. A general construction of fractal interpolation Functions on grids of IRn. Eur. J. Appl. Math. 2007, 18, 449–476. [Google Scholar] [CrossRef][Green Version]
- Gemperline, M.C.; Siller, T.J. Fractal Interpolation. J. Comput. Civ. Eng. 2002, 16, 184–193. [Google Scholar] [CrossRef]
- Mazel, D.S.; Hayes, M.H. Using iterated function systems to model discrete sequences. IEEE Trans. Signal Process. 1992, 40, 1724–1734. [Google Scholar] [CrossRef]
- Barnsley, M.; Elton, J.; Hardin, D.; Massopust, P. Hidden Variable Fractal Interpolation Functions. SIAM J. Math. Anal. 1989, 20, 1218–1248. [Google Scholar] [CrossRef]
- Paramanathan, P.; Uthayakumar, R. Fractal interpolation on the Koch Curve. Comput. Math. Appl. 2010, 59, 3229–3233. [Google Scholar] [CrossRef]
- Keddam, M.; Takenouti, H. Impedance of fractal interfaces: New data on the Von Koch model. Electrochim. Acta 1988, 33, 445–448. [Google Scholar] [CrossRef]
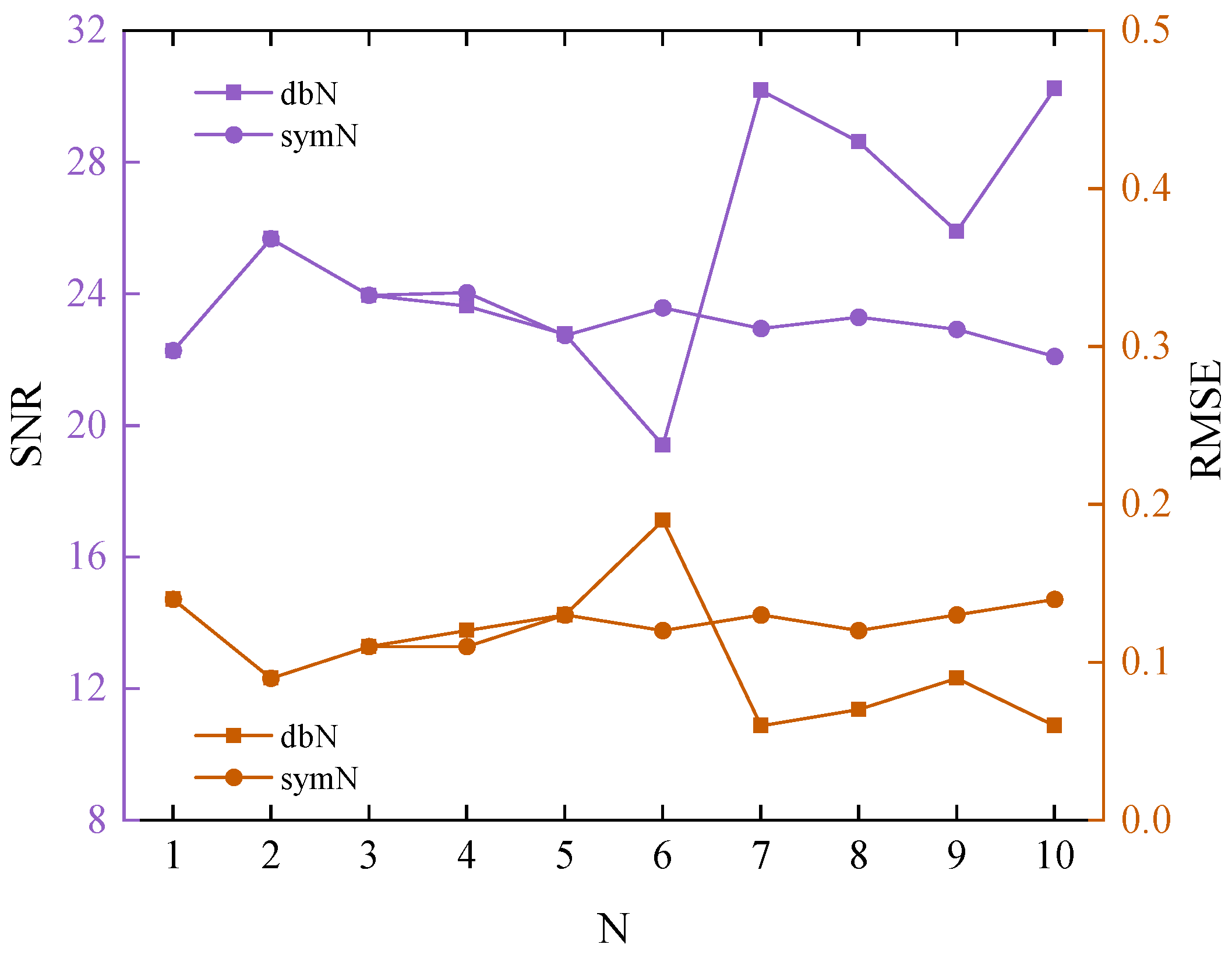





| Wavelet Function | SNR | RMSE |
|---|---|---|
| db N | 25.26 | 0.11 |
| sym N | 23.35 | 0.12 |
| Time Period/d | Monitoring Data (Quantity) | Interpolation Results (Quantity) |
|---|---|---|
| 1–13 | 0.0324 (2) | 0.0384 (13) |
| 13–26 | 0.0818 (5) | 0.1295 (13) |
| 26–40 | 1.8905 (6) | 2.0088 (14) |
| 40–50 | 3.8863 (6) | 4.3266 (10) |
| 50–63 | 4.6987 (6) | 4.8323 (13) |
| 63–75 | 5.2813 (4) | 5.6643 (12) |
| 75–89 | 2.5576 (8) | 2.5132 (14) |
| 89–100 | −0.4147 (9) | −0.3984 (11) |
| 100–124 | 0.2445 (16) | 0.2314 (25) |
| 124–148 | 0.8864 (9) | 0.9232 (24) |
| 148–170 | 0.8730 (6) | 0.9480 (22) |
| 170–194 | 0.3345 (6) | 0.3196 (24) |
| 194–222 | 0.4895 (3) | 0.6553 (28) |
| 222–244 | 0.3798 (3) | 0.3528 (22) |
| 244–264 | 0.3385 (4) | 0.2370 (20) |
| 264–290 | 0.1087 (7) | 0.1184 (26) |
| Monitoring Frequency | Fractal Dimension |
|---|---|
| 1 d/time | 1.2418 |
| 2 d/time | 1.2231 |
| 4 d/time | 1.2261 |
| 6 d/time | 1.2098 |
| 8 d/time | 1.2109 |
| 10 d/time | 1.2055 |
| 12 d/time | 1.1998 |
| 14 d/time | 1.2087 |
| 16 d/time | 1.2139 |
| 18 d/time | 1.2026 |
| 20 d/time | 1.2283 |
| 30 d/time | 1.1921 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; He, P.; Zhang, J.; Xie, L. The Fractal Characteristics of Ground Subsidence Caused by Subway Excavation. Appl. Sci. 2024, 14, 5327. https://doi.org/10.3390/app14125327
Qin Y, He P, Zhang J, Xie L. The Fractal Characteristics of Ground Subsidence Caused by Subway Excavation. Applied Sciences. 2024; 14(12):5327. https://doi.org/10.3390/app14125327
Chicago/Turabian StyleQin, Yongjun, Peng He, Jiaqi Zhang, and Liangfu Xie. 2024. "The Fractal Characteristics of Ground Subsidence Caused by Subway Excavation" Applied Sciences 14, no. 12: 5327. https://doi.org/10.3390/app14125327
APA StyleQin, Y., He, P., Zhang, J., & Xie, L. (2024). The Fractal Characteristics of Ground Subsidence Caused by Subway Excavation. Applied Sciences, 14(12), 5327. https://doi.org/10.3390/app14125327






