Multimodal Shot Prediction Based on Spatial-Temporal Interaction between Players in Soccer Videos
Abstract
1. Introduction
- For the shot prediction from soccer videos, we use a graph that introduces soccer-specific knowledge (players’ importance based on the field positions and team information) with audio-visual information as graph nodes.
- Predicting and obtaining uncertainty with BNNs enables us to provide more robust predictions.
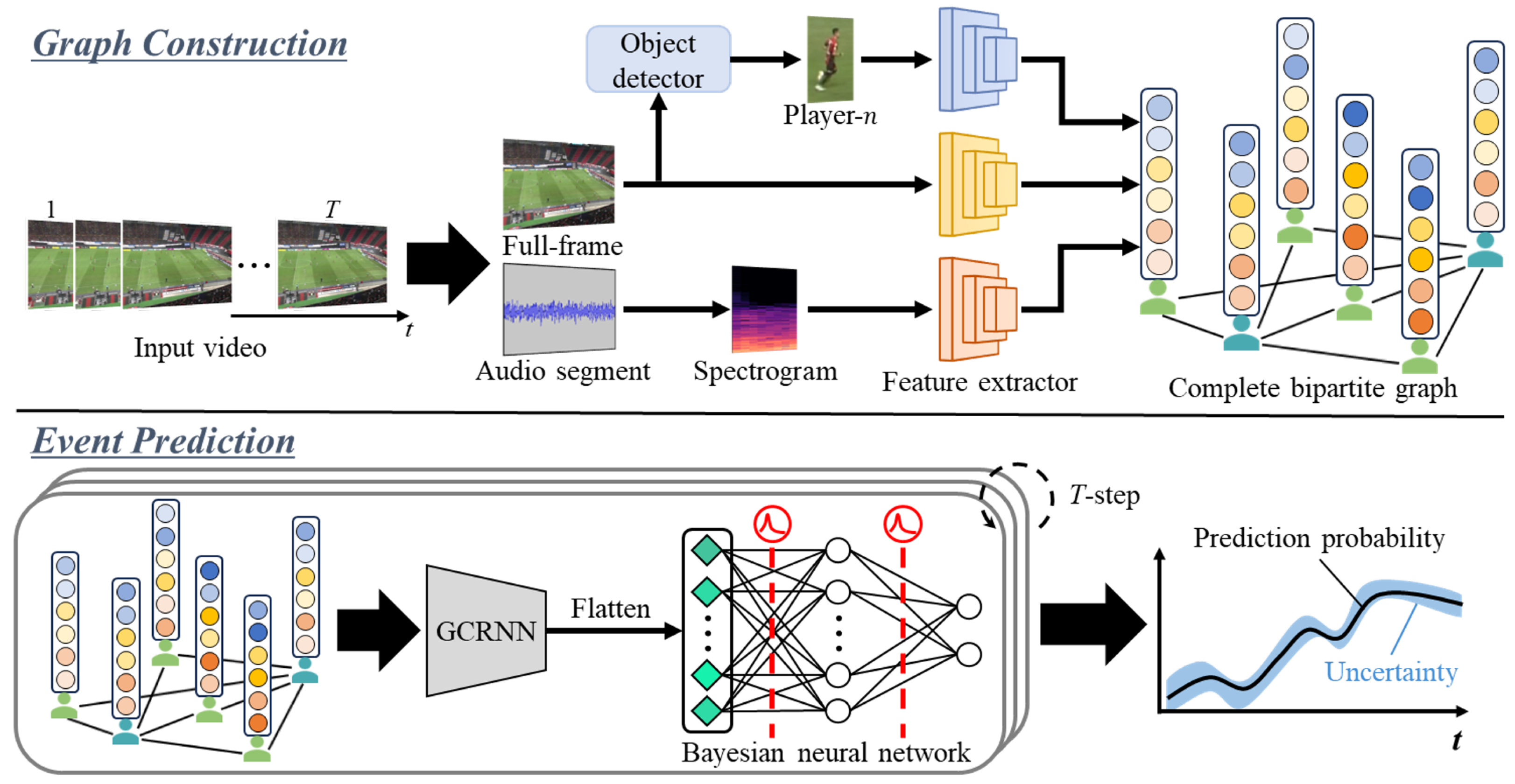
2. Proposed Multimodal Shot Prediction in Soccer Videos
2.1. Graph Construction
2.2. Graph Convolutional Recurrent Neural Network
2.3. Uncertainty-Based Event Prediction
2.3.1. Construction with Bayesian Neural Networks
2.3.2. Loss Function
3. Experiments
3.1. Settings
- DSA [58]:
- This is a method for traffic accident prediction from dashcam videos. This model learns temporal relationships through RNN and the importance of detected objects in the video through Dynamic Spatial Attention (DSA).
- DSTA [59]:
- This is a video-based prediction model for traffic accidents, which uses GRU or LSTM to learn temporal relationships and Dynamic Spatial–Temporal Attention (DSTA) to learn the spatial and temporal importance of detected objects in the dashcam video.
- ViViT [60]:
- This is a video recognition model known as a Video Vision Transformer (ViViT), which learns spatial and temporal dynamics by tokenizing videos into a series of image frames or patches.
3.2. Results and Discussion
3.2.1. Quantitative Results
3.2.2. Qualitative Results
3.2.3. Limitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lord, F.; Pyne, D.B.; Welvaert, M.; Mara, J.K. Methods of performance analysis in team invasion sports: A systematic review. J. Sport. Sci. 2020, 38, 2338–2349. [Google Scholar] [CrossRef] [PubMed]
- Chmait, N.; Westerbeek, H. Artificial intelligence and machine learning in sport research: An introduction for non-data scientists. Front. Sport. Act. Living 2021, 3, 363. [Google Scholar] [CrossRef] [PubMed]
- Van Roy, M.; Yang, W.C.; De Raedt, L.; Davis, J. Analyzing learned Markov decision processes using model checking for providing tactical advice in professional soccer. In Proceedings of the International Joint Conference on Artificial Intelligence Workshop on AI for Sports Analytics, Virtual, 17–19 September 2021. [Google Scholar]
- Wang, J. Predictive Analysis of NBA Game Outcomes through Machine Learning. In Proceedings of the International Conference on Machine Learning and Machine Intelligence, Chongqing, China, 27–29 October 2023; pp. 46–55. [Google Scholar]
- Jones, R.N.; Greig, M.; Mawéné, Y.; Barrow, J.; Page, R.M. The influence of short-term fixture congestion on position specific match running performance and external loading patterns in English professional soccer. J. Sport. Sci. 2019, 37, 1338–1346. [Google Scholar] [CrossRef]
- Goes, F.; Meerhoff, L.; Bueno, M.; Rodrigues, D.; Moura, F.; Brink, M.; Elferink-Gemser, M.; Knobbe, A.; Cunha, S.; Torres, R.; et al. Unlocking the potential of big data to support tactical performance analysis in professional soccer: A systematic review. Eur. J. Sport Sci. 2021, 21, 481–496. [Google Scholar] [CrossRef] [PubMed]
- Forcher, L.; Altmann, S.; Forcher, L.; Jekauc, D.; Kempe, M. The use of player tracking data to analyze defensive play in professional soccer—A scoping review. Int. J. Sport. Sci. Coach. 2022, 17, 1567–1592. [Google Scholar] [CrossRef]
- Akenhead, R.; Nassis, G.P. Training load and player monitoring in high-level football: Current practice and perceptions. Int. J. Sport. Physiol. Perform. 2016, 11, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Nobari, H.; Banoocy, N.K.; Oliveira, R.; Pérez-Gómez, J. Win, draw, or lose? Global positioning system-based variables’ effect on the match outcome: A full-season study on an Iranian professional soccer team. Sensors 2021, 21, 5695. [Google Scholar] [CrossRef] [PubMed]
- Pino-Ortega, J.; Oliva-Lozano, J.M.; Gantois, P.; Nakamura, F.Y.; Rico-Gonzalez, M. Comparison of the validity and reliability of local positioning systems against other tracking technologies in team sport: A systematic review. Proc. Inst. Mech. Eng. Part P J. Sport. Eng. Technol. 2022, 236, 73–82. [Google Scholar] [CrossRef]
- Anzer, G.; Bauer, P. A goal scoring probability model for shots based on synchronized positional and event data in football (soccer). Front. Sport. Act. Living 2021, 3, 624475. [Google Scholar] [CrossRef]
- Simpson, I.; Beal, R.J.; Locke, D.; Norman, T.J. Seq2Event: Learning the Language of Soccer using Transformer-based Match Event Prediction. In Proceedings of the the ACM International Conference on Special Interest Group on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 3898–3908. [Google Scholar]
- Pappalardo, L.; Cintia, P.; Rossi, A.; Massucco, E.; Ferragina, P.; Pedreschi, D.; Giannotti, F. A public data set of spatio-temporal match events in soccer competitions. Sci. Data 2019, 6, 236. [Google Scholar] [CrossRef]
- Biermann, H.; Theiner, J.; Bassek, M.; Raabe, D.; Memmert, D.; Ewerth, R. A unified taxonomy and multimodal dataset for events in invasion games. In Proceedings of the the ACM International Workshop on Multimedia Content Analysis in Sports, Chengdu, China, 20 October 2021; pp. 1–10. [Google Scholar]
- Lucey, P.; Bialkowski, A.; Monfort, M.; Carr, P.; Matthews, I. Quality vs quantity: Improved shot prediction in soccer using strategic features from spatiotemporal data. In Proceedings of the MIT Sloan Sports Analytics Conference, Boston, MA, USA, 28 February–1 March 2014; pp. 1–9. [Google Scholar]
- Decroos, T.; Van Haaren, J.; Dzyuba, V.; Davis, J. STARSS: A spatio-temporal action rating system for soccer. In Proceedings of the the ECML/PKDD Workshop on Machine Learning and Data Mining for Sports Analytics, Skopje, North Macedonia, 18 September 2017; Volume 1971, pp. 11–20. [Google Scholar]
- Power, P.; Ruiz, H.; Wei, X.; Lucey, P. Not all passes are created equal: Objectively measuring the risk and reward of passes in soccer from tracking data. In Proceedings of the the ACM International Conference on Special Interest Group on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1605–1613. [Google Scholar]
- Spearman, W. Beyond expected goals. In Proceedings of the MIT Sloan Sports Analytics Conference, Boston, MA, USA, 23–24 February 2018; pp. 1–17. [Google Scholar]
- Liu, G.; Luo, Y.; Schulte, O.; Kharrat, T. Deep soccer analytics: Learning an action-value function for evaluating soccer players. Data Min. Knowl. Discov. 2020, 34, 1531–1559. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Naik, B.T.; Hashmi, M.F.; Bokde, N.D. A comprehensive review of computer vision in sports: Open issues, future trends and research directions. Appl. Sci. 2022, 12, 4429. [Google Scholar] [CrossRef]
- Deliege, A.; Cioppa, A.; Giancola, S.; Seikavandi, M.J.; Dueholm, J.V.; Nasrollahi, K.; Ghanem, B.; Moeslund, T.B.; Van Droogenbroeck, M. Soccernet-v2: A dataset and benchmarks for holistic understanding of broadcast soccer videos. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Virtual, 25 June 2021; pp. 4508–4519. [Google Scholar]
- Manafifard, M.; Ebadi, H.; Moghaddam, H.A. A survey on player tracking in soccer videos. Comput. Vis. Image Underst. 2017, 159, 19–46. [Google Scholar] [CrossRef]
- Hurault, S.; Ballester, C.; Haro, G. Self-supervised small soccer player detection and tracking. In Proceedings of the the International Workshop on Multimedia Content Analysis in Sports, Seattle, WA, USA, 16 October 2020; pp. 9–18. [Google Scholar]
- Cioppa, A.; Giancola, S.; Deliege, A.; Kang, L.; Zhou, X.; Cheng, Z.; Ghanem, B.; Van Droogenbroeck, M. Soccernet-tracking: Multiple object tracking dataset and benchmark in soccer videos. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, New Orleans, LA, USA, 20 June 2022; pp. 3491–3502. [Google Scholar]
- Fu, X.; Huang, W.; Sun, Y.; Zhu, X.; Evans, J.; Song, X.; Geng, T.; He, S. A Novel Dataset for Multi-View Multi-Player Tracking in Soccer Scenarios. Appl. Sci. 2023, 13, 5361. [Google Scholar] [CrossRef]
- Khaustov, V.; Mozgovoy, M. Recognizing events in spatiotemporal soccer data. Appl. Sci. 2020, 10, 8046. [Google Scholar] [CrossRef]
- Alamuru, S.; Jain, S. Video event detection, classification and retrieval using ensemble feature selection. Clust. Comput. 2021, 24, 2995–3010. [Google Scholar] [CrossRef]
- Mahaseni, B.; Faizal, E.R.M.; Raj, R.G. Spotting football events using two-stream convolutional neural network and dilated recurrent neural network. IEEE Access 2021, 9, 61929–61942. [Google Scholar] [CrossRef]
- Nergård Rongved, O.A.; Stige, M.; Hicks, S.A.; Thambawita, V.L.; Midoglu, C.; Zouganeli, E.; Johansen, D.; Riegler, M.A.; Halvorsen, P. Automated event detection and classification in soccer: The potential of using multiple modalities. Mach. Learn. Knowl. Extr. 2021, 3, 1030–1054. [Google Scholar] [CrossRef]
- Sanabria, M.; Sherly; Precioso, F.; Menguy, T. A deep architecture for multimodal summarization of soccer games. In Proceedings of the International Workshop on Multimedia Content Analysis in Sports, Nice, France, 25 October 2019; pp. 16–24. [Google Scholar]
- Haruyama, T.; Takahashi, S.; Ogawa, T.; Haseyama, M. User-selectable event summarization in unedited raw soccer video via multimodal bidirectional LSTM. ITE Trans. Media Technol. Appl. 2021, 9, 42–53. [Google Scholar] [CrossRef]
- Honda, Y.; Kawakami, R.; Yoshihashi, R.; Kato, K.; Naemura, T. Pass Receiver Prediction in Soccer Using Video and Players’ Trajectories. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, New Orleans, LA, USA, 20 June 2022; pp. 3503–3512. [Google Scholar]
- Fang, J.; Yeung, C.; Fujii, K. Foul prediction with estimated poses from soccer broadcast video. arXiv 2024, arXiv:2402.09650. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Seo, Y.; Defferrard, M.; Vandergheynst, P.; Bresson, X. Structured sequence modeling with graph convolutional recurrent networks. In Proceedings of the International Conference on Neural Information Processing, Siem Reap, Cambodia, 13–16 December 2018; pp. 362–373. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: New York, NY, USA, 2012; Volume 118. [Google Scholar]
- Goka, R.; Moroto, Y.; Maeda, K.; Ogawa, T.; Haseyama, M. Shoot event prediction from soccer videos by considering players’ spatio-temporal relations. In Proceedings of the the IEEE Global Conference on Consumer Electronics, Osaka, Japan, 18–21 October 2022; pp. 193–194. [Google Scholar]
- Goka, R.; Moroto, Y.; Maeda, K.; Ogawa, T.; Haseyama, M. Prediction of shooting events in soccer videos using complete bipartite graphs and players’ spatial-temporal relations. Sensors 2023, 23, 4506. [Google Scholar] [CrossRef] [PubMed]
- Goka, R.; Moroto, Y.; Maeda, K.; Ogawa, T.; Haseyama, M. Shoot Event Prediction in Soccer Considering Expected Goals Based on Players’ Positions. In Proceedings of the International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), PingTung, Taiwan, 17–19 July 2023; pp. 449–450. [Google Scholar]
- Goka, R.; Moroto, Y.; Maeda, K.; Ogawa, T.; Haseyama, M. Prediction of Shoot Events by Considering Spatio-temporal Relations of Multimodal Features. In Proceedings of the International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), PingTung, Taiwan, 17–19 July 2023; pp. 793–794. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Sun, S.b.; Cui, R.y. Player classification algorithm based on digraph in soccer video. In Proceedings of the the IEEE Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 20–21 December 2014; pp. 459–463. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Araújo, D.; Davids, K. Team synergies in sport: Theory and measures. Front. Psychol. 2016, 7, 214015. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.R.; Lopes, R.J.; Louçã, J.; Araújo, D.; Ramos, J. The soccer game, bit by bit: An information-theoretic analysis. Chaos Solitons Fractals 2021, 152, 111356. [Google Scholar] [CrossRef]
- Ruiz, L.; Gama, F.; Ribeiro, A. Gated graph convolutional recurrent neural networks. In Proceedings of the the European Signal Processing Conference, A Coruña, Spain, 2–6 September 2009; pp. 1–5. [Google Scholar]
- Cui, Z.; Henrickson, K.; Ke, R.; Wang, Y. Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4883–4894. [Google Scholar] [CrossRef]
- Elbasani, E.; Njimbouom, S.N.; Oh, T.J.; Kim, E.H.; Lee, H.; Kim, J.D. GCRNN: Graph convolutional recurrent neural network for compound–protein interaction prediction. BMC Bioinform. 2021, 22, 616. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wilson, A.G.; Izmailov, P. Bayesian deep learning and a probabilistic perspective of generalization. Adv. Neural Inf. Process. Syst. 2020, 33, 4697–4708. [Google Scholar]
- Izmailov, P.; Vikram, S.; Hoffman, M.D.; Wilson, A.G.G. What are Bayesian neural network posteriors really like? In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 4629–4640. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural network. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1613–1622. [Google Scholar]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? Adv. Neural Inf. Process. Syst. 2017, 30, 5574–5584. [Google Scholar]
- Diederik, P.K.; Ba, J.L. Adam: A method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Chan, F.H.; Chen, Y.T.; Xiang, Y.; Sun, M. Anticipating accidents in dashcam videos. In Proceedings of the the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 136–153. [Google Scholar]
- Karim, M.M.; Li, Y.; Qin, R.; Yin, Z. A dynamic spatial-temporal attention network for early anticipation of traffic accidents. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9590–9600. [Google Scholar] [CrossRef]
- Arnab, A.; Dehghani, M.; Heigold, G.; Sun, C.; Lučić, M.; Schmid, C. Vivit: A video vision transformer. In Proceedings of the the IEEE International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6836–6846. [Google Scholar]
- Neumann, L.; Zisserman, A.; Vedaldi, A. Future event prediction: If and when. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 2935–2943. [Google Scholar]
- Raghu, M.; Unterthiner, T.; Kornblith, S.; Zhang, C.; Dosovitskiy, A. Do vision transformers see like convolutional neural networks? Adv. Neural Inf. Process. Syst. 2021, 34, 12116–12128. [Google Scholar]


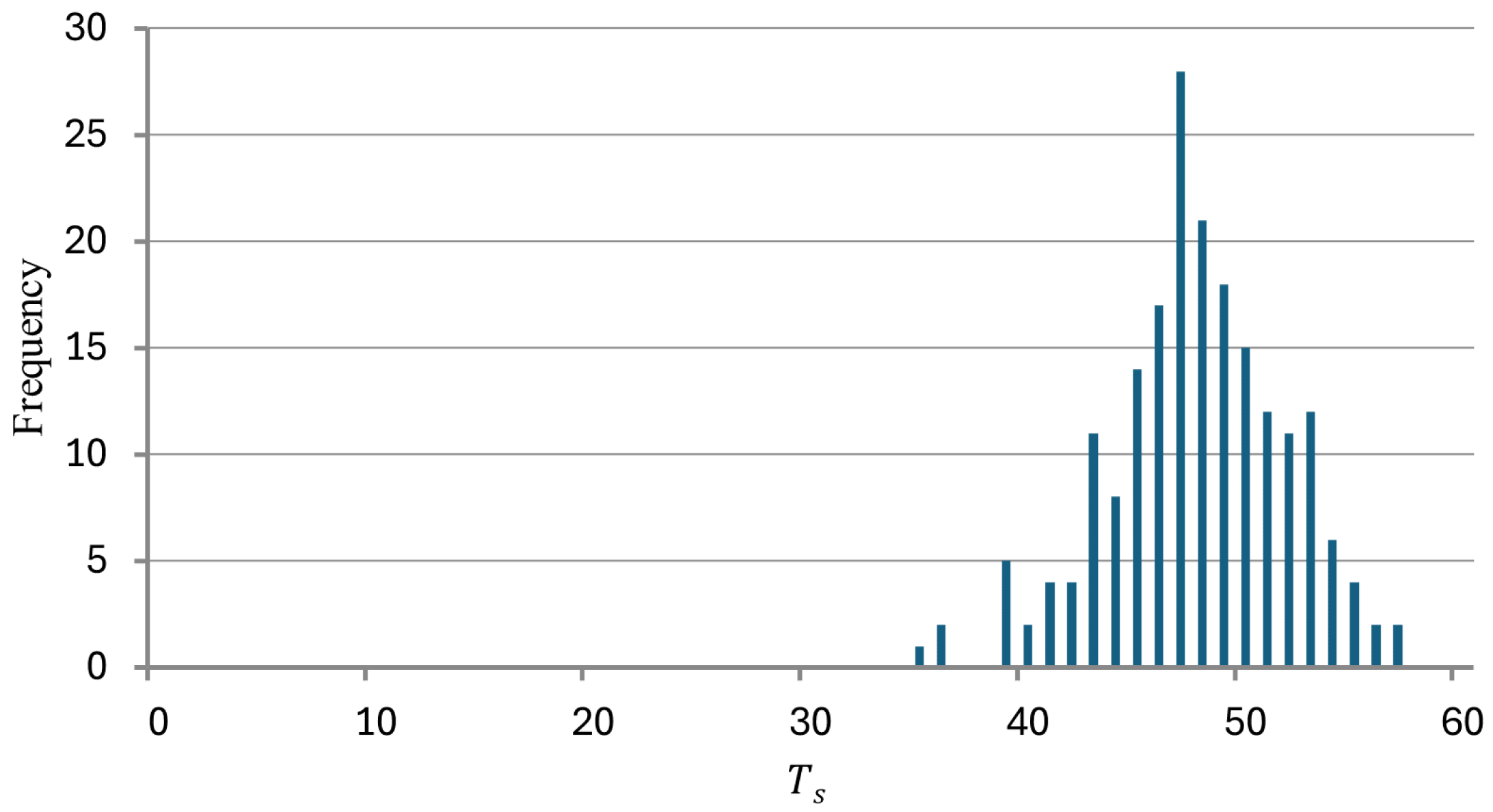
| AP | F1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 10 | t = 20 | t = 30 | t = 40 | t = 50 | t = 60 | t = 10 | t = 20 | t = 30 | t = 40 | t = 50 | t = 60 | |
| Ablation1 | 0.881 | 0.921 | 0.939 | 0.944 | 0.948 | 0.947 | 0.729 | 0.782 | 0.823 | 0.848 | 0.874 | 0.897 |
| Ablation2 | 0.912 | 0.917 | 0.934 | 0.942 | 0.958 | 0.964 | 0.672 | 0.790 | 0.829 | 0.849 | 0.860 | 0.854 |
| Ablation3 | 0.905 | 0.923 | 0.933 | 0.940 | 0.942 | 0.942 | 0.671 | 0.750 | 0.795 | 0.823 | 0.842 | 0.855 |
| Ablation4 | 0.915 | 0.929 | 0.937 | 0.939 | 0.942 | 0.940 | 0.601 | 0.753 | 0.800 | 0.824 | 0.831 | 0.832 |
| DSA [58] | 0.882 | 0.880 | 0.888 | 0.929 | 0.936 | 0.932 | 0.742 | 0.777 | 0.802 | 0.818 | 0.838 | 0.838 |
| DSTA [59] | 0.912 | 0.923 | 0.929 | 0.928 | 0.939 | 0.946 | 0.674 | 0.763 | 0.815 | 0.829 | 0.844 | 0.859 |
| ViViT [60] | 0.736 | 0.744 | 0.766 | 0.770 | 0.760 | 0.755 | 0.679 | 0.682 | 0.676 | 0.679 | 0.675 | 0.682 |
| PM | 0.913 | 0.923 | 0.938 | 0.946 | 0.959 | 0.966 | 0.757 | 0.806 | 0.825 | 0.860 | 0.876 | 0.891 |
| AP | Recall | Precision | F1 | mTTE | |
|---|---|---|---|---|---|
| Ablation1 | 0.934 | 0.807 | 0.882 | 0.839 | 3.46 |
| Ablation2 | 0.941 | 0.781 | 0.891 | 0.824 | 3.63 |
| Ablation3 | 0.927 | 0.797 | 0.849 | 0.801 | 3.46 |
| Ablation4 | 0.926 | 0.766 | 0.884 | 0.816 | 3.61 |
| DSA [58] | 0.920 | 0.786 | 0.859 | 0.820 | 3.71 |
| DSTA [59] | 0.925 | 0.820 | 0.856 | 0.836 | 3.47 |
| PM | 0.948 | 0.828 | 0.896 | 0.858 | 3.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goka, R.; Moroto, Y.; Maeda, K.; Ogawa, T.; Haseyama, M. Multimodal Shot Prediction Based on Spatial-Temporal Interaction between Players in Soccer Videos. Appl. Sci. 2024, 14, 4847. https://doi.org/10.3390/app14114847
Goka R, Moroto Y, Maeda K, Ogawa T, Haseyama M. Multimodal Shot Prediction Based on Spatial-Temporal Interaction between Players in Soccer Videos. Applied Sciences. 2024; 14(11):4847. https://doi.org/10.3390/app14114847
Chicago/Turabian StyleGoka, Ryota, Yuya Moroto, Keisuke Maeda, Takahiro Ogawa, and Miki Haseyama. 2024. "Multimodal Shot Prediction Based on Spatial-Temporal Interaction between Players in Soccer Videos" Applied Sciences 14, no. 11: 4847. https://doi.org/10.3390/app14114847
APA StyleGoka, R., Moroto, Y., Maeda, K., Ogawa, T., & Haseyama, M. (2024). Multimodal Shot Prediction Based on Spatial-Temporal Interaction between Players in Soccer Videos. Applied Sciences, 14(11), 4847. https://doi.org/10.3390/app14114847






