Abstract
In this paper, the vertical vibration behaviour of an experimental scale demonstrator of a railway vehicle carbody fitted with an anti-bending bar system of innovative design is studied to highlight its ability to raise the bending natural frequency of the railway vehicle carbody and to reduce the intensity of the vibration. The anti-bending bar system has been previously proposed by the second author as a new passive method to improve comfort in passenger coaches with long carbodies that have a natural bending frequency located in the range of maximum sensitivity of human beings to vertical vibration. The experimental scale demonstrator consists of an aluminium plate supported on four rubber supports. The aluminium beam reproduces to a scale of 1:10 the length of a passenger coach carbody, and its thickness is set so that the first bending frequency of the plate is close to the usual value of real carbodies. The anti-bending bar system consists of two steel bars arranged longitudinally in the middle of the aluminium plate, near its side edges. Each anti-bending bar is fixed at the ends to the aluminium plate by joints consisting of a clamping arm welded to a fixing flange. The two anti-bending bars oppose the bending movement of the aluminium plate, thus increasing its bending stiffness. This results in increasing the bending natural frequency of the aluminium plate and reduction its vibration. Testing the effectiveness of the anti-bending bar system consists of experimentally determining the frequency response of the aluminium plate acceleration without/with the anti-bending bar system by the impact hammer method. The experimental results show the first bending natural frequency increases from 9.01 Hz to 13.4 Hz and the acceleration amplitude decreases by more than 50% when the anti-bending bar system is used. To confirm these results, a theoretical model of the experimental scale demonstrator based on the finite element method was developed. The results obtained with this model are in line with those obtained experimentally.
1. Introduction
Ride comfort is a sine qua non condition that must be met by all types of passenger trains, whether for urban, commuter or high-speed traffic. A railway vehicle exhibits vibrations in the three directions, vertical, lateral, and longitudinal, which develop practically independently of each other and have their own characteristics. The vertical vibrations are excited by the irregularity of the track longitudinal level [1,2], lateral ones are maintained by the alignment deviations and take the form of hunting motion due to the inverted conicity of the running surfaces of the wheels [3,4], and longitudinal ones are induced by the traction-braking behaviour [5,6].
As for the vertical vibrations of passenger coaches, they affect the ride comfort especially in long and light vehicles intended for high-speed trains, due to the fact that the first natural bending frequency of the carbody is located in the range of highest sensitivity of human beings to vertical vibrations, between 6 and 12 Hz, as an effect of its slenderness [7,8]. In these vehicles, the critical point in terms of the ride comfort is in the middle of the carbody because the bending vibration of the first eigenmode has its ventrum (antinode) here. In contrast, the critical points of ordinary vehicles are located at the ends of the carbody [9].
Active, semi-active and passive systems have been proposed to improve the ride comfort to vertical vibration in passenger coaches [10,11,12,13,14,15,16,17]. They are designed either to isolate the carbody from vibrations using active/semi-active suspension [10,11,12], or to reduce the structural vibration of the carbody through the damping provided by the active/passive suspension [13,14,15,16,17].
In general, a passive system for reducing the vertical vibration of the carbody is simpler to implement, cheaper and requires lower maintenance costs compared to a semi-active or active system.
Many passive systems work on the dynamic absorber principle by elastically attaching a mass to the vehicle carbody. In this way, the bending frequency of the carbody can be increased and taken out of the high sensitivity range mentioned above. This solution has been studied in several papers to improve ride comfort in multiple high-speed electric units [18,19,20,21,22].
The concept of a new passive system for reducing the bending vibration of a railway vehicle carbody was presented in ref. [17]. The functional principle is shown in Figure 1, where the railway vehicle carbody is provided with four rigid supports—two fixed on each side of the carbody chassis, symmetrically in relation to the middle of the carbody, in which two steel bars, called the anti-bending bars, are mounted. When the carbody bends, the cross sections in which the supports work rotate in the opposite direction so that the anti-bending bars are either compressed (Figure 1b) or stretched (Figure 1c). In both situations, the anti-bending bars develop longitudinal forces (red arrows) which, reduced to the neutral axis of the carbody, cause moments that oppose the bending of the carbody (blue curved arrows) and longitudinal forces (blue straight arrows). For clarity, Figure 1a shows the other main components of a four-axle vehicle: wheelset, bogie chassis, primary suspension and secondary suspension.
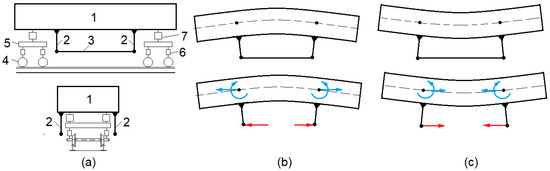
Figure 1.
The functional principle of the passive system with anti-bending bars: (a) scheme of vehicle with anti-bending bars: 1. carbody; 2. support; 3. anti-bending bar; 4. wheelset; 5. bogie chassis; 6. primary suspension; 7. secondary suspension; (b) carbody when the anti-bending bars are compressed; (c) carbody when the anti-bending bars are stretched.
Effect of the anti-bending bar system on the frequency response function of the carbody and on the comfort index in a passenger coach traveling at speeds of up to 300 km/h was investigated in paper [17]. The calculations were performed based on a continuous-discrete analytical model developed for a vehicle like the one in Figure 1a. The carbody was modelled as a Euler–Bernoulli beam, while lumped parameter models were used for the bogie chassis, wheelsets and suspension elements. The anti-bending bars were modelled as ideal elastic elements, neglecting their bending effect.
Figure 2 shows an example regarding the change in the dynamic behaviour of the carbody when fitted with an anti-bending bar system; the calculated speed was 270 km/h. First, the figure graphs show the acceleration power spectral density (acceleration is weighted accordingly Guidelines for Evaluating Passenger Comfort In Relation to Vibration in Railway Vehicles to reflect the sensitivity of the human being to vertical vibrations [23]) for the carbody variant without anti-bending bar system (red line) at the carbody centre (Figure 2a), above the front bogie (Figure 2b) and above the rear bogie (Figure 2c). The carbody centre without anti-bending bars exhibits an absolute maximum at 8 Hz in the acceleration power spectral density corresponding to the bending frequency. This peak is larger than the one due to the carbody bounce located at approx. 1.17 Hz. Above the bogies, a peak at 1.4 Hz due to the pitch motion is added next to the bounce peak and surpasses the bending peak. The vibration behaviour of the carbody with the anti-bending bar system changes radically in terms of the importance of the carbody bending vibration as shown by the three variants depicted in Figure 2. The anti-bending bar system is sized so that the bending frequency of carbody reaches 10 Hz (blue line), 12 Hz (green line) and 14 Hz (yellow line). The effect of the anti-bending bar system is to increase the bending frequency of the carbody and reduce the acceleration in the frequency range corresponding to its bending, thus contributing to the improvement of ride comfort, especially in the middle of the carbody.
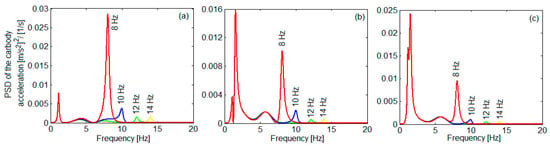
Figure 2.
Influence of the anti-bending bar system in terms of PSD of the carbody acceleration at 270 km/h: (a) at the carbody centre; (b) above the front bogie; and (c) above the rear bogie [17].
The method of reducing vertical vibrations with the help of the anti-bending bar system is advantageous due to the simplicity of the construction whose manufacturing, assembly and maintenance costs are reduced. From the point of view of an anti-bending bar system design, the parameters of the anti-bending bars are calculated by starting from the bending natural frequency of the vehicle carbody and forcing it to reach a convenient value above 12 Hz so that the ride comfort in vertical vibrations is assured.
To demonstrate the feasibility of the new concept of reducing the vibration of the carbody of the railway vehicles using an anti-bending bar system, an original dedicated experimental scale demonstrator system was proposed in ref. [24]. Figure 3 shows the diagram of the experimental scale demonstrator system for the carbody with anti-bending bar system, which consists of the scale model of the vehicle carbody, which is placed on four elastic rubber elements (suspension elements); rubber is a material often used in the suspension of railway vehicles [25,26].

Figure 3.
Sketch of experimental demonstrator system for the carbody with anti-bending bar system (after [24]).
The scale model of the carbody is an aluminium plate sized so that the first bending eigenfrequency of the beam–spring assembly is in the typical range where the natural bending frequency of the carbody on the vehicle suspension is usually found. The anti-bending bar system is mounted under the aluminium beam on its sides.
In paper [24], a discrete–continuous-type model like that used in ref. [17] was presented and utilised to evaluate the influence of the anti-bending bar system on the frequency response function of the reduced scale model of the vehicle carbody.
The use of scale models of the railway vehicle carbody to experiment in laboratory conditions with different vibration reduction methods is widely used due to the advantages of these models over 1:1 scale model, the most important of which is related to the cost of manufacturing and equipping for tests. For example, a passive method of improving the vibration behaviour of a light-carbody railway vehicle by increasing structural damping by means of viscoelastic patches was tested on a scale model in the paper [27]. A 1:24.5 scale model of the carbody of a Shinkansen vehicle was used to verify the results of the numerical simulation on the influence of the traction rod on the vibration behaviour [28].
This paper aims to test the effectiveness of the anti-bending bar system to reduce the vertical bending vibrations of the railway vehicle carbody using an experimental scale demonstrator. That is why the experimental scale demonstrator for the carbody with anti-bending bar system built as described above is presented together with the measuring equipment. Applying the impact hammer method, the frequency response function in the middle of the scale model of the carbody without/with an anti-bending bar system was determined and analysed. The results show that by using the anti-bending bar system, the bending eigenfrequency of the scale model of the carbody increases from 9.0 Hz to 13.4 Hz, and the amplitude of frequency response function decreases by over 50%. These results are remarkable and prove the effectiveness of this system in improving vertical ride comfort in railway vehicles. To substantiate this conclusion, a finite element model of the experimental scale demonstrator for the carbody was developed in which the parameter values of the scale model of the carbody were implemented. As for rubber supports, their stiffness was determined experimentally by means of the frequency response function of a rail coupon weighing close to that of the scale model of the carbody resting on the rubber supports. The results obtained with the finite element model are close to those obtained experimentally, which confirm the successful verification of the effectiveness of the method of reducing vertical bending vibrations of the railway vehicle carbody based on the use of anti-bending bar system.
2. Experimental Scale Demonstrator for Carbody with Anti-Bending Bar System
This section presents the physical realization of the experimental scale demonstrator for carbodies to test the effectiveness of the anti-bending bar system to reduce vertical vibration.
Figure 4 shows the experimental scale demonstrator in which the scale model of the carbody is without the anti-bending bar system (Figure 4a) and with the anti-bending bar system (Figure 4b). The scale model of the carbody is made of an aluminium plate 14 mm thick and corresponds to the carbody of a passenger coach reduced to the scale of 1:10 in terms of length (2600 mm). For reasons of static stability, the width of the scale model of the carbody was chosen to be 400 mm, and it should be emphasized that this dimension has no influence on the frequencies of its bending eigenmodes. The mass of the scale model of the carbody is 39.3 kg.

Figure 4.
Experimental scale demonstrator system: (a) carbody scale model without anti-bending bar system; (b) carbody scale model with anti-bending bar system.
Each anti-bending bar is made of steel with a diameter of 8 mm and is fixed by tightening into two T-shaped steel supports that are secured to the scale model of the carbody by 4 screws (Figure 5a). The steel support leg is 15 mm thick, and its sole is a square plate 80 mm wide and 6 mm thick. The anti-bending bars are mounted in a plane 60 mm below the plane of the neutral fibre of the scale model of the carbody, and the working length of the anti-bending bars is 900 mm. The total mass of the anti-bending bar system is 4.4 kg.

Figure 5.
Details of the experimental scale demonstrator system: (a) support of the anti-bending bar; (b) rubber support.
The scale model of the carbody rested on 4 rubber supports placed at distance of 1900 mm, corresponding to the vehicle wheelbase reduced to 1:10 scale. Each rubber support was cylindrical in shape with an outer diameter of 50 mm, an inner diameter of 17 and a height of 40 mm.
Rubber supports were placed on 2 rigid sheet metal supports fixed to the laboratory floor.
For the experimental determination of the frequency response function of the scale model of the carbody, the impact hammer method was used, which has the advantage of being expedient over other methods such as harmonic excitation by means of a vibrator. A Bruel&Kjaer (Nærum, Denmark) accelerometer type 4514 and an N.I. impact hammer, type PCB Modally Tuned® (PCB Piezotronics, Depew, NY, USA), model 086C03 were utilized (Figure 6). For the acquisition and processing of experimental data, a NI cDAQ-9174 (Emerson, Austin, TX, USA) chassis equipped with a specialized NI 9234 module was used (Figure 6).

Figure 6.
Components of the measurement system: 1. accelerometer; 2. impact hammer; 3. NI cDAQ-9174 type chassis; 4. NI 9234 module.
Figure 7 shows the assembly for the experimental determination of the frequency response function of a rail coupon E49 [29], 820 mm long, placed on the 4 rubber supports used in the experimental scale demonstration model. With the help of the frequency response function, the stiffness of the rubber supports was obtained for use in numerical simulations performed with the finite element model. The mass of the rail coupon was 40.4 kg, very close to the mass of the scale model of the carbody. In this way, the stiffness of the rubber supports was determined when they worked in practically the same conditions as when supporting the scale model of the carbody. The advantage lies in the fact that the rigid vibration mode of the rail coupon has a much lower frequency than the frequency of its first natural bending mode, which allows a more accurate determination of the stiffness of the rubber supports.

Figure 7.
Set-up for determining the stiffness of the rubber support.
3. Finite Element Model of Experimental Scale Demonstrator for Carbody without/with Anti-Bending Bar System
In this section is presented the finite element model elaborated for the theoretical substantiation of research results. Models based on the finite element method are frequently applied for the analysis of load-bearing structures of railway vehicles [30,31,32].
A finite element model was built in ANSYS Workbentch based on the CAD model of the experimental scale demonstrator for the carbody with anti-bending bar system (Figure 8). For comparison, a finite element model for the experimental scale demonstrator for the carbody without anti-bending bars was also developed as a reference from the corresponding CAD model (Figure 9).
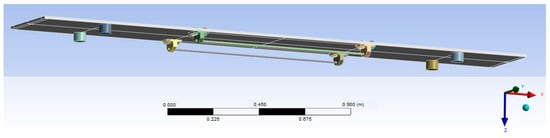
Figure 8.
CAD model for experimental scale demonstrator for the carbody with anti-bending bar system.
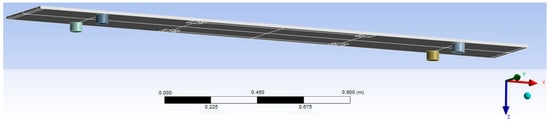
Figure 9.
CAD model for experimental scale demonstrator for the carbody without anti-bending bar system.
Both finite element models are made up of quadratic finite elements: TETRA10 and HEXA20, i.e., SOLID187 and SOLID186 in Ansys. Figure 10 shows the discretization of the model for the experimental scale demonstrator for the carbody with anti-bending bar system.
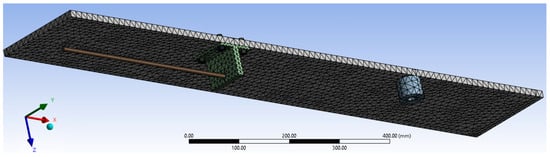
Figure 10.
Discretization of element finite model for experimental scale demonstrator for the carbody with anti-bending bar system (1/4 model).
The finite element model of the experimental scale demonstrator for the carbody without anti-bending bar system has 35,622 finite elements with 72,950 nodes, and the finite element model of the experimental scale demonstrator for carbody with the anti-bending bar system has 52,550 finite elements with 115,273 nodes.
4. Experimental and Theoretical Results
The structure of this section is as follows. In Section 4.1. the frequency response functions are presented in the form of acceleration resulting from experiments carried out on the scale experimental demonstrator of the carbody without/with anti-bending bar system.
The experimental determination of the stiffness of the rubber support based on the acceleration of the rail coupon resting on the rubber supports and an analytical model thereof is given in Section 4.2. The reason for this subsection lies in the fact that the value of the stiffness of the rubber support enters the finite element model of the experimental scale demonstrator of the carbody.
For comparison with the experimental results, theoretical results on the acceleration of the scale model of the carbody obtained using the finite element model of the experimental scale demonstrator of the carbody are also presented in Section 4.3.
4.1. Acceleration Measured on the Scale Model of the Carbody
Figure 11 shows the accelerance in the centre of the scale model of the carbody without anti-bending bar system, obtained by the impact hammer method. The accelerometer was glued in the middle of the model, and the hammer blow was applied to approx. 25 mm of accelerometer along the longitudinal axis of the model. The error of localization of the hammer blow is approx. 1% of the length of the scale model of the carbody. In this way, only symmetric bending modes can be considered to have been excited, the contribution of the anti-symmetric modes being marginal. In addition, acceleration measurement at the middle of the scale model of the carbody ensures that only symmetrical bending modes are caught, the most important of which, for the carbody vibration problem in railway vehicles, is the first bending mode, as shown.
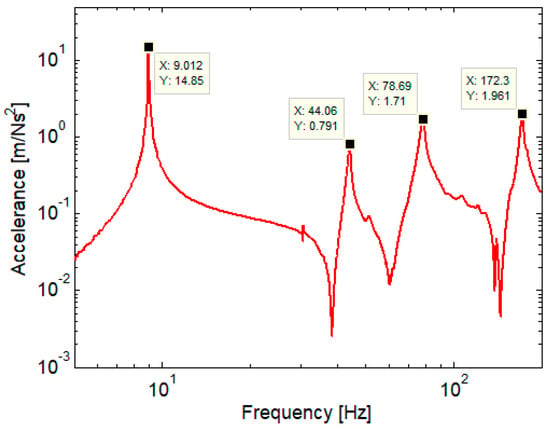
Figure 11.
Accelerance experimentally determined in the middle of the scale model of the carbody without anti–bending bar system.
Although the frequency range of interest is between 5 and 20 Hz, it has been preferred to represent accelerance over a wider range in order to have a comprehensive picture of the vibration characteristics of the experimental scale demonstrator of the carbody. In the presented frequency range (5–200 Hz), it is possible to identify the bending modes of the scale model of the carbody located at 9.01 Hz, 44.06 Hz, 78.69 Hz and 172.3 Hz. The highest accelerance value is at the level of the first bending mode, which is 14,85 m/Ns2. The other peaks are much smaller, at 0.791 m/Ns2, 1.71 m/Ns2 and 1.961 m/Ns2.
Figure 12 shows the accelerance in the middle of the scale model of the carbody with anti-bending bar system, determined under the same conditions as above. The frequency of the first bending mode of the scale model increases to 13.44 Hz because of the anti-bending bar system. The other bending modes also have their frequency changed, but in a much smaller proportion, at 51.56 Hz, 92.63 Hz and 165.8 Hz. It is interesting to note the appearance of the local mode at 47.44 Hz, which can be attributed to the resonance of the anti-bending bar system.
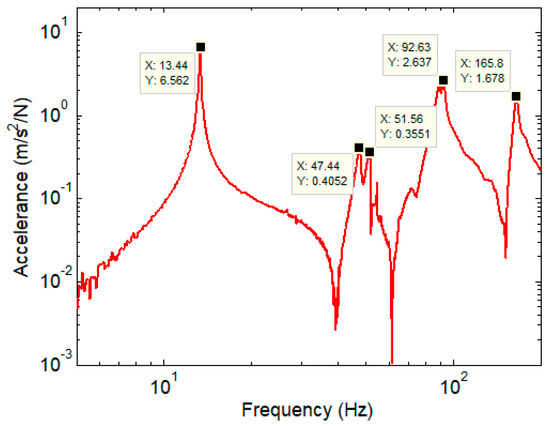
Figure 12.
Accelerance experimentally determined in the middle of the scale model of the carbody with anti–bending bar system.
The influence of the anti-bending bar system is also manifested in the values of accelerance peaks, especially in the first bending mode. Here, the accelerance drops to less than half of the value recorded in the scale model of the carbody without anti-bending bar system, i.e., 6.562 m/Ns2. The other accelerance peak values also change due to the presence of the anti-bending bar system, but to a much lesser extent.
4.2. Determination of Rubber Support Stiffness
Figure 13 shows the accelerance of the rail coupon resting on the rubber supports of the scale model of the carbody (see Figure 7). To reduce the influence of the first bending mode on dynamic response, rubber supports were positioned at the two nodes of the first bending mode. The accelerations were measured above the rubber supports, and the hammer blow was applied to the middle of the rail coupon. Figure 13 shows the accelerance obtained from averaging the two measured acceleration. The resonant frequency of the rigid vibration mode is located at 58 Hz, while the first bending mode has its resonance at 1176 Hz.
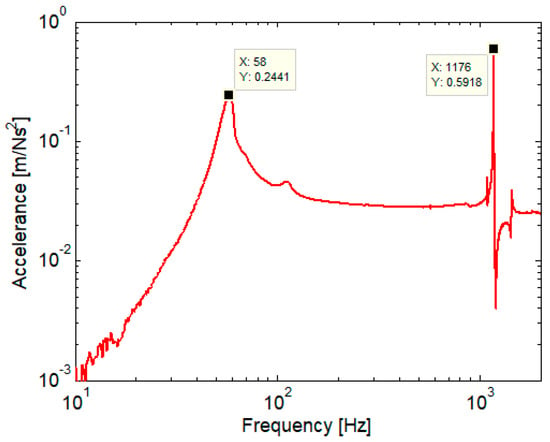
Figure 13.
Rail coupon acceleration experimentally determined above to rubber supports.
To determine the stiffness of rubber supports, an analytical model of the experimental system for measuring the accelerance of the rail coupon was developed (Figure 14). The rail coupon is modelled as a free-free Timoshenko beam, and the rubber supports are considered as elastic elements with hysteretic damping.
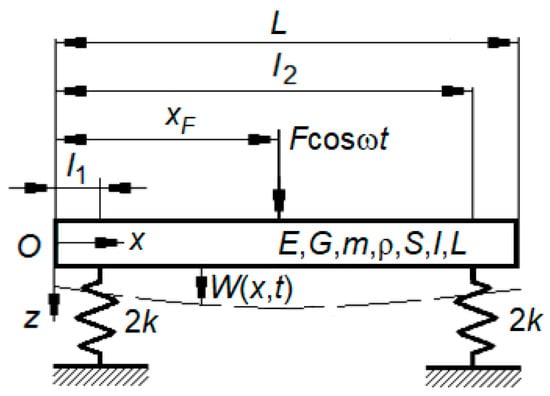
Figure 14.
Rail coupon model on rubber supports.
The equations of motion for steady-state harmonic behaviour can be deduced as follows
where m and ρ are the mass per unit length and density of the beam material, S and I are the area and moment of inertia of the cross-section, E and G are the longitudinal and transverse modulus of elasticity, κ—shear coefficient, —complex stiffness of the rubber support (, where η is the loss factor of the rubber support, and i2 = −1), , are the complex amplitudes of displacement and angle of rotation of the beam in the x-section of the reference system Oxz, the complex amplitude of the harmonic excitation force of angular frequency ω, l1 and l2 determine the position of the rubber supports, xF = L/2 is the position of the excitation force, where L is the length of the beam and δ(.) is Dirac’s delta function. The last term in Equation (1) represents the sum of the two elastic forces in the rubber supports.
The following boundary conditions shall be considered:
The following equation is obtained from Equation (1) by removing the angle of rotation of the section
where .
The solution of Equation (3) can be written as
where
Gw(x, ξ) is Green’s function associated with the free-free Timoshenko beam.
Taking x = l1,2, it obtains
Considering xF = L/2 și l2 = L − l1, it follows for the reason of symmetry
Rail displacement above the rubber supports results
and the corresponding accelerance
Figure 15 shows the accelerance of the rail coupon in the rubber supports section for the following model parameter values: E = 210 GPa, G = 81 GPa, κ = 0.4, ρ = 7850 kg/m3, m = 49.4 kg/m, S = 62.93 × 10−4 m2, I = 1816 × 10−8 m4, L = 0.82 m, l1 = 0.184 m, l2 = 0.636 m and xF = 0.41 m; loss factor of rail coupon material (steel) ηsteel = 0.17%. With these values, the peak due to the first bending mode of the rail coupon has the frequency 1198 Hz and the value 0.5994 m/Ns2.
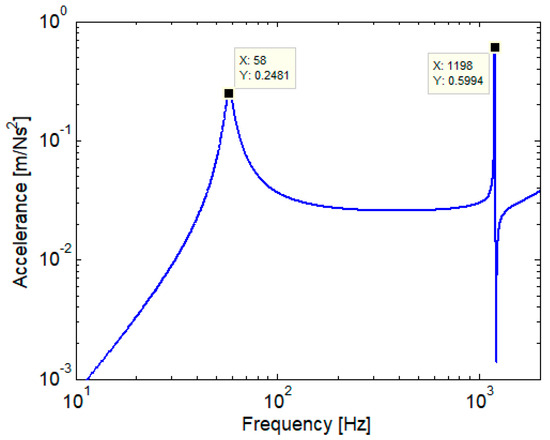
Figure 15.
Accelerance of rail coupon above the rubber supports.
As regards the stiffness and loss factor of the rubber supports, these have been determined by tapping so that the peak corresponding to the rigid mode of vibration is close to that obtained experimentally. Taking the stiffness of the rubber support k = 1.329 MN/m and the loss factor η = 0.1, the rigid mode peak has the frequency 58 Hz and the value 0.2481 m/Ns2.
Given the proximity between the experimental and theoretical results, the above value of the rubber support stiffness shall be retained for insertion into the finite element model of the experimental scale demonstrator of the carbody.
4.3. Accelerance of the Scale Model of the Carbody—Theoretical Results
For reasons of double reflective symmetry and symmetrical loads, numerical simulations of the accelerance of the scale model of the carbody are performed on a quarter of the finite element model of the experimental scale demonstrator of the carbody in order to reduce the simulation time (see Figure 10). Harmonic analysis was performed with the modal superposition method [33,34].
Figure 16 shows accelerance in the middle of the scale model of the carbody without the anti-bending bar system calculated using the finite element model considering the harmonic excitation force located in the centre of symmetry of the model.
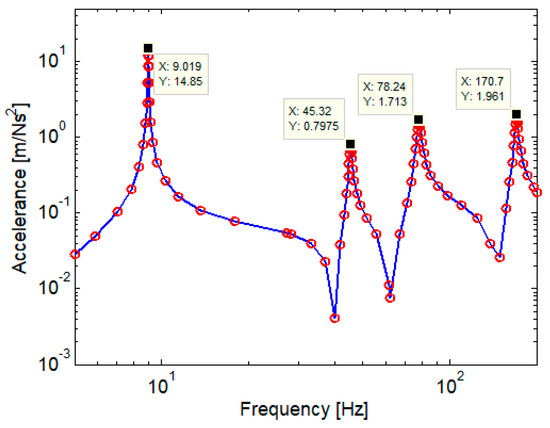
Figure 16.
Acceleration in the middle of the scale model of the carbody without anti–bending bar system (FEM model).
The material constants are: aluminium density ρAl = 2700 kg/m3, Young’s modulus 70 GPa and Poisson coefficient νAl = 0.33. The dimensions of the CAD model are as shown in Section 2.
The accelerance peaks are located at 9.019 Hz, 45.32 Hz, 78.24 Hz and 170.7 Hz with the following values: 14.85 m/Ns2, 0.7975 m/Ns2, 1.713 m/Ns2 and 1.961 m/Ns2.
Figure 17 shows accelerance in the middle of the scale model of the carbody with anti-bending bar system. Numerical simulation using the finite element model shows that due to the use of the anti-bending bar system, the accelerance peak corresponding to the first bending mode of the scale model of the carbody increases to 13.81 Hz, and its amplitude decreases to 6.494 m/Ns2.
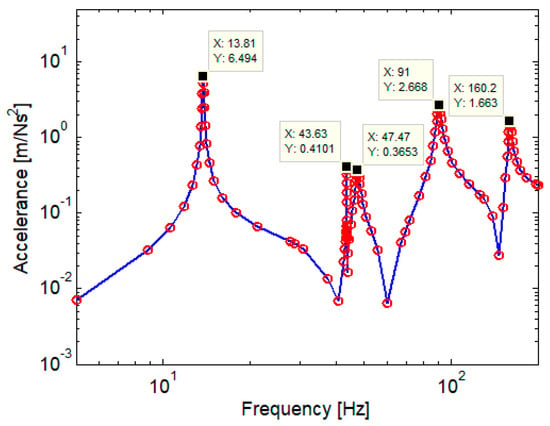
Figure 17.
Accelerance in the middle of the scale model of the carbody with anti–bending bar system (FEM model).
In both simulations, modal damping was determined by explorations based on experimental results on acceleration peaks.
Table 1 and Table 2 summarise the comparison between the experimental results and those obtained with the finite element model in terms of vibration mode frequencies of the scale model of the carbody without/with anti-bending bar system. Errors were calculated against experimental values.

Table 1.
Vibration modes frequency of the scale model of the carbody without anti-bending bar system.

Table 2.
Vibration modes frequency of the scale model of the carbody with anti-bending bar system.
In general, the errors are of several percentage points, which is acceptable. The errors are greater in the case of the scale model of the carbody with anti-bending bar system because its structure is more complicated, and in modelling, these intervene with a series of simplifying assumptions regarding the contacts between components, the constraints generated by the own weight and the tightening of the anti-bending bars, etc.
Regarding Table 2, it should be noted that mode 2 is of the carbody, as shown in Figure 18a, where this mode is shown for the carbody without an anti-bending bar system. When the carbody is fitted with the anti-bending bar system, it also drives the anti-bending bars in an anti-phase motion (Figure 18b). In contrast, mode 2* corresponds only to the vibration of the anti-bending bars—the vibration of the carbody is insignificant (Figure 19).
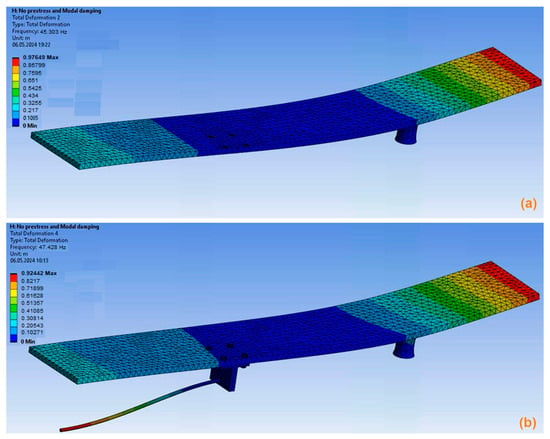
Figure 18.
Carbody vibration mode 2: (a) no anti-bending bar system; (b) with anti-bending bar system.

Figure 19.
Vibration mode of anti-bending bars (mode 2*).
Table 3 shows the comparison in terms of damping in the finite element models of the scale demonstrator of the carbody without/with anti-bending bar system. The damping of the first three bending modes of the scale model of the carbody increases due to the anti-bending bar system which introduces some structural damping, while the fourth is not modified.

Table 3.
Damping vibration modes of scale models of the carbody without/with anti-bending bar system.
5. Conclusions
In this paper, the effectiveness of a new method of reducing the vertical vibration of the passenger coach carbody based on equipping the carbody with anti-bending bar system was tested under laboratory conditions.
For this, an experimental scale demonstrator of the carbody of a passenger coach was built so that the first bending frequency was in the range of maximum sensitivity of human beings to vertical vibrations as happens in the case of these types of rail vehicles.
The frequency response functions of the scale model of the carbody without/with anti-bending bar system were experimentally determined by the impact hammer method.
To substantiate the research, two finite element models were developed for the experimental scale demonstrator of the carbody without/with anti-bending bar system, and the vertical vibration modes were determined and the frequency response function (accelerance) was calculated.
The results of the research showed the following advantages of using the anti-bending bar system:
- -
- The first bending frequency of the scale model of the carbody increases from 9.01 Hz to 13.4 Hz and thus goes out of the zone of maximum sensitivity of the human being to vertical vibrations;
- -
- Peak accelerance corresponding to the first bending frequency of the carbody decreases from 14.85 m/Ns2 to 6.562 m/Ns2;
- -
- Damping of the first three bending modes of the scale model of the carbody increases especially in the first two modes, by 60% in the first mode and by 71% in the second mode.
In addition to the above, it follows that the use of the anti-bending bar system can significantly contribute to improving comfort in passenger coaches.
Further research could be focused on a full-scale passenger coach with an anti-bending bar system starting from the CAD and finite element models to obtain a better image of the possibilities of improving comfort by using the anti-bending bar system method.
Author Contributions
Conceptualization, T.M. and M.D.; methodology, T.M.; software, T.M., Ș.S. and M.A.G.; validation, T.M. and Ș.S.; formal analysis, T.M., M.D. and I.I.A.; investigation, T.M., M.D. and M.A.G.; resources, T.M., M.D. and I.I.A.; writing—original draft, T.M.; writing—review and editing, T.M., M.D. and Ș.S.; project administration, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Ministry of Research, Innovation and Digitization, CCCDI—UEFISCDI, project number PN-III-P2-2.1-PED-2021-0319, within PNCDI III.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sadeghi, J.; Rabiee, S.; Khajehdezfuly, A. Effect of rail irregularities on ride comfort of train moving over ballast-less tracks. Int. J. Struct. Stab. Dyn. 2019, 19, 1950060. [Google Scholar] [CrossRef]
- Jing, L.; Wang, K.; Zhai, W. Impact vibration behavior of railway vehicles: A state-of-the-art overview. Acta Mech. Sin. 2021, 37, 1193–1221. [Google Scholar] [CrossRef]
- Kim, P.; Seok, J. Bifurcation analysis on the hunting behavior of a dual-bogie railway vehicle using the method of multiple scales. J. Sound Vib. 2010, 329, 4017–4039. [Google Scholar] [CrossRef]
- Kaise, I.; Poll, G.; Voss, G.; Vinolas, J. The impact of strcutural flexibilities of wheelsets and rails on the hunting behaviour of a railway vehicle. Veh. Syst. Dyn. 2019, 57, 564–594. [Google Scholar] [CrossRef]
- Popa, G. Determining the optimal operating regime of the traction motors for constant power operation of the vehicle. In Proceedings of the 2006 IEEE International Conference on Automation, Quality and Testing, Robotics, AQTR, Cluj-Napoca, Romania, 25–28 May 2006; Volume 205–208, p. 4022848. [Google Scholar]
- Cole, C.; Spiryagin, M.; Wu, Q.; Sun, Y.Q. Modelling, simulation and applications of longitudinal train dynamics. Veh. Syst. Dyn. 2017, 55, 1498–1571. [Google Scholar] [CrossRef]
- Fu, B.; Bruni, S. An examination of alternative schemes for active and semi-active control of vertical car-body vibration to improve ride comfort. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2022, 236, 386–405. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, B.K.; Thompson, C. A comparison study of ride comfort indices between Sperling’s method and EN 12299. Int. J. Rail Transp. 2019, 7, 279–296. [Google Scholar] [CrossRef]
- Dumitriu, M. On the critical points of vertical vibration in a railway vehicle. Arch. Mech. Eng. 2014, 61, 115–140. [Google Scholar] [CrossRef]
- Palomares, E.; Morales, A.L.; Nieto, A.J.; Chicharro, J.M.; Pintado, P. Comfort improvement in railway vehicles via optimal control of adaptive pneumatic suspensions. Veh. Syst. Dyn. 2022, 60, 1702–1721. [Google Scholar] [CrossRef]
- Lewis, T.D.; Jiang, J.Z.; Neild, S.A.; Gong, C.; Iwnicki, S.D. Using an inerter-based suspension to improve both passenger comfort and track wear in railway vehicles. Veh. Syst. Dyn. 2020, 58, 472–493. [Google Scholar] [CrossRef]
- Sugahara, Y.; Kojima, T. Suppression of vertical vibration in railway vehicle carbodies through control of damping force in primary suspension: Presentation of results from running tests with meter-gauge car on a secondary line. WIT Trans. Built Environ. 2018, 181, 329–337. [Google Scholar]
- Gong, D.; Wang, K.; Duan, Y.; Zhou, J. Car body floor vibration of high-speed railway vehicles and its reduction. J. Low Freq. Noise Vibr. Act. Control 2020, 39, 925–938. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W.J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber. J. Vib. Control 2013, 19, 649–657. [Google Scholar] [CrossRef]
- Graa, M. Modeling and control for vertical rail vehicle dynamic vibration with comfort evaluation. Int. J. Math. Model. Methods Appl. Sci. 2017, 11, 240–245. [Google Scholar]
- Gong, D.; Zhou, J.; Sun, W. Passive control of railway vehicle car body flexural vibration by means of under frame dampers. J. Mech. Sci. Technol. 2017, 31, 555–564. [Google Scholar] [CrossRef]
- Dumitriu, M. A new approach to reducing the carbody vertical bending vibration of railway vehicles. Veh. Syst. Dyn. 2017, 55, 1787–1806. [Google Scholar] [CrossRef]
- Huang, C.; Zeng, J. Suppression of the flexible carbody resonance due to bogie instability by using a DVA suspended on the bogie frame. Veh. Syst. Dyn. 2022, 60, 3051–3070. [Google Scholar] [CrossRef]
- Huang, C.; Zeng, J.; Luo, G.; Shi, H. Numerical and experimental studies on the car body flexible vibration reduction due to the effect of car body-mounted equipment. Proc. IMechE Part F J. Rail Rapid Transit. 2018, 232, 103–120. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, J.; Gong, D.; You, T.; Che, J. Research on multi-point connection of under-chassis equipment suspension system in high-speed trains. AIP Adv. 2021, 11, 125315. [Google Scholar] [CrossRef]
- Guo, J.; Shi, H.; Li, F.; Wu, P. Field measurements of vibration on the car body-suspended equipment for high-speed rail vehicles. Shock Vib. 2020, 2020, 6041543. [Google Scholar] [CrossRef]
- Zhu, T.; Lei, C.; Xiao, S.; Yu, J.P. Suspension stiffness selecting method of elastic suspension equipment under vehicle. J. Traffic Transp. Eng. 2018, 18, 111–118. [Google Scholar]
- UIC 513R; Guidelines for Evaluating Passenger Comfort in Relation to Vibration in Railway Vehicles. International Union of Railways: Paris, France, 1994.
- Dumitriu, M.; Mazilu, T.; Apostol, I.I. Scale models to verify the effectiveness of the methods to reducing the vertical bending vibration of the railway vehicles carbody: Applications and design elements. Appl. Sci. 2023, 13, 2368. [Google Scholar] [CrossRef]
- Sebeșan, I.; Spiroiu, M.A.; Arsene, S.; Popa, G.; Dinu, G. Deformation analysis of clouth-type springs of railway vehicles suspension. Mater. Plast. 2015, 52, 560–563. [Google Scholar]
- Tiwari, V.; Sharma, S.C.; Harsha, S.P. Ride comfort analysis of high-speed rail vehicle using laminated rubber isolator based secondary suspension. Veh. Syst. Dyn. 2023, 61, 2689–2715. [Google Scholar] [CrossRef]
- Melero, M.; Nieto, A.J.; Morales, A.L.; Palomares, E.; Chicharro, J.M.; Ramiro, C.; Pintado, P. Experimental analysis of constrained layer damping structures for vibration isolation in lightweight railway vehicles. Appl. Sci. 2022, 12, 8220. [Google Scholar] [CrossRef]
- Bokaeian, V.; Rezvani, M.A.; Arcos, R. A numerical and scaled experimental study on ride comfort enhancement of high-speed rail vehicle through optimizing traction rod stiffness. J. Vib. Control 2021, 27, 2548–2563. [Google Scholar] [CrossRef]
- EN 13674-1; Railway Applications—Track—Rail—Part 1: Vignole Railway Rails 46 kg/m and Above. Polski Komitet Normalizacyjny: Warszawa, Poland, 2002.
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-element model calibration of a railway vehicle based on experimental modal parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Manea, I.; Popa, G.; Ghiță, G.; Prenta, G. Applying the experimental modal analysis to validate the railway frame bogie design. Proceeding Rom. Acad. Ser. A 2016, 17, 48–56. [Google Scholar]
- Maglio, M.; Vernersson, T.; Nielsen, J.C.O.; Pieringer, A.; Söderström, P.; Regazzi, D.; Cervello, S. Railway wheel tread damage and axle bending stress—Instrumented wheelset measurements and numerical simulation. Int. J. Rail Transp. 2022, 10, 275–297. [Google Scholar] [CrossRef]
- Bottega, W. Engineering Vibrations, Taylor& Francis; Boca Raton: London, UK; New York, NY, USA, 2013. [Google Scholar]
- Mukhopadhyay, M. Finite Element Method in Vibration Analysis. In Structural Dynamics; Springer: Cham, Switzerland, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).