State of the Art on Relative Permeability Hysteresis in Porous Media: Petroleum Engineering Application
Abstract
1. Introduction
2. Mathematical Models
- (1)
- The measurement of two-phase oil-gas relative permeability data does not necessarily occur at connate water saturation.
- (2)
- Due to experimental errors, often does not equal .
2.1. Two-Phase Relative Permeability Hysteresis Model
- (1)
- Land Model [37]
- (2)
- Killough Model [34]
- (3)
- Carlson Model [35]
- (4)
- Beattie Model [38]
- (5)
- Delshad Model [26]
- (6)
- Kjosavik Model [39]
- (7)
- Spiteri Model [10]
2.2. Three-Phase Relative Permeability Hysteresis Model
- (1)
- (2)
- Larsen and Skauge Model [36]
- (3)
- Egermann Model [12]
- (4)
- F. J. Fayers Model [43]
- (5)
- UTHYST Model [16]
- (6)
- WAG-HW Model [16]
- (7)
- Aghabozorgi Model [44]
- (8)
- Sigmoid Model [45]
2.3. Forward Calculation of Phase Permeability Based on Digital Core
2.4. Summary of the Model Study
2.4.1. Two-Phase Relative Permeability Model
2.4.2. Three-Phase Relative Permeability Model
3. Experimental Studies
3.1. Direct Relative Permeability Measurements
3.2. Flowthrough Measurements
| Author | Rock Property | Porosity (%) | Permeability (mD) | Wettability | Saturation Path | Temperature (°C) | Pressure (MPa) | IFT (mN/m) | Flow Rate (mL/min) | Hysteresis Effect |
|---|---|---|---|---|---|---|---|---|---|---|
| Batycky et al. [52] (1981) | Sandstone | 21.5 | 476 | Water-wet | DIDI | / | / | 50 | 0.92 | Both |
| Saraf et al. [51] (1982) | Sandstone | 23 | 510–580 | Water-wet | DDI | 24 ± 1 | 10.2 | / | 2 | Both |
| Van Spronsen et al. [60] (1982) | Sandstone | / | / | / | DDI | / | / | / | / | / |
| Fulcher et al. [61] (1985) | Sandstone | 19.02–26.5 | 123.2–531.6 | Water-wet | DI | 25 | 1.38 | 1 | 1.33–6.67 | Both |
| Oak et al. [62] (1990) | Sandstone | / | 210 | Water-wet | DDI/IID | 21 ± 0.6 | 5.5 | / | 0.001~30 | Displacement |
| Hawkins et al. [7] (1992) | Synthetic core | / | / | Oil-wet | IDID | / | / | / | / | Both |
| Eleri et al. [63] (1995) | Sandstone | 24.09 | 11.15 | Water-wet | IDD | / | / | 0.5 | Both | |
| Braun & Holland et al. [6] (1995) | Sandstone | 22.3 | 512 | Mix-wet/Water-wet | DID | 22.8 | 6.9 | / | 2 | Both |
| Bennion et al. [13] (1998) | Sandstone | 6.2/9.8 | 0.19/0.26 | Water-wet | / | / | 3.6 | / | / | Both |
| Egermann et al. [12] (2000) | / | 23 | 215 | Water-wet | DIDI | / | 1 | 4.8 | 0.17 | / |
| Element et al. [53] (2003) | Sandstone | 19 | 393/328 | Water-wet/Mix-wet | IDIDIDID/DIDIDIDI | / | 2.5 | / | 0.07 | Both |
| Fatemi et al. [64,65] (2012–2013) | Sandstone | 18.3 | 65 | Mix-wet | IDIDI/DIDID | 37.8 | 12.8 | 0.04 | 0.83–1.67 | Both |
| Fatemi et al. [64,65] (2012–2013) Dernaika MR et al. [66] (2013) | Sandstone | 17 | 1000 | Water-wet | DID/DIDIDI | 37.8 | 12.8 | 0.04 | 0.62–1.25 | Both |
| Fatemi et al. [64,67] (2012–2013) Dernaika MR et al. [66] (2013) Shahverdi et al. [50] (2014) | Carbonate | 17.4–27.9 | 0.98–46 | Water-wet | / | / | / | / | 0.33, 0.5 | / |
| Sandstone | 18 | 65 | / | 38 | 12.7 | / | / | / | ||
| Shahverdi et al. [50] (2014) Duchenne et al. [68] (2015) | Sandstone | 16.1 | 71 | / | 93 | 12.7 | / | / | / | |
| Shahverdi et al. [50] (2014) Duchenne et al. [68] (2015) Duchenne et al. [18] (2016) | limestone | 17 | 11 | / | IDID | 145 | 31 | / | 0.03/0.07/0.13 | / |
| Sandstone | 18.2 | 65 | Mix-wet | DIDIDIDI | 38 | 8.4/12.3/12.7 | 2.7/0.15/0.04 | 0.42 | Both | |
| Shahverdi et al. [5] (2016) | Sandstone | 17.6/18.2 | 1000/65 | Mix-wet/Water-wet | IDID/IDIDID | 37.8 | 12.8 | 0.047/55/60 | 0.21–3.33 | Both |
| Wang et al. [59] (2016) | Sandstone | 15/12 | 50.42/56.68 | Oil-wet/Water-wet | DI | 70 | 6.9 | / | 0.35 | / |
| Fatemi et al. [55] (2018) | Carbonate | 20/16 | 260/40 | Oil-wet | IDIDIDID | 58.7 | 12.7 | / | 0.33 | / |
| Alkhazmi et al. [17] (2018) | Carbonate | 15 | 45 | Water-wet | IDIDID | 38 | 12.7 | 0.04 | \ | / |
| Reza et al. [54] (2021) | Carbonate | 17.7–27.1 | 2.3–64.5 | Water-wet | DID | 60 | 10.3 | / | 0.2 | Displacement |
| Zhu Sinan et al. [69] (2021) | Sandstone | 4.6/13.8/16.5 | 1.65/19.34/49 | / | DIDIDIDIDI | / | / | / | / | Both |
| Alnuaimi et al. [57] (2021) | Carbonate | 29 | 16.25 | Mix-wet | IDIDIDIDID/DIDID | 133.3 | 12.7 | / | / | Both |
3.3. Summary of Experimental Research
- (1)
- Permeability
- (2)
- Porosity
- (3)
- Wettability
- (4)
- Miscibility
- (5)
- Cyclic times
4. Applications
4.1. The Impact of Relative Permeability Hysteresis on Recovery
- (2)
- Reduction of water coning [71]
- (3)
- (4)
- Gas blocking [13]
- (5)
- Water blocking [13]
- (2)
- Decrease in recovery [11]
- (3)
- Phase trapping [11]
- (4)
- Early breakthrough of gas and water [11]
| Author | Application | Two Phase or Three Phase | Injection Method | Gas | Phenomena and Conclusions |
|---|---|---|---|---|---|
| J.R. Christensen et al. [78] (1998) | Reservoir | Two-phase | WAG | Natural gas | WAG injection has better accessibility and lower residual oil saturation than water injection. |
| D. J. Element et al. [53] (2003) | Core experiment | Three-phase | WAG | N2 | The hysteresis cycle is irreversible. Reduce residual oil saturation by capturing gas with water. |
| Hamidreza Shahverdi et al. [79] (2011) | Core experiment | Three-phase | WAG | Mixture of methane (C1) and n-butane (n-C4) | The three-phase kr values of water and gas depend on two independent saturation levels. The kr values of three-phase water, oil, and gas are significantly lower than their corresponding two-phase values. |
| S. Mobeen Fatemi et al. [80] (2012) | Core experiment | Two-phase | WAG | Mixture of methane (C1) and n-butane (n-C4) | As the WAG cycle increases, the hysteresis effect weakens. Compared to krw, the cyclic hysteresis of krg is more pronounced. |
| Pedram Mahzari et al. [81] (2016) | Core experiment | Three-phase | WAG | Mixture of methane (C1) and n-butane (n-C4) | Adding WAG hysteresis parameters during fitting experiments instead of using the measured values of these parameters can significantly reduce simulation errors. |
| Ehsan Ranaee et al. [82] (2019) | Reservoir | Three-phase | WAG | Natural gas | The combined effect of relative permeability hysteresis and reservoir heterogeneity on WAG. |
| M. Kowsari et al. [83] (2022) | Reservoir | Three-phase | WAG | Methane (C1) | The optimal WAG parameters may be influenced by the choice of hysteresis models. |
4.2. The Impact of Relative Permeability Hysteresis on CO2 Sequestration
- (1)
- The choice of three-phase relative permeability models and phase trapping models significantly affects the prediction of CO2 sequestration capacity. The impact of three-phase relative permeability models is less important than that of phase trapping models, and the choice of phase trapping models may affect the impact of three-phase relative permeability models.
- (2)
- Injecting water after gas injection disrupts connected gas clusters, as the wetting phase traps the non-wetting phase due to phase trapping, enhancing gas trapping and immobilization. In processes with strong flow reversals, the effect of phase trapping is significant, making gas-water alternation a potentially effective CO2 sequestration strategy.
4.3. Effect of Relative Permeability Hysteresis on Hydrogen Storage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heaviside, J. Measurement of relative permeability. In Interfacial Phenomena in Petroleum Recovery; Morrow, N.R., Ed.; Dekker: New York, NY, USA, 1991; pp. 377–412. [Google Scholar]
- Honarpour, M.; Koederitz, L.; Harvey, A. Relative Permeability of Petroleum Reservoirs; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–143. [Google Scholar]
- Masalmeh, S. Experimental measurements of capillary pressure and relative permeability hysteresis. In Proceedings of the Paper SCA 2001-23 presented at the SCA Conference, Edinburgh, Scotland, September 2001; Available online: https://www.jgmaas.com/SCA/2001/SCA2001-23.pdf (accessed on 12 May 2024).
- Jerauld, G.R.; Salter, S.J. The effect of pore-structure on hysteresis in relative permeability and capillary pressure: Pore-level modeling. Transp. Porous Media 1990, 5, 103–151. [Google Scholar] [CrossRef]
- Shahverdi, H.; Sohrabi, M. Relative Permeability Characterization for Water-Alternating-Gas Injection in Oil Reservoirs. SPE J. 2016, 21, 799–808. [Google Scholar] [CrossRef]
- Braun, E.M.; Holland, R.F. Relative permeability hysteresis; laboratory measurements and a conceptual model. SPE Reserv. Eng. 1995, 10, 222–228. [Google Scholar] [CrossRef]
- Hawkins, J.T.; Bouchard, A.J. Reservoir-engineering implications of capillary-pressure and relative-permeability hysteresis. Log Anal. 1992, 33, 415–420. [Google Scholar]
- Shi, L.; Wang, J.M.; Liao, G.Z. Mechanism of gas-water flow at pore-level in aquifer gas storage. J. Cent. South Univ. 2013, 20, 3620–3626. [Google Scholar] [CrossRef]
- Alkhazmi, B.; Farzaneh, S.A.; Sohrabi, M. A comprehensive and comparative experimental study of the effect of wettability on the performance of near miscible wag injection in sandstone rock. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. [Google Scholar]
- Spiteri, E.J.; Juanes, R. Impact of relative permeability hysteresis on the numerical simulation of WAG injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004; SPE: Richardson, TX, USA; p. 89921. [Google Scholar]
- Vieira, R.A.; Cardoso, M.A.; Pizarro, J.O. An integrated WAG characterization study for an offshore oilfield. In Proceedings of the Offshore Technology Conference Brasil, Rio de Janeiro, Brazil, 29–31 October 2019; p. D031S033R001. [Google Scholar]
- Egermann, P.; Vizika, O.; Dallet, L. Hysteresis in Three-Phase Flow: Experiments, Modeling and Reservoir Simulations. In Proceedings of the SPE European Petroleum Conference, Aberdeen, UK, 29–31 October 2000; p. 65127. [Google Scholar]
- Bennion, D.B.; Thomas, F.B.; Jamaluddin, A.K.; Ma, T. The Effect of Trapped Critical Fluid Saturations on Reservoir Permeability and Conformance. 1998. Available online: https://www.osti.gov/etdeweb/biblio/638855 (accessed on 31 March 2024).
- Flett, M.; Gurton, R.; Taggart, I. The Function of Gas-Water Relative Permeability Hysteresis in the Sequestration of Carbon Dioxide in Saline Formations. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 18–20 October 2004. [Google Scholar]
- Hosseini, S.J. Investigating the Effect of Hysteresis modelling on Numerical Simulation of Immiscible WAG Injection. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 7–9 February 2012; p. IPTC-15055. [Google Scholar]
- Beygi, M.R.; Delshad, M.; Pudugramam, V.S. Novel Three-Phase Compositional Relative Permeability and Three-Phase Hysteresis Models. SPE J. 2015, 20, 21–34. [Google Scholar] [CrossRef]
- Alkhazmi, B.; Farzaneh, S.A.; Sohrabi, M. An Experimental Investigation of WAG Injection Performance under Near-Miscible Conditions in Carbonate Rock and Comparison with Sandstone. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22–26 April 2018. [Google Scholar]
- Duchenne, S.; de Loubens, R.; Joubert, T. Extended Three-Phase Relative Permeability Formulation and its Application to the History-Matching of Multiple WAG Corefloods under Mixed-Wet Conditions. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 31 October–3 November 2016. [Google Scholar]
- Corey, A.T.; Rathjens, C.H.; Henderson, J.H. Three-Phase Relative Permeability. J. Pet. Technol. 1956, 8, 63–65. [Google Scholar] [CrossRef]
- Stone, H.L. Probability Model for Estimating Three-Phase Relative Permeability. J. Pet. Technol. 1970, 22, 214–218. [Google Scholar] [CrossRef]
- Stone, H.L. Estimation of Three-Phase Relative Permeability and Residual Oil Data. J. Can. Pet. Technol. 1973, 12. [Google Scholar] [CrossRef]
- Dietrich, J.; Bondor, P. Three-Phase Oil Relative Permeability Models. Soc Pet. Eng. 1976, 6044. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Elsevier Applied Science Publishers: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Heiba, A.A.; Davis, H.T.; Scriven, L.E. Statistical network theory of three-phase relative permeabilities. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, Oklahoma, 15–18 April 1984; SPE: Richardson, TX, USA; p. 12690. [Google Scholar]
- Baker, L.E. Three-Phase Relative Permeability Correlations. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, OK, USA, 16–21 April 1988; p. 17369. [Google Scholar]
- Delshad, M.; Lenhard, R.J.; Oostrom, M. A Mixed-Wet Hysteretic Relative Permeability and Capillary Pressure Model for Reservoir Simulations. SPE Reserv. Eval. Eng. 2003, 6, 328–334. [Google Scholar] [CrossRef]
- Kokal, S.; Maini, B.B. An Improved Model for Estimating Three-Phase Oil-Water-Gas Relative Permeabilities From Two-Phase Oil-Water And Oil-Gas Data. J. Can. Pet. Technol. 1990, 29. [Google Scholar] [CrossRef]
- Moulu, J.C.; Vizika, O.; Kalaydjian, F. New model for three-phase relative permeabilities based on a fractal representation of the porous medium. In Proceedings of the 1997 SPE Annual Technical Conference and Exhibition, Part Sigma, San Antonio, TX, USA, 5–8 October 1997. [Google Scholar]
- Moulu, J.C.; Vizika, O.; Egermann, P. New three-phase relative permeability model for various wettability conditions. In Proceedings of the 1999 SPE Annual Technical Conference and Exhibition: ‘Reservoir Engineering’, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Blunt, M.J. An empirical model for three-phase relative permeability. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; SPE: Richardson, TX, USA; p. 56474. [Google Scholar]
- Yuen, B.B.W.; Siu, A.L.W.; Shenawi, S.H. A New Three-Phase Oil Relative Permeability Simulation Model Tuned by Experimental Data. In Proceedings of the International Petroleum Technology Conference: IPTC, Kuala Lumpur, Malaysia, 3–5 December 2008; p. 12227. [Google Scholar]
- Hustad, O.S.; Browning, D.J. A Fully Coupled Three-Phase Model for Capillary Pressure and Relative Permeability for Implicit Compositional Reservoir Simulation. SPE J. 2010, 15, 1009–1025. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Sohrabi, M. Accurate Modeling of Relative Permeability Hysteresis in Water Alternating Gas Experiments. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–13 November 2019; SPE: Richardson, TX, USA; p. D031S074R002. [Google Scholar]
- Killough, J.E. Reservoir Simulation With History-Dependent Saturation Functions. Soc. Pet. Eng. J. 1976, 16, 37–48. [Google Scholar] [CrossRef]
- Carlson, F.M. Simulation of Relative Permeability Hysteresis to the Nonwetting Phase. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 4–7 October 1981; p. 10157. [Google Scholar]
- Larsen, J.A.; Skauge, A. Methodology for numerical simulation with cycle-dependent relative permeabilities. SPE J. 1998, 3, 163–173. [Google Scholar] [CrossRef]
- Land, C.S. Calculation of Imbibition Relative Permeability for Two- and Three-Phase Flow from Rock Properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
- Beattle, C.I.; Boberg, T.C.; Mcnab, G.S. Reservoir Simulation of Cyclic Steam Stimulation in the Cold Lake Oil Sands. SPE Reserv. Eng. 1991, 6, 200–206. [Google Scholar] [CrossRef]
- Kjosavik, A.; Ringen, J.K.; Skjaeveland, S.M. Relative permeability correlation for mixed-wet reservoirs. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 3–5 April 2000; SPE: Richardson, TX, USA; p. 59314. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J. A model for hysteretic constitutive relations governing multiphase flow: 1. Saturation-pressure relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.H. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fayers, F.J.; Foakes, A.P.; Lin, C.Y. An Improved Three Phase Flow Model Incorporating Compositional Variance. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 3–5 April 2000. [Google Scholar]
- Aghabozorgi, S.; Sohrabi, M.; Facanha, J. Estimation of Three-phase Oil Relative Permeability in WAG Experiments. In Proceedings of the Offshore Technology Conference Brasil, Rio de Janeiro, Brazil, 29–31 October 2019. [Google Scholar]
- Ranaee, E.; Porta, G.M.; Riva, M. Prediction of three-phase oil relative permeability through a sigmoid-based model. J. Pet. Sci. Eng. 2015, 126, 190–200. [Google Scholar] [CrossRef]
- Liu, Z.; Herring, A.; Arns, C. Pore-scale characterization of two-phase flow using integral geometry. Transp. Porous Media 2017, 118, 99–117. [Google Scholar] [CrossRef]
- Mcclure, J.E.; Armstrong, R.T.; Berrill, M.A. Geometric state function for two-fluid flow in porous media. Phys. Rev. Fluids 2018, 3, 84306. [Google Scholar] [CrossRef]
- Purswani, P.; Johns, R.T.; Karpyn, Z.T. Predictive modeling of relative permeability using a generalized equation of state. SPE J. 2021, 26, 191–205. [Google Scholar] [CrossRef]
- AL-Zubaidi, F.; Mostaghimi, P.; Niu, Y. Effective permeability of an immiscible fluid in porous media determined from its geometric state. Phys. Rev. Fluids 2023, 8, 64004. [Google Scholar] [CrossRef]
- Shahverdi, H.; Sohrabi, M. Modeling of Cyclic Hysteresis of Three-Phase Relative Permeability During Water-Alternating-Gas Injection. SPE J. 2015, 20, 35–48. [Google Scholar] [CrossRef]
- Saraf, D.N.; Batycky, J.P.; Jackson, C.H. An Experimental Investigation of Three-Phase Flow of Water-Oil-Gas Mixtures Through Water-Wet Sandstones. In Proceedings of the SPE Western Regional Meeting, San Francisco, CA, USA, 24–26 March 1982. [Google Scholar]
- Batycky, J.P.; Mccaffery, F.G.; Hodgins, P.K. Interpreting Relative Permeability and Wettability From Unsteady-State Displacement Measurements. Soc. Pet. Eng. J. 1981, 21, 296–308. [Google Scholar] [CrossRef]
- Element, D.J.; Masters, J.H.K.; Sargent, N.C. Assessment of Three-Phase Relative Permeability Models Using Laboratory Hysteresis Data. In Proceedings of the International Improved Oil Recovery Conference, Asia Pacific, Kuala Lumpur, Malaysia, 20–21 October 2003. [Google Scholar]
- Sedaghatinasab, R.; Kord, S.; Moghadasi, J. Relative Permeability Hysteresis and Capillary Trapping during CO2 EOR and Sequestration. Int. J. Greenh. Gas Control 2021, 106, 103262. [Google Scholar] [CrossRef]
- Fatemi, M.; Sohrabi, M. Mechanistic study of enhanced oil recovery by gas, WAG and SWAG injections in mixed-wet rocks: Effect of gas/oil IFT. Exp. Therm. Fluid Sci. 2018, 98, 454–471. [Google Scholar] [CrossRef]
- Zhu, S.; Sun, J.; Wei, G. Numerical simulation correction method for injection and production relative permeability hysteresis in water-drive gas storage reservoirs. Pet. Explor. Dev. 2021, 166–174. [Google Scholar] [CrossRef]
- Alnuaimi, L.O.; Sohrabi, M.; Aghabozorgi, S. Simulation of Immiscible WAG Experiments Performed in Carbonate Rocks: The Impact of Heterogeneity on Hysteresis Phenomenon. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 15–18 December 2021. [Google Scholar]
- Dernaika, M.R.; Kalam, M.Z.; Basioni, M.A. Hysteresis of Capillary Pressure, Resistivity Index and Relative Permeability in Different Carbonate Rock Types. Petrophysics 2012, 53, 316–332. [Google Scholar]
- Wang, X.; Alvarado, V. Analysis of capillary pressure and relative permeability hysteresis under low-salinity waterflooding conditions. Fuel 2016, 180, 228–243. [Google Scholar] [CrossRef]
- Van Spronsen, E. Three-phase relative permeability measurements using the centrifuge method. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 4–7 April 1982; SPE: Richardson, TX, USA; p. 10688. [Google Scholar]
- Fulcher, R.A.; Ertekin, T.; Stahl, C.D. Effect of Capillary Number and Its Constituents on Two-Phase Relative Permeability Curves. J. Pet. Technol. 1985, 37, 249–260. [Google Scholar] [CrossRef]
- Oak, M.J.; Baker, L.E.; Thomas, D.C. Three Phase Relative Permeability of Berea Sandstone. J. Pet. Technol. 1990, 42, 1054–1061. [Google Scholar] [CrossRef]
- Eleri, O.O.; Graue, A.; Skauge, A. Steady-State and Unsteady-State Two-Phase Relative Permeability Hysteresis and Measurements of Three-Phase Relative Permeabilities Using Imaging Techniques. In Proceedings of the 1995 SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar]
- Fatemi, S.M.; Sohrabi, M.; Jamiolahmady, M. Experimental and Theoretical Investigation of Gas/Oil Relative Permeability Hysteresis under Low Oil/Gas interfacial Tension and Mixed-Wet Conditions. Energy 2012, 26, 4366–4382. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Sohrabi, M. Recovery Mechanisms and Relative Permeability for Gas/Oil Systems at Near-Miscible Conditions: Effects of Immobile Water Saturation, Wettability, Hysteresis, and Permeability. Energy Fuels 2013, 27, 2376–2389. [Google Scholar] [CrossRef]
- Dernaika, M.R.; Basioni, M.A.; Dawoud, A. Variations in Bounding and Scanning Relative Permeability Curves With Different Carbonate Rock Types. SPE Reserv. Eval. Eng. 2013, 16, 265–280. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Sohrabi, M. Experimental Investigation of Near-Miscible Water-Alternating-Gas Injection Performance in Water-Wet and Mixed-Wet Systems. SPE J. 2013, 18, 114–123. [Google Scholar] [CrossRef]
- Duchenne, S.; de Loubens, R.; Petitfrere, M. Modeling and Simultaneous History-Matching of Multiple WAG Coreflood Experiments at Reservoir Conditions. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015. [Google Scholar]
- Sinan, Z.; Junchang, S.; Guoqi, W. Numerical simulation-based correction of relative permeability hysteresis in water-invaded underground gas storage during multi-cycle injection and production. Pet. Explor. Dev. 2021, 48, 190–200. [Google Scholar]
- Teklu, T.W.; Li, X.; Zhou, Z. Fracture and Matrix Permeability Hysteresis in Organic Rich Mudrocks. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Bennion, D.B.; Thomas, F.B.; Bietz, R. Hysteretic Relative Permeability Effects and Reservoir Conformance—An Overview; Hycal Energy Research Laboratories Ltd.: Calgary, AB, Canada, 1996. [Google Scholar]
- Hadlow, R. Update of Industry Experience with CO2 Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washing, DC, USA, 4–7 October 1992. [Google Scholar]
- Edlmann, K.; Hinchliffe, S.; Heinemann, N. Cyclic CO2–H2O injection and residual trapping: Implications for CO2 injection efficiency and storage security. Int. J. Greenh. Gas Control 2019, 80, 1–9. [Google Scholar] [CrossRef]
- Jia, W.; McPherson, B.; Pan, F.; Dai, Z.; Moodie, N.; Xiao, T. Impact of Three-Phase Relative Permeability and Hysteresis Models on Forecasts of Storage Associated with CO2-EOR. Water Resour. Res. 2018, 54, 1109–1126. [Google Scholar] [CrossRef]
- Altundas, Y.B.; Ramakrishnan, T.S.; Chugunov, N.; de Loubens, R. Retardation of CO2 Caused by Capillary Pressure Hysteresis: A New CO2 Trapping Mechanism. SPE J. 2011, 16, 784–794. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Zhou, D. Impact of Relative Permeability Hysteresis on Water-Alternating-Gas WAG Injectivity: Modeling and Experimental Study. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Jarrell, P.M. Practical Aspects of CO2 Flooding; Society of Petroleum Engineers: Richardson, TX, USA, 2002. [Google Scholar]
- Christensen, J.R.; Stenby, E.H.; Skauge, A. Compositional and Relative Permeability Hysteresis Effects on Near-Miscible WAG. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 19–22 April 1998. [Google Scholar]
- Shahverdi, H.; Sohrabi, M.; Fatemi, M. Three-phase relative permeability and hysteresis effect during WAG process in mixed wet and low IFT systems. J. Pet. Sci. Eng. 2011, 78, 732–739. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Sohrabi, M. Experimental and Theoretical Investigation of Water/Gas Relative Permeability Hysteresis: Applicable to Water Alternating Gas (WAG) Injection and Gas Storage Processes. In Proceedings of the Abu Dhabi International Petroleum Conference and Exhibition, Abu Dhabi, United Arab Emirates, 11–14 November 2012. [Google Scholar]
- Mahzari, P.; Sohrabi, M. An Improved Approach for Estimation of Flow and Hysteresis Parameters Applicable to WAG Experiments. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016. [Google Scholar]
- Ranaee, E.; Inzoli, F.; Riva, M. Hysteresis effects of three-phase relative permeabilities on black-oil reservoir simulation under WAG injection protocols. J. Pet. Sci. Eng. 2019, 176, 1161–1174. [Google Scholar] [CrossRef]
- Kowsari, M.; James, L.A.; Haynes, R.D. The Effect of Relative Permeability Hysteresis on the Design of an Optimal Water-Alternating-Gas (WAG) Process. SPE Reserv. Eval. Eng. 2022, 25, 125–145. [Google Scholar] [CrossRef]
- Foroudi, S.; Gharavi, A.; Fatemi, M. Assessment of two-phase relative permeability hysteresis models for oil/water, gas/water and gas/oil systems in mixed-wet porous media. Fuel 2022, 309, 122150. [Google Scholar] [CrossRef]
- Rogers, J.D.; Grigg, R.B. A Literature Analysis of the WAG Injectivity Abnormalities in the CO2 Process. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 17–21 April 2001; pp. 375–386. [Google Scholar]
- Ligero, E.L.; Schiozer, D.J. Miscible WAG-CO2 Light Oil Recovery from Low Temperature and High Pressure Heterogeneous Reservoir. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Maracaibo, Venezuela, 21–23 May 2014. [Google Scholar]
- Laboissiere, P.; Mello, S.F.; Trevisan, O.V.; Schiozer, D.J. Relative Permeability Effects on the Miscible CO2 WAG Injection Schemes Trough Compositional Simulations of Brazilian Small Scale Water-Wet Synthetic Pre-Salt Reservoir. In Proceedings of the Offshore Technology Conference Brasil, Rio de Janeiro, Brazil, 29–31 October 2013. [Google Scholar]
- Dietrich, J.K. Relative Permeability During Cyclic Steam Stimulation of Heavy-Oil Reservoirs. J. Pet. Technol. 1981, 33, 1987–1989. [Google Scholar] [CrossRef]
- Christensen, J.R.; Larse, M.; Nicolaisen, H. Compositional Simulation of Water-Alternating-Gas Processes: SPE Annual Technical Conference and Exhibition. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000; p. 62999. [Google Scholar]
- Spiteri, E.J.; Juanes, R.; Blunt, M.J. A new model of trapping and relative permeability hysteresis for all wettability characteristics. SPE J. 2008, 13, 277–288. [Google Scholar] [CrossRef]
- Juanes, R.; Spiteri, E.J.; Orr, F.M. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour. Res. 2006, 42, W12411–W12418. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, D.; Li, J. Numerical simulation of near-miscible WAG considering hysteresis effect. Fault-Block Oil Gas Field 2008, 87–90. [Google Scholar]
- Jiang, T.; Li, J.; Gao, W. Numerical simulation study on the characteristics of unsteady flow in gas-water alternating injection. Pet. Geol. Recovery Effic. 2009, 47–50, 114. [Google Scholar]
- Karkooti, H.; Masoudi, R.; Arif, A.M. Evaluation of the Impact of Relative Permeability Hysteresis and Three Phase Modeling on the Performance of Water Alternative Gas EOR Processes. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 19–21 July 2011. [Google Scholar]
- Shahrokhi, O.; Fatemi, M.; Sohrabi, M. Assessment of Three Phase Relative Permeability and Hysteresis Models for Simulation of Water-Alternating-Gas (WAG) Injection in Water-wet and Mixed-wet Systems. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 12–16 April 2014. [Google Scholar]
- Kamali, F.; Hussain, F.; Cinar, Y. An Experimental and Numerical Analysis of Water-Alternating-Gas and Simultaneous-Water-and-Gas Displacements for Carbon Dioxide Enhanced Oil Recovery and Storage. SPE J. 2017, 22, 521–538. [Google Scholar] [CrossRef]
- Huang, J.; Pan, G.; Wu, J. Study on cyclic water injection in offshore low-volatility oil reservoirs considering hysteresis effect. Spec. Oil Gas Reserv. 2018, 112–117. [Google Scholar] [CrossRef]
- Zayer, H.A.; Sohrabi, M. Numerical Simulation Guideline of Oil Recovery by Cycle-DependentThree-Phase Process Using Coreflood Experiments. In Proceedings of the SPE Europec featured at 82nd EAGE Conference and Exhibition, Amsterdam, The Netherlands, 8–11 December 2020. [Google Scholar]
- Rezaei, A.; Hassanpouryouzband, A.; Molnar, I. Relative permeability of hydrogen and aqueous brines in sandstones and carbonates at reservoir conditions. Geophys. Res. Lett. 2022, 49, e2022GL099433. [Google Scholar] [CrossRef]
- Ali, A.A. Numerical Analysis for Relative Permeability Hysteresis Models in Reservoir Simulation of CO2 Trapping in Underground Carbon Storage. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022. [Google Scholar]
- Lysyy, M.; Føyen, T.; Johannesen, E.B. Hydrogen relative permeability hysteresis in underground storage. Geophys. Res. Lett. 2022, 49, e2022GL100364. [Google Scholar] [CrossRef]
- Hashemi, A.; Shadizadeh, S.R. The impact of reservoir properties on pseudo functions: Upscaling of relative permeability. Pet. Sci. Technol. 2014, 32, 772–782. [Google Scholar] [CrossRef]
- Bo, Z.; Boon, M.; Hajibeygi, H. Impact of experimentally measured relative permeability hysteresis on reservoir-scale performance of underground hydrogen storage (UHS). Int. J. Hydrogen Energy 2023, 48, 13527–13542. [Google Scholar] [CrossRef]
- Pfeiffer, W.T.; Bauer, S. Subsurface porous media hydrogen storage–scenario development and simulation. Energy Procedia 2015, 76, 565–572. [Google Scholar] [CrossRef]
- Hagemann, B.; Rasoulzadeh, M.; Panfilov, M. Mathematical modeling of unstable transport in underground hydrogen storage. Environ. Earth Sci. 2015, 73, 6891–6898. [Google Scholar] [CrossRef]
- Feldmann, F.; Hagemann, B.; Ganzer, L. Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages. Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar] [CrossRef]
- Alvaro, A.S.; Abarca, V.; Grandia, F. Assessment of feasible strategies for seasonal underground hydrogen storage in a saline aquifer. Int. J. Hydrogen Energy 2017, 42, 16657–16666. [Google Scholar]
- Katarzyna, T. Numerical simulation of hydrogen injection and withdrawal to and from a deep aquifer in NW Poland. Int. J. Hydrogen Energy 2020, 45, 2068–2083. [Google Scholar]
- Mahdi, D.S.; AL-khdheeawi, E.A.; Yuan, Y. Hydrogen underground storage efficiency in a heterogeneous sandstone reservoir. Adv. Geo-Energy Res. 2021, 5, 437–443. [Google Scholar] [CrossRef]
- Kanaani, M.; Sedaee, B.; Asadian-Pakfar, M. Role of cushion gas on underground hydrogen storage in depleted oil reservoirs. J. Energy Storage 2022, 45, 103783. [Google Scholar] [CrossRef]
- Okoroafor, E.R.; Saltzer, S.D.; Kovscek, A.R. Toward underground hydrogen storage in porous media: Reservoir engineering insights. Int. J. Hydrogen Energy 2022, 47, 33781–33802. [Google Scholar] [CrossRef]
- Delshad, M.; Umurzakov, Y.; Sepehrnoori, K. Hydrogen storage assessment in depleted oil reservoir and saline aquifer. Energies 2022, 15, 8132. [Google Scholar] [CrossRef]
- Wang, G.; Pickup, G.; Sorbie, K. Scaling analysis of hydrogen flow with carbon dioxide cushion gas in subsurface heterogeneous porous media. Int. J. Hydrogen Energy 2022, 47, 1752–1764. [Google Scholar] [CrossRef]
- Pan, B.; Liu, K.; Ren, B. Impacts of relative permeability hysteresis, wettability, and injection/withdrawal schemes on underground hydrogen storage in saline aquifers. Fuel 2023, 333, 126516. [Google Scholar] [CrossRef]


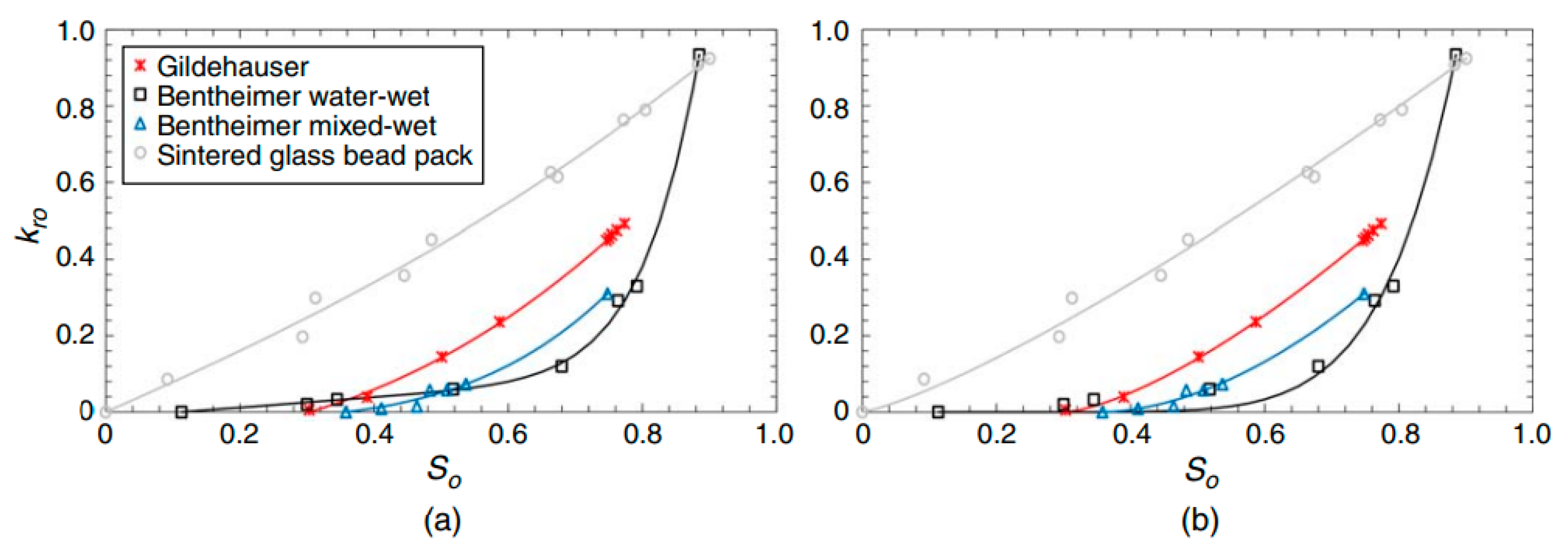
| Hysteresis Model | Application | Wettability | Assumed Conditions/Applicable Conditions | ||
|---|---|---|---|---|---|
| Water | Oil | Gas | |||
| Two-phase hysteresis (related to saturation direction) | |||||
| Land et al. [37] (1968) | No | No | Yes | Water-wet | Capture occurs only during imbibition. |
| Killough et al. [34] (1976) | No | No | Yes | Water-wet | Capture occurs only during imbibition; there is no hysteresis effect in the relative permeability curves of the wetting phase; imbibition relative permeability curves are reversible. |
| Carlson et al. [35] (1981) | Yes | Yes | Yes | Water-wet | Capture occurs only during imbibition; there is no hysteresis effect in the relative permeability curves of the wetting phase; all imbibition curves are parallel. |
| Beattie et al. [38] (1991) | Yes | Yes | No | Water-wet | Assume that the water-phase permeability depends only on water saturation. |
| Kjosavik et al. [39] (2002) | Yes | Yes | No | Mix-wet | Assume that each injection cycle of kr should return to the starting point of the previous displacement and form a closed scanning loop. |
| Delshad et al. [26] (2003) | Yes | Yes | No | Mix-wet | Assume that Sor has a maximum value at and is zero at = 1. |
| Spiteri et al. [10] (2008) | Yes | Yes | No | Water-wet | The captured non-wetting saturation does not always monotonically change with the initial non-wetting saturation. |
| Three-phase hysteresis (related to saturation history: saturation direction and path) | |||||
| Parker and Lenhard et al. [40,41] (1987) | Yes | Yes | Yes | Both | Consider the effect of pore blocking by gas trapped in water and oil phases, as well as oil trapped in the water phase. |
| Larsen and Skauge et al. [36] (1998) | Yes | No | Yes | Water-wet | Gas-water phase permeability is consistent during both two-phase and three-phase flow processes; oil phase permeability in three-phase flow is calculated using the Stone I model; there is no hysteresis effect in the oil phase. |
| Egermann et al. [12] (2000) | Yes | Yes | Yes | Both | CL, CT, and CU represent the Land, capture, and uncaptured constants, respectively. |
| F.J.Fayers et al. [43] (2000) | Yes | Yes | Yes | Mix-wet | It is assumed that the hysteresis for each phase depends only on the saturation of that phase. Consideration of component effects. |
| UTHYST Beygi et al. [16] (2013) | Yes | Yes | Yes | Both | Any relative permeability model containing capture saturation. |
| Sigmoid et al. [45] (2014) | Yes | Yes | Yes | Water-wet | Oil remobilization induced by gas injection in water-wet media; a smooth transition towards the layer-drainage regime for low oil saturations; the consequent reduction of residual oil saturation in a three-phase system. |
| WAG-HW Shahverdi and Sohrabi et al. [50] (2015) | Yes | Yes | Yes | Both | Application of hysteresis methods suitable for WAG simulations, based on three-phase relative permeability data obtained from WAG experiments. |
| Aghabozorgi et al. [44] (2019) | Yes | No | Yes | Both | It is assumed that the relative permeability of gas and water depends only on their saturation. Water saturation fluctuates within a certain range of saturations. |
| Author | Time | Model | Research Target | |
|---|---|---|---|---|
| Displacement | CO2 Sequestration | |||
| J.K. Dietrich et al. [88] | 1981 | J.K. Dietrich | √ | |
| J.R. Christensen et al [89] | 2000 | Larsen and Skauge | √ | |
| M. Delshad et al. [26] | 2003 | UTCHEM | √ | |
| Matthew Flett et al. [14] | 2004 | Land | √ | |
| Elizabeth.J et al. [90] | 2006 | Carlson, Kilough, Larsen and Skauge | √ | |
| Juancs R et al. [91] | 2008 | Kilough | √ | |
| Liu Zixiong et al. [92] | 2008 | FJ Fayers | √ | |
| Hustad et al. [32] | 2010 | Hustad | √ | |
| Jiang Tao et al. [93] | 2009 | \ | √ | |
| Altundas et al. [75] | 2011 | Land | √ | |
| Hooman Karkooti et al. [94] | 2011 | Larsen and Skauge | √ | |
| Hoseini et al. [15] | 2011 | Carlson, Kilough, Larsen and Skauge | √ | |
| Shahrokhi et al. [95] | 2014 | Carlson, Killough and Jargon | √ | |
| Duchenne et al. [68] | 2015 | Larsen and Skauge | √ | |
| Wang et al. [59] | 2016 | Land | √ | |
| Fatemeh et al. [96] | 2017 | Larsen and Skauge | √ | |
| Wei Jia et al. [74] | 2018 | Larsen and Skauge, Carlson, Land | √ | |
| Huang Jianting et al. [97] | 2018 | \ | √ | |
| Vieira, R.A. et al. [11] | 2019 | Larsen and Skauge | √ | |
| Zayer et al. [98] | 2020 | Larsen and Skauge | √ | |
| Rezaei, A. et al. [99] | 2021 | Kilough | √ | |
| Zhu Sinan et al. [56] | 2021 | Carlson, Kilough | √ | |
| Alnuaimi et al. [57] | 2021 | Aghabozorgi | √ | |
| Kowsari et al. [83] | 2022 | Carlson, Kilough | √ | |
| Ammar Al Ali et al. [100] | 2022 | Patterson | √ | |
| Author | Time | Software | Hydrogen Storage Site | Model | Whether Hysteresis Exists | Main Finding |
|---|---|---|---|---|---|---|
| Pfeiffer et al. [104] | 2015 | Eclipse | Saline layer | Corey | No | Porous media hydrogen storage must address issues such as the resistance of caprock rocks to hydrogen permeation and gas diffusion. |
| Hagemann et al. [105] | 2015 | DuMux | aquifers | Brooks–Corey | No | For low injection rates, gravitational forces dominate hydrogen movement, while for high injection rates, viscous forces become dominant, and displacement becomes unstable. |
| Feldmann F. et al. [106] | 2016 | DuMux, COMSOL | Depleted gas reservoir | Brooks–Corey | No | The gravitational override and viscous fingering in the aquifer structure complicate the effective displacement of natural fluids. |
| Alvaro, A.S. et al. [107] | 2017 | COMSOL | saline layer | Brooks–Corey | No | If there are several shallow oil wells beneath the caprock, a large amount of H2 can be recovered. Rising appears to be the main limitation for brine aquifer storage in the absence of other buffering gases. |
| Katarzyna Lubońet al [108] | 2020 | petraSim-TOUGH2 | aquifers | Van Genuchten-Mualem | No | Maximum hydrogen saturation occurs around the injection well, and hydrogen diffuses along the top surface of the reservoir in contact with the caprock, likely due to the lack of viscous fingering and the low viscosity and density of hydrogen, which may impact the geometry of underground storage. |
| Lysyy et al. [101] | 2021 | Eclipse | Depleted field | Field data | No | When injecting pure hydrogen only, most injected hydrogen (>84%) remains underground as a buffering gas. Unrecovered hydrogen accumulates in the uppermost layer. Injecting formation gases as buffering gases leads to higher hydrogen recovery rates. |
| D.S. Mahdi, et al. [109] | 2021 | TOUGH2 | Water layer | van Genuchten-Mualem | Gas-liquid hysteresis | Caprock and injection rates have significant impacts on hydrogen leakage, as well as on the amount of hydrogen captured and recovered. Without caprock, higher injection rates increase H2 leakage. |
| M. Kanaani et al. [110] | 2022 | CMG-GEM | Depletion of condensate reservoirs | Field data | No | Methane performs better as a buffering gas compared to nitrogen and carbon dioxide. Buffer gas injection reduces the negative effects of gravitational segregation. |
| Okoroaf et al. [111] | 2022 | Eclipse | Depleted gas reservoir | Experimental data | No | The main factors affecting hydrogen recovery are reservoir depth, dip angle, current pressure, and flow rate. |
| M. Delshad, et al. [112] | 2022 | CMG-GEM | Depleted reservoirs and aquifers | Experimental data | No | Lateral diffusion of hydrogen is greater in aquifers and natural gas scenarios, and in saline aquifers, the presence of reliable caprock/seal layers needs to be evaluated. |
| Wang et al. [113] | 2022 | CMG-GEM | Depleted field | Experimental data | Gas- hysteresis | Capillary pressure is not a key factor in H2 recovery performance, and the H2 recovery rate is not strongly dependent on gas sweep efficiency. |
| B. Pan et al. [114] | 2023 | CMG-IMEX | aquifers | Displacement and imbibition data | Yes | H2 recovery rate is reduced by hydrogen-brine relative permeability hysteresis, and higher H2 recovery rates result in greater hydrogen recovery, but also increased water production. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, Y.; Guo, P.; Liu, Y.; Wang, S.; Cao, S.; Zhang, J.; Sun, W.; Qi, D.; Ji, Q. State of the Art on Relative Permeability Hysteresis in Porous Media: Petroleum Engineering Application. Appl. Sci. 2024, 14, 4639. https://doi.org/10.3390/app14114639
Lan Y, Guo P, Liu Y, Wang S, Cao S, Zhang J, Sun W, Qi D, Ji Q. State of the Art on Relative Permeability Hysteresis in Porous Media: Petroleum Engineering Application. Applied Sciences. 2024; 14(11):4639. https://doi.org/10.3390/app14114639
Chicago/Turabian StyleLan, Yubo, Ping Guo, Yong Liu, Shuoshi Wang, Sheng Cao, Jiang Zhang, Wenjing Sun, Dongyan Qi, and Qiang Ji. 2024. "State of the Art on Relative Permeability Hysteresis in Porous Media: Petroleum Engineering Application" Applied Sciences 14, no. 11: 4639. https://doi.org/10.3390/app14114639
APA StyleLan, Y., Guo, P., Liu, Y., Wang, S., Cao, S., Zhang, J., Sun, W., Qi, D., & Ji, Q. (2024). State of the Art on Relative Permeability Hysteresis in Porous Media: Petroleum Engineering Application. Applied Sciences, 14(11), 4639. https://doi.org/10.3390/app14114639






