Constitutive Characteristics of Rock Damage under Freeze–Thaw Cycles
Abstract
1. Introduction
2. Experimental Setup
3. Preparation of Samples and Their Associated Physical Characteristics
- Cooling stage: cooling freezing, freeze–thaw test box temperature gradually decreased from room temperature and stabilized at −20 °C, cooling process time is about 100 min.
- Freezing stage: constant temperature freezing, freeze–thaw test box to maintain −20 °C ambient temperature, constant temperature for 4 h.
- heating stage: heating and melting, freeze–thaw box placed automatically into the test box, slightly higher than 20 °C warm water to heat the frozen sample, the box temperature gradually stabilized at 20 °C, the heating process time about 100 min.
- Melting stage: constant temperature water bath, freeze–thaw box environment temperature maintained at 20 °C constant temperature, the sample immersed in 20 °C warm water bath, heating for 4 h.
- The warm water in the freeze–thaw test box is discharged to complete a full FTC test cycle and enter the next FTC stage until the preset number of FTCs.
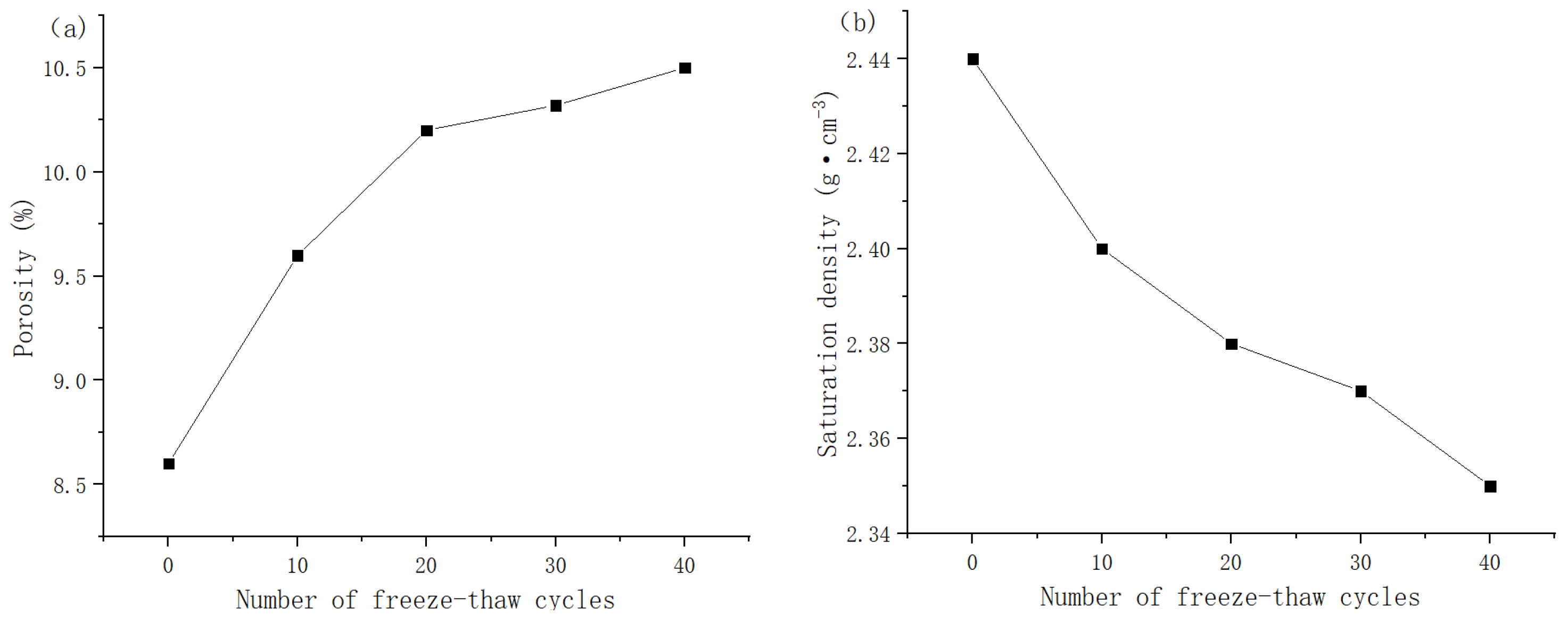
3.1. Rock Porosity and Saturation Density
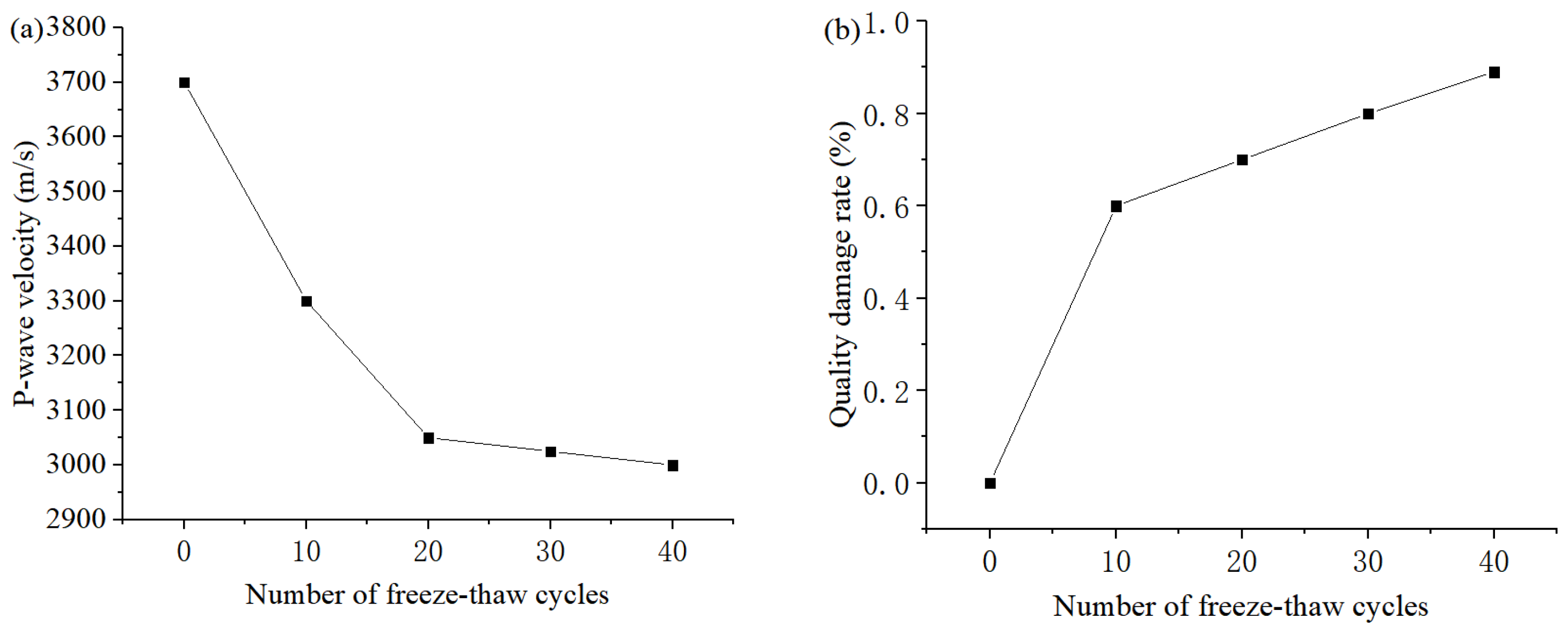
3.2. Rock Mass Loss Rate and P-Wave Velocity
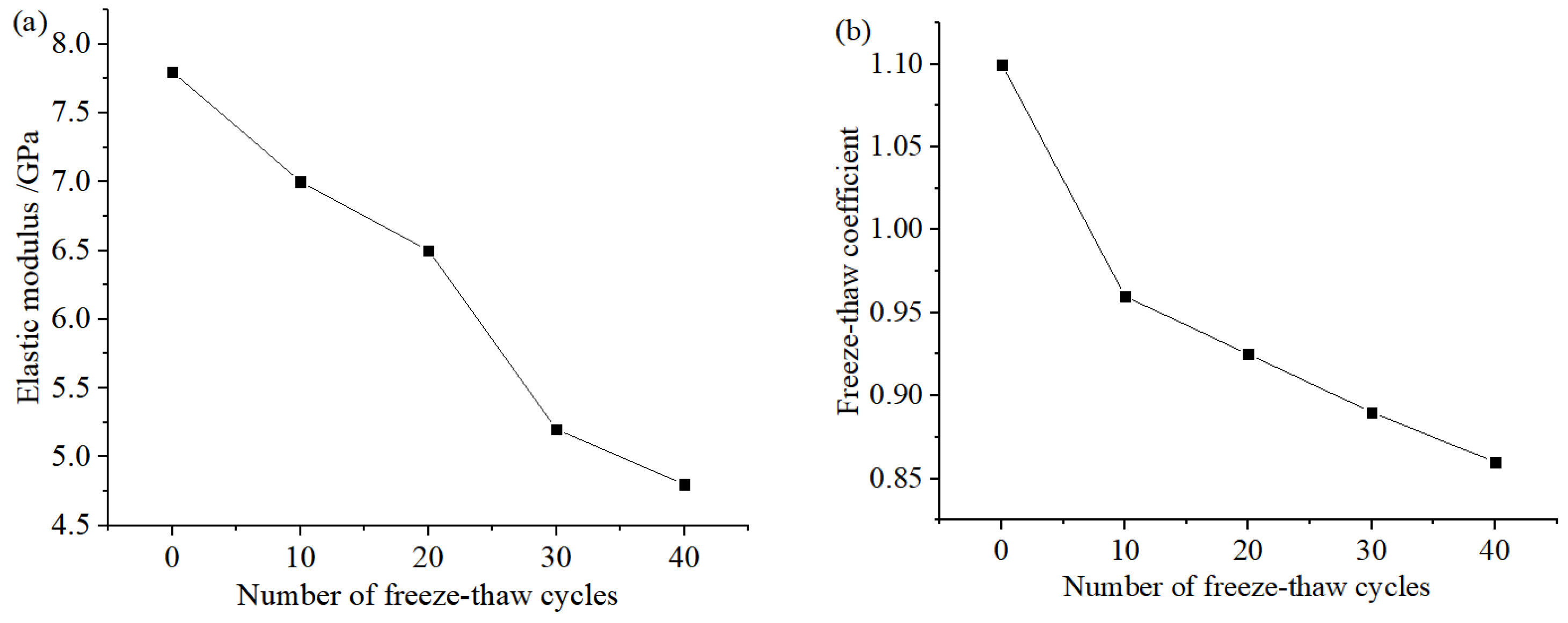
3.3. Analysis of Strength Loss Rate
3.4. Static Compression Test of Rock Damaged by FTC
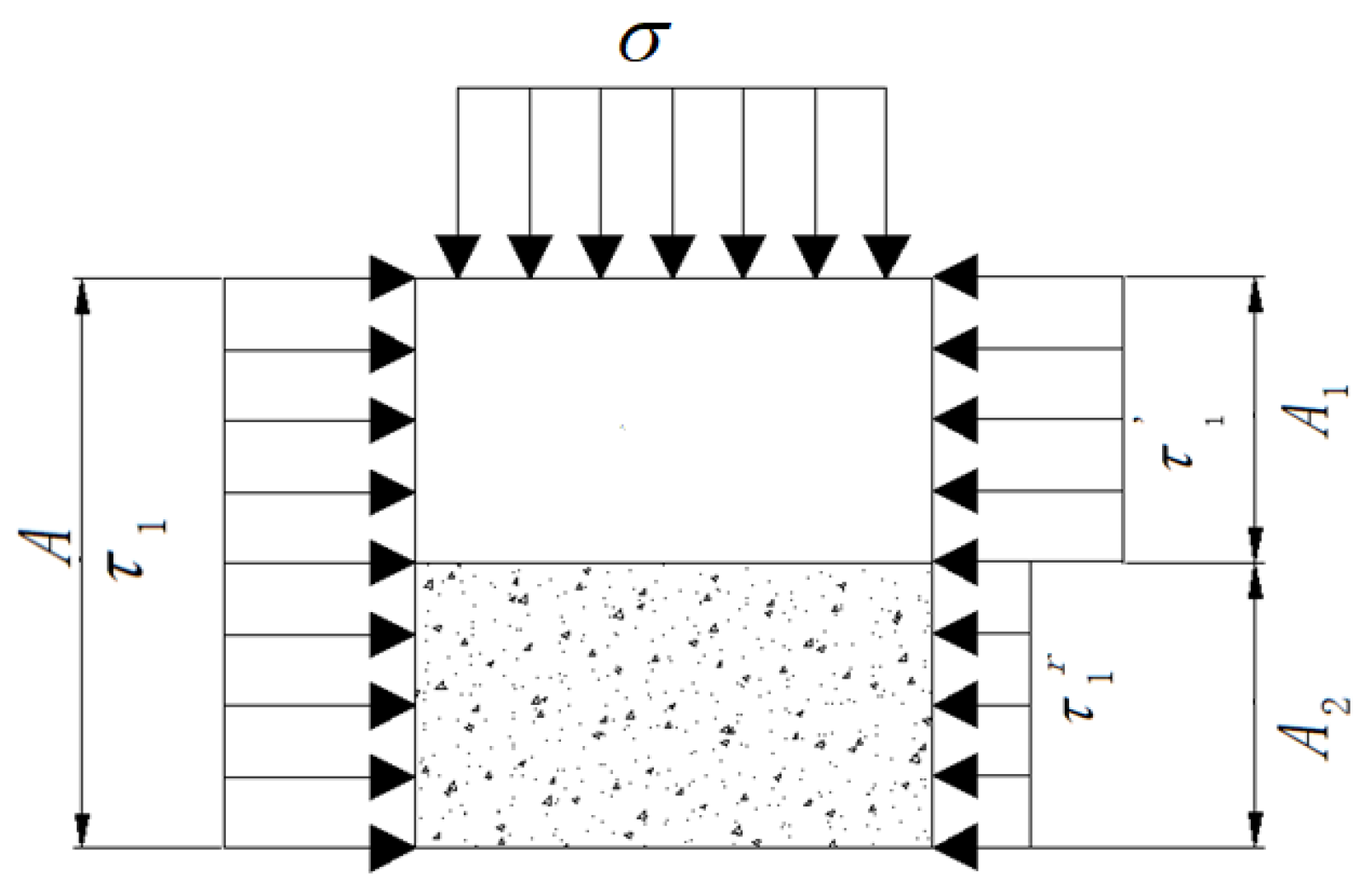
4. Constitutive Relationship and Damage Variables
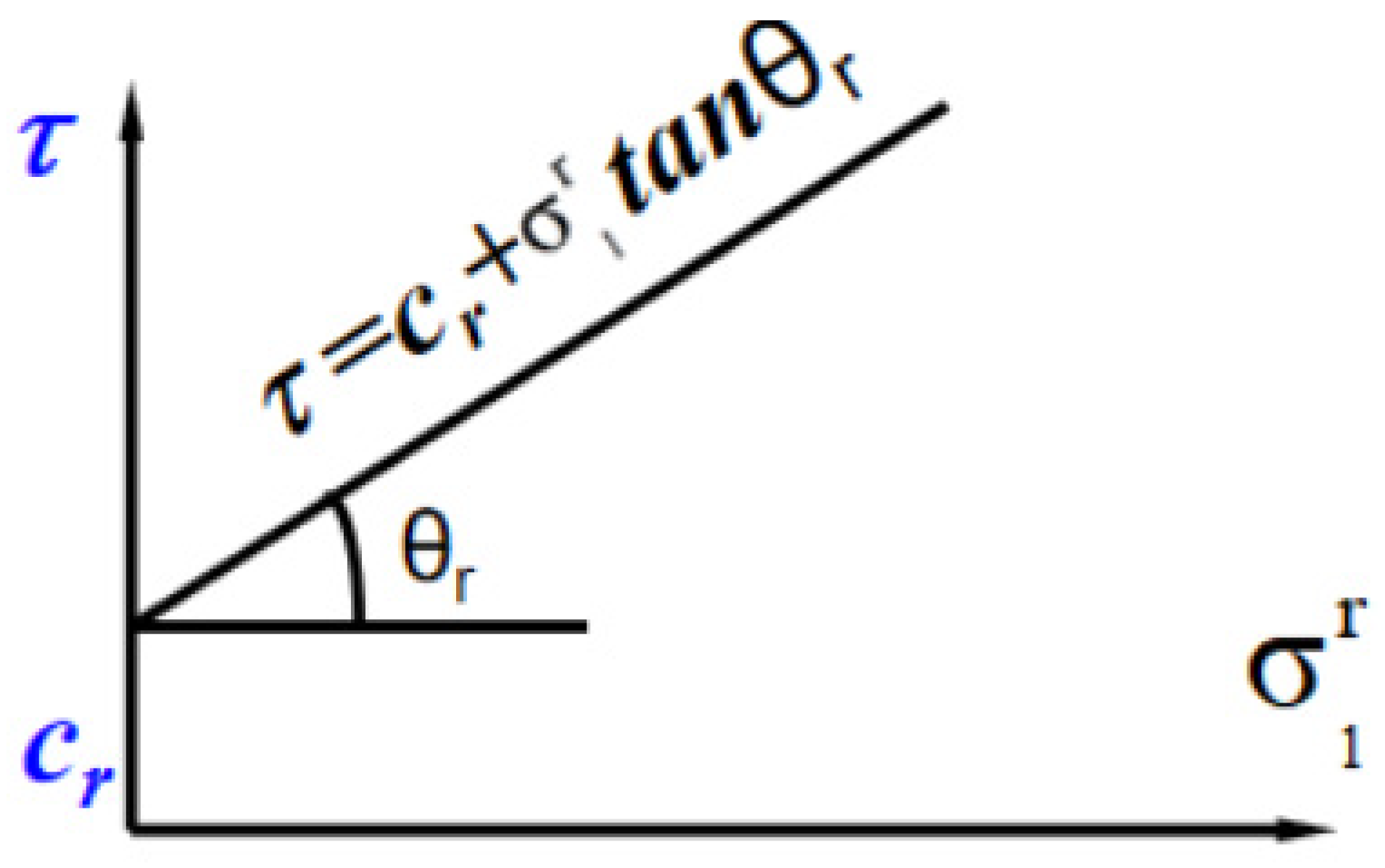
4.1. Establishment of the Constitutive Model
4.2. Determination of Parameters of Rock Damage Constitutive Model
5. Discussion
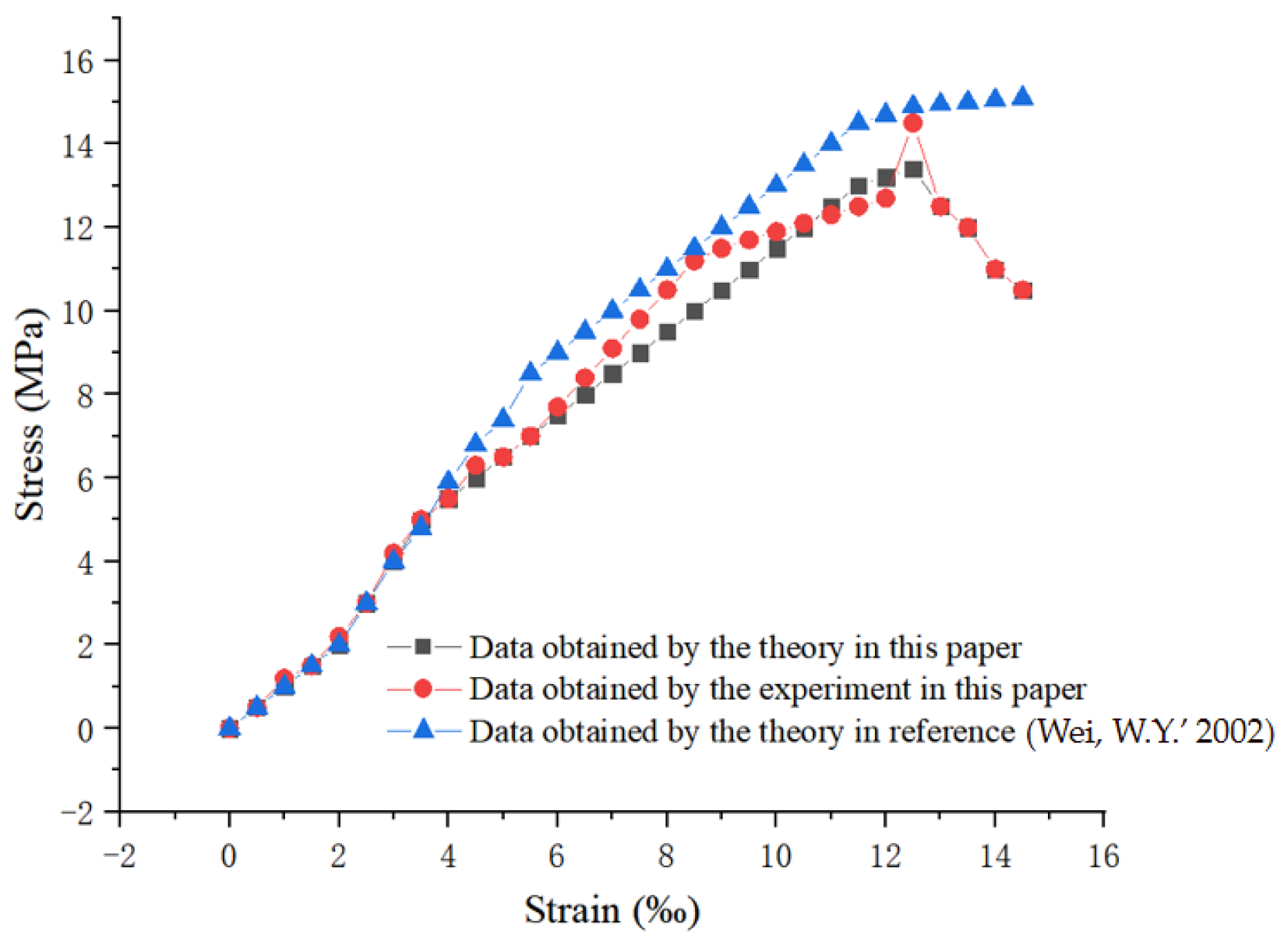
5.1. Comparison of Theoretical Models
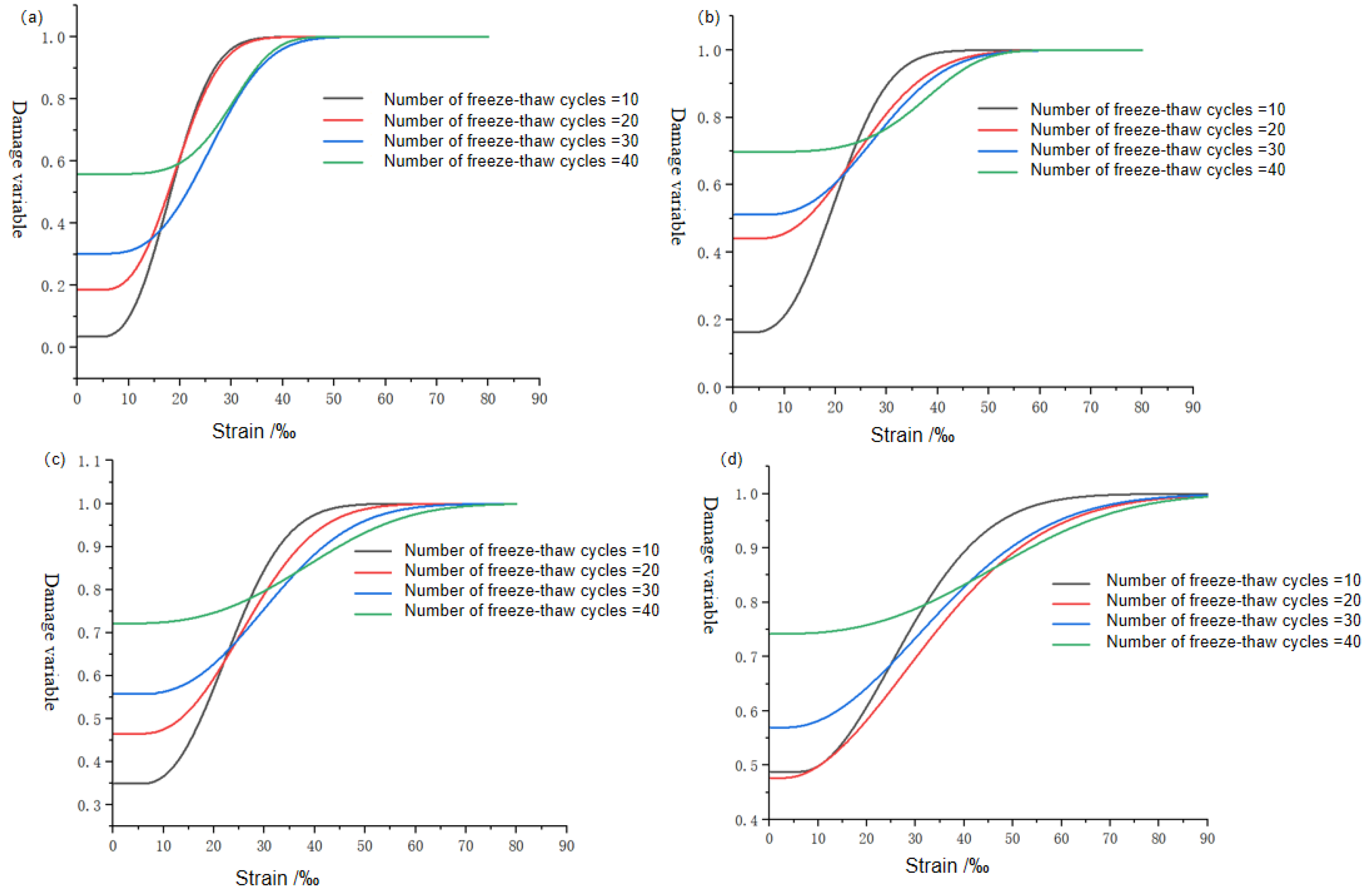
5.2. Damage Percentage Analysis of Rocks under Different FTCs
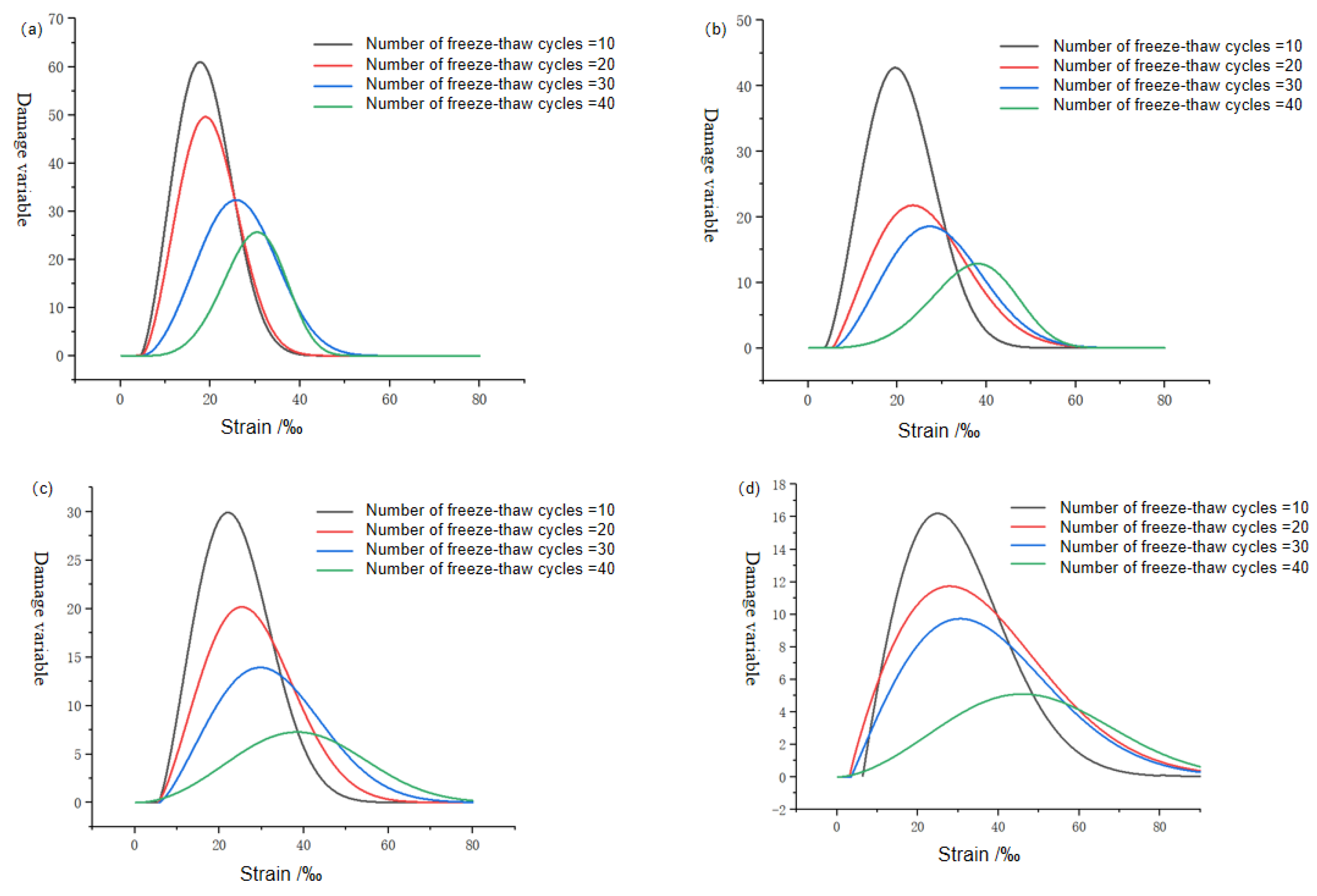
5.3. Analysis of Damage Evolution Rate of Rocks under Different FTCs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Z.; Kong, L.; Wang, M.; Wang, J. Effects of remolding and wetting-drying-freezing-thawing cycles on the pore structures of Yanji mudstones. Cold Reg. Sci. Technol. 2020, 174, 103037. [Google Scholar] [CrossRef]
- Soltani, A. Comments on “effect of wetting–drying–freezing–thawing cycles on the swelling behaviour of the Yanji mudstone”[Environ Earth Sci (2019) 78: 435]. Environ. Earth Sci. 2019, 78, 512. [Google Scholar] [CrossRef]
- Wang, J.; Song, C.; Hou, A.; Miao, Y.; Yang, G.; Zhang, J. Effects of freezing-thawing cycle on peatland active organic carbon fractions and enzyme activities in the Da Xing’anling Mountains, Northeast China. Environ. Earth Sci. 2014, 72, 1853–1860. [Google Scholar] [CrossRef]
- Zeng, Z.; Kong, L. Effect of wetting–drying–freezing-thawing cycles on the swelling behavior of the Yanji mudstone. Environ. Earth Sci. 2019, 78, 435. [Google Scholar] [CrossRef]
- Martinez, J.; Benavente, D.; Gomez-Heras, M.; Marco-Castaño, L.; García-del-Cura, M.Á. Non-linear decay of building stones during freeze-thaw weathering processes. Constr. Build. Mater. 2013, 38, 443–454. [Google Scholar] [CrossRef]
- Yamabe, T.; Neaupane, K.M. Determination of some thermo-mechanical properties of Sirahama rock under subzero temperature condition. Int. J. Rock Mech. Min. Sci. 2001, 38, 1029–1034. [Google Scholar] [CrossRef]
- Park, C.; Synn, J.H.; Shin, H.S.; Cheon, D.S.; Lim, H.D.; Jeon, S.W. Experimental study on the thermal characteristics of rock at low temperatures. Int. J. Rock Mech. Min. Sci. 2004, 41, 81–86. [Google Scholar] [CrossRef]
- Sondergeld, C.H.; Rai, C.S. Velocity and resistivity changes during FTC in Berea rock. Geophysics 2007, 72, E99–E105. [Google Scholar] [CrossRef]
- Del Roa, L.M.; Lopez, F.; Esteban, F.J.; Tejado, J.J.; Mota, M.I.; González, I.; Ramos, A.; San Emeterio, J.L. Ultrasonic study of alteration processes in granites caused by freezing and thawing. In Proceedings of the IEEE Ultrasonics Symposium 2005, Rotterdam, The Netherlands, 18–21 September 2005. [Google Scholar]
- Janach, W. The role of bulking in brittle failure of rocks under rapid compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 177–186. [Google Scholar] [CrossRef]
- Lankford, J. The role of tensile microfracture in the strain rate dependence of compressive strength of fine-grained limestone—Analogy with strong ceramics. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 173–175. [Google Scholar] [CrossRef]
- Olsson, W.A. The compressive strength of tuff as a function of strain rate from 10−6 to 103/sec. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 115–118. [Google Scholar] [CrossRef]
- Zhou, K.P.; Li, B.; Li, J.L.; Deng, H.W.; Feng, B.I.N. Microscopic damage and dynamic mechanical properties of rock under freeze-thaw environment. Trans. Nonferrous Met. Soc. China 2015, 25, 1254–1261. [Google Scholar] [CrossRef]
- Kawakata, H.; Cho, A.; Yanagidani, T.; Shimada, M. The observations of faulting in westerly granite under triaxial compression by X-ray CT scan. Int. J. Rock Mech. Min. Ences 1997, 34, 151.e1–151.e12. [Google Scholar] [CrossRef]
- Kawakata, H.; Cho, A.; Kiyama, T.; Yanagidani, T.; Kusunose, K.; Shimada, M. Three-dimensional observations of faulting process in Westerly granite under uniaxial and triaxial conditions by X-ray CT scan. Tectonophysics 1999, 313, 293–305. [Google Scholar] [CrossRef]
- Kyoya, T.; Baek, Y.; Onda, C. On deterioration of Oya-tuff in freezing-thawing cycle and its quantitative description. Doboku Gakkai Ronbunshu 2000, 652, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhai, C.; Qin, L.; Xu, J.; Yu, G. Coal pore characteristics at different freezing temperatures under conditions of freezing-thawing cycles. Environ. Earth Sci. 2018, 77, 525. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N.; Singh, K. Effect of Curing on Micro-Physical Performance of Polypropylene Fiber Reinforced and Silica Fume Stabilized Expansive Soil Under Freezing Thawing Cycles. Sci. Rep. 2020, 10, 7624. [Google Scholar] [CrossRef] [PubMed]
- Sellares, J.; Mas, S.; Melo, E.; Sanchez, F.; Marin, J.; Gea, J.; Barreiro, E. Oxidative stress time course in the rat diaphragm after freezing-thawing cycles. Respir. Physiol. Neurobiol. 2006, 155, 156–166. [Google Scholar] [CrossRef] [PubMed]
- GBT 50266-2013; Test Method Standard for Engineering Rock Mass. China Planning Press: Beijing, China, 2013. (In Chinese)
- Wei, W.Y.; Wei, L.D. Study on statistical damage constitutive model of rock. Chin. J. Rock Mech. Eng. 2002, 21, 787–791. (In Chinese) [Google Scholar]

| Mean Compressive Strength at Unfrozen and Thawing Saturation (MPa) | 0 Times of FTC | 10 Times of FTC | 20 Times of FTC | 30 Times of FTC | 40 Times of FTC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Saturated Water Compressive Strength (MPa) | Loss Rate of Freeze–Thaw Strength (%) | Saturated Water Compressive Strength (MPa) | Loss Rate of Freeze–Thaw Strength (%) | Compressive Strength in Saturated Water (MPa) | Loss Rate of Freeze–Thaw Strength (%) | Compressive Strength in Saturated Water (MPa) | Loss Rate of Freeze–Thaw Strength (%) | Saturated Water Compressive Strength (MPa) | Loss Rate of Freeze–Thaw Strength (%) | |
| 125.7 | 119.5 | 0 | 116.9 | 7.00 | 113.2 | 9.94 | 111.7 | 11.14 | 105.6 | 15.99 |
| Number of FTCs | Confining Pressure/MPa | Extreme Stress /MPa | Modulus of Elasticity /GPa |
|---|---|---|---|
| 10 | 0 | 4.23 | 0.867 |
| 10 | 2 | 14.5 | 1.295 |
| 10 | 5 | 19.6 | 1.452 |
| 10 | 10 | 24.3 | 1.565 |
| 20 | 0 | 3.8 | 0.761 |
| 20 | 2 | 12.7 | 1.156 |
| 20 | 5 | 18.9 | 1.289 |
| 20 | 10 | 23.5 | 1 325 |
| 30 | 0 | 3.74 | 0.529 |
| 30 | 2 | 11.3 | 0.890 |
| 30 | 5 | 18.1 | 1.066 |
| 30 | 10 | 22.9 | 1.240 |
| 40 | 0 | 3.3 | 0.515 |
| 40 | 2 | 10.5 | 0.710 |
| 40 | 5 | 17.2 | 0.917 |
| 40 | 10 | 21.2 | 0.932 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, Z.; Cao, H.; Wu, T. Constitutive Characteristics of Rock Damage under Freeze–Thaw Cycles. Appl. Sci. 2024, 14, 4627. https://doi.org/10.3390/app14114627
Li Y, Wang Z, Cao H, Wu T. Constitutive Characteristics of Rock Damage under Freeze–Thaw Cycles. Applied Sciences. 2024; 14(11):4627. https://doi.org/10.3390/app14114627
Chicago/Turabian StyleLi, Yaoxin, Zhibin Wang, Haiqing Cao, and Tingyao Wu. 2024. "Constitutive Characteristics of Rock Damage under Freeze–Thaw Cycles" Applied Sciences 14, no. 11: 4627. https://doi.org/10.3390/app14114627
APA StyleLi, Y., Wang, Z., Cao, H., & Wu, T. (2024). Constitutive Characteristics of Rock Damage under Freeze–Thaw Cycles. Applied Sciences, 14(11), 4627. https://doi.org/10.3390/app14114627







