Optimal Concordant Tests
Abstract
1. Introduction
2. Methods
2.1. Pearson’s Concordant Test
2.2. Concordant Tests Based on Gamma Distribution
2.3. Optimal Concordant Test
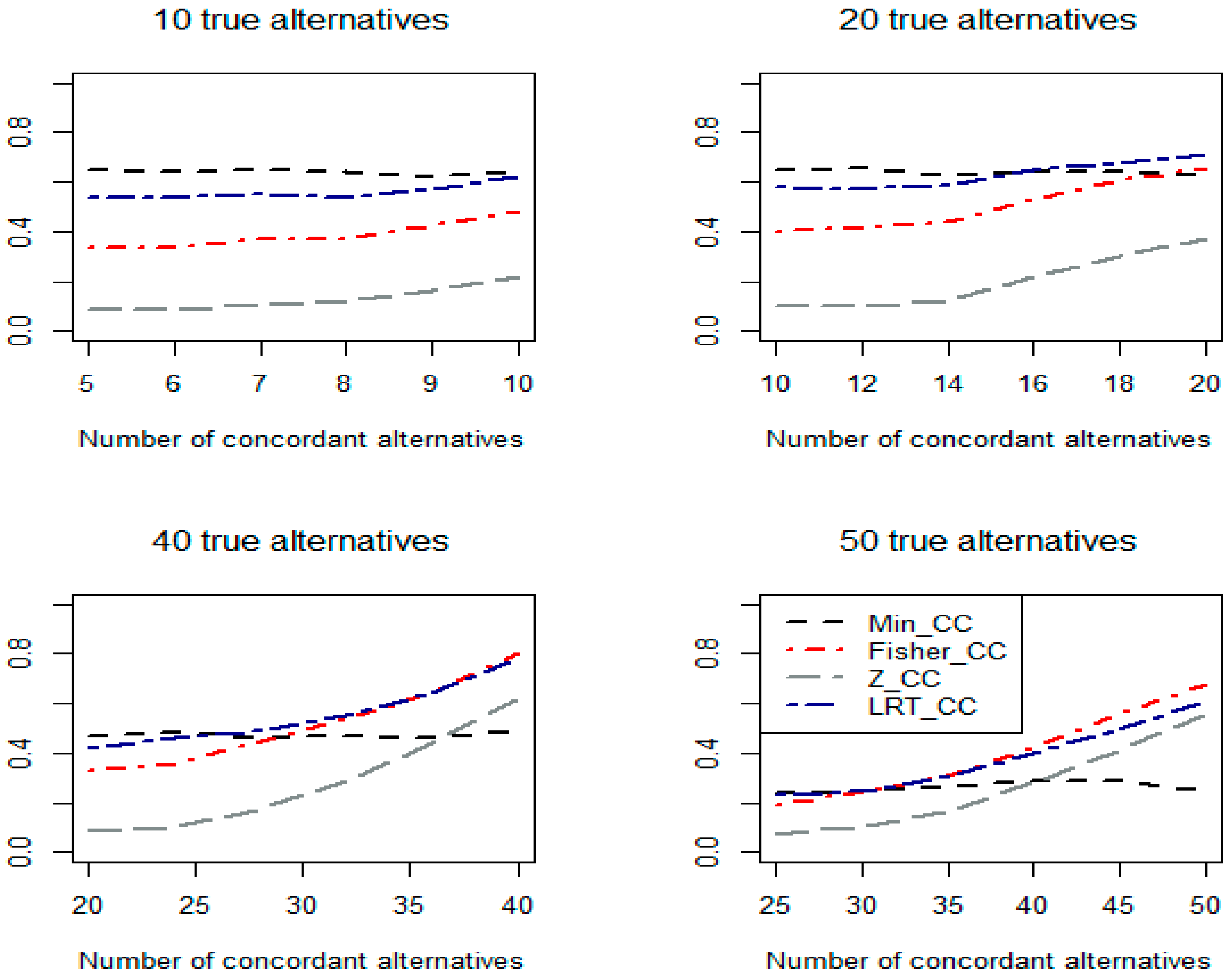
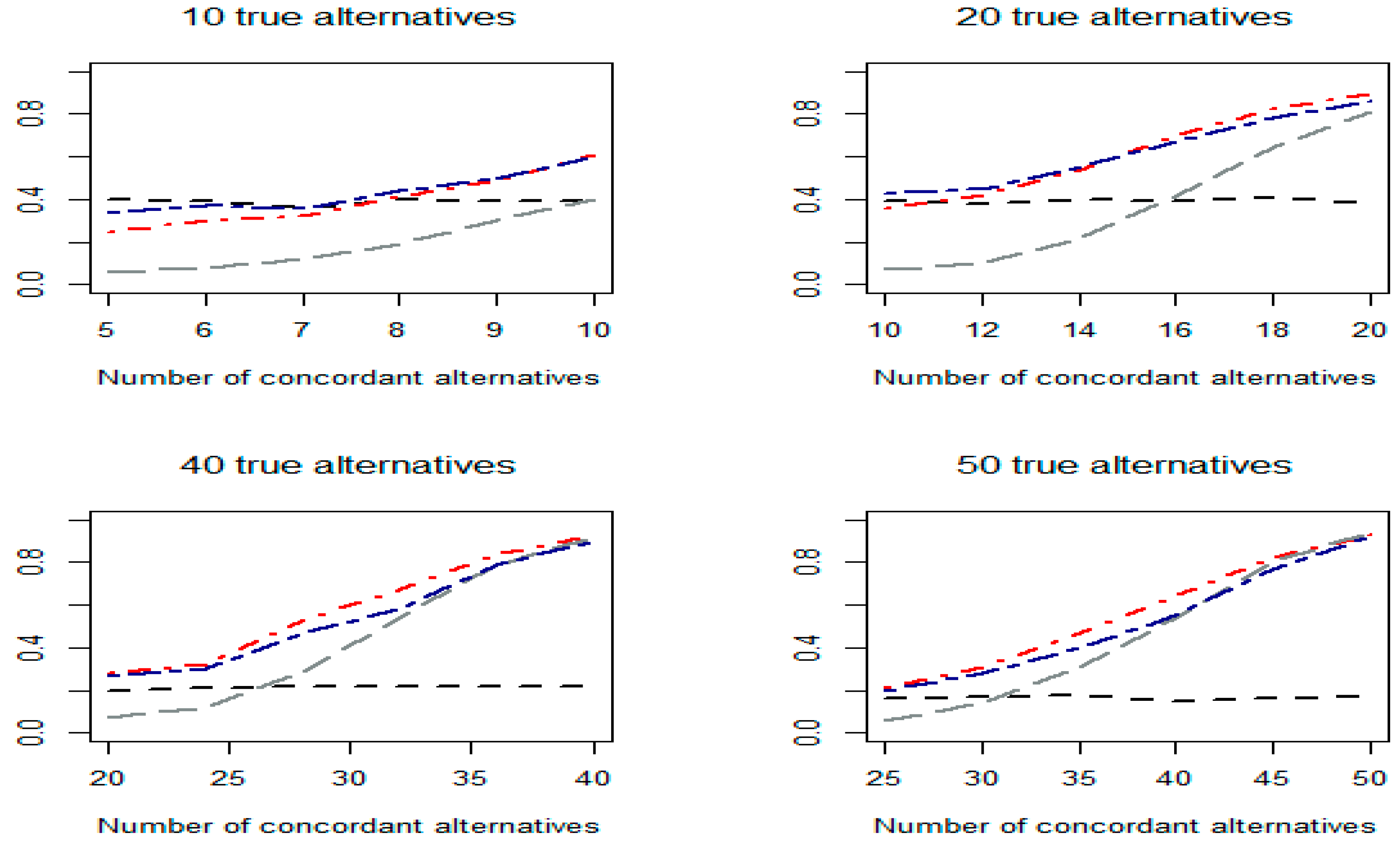
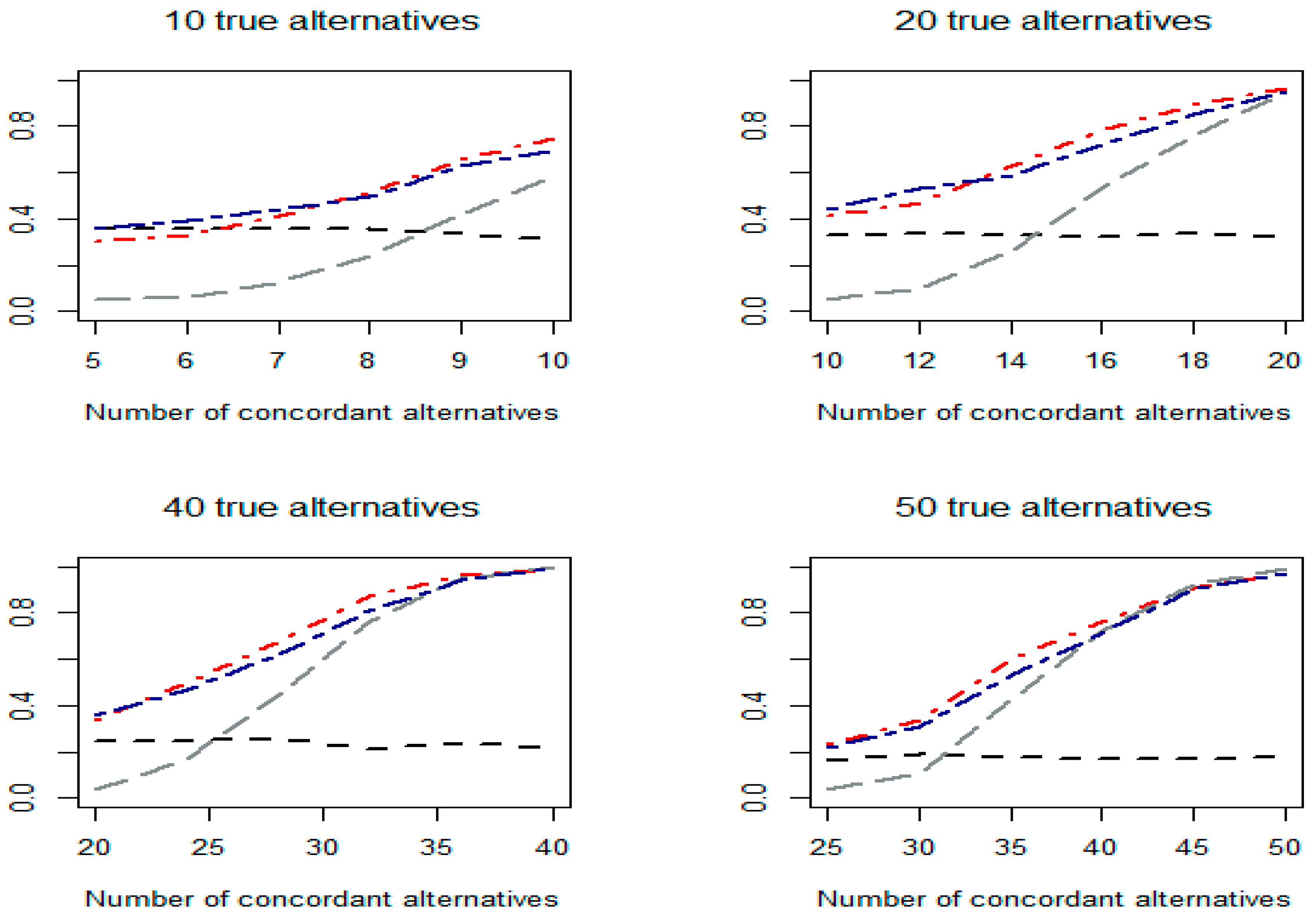
3. Results
3.1. Numeric Results from Simulation Study
3.2. Real Data Application
4. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Owen, A.B. Karl Pearson’s meta-analysis revisited. Ann. Stat. 2009, 37, 3867–3892. [Google Scholar] [CrossRef] [PubMed]
- Hedges, L.; Olkin, I. Statistical Methods for Meta-Analysis; Academic: San Diego, CA, USA, 1985. [Google Scholar]
- Chen, Z.; Zhang, G.; Li, J. Goodness-of-fit test for meta-analysis. Sci. Rep. 2015, 5, 16983. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. Statistical Methods for Research Workers, 4th ed.; Oliver and Boyd: Edinburgh, UK, 1932. [Google Scholar]
- Pearson, K. On a New Method of Determining “Goodness of Fit”. Biometrika 1934, 26, 425–442. [Google Scholar]
- Tippett, L.H.C. Methods of Statistics; Williams Norgate: London, UK, 1931. [Google Scholar]
- Stouffer, S.A.; Suchman, E.A.; Devinney, L.C.; Star, S.A.; Williams, R.M., Jr. The American Soldier: Adjustment During Army Life. (Studies in Social Psychology in World War II); Princeton Univ. Press: Princeton, NJ, USA, 1949; Volume 1. [Google Scholar]
- Lancaster, H. The combination of probabilities: An application of orthonormal functions. Aust. J. Stat. 1961, 3, 20–33. [Google Scholar] [CrossRef]
- Chen, Z.; Nadarajah, S. On the optimally weighted z-test for combining probabilities from independent studies. Comput. Stat. Data Anal. 2014, 70, 387–394. [Google Scholar] [CrossRef]
- Chen, Z. Optimal Tests for Combining p-Values. Appl. Sci. 2022, 12, 322. [Google Scholar] [CrossRef]
- Birnbaum, A. Combining Independent Tests of Significance. J. Am. Stat. Assoc. 1954, 49, 559–574. [Google Scholar]
- Chen, Z. Robust tests for combining p-values under arbitrary dependency structures. Sci. Rep. 2022, 12, 3158. [Google Scholar] [CrossRef] [PubMed]
- Esary, J.D.; Proschan, F.; Walkup, D.W. Association of random variables, with applications. Ann. Math. Stat. 1967, 38, 1466–1474. [Google Scholar] [CrossRef]
- Self, S.G.; Liang, K.-Y. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc. 1987, 82, 605–610. [Google Scholar] [CrossRef]
- Bachmann, S.; Finger, C.; Huss, A.; Egger, M.; Stuck, A.E.; Clough-Gorr, K.M. Inpatient rehabilitation specifically designed for geriatric patients: Systematic review and meta-analysis of randomised controlled trials. Bmj 2010, 340, c1718. [Google Scholar] [CrossRef] [PubMed]
- Riley, R.D.; Higgins, J.P.; Deeks, J.J. Interpretation of random effects meta-analyses. Bmj 2011, 342, d549. [Google Scholar] [CrossRef] [PubMed]
- Cochran, W. Some methods for strengthening the common chi-square tests. Biometrics 1954, 10, 417–451. [Google Scholar] [CrossRef]
- Lancaster, H. The derivation and partition of χ2 in certain discrete distributions. Biometrika 1949, 36, 117–129. [Google Scholar] [CrossRef]
- Chen, Z. A new association test based on Chi-square partition for case-control GWA studies. Genet. Epidemiol. 2011, 35, 658–663. [Google Scholar] [CrossRef]
| Study | OR | 95% CI | Study | OR | 95% CI | Study | OR | 95% CI |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.11 | 0.51, 2.39 | 5 | 0.88 | 0.39, 1.95 | 9 | 1.06 | 0.63, 1.79 |
| 2 | 0.97 | 0.78, 1.21 | 6 | 1.28 | 0.71, 2.30 | 10 | 2.95 | 1.54, 5.63 |
| 3 | 1.13 | 0.73, 1.72 | 7 | 1.19 | 0.69, 2.08 | 11 | 2.36 | 1.18, 4.72 |
| 4 | 1.08 | 0.42, 2.75 | 8 | 3.82 | 1.37, 10.60 | 12 | 1.68 | 1.05, 2.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z. Optimal Concordant Tests. Appl. Sci. 2024, 14, 4536. https://doi.org/10.3390/app14114536
Chen Z. Optimal Concordant Tests. Applied Sciences. 2024; 14(11):4536. https://doi.org/10.3390/app14114536
Chicago/Turabian StyleChen, Zhongxue. 2024. "Optimal Concordant Tests" Applied Sciences 14, no. 11: 4536. https://doi.org/10.3390/app14114536
APA StyleChen, Z. (2024). Optimal Concordant Tests. Applied Sciences, 14(11), 4536. https://doi.org/10.3390/app14114536







