Advancing Visible Spectroscopy through Integrated Machine Learning and Image Processing Techniques

Abstract

This research introduces an approach to visible spectroscopy leveraging image processing techniques and machine learning (ML) algorithms. The methodology involves calculating the hue value of an image and deriving the corresponding dominant wavelength. Initially, a six-degree polynomial regression supervised machine learning model is trained to establish a relationship between the hue values and dominant wavelengths. Subsequently, the ML model is employed to analyse the visible wavelengths emitted by various sources, including sodium vapour, neon lamps, mercury vapour, copper vapour lasers, and helium vapour. The performance of the proposed method is evaluated through error analysis, revealing remarkably low error percentages of 0.04%, 0.01%, 3.7%, 1%, and 0.07% for sodium vapour, neon lamp, copper vapour laser, and helium vapour, respectively. This approach offers a promising avenue for accurate and efficient visible spectroscopy, with potential applications in diverse fields such as material science, environmental monitoring, and biomedical research. This research presents a visible spectroscopy method harnessing image processing and machine learning algorithms. By calculating hue values and identifying dominant wavelengths, the approach demonstrates consistently low error rates across diverse light sources.

1. Introduction

Visible spectroscopy, a fundamental technique in analytical chemistry and material science, plays a pivotal role in characterising the spectral properties of various substances based on their interaction with light. Traditional spectroscopic methods often rely on the complex instrumentation and manual interpretation of spectral data, posing challenges in terms of accuracy and efficiency. However, recent advancements in machine learning (ML) and image processing have opened new avenues for improving the accuracy and automation of spectroscopic analysis. This paper introduces a methodology that combines ML algorithms with image processing techniques to enhance visible spectroscopy. By leveraging the power of ML, which excels in pattern recognition and data analysis, in conjunction with image processing, which enables the extraction of valuable spectral information from visual data, this approach aims to overcome the limitations of traditional spectroscopic methods. The foundation of this methodology lies in the integration of polynomial regression with ML algorithms. The machine learning model employed is a polynomial regression of six degree, a supervised learning approach designed to capture complex relationships between input features and the target variable by fitting a polynomial equation. The algorithm learns from labelled data to determine the coefficients of the polynomial equation that best fits the training data, thereby enabling it to make predictions on unseen data. This model is adept at capturing nonlinear patterns in the data, though caution must be exercised to prevent overfitting, potentially requiring regularisation techniques for improved generalisation. Polynomial regression serves as a mathematical framework for modelling the relationship between hue values extracted from images and the corresponding dominant wavelengths. By fitting polynomial functions to the dataset, the methodology captures complex spectral patterns and enables the accurate prediction of dominant wavelengths. Polynomial regression is often preferred in scenarios where the relationship between the independent and dependent variables is non-linear. Unlike simple linear regression, which assumes a linear relationship between the variables, polynomial regression allows for more flexible modelling through fitting a polynomial function to the data. This flexibility enables polynomial regression to capture complex patterns and variations in the data that cannot be adequately represented by a straight line. One of the key advantages of polynomial regression is its ability to model curvature in the data. By introducing polynomial terms of a higher degree, the model can better capture the curvature and non-linearity present in many real-world datasets. This makes polynomial regression a valuable tool for predicting outcomes in fields such as finance, economics, and engineering, where relationships between variables may be more intricate and nuanced.

Additionally, polynomial regression can provide improved accuracy compared to linear regression when the underlying relationship between the variables is non-linear. By allowing the model to flexibly adapt to the data, polynomial regression can yield more accurate predictions and better capture the true underlying patterns in the data.

Furthermore, the utilisation of image processing techniques enables the extraction of hue values from images of vapour sources, thereby providing quantitative inputs for ML algorithms. This integrated approach facilitates the automated analysis of spectral data, eliminating the need for manual interpretation and enhancing the efficiency of spectroscopic analysis. The significance of this research lies in its potential to revolutionise visible spectroscopy through offering a robust and automated methodology for spectral analysis. By harnessing the capabilities of machine learning and image processing, researchers can achieve unprecedented levels of accuracy and efficiency in characterising the spectral properties of various substances. This paper presents the methodology, experimental results, and implications of this approach, highlighting its potential applications in diverse fields such as material science, environmental monitoring, and biomedical research.

2. Literature Review

The literature review explores the growing field of spectroscopy, which is crucial in various scientific and industrial fields due to advancements in image processing and machine learning. This field is widely used in natural surface characterisation, sensor calibration, material analysis, and environmental sensing.

Milton et al. [1] provided a comprehensive review of field spectroscopy, emphasising its applications in characterising natural surfaces and supporting sensor calibration. Building on this, John-Herpin et al. [2] introduced a technique utilising visible light for infrared spectroscopy, highlighting its potential in material analysis and environmental sensing. Pholpho et al. [3] presented a study on classifying bruised longan fruits using visible spectroscopy, demonstrating its industrial applications. Similarly, Wang and ElMasry [4] developed a spectrophotometric method for detecting surface bruises on apples, offering an automated quality control approach in fruit processing. Beberniss and Ehrhardt [5] discussed the impact of high-speed computers on theoretical spectroscopy, which enabled detailed analyses and facilitated collaborations in experimental research. In another domain, Van Vliet and De Groot [6] reviewed high-pressure sodium discharge lamps, focusing on advancements in design and their applications for outdoor lighting. Kitsinelis et al. [7] investigated medium-pressure mercury discharge lamps as intense white light sources, providing insights into their atomic emission spectra and potential applications.

Further extending the exploration of discharge characteristics, Trunec et al. [8] studied atmospheric pressure glow discharge in neon, shedding light on its behaviour in different gas mixtures. Complementing this, Golubovskii et al. [9] utilised numerical simulations to analyse homogeneous barrier discharge in helium, contributing to the understanding of plasma physics. Amendola and Meneghetti [10] proposed a method for sizing gold nanoparticles using UV-vis spectroscopy, offering a practical approach for nanoparticle characterisation. Finally, Godiksen et al. [11] employed electron paramagnetic resonance spectroscopy to identify and quantify copper sites in zeolites, enhancing our understanding of their catalytic properties.

Windom et al. [12] utilised Raman spectroscopy to study molybdenum disulfide and trioxide, demonstrating their applications in tribological systems. Rauscher et al. [13] highlighted the need for improved detector technologies for spectroscopic biosignature characterisation in space telescopes, underscoring the significance of advanced detection techniques. Kurniastuti et al. [14] developed a method for determining Hue Saturation Value (HSV) colour features in kidney histology images, enabling automated segmentation. Similarly, Cantrell et al. [15] investigated the Hue parameter in the HSV colour space for bitonal optical sensors, demonstrating its superior precision in sensing applications. Ma et al. [16] proposed a computational framework for turbid water single-pixel imaging, which enhanced image recovery in underwater environments. This work was complemented by Steinegger et al. [17], who discussed various aspects of spectroscopies related to pH values and the benefits of different materials and their applications. Wang et al. [18] designed a refinement module to optimise the details of underwater images, achieving better visual effects and reporting the effectiveness of the proposed UIE-Convformer. In the realm of medical diagnosis, Simbolon et al. [19] employed colour segmentation in CT scans for pneumonia detection, demonstrating the significant potential of visual computing techniques in healthcare applications. Garaba et al.’s [20] study on the effectiveness of the Forel-Ule Colour Index (FUI) scale in assessing natural water properties revealed its versatility in measuring water quality through ocean colour remote sensing products, handheld scales, and mobile apps. Verma et al. [21] developed MPR for haze removal from images, enhancing methods and addressing challenges in environmental monitoring and medical diagnostics using advanced spectroscopy and imaging technologies.

Kang et al. [22] reported that the machine learning-assisted fluorescence hyperspectral technique was beneficial for classifying rice varieties. Blake et al.‘s [23] literature review on machine learning methods for cancer classification using Raman spectroscopy data highlighted the popularity of deep learning models, the need to address methodological challenges, and the need for benchmark datasets. Ede [24] discussed the future scope of deep learning in the field of electron microscopy, pointing towards its potential for significant advancements. Carey et al. [25] utilised machine learning and genetic programming to analyse spectroscopic data, providing insights into material composition and enabling informed decision-making through interpretable rules. In a related study, Li et al. [26] presented a methodology for dermatological disease detection using image processing and machine learning, showcasing the potential of these techniques in improving diagnostic accuracy and efficiency in dermatology. Rodellar et al. [27] focused on image processing and machine learning for the morphological analysis of blood cells, highlighting the utility of these techniques in automating cell image analysis and supporting clinical diagnosis. Carey et al. [28] machine learning method interprets vibrational spectroscopy data, creating interpretable rules for explanatory analysis.

Zeng et al. [29] developed a method for the speciation of arsenic using liquid phase microextraction coupled with flame atomic absorption spectroscopy, demonstrating its applicability in environmental and biological sample analysis. Similarly, Bai and Fan [30] proposed a flow injection micelle-mediated methodology for the determination of lead using electrothermal atomic absorption spectrometry, showcasing its sensitivity and accuracy in trace lead detection. Li et al.‘s [31] study utilised image-based modelling and deep learning to predict the mechanical properties of heterogeneous materials, highlighting the potential of deep learning to establish implicit mappings between macroscale and mesoscale structures, providing insights for material behaviour optimisation. Additionally, Zhang et al. [32] explored the performance of classification models for toxins based on Raman spectroscopy using machine learning algorithms. Their study demonstrated the effectiveness of preprocessing methods and classification models in accurately identifying protein toxins, offering promising avenues for toxin detection and public health protection.

In recent years, advancements in imaging technology revolutionised various industries, including agriculture, food processing, and pharmaceuticals. For instance, Kruse et al. [33] introduced the Spectral Image Processing System (SIPS), facilitating the interactive visualisation and analysis of imaging spectrometer data. Yang et al. [34] investigated the identification of the geographic origin of peaches using visible-near infrared spectroscopy, fluorescence spectroscopy, and image processing technology. Similarly, Simon et al. [35] compared external bulk video imaging (BVI) with focused beam reflectance measurement (FBRM) and ultraviolet-visible (UV/vis) spectroscopy for identifying metastable zones in crystallisation processes. Furthermore, Vong and Larbi [36] evaluated processed image data obtained from different commercial cameras for visible spectroscopy applications. Liu et al. [37] provided a comprehensive review of wavelength selection techniques for hyperspectral image processing in the food industry. Plaza et al. [38] showcased recent advancements in hyperspectral image processing techniques, focusing on algorithms for handling high-dimensional data and integrating spatial and spectral information, highlighting their potential for innovation across various industries.

Yonezawa et al. [39] created MOLASS, an analytical software that automates the processing of matrix data from SAXS, UV-visible spectroscopy, and SEC-SAXS, using matrix optimisation with low-rank factorisation. Building on advancements in educational tools, Grasse et al. [40] introduced a method for teaching UV-Vis spectroscopy using a 3D-printable smartphone spectrophotometer, thus addressing accessibility issues associated with traditional laboratory equipment in educational settings. Green et al.’s [41] study on imaging spectroscopy and the Air-borne Visible/Infrared Imaging Spectrometer (AVIRIS) provides a comprehensive analysis of its diverse applications in Earth remote sensing research, including environmental monitoring and Earth observation.

Shakya et al. [42] introduced a visible light spectroscopy method using plasmonic colour filter arrays, which offers a spatial resolution of 1.4 mm and a video rate of up to 30 frames per second, demonstrating its feasibility and potential in hyper-spectral imaging systems for improved spectral resolution and accuracy. Usami et al. [43] developed a real-time terahertz imaging system with a spatial resolution of 1.4 mm and a video rate of up to 30 frames per second for materials science and imaging applications. Delaney et al.’s [44] study utilised reflectance imaging spectroscopy for pigment mapping in paintings, demonstrating the effectiveness of hyperspectral imaging cameras in identifying and mapping artist pigments. Al Ktash et al. [45] used UV-Vis/NIR spectroscopy and hyperspectral imaging to identify raw cotton types, revealing proteins, hydrocarbons, and hy-droxyl groups as dominant structures. Baka et al. [46] developed a UV-Vis spectroscopy method for measuring transformer oil’s interfacial tension, offering a cost-effective and rapid alternative for transformer maintenance. Haffert et al. [47] developed VIS-X, a high-resolution spectrograph for the Magellan Clay 6.5 m telescope, enhancing sensitivity to protoplanetary systems and providing insights into planet formation processes in the visible spectrum. Van der Woerd et al. [48] conducted a study on the use of hue-angle products in optical satellite sensors for water quality monitoring, revealing accurate colour properties from ocean colour satellite instruments since 1997.

The identified literature gap revealed a lack of processes utilising image processing for visible spectroscopy. This research addressed this gap by conducting a visible spectroscopy of chemical element vapours through the integration of machine learning and image processing techniques.

3. Methodology

Visible spectroscopy plays a crucial role in various scientific and industrial applications, facilitating the analysis of materials based on their spectral characteristics. In recent years, the integration of image processing techniques and machine learning algorithms has emerged as a promising approach to enhance the accuracy and efficiency of spectroscopic methods. This research aims to leverage such advancements by developing a methodology for visible spectroscopy using polynomial regression and machine learning algorithms.

The TAS-990 Atomic Absorption Spectrophotometer was used by the researchers for the spectroscopy of different vapours and stands out as one of the most precise spectrometers available, renowned for its exceptional accuracy in providing data on elemental emissions (See

Table 1. Specifications of the spectrometer.

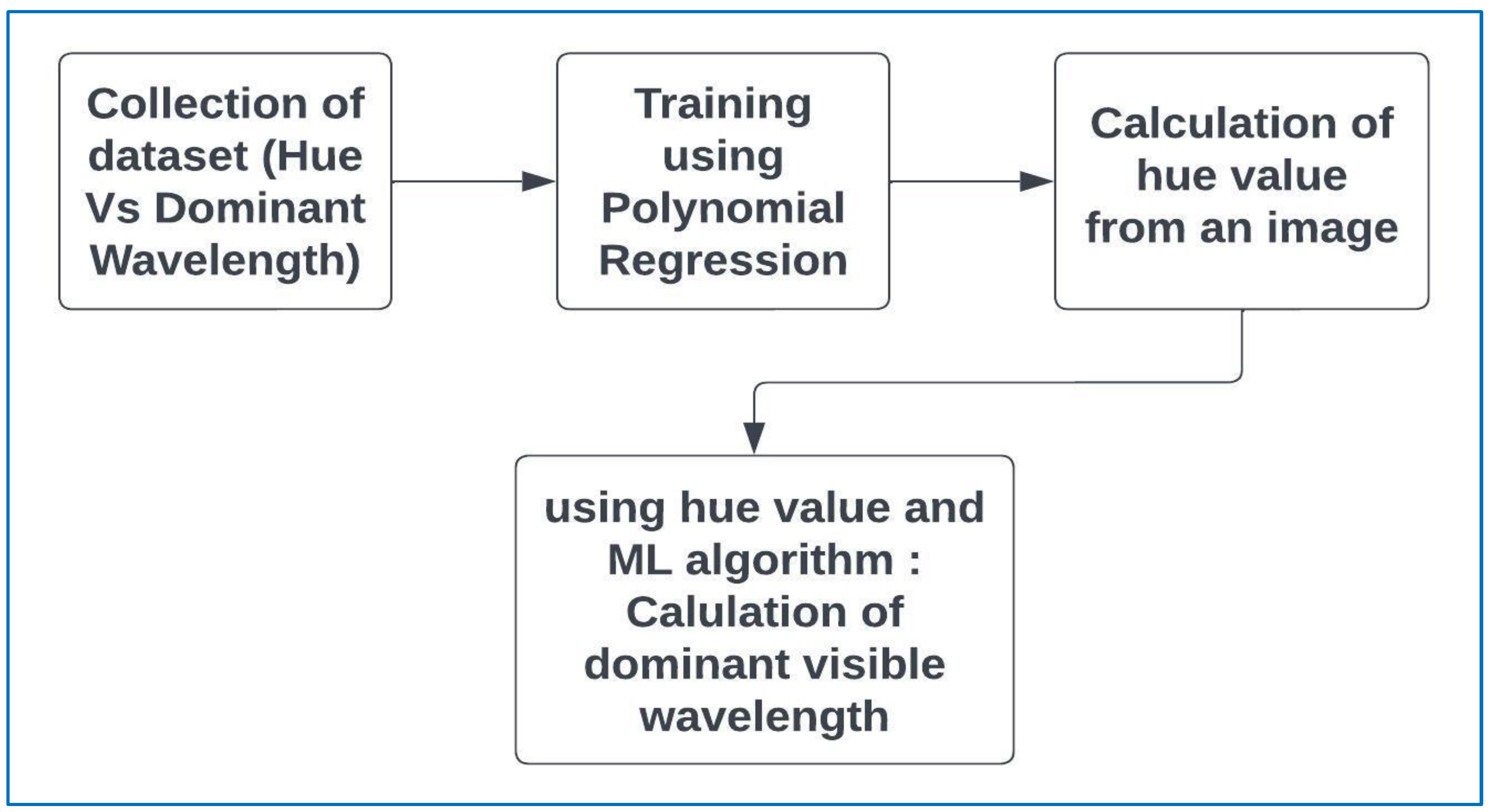
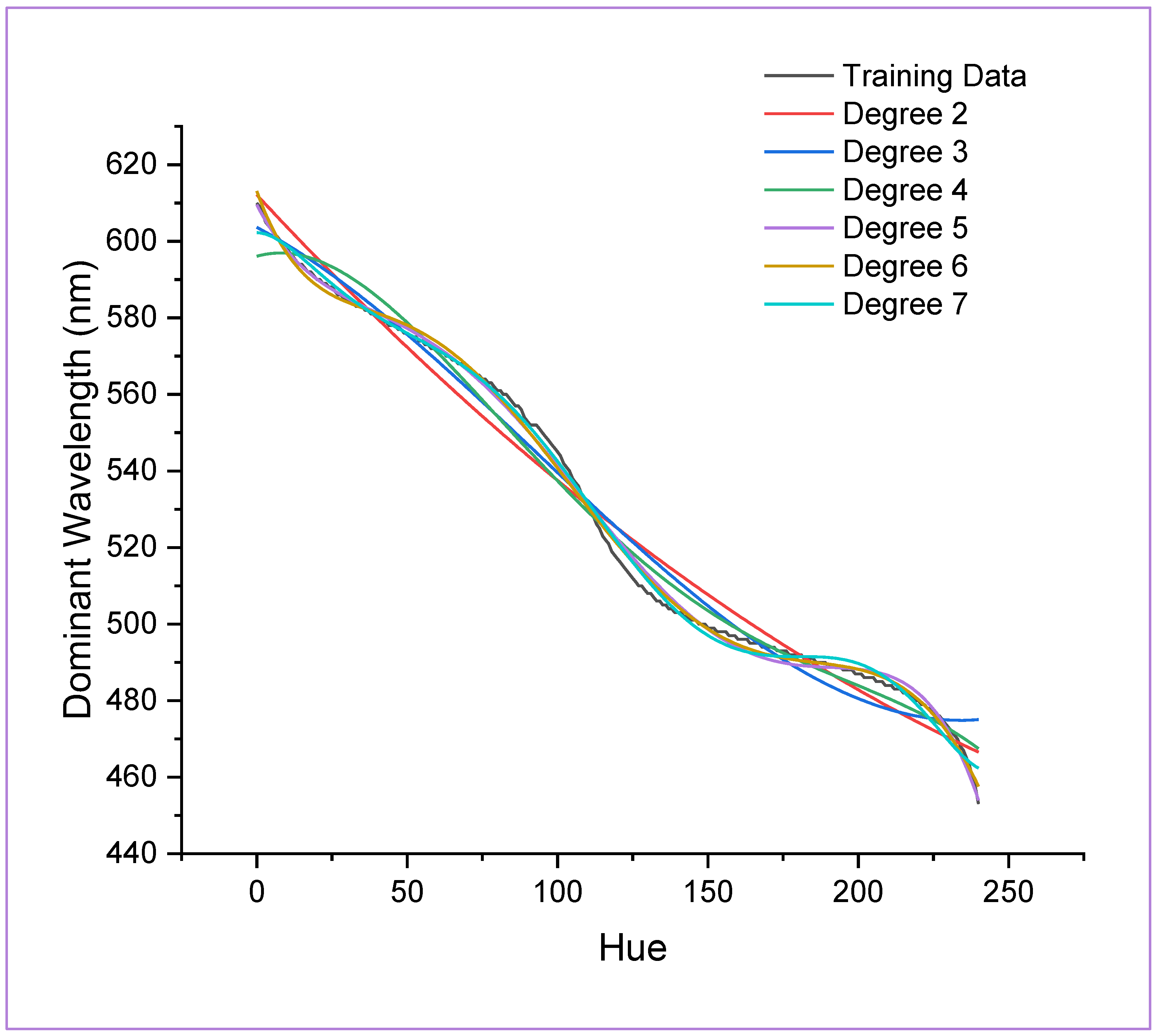
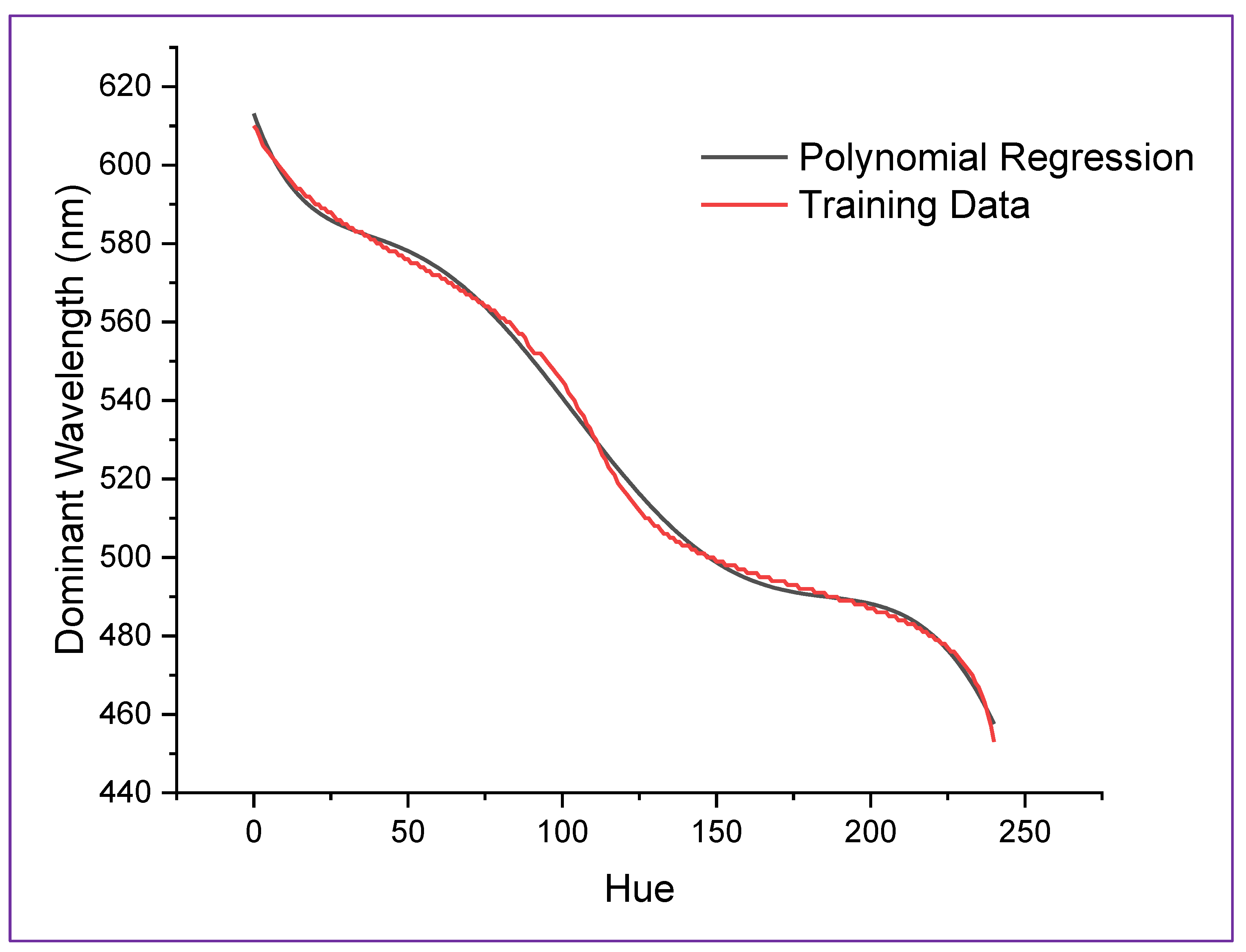
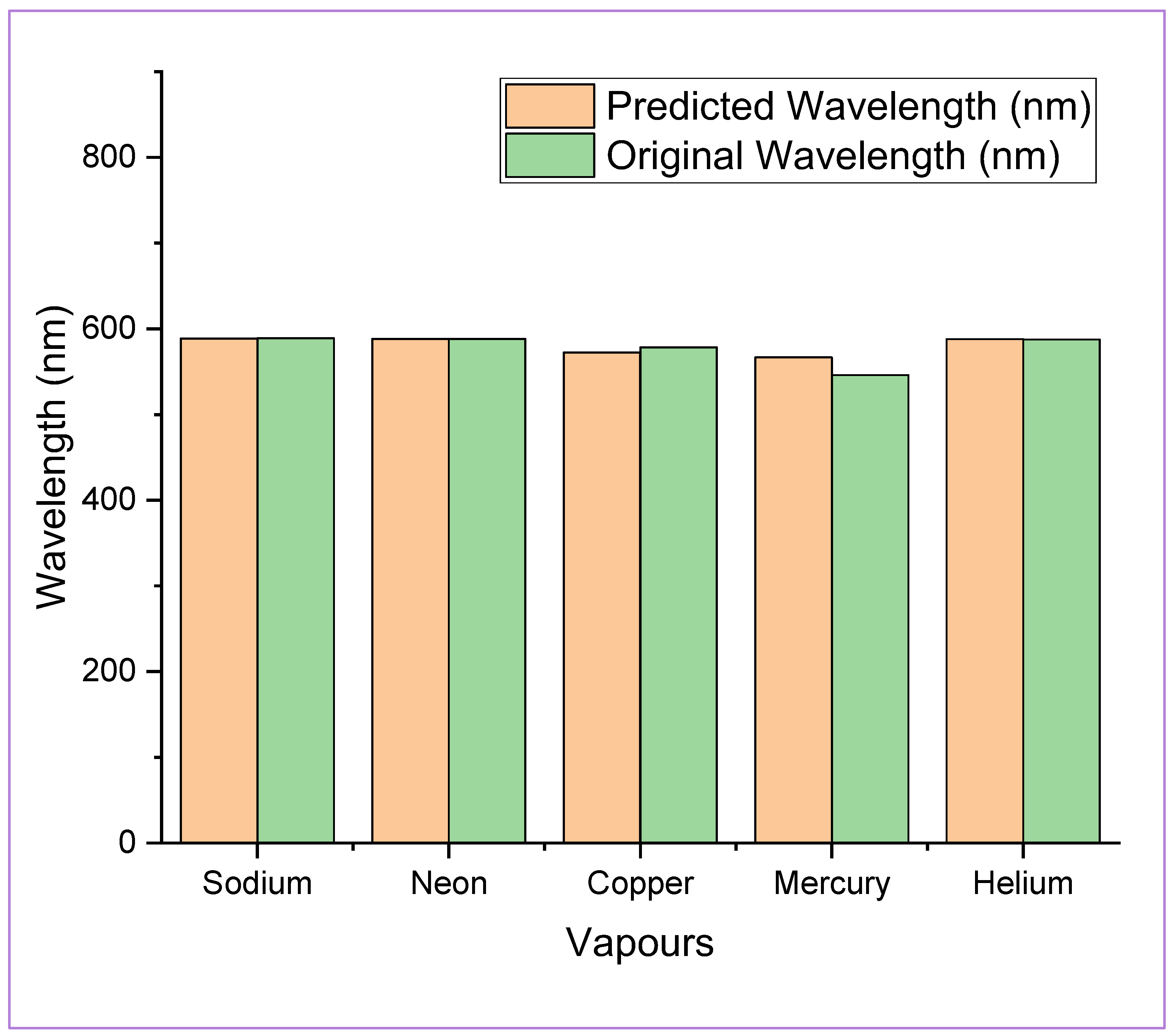
Feature	Specification
Technique	Atomic Absorption Spectroscopy (AAS)
Wavelength Range	190 nm to 900 nm
Spectral Bandwidth	0.1, 0.2, 0.4, 1.0, 2.0 nm (selectable)
Wavelength Accuracy	±0.25 nm
Wavelength Repeatability	±0.15 nm
Baseline Drift	≤0.005 Abs/30 min
Background Correction	Deuterium lamp background correction
Atomisation Methods	Flame Atomiser, Graphite Furnace Atomiser
Heating temperature range (Graphite Furnace)	Room temperature~2650 °C
Lamp Type	Hollow Cathode Lamp (HCL)
Number of Lamp Positions	8 (automatic turret)
Sample Types	Liquids, Solids
Precision (RSD)	≤3%
Software Compatibility	Windows Platform

for its features and specifications).

Artificial intelligence (AI) encompasses a broad spectrum of technologies and techniques aimed at enabling machines to mimic human cognitive functions, learn from data, and make autonomous decisions. Within the realm of AI, machine learning is a pivotal subfield that empowers systems to improve their performance on tasks through experience. One notable technique within machine learning is polynomial regression, which is a type of regression analysis where the relationship between the independent variable (or variables) and the dependent variable is modelled as an nth-degree polynomial function. Polynomial regression extends linear regression to capture more complex relationships between variables, making it particularly useful when the data do not follow a strictly linear pattern. By fitting a polynomial curve to the data points, polynomial regression enables AI systems to uncover intricate patterns and trends, thus enhancing their predictive capabilities. In the context of AI, polynomial regression finds applications in various domains, including finance, economics, engineering, and the sciences. For instance, in finance, polynomial regression can be employed to model stock price movements, considering factors beyond linear trends. Similarly, in climate science, it can aid in analysing the nonlinear relationships between atmospheric variables. Moreover, polynomial regression serves as a fundamental building block for more advanced AI techniques, such as neural networks. Neural networks often leverage polynomial regression as an activation function within their layers, allowing them to learn and represent nonlinear relationships in data. In summary, polynomial regression plays a crucial role in the AI landscape by enabling systems to model and understand nonlinear phenomena, thereby advancing their capabilities in prediction, decision-making, and pattern recognition.

The research begins by acquiring a dataset containing hue versus dominant wavelength values. In Van der Woerd and Wernand’s [48] study, the generation of the dataset, hue values, and corresponding wavelengths involves a multi-step process. Initially, 500 simulated satellite remote sensing reflectance (Rrs) spectra are utilised, and corrected for atmospheric influences and other optical properties. These Rrs spectra are functions of wavelength, representing the measured light intensity at different wavelengths. Tristimulus values are then determined through integrating Rrs with standard colorimetry two-degree Colour Matching Functions (CMFs), which serve as weighting functions based on the sensitivity of human vision to different wavelengths. For each sensor used in the study, such as SeaWiFS, MODIS, MERIS, OLCI, Landsat, and MSI, weights (M) are precalculated based on CMFs and the central wavelengths of each sensor’s spectral bands. These sensors typically have narrow spectral bands, ensuring the accurate measurement of Rrs at specific wavelengths. Subsequently, the offset for hue angles is determined by comparing the reconstructed sensor spectrum with the original hyperspectral spectrum. This comparison ensures the accuracy of hue angle calculations across different sensors. For instruments with broad spectral bands, such as the MSI on Sentinel-2 or MODIS 500-m product, which have a varying detection efficiency within each band described using the Spectral Response Function (SRF), a similar approach is followed. Weights are precalculated based on the mean wavelength of each band, and Rrs is derived by folding IOCCG and field spectra with the sensor’s SRF. This process allows for the determination of hue angles from the derived Rrs values, which are then compared with the original hyperspectral data to assess accuracy. In summary, the dataset, hue values, and corresponding wavelengths are generated through a meticulous process involving the correction of Rrs spectra, integration with CMFs, the pre-calculation of weights based on sensor characteristics, and the folding of spectra with sensor SRFs to derive Rrs values for each sensor band, ultimately allowing for the accurate determination of hue angles. In this study, a total of 241 data were used, with variations across different materials and their corresponding hue values being calculated. A breakdown of the dataset distribution for each light source could provide further insight into the distribution and composition of the samples. The hue value represents the colour information extracted from an image, while the dominant wavelength corresponds to the peak wavelength of the emitted light. This dataset serves as the foundation for establishing a mathematical relationship between hue values and dominant wavelengths.

To model this relationship, polynomial regression is initially applied to the dataset. To model the relationship between the independent variable X (representing the hue value) and the dependent variable y (representing the hue value of an image), we initially employed polynomial regression on the dataset. Polynomial regression is a statistical technique utilised to fit a polynomial function to observed data points, allowing us to capture potentially nonlinear relationships between variables.

In the provided code snippet that is

Table 2. Code snippet of polynomial regression.

Steps	Code	Comment
1.	X_train, X_test, y_train, y_test = train_test_split (X, Y, test_size = 0.2, random_state = 0)	Splitting the data into training and testing sets
2.	poly_reg = PolynomialFeatures (degree = 6)	Creating polynomial features with specified degree
3.	X_poly = poly_reg.fit_transform (X_train)	Transforming the training features into polynomial features
4.	pol_reg = LinearRegression ()	Initialising linear regression model
5.	pol_reg.fit (X_poly, y_train)	Fitting the polynomial features to the target variable

, the dataset is divided into training and testing sets using the “train_test_split” function, where X and Y represent the independent and dependent variables, respectively, with a test size of 20% and a specified random state for reproducibility.

In this study, polynomial regression models with degrees ranging from 2 to 5 are constructed and evaluated. However, upon analysis, it is observed that these models exhibit significant errors and fail to adequately capture the underlying patterns in the data.

Recognising the need for a more flexible and expressive model, a 6th-degree polynomial regression model is subsequently employed. The decision to increase the polynomial degree is motivated by the desire to capture higher-order relationships and finer details in the dataset. Remarkably, the 6th-degree polynomial regression model demonstrates improved performance, exhibiting better alignment with the dataset and reduced errors compared to lower-degree models. This highlights the importance of selecting an appropriate model complexity to accurately represent the underlying data distribution.

The successful implementation of the 6th-degree polynomial regression model lays the groundwork for further advancements in the research. With an effective mathematical model in place, the next step involves integrating machine learning algorithms to enhance the spectroscopic analysis process. Specifically, the developed model serves as a basis for training machine learning algorithms to predict dominant wavelengths based on hue values extracted from input images.

By combining polynomial regression with machine learning algorithms, the proposed methodology offered a framework for visible spectroscopy. This integrated approach leverages the strengths of both techniques, enabling accurate and efficient analysis of spectral data. The ML algorithms were integrated into another algorithm, which calculated the corresponding wavelength values based on hue values extracted from images of different vapours. The hue value is calculated using OpenCV framework. OpenCV calculates the hue value of an image using the HSV (Hue, Saturation, Value) colour space. In this colour space, hue represents the dominant wavelength of light, effectively denoting the colour itself. To calculate the hue value of an image, OpenCV first converts the image from the default BGR (Blue, Green, Red) colour space to HSV. This conversion separates the colour information from the brightness and intensity components, facilitating easier manipulation and analysis of colours. Once the image is in the HSV colour space, OpenCV extracts the hue component, which ranges from 0 to 179 degrees or 0 to 255, depending on the data type used. This hue component is essentially a measure of the colour’s position on the colour wheel, with red at 0 degrees, green at 120 degrees, and blue at 240 degrees. By isolating the hue component, OpenCV effectively quantifies the colour of each pixel in the image, providing a numerical representation of its hue. This combined approach enabled the ML model to accurately predict the dominant wavelengths associated with the hue values obtained from the input images. In simpler terms, the algorithm processed the images to extract hue values, which were then fed into the ML model to determine the corresponding wavelengths, as shown in Figure 1. This allowed the system to effectively analyse various vapour sources and provide accurate spectral information based on the visual data input.

In this study, machine learning algorithms were seamlessly integrated into an image processing framework, orchestrating the extraction of hue values from images capturing different vapours. This synergistic approach facilitated the ML model’s ability to make precise predictions regarding the predominant wavelengths corresponding to these hue values derived from the input imagery. The experiment encompassed the examination of sodium vapour, neon lamp, copper vapour laser, and helium vapour, where their respective hue values were utilised to deduce their dominant wavelengths, as shown in Figure 2. This methodological fusion empowered the system to adeptly scrutinise diverse vapour sources, harnessing visual data input to furnish valuable spectral insights.

The significance of this phase lies in its ability to bridge the gap between visual information and spectral data through a systematic and data-driven approach. By acquiring images of different vapours along with their known dominant wavelengths, researchers can establish a robust dataset for training ML algorithms. This dataset serves as a foundation for teaching the ML model to recognise and associate specific hue values extracted from the vapour images with their corresponding dominant wavelengths.

Moreover, the development of an algorithm to process these images and extract hue values adds a layer of sophistication to the analysis process. This algorithm plays a pivotal role in preprocessing the visual data and converting it into a format suitable for ML analysis. By calculating the hue values from the images, the algorithm provides quantitative inputs that can be directly fed into the ML model.

The integrated approach of combining image processing with ML techniques offers several significant advantages. It enables the ML algorithm to learn complex patterns and relationships between hue values and dominant wavelengths. Through iterative training on a diverse dataset of vapour images, the ML model can refine its predictions and improve its accuracy over time.

Combining polynomial regression with machine learning (ML) algorithms represents a powerful synergy that enhances the methodology for visible spectroscopy in several ways.

Firstly, polynomial regression provides a mathematical framework to model the relationship between hue values and dominant wavelengths. By fitting a polynomial function to the dataset, it captures the underlying patterns and trends in the spectral data. This allows for more accurate predictions of dominant wavelengths based on hue values extracted from images. The use of polynomial regression ensures that the model can effectively handle nonlinear relationships and complex spectral variations, which are common in visible spectroscopy.

On the other hand, ML algorithms bring additional capabilities to the methodology. These algorithms have the ability to learn from data, recognise patterns, and make predictions without being explicitly programmed. By integrating ML techniques, the methodology gains the advantages of adaptability and scalability. ML algorithms can iteratively refine their predictions based on new data, leading to continuous improvement in accuracy and performance over time. Moreover, ML algorithms can handle complex datasets with high dimensionality, making them well-suited for analysing diverse vapour sources with varying spectral characteristics. Unlike traditional spectroscopic methods that may be limited to specific types of samples or conditions, ML algorithms can generalise patterns across different vapour sources. This flexibility enables the methodology to accommodate a wide range of applications and scenarios, from industrial process monitoring to environmental sensing. Furthermore, the combination of polynomial regression with ML algorithms offers a robust framework for spectroscopic analysis. Polynomial regression provides a solid mathematical foundation, while ML algorithms add a layer of intelligence and adaptability. This dual approach ensures that the methodology is both accurate and versatile, capable of handling the complexities inherent in visible spectroscopy. Overall, through integrating polynomial regression with ML algorithms, the methodology for visible spectroscopy becomes more than the sum of its parts. It offers a comprehensive and effective framework for analysing spectral data, enhancing accuracy, and enabling the analysis of diverse vapour sources. This synergy between mathematical modelling and machine learning represents a significant advancement in spectroscopic techniques, with wide-ranging applications across various scientific and industrial fields.

4. Results and Discussions

In this study, polynomial regression models spanning degrees 2 to 5 were formulated and assessed. However, upon examination, it was noted that these models yielded notable errors and struggled to accurately depict the inherent patterns within the dataset. The resultant curves displayed a poor alignment with the data points, highlighting the constraints associated with the selected polynomial degrees, as illustrated in Figure 3.

According to Figure 3, the coefficient of determination for polynomial regression for the second degree is 97.77%, the third degree is 98.31%, the fourth degree is 98.69%, the fifth degree is 99.71%, the sixth degree is 99.77%, and the seventh degree is 99.72%. It can be seen that the fifth degree, sixth degree, and seventh degree polynomial regressions are equivalent. However, among all, the sixth degree of polynomial regression has the highest coefficient of determination. Notably, the sixth degree polynomial regression model highlights enhanced performance, displaying superior alignment with the dataset and diminished errors. For a more clear interpretation, the sixth degree polynomial regression has been shown with training data in Figure 4.

After applying sixth-degree polynomial regression, the machine learning model generates a curve, as shown in Figure 5.

Table 3. Comparison of dataset based wavelength i.e., training data (Van der Woerd and Wernand [48]) and ML-based wavelength i.e., polynomial regression.

Hue	Training Data [48]	Polynomial Regression	Hue	Training Data [48]	Polynomial Regression	Hue	Training Data [48]	Polynomial Regression
0	610	613.13	81	561	558.97	162	496	493.99
1	609	611.02	82	560	558.10	163	496	493.70
2	607	609.04	83	560	557.22	164	495	493.42
3	605	607.17	84	559	556.32	165	495	493.16
4	604	605.42	85	558	555.41	166	495	492.90
5	603	603.76	86	557	554.49	167	495	492.67
6	602	602.21	87	557	553.56	168	494	492.44
7	601	600.75	88	556	552.62	169	494	492.23
8	600	599.39	89	554	551.67	170	494	492.03
9	599	598.10	90	553	550.72	171	494	491.84
10	598	596.90	91	552	549.75	172	494	491.66
11	597	595.78	92	552	548.77	173	493	491.49
12	596	594.73	93	552	547.79	174	493	491.33
13	595	593.75	94	551	546.80	175	493	491.18
14	594	592.83	95	550	545.81	176	493	491.04
15	594	591.97	96	549	544.81	177	492	490.91
16	593	591.17	97	548	543.80	178	492	490.78
17	592	590.43	98	547	542.79	179	492	490.66
18	592	589.73	99	546	541.78	180	492	490.54
19	591	589.08	100	545	540.76	181	492	490.43
20	590	588.47	101	544	539.75	182	491	490.33
21	590	587.90	102	542	538.73	183	491	490.23
22	589	587.37	103	541	537.71	184	491	490.13
23	589	586.88	104	540	536.69	185	491	490.03
24	588	586.41	105	538	535.67	186	490	489.93
25	588	585.97	106	537	534.65	187	490	489.84
26	587	585.56	107	536	533.63	188	490	489.74
27	586	585.17	108	534	532.61	189	490	489.64
28	586	584.81	109	533	531.60	190	489	489.54
29	585	584.46	110	531	530.59	191	489	489.44
30	585	584.12	111	530	529.59	192	489	489.33
31	584	583.80	112	528	528.59	193	489	489.22
32	584	583.50	113	526	527.59	194	489	489.10
33	583	583.20	114	525	526.60	195	488	488.97
34	583	582.91	115	523	525.62	196	488	488.83
35	583	582.63	116	522	524.64	197	488	488.69
36	582	582.35	117	521	523.67	198	488	488.53
37	582	582.07	118	519	522.71	199	487	488.37
38	581	581.79	119	518	521.76	200	487	488.19
39	581	581.52	120	517	520.81	201	487	488.00
40	580	581.24	121	516	519.88	202	486	487.79
41	580	580.96	122	515	518.96	203	486	487.57
42	579	580.67	123	514	518.04	204	486	487.33
43	579	580.38	124	513	517.14	205	486	487.07
44	578	580.08	125	512	516.25	206	485	486.79
45	578	579.78	126	511	515.37	207	485	486.50
46	578	579.46	127	510	514.51	208	485	486.18
47	577	579.14	128	510	513.66	209	484	485.84
48	577	578.80	129	509	512.82	210	484	485.47
49	576	578.45	130	508	511.99	211	484	485.08
50	576	578.09	131	508	511.18	212	483	484.67
51	575	577.72	132	507	510.38	213	483	484.23
52	575	577.34	133	506	509.60	214	483	483.76
53	575	576.93	134	506	508.83	215	482	483.25
54	574	576.52	135	505	508.07	216	482	482.72
55	574	576.09	136	505	507.34	217	481	482.16
56	573	575.64	137	504	506.61	218	481	481.56
57	573	575.18	138	504	505.91	219	480	480.93
58	572	574.70	139	503	505.22	220	480	480.26
59	572	574.20	140	503	504.54	221	479	479.56
60	572	573.69	141	503	503.89	222	479	478.82
61	571	573.16	142	502	503.25	223	478	478.04
62	571	572.61	143	502	502.62	224	478	477.21
63	570	572.04	144	501	502.02	225	477	476.35
64	570	571.46	145	501	501.43	226	476	475.44
65	569	570.86	146	501	500.86	227	476	474.49
66	569	570.24	147	500	500.30	228	475	473.49
67	568	569.61	148	500	499.76	229	474	472.45
68	568	568.95	149	500	499.24	230	473	471.36
69	567	568.28	150	499	498.74	231	472	470.22
70	567	567.60	151	499	498.25	232	471	469.03
71	566	566.89	152	499	497.78	233	470	467.79
72	566	566.17	153	498	497.33	234	468	466.49
73	565	565.43	154	498	496.89	235	467	465.15
74	565	564.68	155	498	496.48	236	465	463.74
75	564	563.91	156	498	496.07	237	463	462.29
76	564	563.12	157	497	495.69	238	460	460.77
77	563	562.32	158	497	495.32	239	457	459.20
78	563	561.51	159	497	494.96	240	453	457.57
79	562	560.68	160	496	494.62
80	561	559.83	161	496	494.30

provides a comparison between the wavelengths in the dataset and the corresponding wavelengths at certain points after training. The results presented in

Table 4. Predicted wavelength of different vapours.

Vapour	Predicted Wavelength (nm)	Original Wavelength (nm)	Error Percentage
Sodium	588.73231	589	0.04%
Neon	588.14	588.2	0.01%
Copper	572.38412	578.2	1%
Mercury	566.5212	546.074	3.7%
Helium	587.97620	587.562	0.07%

indicate the performance of the proposed methodology in predicting the dominant wavelengths emitted by various vapour sources compared to their known or original values. The methodology involves a combination of polynomial regression and machine learning algorithms to analyse spectral data extracted from images.

The original wavelengths (in nm) for various vapour lamps are as follows: sodium (589), neon (588.2), copper (578.2), mercury (546.074), and helium (587.562) [22,23,24,25,26].

For sodium (Na), the predicted dominant wavelength is found to be 588.73231 nm, while the original value is 589 nm. This results in a very low error percentage of 0.04%, indicating a highly accurate prediction.

Similarly, for neon (Ne), the predicted wavelength is 588.14 nm, slightly lower than the original value of 588.2 nm, resulting in an error percentage of only 0.01%. This demonstrates a high level of precision in predicting the dominant wavelength of neon vapour.

However, for copper (Cu), there is a larger discrepancy between the predicted wavelength (572.38412 nm) and the original value (578.2 nm), resulting in an error percentage of 1%. While this error is relatively small, it suggests that there may be some limitations or challenges in accurately predicting the spectral characteristics of copper vapour using the current methodology.

The results for mercury (Hg) indicate a more significant error, with the predicted wavelength (566.5212 nm) deviating considerably from the original value (546.074 nm). The error percentage in this case is 3.7%, indicating that the methodology may struggle to accurately predict the dominant wavelength of mercury vapour, potentially due to the complex spectral characteristics of mercury emissions.

Lastly, for helium (He), the predicted wavelength (587.97620 nm) is very close to the original value of 587.562 nm, resulting in a relatively low error percentage of 0.07%. This indicates that the methodology performs well in predicting the dominant wavelength of helium vapour with a high level of accuracy.

Overall, the results, as shown in Table 1 and Figure 5, demonstrate the effectiveness of the proposed methodology in predicting the dominant wavelengths of vapour sources, with generally low error percentages across different elements. While some discrepancies exist, particularly for elements like copper and mercury, the methodology shows promise for a wide range of applications in visible spectroscopy. Further refinement and optimisation may be necessary to improve accuracy, particularly for elements with complex spectral characteristics.

This approach enhances the versatility and applicability of spectroscopic analysis. By leveraging image data, researchers can analyse vapour sources in real-world scenarios, capturing variations in lighting conditions, camera settings, and other environmental factors. This capability is particularly valuable for field applications where traditional spectroscopic instruments may be impractical or inaccessible.

Furthermore, the ability to accurately predict dominant wavelengths based on hue values extracted from vapour images holds immense potential for various scientific and industrial applications. For instance, in environmental monitoring, this methodology could be employed to identify and quantify pollutants or trace gases based on their spectral signatures. In material science, it could aid in the characterisation of materials based on their optical properties.

Overall, the integration of image processing and ML techniques in spectroscopic analysis represents a significant advancement with far-reaching implications. By leveraging visual data to enhance spectral analysis, researchers can unlock new insights into the composition, behaviour, and properties of vapour sources, paving the way for solutions in diverse fields.

5. Conclusions

In conclusion, the presented research offers a methodology for visible spectroscopy through integrating polynomial regression with machine learning algorithms. The results demonstrate the effectiveness of this approach in accurately predicting the dominant wavelengths emitted by various vapour sources. The methodology achieves low error percentages for most elements, indicating a high precision in wavelength prediction. Specifically, for sodium, neon, and helium, the error percentages are exceptionally low at 0.04%, 0.01%, and 0.07%, respectively. Despite minor discrepancies observed in elements like copper and mercury, with error percentages of 1% and 3.7%, respectively, the overall performance of the methodology remains good.

The combination of polynomial regression and machine learning provides a robust framework for spectroscopic analysis, enhancing the accuracy and versatility of the methodology. While some discrepancies exist, particularly for elements with complex spectral characteristics such as copper and mercury, overall, the methodology shows promise for a wide range of applications in visible spectroscopy.

Further refinement and optimisation may be necessary to improve accuracy, particularly for elements with challenging spectral profiles. Additionally, future research could explore the scalability of the methodology to analyse a broader range of vapour sources and its applicability in real-world scenarios.

Overall, this research represents a significant advancement in visible spectroscopy, offering a comprehensive and effective approach that holds promise for various scientific and industrial applications. With continued development and validation, the methodology has the potential to contribute to advancements in fields such as colorimetric assay, the analysis of transition metal complexes, and the analysis of natural pigments.