Abstract
The process of concrete production involves mixing cement, water, and other materials. The quantity of each of these materials results in a performance that is particularly estimated in terms of compressive or flexural strength. It has been observed that the final performance of concrete has a high variance and that traditional formulation methods do not guarantee consistent results. Consequently, designs tend to be over-designed, generating higher costs than required, to ensure the performance committed to the client. This study proposes the construction of predictive machine learning models to estimate compressive or flexural strength and concrete slump. The study was carried out following the Team Data Science Process (TDSP) methodology, using a dataset generated by the Colombian Ready Mix (RMX) company Cementos Argos S.A. over five years, containing the quantity of materials used for different concrete mixes, as well as performance metrics measured in the laboratory. Predictive models such as XGBoost and neural networks were trained, and hyperparameter tuning was performed using advanced techniques such as genetic algorithms to obtain three models with high performance for estimating compressive strength, flexural strength, and slump. This study concludes that it is possible to use machine learning techniques to design reliable concrete mixes that, when combined with traditional analytical methods, could reduce costs and minimize over-designed concrete mixes.
1. Introduction
1.1. Constituted Materials and Mixture Design of Concrete
After water, concrete is the most used material in the world with an annual production of approximately 4.1 billion tons of cement [1] and a consumption of around 14 billion cubic meters of concrete [2]. In per capita terms, cement production exceeds three times the production of steel or wood [3]. Since ancient times, concrete has been able to satisfy the needs for housing and infrastructure applications. Concrete is an easy-to-use material that is in a plastic state when freshly manufactured, allowing it to flow through formwork to acquire the designed shapes. It has a low price and can be manufactured in almost all regions of the planet [4]. Concrete production involves mixing various materials from different qualities based on pre-established designs depending on the desired performance properties and the characteristics of the materials available at the concrete plants [5].
Concrete is mainly composed of cement, supplementary cementitious materials such as fly ash, slag, clays, silica fume, fine aggregate, coarse aggregate, water, and chemical admixtures that allow modification of the characteristics of the mixture based on application needs. Cement is a binding material with adhesive and cohesive properties that allow it to bond different mineral fragments to form a compact structure with adequate strength and durability [6]. Once it comes into contact with water, the hydration process begins, undergoing a series of chemical reactions that lead to the formation of calcium silicate hydrates (C-S-H). This gel gains strength over time, transforming it into a compound with the mechanical properties necessary for structural applications.
Supplementary cementitious materials (SCMs) are alternative binders that allow the reduction of the amount of clinker used in blended cements or as cement substitutes in concrete production. Since the 1970s, quantifiable methods such as the cement factor have been developed [7], as well as more recent standards such as ASTM C618 [8], which allows the determination of the pozzolanic activity of fly ash or natural pozzolans for use in concrete, ensuring the correct performance of the mixes. Among these materials are fly ash (FA), natural pozzolans (NP) or artificial pozzolans (AP), silica fume (SF), and ground granulated blast furnace slag (GGBFS) [9].
Water is a component that enables the reaction in cement and imparts plasticity to concrete. The mixture of cementitious material and water is known as paste. During the hydration process, cement undergoes chemical reactions that give it the property of setting and hardening to form a solid material [6]. The proportion of the amount of water to the amount of cement is known as the water-to-cement ratio (w/c). This ratio represents one of the most determining and influential factors in concrete properties such as strength, slump, and durability.
Fine and coarse aggregates occupy between 60% and 75% of the volume of concrete and influence its properties in both fresh and hardened states [10]. Fine aggregate refers to natural sands or crushed rock with particle sizes smaller than 4.75 mm, while coarse aggregate consists of rocks with particle sizes larger than 4.75 mm; both can be extracted directly from rock formations or deposits transported by rivers. Aggregates must meet quality standards that guarantee their optimal use in concrete mixes, thus complying with characteristics of hardness, purity, durability, low clay content, or other fine materials that in large proportions can affect the hydration process and the bonding of the cement paste.
Chemical admixtures are used to control the physical and mechanical properties of concrete mixes in the fresh or hardened state. Understanding the effect of using admixtures in concrete mixes allows the achievement of optimal concrete performance, meeting required properties and contributing to durability in the hardened state [11]. Generally, admixtures are dosed based on the the amounts of cementitious materials, water, or aggregate depending on the intended use.
Concrete mix designs can vary depending on the availability of raw materials, physicochemical variations of the cement, climatic changes affecting aggregate moisture, and admixture technology, among other external conditions. These changes directly influence the physical and chemical properties of concrete in both the fresh and hardened states, sometimes resulting in high variability in the expected results for different designs. Compressive strength is one of the main mechanical characteristics of concrete. It is defined as the capacity to withstand a load per unit area, and many factors can influence compressive strength, such as cement content, cement type, aggregate quantities and quality, SMCs type, and temperature, among others [12]. Compressive strength can be evaluated in different ways; however, it is not only a lengthy process due to the number of variables but may also require intensive testing and qualified personnel [13].
While the optimization and automation of processes have been achieved by incorporating quality and production control software, the cement and concrete industry presents significant challenges for companies dedicated to their manufacture. One of the main difficulties in applying computational modeling techniques is the complexity of the physicochemical phenomena that govern the behavior of cement and concrete, as well as the high variability in their production processes. Consequently, there is a need to generate practical digital alternatives that allow for understanding the complexity of the products to generate solutions that guarantee their quality.
1.2. Artificial Intelligence Applied to Concrete Production
In recent years, the use of artificial intelligence techniques to estimate and model a wide range of problems has increased, especially in civil engineering [14]. In our review of the literature, we found the application of artificial intelligence techniques in the concrete production process. The central interest has focused on predicting compressive strength using supervised machine learning techniques. The use of artificial intelligence techniques and statistical approaches such as artificial neural networks [15], adaptive neuro-fuzzy inference systems (ANFIS) [16], genetic programming [17], support vector machines [18], regression or classification trees [19], and some ensemble methods [20], has been very relevant in predicting concrete compressive strength based on mix proportions [21]. This application is quite useful due to the complexity and uncertainty of its calculation, caused by the variable nature of the materials, the quality of the machinery, and the use of chemical and mineral admixtures.
In Table 1 and Table 2, the literature findings are summarized, identifying the variables to predict, describing the analyzed data, and outlining the methods applied.

Table 1.
Overview of AI techniques found in the literature for prediction of concrete strength.

Table 2.
Overview of AI techniques found in the literature for prediction of concrete slump.
Algorithms based on artificial intelligence techniques have proven to be relevant in exploring the properties of complex systems when there are sufficient data for training. This study presents a solution to forecast the compressive strength, flexural strength, and slump of concrete based on the quantities of the materials in the mix. For compressive strength, the best model identified was a single-hidden-layer multi-layer perceptron regressor with 134 units, achieving a mean absolute percentage error (MAPE) of 11.4% measured through cross-validation. For flexural strength, a single-hidden-layer multi-layer perceptron regressor with 178 units achieved a MAPE of 14%. Regarding slump, the best-performing model was a single-hidden-layer multi-layer perceptron regressor with 193 units, which achieved a MAPE of 7%. MAPE is calculated as shown in Equation (2), representing the average percentage error of the prediction relative to the actual value.
2. Materials and Methods
This project was developed following the TDSP methodology, which was developed by Microsoft and influenced by the classic methodology for data mining, the Cross-Industry Standard Process for Data Mining (CRISP-DM), and the agile framework of Scrum. This methodology includes best practices and structures from Microsoft and other industry leaders to help successfully implement data science initiatives [37]. TDSP provides a lifecycle to structure the development of data science projects.
2.1. Business Understanding
In this phase, collaboration with the client and other stakeholders is essential to comprehensively understand and identify the business challenges. Subsequently, it is imperative to pinpoint the data sources that aid in addressing the predefined questions aligned with the project’s objectives. Finally, key variables are specified as inputs to the model, alongside performance metrics, to gauge the project’s success [37].
Cementos Argos S.A. is committed to fostering a culture of innovation, research, and development to uphold its competitive edge and progress toward sustainability. To this end, it advocates for synergies between the cement and concrete industry challenges and academic solutions [38]. Despite the longstanding and widespread use of cement and concrete production processes, considerable uncertainty remains regarding the behavior of the final product in terms of setting, strength, and slump. This uncertainty primarily stems from the multitude of variables influencing product formulation and the limitations in the manufacturing process for measuring these variables. Due to the inherent properties of cement and concrete, the performance of the final product is often unknown until the mixture has fully cured, as there is a lack of reliable estimation models. This typically occurs several days after the initial mixing. Consequently, any adjustments to the quantities or characteristics of the materials used in the production process are subject to a certain delay [39].
2.1.1. Data Sources
The database used in this study was constructed from 2019 over a five-year period, containing the amount of material dosed to form different concrete mixes, as well as the flexural or compressive strength, and the slump measured at the plant’s laboratory from real production samples. For the development of the concrete compressive strength prediction model, an initial dataset with 20,108 records and 92 variables was used. For the flexural strength model, an initial dataset with 607 records and 92 variables was used. For the slump model, an initial dataset with 21,335 records and 92 variables was used. These datasets include, among others, the following input variables: The amount of free water; the amount of cement; the amount of fine aggregate, its moisture content, and its source; the amount of coarse aggregate, its moisture content, and its source; and the amount of SCMs. Regarding the admixtures used for concrete production, three groups were created: retarder, superplasticizer, and hydration controller, each with their respective amounts. The records include the plant code where the dosing process was carried out, along with the respective output variables for the predictive models: slump, flexural strength, or compressive strength after 28 days.
2.1.2. Solution Design and Performance Metrics
To solve the problem of predicting concrete quality from mixture characteristics, the solution design is shown in Figure 1. The data collected by the RMX company to predict the target variables are prepared by a cleaning process and a feature engineering. Then, the prepared data are used to create and compare the performance of several supervised machine learning methods. The comparison is made through error measurements in the predictions using a 10 fold-cross validation procedure.
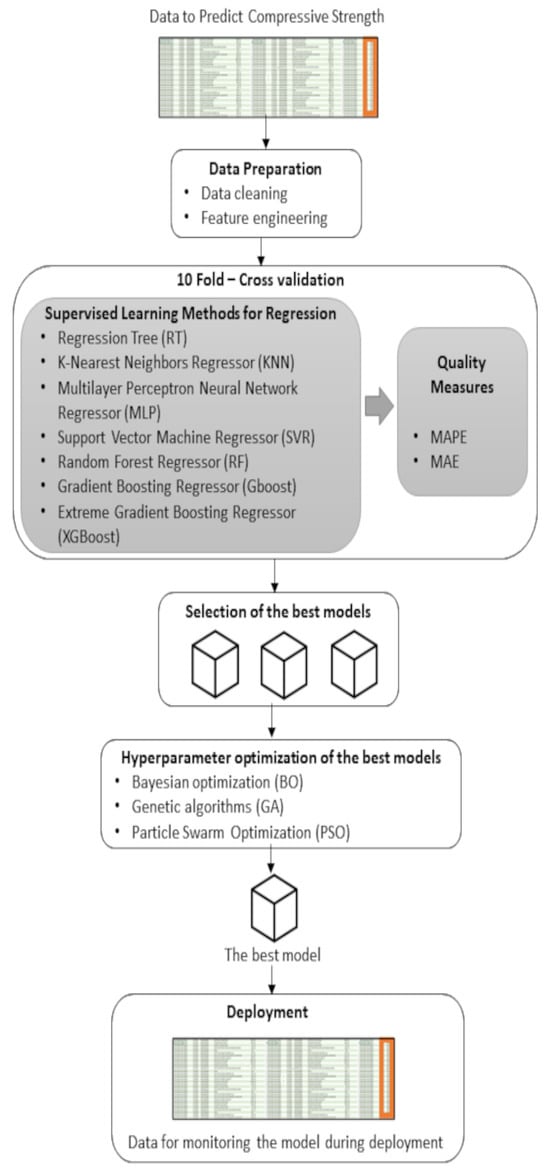
Figure 1.
Methodology for model training and evaluation.
To compare the results of the models, their predictive ability is measured using the mean absolute error (MAE), which measures the average magnitude of the errors in a set of predictions without considering their sign, and the MAPE, which expresses accuracy as a percentage of the error and can be easier to interpret than other accuracy measurement statistics.The mathematical formulae for these two evaluation metrics are shown in Equations (1) and (2).
The methods with the best performance are selected for a hyperparameter optimization process aimed at improving the predictive performance of the models. This optimization allows for finding the best configuration and selecting the prediction model with the best performance. Finally, the best model is deployed on a web platform, and its predictive capability is validated on a monitoring dataset over a new period of time.
This solution design is implemented using the Python (version 3.10.12) language and the libraries NumPy, pandas, Matplotlib, seaborn, scikit-learn, XGBoost, Scikit-Optimize, sklearn-genetic, and Joblib.
2.2. Data Acquisition and Understanding
There are three main tasks addressed in this stage. First, the data are made available in the target analytical environment. Once there, they are explored to determine if their quality is good enough to answer the objective question. Finally, a data pipeline is configured to process new data or update them periodically [37]. In this study, the data are accessed from a relational database in the cloud under the Azure SQL service, which is updated daily. Access is achieved from Google Colaboratory using the pyodbc and pandas packages. For the development of this project, data from a five-year period were taken, and the records from the first 55 months were used for training and the rest for monitoring.
2.2.1. Statistical Description of the Data
In a Google Colab notebook, each of the tables was loaded, and a general descriptive analysis of the data was performed. The number of rows and columns, data types, and the presence of empty records were reviewed. For numerical variables, the mean, standard deviation, minimum value, maximum value, and quartiles were calculated. For categorical variables, the unique values and their frequency distribution were listed. Subsequently, a quick analysis was performed using the Pandas Profiling package [40], which provides visualizations to help understand the distribution of each variable and generates alerts when a variable has only one value, is empty, has a high percentage of nulls or zeros, and when there are linear relationships between variables. With the information obtained and after conducting an analysis with experts in the field of concrete production, the data cleaning process was carried out.
2.2.2. Data Cleaning
To apply machine learning methods, different cleaning processes were developed for each of the tables containing information: According to the criteria of an expert in concrete mixes, columns that would not be useful for training the models were removed. Empty columns were removed. Duplicate records were removed. Adjustments were made to the quantities, as in some cases, where different units of measurement were used.
2.3. Modeling
In this phase, the objective is to create a machine learning model that predicts the target variable with the highest precision and is suitable for deployment in production. Three specific activities are undertaken to develop this stage: Feature engineering (data transformation and feature selection), model training (training the model and tuning its hyperparameters), and finally, evaluating whether the model performance meets production requirements [37].
2.3.1. Feature Engineering
- Data Transformation
In accordance with the specific recommendations provided by experts, the following adjustments were made to the datasets:
- Variables were grouped together because the components they represent are similar and only differ in brand or reference. The quantities of each grouped variable were summed to create a new single variable.
- All predictor variables were standardized to the production of one cubic meter of concrete. This was implemented by dividing each component quantity by the amount of concrete produced.
- For outlier treatment, quality rules established by concrete production experts were used.
- To facilitate model convergence, input variables were standardized using a standard scaler, and categorical variables were converted to numerical using a one hot encoder.
- Feature Selection
To define the input variables that are relevant in the model, linear and non-linear analyses of the input variables with respect to the target variable were conducted. For the relationship analysis, the mutual information measure was used to estimate both linear and non-linear relationships between variables. Additionally, a linear relationship analysis was performed using the Pearson correlation coefficient to observe dependencies between independent and perhaps not so independent variables.
2.3.2. Building of Predictive Models
The following models were trained using the training dataset:
- Regression Tree (RT): These divide the data into homogeneous subsets through binary partitions. The most discriminative variable is first selected as the root node to split the dataset into nodes or branches. The partitioning is repeated until the nodes are homogeneous enough to be definitive. Thus, in a tree structure, the terminal nodes (called leaves) represent class labels, and the branches represent conjunctions of features leading to those class labels [20].
- K-Nearest Neighbors Regressor (KNN): This method predicts for a given data point based on the average of the target values of the K-nearest neighbors. The main advantage of KNN regression is that it is simple to apply and can perform well in practice, especially if there is a clear pattern in the data. However, KNN regression can be computationally expensive as it requires calculating distances between all data points in the training set for each prediction [41].
- Multi-Layer Perceptron Neural Network Regressor (MLP): A computational model inspired by biological neural networks, featuring a layered organization of neurons where the input layer represents the predictor variables, the output layer represents the target variable, and the hidden layers perform nonlinear mappings of the data [42].
- Support Vector Machine Regressor (SVR): Constructs a hyperplane supported by as many data points as possible, called support vectors. They are known for using the kernel trick to increase the dimensionality of the data and achieve prediction [43].
- Random Forest Regressor (RF): Constructs a large number of decision trees at training time, and the prediction outputs are subjected to a vote by the individual trees. The basic concept behind this is that a group of weak classifiers can be joined together to build a strong prediction [44].
- Gradient Boosting Regressor (GBoost):Gradient boosting is an ensemble of multiple models, typically decision trees. The fundamental concept behind this algorithm is that each tree is trained using the errors (residuals) from all the preceding trees. Additionally, the negative gradient of the loss function in the current model is employed as an estimate for these errors in the boosted tree algorithm, which helps adjust the regression or classification tree [27].
- Extreme Gradient Boosting Regressor (XGBoost): It is a technique based on decision trees that takes into account data dispersion for approximate tree learning. It is a gradient boosting algorithm optimized through parallel processing, tree pruning, handling of missing values, and regularization to avoid overfitting and bias [45].
To select the models with the best performance, MAPE of the models was compared using a 10-fold cross-validation. The training sets are divided into 10 groups, selecting one as the test set in each iteration. The remaining 9 groups are used as the training set, and the model is trained and evaluated 10 times. The MAPE metric is calculated as the average of these 10 evaluations. Using 10-fold cross-validation can effectively avoid overfitting or underfitting and improve the reliability of the final prediction [23].
2.3.3. Model Optimization
The three models with the best performance were selected for a hyperparameter optimization process. The optimal combination of these values allows for maximizing the model’s performance and reducing the error percentage. Three optimization techniques were used: Bayesian optimization, genetic algorithms, and particle swarm optimization.
- Bayesian Optimization (BO):
In this case, the hyperparameter tuning can be viewed as the optimization of an unknown black-box function. Bayesian optimization works by assuming that the unknown function is sampled from a Gaussian process and maintains a posterior distribution for this function as observations are made, or in this case, as the results of running experiments of learning algorithms with different hyperparameters are observed. To choose the hyperparameters for the next experiment, one can optimize the expected improvement over the current best result or the upper confidence bound of the Gaussian process. This has been shown to be efficient in the number of experiments needed to find the global minimum of the black-box function [46]. This process was implemented using the BayesSearchCV function from the skopt (Scikit-Optimize) package.
- Genetic Algorithms (GA):
A genetic algorithm is a heuristic, biology-inspired approach based on the evolutionary process that represents an optimization procedure in a binary search space. It runs multiple times through an evolutionary cycle, which involves the selection of individuals, crossover to create offspring, and occasional mutation. After each cycle, the fitness function of each individual is calculated, and the best ones are selected to survive and reproduce. The process of generating new populations continues until a termination check is met, with the condition that each rule in the population satisfies a predefined fitness threshold [47]. The GASearch library was used for hyperparameter optimization in this case.
- Particle Swarm Optimization (PSO):
Inspired by the group behavior of bird flocks and fish schools, this method is based on collective intelligence. The algorithm consists of a group of particles moving through the search space, adjusting their positions based on their own experience and that of other particles. The goal is to find a solution that minimizes a given objective function. This is achieved through iterations, improving the position until no further improvement can be found or a maximum number of iterations is reached. PSO has been shown to have wide optimization capabilities due to its simple concept, easy implementation, scalability, robustness, and rapid convergence [48]. The pyswarm library was used for this purpose.
- Tuned Hyperparameters:
Table 3 shows the description of tuned hyperparameters.

Table 3.
Tuned Hyperparameters Description.
2.3.4. Model Evaluation
The final predictive models were evaluated to observe their generalization ability by measuring the mean absolute percentage error (MAPE) and mean absolute error (MAE) using a 10-fold cross-validation.
2.4. Deployment
The model and the data processing pipeline should be deployed in a production environment for consumption by the application [37]. This phase also includes monitoring the model in production to validate the operation of the deployed model and confirm that the pipeline meets the client’s requirements.
3. Results
The TDSP methodology enabled effective collaboration in a team composed of experts in machine learning and experts in concrete manufacturing. The results obtained in the different stages of the methodology are presented below.
3.1. Business Understanding
One of the objectives of the project developed by Cementos Argos S.A. was to reduce the over-design of concrete mixes, ensuring that the mix performance meets client expectations. This over-design stems from the uncertainty inherent in traditional models for concrete mix design. Figure 2 shows the difference between the final performance metrics (compressive strength, flexural strength, and slump) and those requested by the client (committed metrics). For compressive strength, a mode close to 10 MPa excess is observed; for flexural strength, a mode close to 1.2 MPa; and for slump, a mode of 20 mm. With this in mind, the following performance goals for predictive models can be defined: for compressive strength, an MAE less than 10 MPa; for flexural strength, an MAE less than 1.2 MPa; and for slump estimation, an MAE less than 20 mm. The literature review allowed us to define performance goals, as in the case of compressive strength prediction, where [27] concludes that a model with has a high level of accuracy. However, we consider that the results of other research are not comparable to ours due to the number of samples used to train and evaluate the models; whereas most studies barely reach a thousand samples, our study contains more than 20,000.
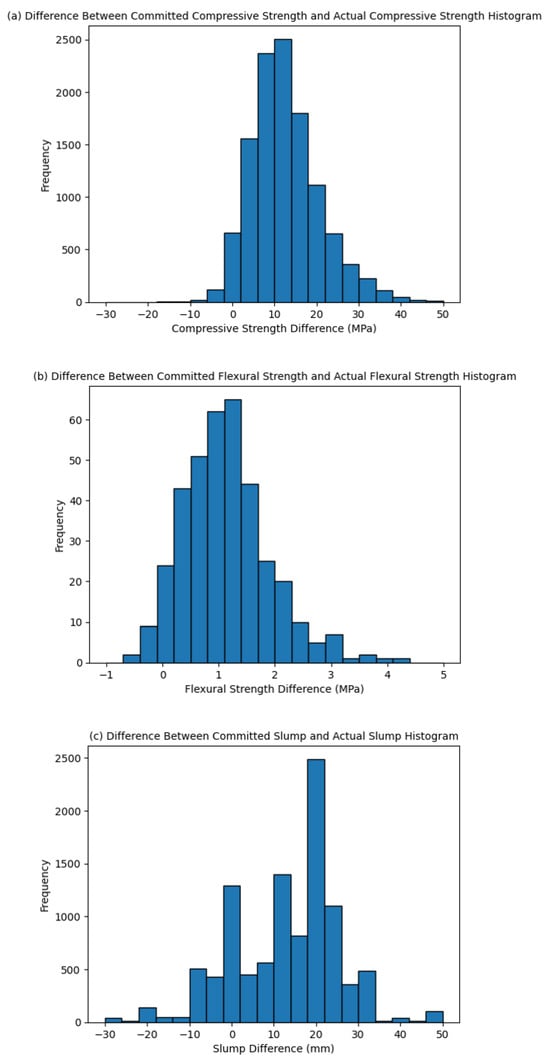
Figure 2.
(a) Compressive Strength Difference. (b) Flexural Strength Difference. (c) Slump Difference.
3.2. Data Acquisition and Understanding
Data from January 2019 to July 2023 are used to create the models, initially comprising 91 variables. The datasets contain 20,725 data records for building the compressive strength prediction model; 607 data records for building the flexural strength prediction model; and 21,335 data records for building the slump prediction model. Figure 3 shows the distributions of the output variables in each dataset.
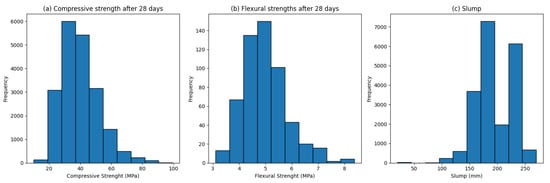
Figure 3.
(a) Compressive Strength Data Distribution. (b) Flexural Strength Data Distribution. (c) Slump Data Distribution.
To apply machine learning methods, it is necessary for the data to be of good quality, which is why outlier and null cleaning are performed. Outlier cleaning was carried out by evaluating quality rules defined by concrete production experts, as presented in Table 4. Records with values outside the established ranges were removed, as well as records that did not have a value for compressive strength, flexural strength, or slump.

Table 4.
Definition of maximum and minimum values for concrete components.
At the end of the data cleaning process, a dataset with 20,108 rows was obtained for the compressive strength model, a dataset with 551 rows for the flexural strength model, and a dataset with 20,662 rows for the slump model.
3.3. Modeling
3.3.1. Feature Engineering
The transformations applied to the variables are described below:
- Variables were grouped because the components they represent are similar and only differ in brand or reference. The quantities of each grouped variable were summed to create a new single variable. For example, instead of having three references for cement, a single variable called “Cement 1” was kept. Similarly, instead of having five references for a retarding admixture, a single variable called “Admixture_1 Retarding” was kept.
- Variables with zero values were removed.
- In order to observe the influence of different independent variables on the output variable, linear and non-linear relationship analyses were conducted using the mutual_info_regression method, this method quantifies the interdependence of two variables, a higher mutual information suggests a stronger correlation between the variables [49]. Unlike the linear correlation coefficient, mutual information is sensitive to dependencies that may not be apparent in the covariance [50]. For 28-day compressive strength, it was found that in addition to cement, retarding and superplasticizer admixtures, supplementary cementitious materials, and free water, there is also a relationship with the moisture content of the aggregates and their sources. In the case of 28-day flexural strength, the results are similar, but there is a stronger relationship with the superplasticizing admixtures than with the retarding agents, and there is a stronger relationship with the plant where the concrete is produced. Finally, in the prediction of slump, it was found that water has a stronger relationship than in the strength predictions.
- Pearson correlation was analyzed to detect dangerously high relationships between independent variables, verifying that there are no correlations greater than 0.8 or less than −0.8 between independent variables, unless they correspond to the quantity of aggregate and its moisture content from the same source. This way, the existence of redundant variables is ruled out.
- All independent variables were scaled to the production of one cubic meter of concrete.
At the end of the data transformation process, a dataset with 20,108 rows and 47 columns was obtained for the compressive strength model, a dataset with 551 rows and 41 columns for the flexural strength model, and a dataset with 20,662 rows and 47 columns for the slump model.
3.3.2. Predictive Models
A 10-fold cross-validation was performed over the training set to compare the predictive methods RT, KNN, MLP, support vector regressor SVR, RF, GBoost, and XGBoost in predicting compressive strength. An analysis of variance (ANOVA) was conducted to assess whether there are significant differences in the performance of the machine learning methods; however, there was not enough evidence to reject the null hypothesis that there are no significant differences between the methods. The same results were found using the Tukey method, where no significant differences were found between each pair of methods. Consequently, the methods were compared using boxplots (Figure 4), where a smaller spread suggests higher consistency in the model’s performance. It can be seen that RT and KNN have the highest errors. SVR has a very high error in one of the cross-validation iterations, which significantly increases its average MAPE. XGBoost has a median biased towards higher values, which could indicate the presence of outliers or a skewed distribution. Finally, the three methods with the best performance were selected: MLP, RF, and GBoost.
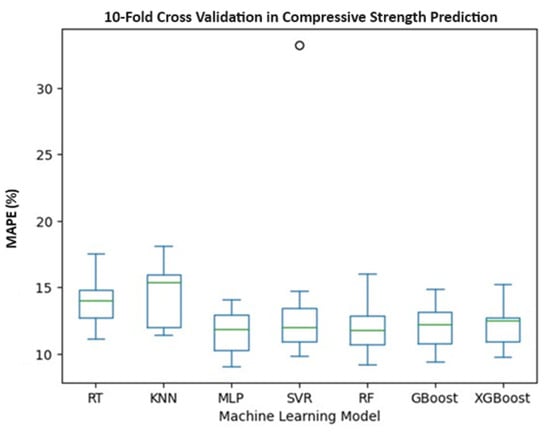
Figure 4.
Performance Comparison.
3.3.3. Hyperparameter Optimization
The MLP, RF, and GBoost models were selected to undergo a hyperparameter tuning process using the BO, GA, and PSO optimization algorithms. Finding the optimal combination of values for the training parameters helps maximize the model’s performance on the target dataset and reduce the error percentage.
Table 5, Table 6 and Table 7 present the values obtained for each of the hyperparameters in predicting 28-day compressive strength. Additionally, the MAPE value resulting from evaluating the final model on the test data is provided.

Table 5.
MLP Optimization Results.

Table 6.
RF Optimization Results.

Table 7.
GBoost Optimization Results.
For the RF algorithm, the hyperparameters obtained with GA are selected, resulting in a MAPE of 11.96%. For the MLP method, the hyperparameters obtained with GA are selected, resulting in a MAPE of 11.42%. Finally, for the GBoost method, the hyperparameters obtained with BO are selected, resulting in a MAPE of 12.1%. Figure 5 presents the results of the 10-fold cross-validation to compare the optimized predictive methods, where the model obtained with MLP is selected because it has the lowest MAPE and the smallest spread, suggesting higher consistency in the model’s performance.
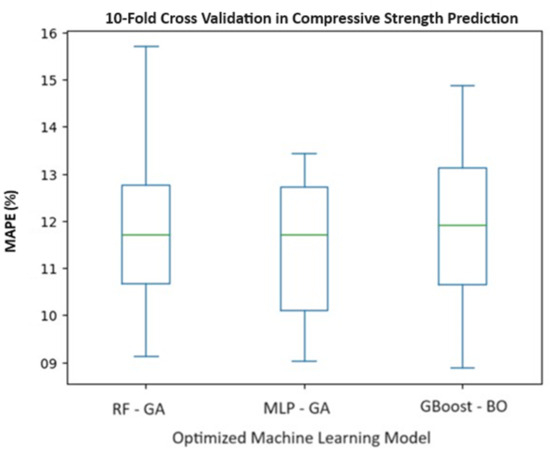
Figure 5.
10-Fold Cross Validation Optimized Models.
After determining that the MLP method optimized with GA achieved a lower MAPE in predicting compressive strength, an optimized MLP model with GA is created to predict flexural strength and slump. The evaluation metrics resulting from a cross-validation of the final models are presented in Table 8.

Table 8.
Final Model Description and Performance.
In the three predictive models, the differences between the errors in the training and test sets were found to be relatively small, suggesting that the model generalizes well to new data and does not suffer from overfitting. Overfitting occurs when a model fits too closely to the training data and does not generalize well to new data, which would be reflected in a significant discrepancy between performance in the training and test sets.
3.4. Deployment
To deploy the models, we developed three pipelines that include normalizing numerical variables (StandardScaler), creating dummy variables (OneHotEncoder), and applying the model (MLPRegressor), as shown in Figure 6.
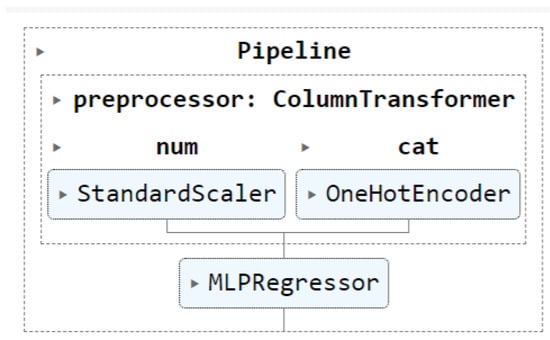
Figure 6.
Pipeline for Data Preparation and Model Application.
To validate the quality of the three models, we selected a monitoring dataset containing records from August to November 2023. The following figures present the prediction obtained by the final models vs. the actual values in the monitoring dataset. Ideally, the points on the graph should be close to the diagonal line, which represents a perfect prediction where the predicted value is exactly equal to the actual value. Alignment close to the diagonal indicates that the model is making accurate and reliable predictions. The dispersion around the diagonal line is normal due to the inherent limitations of any predictive model. The compressive strength (Figure 7) and flexural strength (Figure 8) graphs show a distribution along the diagonal, representing reliable predictions. In the slump graph (Figure 9), a distribution along the diagonal is also observed, except for 10 predictions that deviate considerably from the diagonal.
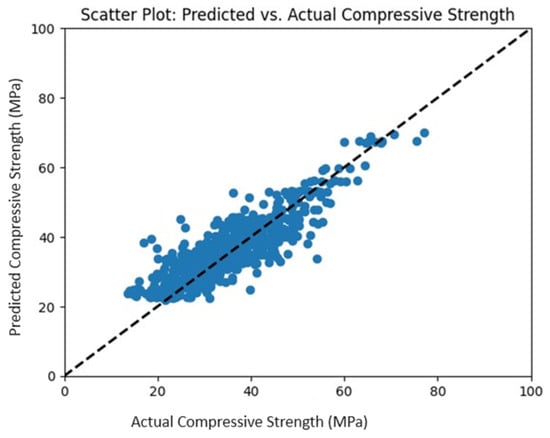
Figure 7.
Actual vs. Predicted Compressive Strength Applied on Test Data.
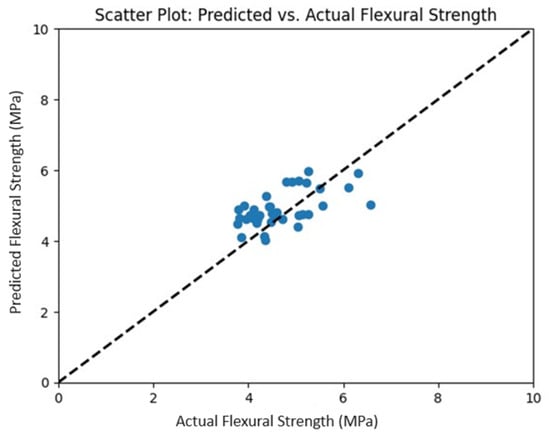
Figure 8.
Actual vs. Predicted Flexural Strength Applied on Test Data.
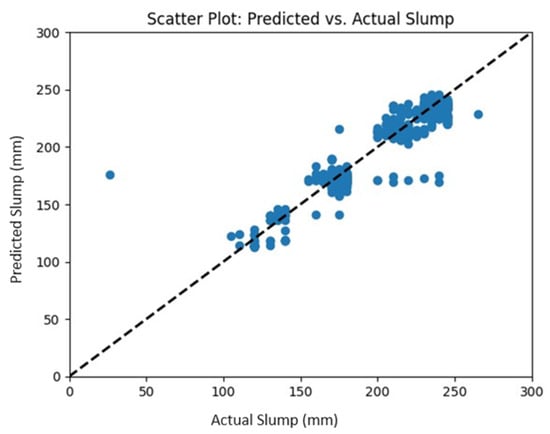
Figure 9.
Actual vs. Predicted Slump Applied on Test Data.
In the monitoring of the three models, points deviating from the diagonal can be observed through visual inspection, as they exhibit a significantly greater distance compared to the other data points. Predictive models applied to real-world data are subject to imperfections, which can manifest as discrepancies in the real vs. predicted value graph. The data collected from real-world sources often carry inherent noise and variability, which can obscure patterns and undermine prediction precision. Moreover, actual measurements of compression, flexion, and slump may be influenced by meteorological factors not considered in predictive models.
For deployment, a cloud-based prediction platform was implemented, operating as Software as a Service (SaaS). This platform contains the necessary information for the model’s operation, including a joblib file with the data processing pipeline and the trained prediction models. On this platform, users can input the amounts of concrete mixture and obtain the desired prediction results by clicking a button. It is important to highlight that this predictive-capable platform underwent socialization and validation with personnel from the concrete production field.
4. Discussion
Unlike other studies, the present study predicts, in addition to the traditional compressive strength of concrete, flexural strength and slump values.
For the estimation of compressive and flexural strength of concrete at 28 days, as well as slump, several supervised learning models (LR, RT, KNN, MLP, SVR, RF, GBoost, and XGBoost) were trained and their performance tested. Using cross-validation, MAPE was measured to assess the predictive abilities of each model. The results from the training phase indicated that the supervised learning models developed in this study performed well in predicting concrete performance variables. Among these models, the MLP model proved to be the most effective compared to the others. For compressive strength estimation, a MLP with a hidden layer of 134 units achieved a MAE of 4.3 MPa and MAPE of 11.4%. For flexural strength estimation, a MLP with a hidden layer of 178 units achieved a MAE of 0.7 MPa and MAPE of 14%. For slump estimation, an MLP with a hidden layer of 193 units achieved an MAE of 11.7 mm and MAPE of 7%.
Since the best method for predicting compressive strength was MLP and the best optimization technique was GA, MLP with GA optimization was selected to build the prediction model for flexural strength and slump. The performance of the models obtained demonstrated that this solution is valid, and models with acceptable performance can be obtained in less time than traditional model selection methods.
Instead of using the traditional grid search for hyperparameter tuning, we used different methods (GA, BO, PSO). The method that proved to optimize the hyperparameters most effectively was a GA.
The data acquisition and understanding phase has been crucial for the success of our study. We have leveraged an extensive dataset collected over a period of more than five years to train and validate our predictive models. The availability of detailed data on compressive strength, flexural strength, and slump has allowed us to develop robust and reliable models. Data cleaning and preparation have been critical aspects of our modeling process. The identification and removal of outliers and null values have ensured the integrity and quality of our datasets. Furthermore, the application of quality rules defined by experts in concrete production has improved the relevance and accuracy of our models.
In the modeling phase, feature engineering operations have allowed us to understand the influence of various independent variables on the performance properties of concrete. Using the mutual_info_regression method, we have identified linear and non-linear relationships between the independent variables and the target variables, including compressive strength, flexural strength, and slump of concrete. Our findings confirm that in addition to cement, other components such as retarding and superplasticizing admixtures, supplementary cementitious materials, and water also significantly influence the compressive and flexural strength of concrete. Furthermore, we have observed that the concrete production plant and the source of aggregates can also significantly affect these properties.
In order to compare our results with other articles, the and root mean square error (RMSE) measures were calculated. is a statistical measure quantifying the model’s ability to explain the variance in the target variable, representing its goodness-of-fit relative to the total variance in the data. The RMSE is a statistical measure representing the square root of the average of the squared errors between a model’s predictions and the actual values. A close to 1 indicates a good fit of the model to the data, while a low RMSE indicates good accuracy in the model’s predictions.
Our predictive model for 28-days-compressive strength, trained with 19,294 data instances, achieved = 0.79 and RMSE = 5.1 MPa in a 10-fold-cross-validation. In the study outlined in [27], where 1030 sets of concrete compressive strength were analyzed using 5-fold-cross-validation, a = 0.9 and a RMSE = 4.8 MPa were obtained. Our predictive model, trained with a significantly larger dataset, achieved similar performance in RMSE but lower in . However, we consider that the results of the other research are not comparable to ours due to the number of input variables and samples used to train and evaluate the models. Additionally, in the other research, the age of the concrete is an input instance, a variable that may have small values, favoring the measurement. Theoretically, higher concrete age is expected to result in lower predictive capability.
Our predictive model for 28-day flexural strength, trained with 514 data instances, yielded an = 0.69, RMSE = 0.57 MPa, and MAE = 0.7 MPa in 10-fold-cross-validation. Conversely, the study outlined in [31] reported an = 0.96, RMSE = 1.8 MPa, and MAE = 1.3 MPa in a 10-fold-cross-validation in the prediction of 28-days flexural strength using 173 data points. In the other research, a higher was achieved but with poorer RMSE and MAE values using a smaller dataset.
Finally, the predictive slump model, trained with 19,536 data instances, achieved = 0.84 and RMSE = 11.3 mm during 10-fold-cross-validation. In the study outlined in [35], modeling with a neural network on 103 data instances using a 70–30% train–test split yielded an of 0.95 and an RMSE of 2.781 cm (equivalent to 27.81 mm). We consider that the results are not directly comparable due to significant differences in the quantity of data. Nonetheless, our model achieved a lower RMSE compared to the neural network model in the cited study.
The models were deployed on a web platform, then were monitored on an independent dataset. In the monitoring of the final models, prediction vs. actual value graphs were created (Figure 7, Figure 8 and Figure 9). The proximity of the points to the diagonal line in these graphs indicates the accuracy and reliability of the predictions. Overall, a consistent distribution along the diagonal was observed in the compressive and flexural strength graphs, suggesting reliable predictions in these aspects. However, in the slump graph, although most predictions aligned with the diagonal, considerable deviations were identified in a small number of cases.
The and RMSE metrics were also calculated during the monitoring phase. In this phase the predictive model for compressive strength (Figure 7) obtained an of 0.77 and an RMSE of 5.0 MPa. This suggests that the model explains approximately 77% of the variability in the compressive strength data, which is acceptable given the low values of MAE = 4.36 MPa and MAPE = 11.41% in the cross-validation. During the monitoring of the flexural model (Figure 8), we obtained an of 0.73 and an RMSE of 0.55 MPa, which indicates that approximately 73% of the variability in the dependent variable can be explained by the prediction model. The low values of MAE = 0.7 MPa and MAPE = 14.05% in the cross-validation enhance the reliability of the model. Finally, during the slump model monitoring (Figure 9), we obtained an of 0.91 and RMSE of 9.9 MPa. This suggests that the model explains approximately 91% of the variability in slump data. The model’s quality is also verified by the MAE = 11.7 mm and MAPE = 7.27% obtained in the cross-validation. Given the strong performance of the slump prediction model, demonstrated by the high values of and low values of MAE and MAPE, the presence of 10 deviations in the predictions (Figure 9) could be attributed to either uncommon values in the input variables or atypical slump measurements, possibly influenced by factors not considered in the model, such as meteorological conditions.
For future research directions, several areas can be considered to expand and improve the scope and application of the developed predictive models. The incorporation of new variables is proposed, where the inclusion of additional variables such as environmental conditions, specific material characteristics, or production process details could enhance the predictive capacity of the models and offer a more comprehensive understanding of the factors influencing concrete properties. Additionally, the construction of an optimization tool is proposed to determine the quantity of components necessary for a concrete mix to achieve a desired strength or slump within specified constraints. In this regard, the use of a heuristic algorithm that uses the flexural or compressive strength estimator presented in this study as input is suggested.
5. Conclusions
In this study, predictive models were developed for concrete compressive strength, flexural strength, and slump values using various supervised learning techniques. The models were developed following the TDSP methodology. The following conclusions are drawn:
- Various supervised learning models were trained and tested to estimate compressive and flexural strength, as well as slump, revealing promising performance. Among these models, the MLP demonstrated superior efficacy in a 10-fold-cross-validation.
- The MLP model achieved an MAE of 4.36 MPa and an MAPE of 11.41% for compressive strength estimation, indicating its robust predictive power. The results are in line with the established objectives of an MAE below 10 MPa.
- The MLP model for flexural strength prediction achieved an MAE of 0.7 MPa and an MAPE of 14.05%. These results align with the established goal of achieving an MAE less than 1.2 MPa.
- The MLP model for slump prediction achieved an MAE of 11.7 mm and an MAPE of 7.27%. These findings are consistent with the target of achieving an MAE under 20 mm.
- Our approach differed from conventional methods by utilizing GA, BO, and PSO for hyperparameter tuning, with GA proving to be the most effective.
- Comparisons with other studies underscored our models’ competitive performance despite the differences in dataset size and attributes. While our models achieved comparable RMSE values, slight disparities in values were noted, likely attributed to dataset variations. Nonetheless, our predictive models for compressive strength, flexural strength, and slump exhibited promising accuracy and reliability.
- Regarding the datasets constructed for this study, it is important to highlight that in the observed studies, no comparable datasets were found with ours. Unlike our case, it is common to find that studies conclude that they need larger datasets.
- Finally, our study stands out from other research endeavors by executing the deployment process within a real-world environment. In the deployment phase, a meticulous process was executed to implement the predictive models in an operational environment.
Author Contributions
Conceptualization, J.F.V. and A.I.O.; data curation, J.F.V., A.I.O., N.A.O., and E.O.; formal analysis, J.F.V., A.I.O., and J.M.L.; funding acquisition, J.F.V. and A.I.O.; investigation, J.F.V., A.I.O., N.A.O., E.O., A.G., and J.M.L.; methodology, J.F.V., A.I.O., and E.O.; project administration, J.F.V. and A.I.O.; resources, J.F.V. and A.I.O.; software, J.F.V., A.I.O., N.A.O., and E.O.; supervision, J.F.V. and A.I.O.; validation, J.F.V., A.I.O., A.G., and J.M.L.; visualization, J.F.V. and A.I.O.; writing—original draft, J.F.V., A.I.O., N.A.O., and E.O.; writing—review and editing, J.F.V., A.I.O., A.G., and J.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Minciencias Colombia, grant number 193-2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article are proprietary industry data. However, a portion of the compressive strength dataset will be made available by the authors on request.
Conflicts of Interest
Author Ana Gómez was employed by the company Cementos Argos. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AP | Artificial pozzolans |
| BO | Bayesian optimization |
| CRISP-DM | Cross-Industry Standard Process for Data Mining |
| C-S-H | Calcium silicate hydrate |
| FA | Fly ash |
| GA | Genetic algorithm |
| GBoost | Gradient boosting |
| GGBFS | Ground granulated blast furnace slag |
| KNN | K-nearest neighbors |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MLP | Multi-layer perceptron regressor |
| NP | Natural pozzolans |
| PSO | Particle swarm optimization |
| RF | Random forest |
| RMX | Ready mix |
| RT | Regression trees |
| SaaS | Software as a Service |
| SCMs | Supplementary cementitious materials |
| SF | Silica fume |
| SVR | Support vector regressor |
| TDSP | The Team Data Science Process |
| XGBoost | Extreme gradient boosting |
References
- Cement Production Global 2023|Statista. Available online: https://www.statista.com/statistics/1087115/global-cement-production-volume/ (accessed on 4 November 2022).
- Cement and Concrete around the World. Available online: https://gccassociation.org/concretefuture/cement-concrete-around-the-world/ (accessed on 10 November 2022).
- Monteiro, P.J.; Miller, S.A.; Horvath, A. Towards sustainable concrete. Nat. Mater. 2017, 16, 698–699. [Google Scholar] [CrossRef] [PubMed]
- Damme, H.V. Concrete material science: Past, present, and future innovations. Cem. Concr. Res. 2018, 112, 5–24. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill Education: New York, NY, USA, 2014; pp. 95–108. [Google Scholar]
- Telechea, S.; Diego, S.; Tecnología del Concreto y del Mortero, 5ta Edición. Tecnolog 2001. Available online: https://www.academia.edu/49045048/ (accessed on 9 March 2024).
- Smith, I.A. The Design of Fly-Ash Concretes. Proc. Inst. Civ. Eng. 1967, 36, 769–790. [Google Scholar] [CrossRef]
- ASTM C618-23; Standard Specification for Coal Ash and Raw or Calcined Natural Pozzolan for Use in Concrete. American Society for Testing: West Conshohocken, PA, USA, 2023.
- Moreno, J.D. Materiales Cementantes Suplementarios y Sus Efectos en el Concreto. 2018. Available online: https://360enconcreto.com/blog/detalle/efectos-de-cementantes-suplementarios/ (accessed on 9 December 2023).
- Kosmatka, S.; Kerkhoff, B.; Panarese, W. Design and Control of Concrete Mixtures, EB001. In Design and Control of Concrete Mixtures; Canadian Portland Cement Association: Portland, ON, Canada, 2002; pp. 57–72. [Google Scholar]
- Nagrockienė, D.; Girskas, G.; Skripkiūnas, G. Properties of concrete modified with mineral additives. Constr. Build. Mater. 2017, 135, 37–42. [Google Scholar] [CrossRef]
- Osorio, J.D. Resistencias del Concreto|ARGOS 360. 2019. Available online: https://www.360enconcreto.com/blog/detalle/resistencia-mecanica-del-concreto-y-compresion (accessed on 10 November 2022).
- Nguyen, T.T.; Duy, H.P.; Thanh, T.P.; Vu, H.H. Compressive Strength Evaluation of Fiber-Reinforced High-Strength Self-Compacting Concrete with Artificial Intelligence. Adv. Civ. Eng. 2020, 2020, 3012139. [Google Scholar] [CrossRef]
- Azizifar, V.; Babajanzadeh, M. Compressive Strength Prediction of Self-Compacting Concrete Incorporating Silica Fume Using Artificial Intelligence Methods. Civ. Eng. J. 2018, 4, 1542. [Google Scholar] [CrossRef]
- Hassoun, M.H.; Intrator, N.; McKay, S.; Christian, W. Fundamentals of Artificial Neural Networks. Proc. IEEE 1996, 10, 137. [Google Scholar] [CrossRef]
- Chen, S.C.; Le, D.K.; Nguyen, V.S. Adaptive Network-Based Fuzzy Inference System (ANFIS) Controller for an Active Magnetic Bearing System with Unbalance Mass. Lect. Notes Electr. Eng. 2014, 282 LNEE, 433–443. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.; Saitta, L. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Grajski, K.A.; Breiman, L.; Prisco, G.V.D.; Freeman, W.J. Classification of EEG spatial patterns with a tree-structured methodology: CART. IEEE Trans. Bio-Med. Eng. 1986, 33, 1076–1086. [Google Scholar] [CrossRef] [PubMed]
- Young, B.A.; Hall, A.; Pilon, L.; Gupta, P.; Sant, G. Can the compressive strength of concrete be estimated from knowledge of the mixture proportions?: New insights from statistical analysis and machine learning methods. Cem. Concr. Res. 2019, 115, 379–388. [Google Scholar] [CrossRef]
- Ahmad, M.; Hu, J.L.; Ahmad, F.; Tang, X.W.; Amjad, M.; Iqbal, M.J.; Asim, M.; Farooq, A. Supervised Learning Methods for Modeling Concrete Compressive Strength Prediction at High Temperature. Materials 2021, 14, 1983. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zhou, M.; Yuan, H.; Sabri, M.M.S.; Li, X. Prediction of the Compressive Strength for Cement-Based Materials with Metakaolin Based on the Hybrid Machine Learning Method. Materials 2022, 15, 3500. [Google Scholar] [CrossRef]
- Moradi, N.; Tavana, M.H.; Habibi, M.R.; Amiri, M.; Moradi, M.J.; Farhangi, V. Predicting the Compressive Strength of Concrete Containing Binary Supplementary Cementitious Material Using Machine Learning Approach. Materials 2022, 15, 5336. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Salami, B.A.; Jamal, A.; Amin, M.N.; Usman, M.; Al-Faiad, M.A.; Abu-Arab, A.M.; Iqbal, M. Prediction Models for Estimating Compressive Strength of Concrete Made of Manufactured Sand Using Gene Expression Programming Model. Materials 2022, 15, 5823. [Google Scholar] [CrossRef] [PubMed]
- Silva, V.P.; de Alencar Carvalho, R.; da Silva Rêgo, J.H.; Evangelista, F. Machine Learning-Based Prediction of the Compressive Strength of Brazilian Concretes: A Dual-Dataset Study. Materials 2023, 16, 4977. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Tang, Z.; Kang, Q.; Zhang, X.; Li, Y. Machine Learning-Based Method for Predicting Compressive Strength of Concrete. Processes 2023, 11, 390. [Google Scholar] [CrossRef]
- Kumar, A.; Arora, H.C.; Kapoor, N.R.; Mohammed, M.A.; Kumar, K.; Majumdar, A.; Thinnukool, O. Compressive Strength Prediction of Lightweight Concrete: Machine Learning Models. Sustainability 2022, 14, 2404. [Google Scholar] [CrossRef]
- Ali, A.; Riaz, R.D.; Malik, U.J.; Abbas, S.B.; Usman, M.; Shah, M.U.; Kim, I.H.; Hanif, A.; Faizan, M. Machine Learning-Based Predictive Model for Tensile and Flexural Strength of 3D-Printed Concrete. Materials 2023, 16, 4149. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Akmal, U.; Shah, S.A.; Salmi, A.; Awad, Y.A.; Shah, L.A.; Iftikhar, Y.; Javed, M.H.; Khan, M.I. Application of Machine Learning Techniques for Predicting Compressive, Splitting Tensile, and Flexural Strengths of Concrete with Metakaolin. Materials 2022, 15, 5435. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Wu, R.; Sufian, M.; Kahla, N.B.; Atig, M.; Deifalla, A.F.; Accouche, O.; Azab, M. Flexural Strength Prediction of Steel Fiber-Reinforced Concrete Using Artificial Intelligence. Materials 2022, 15, 5194. [Google Scholar] [CrossRef] [PubMed]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Cihan, M.T. Prediction of Concrete Compressive Strength and Slump by Machine Learning Methods. Adv. Civ. Eng. 2019, 2019, 3069046. [Google Scholar] [CrossRef]
- Zhang, X.; Akber, M.Z.; Zheng, W. Predicting the slump of industrially produced concrete using machine learning: A multiclass classification approach. J. Build. Eng. 2022, 58, 104997. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, J.; Zhang, Y.; Fu, L.; Luo, Y.; Liu, Y.; Li, L. Research on Hyperparameter Optimization of Concrete Slump Prediction Model Based on Response Surface Method. Materials 2022, 15, 4721. [Google Scholar] [CrossRef] [PubMed]
- Jaf, D.K.I. Soft Computing and Machine Learning-Based Models to Predict the Slump and Compressive Strength of Self-Compacted Concrete Modified with Fly Ash. Sustainability 2023, 15, 11554. [Google Scholar] [CrossRef]
- Jani, M. What Is the Team Data Science Process? 2022. Available online: https://learn.microsoft.com/en-us/azure/architecture/ai-ml/ (accessed on 9 March 2024).
- ARGOS. Centro Argos Para la Innovación. 2021. Available online: https://argos.co/centro-argos-para-la-innovacion/ (accessed on 29 May 2022).
- Osorio, J.D. Resistencia mecáNica del Concreto y Resistencia a la Compresión. 2018. Available online: https://360enconcreto.com/blog/detalle/resistencia-mecanica-del-concreto-y-compresion/ (accessed on 7 December 2023).
- PyPI. Pandas-Profiling. 2023. Available online: https://pypi.org/project/pandas-profiling/ (accessed on 9 March 2024).
- Singh, A. KNN Algorithm: Guide to Using K-Nearest Neighbor for Regression. 2023. Available online: https://www.analyticsvidhya.com/blog/2018/08/k-nearest-neighbor-introduction-regression-python/ (accessed on 9 March 2024).
- Lek, S.; Park, Y.S. Artificial Neural Networks. In Encyclopedia of Ecology, Five-Volume Set; PHI Learning Pvt. Ltd.: Delhi, India, 2008; pp. 237–245. [Google Scholar] [CrossRef]
- Gholami, R.; Fakhari, N. Support Vector Machine: Principles, Parameters, and Applications. In Handbook of Neural Computation; Academic Press: Cambridge, MA, USA, 2017; pp. 515–535. [Google Scholar] [CrossRef]
- Shrivastava, D.; Sanyal, S.; Maji, A.K.; Kandar, D. Bone cancer detection using machine learning techniques. In Smart Healthcare for Disease Diagnosis and Prevention; Academic Press: Cambridge, MA, USA, 2020; pp. 175–183. [Google Scholar] [CrossRef]
- Morde, V. XGBoost Algorithm: Long May She Reign! 2019. Available online: https://towardsdatascience.com/https-medium-com-vishalmorde-xgboost-algorithm-long-she-may-rein-edd9f99be63d (accessed on 10 November 2023).
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Hamdia, K.M.; Zhuang, X.; Rabczuk, T. An efficient optimization approach for designing machine learning models based on genetic algorithm. Neural Comput. Appl. 2021, 33, 1923–1933. [Google Scholar] [CrossRef]
- Qolomany, B.; Maabreh, M.; Al-Fuqaha, A.; Gupta, A.; Benhaddou, D. Parameters optimization of deep learning models using Particle swarm optimization. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference, IWCMC 2017, Valencia, Spain, 26–30 June 2017; pp. 1285–1290. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, X.; Shi, L.; Gong, L. Time Series Feature Selection Method Based on Mutual Information. Appl. Sci. 2024, 14, 1960. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E—Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2004, 69, 16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).