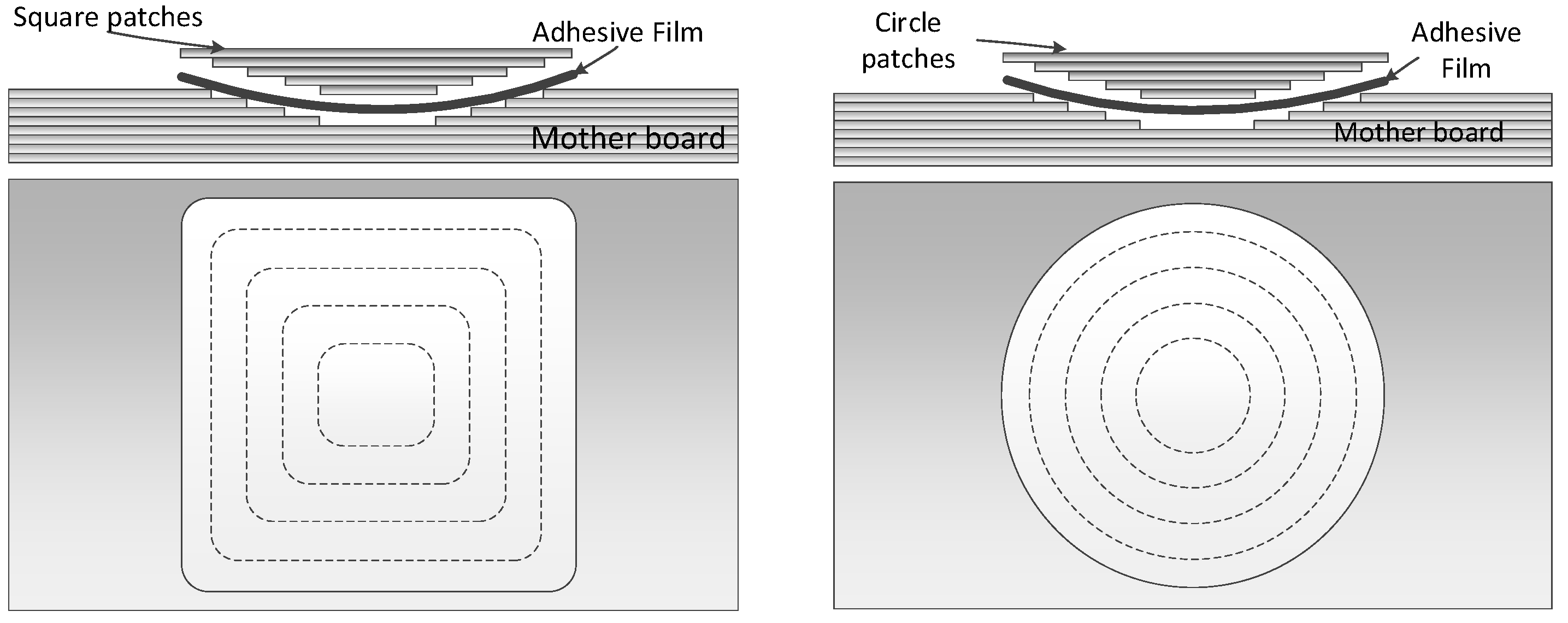
Figure 1.
Different shapes of composite material repair patches.
Figure 1.
Different shapes of composite material repair patches.
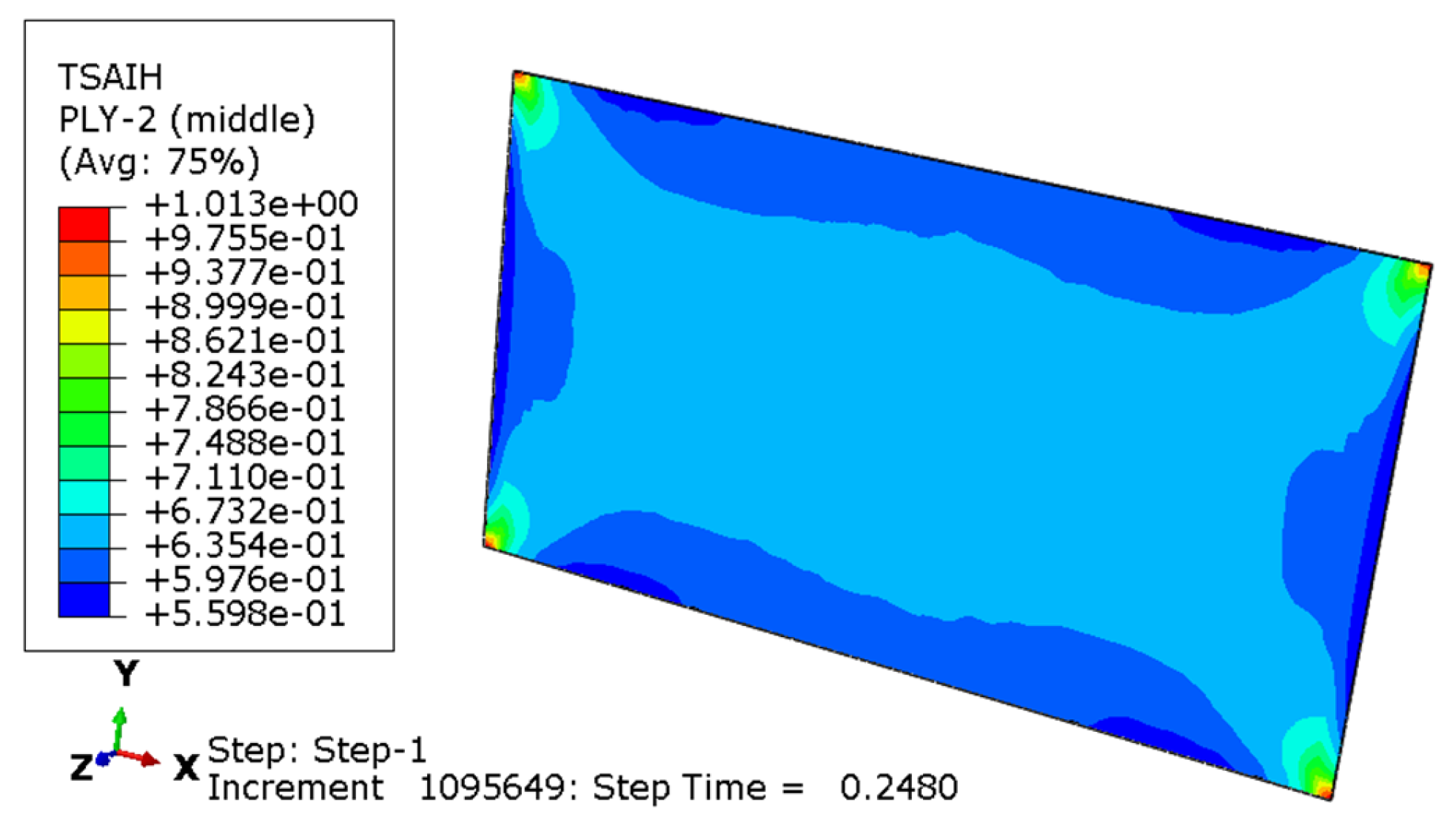
Figure 2.
The first layer’s failure coefficient cloud map.
Figure 2.
The first layer’s failure coefficient cloud map.
Figure 3.
The second layer’s failure coefficient cloud map.
Figure 3.
The second layer’s failure coefficient cloud map.
Figure 4.
The third layer’s failure coefficient cloud map.
Figure 4.
The third layer’s failure coefficient cloud map.
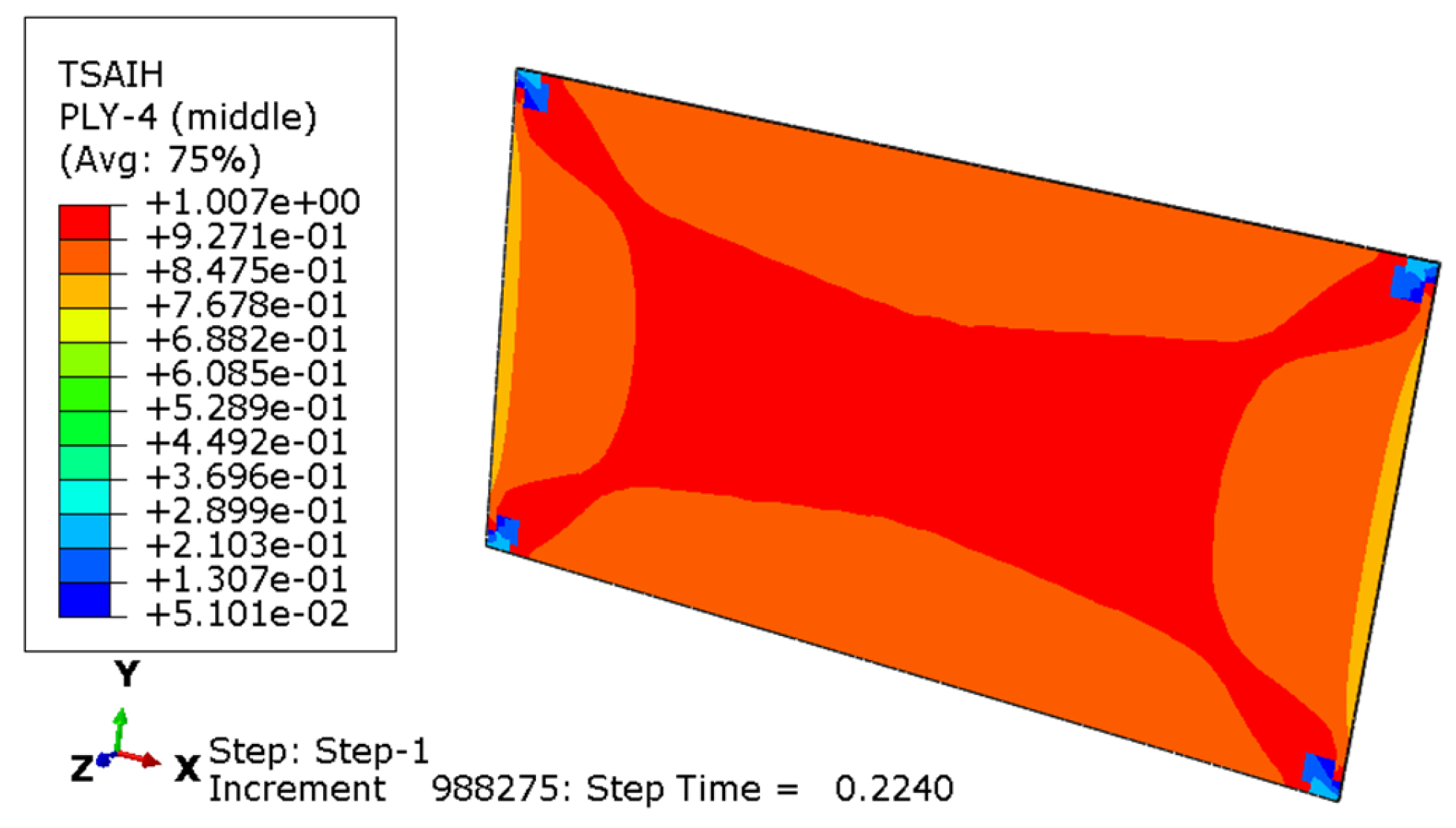
Figure 5.
The fourth layer’s failure coefficient cloud map.
Figure 5.
The fourth layer’s failure coefficient cloud map.
Figure 6.
The force–displacement curve of healthy composite laminates.
Figure 6.
The force–displacement curve of healthy composite laminates.
Figure 7.
Rectangular perforated panel and its patch.
Figure 7.
Rectangular perforated panel and its patch.
Figure 8.
Circle perforated panel and its patch.
Figure 8.
Circle perforated panel and its patch.
Figure 9.
Experimental equipment condition.
Figure 9.
Experimental equipment condition.
Figure 10.
Experimental specimen loading condition.
Figure 10.
Experimental specimen loading condition.
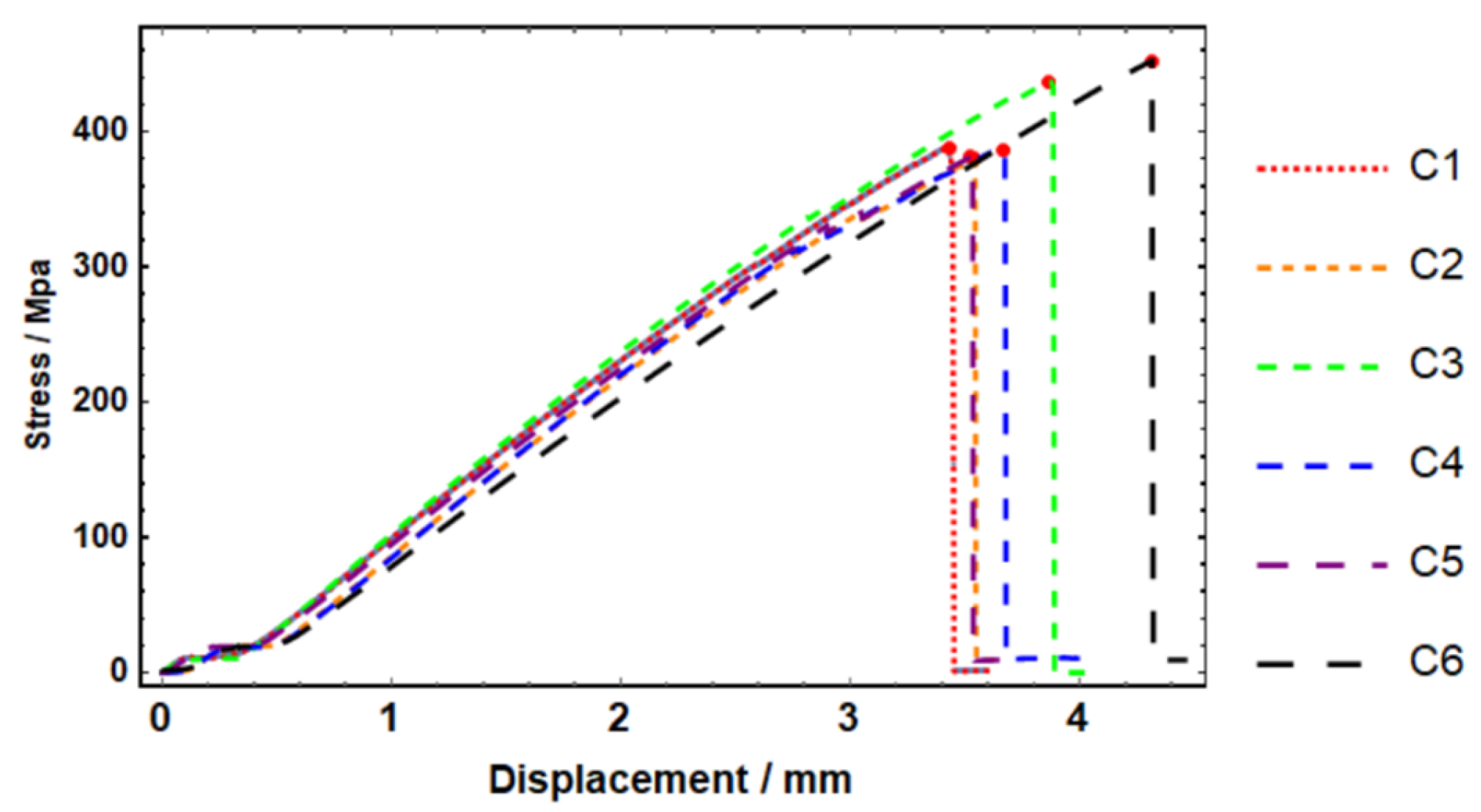
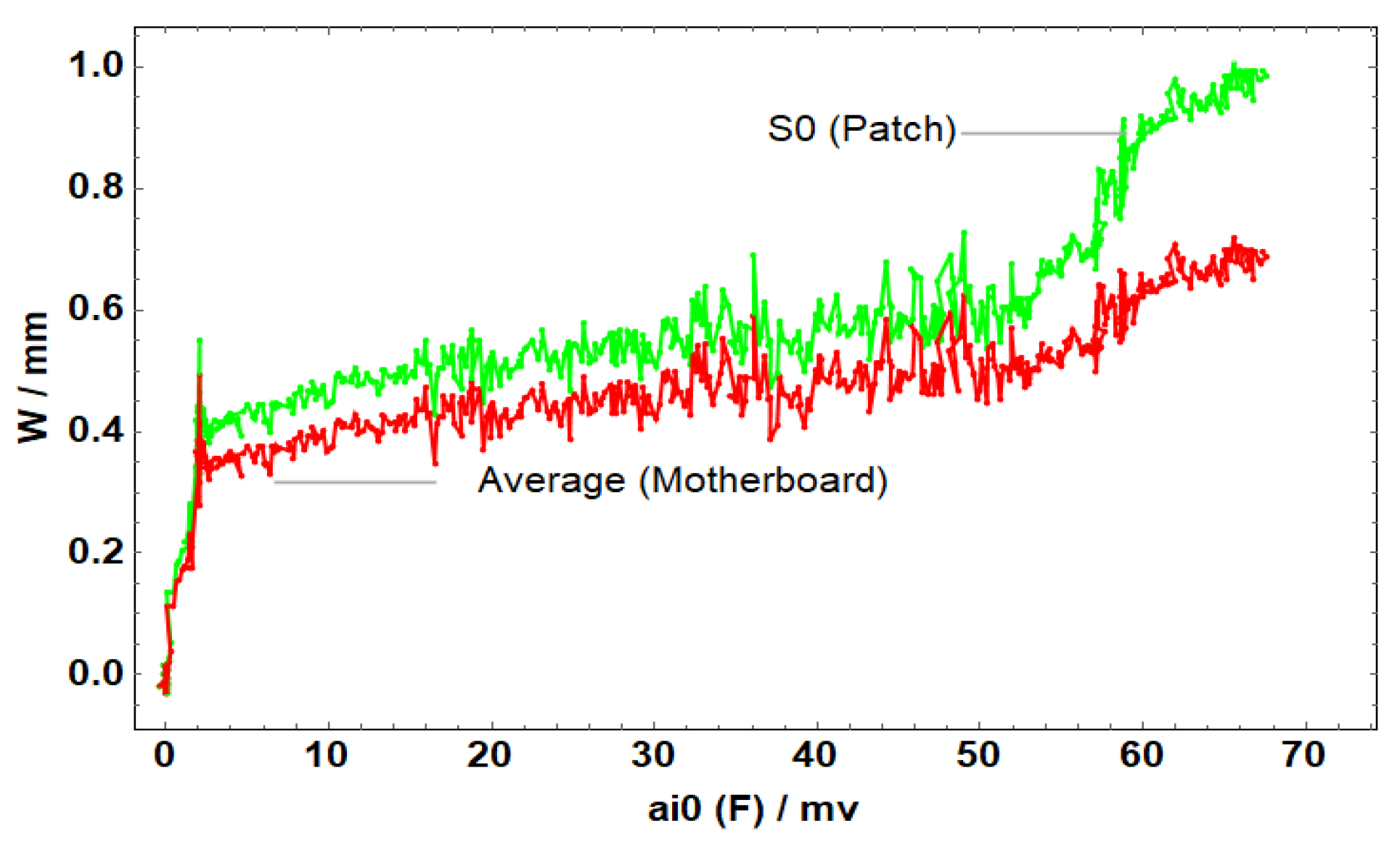
Figure 11.
Stress–displacement curve of circular patch specimens.
Figure 11.
Stress–displacement curve of circular patch specimens.
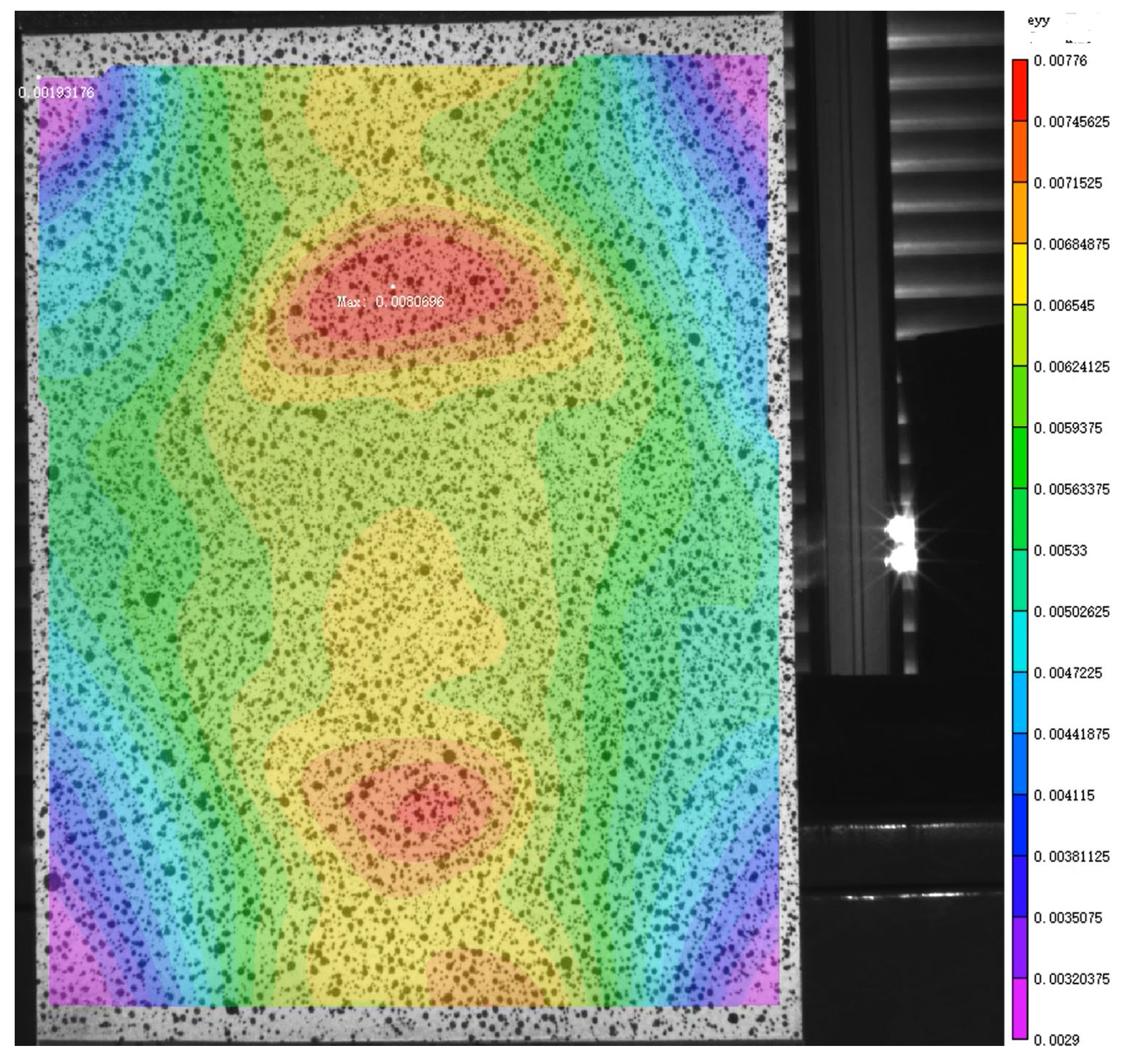
Figure 12.
Y−direction strain before fracture of the specimen with a circular patch.
Figure 12.
Y−direction strain before fracture of the specimen with a circular patch.
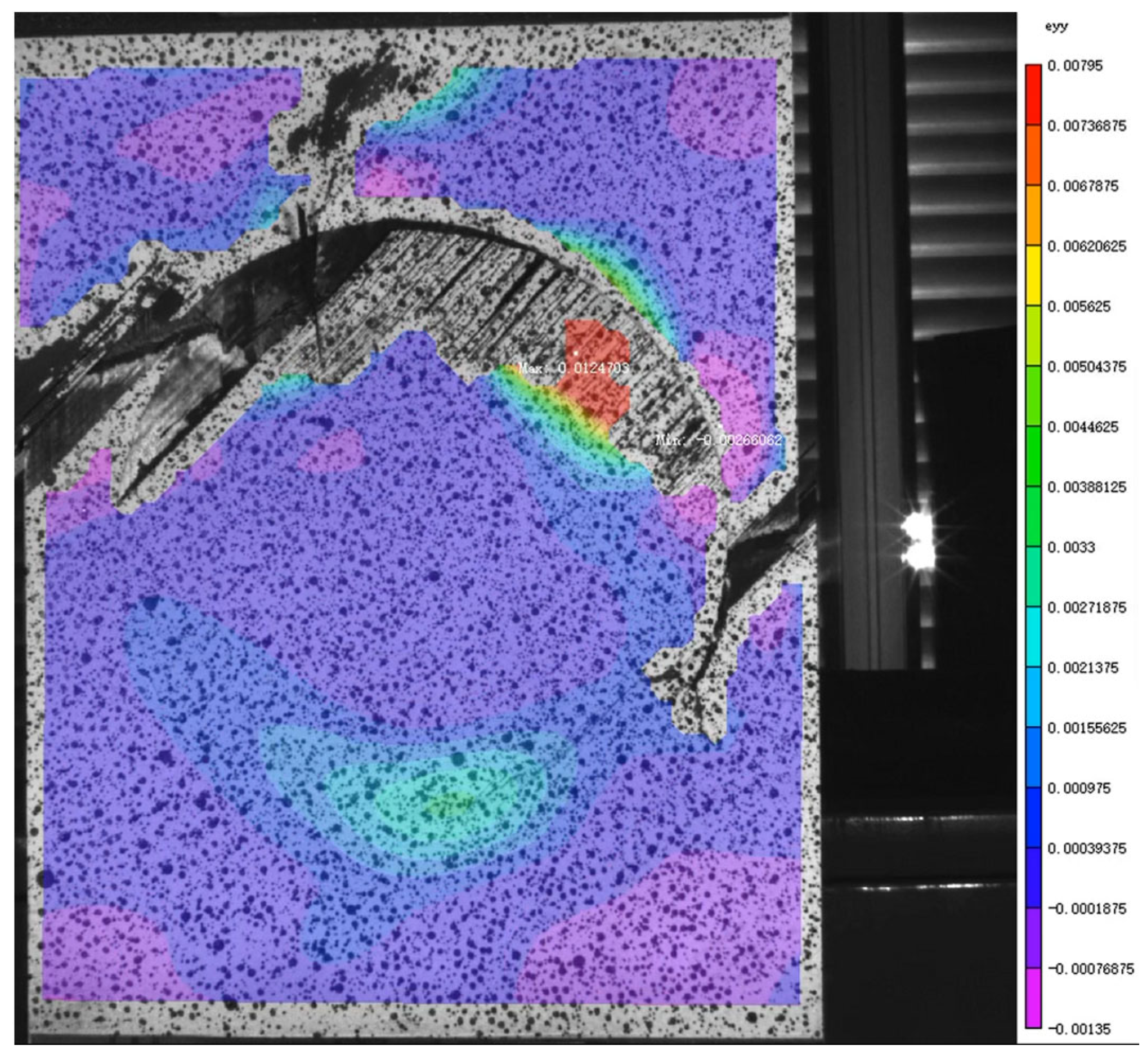
Figure 13.
Y−direction strain after fracturing of specimen with a circular patch.
Figure 13.
Y−direction strain after fracturing of specimen with a circular patch.
Figure 14.
The patch area (Black circle) of the circular repaired plate for DIC test.
Figure 14.
The patch area (Black circle) of the circular repaired plate for DIC test.
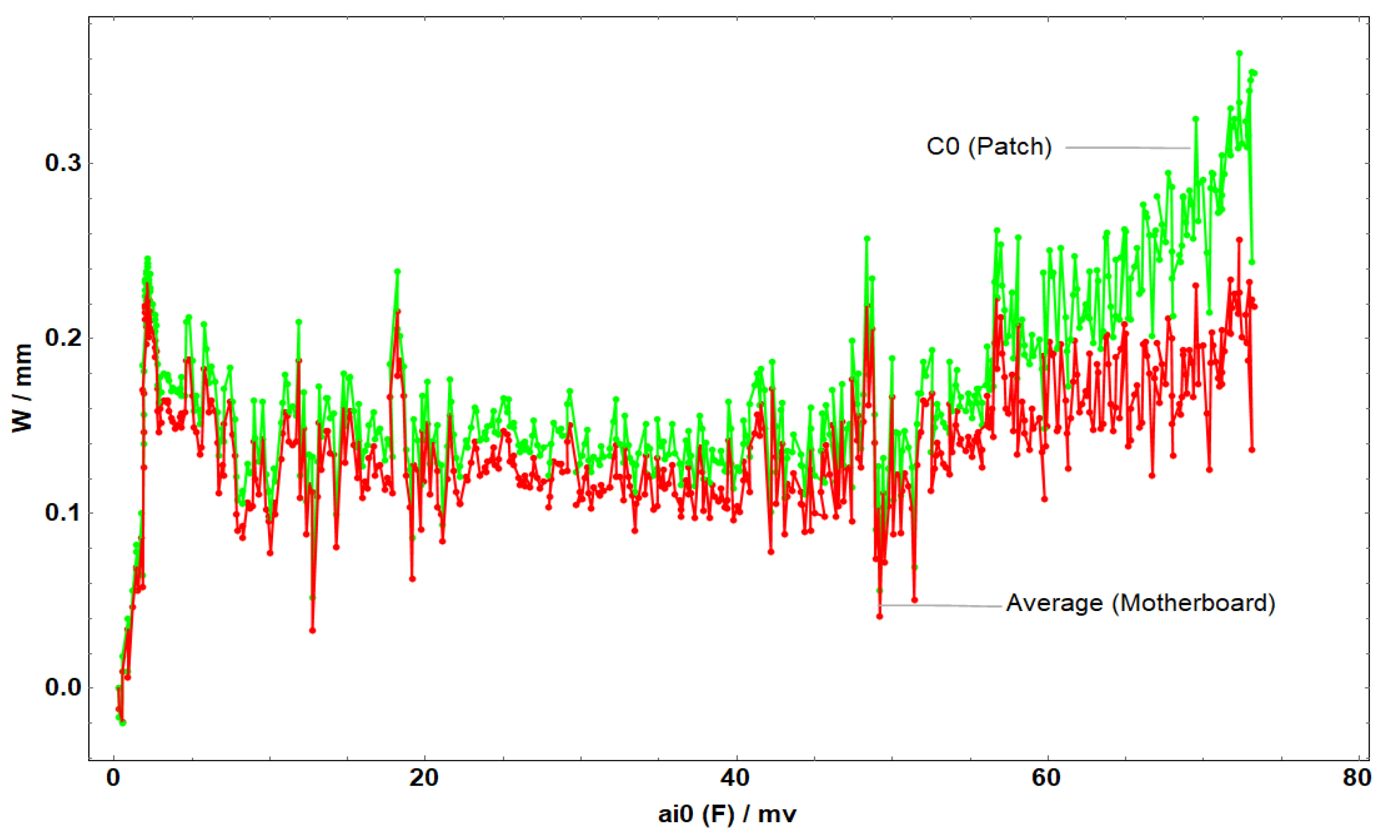
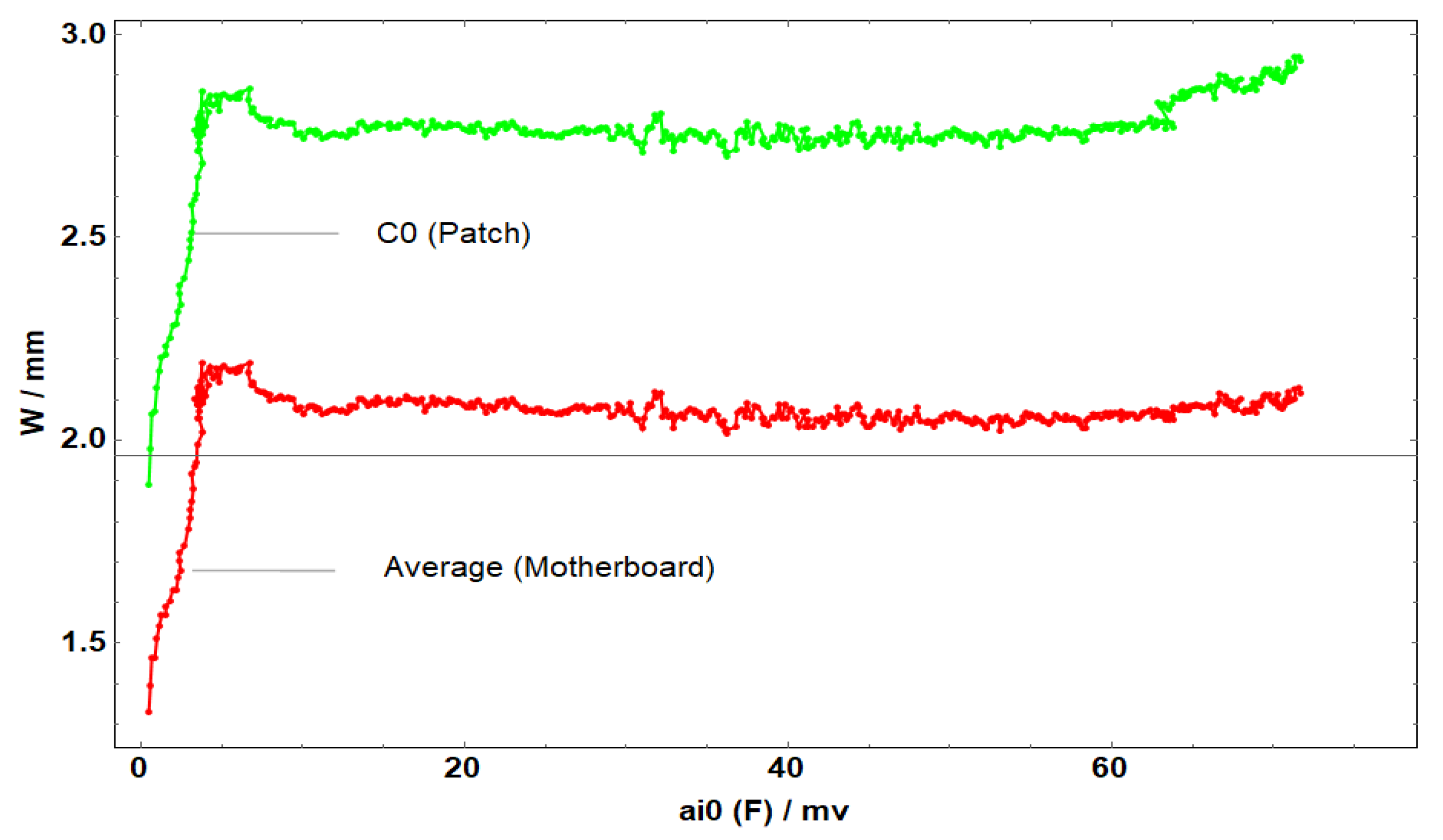
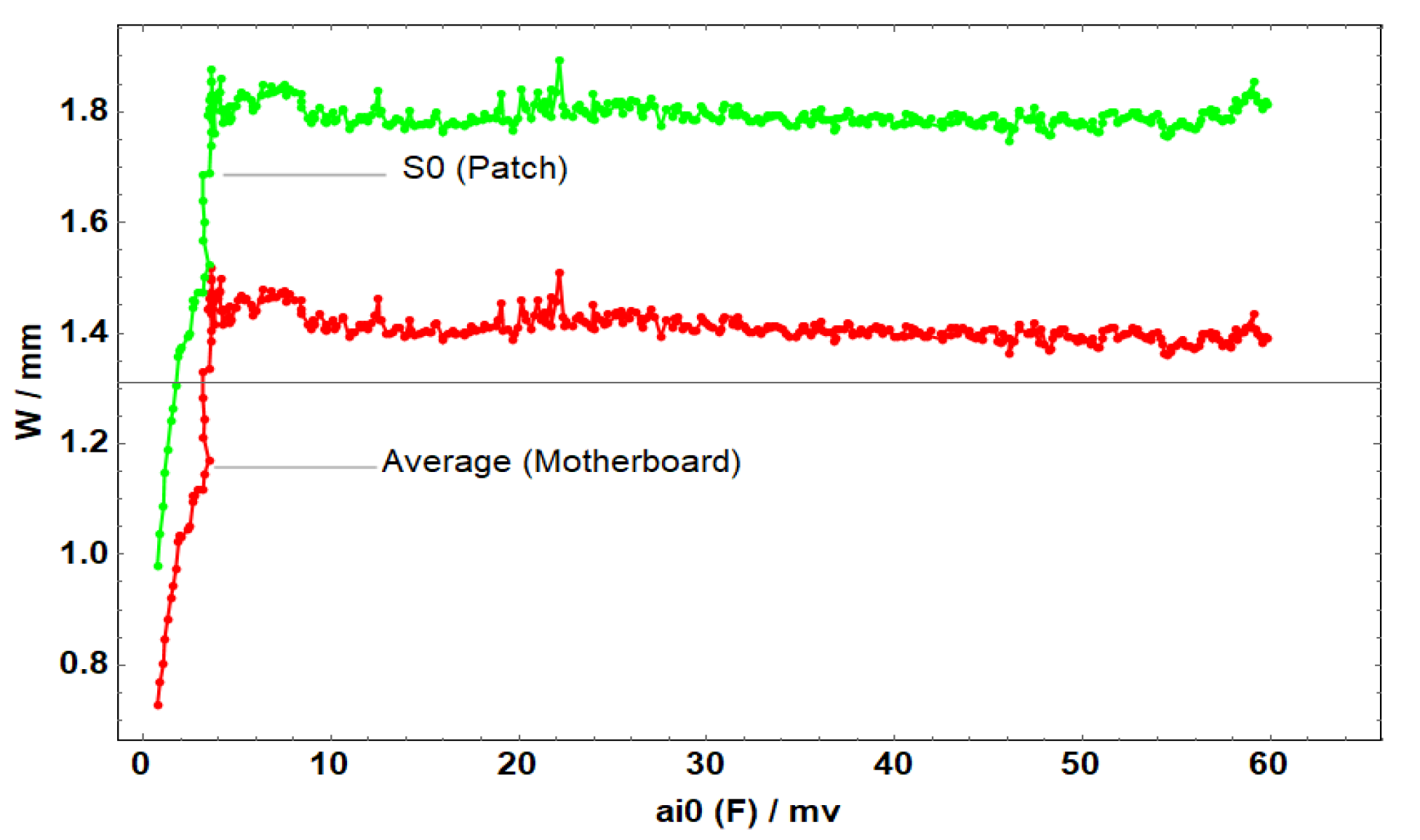
Figure 15.
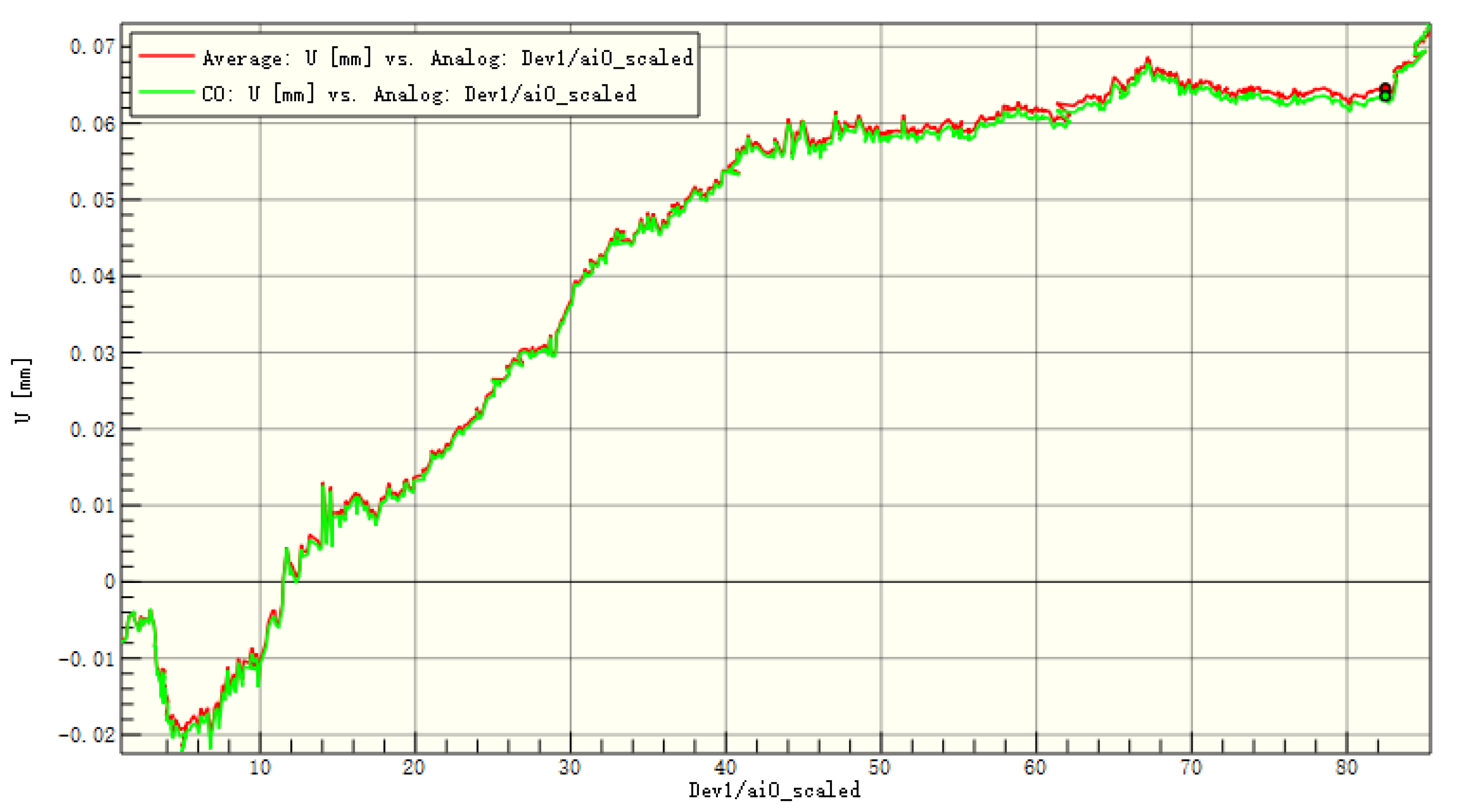
Average displacement of the entire board and the patch in the x-direction of C1.
Figure 15.
Average displacement of the entire board and the patch in the x-direction of C1.
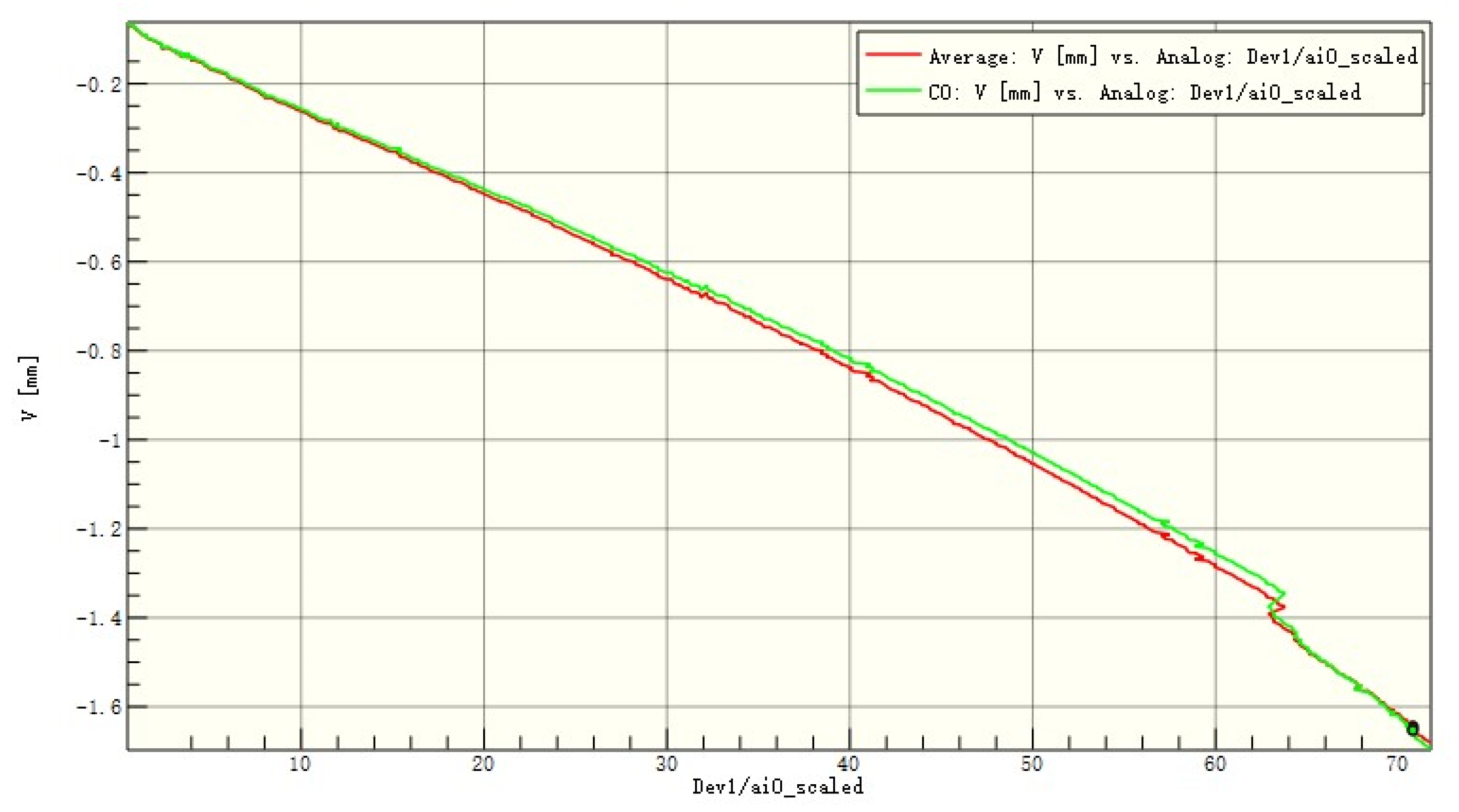
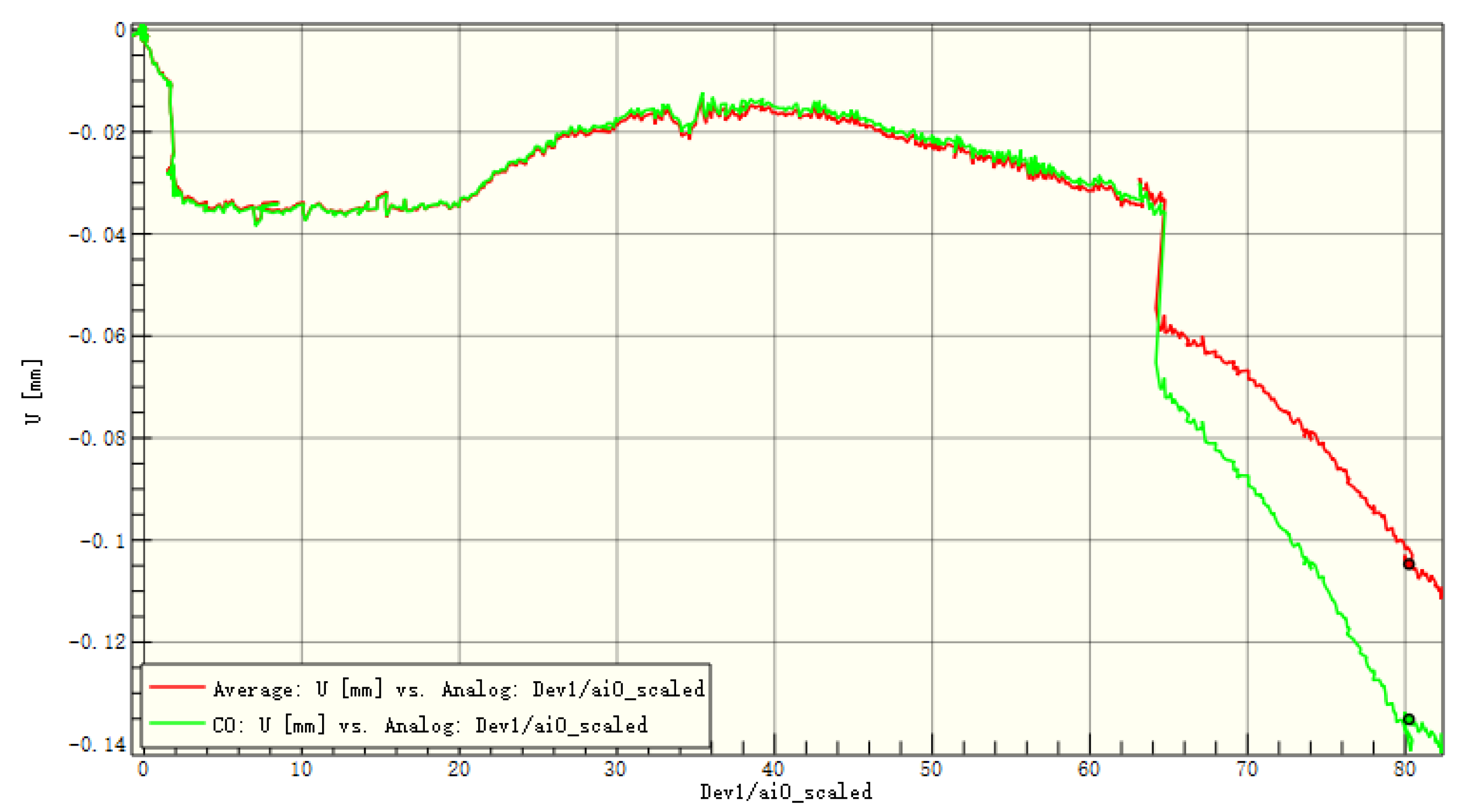
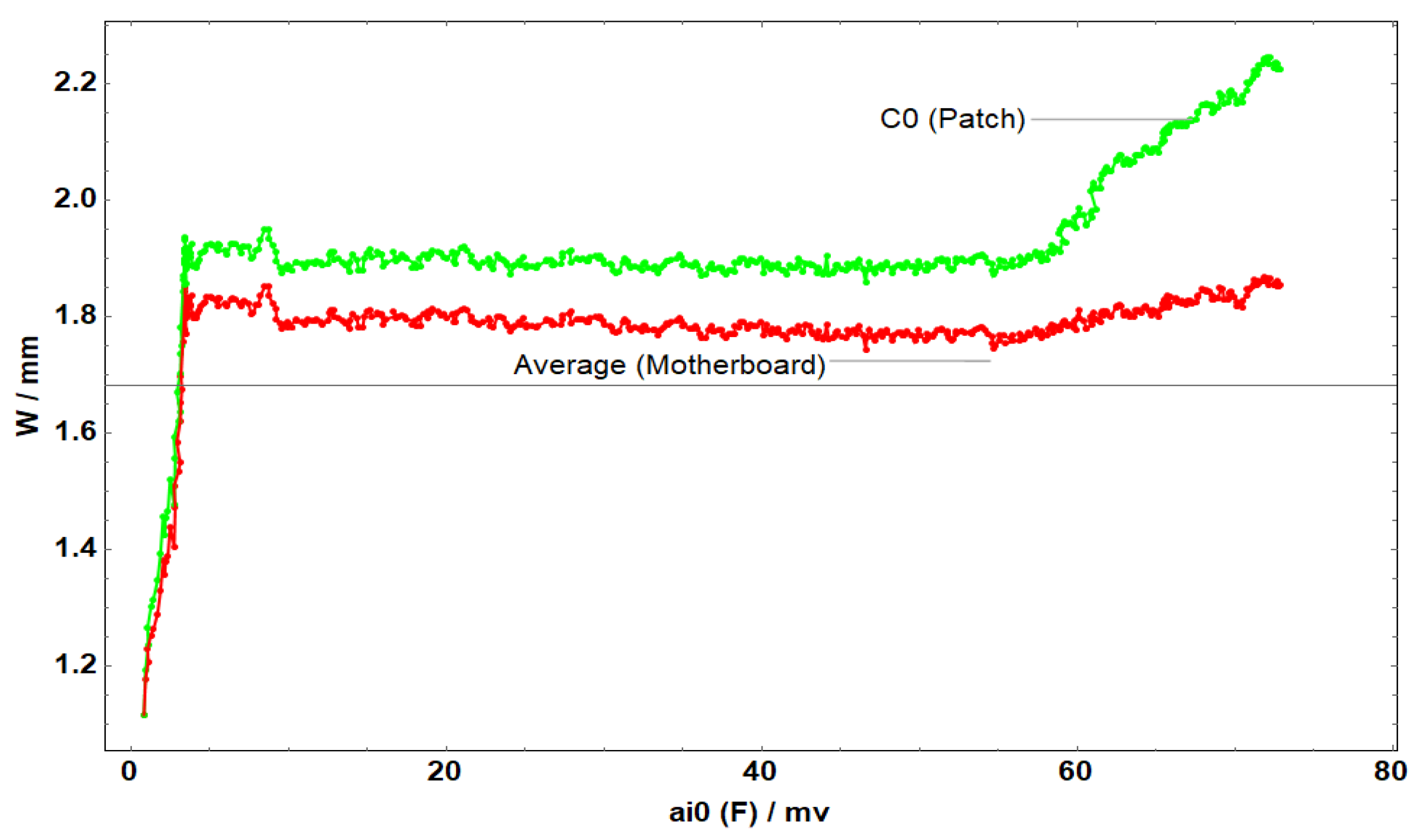
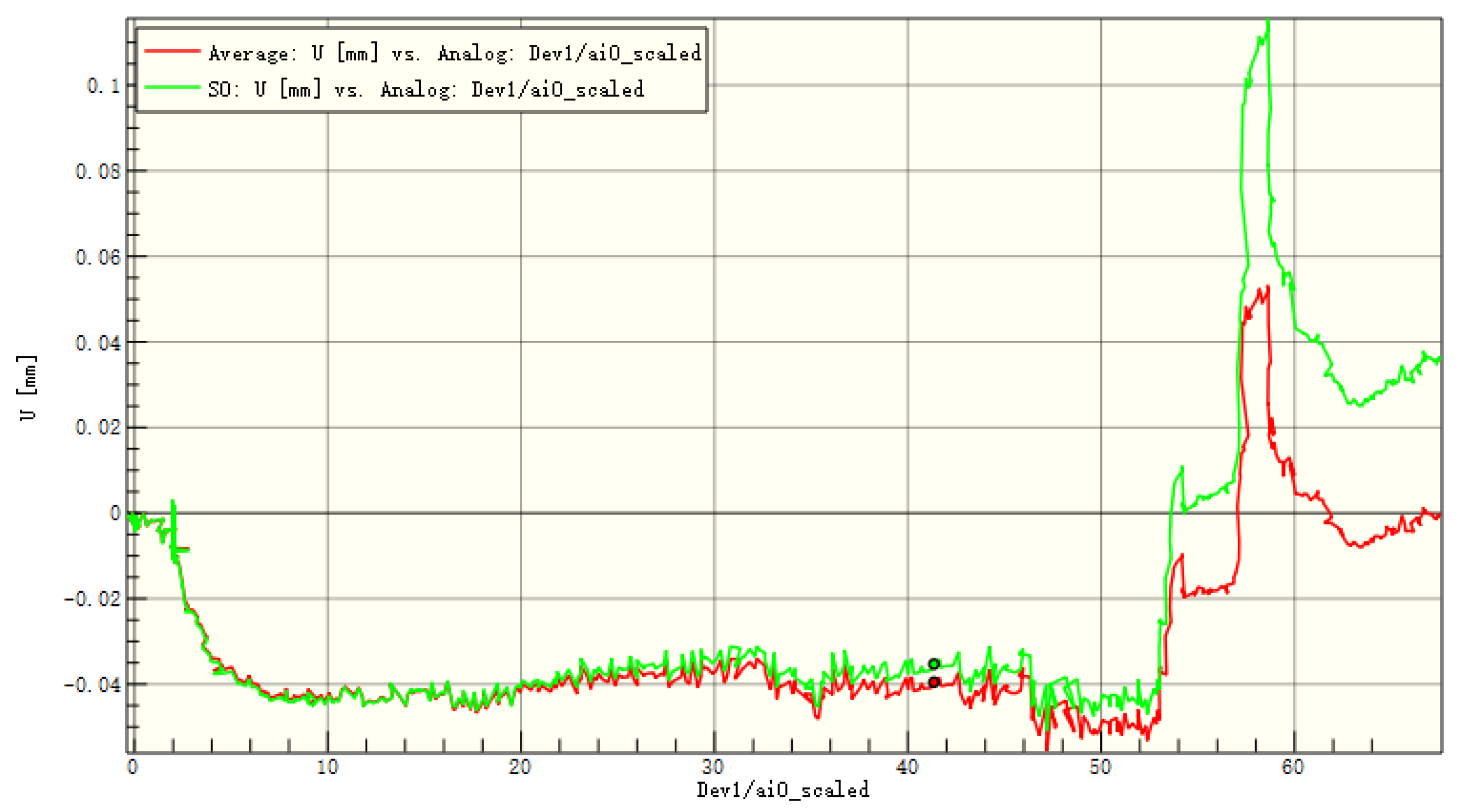
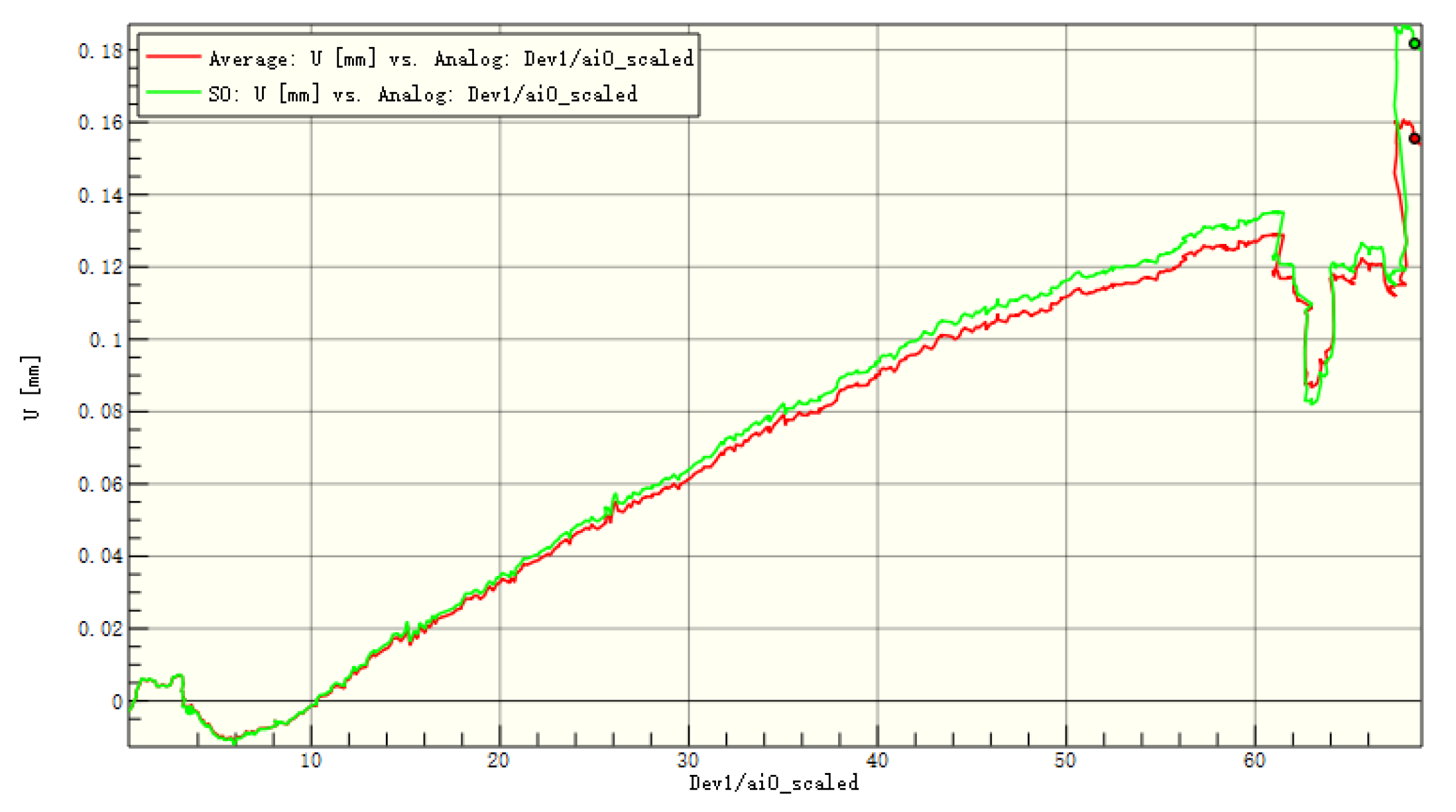
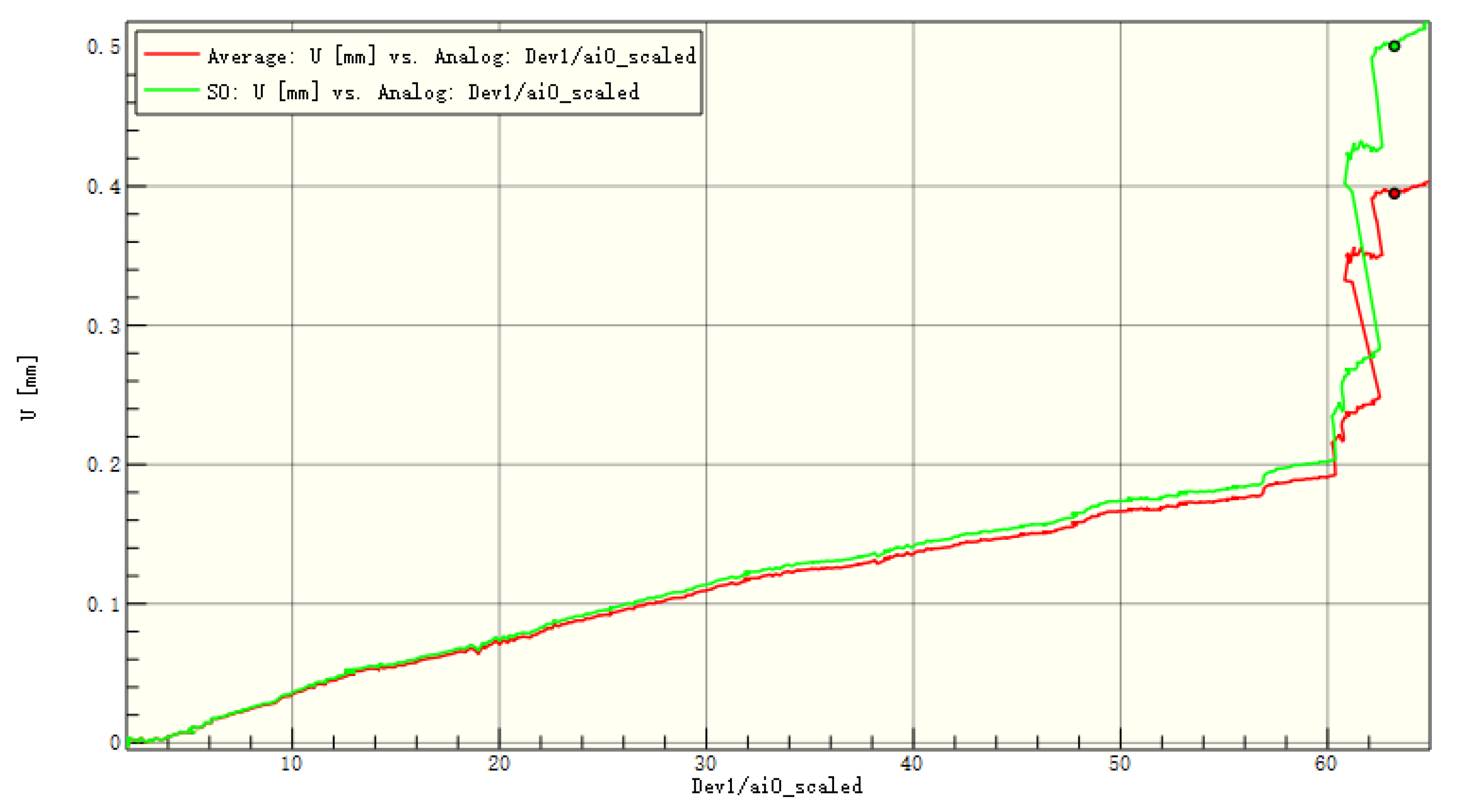
Figure 16.
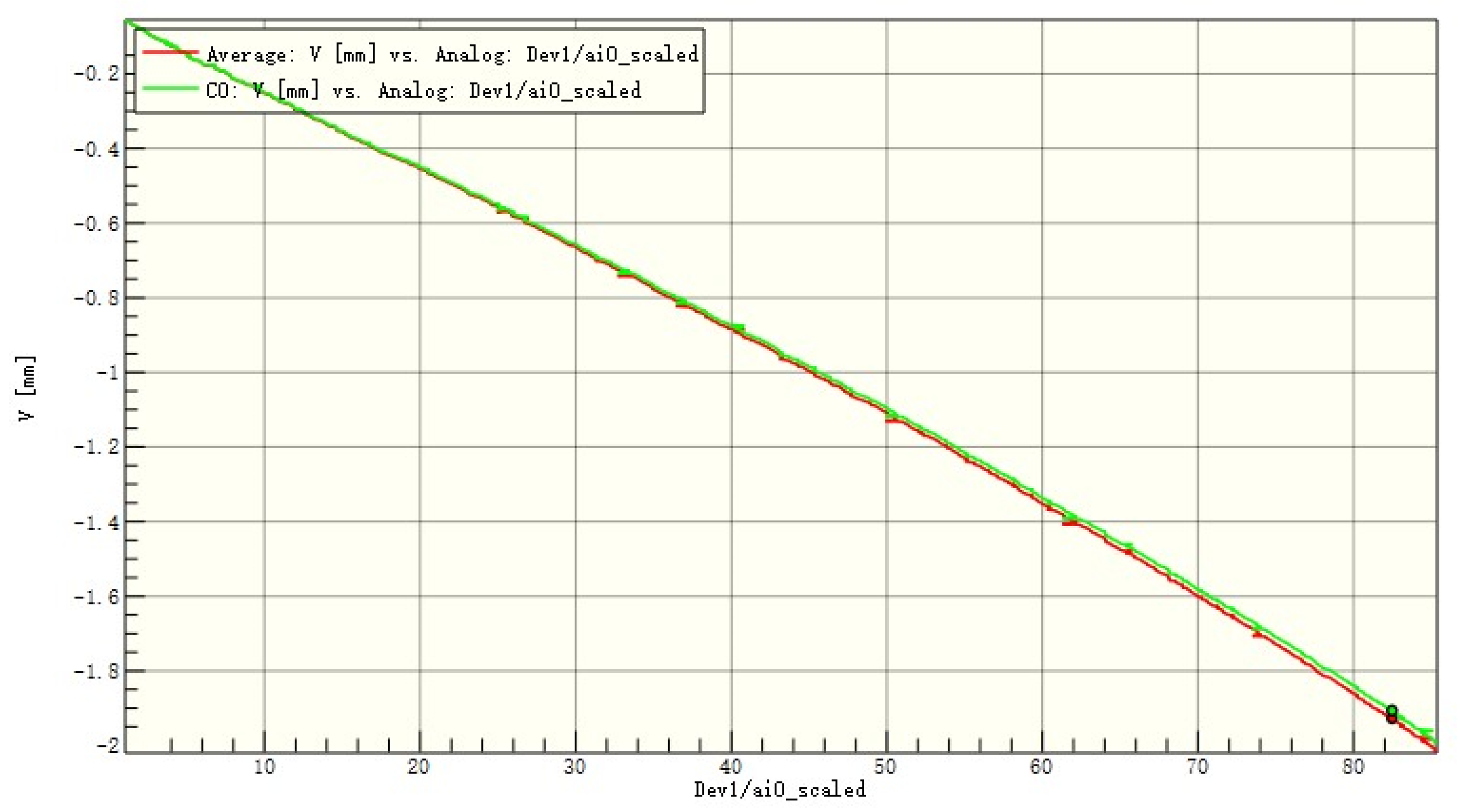
Average displacement of the entire board and the patch in the y-direction of C1.
Figure 16.
Average displacement of the entire board and the patch in the y-direction of C1.
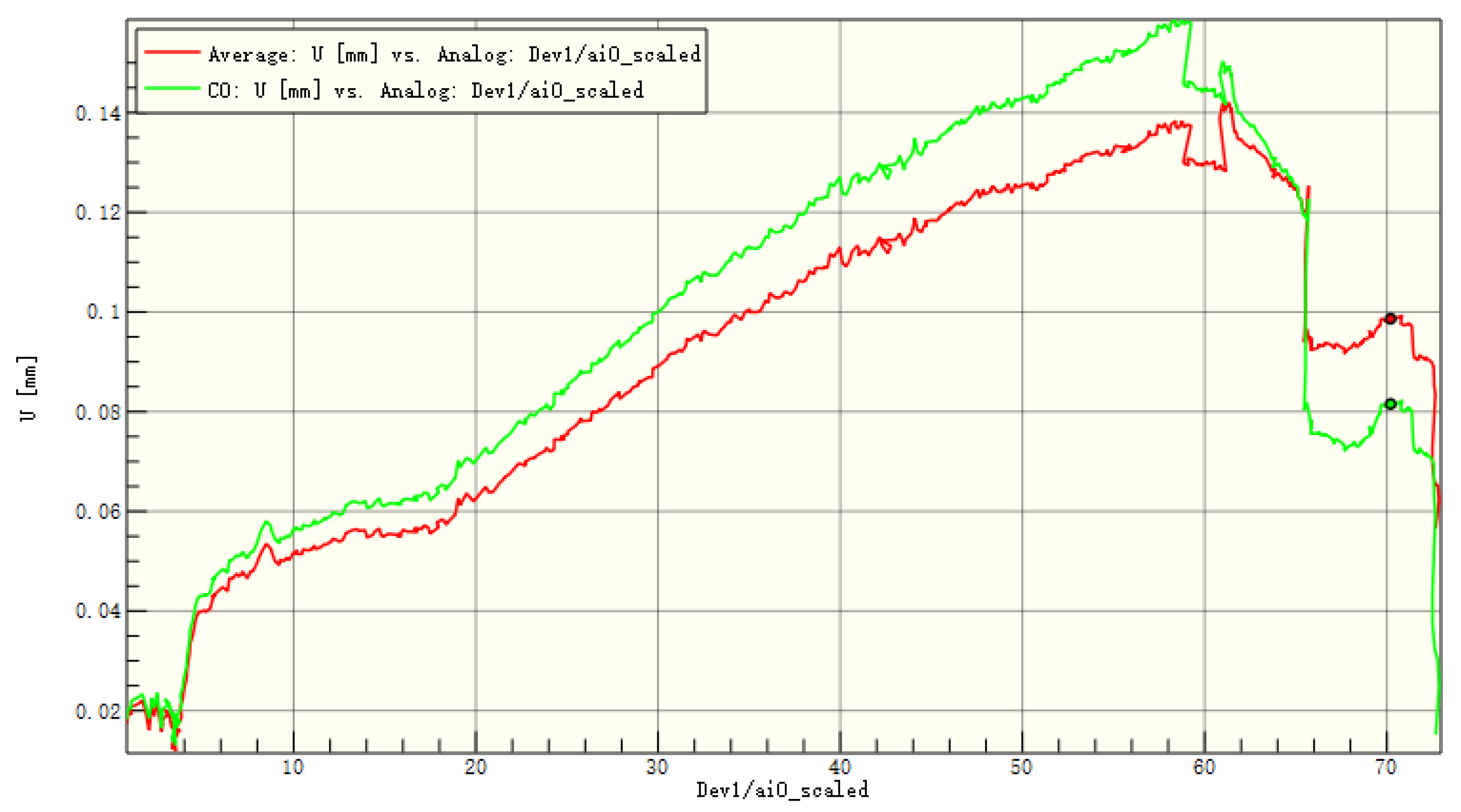
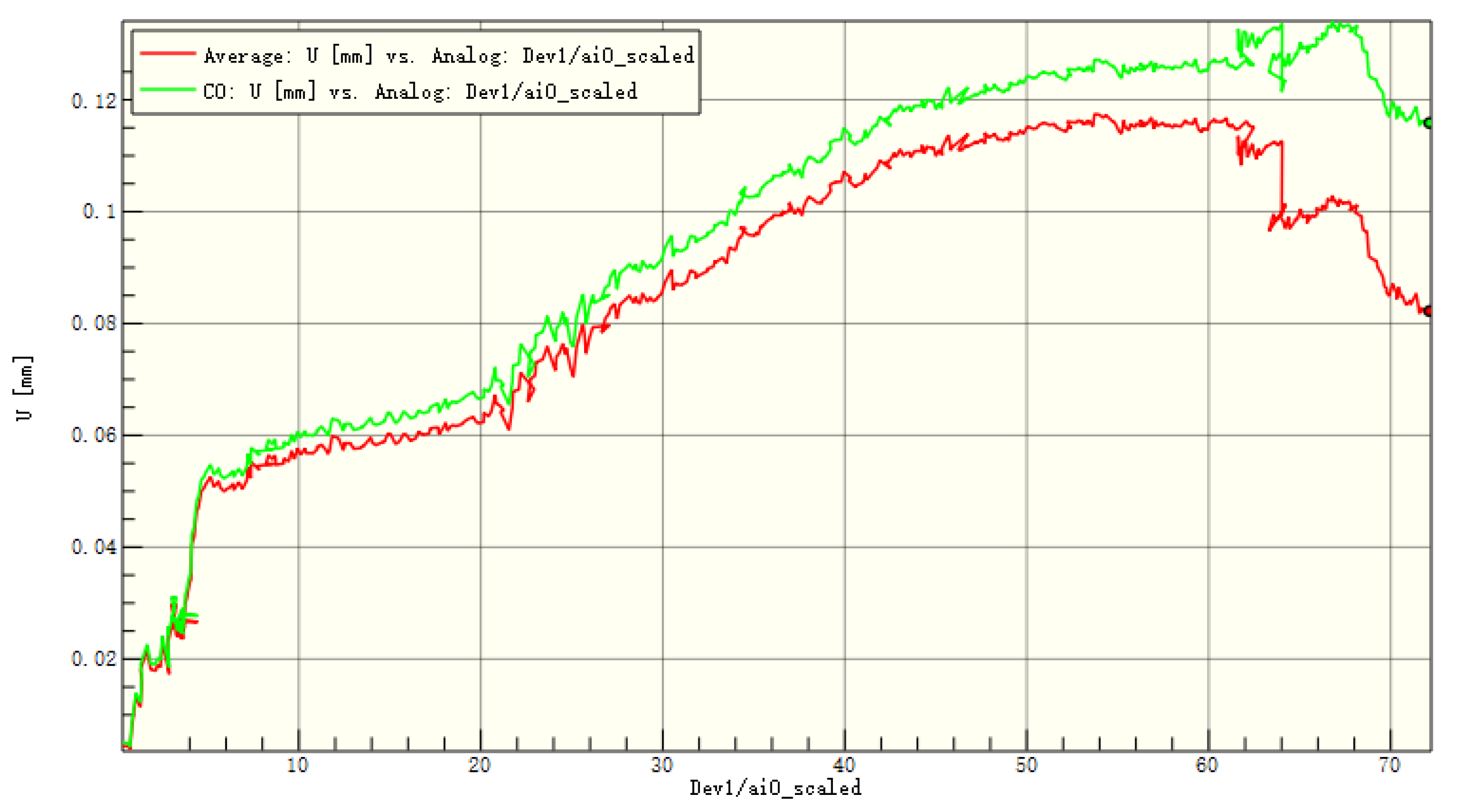
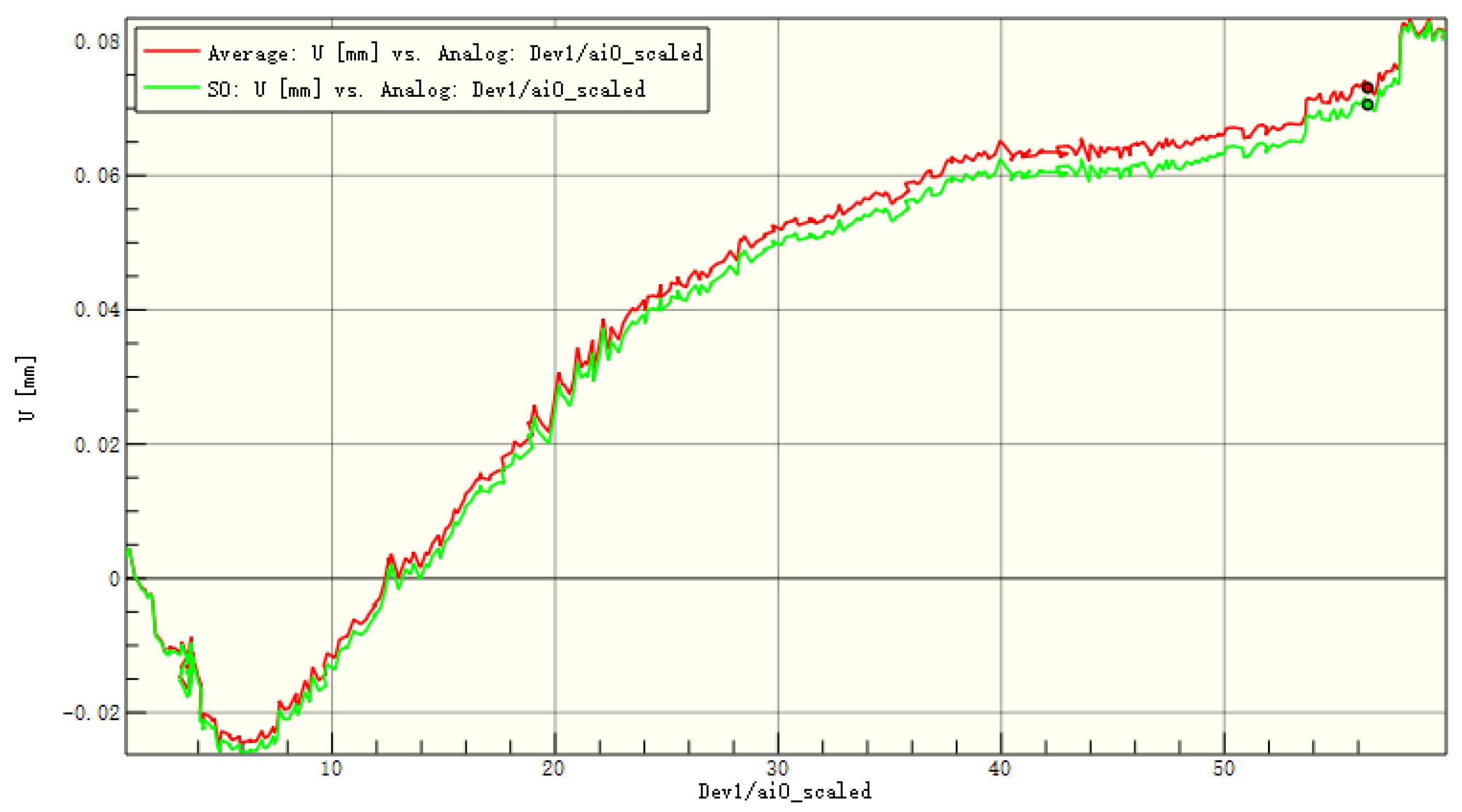
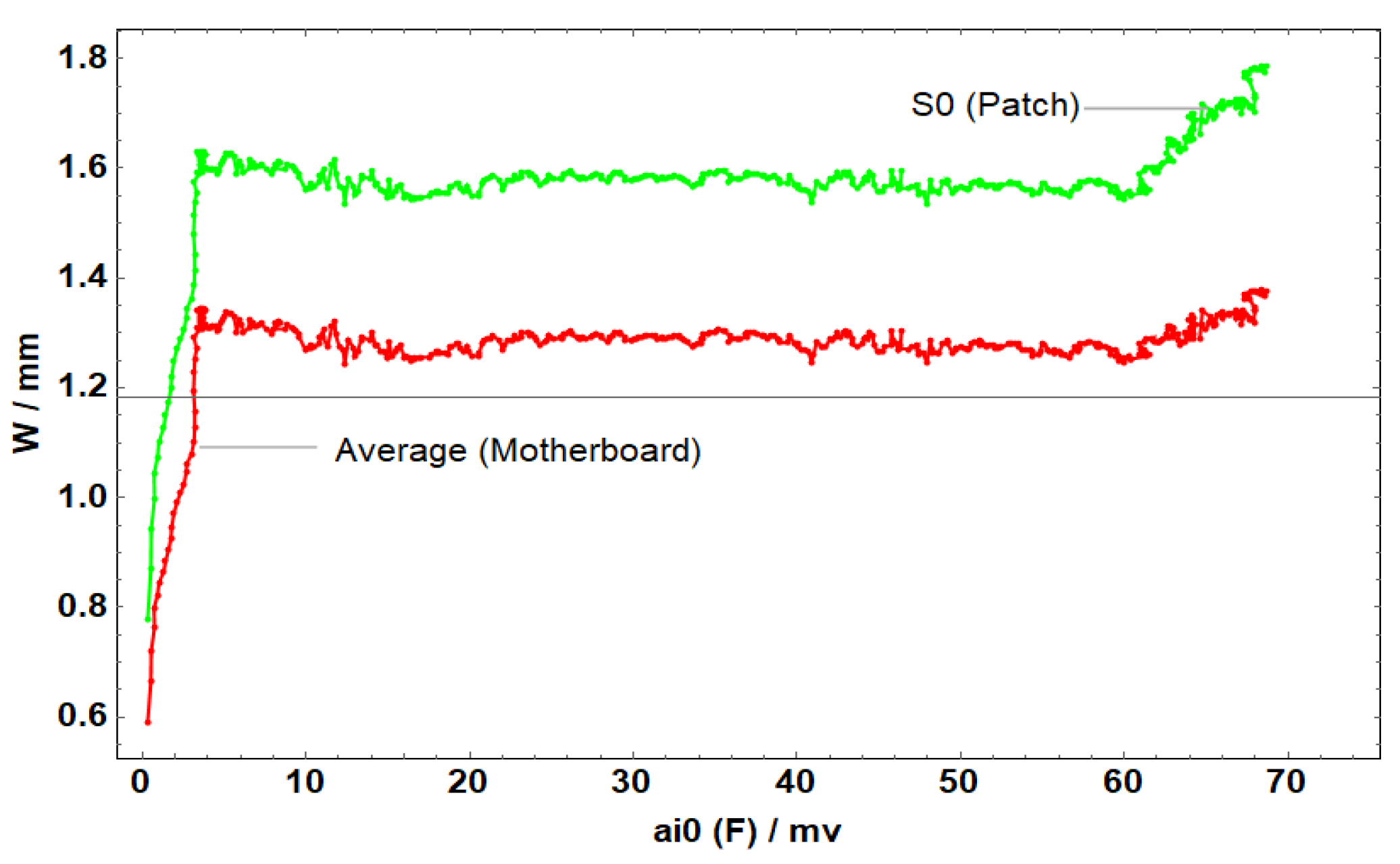
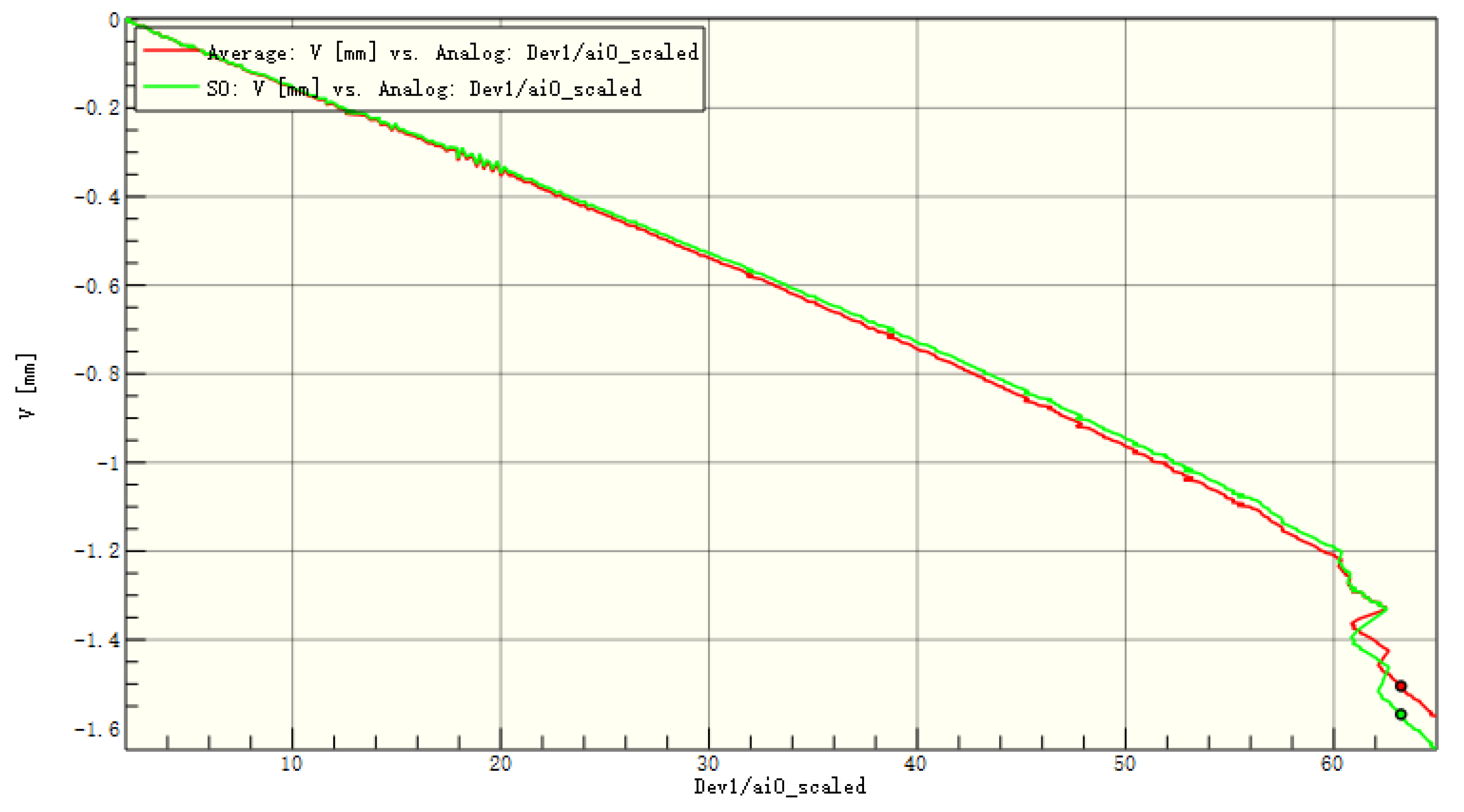
Figure 17.
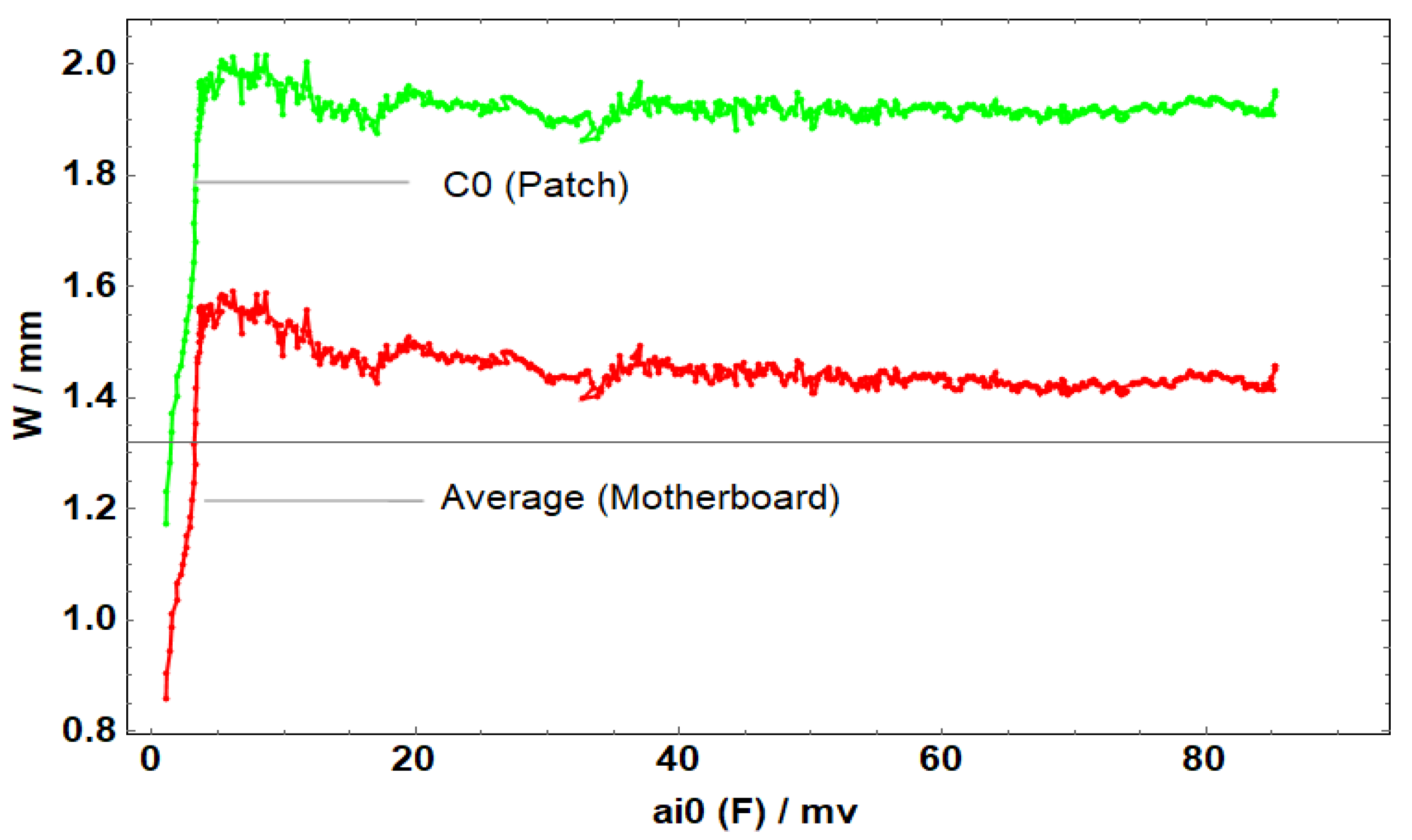
Average displacement of the entire board and the patch in the z-direction of C1.
Figure 17.
Average displacement of the entire board and the patch in the z-direction of C1.
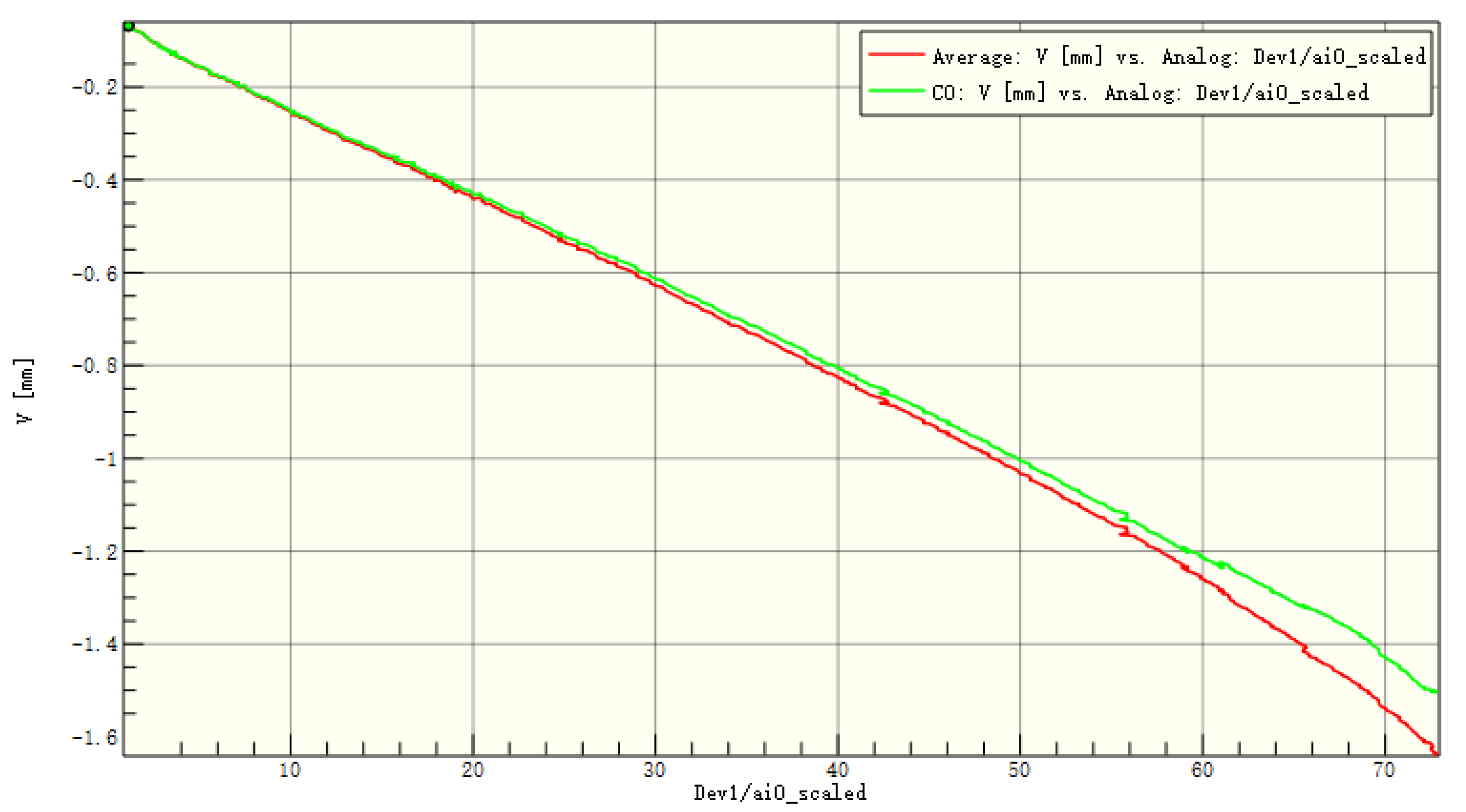
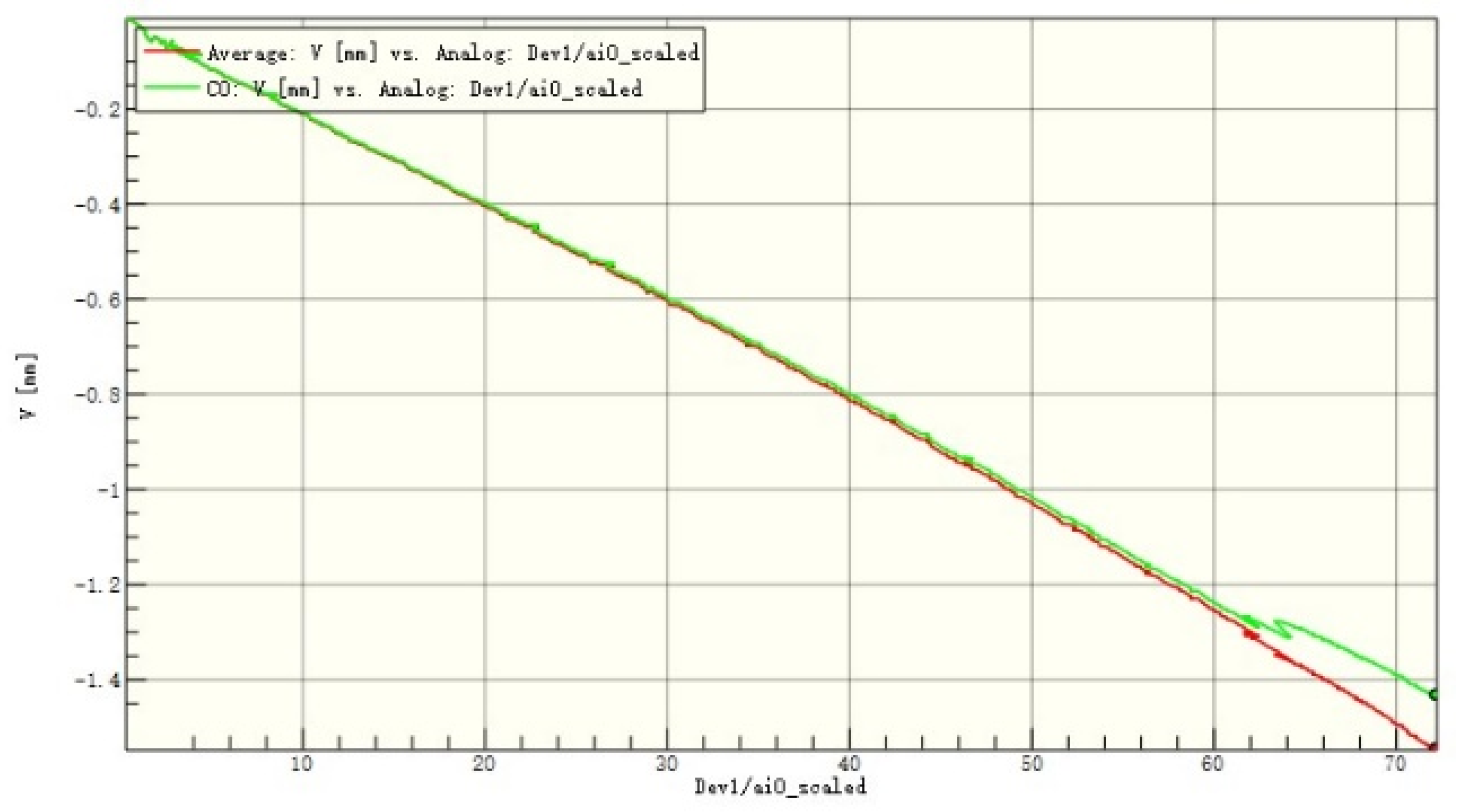
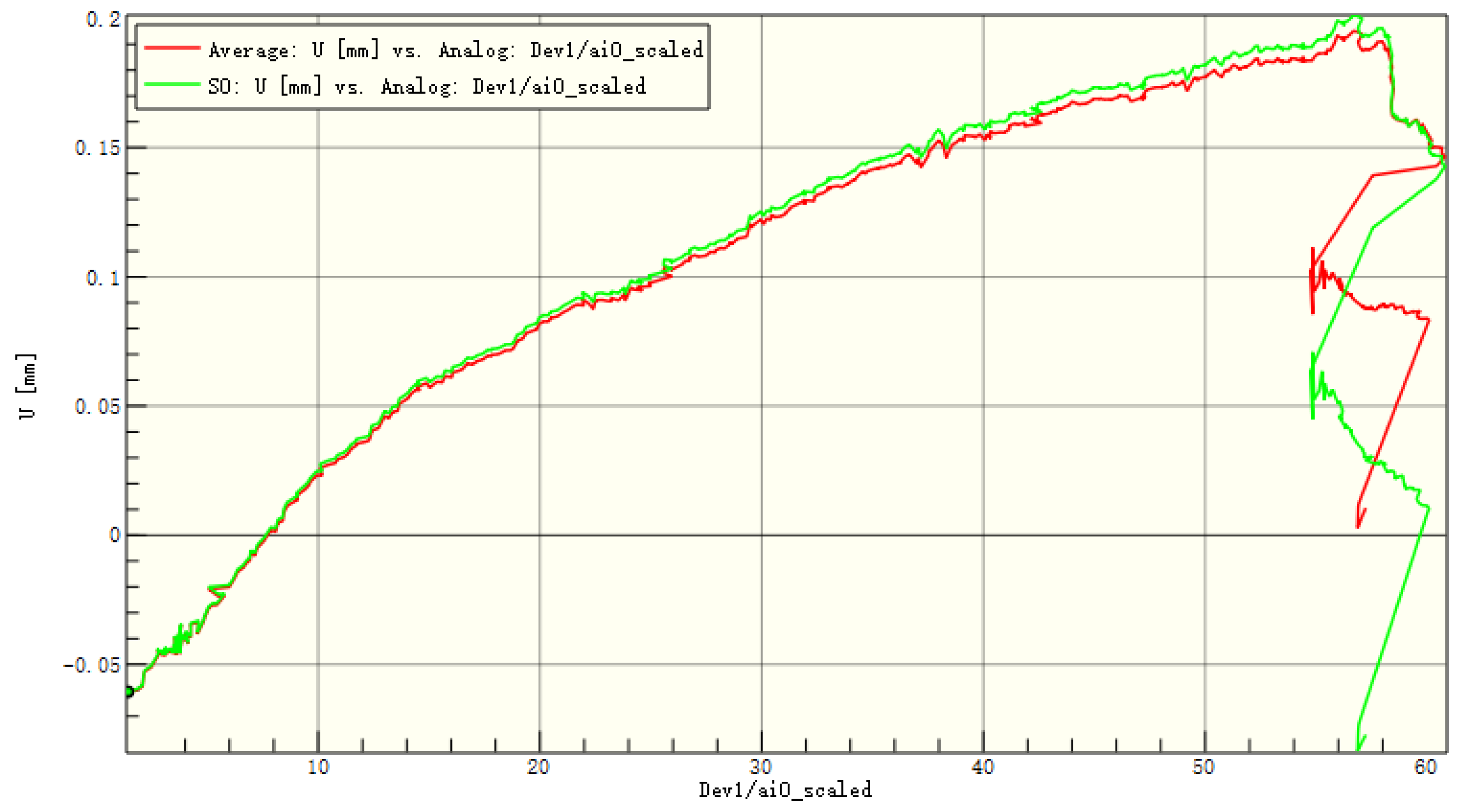
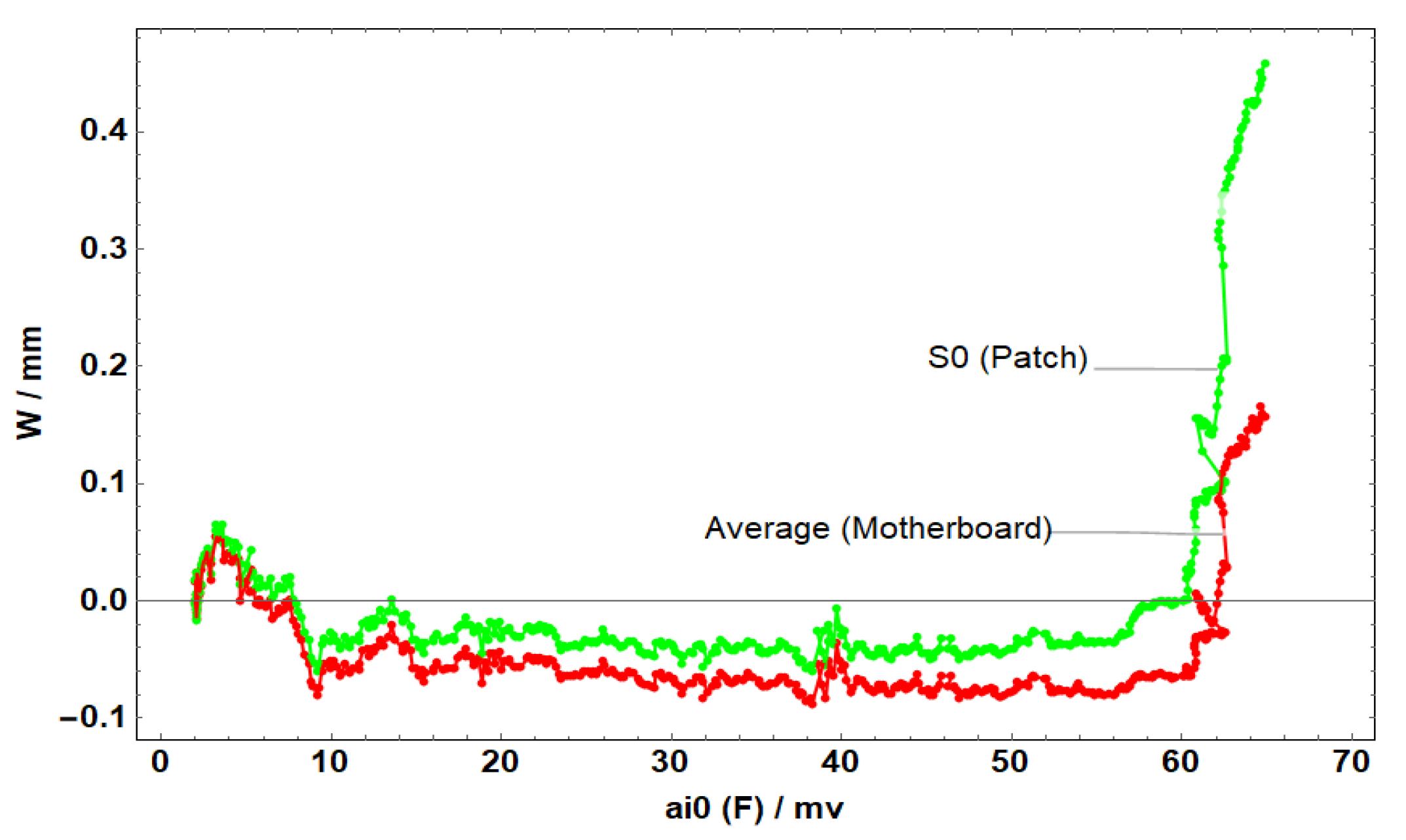
Figure 18.
Average displacement of the entire board and the patch in the x-direction of C2.
Figure 18.
Average displacement of the entire board and the patch in the x-direction of C2.
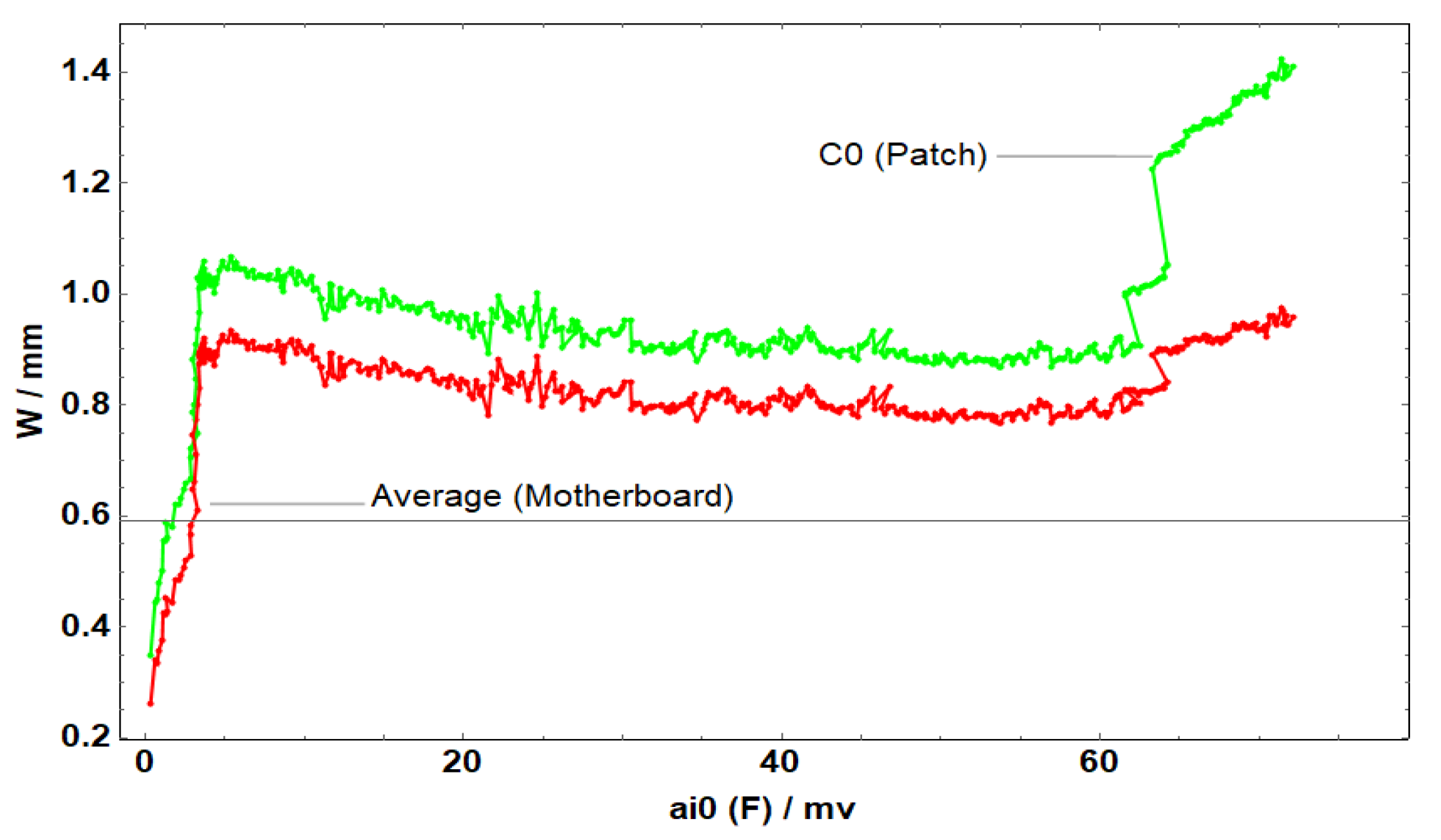
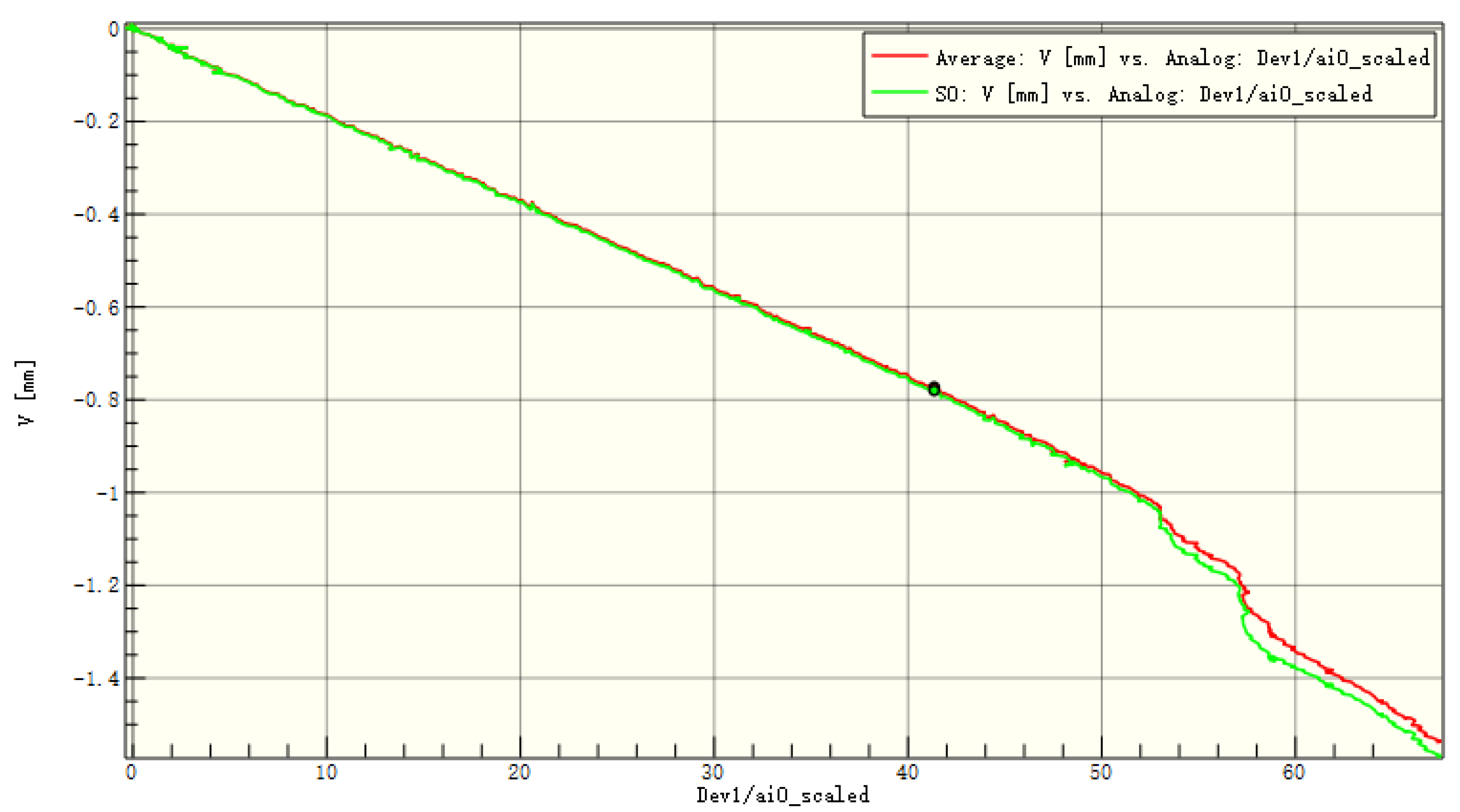
Figure 19.
Average displacement of the entire board and the patch in the y-direction of C2.
Figure 19.
Average displacement of the entire board and the patch in the y-direction of C2.
Figure 20.
Average displacement of the entire board and the patch in the z-direction of C2.
Figure 20.
Average displacement of the entire board and the patch in the z-direction of C2.
Figure 21.
Average displacement of the entire board and the patch in the x-direction of C3.
Figure 21.
Average displacement of the entire board and the patch in the x-direction of C3.
Figure 22.
Average displacement of the entire board and the patch in the y-direction of C3.
Figure 22.
Average displacement of the entire board and the patch in the y-direction of C3.
Figure 23.
Average displacement of the entire board and the patch in the z-direction of C3.
Figure 23.
Average displacement of the entire board and the patch in the z-direction of C3.
Figure 24.
Average displacement of the entire board and the patch in the x-direction of C4.
Figure 24.
Average displacement of the entire board and the patch in the x-direction of C4.
Figure 25.
Average displacement of the entire board and the patch in the y-direction of C4.
Figure 25.
Average displacement of the entire board and the patch in the y-direction of C4.
Figure 26.
Average displacement of the entire board and the patch in the z-direction of C4.
Figure 26.
Average displacement of the entire board and the patch in the z-direction of C4.
Figure 27.
Average displacement of the entire board and the patch in the x-direction of C5.
Figure 27.
Average displacement of the entire board and the patch in the x-direction of C5.
Figure 28.
Average displacement of the entire board and the patch in the y-direction of C5.
Figure 28.
Average displacement of the entire board and the patch in the y-direction of C5.
Figure 29.
Average displacement of the entire board and the patch in the z-direction of C5.
Figure 29.
Average displacement of the entire board and the patch in the z-direction of C5.
Figure 30.
Average displacement of the entire board and the patch in the x-direction of C6.
Figure 30.
Average displacement of the entire board and the patch in the x-direction of C6.
Figure 31.
Average displacement of the entire board and the patch in the y-direction of C6.
Figure 31.
Average displacement of the entire board and the patch in the y-direction of C6.
Figure 32.
Average displacement of the entire board and the patch in the z-direction of C6.
Figure 32.
Average displacement of the entire board and the patch in the z-direction of C6.
Figure 33.
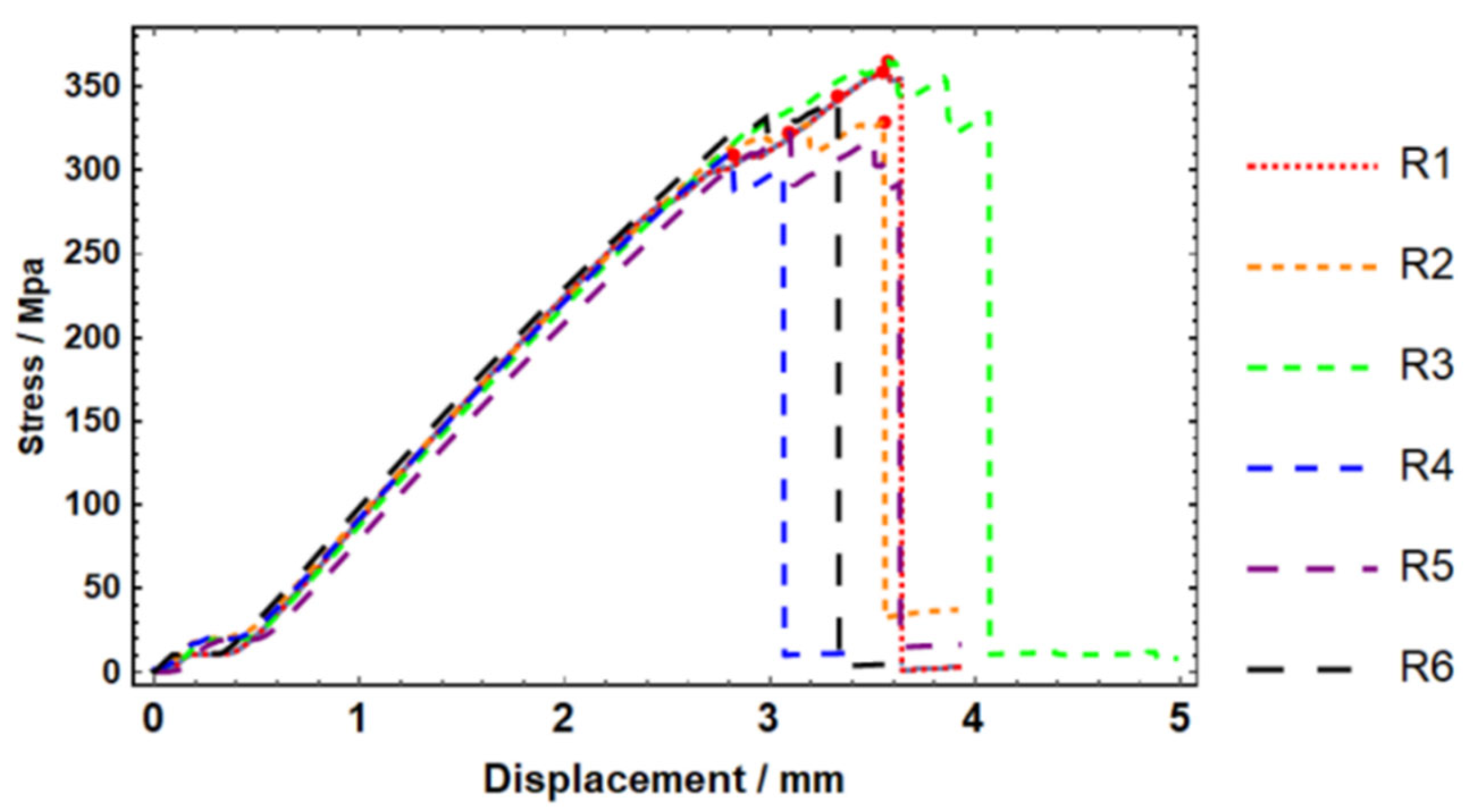
Stress–displacement curve of rounded square patch specimens.
Figure 33.
Stress–displacement curve of rounded square patch specimens.
Figure 34.
Y-direction strain before fracture of the specimen with a square patch.
Figure 34.
Y-direction strain before fracture of the specimen with a square patch.
Figure 35.
Y-direction strain after fracturing of specimen with a square patch.
Figure 35.
Y-direction strain after fracturing of specimen with a square patch.
Figure 36.
The patch area (Black Rectangle) of the rectangle repaired plate for DIC test.
Figure 36.
The patch area (Black Rectangle) of the rectangle repaired plate for DIC test.
Figure 37.
Average displacement of the entire board and the patch in the x-direction of sample R1.
Figure 37.
Average displacement of the entire board and the patch in the x-direction of sample R1.
Figure 38.
Average displacement of the entire board and the patch in the y-direction of sample R1.
Figure 38.
Average displacement of the entire board and the patch in the y-direction of sample R1.
Figure 39.
Average displacement of the entire board and the patch in the z-direction of sample R1.
Figure 39.
Average displacement of the entire board and the patch in the z-direction of sample R1.
Figure 40.
Average displacement of the entire board and the patch in the x-direction of sample R2.
Figure 40.
Average displacement of the entire board and the patch in the x-direction of sample R2.
Figure 41.
Average displacement of the entire board and the patch in the y-direction of sample R2.
Figure 41.
Average displacement of the entire board and the patch in the y-direction of sample R2.
Figure 42.
Average displacement of the entire board and the patch in the z-direction of sample R2.
Figure 42.
Average displacement of the entire board and the patch in the z-direction of sample R2.
Figure 43.
Average displacement of the entire board and the patch in the x-direction of sample R3.
Figure 43.
Average displacement of the entire board and the patch in the x-direction of sample R3.
Figure 44.
Average displacement of the entire board and the patch in the y-direction of sample R3.
Figure 44.
Average displacement of the entire board and the patch in the y-direction of sample R3.
Figure 45.
Average displacement of the entire board and the patch in the z-direction of sample R3.
Figure 45.
Average displacement of the entire board and the patch in the z-direction of sample R3.
Figure 46.
Average displacement of the entire board and the patch in the x-direction of sample R5.
Figure 46.
Average displacement of the entire board and the patch in the x-direction of sample R5.
Figure 47.
Average displacement of the entire board and the patch in the y-direction of sample R5.
Figure 47.
Average displacement of the entire board and the patch in the y-direction of sample R5.
Figure 48.
Average displacement of the entire board and the patch in the z-direction of sample R5.
Figure 48.
Average displacement of the entire board and the patch in the z-direction of sample R5.
Figure 49.
Average displacement of the entire board and the patch in the x-direction of sample R6.
Figure 49.
Average displacement of the entire board and the patch in the x-direction of sample R6.
Figure 50.
Average displacement of the entire board and the patch in the y-direction of sample R6.
Figure 50.
Average displacement of the entire board and the patch in the y-direction of sample R6.
Figure 51.
Average displacement of the entire board and the patch in the z-direction of sample R6.
Figure 51.
Average displacement of the entire board and the patch in the z-direction of sample R6.
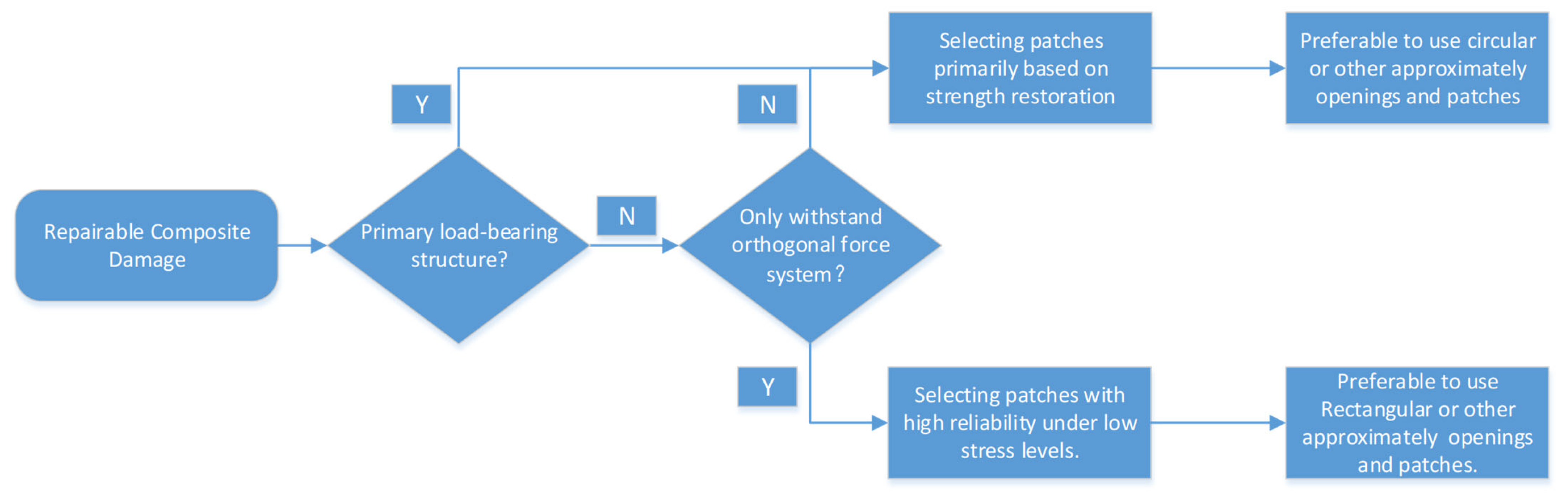
Figure 52.
The method for optimizing the selection of patch shape for composite material repairs is based on strength analysis.
Figure 52.
The method for optimizing the selection of patch shape for composite material repairs is based on strength analysis.
Table 1.
Basic parameters of composite laminated plate.
Table 1.
Basic parameters of composite laminated plate.
| Name | Ply Direction | Size | Single-Layer Thickness | Density |
|---|
| T300 Laminate | [45°/0°/−45°/90°]s | 300 × 162 × 1.2 mm3 | 0.15 mm | 1.80 g/cm3 |
Table 2.
Mechanical properties of composite single-layer plate.
Table 2.
Mechanical properties of composite single-layer plate.
| E1/MPa | E2 = E3/MPa | G12 = G13/MPa | G23/MPa | |
|---|
| 135,000 | 8800 | 5500 | 3308 | 0.33 |
Table 3.
Failure strength of laminated composite plates.
Table 3.
Failure strength of laminated composite plates.
| Ft1/MPa | Fc1/MPa | Ft2/MPa | Fc2/MPa | max/MPa |
|---|
| 1548 | 1226 | 55.5 | 232 | 89.9 |
Table 4.
E51 epoxy resin mixing ratio.
Table 4.
E51 epoxy resin mixing ratio.
| Name | Epoxy | Curing Agent |
|---|
| Percent/% | 80 | 20 |
Table 5.
Material parameters of circular patches obtained from tensile test/MPa.
Table 5.
Material parameters of circular patches obtained from tensile test/MPa.
| | Parameters | Elastic Modulus | Ultimate Failure Strength |
|---|
| Specimens | |
|---|
| C1 | 13,260 | 388.653 |
| C2 | 11,922 | 379.611 |
| C3 | 14,095 | 436.874 |
| C4 | 11,244 | 386.238 |
| C5 | 11,500 | 381.897 |
| C6 | 10,185 | 452.596 |
| Average | 12,034 | 404.311 |
Table 6.
Material parameters of square patches obtained from tensile test/MPa.
Table 6.
Material parameters of square patches obtained from tensile test/MPa.
| | Parameters | Elastic Modulus | Ultimate Failure Strength |
|---|
| Specimens | |
|---|
| R1 | 11,677 | 358.716 |
| R2 | 11,973 | 329.284 |
| R3 | 11,377 | 365.397 |
| R4 | 11,692 | 309.524 |
| R5 | 10,517 | 322.321 |
| R6 | 13,438 | 344.195 |
| Average | 11,779 | 338.239 |
Table 7.
Material parameters of circular patches obtained from tensile test/MPa.
Table 7.
Material parameters of circular patches obtained from tensile test/MPa.
| | Parameters | Elastic Modulus | Ultimate Failure Strength |
|---|
| Specimens | |
|---|
| Circular Patch Specimens | 12,034 | 404.311 |
| Square Patch Specimens | 11,779 | 338.239 |