Abstract
Current orbit uncertainty propagation (OUP) and orbit determination (OD) methods suffer from drawbacks related to high computational burden, limiting their applications in deep space missions. To this end, this paper proposes a multivariate attention-based method for efficient OUP and OD of Earth–Jupiter transfer. First, a neural network-based OD framework is utilized, in which the orbit propagation process in a traditional unscented transform (UT) and unscented Kalman filter (UKF) is replaced by the neural network. Then, the sample structure of training the neural network for the Earth–Jupiter transfer is discussed and designed. In addition, a method for efficiently generating a large number of samples for the Earth–Jupiter transfer is presented. Next, a multivariate attention-based neural network (MANN) is designed for orbit propagation, which shows better capacity in terms of accuracy and generalization than the deep neural network. Finally, the proposed method is successfully applied to solve the OD problem in an Earth–Jupiter transfer. Simulations show that the proposed method can obtain a similar estimation to the UKF while saving more than 90% of the computational cost.
1. Introduction
Orbit uncertainty propagation (OUP) and orbit determination (OD) are essential in space missions such as near-Earth missions [1,2,3], asteroid exploration missions [4,5,6], lunar exploration missions [7], Venus exploration missions [8], and Jupiter exploration missions [9,10]. Among these space missions, deep space exploration missions rely on extremely accurate OUP and OD techniques. The OUP involves predicting the orbital states (and the associated uncertainties), whereas the OD involves determining the precise position and velocity of a space target, such as a spacecraft or an asteroid, with respect to a reference frame [11,12,13].
Accurate OUP and OD are crucial for many deep space missions, including spacecraft navigation, design of trajectory correction maneuvers, planetary exploration, and more [14,15]. High accuracy helps to optimize and design robust trajectories that consider uncertainties, which is particularly important for mission planning and execution [16,17]. Additionally, it enables the prediction of future spacecraft positions and velocities [18,19], which is useful for coordinating operations and avoiding collisions with other objects in deep space [20,21,22].
Classic OUP methods include Monte Carlo simulation [23], unscented transform (UT) [24,25,26], cubature rule [27], state transition matrix [28,29], state transition tensor (STT) [30,31,32,33], and Gaussian mixture model (GMM) [34]. Park and Scheeres investigated the OUP problem of a spacecraft on a Sun–Earth L1 orbit [32,33]. Kim and Park derived an STM for OUP of a fly-by spacecraft [35]. Boone and McMahon analyzed the stability of the Europa Lander orbit using STT [36]. Qiao et al. proposed a semi-analytical uncertainty propagation method for a heliocentric constellation based on STT techniques [31].
In general, OD can be performed for a deep space probe using optical [37], pulsar-based [10], and doppler-Range radio [35] measurements. Qiao et al. investigated the possibility of optical navigation during the approach of an asteroid [5]. They performed observability analysis for the optical navigation and proposed an observability improvement method based on maneuvers. Mortari and Conway proposed a weighted least squares method for state estimation of interplanetary orbits using multi-angle measurements [38]. Christian investigated the possibility of deep-space optical navigation using a planet’s centroid and apparent diameter in images [39]. Compared with angle-only measurements, the use of the apparent diameter can improve the observability of optical navigation. Christian further investigated the pose estimation and optical navigation methods using the features of the rotating celestial bodies (e.g., asteroids) and spheroidal planets with banded atmospheres (e.g., Jupiter) [9]. Andreis et al. analyzed the performance of optical navigation of a CubeSat in an Earth–Mars transfer [11]. Ma et al. reviewed deep space navigation methods and concluded that the conventional doppler-rRange radio navigation method can hardly satisfy the deep space mission requirement of high performance in real-time accuracy and coverage [10]. In addition, they found that the higher frequency of pulsars leads to a better navigation solutions compared to optical navigation. Ely et al. compared deep-space navigation methods using optical, pulsar-based, and radiometric measurements and concluded that significant pulsar time-of-arrival measurement noise limits its utility for approach and entry navigation [40].
The least squares (LS) and Kalman filter are two basic methods for OD [41,42]. In LS-based OD, a set of measurements, such as range and angle measurements, is used to estimate the initial state vector of a spacecraft. The basic idea of LS is to minimize the difference between the observed and predicted measurements by adjusting the initial state vector [43]. This adjustment is done by solving a system of linear equations, where the solution corresponds to the state vector that best fits the observations in a least-squares sense. LS-based OD is widely used in space-related applications such as satellite navigation and OD of space debris and asteroids. However, LS has limitations for onboard applications as it is a batch method that requires high computational cost.
The Kalman filter and its variants belong to the category of sequential methods, requiring a lower computational cost than LS. Commonly used Kalman filters include (to name a few) the extended Kalman filter (EKF), unscented Kalman filter (UKF) [24,25], cubature Kalman filter (CKF) [27], and Gaussian mixture filter (GMF) [44]. In order to effectively filter data on onboard applications, two fundamental prerequisites must be fulfilled, namely, achieving high accuracy while maintaining low complexity. Nevertheless, these requirements can sometimes be in conflict with one another [45]. For instance, the UKF is recognized for its superior accuracy compared to the EKF; however, its computational cost is significantly higher due to the integration of over ten sigma points [30,46].
Several research studies have been carried out recently to improve the efficiency of the OUP and OD methods for onboard applications. Greco and Vasile developed a surrogate-based particle filter in which a surrogate model replaces the orbit integrations in the OUP process of a conventional particle filter [47]. Zhou et al. developed an adaptive order-switching Kalman filter (AOSKF) for cislunar OD [45]. In AOSKF, a deep neural network (DNN) is employed to detect highly nonlinear points and the OUP’s orders are adaptively adjusted according to the nonlinear detection results. More recently, Zhou et al. proposed a DNN-based orbital uncertainty propagation and estimation framework for low-Earth orbit (LEO) spacecraft in which the computational cost is significantly reduced [46]. In this method, the orbit propagation process in the conventional UKF is replaced by a DNN-based prediction process. However, such an OUP and OD method can be further improved, as the prediction capacity of the DNN is limited.
Motivated by Zhou et al.’s work [46], this paper aims to improve the computational efficiency of the OD using a neural network. A deep space transfer case, the Earth–Jupiter transfer, is taken as an example to show the performance of such a method. Compared with Zhou et al.’s work, the innovations of this paper can be summarized as follows:
- A multivariate attention-based neural network (MANN), rather than a simple DNN, is designed and utilized to replace the orbit integration process in the UT and UKF. It will be shown that the designed MANN has a much more advanced performance than the DNN in the investigated problem.
- An Earth–Jupiter transfer case, rather than an LEO case, is considered in this work. The input structure of the sample is comprehensively discussed and carefully designed.
- A method for fast generating a large number of samples for the Earth–Jupiter transfer case is presented.
The remainder of this paper is organized as follows. Section 2 describes the neural network-based OD framework. Section 3 discusses the construction of the samples and introduces the structure and training process of the MANN. Numerical simulations are provided in Section 4 and conclusions in Section 5.
2. Neural Network-Based Orbit Uncertainty Propagation Orbit Determination Framework
2.1. Orbit Uncertainty Propagation
In this work, the dynamics of a spacecraft during the transfer from Earth to Jupiter considers the point-mass gravitational accelerations and the Solar Radiation Pressure (SRP) perturbations; thus, the high-fidelity dynamics model can be written as
where represents the state vector (with and being the position and velocity vectors, respectively) of the spacecraft in the heliocentric inertial coordinate, , , and denote the gravitational constants of the Sun, Mars, Earth, and Jupiter, respectively, , , and are the position vectors of the Earth, Mars, and Jupiter in the heliocentric inertial coordinate, is the reflection coefficient, is the area-to-mass ratio, and is the reference value of the SRP at a distance of 1 AU (1 AU = 149,597,870 km, and ) from the Sun [8,11]. Note that in this work the ephemeris data of the Earth, Mars, and Jupiter come from the Jet Propulsion Laboratory’s Development Ephemerides (DE432). In this work, the J2 term of the Earth and the propulsion term are not considered in order to simplify the problem (as in [11]). In addition, we define
and in the remainder of this paper, given the initial epoch and the corresponding initial orbital state , the solution flow of the ordinary differential equation in Equation (1) can be represented as .
Orbit deviation propagation is the premise of orbit determination [46]. This is because orbit deviation propagation, also called the orbit uncertainty propagation technique, can help predict the uncertainties, which is necessary to calculate the Kalman gain in a Kalman filter framework. In addition, it can help provide gradient information for the LSM. As shown in Figure 1, the black solid line and the black dashed line represent the nominal orbit and the neighboring orbit, respectively, under the high-fidelity dynamics model. Let be the initial orbital state of the neighboring orbit, with being the initial deviation between the nominal and neighboring orbits. By propagating the orbits under high-fidelity dynamics, the orbital states of the nominal and neighboring orbits at any given epoch t can be obtained as and . The orbit deviation between the nominal and neighboring orbits at a given epoch t is defined as
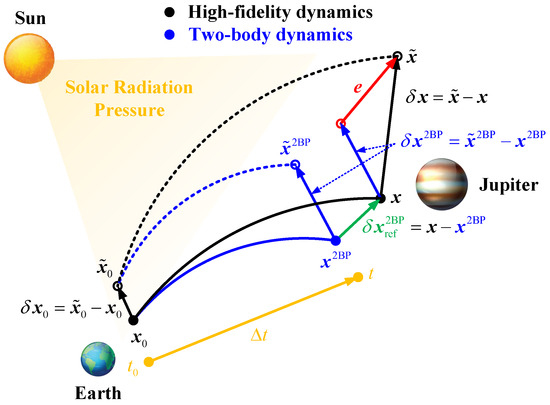
Figure 1.
An illustration of the orbit deviation propagation framework.
The orbit deviation propagation is used to calculate or predict the deviation given the initial state of the nominal orbit and the initial deviation . In general, there are two ways to calculate the deviation . The first is to propagate the neighboring orbit directly and calculate the deviation using Equation (3). The other is to approximate the deviation using techniques such as state transition matrix (STM), state transition tensor (STT), or polynomial chaos (PC). Both approaches require numerical integrations, making its computational cost unacceptable for certain onboard applications, especially CubeSat-like platforms with limited computational capacity.
Recently, a novel neural network-based method was developed in [46] to significantly improve the computational cost of the OD of an LEO spacecraft. This work extends such an idea to solve the OD problem of an Earth–Jupiter transfer spacecraft with the framework shown in Figure 1. In Figure 1, the orbits propagated using high-fidelity and two-body dynamics (considering only the Sun’s gravitational force) are represented by black and blue lines, respectively. In addition, the orbital state propagated by the two-body dynamics is distinguished using a superscript “2BP”. For example, and represent the orbital states of the nominal and neighboring orbits under the two-body dynamics. Under the two-body dynamics, the orbit deviation in Equation (3) has an analytical solution (i.e., can be analytically computed). The detailed expressions for the orbit deviation propagation under the two-body dynamics are well presented in [46,48]. As shown in Figure 1, we define , which represents the residual between the true (under the high-fidelity dynamics) and two-body orbit deviation propagation solutions. If the residual can be predicted using a neural network, then the value of can be obtained without additional numerical integrations, which can significantly reduce the computational burden.
In this work, a multivariate attention-based neural network (MANN) is developed to predict the residual . The designed structure and the training process of the MANN will be introduced in the next section. Let be the prediction of the MANN; then, the orbit deviation propagation solution can be rewritten as
In the following subsection, the solution in Equation (4) is combined with a UT method (denoted as MANN-UT) to improve the OD efficiency of the conventional UKF method.
2.2. Orbit Determination Method
The framework of the MANN-UT is illustrated in Figure 2. Given the mean of the initial state and its associated covariance , thirteen sigma points () can be obtained under the UT framework as follows:
where is the dimension of the orbit state, is an adjusted factor, is the i-th column of the matrix , , and is computed using the Cholesky decomposition. In this work, and .
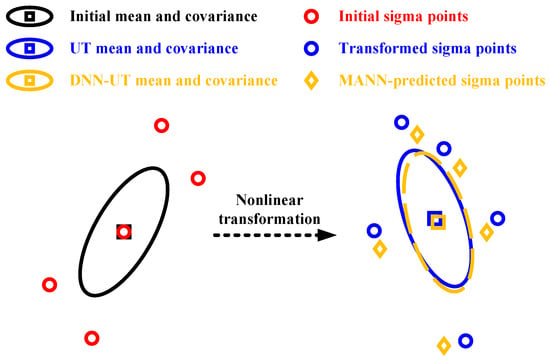
Figure 2.
An illustration of the framework of MANN-UT.
In the conventional UT framework, the thirteen sigma points in Equation (5) are propagated from the initial epoch to a given future epoch t using high-fidelity dynamics; thus, we have (). After weighing these propagated sigma points, the mean and covariance can be computed as
where and represent the mean and covariance at epoch t and and are the weights of the mean and covariance , with their expressions provided by
where is used in this work.
Using Equation (4), the propagated sigma points can be written as
where denotes the two-body orbital deviation of the i-th sigma point.
In addition, the covariance can be rewritten as
Motivated by [46], by applying such a MANN-UT method into a UKF framework, a MANN-assisted UKF (denoted as MANN-UKF) is presented herein.
First, the OD system of the Earth–Jupiter transfer orbit can be written as
where and represent the orbital state at epochs and , respectively, is the measurement vector at epoch , denotes the measurement model, is the process noise, and is the measurement noise. We assume that the process and measurement noises are zero-mean Gaussian errors, with their covariance being and , respectively, i.e., and . Note that Equation (11) is a discrete format of the OD system, which should be distinguished from Equations (1)–(10).
Based on the MANN-UT presented in Equations (9) and (10), the process of the MANN-UKF is provided as follows:
- A.
- Time Update
- Given the estimated state and the associated covariance at epoch , calculate the predicted state and the associated covariance :
- B.
- Measurement update
- Calculate the Cholesky decomposition of and generate sigma points .
- Calculate the predicted measurement and the associated covariance and :
- When the measurement has been collected, calculate the estimated state and the associated covariance at epoch :
Compared with traditional UKF, the advantage of using the proposed MANN-UKF is that it actually only needs to integrate one sigma sample point to calculate the prediction state and covariance matrix instead of integrating all thirteen sigma sample points, as the remaining twelve sigma sample points can be predicted by MANN. The estimation accuracy of MANN-UKF may be worse than that of UKF because of the inevitable prediction error when using MANN. This section introduces a neural network-assisted Earth–Jupiter transfer OD system, wherein MANN construction and training are shown in the next section.
3. Construction and Training of the Multivariate Attention Neural Network
3.1. Sample Construction
As shown in Figure 1, the goal of MANN is to predict . The variables that are related to are provided as follows:
- The initial state of the nominal orbit: .
- The initial deviation: .
- The orbital state of the nominal orbit at the epoch t: .
- The orbit deviation propagated using the two-body dynamics: .
Apart from the four variables, there are some other variables that are available and can be potentially helpful in predicting :
- The deviation between the nominal orbits propagated using the high-fidelity and two-body dynamics: . This variable is expected to carry the information on the errors between the high-fidelity and two-body dynamics.
- The state vectors of the Earth, Mars, and Jupiter in the heliocentric inertial coordinate at the initial epoch : , , and . These variables contain information about the gravitational perturbation of the third body. Here, both the position of the perturbed object and the velocity of the perturbed bodies are considered, as the positions of the perturbed bodies in have an effect on the orbital propagation and adding the velocities of the perturbed bodies to the sample helps to provide information about the position of the perturbed bodies at future times.
- The propagated interval: . This is an important variable, as a longer propagated interval usually indicates more significant orbital deviations.
- The variable related to the SRP: .
Therefore, the input structure of the sample is designed as follows:
and the structure of the sample is designed as
Based on the above discussion of the input and output of the sample, a method is developed to quickly generate a large number of samples.
Step 1: Generate ten Earth–Jupiter transfer orbits between 1 January 2024 and 31 December 2033.
Step 1.1: Divide the above periods (1 January 2024–31 December 2033.) with an interval of 1 year. For each time interval, optimize the launch window. The corresponding steps are as presented in Step 1.2–Step 1.3;
Step 1.2: Two-impulse transfer is employed. The launch time JD0 and transfer time ToF (Time-of-flight, unit: day) are taken as the optimization variables. At the launch epoch, the C3 is constrained to be no more than 100 km2/s2, and at the arrival epoch the spacecraft is required to enter an orbit with an eccentricity of 0.98 and a height of 10,000 km at the perigee of the Jupiter. Let and be the magnitudes of the position vectors of spacecraft and Jupiter at the arrival epoch heliocentric inertial coordinate, respectively; then, the velocity increment that is required for the spacecraft to enter the Jupiter orbit can be expressed as shown below.
Taking the magnitude of the velocity increment as the objective, the optimization problem can be provided as follows:
In this work, the Lambert transfer is solved using the Python toolkit lamberthub (https://pypi.com.cn/project/lamberthub/, accessed on 8 May 2024).
Step 1.3: The differential evolution (DE) algorithm is used to optimize the problem in Equation (24). The range of launch time JD0 is determined by Step 1.1 and the range of ToF is set as [10 days, 5 years]. The population is set to 50 and the number of maximal iterations is set to 100. In this study, the DE algorithm is realized through the Python toolkit geatpy (https://pypi.com.cn/project/geatpy/, accessed on 8 May 2024). The ten obtained Earth–Jupiter transfer orbits are shown in Figure 3.
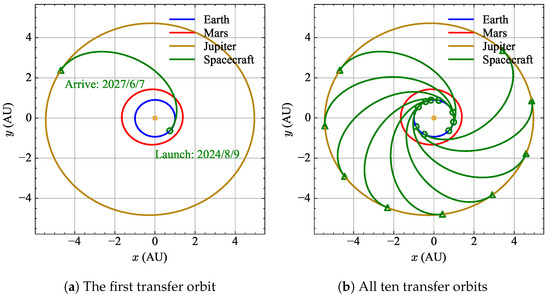
Figure 3.
Optimized Earth–Jupiter transfer orbits.
Step 2: For the ten Earth–Jupiter transfer orbits obtained in Step 1, high-fidelity dynamics (i.e., Equation (1)) are used for orbit propagation. In order to avoid singularities at the Earth’s or Jupiter’s center, we remove the 60-day orbits at the beginning and end of the transfer orbits under two-body dynamics in Step 1. Taking the orbit state at the 60th day as the initial value and randomly generating c (variable of the SRP) between 0 and 0.1, orbit propagation is performed using high-fidelity dynamics.
Step 3: Each transfer orbit obtained in Step 2 under the high-precision dynamics is divided into ten orbits according to the time. For each split orbit, 100 initial deviations are randomly generated, where the position deviation is no more than 104 km per axis and the velocity deviation is no more than 0.1 km/s per axis. Additionally, the propagated time is randomly divided into ten epochs and a sample is constructed for each epoch according to Equation (22). Through the above methods, a total of 105 samples are obtained.
Note that one of the drawbacks of such neural network-based methods is that they cannot be employed in cases for which they are not trained. The performance of the neural network will degrade if it is trained under the dynamics in (1) and then employed under another dynamics. Therefore, if we want to consider additional accelerations, such as the J2 term of the Earth and the propulsion term, the samples must be regenerated and the neural network should be retrained.
3.2. Structure of the Neural Network
In recent years, due to the rise of Chat-GPT, transformers (including improved versions such as iTransformer, Informer, Autoformer, Crossformer, etc.) have received significant attention in the fields of natural language processing (NLP) and computer vision (CV). In transformer-based architectures, the most crucial portion is the multi-head attention mechanism. The multi-head attention mechanism captures the dependencies between different variables by applying different weights. In recent years, some scholars have found that in NLP and CV contexts, network architectures based on a multi-head attention mechanisms exhibit better capacity than conventional neural networks such as RNN, DNN, and CNN. Inspired by the relevant research work, in this paper we construct a neural network model based on a multi-head attention mechanism, which is applied to solve the orbit deviation propagation problem in the Earth–Jupiter transfer process.
The structure of the Multivariate Attention-based Neural Network (MANN) constructed in this paper is shown in Figure 4.
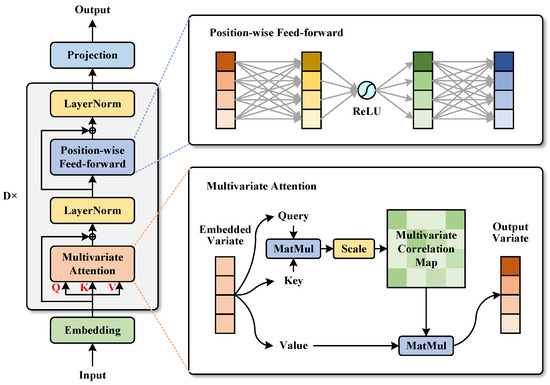
Figure 4.
Structure of the designed MANN.
In Figure 4, the MANN developed in this paper is similar to the encoder module of the standard Transformer. As shown on the left side of Figure 4, the MANN consists of an embedding module, D (Depth) processing modules e (shown by gray in Figure 4) connected sequentially, and a projection module. Each processing module contains a multivariate attention layer, two normalization layers, and a feed-forward layer.
The main role of the embedding module is to expand the sample input into a dim-dimensional vector , with the expression provided as follows:
where is a user-defined parameter.
At the multi-head attention mechanism layer, for the i-th attention mechanism, the calculation process is as follows:
Step 1: Calculate the three vectors , , and using linear transformation:
where and .
Step 2: Calculate the scores by the sum dot product of and :
Step 3: Scale the scores calculated in Step 2. In this paper, the scores are divided by 8, which allows the MANN to have a more stable gradient. Then, the result is normalized by softmax:
Step 4: Multiply the output from Step 3, , with the vector to obtain the output of the i-th head:
Step 5: Combine the outputs of all the heads and multiply them by the weight matrix :
Step 6: Map the output of Step 5 linearly to obtain the output with the dimension same as that of :
The above multi-head attention mechanism layer can be written as follows:
The normalization layer is mainly used to improve training convergence, and can be expressed as
The function of the feed-forward layer is to extract deeper features of the input data through linear transformation:
The second normalization layer can be written as
Finally, the projection module maps the data to required dimensions:
The above process can be summarized as follows:
For the MANN architecture described above, the user-defined parameters include the depth (D) of the processing module (in gray), the output dimension (dim) of the embedding module, the number of multivariate attention heads in the module, and the dimensions of the heads in the embedding module.
3.3. Training of the Neural Network
For the MANN described in the previous subsection, the neural network model is constructed in the Pytorch environment in this work. During the training process, the generated 100,000 samples are divided into two groups: a training dataset including 80% of the samples and a validation dataset including the remaining 20% of the samples. The MANN is trained for 1000 iterations, and in each iteration, the training dataset is randomly shuffled into ten batches (each batch contains 8000 samples). The mean square error (MSE) is used as the loss function of neural network optimization, and Adaptive Moment Estimation (Adam) is used to optimize the neural network. We set each multivariate attention layer in the MANN to contain four heads, each with a dimension of 64. We first considered two sizes of MANN: one with depth 2 and dim 16, and a second with depth 8 and dim 256. The training results for the two sizes of MANN are shown in Figure 5a,b. As can be seen from Figure 5a,b, there is no apparent overfitting phenomenon when the MANN is used. In addition, there is no obvious deviation between the MSE loss value of the training dataset and the validation dataset. Meanwhile, the minimum value of the MSE loss in the validation dataset of the first small-size MANN is about 10−7, while that in the validation dataset of large-size MANN is about 10−8, indicating that increasing the depth and dimension of the MANN can help to improve the prediction results of neural networks.
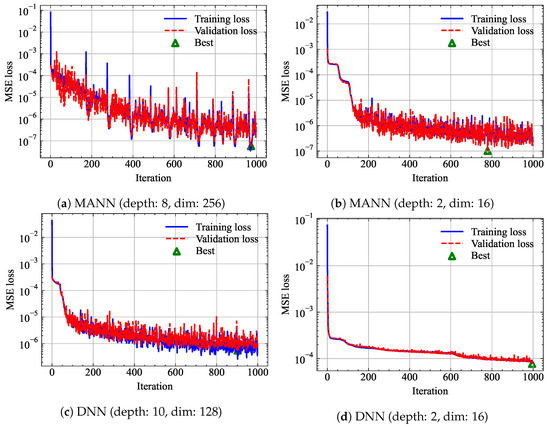
Figure 5.
Time histories of the MSE losses of the MANN and DNN.
Figure 5c,d shows the training process of a traditional DNN to show the advantages of the MANN neural network. As shown in Figure 5c, the DNN shows obvious overfitting in the training process, and the MSE loss in the training dataset is significantly smaller than the MSE loss in the validation dataset. At the same time, the MSE loss values of the DNN are at least one order of magnitude larger than those of the MANN. This shows that the developed MANN has advantages in prediction accuracy and generalization compared with the traditional DNNs.
The training performances of MANNs and DNNs with different sizes are provided in Table 1 and Table 2. It can be seen from Table 1 and Table 2 that the MANN has significant advantages over the DNNs when the structure size is small. For example, with depth 2 and dim 16, the minimal MSE loss of the validation dataset of MANN is while that of DNN is . The minimal MSE loss of the validation dataset of the MANN is less than the order of , while that of the DNN is larger than in most cases. In the following simulation, the MANN with the smallest MSE loss (shown in bold in Table 1) is adopted as the neural network to predict the .

Table 1.
Training performance of MANNs with different sizes.

Table 2.
Training performance of DNNs with different sizes.
4. Simulation Results
W take the first orbit (i.e., the orbit departing on 9 August 2024 in Figure 3a) as an example for simulation. Note that as the initial deviations are different, the samples in this simulation are not in the training or validation datasets to show the performance of the MANN in a case for which it is not trained. After deleting 60 days at the beginning and ending epochs, the total flight time is about 911.7 days. The parameters for the simulations are listed in Table 3. We assume that a total of ten measurements can be obtained during the transfer process, i.e., the measurement interval is about 91 days (no measurement is available at the initial epoch). Assume that the position vectors can be measured. In general, the position vectors can be measured by observing planets or beacons. For example, by observing two different planets and obtaining the corresponding line-of-sight vectors, we can compute its own-position vector. Therefore, the measurement model is written as follows:

Table 3.
Parameters for the simulations.
First, a single simulation was performed, with the initial position errors set to 10,000 km per axis and the initial velocity error set to 0.1 km/s per axis. The standard deviation of the measurements was set as 1000 km per axis. The initial covariance was set as
The single simulation results are shown in Figure 6 and Figure 7. In Figure 6 and Figure 7, the blue curve is the OD error of the single simulation and the red curve is the standard deviation forecast by the MANN-UKF and UKF. As can be seen from Figure 6 and Figure 7, the OD errors of both methods are within the boundaries. In Figure 6 and Figure 7, the symbol denotes the STD of estimated errors, which is calculated analytically using Equation (20). The values of the estimated STDs converge in the first 100 days. The position and velocity STDs at the initial epoch are 10,000 km and 0.01 km/s, respectively. The STDs of the position estimated errors converge to approximately 300 km at the ending epoch.
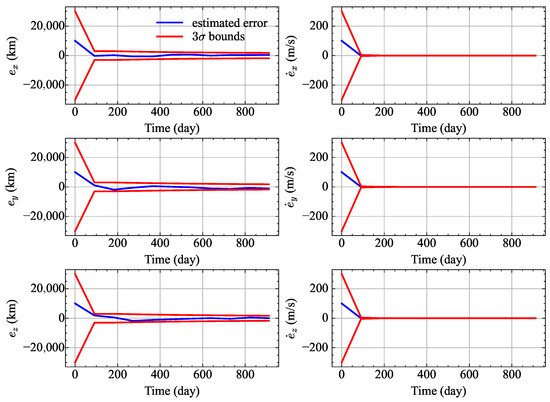
Figure 6.
Orbit determination errors of the single simulation of MANN-UKF.
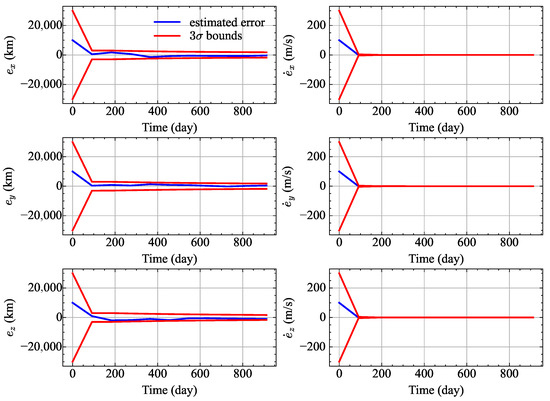
Figure 7.
Orbit determination errors of the single simulation of UKF.
Figure 8 shows the Mahalanobis distance (MD) results of the two methods in the single simulation, with the MD defined as follows:
where and represent the true orbit and the estimated orbit, respectively, and is the estimated covariance matrix. The Mahalanobis distance is a statistical measure used to compare a set of observations or variables. It takes into account the covariance between variables, unlike other distance measures such as Euclidean distance. Essentially, it measures the distance between a point and a distribution or a set of points, taking into account the correlation between the variables. In Equation (42), a value of MD closer to 1 indicates better uncertainty estimation performance [46]. As can be seen from Figure 8, at the ending epoch, the estimation performance of MANN-UKF is slightly worse than that of UKF. This is because the MANN method has lower prediction accuracy when the deviation is slight [46].
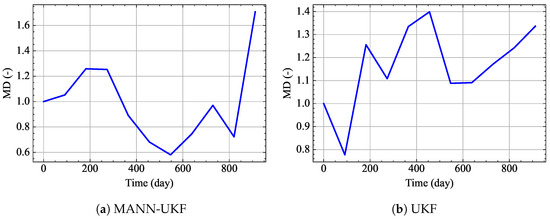
Figure 8.
MD results of the single simulation.
A Monte Carlo (MC) simulation was further carried out, with the results shown below. For each method, 100 MC simulations were performed; for each MC simulation, the initial guess was obtained by the following equation:
The MC simulation results are shown in Figure 9 and Figure 10. In Figure 9 and Figure 10, the boundaries were statistically obtained based on the results of 100 MC simulations. The curve of one standard deviation for both methods is provided in Figure 11. As shown in Figure 11, the convergence tendency of estimation accuracy of MANN-UKF and UKF is very close. For example, during the epochs from 200 days to 600 days, the MANN-UKF is slightly more accurate than the UKF in terms of the estimated errors along the x-axis. Slight differences exist as initial estimations are randomly generated in the MC simulation. However, around the ending epoch the performance of MANN-UKF is slightly worse than that of UKF. This is because around the ending epoch the estimation error is smaller than that in the early stage, and the prediction accuracy of MANN decreases, resulting in the decline of the prediction accuracy. As a result, the performance of MANN-UKF decreases.
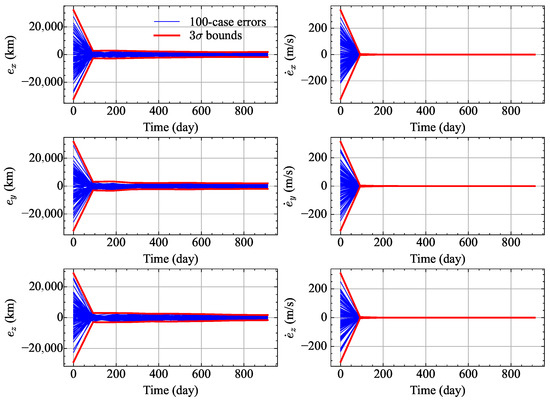
Figure 9.
MC results of MANN-UKF.
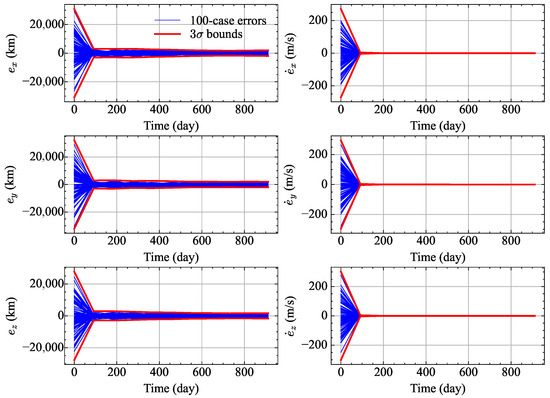
Figure 10.
MC results of UKF.
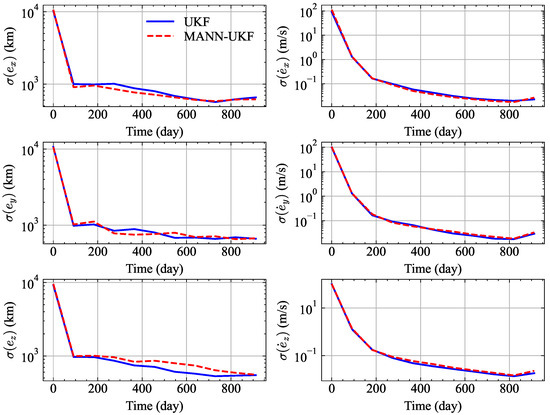
Figure 11.
MC results comparing MANN-UKF and UKF.
Figure 12 and Figure 13 are Box and Whisker Plots. The line splitting the box in two represents the median value. The upper edge and lower edge of the box represent the upper quartile and lower quartile respectively. The values at which the vertical lines stop at are the values of the upper and lower values of the data. The single points on the diagram show the outliers.
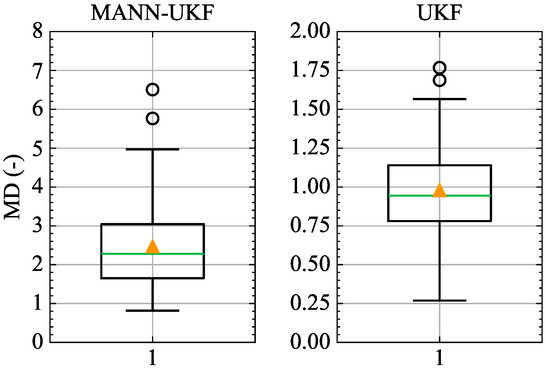
Figure 12.
Comparison of MD between MANN-UKF and UKF in the MC simulations.
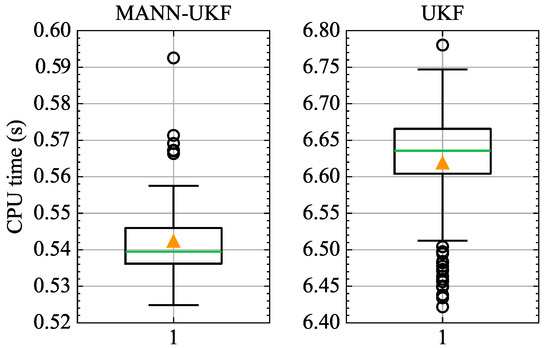
Figure 13.
Comparison of CPU times between MANN-UKF and UKF.
As shown in Figure 12, the MDs of UKF are around 1, while the MC of MANN-UKF are between 1 and 5. This is again due to the decline in the prediction accuracy of the MANN when the deviation is small, resulting in inaccurate prediction of the covariance matrix.
The primary purpose of the proposed MANN-UKF method is to reduce the computational cost in OD. Figure 13 and Table 4 compare the CPU times of the two methods. The CPU time of the UKF method is about 6.6 s, while the proposed MANN-UKF method only needs about 0.54 s. The proposed method saves on CPU time by more than 90%.

Table 4.
CPU times of MANN-UKF and UKF.
Apart from the above case, a second case is presented to investigate the performance of the proposed method. The parameters of the second case are shown in Table 5. In this case, line-of-sight (LOS) measurements are employed instead of the measurement model in Equation (40). We assume that the spacecraft can obtain the LOS measurements (from the spacecraft to the Jupiter) using optical sensors. The LOS measurement model is represented as follows [42,49,50]:

Table 5.
Parameters for the simulations (second case).
In this simulation, the STDs of the LOS measurements are set as per axis (similar to [42]). One hundred MC runs were performed using two algorithms, with the estimated STDs shown in Figure 14. It can be seen from Figure 14 that the proposed MANN-UKF can output OD solutions with accuracy and convergence similar to those of the UKF.
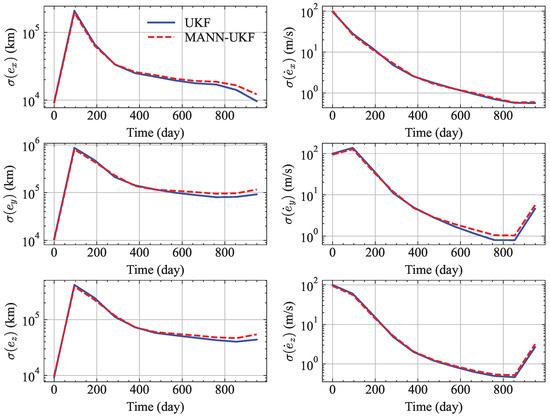
Figure 14.
MC results comparisons between MANN-UKF and UKF (second case).
5. Conclusions
This paper proposes a multivariate attention neural network (MANN)-based orbit uncertainty propagation (OUP) and orbit determination (OD) method for Earth–Jupiter transfer. The proposed method relies on a carefully designed MANN for orbit deviation propagation, which is further employed to predict uncertainties for Earth–Jupiter transfer OD. Training results show that the MANN outperforms conventional deep neural networks (DNNs) regarding accuracy and generalization. The minimal loss of the MANN is lower than , which is at least two orders of magnitude smaller than that of a conventional DNN. Using the proposed MANN-based method, the orbit estimation errors quickly converge. Orbit estimation results reveal that the MANN-based method has accuracy close to that of an unscented Kalman filter (UKF) while saving more than 90% of the computational time of UKF. Moreover, the Mahalanobis distance results show that the proposed method has worse uncertainty estimation performance than the UKF method. In the future, more complex dynamics should be considered to test the robustness of the proposed method. In addition, combining the MANN with other estimation methods, such as a cubature Kalman filter or Gaussian sum filter, is suggested.
Author Contributions
Methodology, Z.Z.; Writing—review & editing, Y.S.; Supervision, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 62394353).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bechini, M.; Gu, G.; Lunghi, P.; Lavagna, M. Robust spacecraft relative pose estimation via CNN-aided line segments detection in monocular images. Acta Astronaut. 2024, 215, 20–43. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, S.; Qin, T. Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation. Appl. Sci. 2022, 12, 7660–7671. [Google Scholar] [CrossRef]
- Christian, J.A. Optical Navigation Using Iterative Horizon Reprojection. J. Guid. Control Dyn. 2016, 39, 1092–1103. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, H.; Li, S.; Zhou, Y. On-board modeling of gravity fields of elongated asteroids using Hopfield neural networks. Astrodynamics 2023, 7, 101–114. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Zhao, Z.; Qin, T. Asteroid Approaching Orbit Optimization Considering Optical Navigation Observability. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5165–5179. [Google Scholar] [CrossRef]
- Ogawa, N.; Terui, F.; Mimasu, Y.; Yoshikawa, K.; Ono, G.; Yasuda, S.; Matsushima, K.; Masuda, T.; Hihara, H.; Sano, J.; et al. Image-based autonomous navigation of Hayabusa2 using artificial landmarks: The design and brief in-flight results of the first landing on asteroid Ryugu. Astrodynamics 2020, 4, 89–103. [Google Scholar] [CrossRef]
- Qi, Y.; De Ruiter, A. Study of correction maneuver for lunar flyby transfers in the real ephemeris. J. Guid. Control Dyn. 2018, 41, 2112–2132. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Huo, Z.; Meng, L.; Huang, J. Near-Earth Asteroid Surveillance Constellation in the Sun-Venus Three-Body System. Space Sci. Technol. 2022, 2022, 9864937. [Google Scholar] [CrossRef]
- Christian, J.A. Pole Estimation and Optical Navigation Using Circle of Latitude Projections. J. Guid. Control Dyn. 2023, 47, 407–416. [Google Scholar] [CrossRef]
- Ma, X.; Fang, J.; Ning, X. An overview of the autonomous navigation for a gravity-assist interplanetary spacecraft. Prog. Aerosp. Sci. 2013, 63, 56–66. [Google Scholar] [CrossRef]
- Andreis, E.; Franzese, V.; Topputo, F. Onboard Orbit Determination for Deep-Space CubeSats. J. Guid. Control Dyn. 2022, 45, 1466–1480. [Google Scholar] [CrossRef]
- Zhou, X.; Qin, T.; Meng, L. Maneuvering Spacecraft Orbit Determination Using Polynomial Representation. Aerospace 2022, 9, 257. [Google Scholar] [CrossRef]
- Bețco, D.; Pârvu, P.V.; Ciudin, S. Autonomous navigation for the Martian Inspection Drone. Acta Astronaut. 2024, 216, 55–63. [Google Scholar] [CrossRef]
- Fossà, A.; Losacco, M.; Armellin, R. Perturbed initial orbit determination. Astrodynamics 2024, 1–6. [Google Scholar] [CrossRef]
- Yin, W.; Shi, Y.; Shu, L.; Gao, Y. Autonomous navigation of an asteroid orbiter enhanced by a beacon satellite in a high-altitude orbit. Astrodynamics 2024. [Google Scholar] [CrossRef]
- Capuano, V.; Harvard, A.; Chung, S.J. On-board cooperative spacecraft relative navigation fusing GNSS with vision. Prog. Aerosp. Sci. 2022, 128, 100761. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Comparative evaluation of three machine learning algorithms on improving orbit prediction accuracy. Astrodynamics 2019, 3, 325–343. [Google Scholar] [CrossRef]
- Sun, Q.; Gutiérrez, J.L.R.; Yu, X. Deep Neural Network-Based 4-Quadrant Analog Sun Sensor Calibration. Space Sci. Technol. 2023, 3, 24. [Google Scholar] [CrossRef]
- Izzo, D.; Märtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Yu, Z.; Cui, P.; Crassidis, J.L. Design and optimization of navigation and guidance techniques for Mars pinpoint landing: Review and prospect. Prog. Aerosp. Sci. 2017, 94, 82–94. [Google Scholar] [CrossRef]
- Ge, D.; Cui, P.; Zhu, S. Recent development of autonomous GNC technologies for small celestial body descent and landing. Prog. Aerosp. Sci. 2019, 110, 100551. [Google Scholar] [CrossRef]
- Li, R.; Sun, C.; Yu, X.; Zhang, L.; Wei, J.; Fang, Q. Space Noncooperative Target Trajectory Tracking Based on Maneuvering Parameter Estimation. Space Sci. Technol. 2024, 3, 78. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, Z. A review of uncertainty propagation in orbital mechanics. Prog. Aerosp. Sci. 2017, 89, 23–39. [Google Scholar] [CrossRef]
- Garcia, R.V.; Pardal, P.; Kuga, H.K.; Zanardi, M.C. Nonlinear filtering for sequential spacecraft attitude estimation with real data: Cubature Kalman Filter, Unscented Kalman Filter and Extended Kalman Filter. Adv. Space Res. 2019, 63, 1038–1050. [Google Scholar] [CrossRef]
- Yan, H.; Liu, H.; Sun, X.; Xu, M. Accuracy Evaluation of Marginalized Unscented Kalman Filter. Space Sci. Technol. 2024, 3, 85. [Google Scholar] [CrossRef]
- Zhou, X.; Jia, F.; Li, X. Configuration Stability Analysis for Geocentric Space Gravitational-Wave Observatories. Aerospace 2022, 9, 519. [Google Scholar] [CrossRef]
- Santos-León, J.C.; Orive, R.; Acosta, D.; Acosta, L. The Cubature Kalman Filter revisited. Automatica 2021, 127, 109541. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Li, X. Analytical configuration uncertainty propagation of geocentric interferometric detection constellation. Astrodynamics 2023, 7, 271–284. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, Y.; Qiao, D.; Huo, Z. An adaptive surrogate model-based fast planning for swarm safe migration along halo orbit. Acta Astronaut. 2022, 194, 309–322. [Google Scholar] [CrossRef]
- Roa, J.; Park, R.S. Reduced Nonlinear Model for Orbit Uncertainty Propagation and Estimation. J. Guid. Control Dyn. 2021, 44, 1578–1592. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Li, X. Feasible domain analysis of heliocentric gravitational-wave detection configuration using semi-analytical uncertainty propagation. Adv. Space Res. 2023, 72, 4115–4131. [Google Scholar] [CrossRef]
- Park, R.S.; Scheeres, D.J. Nonlinear mapping of Gaussian statistics: Theory and applications to spacecraft trajectory design. J. Guid. Control Dyn. 2006, 29, 1367–1375. [Google Scholar] [CrossRef]
- Park, R.S.; Scheeres, D.J. Nonlinear semi-analytic methods for trajectory estimation. J. Guid. Control Dyn. 2007, 30, 1668–1676. [Google Scholar] [CrossRef]
- Sun, P.; Colombo, C.; Trisolini, M.; Li, S. Hybrid Gaussian Mixture Splitting Techniques for Uncertainty Propagation in Nonlinear Dynamics. J. Guid. Control Dyn. 2022, 46, 770–780. [Google Scholar] [CrossRef]
- Kim, Y.; Park, S.Y. Perturbative analysis on orbital kinematics of flybys and applications to Doppler observation. J. Guid. Control Dyn. 2015, 38, 1690–1698. [Google Scholar] [CrossRef]
- Boone, S.; McMahon, J. Directional State Transition Tensors for Capturing Dominant Nonlinear Effects in Orbital Dynamics. J. Guid. Control Dyn. 2022, 46, 431–442. [Google Scholar] [CrossRef]
- Hu, R.; Huang, X.; Xu, C. Integrated visual navigation based on angles-only measurements for asteroid final landing phase. Astrodynamics 2023, 7, 69–82. [Google Scholar] [CrossRef]
- Mortari, D.; Conway, D. Single-point position estimation in interplanetary trajectories using star trackers. Celest. Mech. Dyn. Astron. 2017, 128, 115–130. [Google Scholar] [CrossRef]
- Christian, J.A. Optical Navigation Using Planet’s Centroid and Apparent Diameter in Image. J. Guid. Control Dyn. 2014, 38, 192–204. [Google Scholar] [CrossRef]
- Ely, T.; Bhaskaran, S.; Bradley, N.; Lazio, T.J.W.; Martin-Mur, T. Comparison of Deep Space Navigation Using Optical Imaging, Pulsar Time-of-Arrival Tracking, and/or Radiometric Tracking. J. Astronaut. Sci. 2022, 69, 385–472. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, X.; Peng, H.; Chen, G.; Shen, D.; Blasch, E.; Sheaff, C.B. Gaussian-Binary classification for resident space object maneuver detection. Acta Astronaut. 2021, 187, 438–446. [Google Scholar] [CrossRef]
- Zhou, X.; Qin, T.; Macdonald, M.; Qiao, D. Observability analysis of cooperative orbit determination using inertial inter-spacecraft angle measurements. Acta Astronaut. 2023, 210, 289–302. [Google Scholar] [CrossRef]
- Prabhu, K.; Majji, M.; Alfriend, K.T. Least Sum of Absolute Residuals Orbit Determination. J. Guid. Control Dyn. 2021, 45, 468–480. [Google Scholar] [CrossRef]
- Schiemenz, F.; Utzmann, J.; Kayal, H. Adaptive Gaussian Mixture based orbit determination with combined atmospheric density uncertainty consideration. Adv. Space Res. 2020, 66, 1609–1634. [Google Scholar] [CrossRef]
- Zhou, X.; Qiao, D.; Li, X. Adaptive Order-Switching Kalman Filter for Orbit Determination Using Deep-Neural-Network-Based Nonlinearity Detection. J. Spacecr. Rocket. 2023, 60, 1724–1741. [Google Scholar] [CrossRef]
- Zhou, X.; Qiao, D.; Li, X. Neural Network-Based Method for Orbit Uncertainty Propagation and Estimation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1176–1193. [Google Scholar] [CrossRef]
- Greco, C.; Vasile, M. Robust Bayesian Particle Filter for Space Object Tracking Under Severe Uncertainty. J. Guid. Control Dyn. 2021, 45, 481–498. [Google Scholar] [CrossRef]
- Khatri, Y.; Scheeres, D.J. Nonlinear semi-analytical uncertainty propagation for conjunction analysis. Acta Astronaut. 2023, 203, 568–576. [Google Scholar] [CrossRef]
- Casini, S.; Cervone, A.; Monna, B.; Gill, E. On line-of-sight navigation for deep-space applications: A performance analysis. Adv. Space Res. 2023, 72, 2994–3008. [Google Scholar] [CrossRef]
- Hu, Y.; Sharf, I.; Chen, L. Three-spacecraft autonomous orbit determination and observability analysis with inertial angles-only measurements. Acta Astronaut. 2020, 170, 106–121. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).