Seismic Resilience Evolution of Shield Tunnel with Structure Degradation
Abstract
:1. Introduction
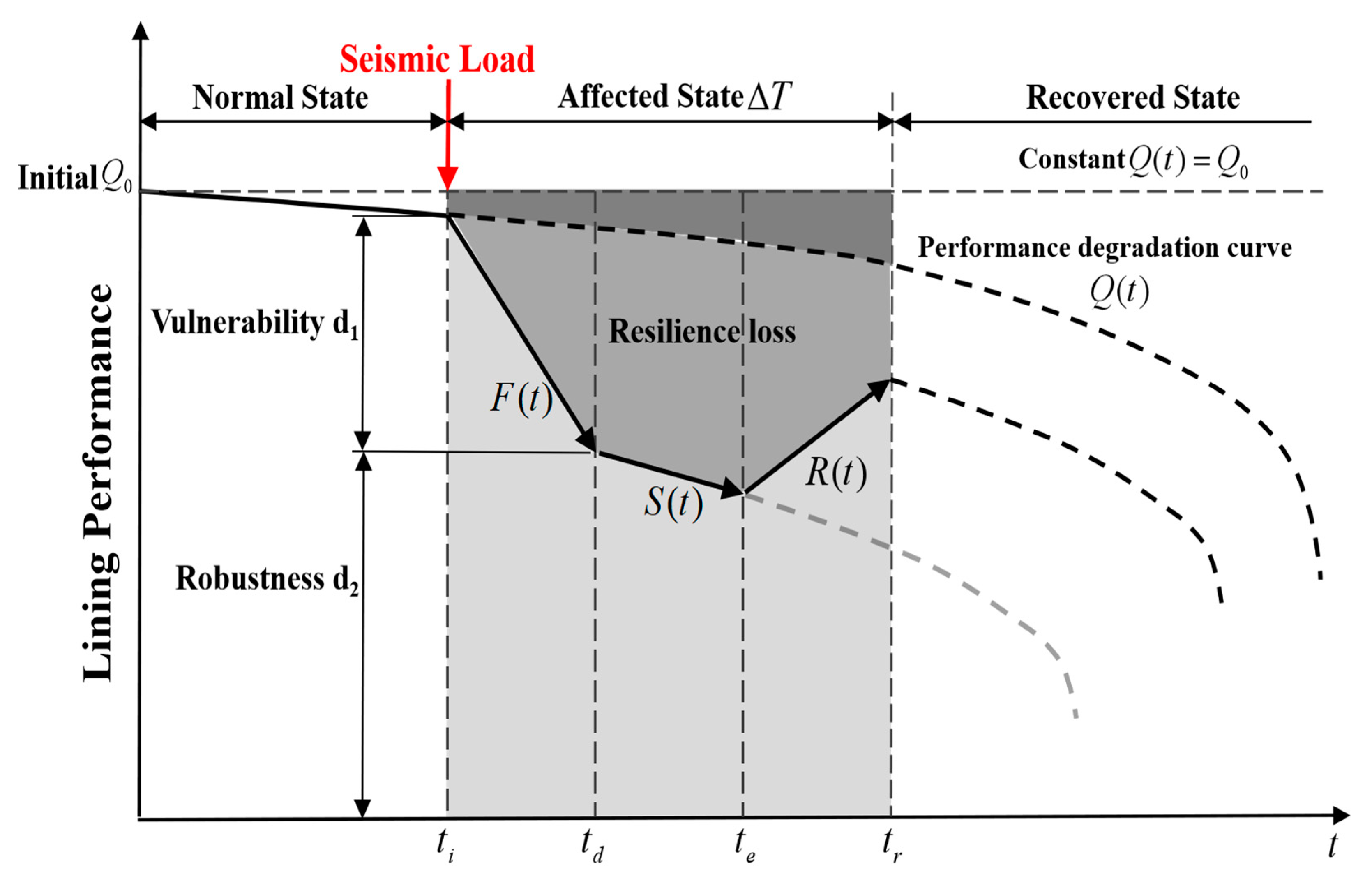
2. Resilience Assessment Model
2.1. Introduction of Resilience Assessment Model
2.2. Resilience Assessment Indicators
3. Numerical Simulation
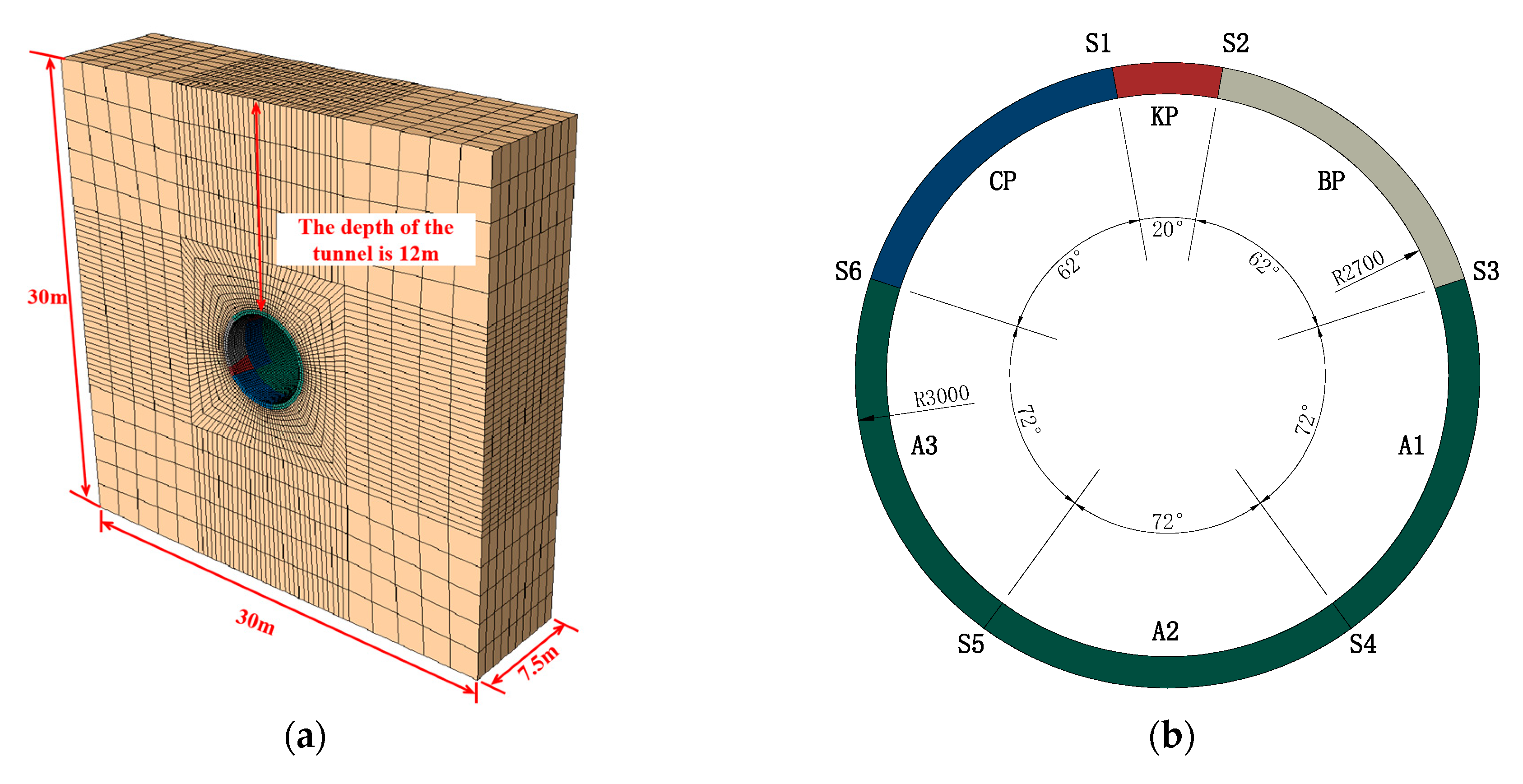
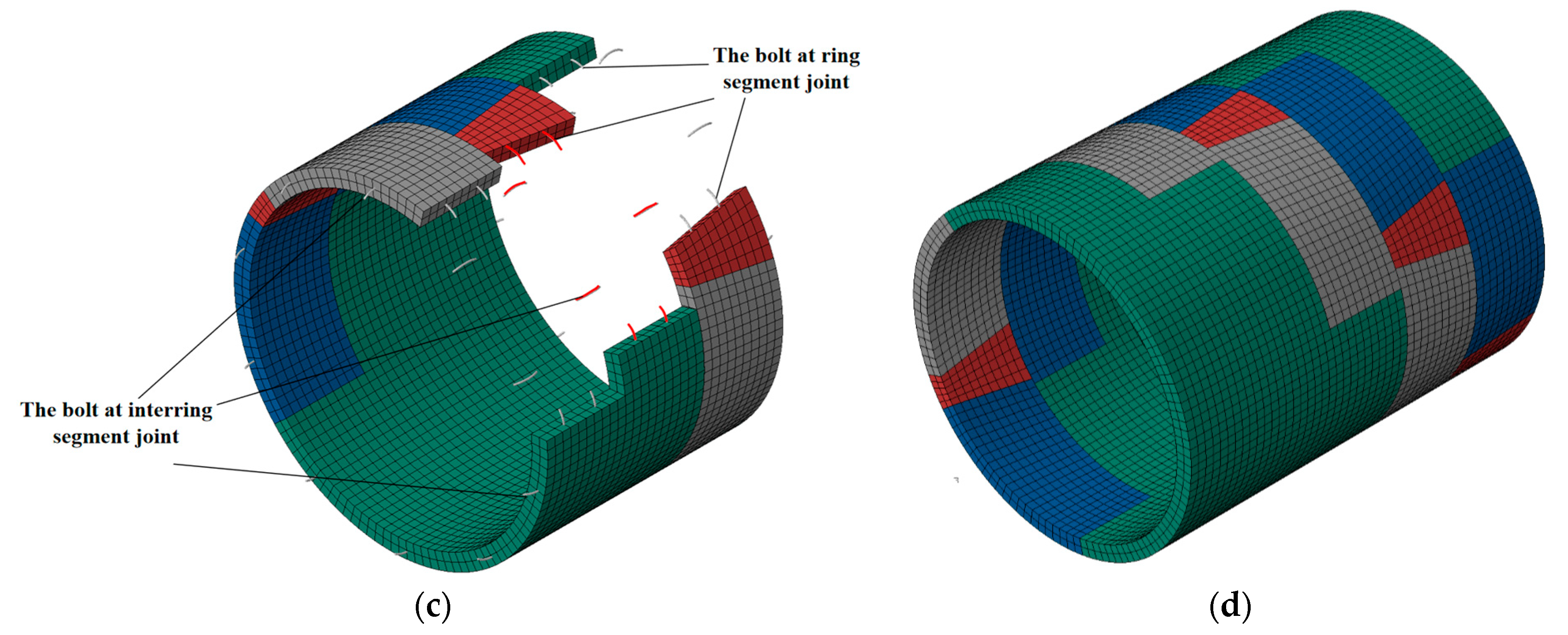
3.1. Establishment of the Finite Element Model
3.1.1. Geometric Dimensions
3.1.2. Material Constitutive
3.1.3. Interaction
3.2. Structure Load
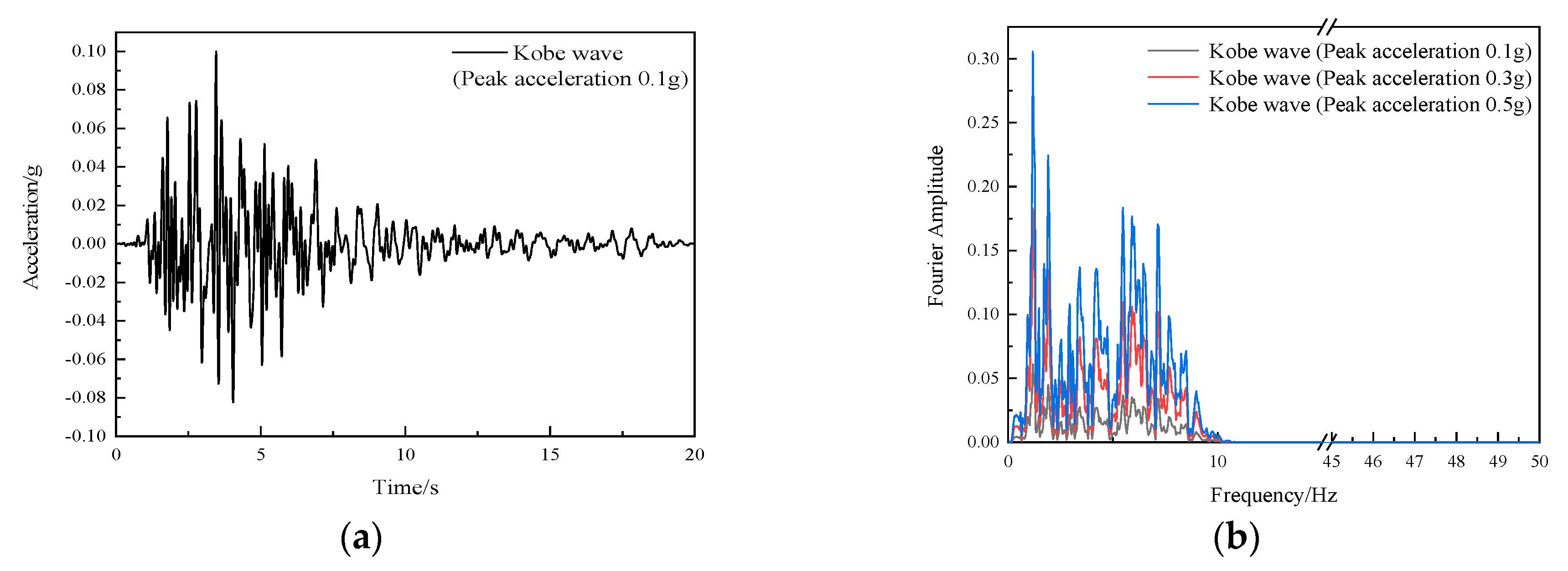
3.2.1. The Selection of Seismic Wave
3.2.2. Boundary Condition and Seismic Input
3.2.3. Preload Loss
4. Tunnel Structure Response Characteristics
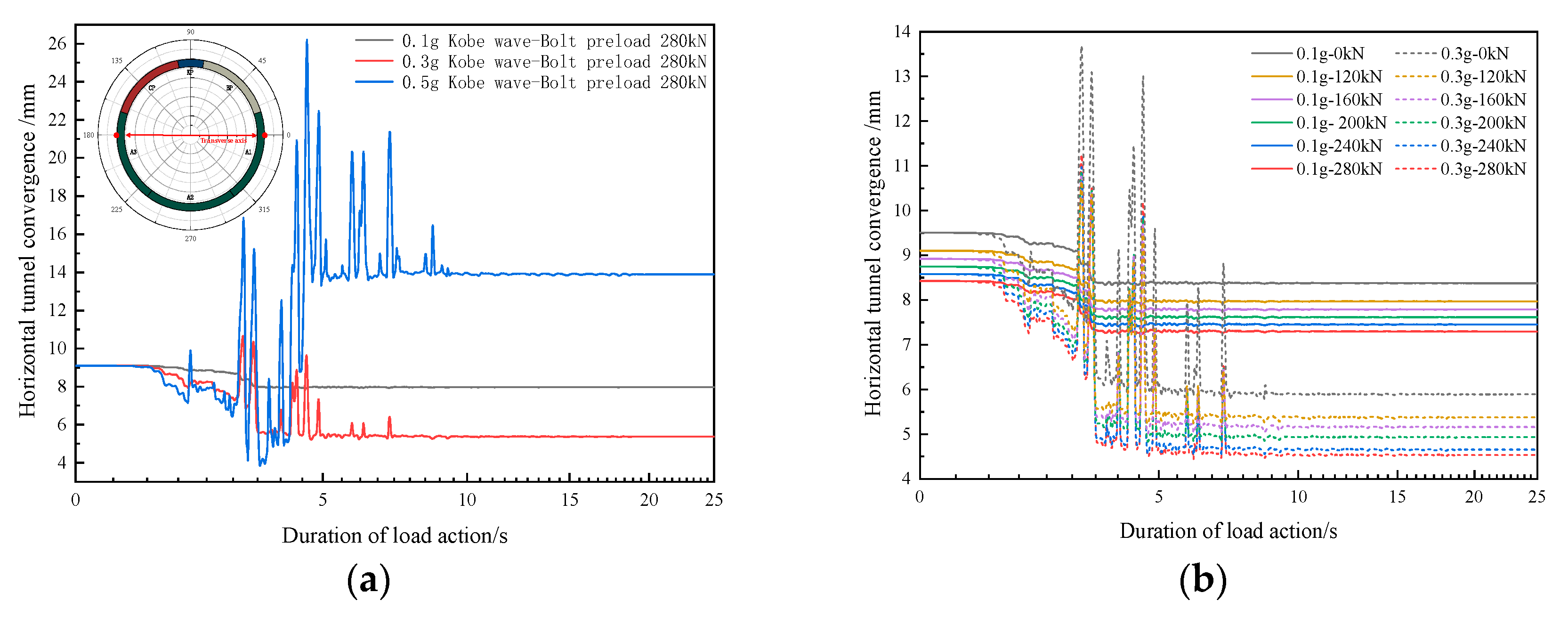
4.1. Lining Horizontal Convergence
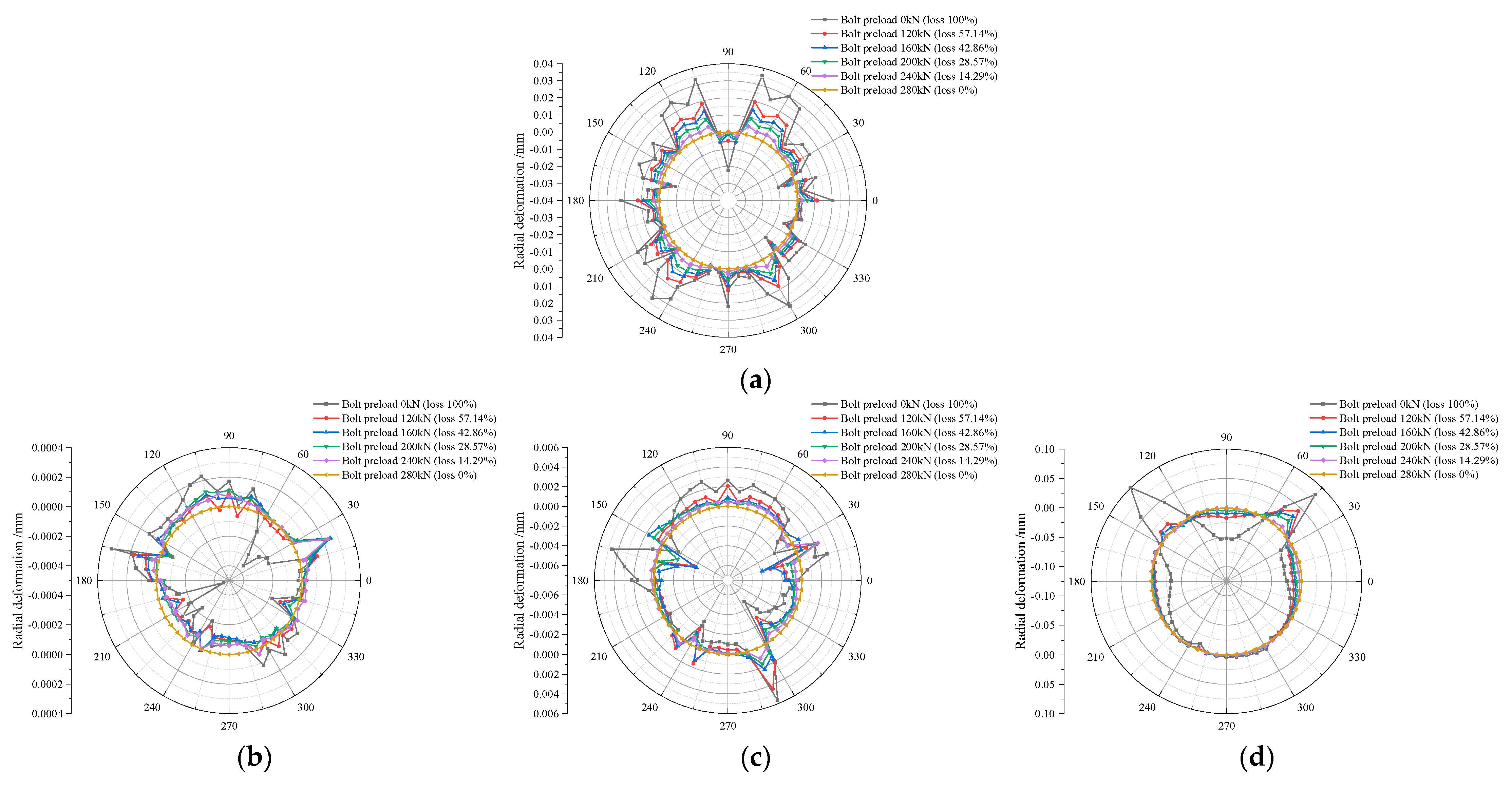
4.2. Radial Deformation of Tunnel
5. Evolution of Tunnel Seismic Resilience
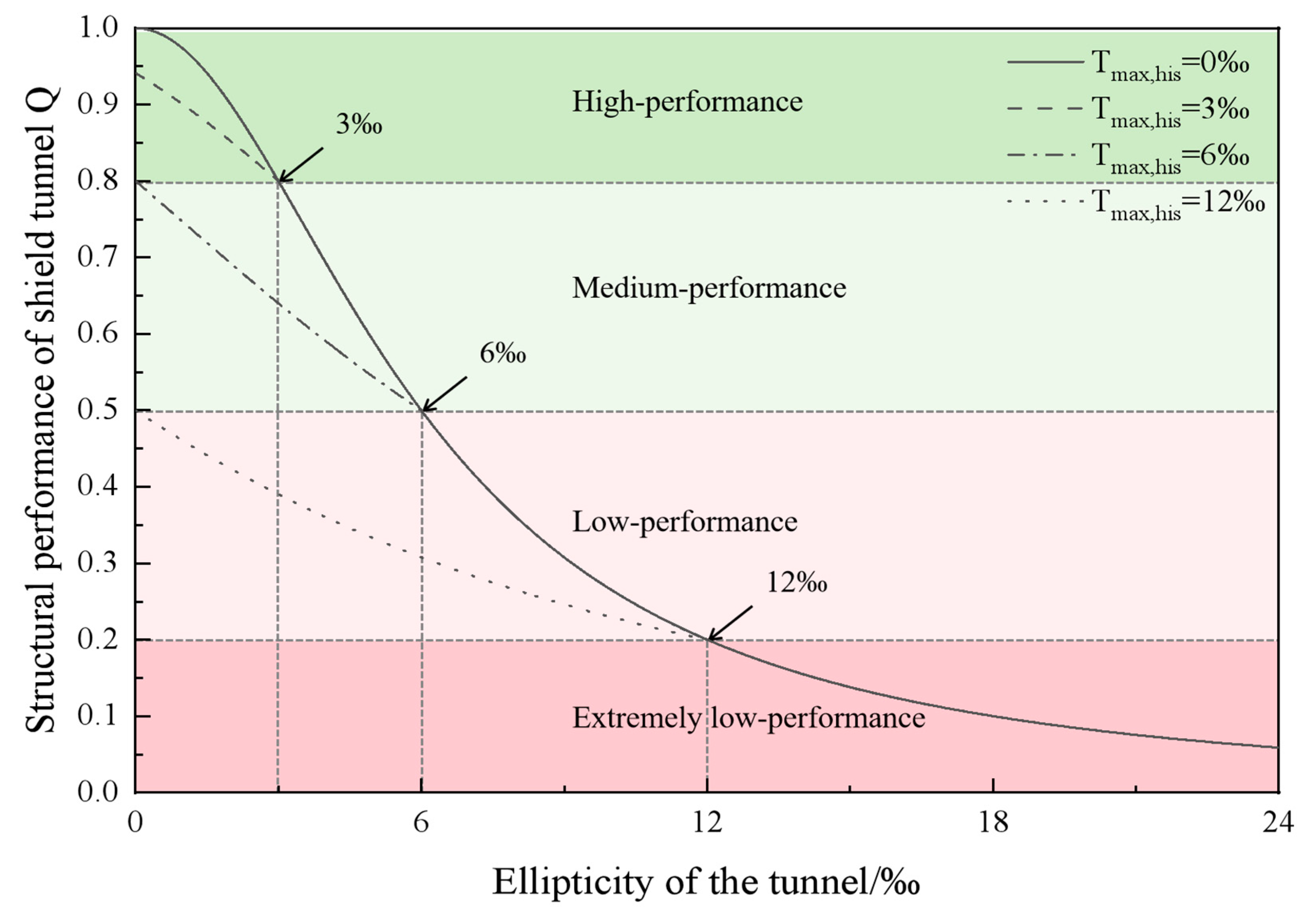
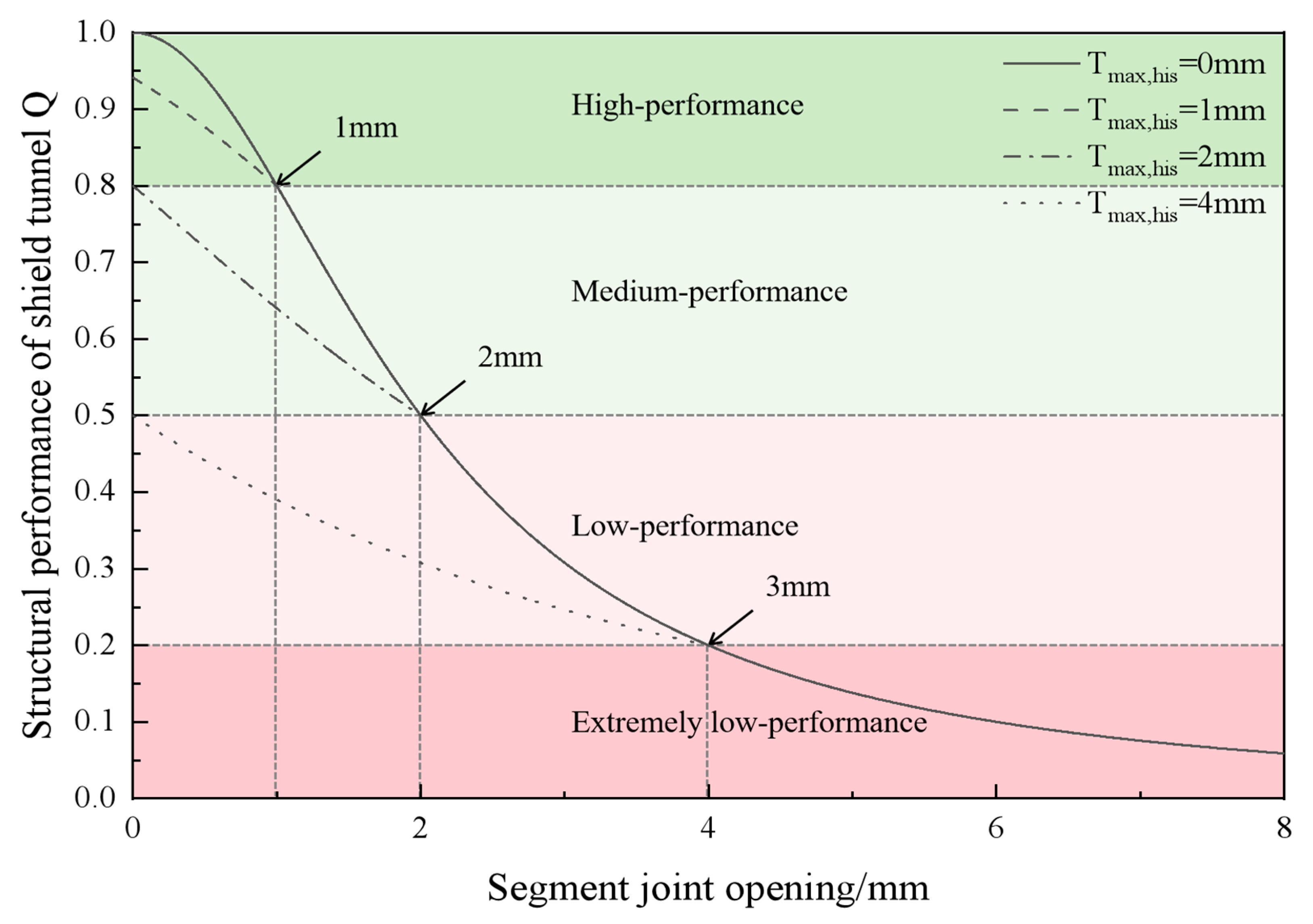
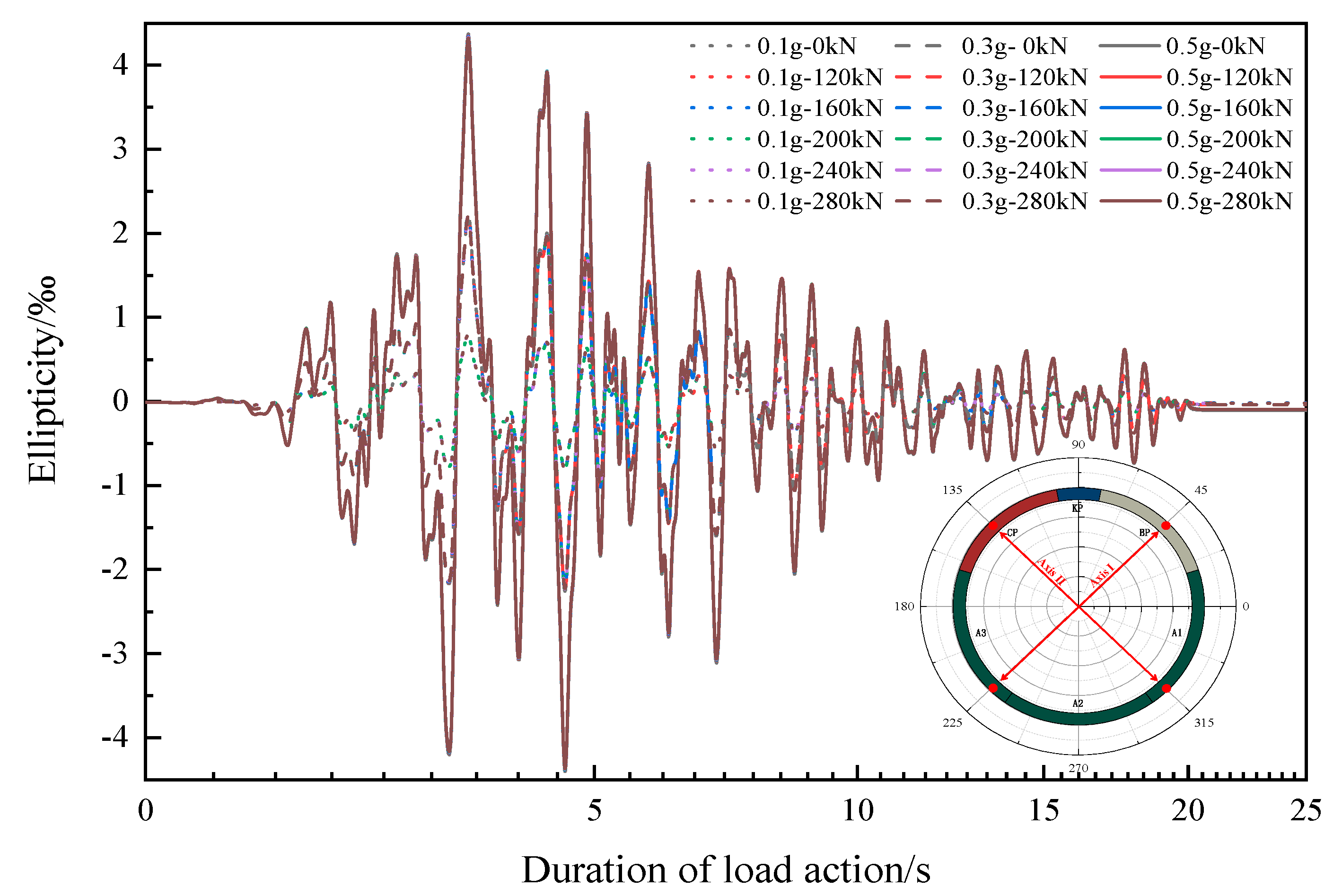
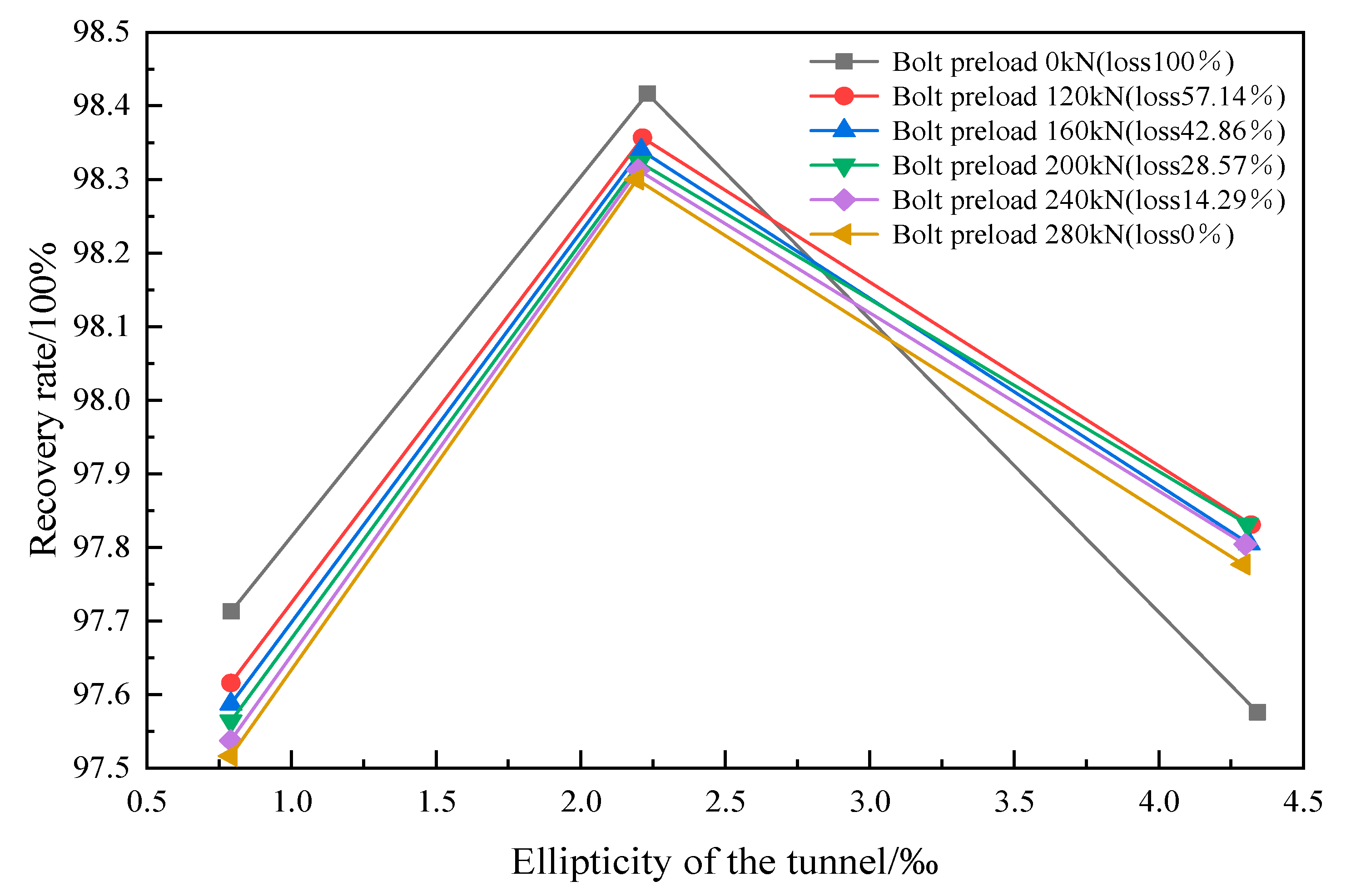
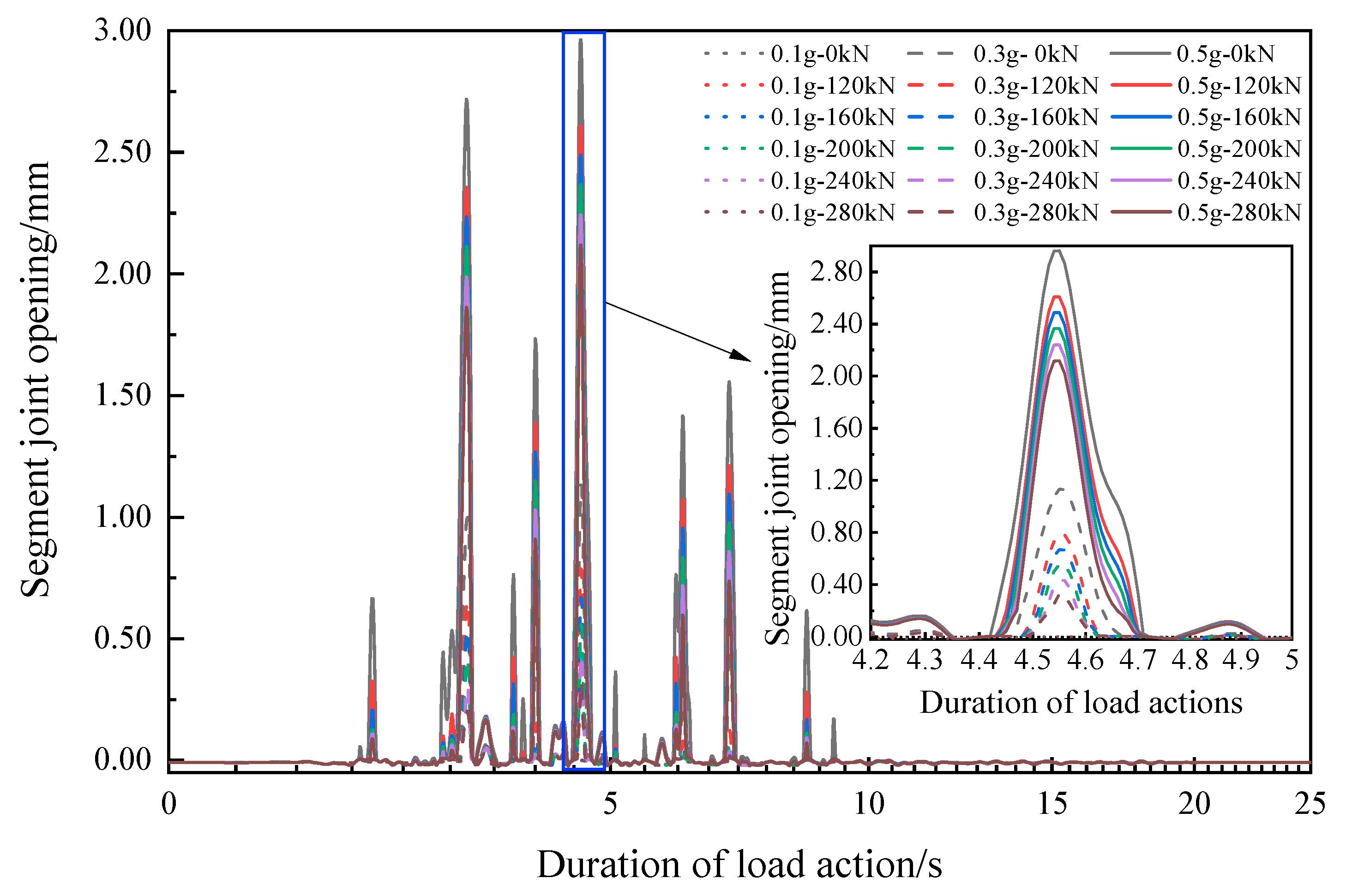
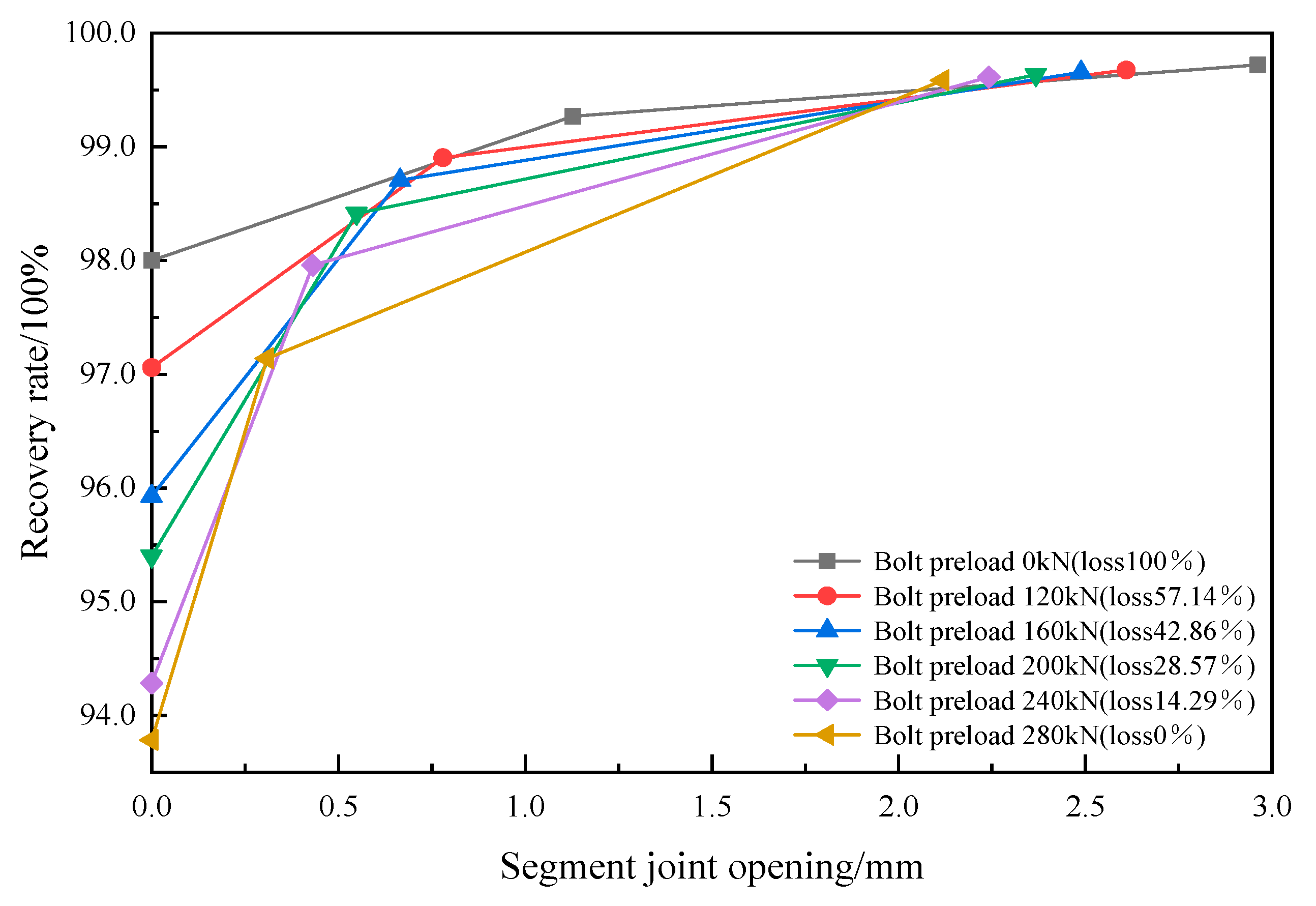
5.1. Performance of Tunnel Lining
- (A)
- Ellipticity
- (B)
- Deformation on Segment Joints
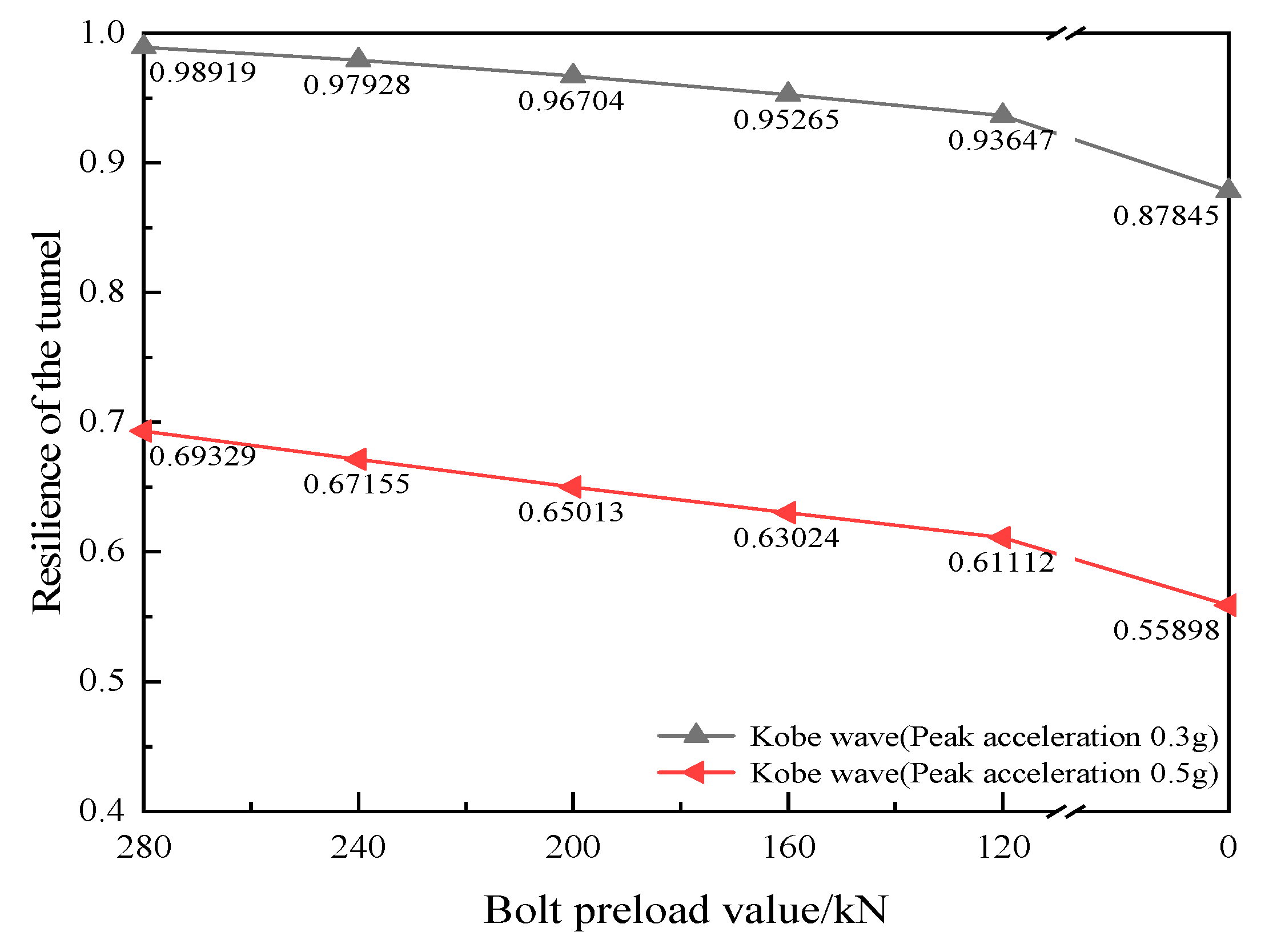
5.2. The Impact of Preload Loss on Resilience
5.3. Classification of Resilience
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, M.; Chen, X.; Wang, X. Analysis and thinking on structural performance evolution of shield tunnel ling. Eng. Mech. 2022, 39, 33–50. (In Chinese) [Google Scholar]
- Shao, H.; Huang, H.; Zhang, D.; Wang, R. Case study on repair work for excessively deformed shield tunnel under accidental surface surcharge in soft clay. Chin. J. Geotech. Eng. 2016, 38, 1036–1043. [Google Scholar]
- Liang, R.; Cao, S.; Xiang, L.; Kang, C.; Chen, F.; Li, Z.; Ke, Z.; Cuo, Y. Experimental investigation on longitudinal mechanical mechanism of shield tunnels subjected to ground surface surcharge. Chin. J. Rock Mech. Eng. 2023, 42, 736–747. [Google Scholar]
- Wang, R.; Zhang, D. Mechanism of transverse deformation and assessment index for shield tunnels in soft clay under surface surcharge. Chin. J. Geotech. Eng. 2013, 35, 1092–1101. [Google Scholar]
- Li, F.; Gou, C.; Xu, D. Study on Structure Inner Forces Affected by Shield Tunnel Segment Joint Bending Stiffness. J. Wuhan Univ. Technol. 2013, 35, 73–78. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, J.; Zhang, C.; Qu, T.; Fu, J.; Wang, S. Linking shear strength to granular skeleton state of continuously graded coarse-grained soils: Insights from discrete element modelling. Comput. Geotech. 2022, 146, 104750. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, X.; Zhang, T.; Sun, J.; Qiu, H.; Diao, Y. Numerical study on mechanical behavior and ultimate bearing capacity of shield segment joints under difffferent load conditions. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2023, 139, 105204. [Google Scholar] [CrossRef]
- Zuo, L.; Li, G.; Feng, K.; Ma, X.; Zhang, L.; Qiu, Y.; Cao, S.; Feng, L. Experimental analysis of mechanical behavior of segmental joint for gas pipeline shield tunnel under unfavorable compression-bending loads. Tunn. Undergr. Space Technol. 2018, 77, 227–236. [Google Scholar] [CrossRef]
- Chen, X.; Shen, J.; Bao, X.; Wu, X.; Tang, W.; Cui, H. A review of seismic resilience of shield tunnels. Tunn. Undergr. Space Technol. 2023, 136, 105075. [Google Scholar] [CrossRef]
- Shen, J.; Bao, X.; Chen, X.; Wu, X.; Cui, H. Prediction of Tunnel Earthquake Damage Based on a Combination Weighting Analysis Method. Symmetry 2022, 14, 1922. [Google Scholar] [CrossRef]
- Li, X.; Lin, X.; Zhu, H.; Wang, X.; Liu, Z. Condition assessment of shield tunnel using a new indicator: The tunnel serviceability index. Tunn. Undergr. Space Technol. 2017, 67, 98–106. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Zhu, H. Condition evaluation of urban metro shield tunnels in Shanghai through multiple indicators multiple causes model combined with multiple regression method. Tunn. Undergr. Space Technol. 2019, 85, 170–181. [Google Scholar] [CrossRef]
- Shadabfar, M.; Mahsuli, M.; Zhang, Y.; Xue, Y.; Ayyub, B.M.; Huang, H.; Medina, R.A. Resilience-Based Design of Infrastructure: Review of Models, Methodologies, and Computational Tools. Asce-Asme J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2022, 8, 03121004. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, D. Resilience analysis of shield tunnel lining under extreme surcharge: Characterization and field application. Tunn. Undergr. Space Technol. 2016, 51, 301–312. [Google Scholar] [CrossRef]
- Lin, X.; Chen, X.; Su, D.; Zhu, M.; Han, K.; Chen, R. Evaluation method for resilience of shield tunnel linings considering multiple disturbances and its application. Chin. J. Geotech. Eng. 2022, 44, 591–601. [Google Scholar]
- Lin, X.; Chen, X.; Su, D.; Han, K.; Zhu, M. An analytical model to evaluate the resilience of shield tunnel linings considering multistage disturbances and recoveries. Tunn. Undergr. Space Technol. 2022, 127, 104581. [Google Scholar] [CrossRef]
- Xu, H.; Li, T.; Xia, L.; Zhao, J.X.; Wang, D. Shaking table tests on seismic measures of a model mountain tunnel. Tunn. Undergr. Space Technol. 2016, 60, 197–209. [Google Scholar] [CrossRef]
- Dong, F.; Zhang, D.; Fang, Q.; Zhu, W.; Chen, L.; Tai, Q. Seismic Response Analysis of Large-Diameter Shield Tunnels Considering the Segment Joint Effect. Mod. Tunn. Technol. 2015, 52, 111–120. [Google Scholar] [CrossRef]
- Xu, H.; Li, T.; Xu, J.; Wang, Y. Dynamic Response of Underground Circular Lining Tunnels Subjected to Incident P Waves. Math. Probl. Eng. 2014, 2014, 1350026. [Google Scholar] [CrossRef]
- Liu, N.; Men, Y.; Peng, J.; Chu, C.; Liu, Y. Dynamic response of shield metro tunnel in earthquake load. Hydrogeol. Eng. Geol. 2010, 37, 58–62. [Google Scholar] [CrossRef]
- Wang, Q.; Geng, P.; Chen, C.; Chen, J.; He, C. Determination of seismic response of reinforced tunnel portal slope using shaking table tests. Tunn. Undergr. Space Technol. 2023, 136, 105072. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, X.; Xia, C.; Wang, C.; Bao, X. Resilience evolution of shield tunnel structure under ground surcharge. Chin. J. Geotech. Eng. 2023, 15, 1547–1564. [Google Scholar]
- Zhang, Y.; Saadat, Y.; Huang, H.; Zhang, D.; Ayyub, B.M. Experimental study on deformational resilience of longitudinal joint in shield tunnel lining. Struct. Infrastruct. Eng. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Ayyub, B.M. Systems Resilience for Multihazard Environments: Definition, Metrics, and Valuation for Decision Making. Risk Anal. 2014, 34, 340–355. [Google Scholar] [CrossRef] [PubMed]
- CJJ/T202-2013[S]; Technical Code for the Protection Structures of Urban Rail Transit. ChineseStandard GB/T: Beijing, China, 2014. (In Chinese)
- GB50446-2017; Code for Construction and Acceptance of Shield Tunnel. ChineseStandard GB/T: Beijing, China, 2008.
- Zhang, W.; Zhang, Q.; Cao, W. Study on Stress and Deformation of Bolt Joints of Shield Tunnel under Static and Seismic Action. Ksce J. Civ. Eng. 2021, 25, 3146–3159. [Google Scholar] [CrossRef]
- JGJ 82-20112011; Technical Pecification for High Strength Bolt Connections of Steel Structures. State Standard of the People’s Republic of China: Shanghai, China, 2011; p. 78.
- GB 50909-20142014; Code for Seismic Design of Urban Rail Transit Structures. State Standard of the People’s Republic of China: Shanghai, China, 2014; p. 185.
- GB50010-2010; Code for Design of Concrete Structures. State Standard of the People’s Republic of China: Shanghai, China, 2011; p. 133.
- Miao, Y.; Yao, E.L.; Ruan, B.; Zhuang, H.Y. Seismic response of shield tunnel subjected to spatially varying earthquake ground motions. Tunn. Undergr. Space Technol. 2018, 77, 216–226. [Google Scholar] [CrossRef]
- Shen, Y.Y.; Zhong, Z.L.; Li, L.Y.; Du, X.L.; El Naggar, M.H. Seismic response of soil-shield tunnel systems in sandwiched liquefiable soil deposits. Tunn. Undergr. Space Technol. 2023, 140, 105322. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, F. Study on transformation method for artificial boundaries in static-dynamic analysis of underground structure. J. Vib. Shock. 2011, 30, 165–170. [Google Scholar]
- Liu, J.; Wang, Z.; Zhang, K.; Pei, Y. 3d finite element analysis of large dynamic machine foundation considering soil-structure interaction. Eng. Mech. 2002, 19, 34–38, 49. [Google Scholar]
- Liu, J.; Gu, Y.; Du, Y. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements. Chin. J. Geotech. Eng. 2006, 28, 1070–1075. [Google Scholar]
- Gu, Y.; Liu, J.; Du, Y. 3D consistent viscous-spring artificial boundary and viscous-spring boundary elemen. Eng. Mech. 2007, 24, 31–37. (In Chinese) [Google Scholar]
- He, J.; Ma, H.; Zhang, B.; Chen, H. Method and realization of seismic motion input of viscous-spring boundary. J. Hydraul. Eng. 2010, 41, 960–969. [Google Scholar]
- Lu, Z.; Zhang, L.; Jiang, J.; You, C.; Zhong, X.; Feng, D.; Chen, S. Characteristic evaluation of passive seismic ellipticity method in urban shield tunnel. J. Appl. Geophys. 2023, 216, 105134. [Google Scholar] [CrossRef]
- Bao, X.; Li, P.; Cui, H.; Zhu, H. Dynamic Response of Complex Soft Clay due to Mero Tunnel Operation. Mod. Tunn. Technol. 2018, 55, 53–60. [Google Scholar]
- He, C.; Geng, P. Research on Practical Seismic Analysis Methods of Shield Tunnel. China J. Highw. Transp. 2020, 33, 15–25. [Google Scholar]
- He, C.; Li, L.; Zhang, J.; Geng, P.; Yan, Q. Seismic damage mechanism of tunnels through fault zones. Chin. J. Geotech. Eng. 2014, 36, 427–434. [Google Scholar]
- Zhou, Y.M.; Wang, J.W.; Yang, H. Resilience of Transportation Systems: Concepts and Comprehensive Review. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4262–4276. [Google Scholar] [CrossRef]
- Amekudzi-Kennedy, A.; Singh, P.; Williams, E.; Cuadra, M.; Ashuri, B.; Woodall, B.; Garrett, A.; Tennakoon, M.; Clark, R.; Dheeraj, A. Developing Transportation Resilience Adaptively to Climate Change. Transp. Res. Rec. 2023, 2023, 03611981231186989. [Google Scholar] [CrossRef]
- Wang, N.X.; Wu, M.; Yuen, K.F. Assessment of port resilience using Bayesian network: A study of strategies to enhance readiness and response capacities. Reliab. Eng. Syst. Saf. 2023, 237, 109394. [Google Scholar] [CrossRef]
- Ren, H.; Rong, C.; Tian, Q.H.; Zhang, W.C.; Shao, D. Evaluation Model for Seismic Resilience of Urban Building Groups. Buildings 2023, 13, 2502. [Google Scholar] [CrossRef]
- Xu, H.; Li, T.; Li, L. Research on Dynamic Response of Underground Circular Lining Tunnel under the Action of P waves. Appl. Mech. Mater. 2011, 99–100, 181. [Google Scholar] [CrossRef]




| No. | Preload/kN | PGA/g | No. | Preload/kN | PGA/g | No. | Preload/kN | PGA/g |
|---|---|---|---|---|---|---|---|---|
| A01 | 280 | 0.1 | B01 | 280 | 0.3 | C01 | 280 | 0.5 |
| A02 | 240 | B02 | 240 | C02 | 240 | |||
| A03 | 200 | B03 | 200 | C03 | 200 | |||
| A04 | 160 | B04 | 160 | C04 | 160 | |||
| A05 | 120 | B05 | 120 | C05 | 120 | |||
| A06 | 0 | B06 | 0 | C06 | 0 |
| Uniaxial Compression | Uniaxial Tension | ||||
|---|---|---|---|---|---|
| Stress /MPa | Inelastic Strain | Damage Factor | Stress /MPa | Cracking Strain | Damage Factor |
| 26.892 | 0 | 0 | 3.423939 | 0 | 0 |
| 38.455 | 6.6 | 0.208666 | 3.257697 | 0.3 | 0.125466 |
| 34.997 | 10.9 | 0.309287 | 2.701560 | 1.1 | 0.349736 |
| 28.692 | 16.2 | 0.420016 | 2.169453 | 1.8 | 0.495345 |
| 23.006 | 21.2 | 0.513588 | 1.561394 | 3.2 | 0.650423 |
| 18.640 | 25.8 | 0.586791 | 1.045034 | 5.8 | 0.778459 |
| 15.401 | 30.2 | 0.643377 | 0.675897 | 10.7 | 0.867185 |
| 12.985 | 34.3 | 0.687565 | 0.430703 | 20.5 | 0.922839 |
| 9.725 | 42.0 | 0.751014 | 0.272294 | 40.0 | 0.955944 |
| 6.315 | 56.6 | 0.824267 | 0.171334 | 78.7 | 0.975075 |
| 3.624 | 84.5 | 0.890016 | 0.107651 | 156.0 | 0.985949 |
| 1.784 | 148.0 | 0.941518 | 0.067876 | 308.0 | 0.992065 |
| 0.032288 | 953.0 | 0.996891 | |||
| Material | Young’s Modulus /MPa | Poisson’s Ratio | Mass Density | Damping Ratio |
|---|---|---|---|---|
| Semi-Weathered granite | 126 | 0.35 | 1.85 | 0.09 |
| Concrete | 34,500 | 0.20 | 2.42 | 0.02 |
| Bolt | 210,000 | 0.3 | 7.85 | 0.05 |
| Preload /kN | Preload Loss Rate /% | Temperatures /°C | Carrying Capacity Redundancy/kN |
|---|---|---|---|
| 280 | 0 | −150.86 | 172.39 |
| 240 | 14.29 | −129.31 | 212.39 |
| 200 | 28.57 | −107.76 | 252.39 |
| 160 | 42.86 | −86.21 | 292.39 |
| 120 | 57.14 | −64.66 | 332.39 |
| 0 | 100 | 0 | 372.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Tao, R.; Bao, X.; Wu, X.; Qiu, T.; Shen, J.; Han, Z.; Chen, X. Seismic Resilience Evolution of Shield Tunnel with Structure Degradation. Appl. Sci. 2024, 14, 72. https://doi.org/10.3390/app14010072
Cui H, Tao R, Bao X, Wu X, Qiu T, Shen J, Han Z, Chen X. Seismic Resilience Evolution of Shield Tunnel with Structure Degradation. Applied Sciences. 2024; 14(1):72. https://doi.org/10.3390/app14010072
Chicago/Turabian StyleCui, Hongzhi, Ran Tao, Xiaohua Bao, Xianlong Wu, Tong Qiu, Jun Shen, Zhen Han, and Xiangsheng Chen. 2024. "Seismic Resilience Evolution of Shield Tunnel with Structure Degradation" Applied Sciences 14, no. 1: 72. https://doi.org/10.3390/app14010072
APA StyleCui, H., Tao, R., Bao, X., Wu, X., Qiu, T., Shen, J., Han, Z., & Chen, X. (2024). Seismic Resilience Evolution of Shield Tunnel with Structure Degradation. Applied Sciences, 14(1), 72. https://doi.org/10.3390/app14010072







