Featured Application
This research study can be utilized to improve the data assimilation process and uncertainty quantification analysis.
Abstract
The reflooding phase, a crucial recovery process after a loss of coolant accident (LOCA) in reactors, involves cooling overheated fuel rods with subcooled water. Its complex nature, notably in its flow regime and heat transfer, makes prediction challenging, resulting in high uncertainty and computation cost. In this study, we utilized the data assimilation (DA) technique to enhance the prediction of reflooding phenomena and subsequently deployed machine learning models to predict the accuracy of the safety and performance analysis code (SPACE) simulation. To generate the dataset for the machine learning model, we employed the sampling method for highly nonlinear system uncertainty analysis (STARU), providing a high-quality dataset for a complex problem such as a reflooding simulation. In this dataset, the physical models were assimilated under their selected uncertainty bands and utilized the effective sampling approach of STARU, generating the high-quality output and efficient enhancement of SPACE predictions. Consequently, the implemented machine learning model can be used to enhance model development and uncertainty quantification (UQ) analysis using the system code.
1. Introduction
Reflooding is a critical recovery process in a reactor following a loss of coolant accident (LOCA). It entails introducing subcooled water from accumulators to cool down overheated fuel rods, mitigating the risk of reactor meltdown—a severe accident in nuclear safety. Despite its significance, the intricacies of the reflooding phase, especially concerning the flow regime and heat transfer, remain challenging to predict [1,2,3].
In pressurized water reactors (PWRs), enhancing predictions related to reflooding is crucial as they influence the effectiveness of the emergency core cooling system (ECCS) during a LOCA [4,5,6,7]. An essential aspect of this is the accurate prediction of quenching time, as once the fuel rods are quenched, they cool to natural convection levels, averting potential fuel meltdown and ensuring safety. Among the complex phenomena during reflooding, saturated film boiling (SFB) [8,9,10], dispersed flow film boiling (DFFB) [11,12], and inverted annular film boiling (IAFB) [13,14] play a pivotal role. Understanding these heat transfer processes is crucial for refining predictions and improving reactor safety analysis [15,16,17].
To enhance the predictions of the system thermal–hydraulics code (TRACE) [18], a combined version of the transient reactor analysis code (TRAC) and the reactor excursion and leak analysis program (RELAP5 [19]), the effects of DFFB and IAFB heat transfers, which usually occur in the reflooding phase in a rod bundle, were examined at the Pennsylvania State University/U.S. Regulatory Commission Rod Bundle Heat Transfer (RBHT) test facility [20]. This test data can enhance the reflood model in the TRACE code. Therefore, the TRACE code’s more accurate and reliable reflood model can be realistically achieved rather than the conservative predictions. Simulating the full-length emergency core cooling heat transfer-separate effects tests and system-effects tests (FLECHT SEASET) and RBHT reflood tests, the existing reflood model of the multidimensional analysis of reactor safety (MARS [21]) code, such as the DFFB and IAFB wall heat transfer models, were improved [22].
Moreover, the effectiveness of ECCS is considerably concentrated in the flooding experiment with blocked arrays (FEBA) with the deformed claddings in the fuel assembly [23]. In the FEBA project, some separate effect test series are carefully investigated with various blockage geometries that simulate the ballooned fuel rod claddings. Consequently, the effects of spacer grids and the heat transfer enhancements of the downstream region for ballooned fuel rods with various blockage ratios were evaluated.
Furthermore, using the safety and performance analysis code (SPACE) [24] and parallel computing platform integrated for uncertainty and sensitivity analysis (PAPIRUS), the wall and vapor temperature of the FEBA and FLECHT SEASET uncertainty propagation were also examined [16]. The uncertainty quantification (UQ) analysis concluded that the predicted cladding temperature was displayed a highly nonlinear behavior in the reflood phase, resulting in a high simulation uncertainty and computation cost. Likewise, the UQ analysis was examined using Markov chain Monte Carlo sampling within the data assimilation (DA) technique of PAPIRUS and SPACE to simulate the FLECHT SEASET reflood tests [25]. It can be inferred that the SFB in the convective heat transfer was identified as the most influential physical model in this DA result after eight months of calculation, indicating a very high computation cost.
It can be revealed that the DA and UQ analysis for the reflooding simulation involved a significant amount of computation and data analysis due to the highly nonlinear system [15,16,25,26]. However, while traditional prediction methods have offered valuable insights, the advent of machine learning presents an opportunity to harness vast amounts of data, refine our predictive capabilities, and achieve unprecedented levels of accuracy. For instance, the machine learning models to predict the velocity of quench front propagation, the minimum film boiling temperature, and the transient boiling curve using fiber temperature measurement data were implemented [27]. Their findings suggest that multilayer perceptrons or deep neural networks (DNNs) can more accurately predict quenching behavior than support vector machine (SVM) and random forest (RF). Shortly after that, they integrated machine learning with minimum film boiling temperature correlations, resulting in predictions that surpassed those from standalone machine learning models [28]. Jin et al. (2023) also explored predictions for rod cladding temperatures during RBHT reflood tests, utilizing both machine learning and the coolant-boiling in rod arrays-two fluid (COBRA-TF) code [29]. Their analysis indicated that artificial neural networks and RF are adept at capturing the intricate phenomena observed during reflooding, yielding precise predictions.
In this study, machine learning models such as linear regression (LR), RF, and DNN to examine the accuracy of the SPACE predictions are implemented. Our work consists of two main tasks, which are (1) to examine the UQ of SPACE for the FLECHT SEASET reflood tests and (2) to implement the machine learning models using the UQ datasets derived from the sampling method for highly nonlinear system uncertainty analysis (STARU) framework. Via these tasks, this study aims to lay the initial foundation for implementing the machine learning models to enhance the efficiency of the UQ analyses for the reflood phenomena. Moreover, these machine learning models are also employed to identify the most influential physical model in simulating the reflood phenomena; this outcome can be utilized to enhance the physical model developments of the system code.
2. Methods and Data Preparation
This section describes the selection of the reflood test data, the comprehensive UQ analysis to generate datasets, and a brief introduction to the machine learning models that can be utilized in this study.
2.1. FLECHT SEASET Reflood Tests
The FLECHT SEASET unblocked test data are designed to observe the reflood phenomena for the unblocked flow in a 17 × 17 fuel rod [30]. Via these reflood tests, many effects have been examined, such as the pressure, initial clad temperature, flooding rate, rod peak power, and subcooling transient effect. Figure 1 illustrates the bundle cross-section of the FLECHT SEASET experiment. This configuration will be modeled using SPACE to calculate the cladding temperatures and quenching times.
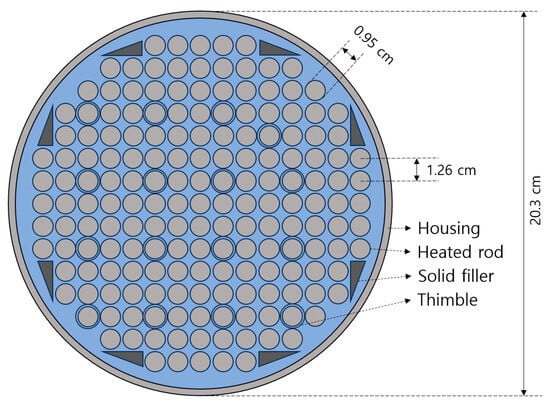
Figure 1.
The FLECHT SEASET bundle cross-section.
In this investigation, nine reflood tests were selected. According to this selection, the features of the unblocked reflood test, such as reflooding rates, powers, initial cladding temperatures, and pressures, are appropriately selected (see Table 1).

Table 1.
The selected FLECHT SEASET reflood tests.
2.2. UQ Analysis
The best estimate plus uncertainty (BEPU) approach is practical to propagate the physical models’ uncertainty and their system states, resulting in a reliable numerical analysis [31,32,33,34]. The results of simulations can be strongly influenced by the selection of physical models and their uncertainty ranges. Therefore, in the validation process of the system code models, UQ analysis can be advantageous to validate the physical models and enhance the simulation results. In this process, the propagation of parameters under their uncertainty ranges and corresponding system states is performed to achieve the specific requirements of model validations.
The UQ analysis for FLECHT SEASET refloods tests was established using the PAPIRUS framework and SPACE [25], revealing a slight improvement in the simulation and high computation costs. Subsequently, STARU [26] was developed to examine and enhance the UQ for nonindependent and high-dimension parameters, resulting in a highly nonlinear relationship between the physical models and their system states. The acceptance probability β and step size ε can be justified in STARU, as can the adjusted multipliers and their uncertainty ranges based on parameters and system responses. This effectively improves the validation process and increases the system code’s reliability. STARU will be used in this study to examine the UQ analysis.
In this implementation, the STARU sampling algorithm (with β = 0.95 and ε = 0.01) and the absolute relative difference (ARD) method for accuracy evaluation were adopted. The cladding temperatures and quenching times were deployed as the primary responses for our investigations. The selected physical models and their uncertainty ranges for this UQ analysis are displayed in Table 2, C1 to C42, corresponding to the adjusted parameters in the UQ analysis. Note that the uncertainty bands were recommended by the DA results, and the obtained samples included uniform and continuous samples. The massive samples for training and testing the machine learning models based on these configurations were generated. It is crucial to confirm that these datasets were of high quality and high fidelity to achieve the efficiency of training and validating the machine learning models.

Table 2.
The selected physical model and uncertainty band for UQ.
2.3. Machine Learning Model
In this section, three machine learning models are described, such as LR, RF, and DNN. In this context, the fundamental models and their corresponding experiment descriptions, such as the selection of the models and hyperparameters, are presented. It can be emphasized that the selection of the hyperparameters is based on trial-and-error examinations before performing an actual analysis.
2.3.1. Linear Regression
In the dynamic landscape of machine learning, regression stands out as a fundamental task, aiming to predict a continuous outcome variable based on one or more predictors. While the concept remains consistent, the methodologies vary widely. There are various methods to predict the relationship between the input and output in machine learning regression tasks. LR is the most common in the regression problem of machine learning that can be implemented to establish the relationship between the dependent and one or more independent variables. It predicts the output by simply fitting the best linear line or hyperplane. LR is the most simple, interpretable, and widely used in statistical modeling. However, it may exhibit a reduced accuracy in cases where the underlying relationship between the input and output is nonlinear, as illustrated in Figure 2.
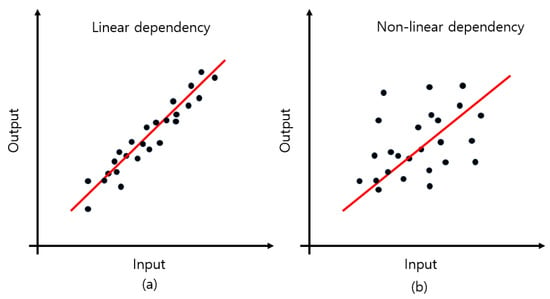
Figure 2.
The dependency in the regression tasks: (a) the linear dependency, (b) the nonlinear dependency. The red line indicates the linear fitting method and the black dots represent the data to be fitted.
2.3.2. Random Forest
In machine learning, RF is an ensemble learning method that creates multiple decision trees during training and produces the average output of individual trees for regression problems; it was initially introduced by Breiman et al. (1984) [35]. This method has a reliable accuracy, can estimate missing values, and can handle large datasets with higher dimensionality. Furthermore, an RF-trained model can identify the most influential input parameters from the output of the dataset by using feature score tracking methods. These scores can be specified by each feature’s contribution to the model’s overall predictive performance. The RF algorithm evaluates the impact of individual features by measuring the decrease in accuracy or impurity when a particular feature is included in the model. Consequently, higher feature importance scores indicate a more influential role in predicting the target variable. These results are presented in the following sections. In this investigation, the number of trees in the RF model is 200, and the random number generator is initialized with a seed value of 10.
2.3.3. Deep Neural Networks
DNNs, composed of multiple hidden layers between the input and output, can estimate the unknown underlying function that maps inputs to outputs of the given datasets. Our DNN model employed the Adam optimization algorithms to justify the learning rates [36]. Furthermore, the output of SPACE prediction’s accuracy is positive real numbers. Therefore, the ReLU activation function was documentationally recommended to be most appropriate [37]. Moreover, the mean squared error (MSE) as the loss function to track the accuracy of the DNN during the training process was deployed; the selected hyperparameters of the DNN model are presented in Table 3.

Table 3.
The selection of the hyperparameters in the machine learning models.
It can be revealed that the DNN predictions may have some noisy results even after sufficient epochs when the MSE reaches an acceptable value. To mitigate these noises, the ModelCheckpoint in Keras [38] during the training process was utilized. This allowed us to capture the best accuracy achieved, ensuring that the best prediction of DNNs could always be obtained despite the presence of noise.
2.4. Dataset
As illustrated in Table 2, the 42 adjustable input parameters, within their respective uncertainty ranges, were utilized for stand-alone DA using the SPACE and STARU. This procedure of running DA generates the system states corresponding to various value sets of the 42 input parameters. These data were subsequently processed and utilized as training and testing datasets for our investigation of machine learning models (see Figure 3 and Figure 4).
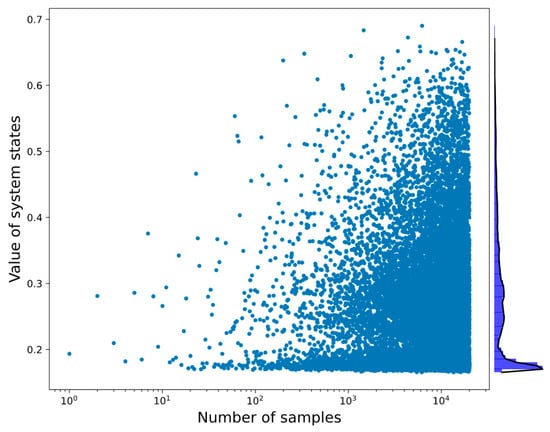
Figure 3.
The system states for the training dataset. The histogram of the system states and their values are displayed on the right edge of this figure, where its value distributions present a total of 20,000 samples.
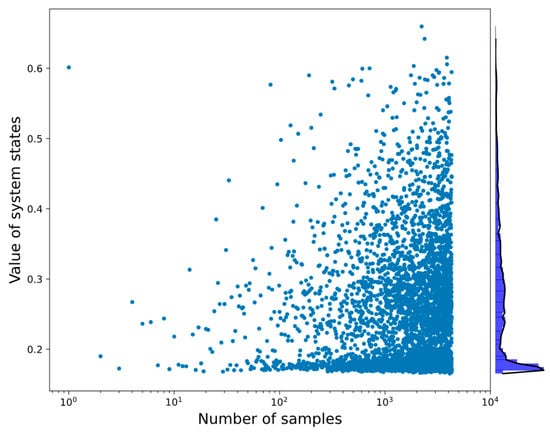
Figure 4.
The system states for the testing dataset. The histogram of the system states and their values are displayed on the right edge of this figure, where its value distributions present a total of 4000 samples.
It can be revealed that a single sample of DA refers to a single simulation of the SPACE, and the values of individual points in Figure 3 and Figure 4 refer to the accuracy of the SPACE simulation compared with the experimental data from reflood tests. This accuracy can be evaluated using the ARD method in which a lower value indicates a higher reliability of the SPACE simulation; this value is also so-called the system state. The combination of a system state value along with the corresponding value of their physical models is the structure of a dataset. In this dataset, the training data for the machine learning models is collected from 20,000 samples of DA; the test data is produced using 4000 samples. Both the training and test datasets include 42 input parameters as input values and their corresponding system states as output values.
2.5. Standard Deviation Method
Finding the most influential parameter, which contributed the most to the system behavior, is crucial in the UQ analysis, reflecting the firm relationship order between the system state and input parameters. These results can be helpful in the model development of the system code to provide more accurate predictions for complex real physical phenomena. In this study, we utilized three methods to identify the most influential physical model, such as standard deviation (STD) evaluation, feature scores, and permutation methods in machine learning models [39].
To identify the most influential parameter using the STD evaluation, the relative accumulative values of the STD for all input parameters are examined. The relative accumulative value of STD would be calculated as follows:
where is the STD value of a specific parameter; is the physical model from 1 to 42 corresponding to their parameters indicated in Table 2, is the total of samples, is the value of the physical model at the ith sample, and is the average value of the physical model k from 1 to n. It revealed that a smaller STD values a higher contribution to the system, resulting in a more sensitive physical model.
To effectively identify the ranked physical model, we plotted the values (see Equation (2)). A higher value of indicates a higher contribution of parameter k, implying a higher influence of parameter k on the system state prediction. The value of parameter is illustrated as
3. Results and Discussions
In this section, the UQ results, the improvements in the prediction of the SPACE, and the results of the machine learning model to predict the accuracy of the SPACE predictions are discussed. Moreover, the most influential physical model identification by the machine learning model and the STD method are also illustrated.
3.1. Uncertainty Quantification Results
A UQ analysis for the nine reflood tests was performed in this analysis, delivering the quenching time and cladding temperature propagation results for the SPACE simulation. As a result, the experimental data of quenching time and cladding temperature for the nine tests were covered by the propagation results from the UQ analysis, implying an appropriate selection of the uncertainty bands for the physical models.
The quenching time and cladding temperature propagations for all reflood tests are illustrated in Figure 5 and Figure 6, respectively. In these results, the term “UQ” referred to the cladding temperature or quenching time results of the UQ analysis, in which the DA method was applied; the nominal prediction referred to the prediction of the SPACE without any adjustment of the physical model; and the measured data referred to the actual data from the experimental work of the FLECHT SEASET reflood tests. The justification for the selected physical models and their corresponding uncertainty ranges, as outlined in Table 2, efficiently enhances the simulation of reflooding phenomena using the SPACE. This result emphasizes the UQ analysis’s reliability, enhancing the code’s predictive capabilities. Furthermore, observing the behaviors of the physical models during the UQ process can be valuable in further developing the physical model in the system code. However, the intricacies of this phenomenon, coupled with the nonlinear dependence of the input parameters on system states, result in a prohibitively high computational cost for the UQ analysis.
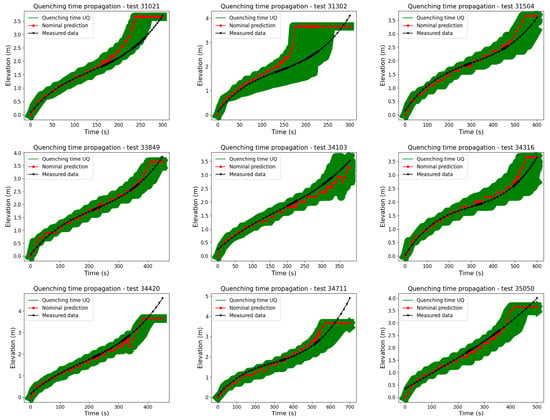
Figure 5.
The quenching time propagation for all the reflood tests.
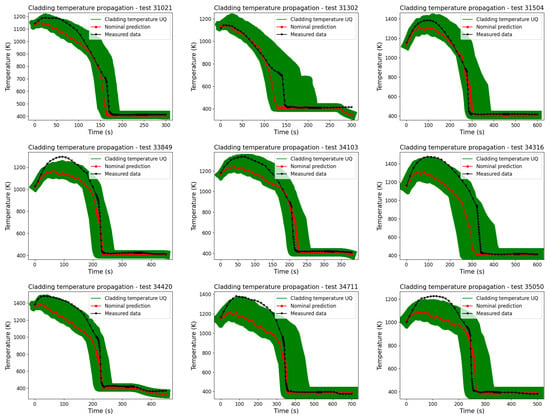
Figure 6.
The cladding temperature propagations.
To address this challenge, we introduced a machine learning model to predict the system behaviors and their corresponding physical models. The objective was for this machine learning model to enhance the UQ results and improve the SPACE prediction for such complex phenomena of the reflooding phase. The expectation is that leveraging machine learning can mitigate the computational demands associated with UQ and sampling algorithms in the DA process, offering a more efficient and effective approach to enhancing the predictive accuracy of the system code.
3.2. Machine Learning Predictions and Comparisons
In this section, the dataset presented in Section 2.4 was employed for training the machine learning models. Within this context, the predictions of machine learning models, including LR, RF, and DNN, were deployed and compared. In the LR, the model assumes a linear relationship between the input features and the output; therefore, for this nonlinear dependency of the system state in the reflooding phenomena prediction, LR may not capture the underlying patterns effectively, resulting in high uncertainty in the prediction compared with the actual values of the test dataset (see Figure 7). These results illustrated that the system states and features are firmly nonlinear dependent. Furthermore, due to these inaccuracies, the ranked parameters most influential to the system state predictions were also not well consistent with the STD evaluation and DNN identification.
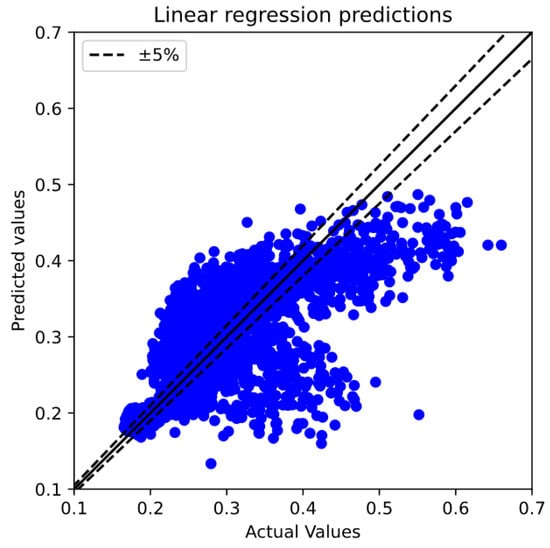
Figure 7.
Linear regression predictions.
In addition, RF is a learning method based on decision trees. It builds multiple decision trees during training and merges them for a more accurate and stable prediction. However, it may not capture highly complex patterns as effectively as DNNs when massive training datasets are employed. It can be illustrated that the predictions of the DNN with selected hyperparameters have the highest accuracy compared to LR and RF (see Figure 7, Figure 8 and Figure 9), delivering an acceptable consistent identification of the most influential physical model. These results trends were also indicated in the previous studies [27,29] where the DNNs tended to capture better predictions compared to RF.
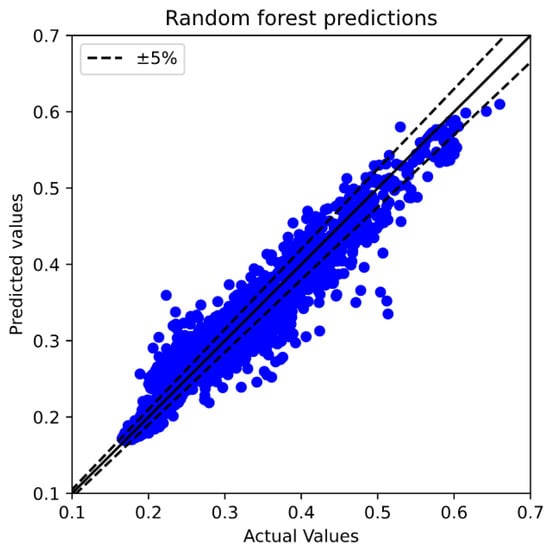
Figure 8.
Random forest predictions.
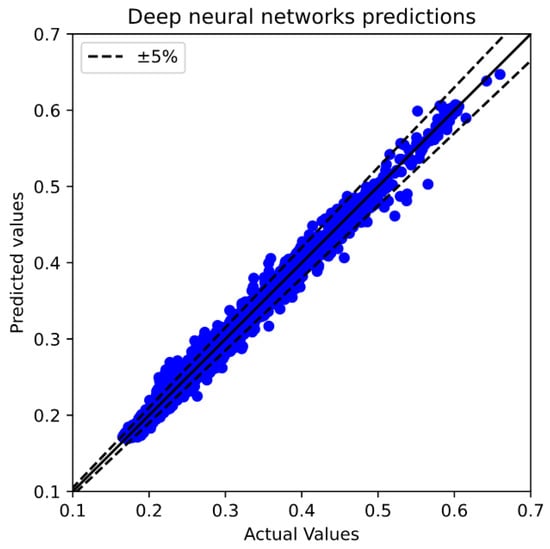
Figure 9.
Deep neural network predictions.
However, DNNs often require large datasets to obtain good predictions. If the dataset is small, a simpler model like LR and RF might better capture the actual system states and identify the most influential physical model, as DNNs may be more unsuitable for overcoming such scenarios. Therefore, the choice between LR, RF, and DNN depends on the nature of the data, the linearity of the system, the correlations between input parameters, the size of the dataset, and the computational cost.
Additionally, we conducted a comparison of computation times. In this analysis, we assumed that each method is tasked with predicting 4000 samples. The findings indicate that the total computation time required by the SPACE is approximately 16,000 min, utilizing an AMD Ryzen Threadripper 3970X computer with 64 processors. In contrast, the LR, RF, and DNN models were executed on a desktop computer with a Core i7-6700 processor, taking a maximum of approximately 3 min, representing a substantial reduction in computation time. The noteworthy reductions presented in Table 4 underscore the potential application of these machine learning models, particularly the DNN.

Table 4.
Computation time comparison.
3.3. Sensitive Physical Model Investigation Results
In this evaluation, the output data of the UQ process are examined, calculating the relative accumulative STD of all the physical models (see Equation (1)). It can be revealed that the system state must reach an equilibrium state before evaluating the STD value of all the parameters, and only the accepted samples are used in this investigation. Our observations reveal that the system state approximately stabilizes after about 1000 iterations, suggesting that a based value is identified (see Figure 10). The based values referred to the enhanced predictions which are achieved. Consequently, the evaluation of the STD will be conducted starting from the 1000th iteration.
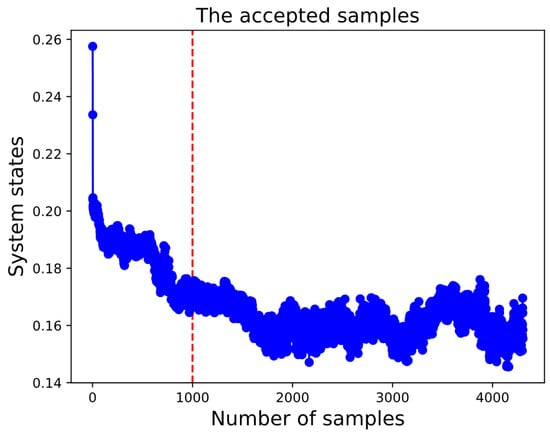
Figure 10.
The system states along with the number of samples. The red-dotted line indicates where the STD calculations will begin.
Figure 11 illustrates the most influential physical model STD analysis, specifically for the C38, corresponding to the SFB heat transfer model in Table 2. This result is consistent with the outcome of previous study [25,26,40], indicating that the film boiling heat transfer is the most crucial physical model in the reflooding phenomena simulation. In addition, the interfacial friction factor for inverted annular flow, slug flow, and interphase heat transfer coefficients for stratified and annular to stratified transition also strongly contribute to this UQ analysis using STD evaluation (see Figure 11). These results are reasonable and consistent with the fact that the contributions of the physical models are not equal but firmly non-negligible. It can be noted that this STD directly reflected the relationship between the adjustment of physical models to their system state predicted by the SPACE. These results can serve as a reference case for further parameters’ influential analyses.
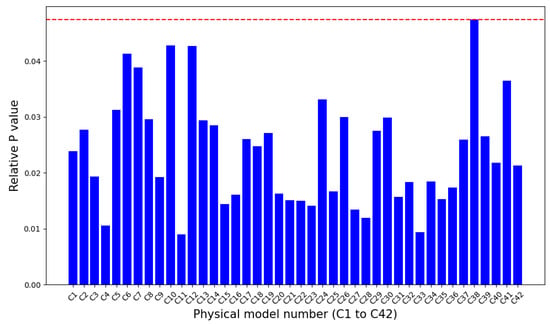
Figure 11.
The relative accumulative p values of all physical models. The red-dotted line indicates the maximum value of the relative p values.
In the LR and RF machine learning problems, the feature scores can be tracked to identify the most influential input parameter; the higher the feature scores, the more influential the parameter. According to the results of LR and RF, the most influential physical model is the droplet entrainment factor. The second order is the SFB in the convective heat transfer model (see Figure 12 and Figure 13).
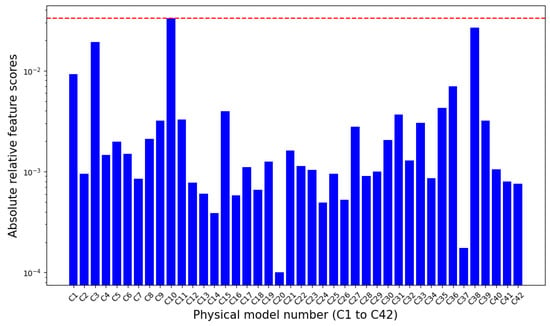
Figure 12.
The absolute relative feature scores of LR. The red-dotted line indicates the maximum value of the absolute relative feature scores.
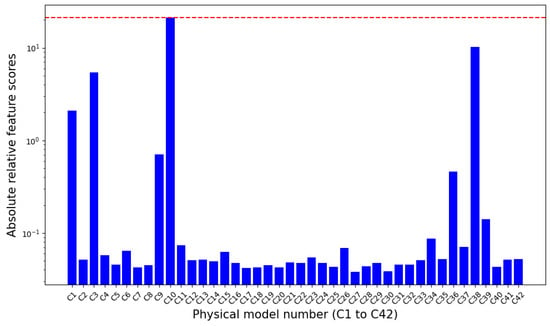
Figure 13.
The absolute relative feature scores of RF. The red-dotted line indicates the maximum value of the absolute relative feature scores.
Furthermore, the permutation feature importance scores can also be used to track the importance of the parameters [35]. In particular, an input parameter is essential in the permutation method if its shuffled values increase the model uncertainties. Conversely, a component is insignificant if its rearranged values produce the model error unaltered, resulting in its negligible contribution to the prediction. In this context, the higher absolute permutation scores illustrated the more influence of that parameter. As a result, the most influential parameter of DNN is SFB, consisting of the STD evaluation results (see Figure 14). However, these results do not imply that we can reduce the dimension of the dataset by neglecting the unimportant component to decrease the computation cost of machine learning predictions. As shown in Figure 11, it can be illustrated that the physical models affect the system states, whether low or high, and this influence is non-negligible. Therefore, retraining the machine learning using a minimum set of influential parameters only may not be sufficient to predict the actual system states that are generated based on the contributions of all these physical models.
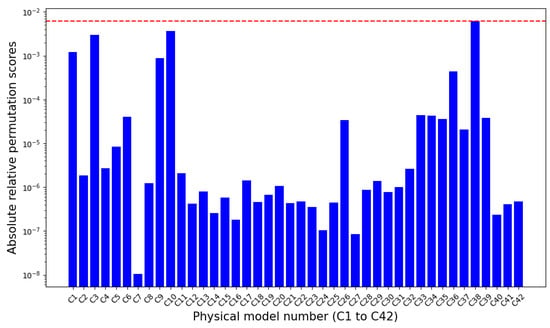
Figure 14.
The absolute relative permutation importance scores of DNN. The red-dotted line indicates the maximum value of the absolute relative permutation scores.
Consequently, these results indicated that the SFB in the convective heat transfer needs to be focused on in the future development of the SPACE to effectively simulate the reflooding phenomena, especially to improve the cladding temperature and quench front velocity calculation.
4. Conclusions
The UQ for the FLECHT SEASET tests using the SPACE was examined using the STARU. We found that all the test case predictions were improved and effectively approximated the experimental data, resulting in an efficient enhancement of SPACE predictions and the effectiveness of the STARU. Moreover, the most influential physical models obtained were consistent with the results of previous studies. Furthermore, we deployed a machine learning model to predict the dependency of the system behaviors corresponding to their physical models and suggest the most influential physical model. As a result, DNN showed a good performance in system state predictions and consistent results in the most influential parameter identification for this problem, delivering a promising application of DNNs in UQ analysis. However, the results are strongly dependent on the dataset structure and complexity of the input parameters and system state relationship. Therefore, future studies should focus on enhancing the performance of the machine learning model and the sampling algorithm in the DA framework to adapt to various datasets and correlations of simulation problems, contributing to obtaining more reliable results and enhancing the efficiency of UQ analysis.
Author Contributions
Conceptualization, N.H.T., K.-D.K. and H.-Y.J.; methodology, N.H.T., K.-D.K. and H.-Y.J.; software, N.H.T., K.-D.K. and H.-Y.J.; validation, N.H.T.; formal analysis, N.H.T.; investigation, N.H.T.; resources, K.-D.K., H.-Y.J. and M.T.V.; data curation, N.H.T.; writing—original draft preparation, N.H.T.; writing—review and editing, N.H.T., K.-D.K., H.-Y.J., N.X.-M., N.N.A., V.-K.H. and M.T.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the computer code licensing requirements.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ARD | Absolute Relative Difference |
| BEPU | Best Estimate Plus Uncertainty |
| COBRA-TF | Coolant-Boiling in Rod Arrays—Two Fluid |
| DA | Data Assimilation |
| DFFB | Dispersed Flow Film Boiling |
| DNN | Deep Neural Network |
| ECCS | Emergency Core Cooling System |
| FEBA | Flooding Experiment with Blocked Arrays |
| FLECHT SEASET | Full-Length Emergency Core Cooling Heat Transfer-Separate Effects Tests and System-Effects Tests |
| IAFB | Inverted Annular Film Boiling |
| LOCA | Loss Of Coolant Accident |
| LR | Linear Regression |
| MARS | Multidimensional Analysis of Reactor Safety |
| MSE | Mean Squared Error |
| PAPIRUS | Parallel Computing Platform Integrated for Uncertainty and Sensitivity Analysis |
| PWR | Pressurized Water Reactor |
| RBHT | Rod Bundle Heat Transfer |
| RELAP | Reactor Excursion and Leak Analysis Program |
| RF | Random Forest |
| SFB | Saturated Film Boiling |
| SPACE | Safety and Performance Analysis Code for Nuclear Power Plants |
| STARU | Sampling Method for Highly Nonlinear System Uncertainty Analysis |
| STD | Standard Deviation |
| SVM | Support Vector Machine |
| TRACE | TRAC/RELAP Advanced Computational Engine |
| UQ | Uncertainty Quantification |
References
- Yadigaroglu, G.; Nelson, R.A.; Teschendorff, V.; Murao, Y.; Kelly, J.; Bestion, D. Modeling of reflooding. Nucl. Eng. Des. 1993, 145, 1–35. [Google Scholar] [CrossRef]
- Andreani, M.; Yadigaroglu, G. Difficulties in modeling dispersed-flow film boiling. Warme Stoffubertrag. 1992, 27, 37–49. [Google Scholar] [CrossRef]
- Yang, B.W.; Bajorek, S.M.; Jin, Y.; Cheung, F.B. Progress in reflood thermal hydraulics studies in the past 40 years. Nucl. Eng. Des. 2021, 376, 111073. [Google Scholar] [CrossRef]
- Zubair, M.; Al Suwaidi, R.R.; Al Souqi, A.A. Behavior of Emergency Core Cooling System (ECCS) during the early stage of Loss of Coolant Accident (LOCA) for APR 1400 with Flownex software. Prog. Nucl. Energy 2021, 141, 103949. [Google Scholar] [CrossRef]
- Takeda, T.; Ohtsu, I. RELAP5 uncertainty evaluation using ROSA/LSTF test data on PWR 17% cold leg intermediate-break LOCA with single-failure ECCS. Ann. Nucl. Energy 2017, 109, 9–21. [Google Scholar] [CrossRef]
- El-Sahlamy, N.M.; Elsaid, A.M. Effect of ECCS cold-leg injection angle on thermal hydraulic characteristics and core recovery during LBLOCA in a PWR. Prog. Nucl. Energy 2021, 142, 104033. [Google Scholar] [CrossRef]
- Safarzadeh, O.; Pourrostam, A. The large-break LOCA uncertainty analysis in a VVER-1000 reactor using TRACE and DAKOTA. Nucl. Eng. Des. 2023, 412, 112459. [Google Scholar] [CrossRef]
- Yukio, S.; Murao, Y. Film Boiling Heat Transfer during Reflood Process; No. JAERI-M—6848; Japan Atomic Energy Research Institute: Ibaraki, Japan, 1976. [Google Scholar]
- Yukio, S. Film boiling heat transfer during reflood phase in postulated PWR loss-of-coolant accident. J. Nucl. Sci. Technol. 1980, 17, 516–530. [Google Scholar] [CrossRef]
- Yoshio, M.; Sugimoto, J. Correlation of heat transfer coefficient for saturated film boiling during reflood phase prior to quenching. J. Nucl. Sci. Technol. 1981, 18, 275–284. [Google Scholar] [CrossRef]
- Akira, O.; Akimoto, H.; Murao, Y. Effect of liquid flow rate on film boiling heat transfer during reflood in rod bundle. J. Nucl. Sci. Technol. 1990, 27, 535–546. [Google Scholar] [CrossRef]
- Ishii, M.; Denten, J.P. Two-phase flow characteristic of inverted bubbly, slug and annular flow in post-critical heat flux region. Nucl. Eng. Des. 1990, 121, 349–366. [Google Scholar] [CrossRef][Green Version]
- Hammouda, N.; Groeneveld, D.C.; Cheng, S.C. Two-fluid modelling of inverted annular film boiling. Int. J. Heat Mass Transf. 1997, 40, 2655–2670. [Google Scholar] [CrossRef]
- Mohanta, L.; Riley, M.P.; Cheung, F.B.; Bajorek, S.M.; Kelly, J.M.; Tien, K.; Hoxie, C.L. Experimental investigation of inverted annular film boiling in a rod bundle during reflood transient. Nucl. Technol. 2015, 190, 301–312. [Google Scholar] [CrossRef]
- Mendizabal, R.; de Alfonso, E.; Freixa, J.; Reventos, F. OECD/NEA Premium Benchmark Final Report; NEA/CSNI/R. 2016, Volume 18. Available online: https://one.oecd.org/document/NEA/CSNI/R(2016)18/En/pdf (accessed on 1 December 2023).
- Jaeseok, H.; Kim, K.D.; Lee, S.-W. Validation and uncertainty quantification for FEBA, FLECHT SEASET, and PERICLES tests incorporating multi-scaling effects. Ann. Nucl. Energy 2018, 111, 499–508. [Google Scholar] [CrossRef]
- Yue, J.; Cheung, F.-B.; Shirvan, K.; Stephen, M.; Tien, B.K.; Chris, L. Hoxie. Development of a droplet breakup model for dry spacer grid in the dispersed flow film boiling regime during reflood transients. Int. J. Heat Mass Transf. 2019, 143, 118544. [Google Scholar] [CrossRef]
- USNRC. TRACE V5.0—Theory Manual; ML120060218; US Nuclear Regulatory Commission: Rockville, MA, USA, 2010. [Google Scholar]
- Fletcher, C.D.; Scuhltz, R.R. RELAP5/MOD3 Code Manual, No. NUREG/CR-5535-Vol. 5, EGG-2596-Vol. 5; Idaho National Engineering Laboratory: Idaho Falls, ID, USA, 1992. [Google Scholar]
- Hochreiter, L.E.; Cheung, F.-B.; Lin, T.F.; Ergun, S.; Sridharan, A.; Ireland, A.; Rosal, E.R. RBHT Reflood Heat Transfer Experiments Data and Analysis; Technical report (NUREG/CR-6980); United States Nuclear Regulatory Commission: Washington, DC, USA, 2012. Available online: https://www.nrc.gov/reading-rm/doc-collections/nuregs/contract/cr6980/index.html (accessed on 1 December 2023).
- Jeong, J.-J.; Ha, K.S.; Chung, B.D.; Lee, W.J. Development of a multi-dimensional thermal-hydraulic system code, MARS 1.3.1. Ann. Nucl. Energy 1999, 26, 1611–1642. [Google Scholar] [CrossRef]
- Moonkyu, H.; Chung, B.-D. MARS Code Reflood Model Improvements and Comparisons with Flecht-Seaset and RBHT Tests. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting, Gyeongju, Republic of Korea, 27–28 October 2011. [Google Scholar]
- Ihle, P.; Rust, K. FEBA: Flooding Experiments with Blocked Arrays: Data Report; Test Series I through IV; Kernforschungszentrum Karlsruhe GmbH: Baden-Württemberg, Germany, 1984. [Google Scholar]
- Sang-Jun, H.; Park, C.-E.; Kim, K.-D.; Ban, C.-H. Development of the SPACE code for nuclear power plants. Nucl. Eng. Technol. 2011, 43, 45–62. [Google Scholar] [CrossRef]
- Tiep, N.H.; Kim, K.D.; Heo, J. Improvement in the accuracy of SPACE prediction for the unblocked FLECHT SEASET reflood tests by data assimilation. Ann. Nucl. Energy 2021, 161, 108462. [Google Scholar] [CrossRef]
- Tiep, N.H.; Kim, K.-D.; Heo, J.; Choi, C.-W.; Jeong, H.-Y. A newly proposed data assimilation framework to enhance predictions for reflood tests. Nucl. Eng. Des. 2022, 390, 111724. [Google Scholar] [CrossRef]
- Mo, K.K.; Hurley, P.; Duarte, J.P. High-resolution prediction of quenching behavior using machine learning based on optical fiber temperature measurement. Int. J. Heat Mass Transf. 2022, 184, 122338. [Google Scholar] [CrossRef]
- Mo, K.K.; Hurley, P.; Duarte, J.P. Physics-informed machine learning-aided framework for prediction of minimum film boiling temperature. Int. J. Heat Mass Transf. 2022, 191, 122839. [Google Scholar] [CrossRef]
- Yue, J.; Bajorek, S.M.; Cheung, F.-B. Validation and Uncertainty Quantification of Transient Reflood Models Using COBRA-TF and Machine Learning Techniques Based on the NRC/PSU RBHT Benchmark. Nucl. Sci. Eng. 2023, 197, 967–986. [Google Scholar] [CrossRef]
- Loftus, M.J.; Hochreiter, L.E.; Conway, C.E.; Dodge, C.E.; Tong, A.; Rosal, E.R.; Valkovic, M.M.; Wong, S. PWR FLECHT SEASET Unblocked Bundle, Forced and Gravity Reflood Task Data Report; Nuclear Regulatory Commission: Rockville, MD, USA, 1981; Volume 1 + 2. [Google Scholar]
- D’Auria, F.; Camargo, C.; Mazzantini, O. The Best Estimate Plus Uncertainty (BEPU) approach in licensing of current nuclear reactors. Nucl. Eng. Des. 2012, 248, 317–328. [Google Scholar] [CrossRef]
- Wilson, G.E. Historical insights in the development of best estimate plus uncertainty safety analysis. Ann. Nucl. Energy 2013, 52, 2–9. [Google Scholar] [CrossRef]
- Queral, C.; Montero-Mayorga, J.; Gonzalez-Cadelo, J.; Jimenez, G. AP1000® Large-Break LOCA BEPU analysis with TRACE code. Ann. Nucl. Energy 2015, 85, 576–589. [Google Scholar] [CrossRef]
- Kovtonyuk, A.; Petruzzi, A.; D’Auria, F.S. Post-BEMUSE Reflood Model Input Uncertainty Methods (PREMIUM) Benchmark Phase II: Identification of Influential Parameters; Nuclear Energy Agency: Paris, France, 2015. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Keras Documentation. 2022. Available online: https://keras.io/api/ (accessed on 3 August 2023).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yoo, J.M.; Cho, Y.J.; Yoon, H.Y.; Jeong, J.J. Analysis of the effect of liquid droplet models on the reflood heat transfer using the CUPID code. Nucl. Eng. Des. 2019, 354, 110148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).