Abstract
This paper addresses the challenges associated with steel pipes used for transporting liquid fluids within buried sections of mining facilities, specifically in areas with heavy mining vehicles. While existing design standards, such as AW-WA M11, and manufacturer recommendations largely consider loads from vehicles like the AASHTO HS20 or Cooper E-80, both weighing below 35 tons, these guidelines inadequately represent the actual loads experienced on certain mining roads, notably those accommodating heavy vehicles, like haul roads. The research presented here focuses on the interaction between soil and buried steel pipes under the substantial loads exerted by mining vehicles with a maximum gross load of up to 612 tons, inclusive of hauled material weight. Utilizing a parametric study with the finite element method, the paper identifies critical variables influencing efforts and deflections calculations in these facilities. The analysis of 108 models, varying parameters related to trench pipe installation conditions, offers insights that empower designers to refine soil trench parameters in mining facilities, mitigating pipe failures and optimizing installation costs. Ultimately, the key influential variables affecting pipe deflection and stress are identified as the trench backfill height and the elasticity modulus of the trench lateral fill.
1. Introduction
Steel pipes that transport water and other fluids over long distances are called pipelines. The determination of the wall thickness of pipes is an important aspect in pipeline design. To determine this thickness, the following factors are considered: the internal pressure, the effects exerted by the installation loads on the pipe itself (flexibility analysis), the effects of occasional internal loads (for example, water hammer), and the effects of occasional external loads (such as surface loads). Considering safety as well as the aforementioned factors, underground pipes installed in mining areas must support high loads (which includes the weight of the mineral hauling vehicle), and thus must be properly analysed (see Figure 1).
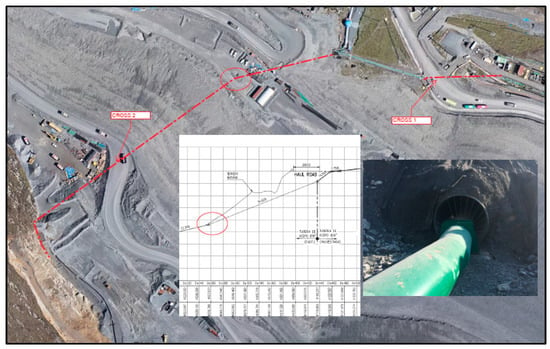
Figure 1.
Example of pipeline installation crossing different accesses and a haul road.
To protect buried pipes from the loads to which they are subjected, some designers use protective jackets, e.g., corrugated steel pipes. These measures represent a significant additional cost in the projects, which is why the pipe is sometimes buried at a certain depth and in direct contact with the ground. In these cases, it must be verified that the stresses caused by dead loads and surface loads are below the allowable values of the pipe material. It is important to design the installation considering the smallest possible size of the trench and selecting filling materials incurring the lowest possible cost.
Generally, trenches are composed of a pipe supported by a bed of fine sand or similar material, a lateral fill installed by means of thin compacted layers and a top fill compacted on the pipe. For this article, a finite element model is proposed within the Abaqus/CAE 2019 software environment, which considers the nonlinearity of the soil material, the nonlinearity of the contact between the pipe and the soil, the nonlinearity of the soil geometry and finally the residual lateral loads with nonlinear soil behaviour due to the compaction of the different layers in the construction stage. Model validation is performed using experimental data obtained at the University of Texas Arlington (UTA) in the Center for Underground Infrastructure Research and Education (CUIRE).
This study demonstrates the importance of the proper selection of soil materials to construct a trench, as well as the importance of considering appropriate conditions for the installation of pipes. A correct selection makes it possible to reduce installation costs and allows the pipe to withstand forces below the allowable values. Varying the width of the trench and choosing a material with a higher degree of elasticity for the side fill are important factors.
This study analyses other factors that can increase deflections in the pipe, such as the variation in the height of the pipe bed or the height of the top fill. Additionally, the position on the pipe of the point subjected to the greatest load is determined. The parametric analysis carried out allows us to understand the behaviour of buried pipes under stresses and deflections generated by truck traffic.
In the mining industry, mined material is transported in mining trucks via haul roads. Some vehicles used in this industry can reach weights (considering both net weight and cargo weight) of up to 612 tons. Therefore, the pipes buried under the haul roads support high loads. To analyse these loads, it is not possible to use the recommendations of the AWWA M11 standard [1], since this standard only provides information for calculations with vehicles up to 35 tons, such as the AASHTO HS20 [2] or Cooper E-80.
The conventional design of buried pipes is based on the maximum deflection of the pipe, which according to AWWA M11 [1] should not exceed 5%. Deflection is measured by dividing the displacement either vertically or horizontally with respect to the pipe diameter. Spangler [3] defined Equation (1), which approximates the horizontal deflection of a steel pipe under the assumption shown in Figure 2.
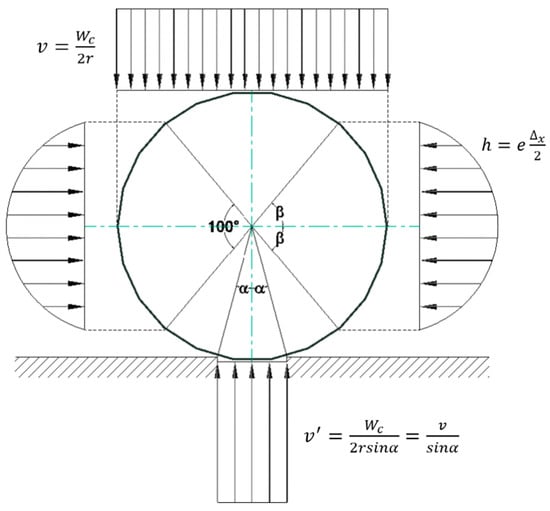
Figure 2.
Spangler’s stress distribution hypothesis [3].
In accordance with Equation (1), the deflection is directly proportional to the following:
- The pipe bedding effect constant , which depends on the pipe bedding angle α;
- The deflection factor for installation time ;
- The dead load , which is commonly estimated using the Marston’s equation or its derivatives;
- The live load , which can be estimated using the Boussinesq or Timoshenko equations or their derivatives;
- The cube of the mean radius of the pipe r.
On the other hand, it is inversely proportional to the sum of the pipe stiffness defined by the following:
- The product of the elasticity modulus, , and the inertia moment of the pipe, ;
- The lateral soil stiffness of the pipe, with value of , where the value 0.061 corresponds to the value of β for an angle of 50° (a typical value in this type of installations, but which may vary depending on the installation). is the modulus of soil reaction obtained from AWWA M11 standard tables [1], which has different recommended values and depends on soil properties, degree of compaction and depth [4].
In some cases, the recommended values of the hybrid module are limiting for certain soil types. For the soil type considered in this article, the most appropriate alternative is the one proposed by Krizek et al. [5], restricted soil modulus (kPa). The restricted modulus is an inherent characteristic of the material and is determined as the gradient of the secant line on the stress–strain curve derived from a soil compression test. This test, which is carried out inside cylindrical containers to avoid lateral expansion of the soil, measures the capacity of the soil to withstand axial compression loads. Alternatively, the restricted modulus can be calculated, based on the Young’s modulus and the Poisson’s ratio of the soil, using Equation (2):
To determine the value of , the load applied to the pipe is taken into account. Using previous research, it is established that E’ is in the range of 0.7 to 1.5, although AWWA M11 [1] suggests considering = . On the other hand, the surface loads produced by the weight of the vehicle and transmitted to the trench through its wheels [6], represent a force on the crown of the pipe, whose value can be estimated using the Timoshenko expression (Equation (3)).
Its impact depends on the following:
- The backfill height over pipe H;
- The external diameter of the pipe ;
- The radius of contact , equivalent to the width of the tire;
- The equivalent contact area of the wheel track on the trench ;
- The impact factor which for the present study was considered to be 2.
The AWWA M11 standard [1] also suggests verifying the resistance of the pipe taking into account the buckling limit (kPa) which is calculated by Equation (4). This limit, , depends on the following:
- The pipe stiffness ;
- Its outside diameter ;
- Modulus of soil reaction ;
- Backfill height over pipe H;
- The water buoyancy factor , which is considered 1.0 for dry soils or those far from humid areas.
Equation (4) does not depend on the width of the trench nor on the elastic modulus of the lateral fill and, given that exceeding this load on the pipe could imply its failure, it is necessary to verify it by other means.
Other researchers, such as Warman et al. [7], propose improvements to the analytical calculations based on the equations of Marston and Spangler [3] introducing more variables in a buried pipe installation. Even so, they continue considering the behaviour of the soil in its elastic state and conventional load values.
The finite element method (FEM) associated with engineering is mainly due to the research of Turner M. J. et al. [8]. They analysed stresses in complex aircraft structures, and their advances soon spread to other areas of engineering (mechanical, civil engineering, etc.). For example, in the geotechnical and pipeline specialties it has been possible for finite element models to adequately simulate the values of experimental tests. Different publications [9,10,11,12,13,14] analyse buried pipes under different installation conditions and materials and use the FEM to simulate the values of experimental studies.
Below are indicated, according to the research carried out by Watkins and Anderson and published in the book Structural Mechanics Buried Pipes [15], some of the main advantages of using the finite element method compared to using more common calculation procedures:
- It allows consideration of the nonlinearity and heterogeneity of the soil;
- It allows consideration of the interface between the pipe and the ground, that is, the slip or adhesion between both surfaces;
- It provides greater precision in the analysis of the vertical and horizontal displacements of the pipe;
- It uses mathematical models that allow the materials of the ground and the pipe to be characterized.
The present study proposes a parametric model that considers the behaviour under real conditions of a pipe trench located in a facility subjected to surface loads. One of the main contributions of this study is to analyse vehicles with a weight much higher than the weight contemplated in the AWWA M11 standard. Using finite elements, it is also determined which parameters that tend to increase the stresses on the pipe are most influential.
The parameters of the finite element model are adjusted through a sensitivity analysis to adequately reproduce Sharma’s experimental tests [16]. The deflections and maximum stresses are determined for steel pipes of 36″, 42″ and 48″ with standard weight thickness and ASTM A53 Grade B material. The surface loads produced by the circulation of mining trucks are considered. Table 1 includes the load capacity for the truck models commonly used in mining.

Table 1.
List of load capacities of heavy vehicles used in mining industry (Typical mining equipment—Peru).
The parametric analysis consists of evaluating 108 models that emerged after modifying the following variables (variables identified in previous equations):
- Pipe outside diameter ;
- Pipe thickness , preselected according to hydraulic calculations;
- Pipe bedding angle , depending on the installation;
- Elasticity modulus of the pipe material, preselected according to the hydraulic calculations ;
- Elasticity modulus of the trench backfill, determined by a soil survey or recommended values (, , …, );
- The recommended geometric values in the typical trench section as width and height;
- The study was carried out using the mining vehicles shown in Table 1 as a reference.
2. Proposed Finite Element Model
Previous researchers [6,9,17,18] have used finite elements to determine and analyse the stresses produced by different external loads on pipelines, in order to determine different failure scenarios. This study analyses buried pipes subjected to external loads higher than those contemplated in the standards applying the finite element method with Abaqus/CAE 2019 software to identify the installation parameters that have the greatest influence on the stresses produced on the pipe and that could lead to failure.
Experimental data from a test carry on at the University of Texas Arlington (UTA) in the Center for Underground Infrastructure Research and Education (CUIRE) by Sharma [16] were used to validate the finite element model.
The procedure developed is summarized in the scheme shown in Figure 3. The following characteristics are taken into account:
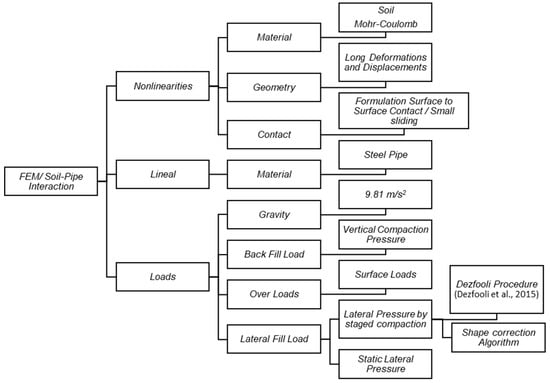
Figure 3.
FEM analysis procedure of a buried pipe in a trench [10].
- The nonlinearity of the material, the contact and the geometry [15,19,20,21];
- The linearity range of the pipe;
- The applied loads, including soil and surface loads as well as lateral loads produced by the compaction process of the layers during installation.
During the construction process of installing pipes in trenches, the compaction of the soil in layers is contemplated, which progressively affects the deflection of the pipe. The lower layers affect the horizontal deflection, reducing the diameter; the upper layers reverse the result, causing the pipe to deflect horizontally toward the walls of the trench. Thus, using a procedure that considers the construction process in stages, proposed by Dezfooli et al. [10] and described in Section 2.3, results are obtained that better approximate reality.
To approximate the nonlinear behaviour of soils, different constitutive models can be used, which model this behaviour based on the soil type and the nature of the problem. Among these models, the following stand out: the Mohr–Coulomb elastoplastic model with perfect plasticity, the plasticity model of Drucker and Prager [22], the Cam clay model [23], the modified Cam clay model [24], Duncan’s hyperbolic model [25], Vermeer’s nonlinear elastoplastic model with hardening [26], the soil model with hardening [27], the undrained soft clay model [28] and the Duncan–Selig [29]. Considering the objectives set out in this article, it is necessary to measure the trends of increase in the stresses of a buried pipe, caused by changes in some variables of the installation, but a high accuracy in the plastic behaviour of the soil is not required. Taking into account these considerations, the Mohr–Coulomb elastoplastic constitutive model is used. Likewise, it is considered that the values required by this model, the friction angle ϕ and cohesion c, can be easily obtained from a conventional and usual soil study in engineering projects.
2.1. Validation of Finite Element Model
The finite element model proposed in this paper has been validated with the experimental results of test 1a presented by Sharma [16] in his study “Development of a Model for Estimation of Buried Large Diameter Thin-Walled Steel Pipe Deflection due to External Loads” (see Figure 4).
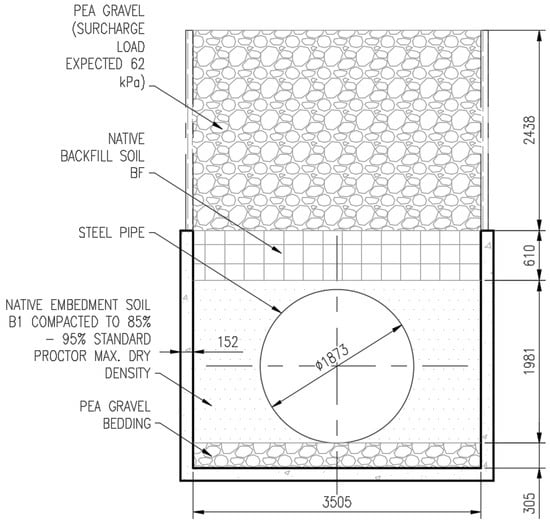
Figure 4.
Installation section for validation test 1a (mm). Adapted from Sharma [16].
For the Sharma’s test [16], a concrete box was previously built in the Center for Underground Infrastructure Research and Education (CUIRE) at Arlington University, and it consists of reinforced concrete walls and slab. Pea gravel bedding of 0.305 m height was placed at the floor of the soil box. Instrumented steel pipe piece was placed longitudinally along the length of the load cell and centrally along the width of the soil box. The pipe was embedded with native material as embedment. The embedment was placed in approximately nine layers compacted above 90% standard proctor density. Density measurement was taken through a nuclear density gage.
A timber frame was constructed above the concrete box to provide 2.438 m high walls on the sides to facilitate additional surcharge load. The surcharge load due to compaction was achieved by 0.610 m of native material and the 2.438 m of pea gravel placed over the embedment.
In Sharma’s test [16] the horizontal and vertical pipe deflection were measured by recording values u1 and u2 (inches), respectively, by means of convergence meters. Also, the micro circumferential deformations in different positions of the pipe were also measured using strain gauges.
During the embedment phase there is a positive peaking deflection in the vertical diameter (u2) and a negative deflection in the horizontal diameter (u1). This behaviour is reversed during the backfill cover and surcharge loading when there is a reduction in the vertical diameter and an increase in the horizontal diameter.
2.1.1. Model Geometry
The test 1a includes the measurement of horizontal and vertical deflections and circumferential deformations on an instrumented steel pipe. The pipe, 72 inches diameter and 0.313 inches thickness, was installed inside a concrete box and buried using a layered clay soil compaction procedure, with an average thickness of 9 inches per layer. To simulate the upper external load and pressure at the pipe crown of approximately 62 kPa, a wooden box was installed.
The results of Test 1a are shown in Section 2.3 along with the FEM simulation.
The geometry of the pipe trench is determined by the pipe, the gravel bed, the compacted lateral layers and the fill over the pipe. In the experimental study [16] the concrete box was represented as a rigid element where lateral displacement was restricted at the walls and vertical displacement at the base. See Figure 5.
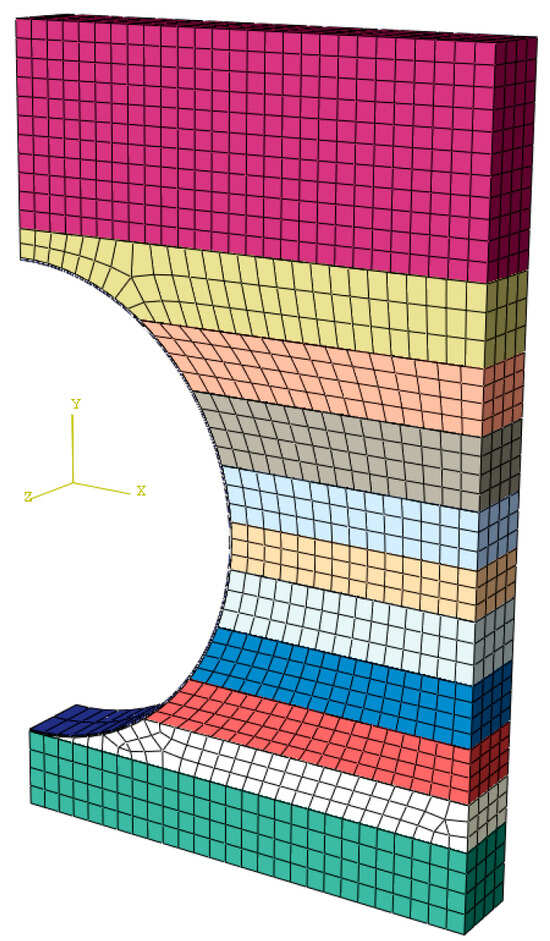
Figure 5.
Finite element model validation—geometry.
The length of the finite element model has been defined according to the sensitivity analysis described in Section 2.2.2.
2.1.2. Boundary and Contact Conditions
A symmetrical model is considered with respect to the central axis of the trench. The boundary conditions imposed on the edges of the model restrict the movements in the lateral nodes in the horizontal direction, in the lower edge of the model in all directions, and the rotations with respect to the X, Y and Z axes. Since a symmetric geometry is involved, it is considered a restriction on the lateral edge coinciding with the direct axis of the trench and the turns in the XY plane, thus allowing the number of model elements and the computational and temporal cost to be reduced. See Figure 6.
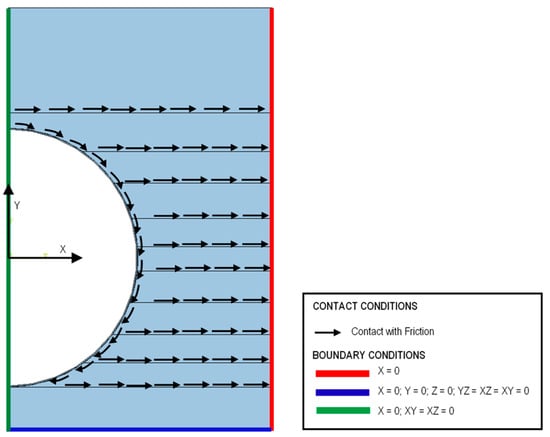
Figure 6.
Model contact and boundary conditions.
The friction angle has been defined according to the sensitivity analysis developed in Section 2.2.3.
2.1.3. Meshing and Element Types
The proposed model contemplates the use of wedge elements with six (6) nodes as well as linear brick elements with eight (8) nodes with reduced integration and “hourglass control” for both the ground and the steel materials. Reduced integration is considered to have sufficient precision with one integration point per element, and thus reduce computational costs (without affecting the results).
The mesh size has been defined according to the sensitivity analysis developed in Section 2.2.4.
2.1.4. Lateral Loads and Numerical Simulation Procedure
Lateral earth pressures on large diameter pipe are important in order to model the behaviour of the pipe–soil system. However, the study of this lateral loads during pipe installation is limited. Dezfooli et al. [10] developed a method to model construction stages across layers, using an algorithm to activate and deactivate soil layers. Figure 7 shows the last three layers considered in the study in contact with the pipe, when only the pipe and a group of soil layers are active. The shared nodes allow the model parts to capture and track modified geometry, according to the deformed shape of neighbouring parts.
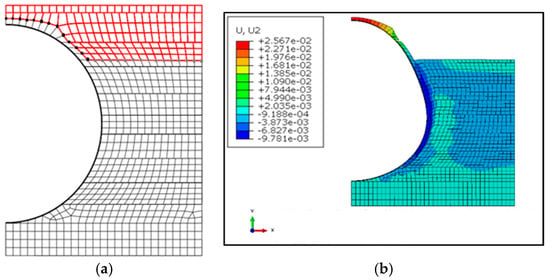
Figure 7.
Shared nodes between active and inactive parts: (a) Black dots are shared nodes between soil and pipe, and grey dots are shared nodes between soil layers. (b) Analysis in finite element software (Deflections U, U2 in meters).
For the case of lateral pressure induced by compaction, a horizontal load is applied to each constructive layer of the compacted soil [10]. The calculated stresses are applied to each soil layer using the equivalent temperature loading (Equation (5)) [10]:
where:
- the cross-sectional area of the soil layer is ;
- the length of each layer is ;
- values are obtained as the product of the pipe thickness and its elasticity modulus;
- , is obtained multiplying the trench wall’s elasticity modulus by the trench wall’s length;
- is the elasticity modulus of the lateral fill;
- α is a virtual thermal coefficient;
- is the lateral soil stress. It is calculated from the value of the undrained cohesion Cu of the soil. Cu is measured in units of pressure. According to Clayton and Symons [30] the lateral soil pressure reaches up to 80% of Cu for soil plasticity indexes of 48%.
The undrained cohesion values, Cu, have been defined according to the sensitivity analysis developed in Section 2.2.1.
Finally, the lateral stresses are introduced into the model through the temperature variation obtained for each layer.
In the finite element model developed, the pipe does not reach its elastic limit and the soil works in its elastoplastic state. The soil failure criterion proposed by Mohr–Coulomb is used. The Mohr–Coulomb criterion relates the maximum and minimum triaxial stresses to the friction angle and the cohesion of the material (Equation (6)). The Mohr–Coulomb criterion defines the yield function, as a measure of how close the normal and shear stress are to the failure surface. The graphical representation is a circumference perpendicular to the hydrostatic axis and corresponds to half of the first invariant of the stress tensor. When the friction angle of the soil is not considered, that is, = 0, the expression is simplified to the Tresca criterion.
This mathematical model has been chosen considering that its parameters are easily obtained with a conventional soil study and the accuracy of the results is sufficient for trend analysis.
2.2. Sensitivity Analysis of the Finite Element Model
The finite element model validation has been finally completed with the adjustment of the following variables: compaction, model length, the friction coefficient, and the size of the mesh. To obtain the appropriate values for these variables the following sensitivity analysis has been performed.
2.2.1. Compaction
Layer compaction during the construction stage generates lateral loads in the soil that affect the pipeline. Its value is directly proportional to a percentage of the shear stress of a compacted and undrained soil. The sensitivity analysis considers the evaluation of the model applying lateral loads between 0.2 to 0.6 of the undrained cohesion, Cu.
As shown in Figure 8, the results indicate that for the first layers (at the height of the base of the pipe or “Haunch Zone”) compaction is not effective, since low pressures are present (approximately 20% of the Cu). For layers above the first two, the percentage increases and is between 30% to 60% of Cu. In the last two layers, the percentage is 40%. The lateral pressure is maximal in the central lateral zone of the pipe or “Springline”.
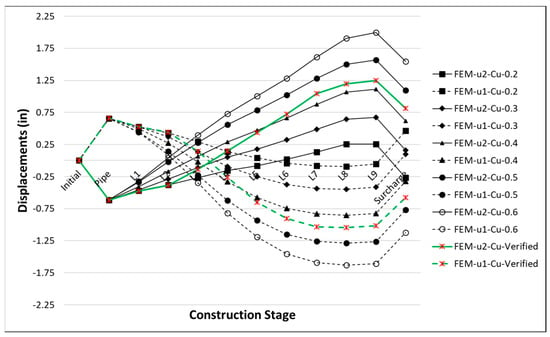
Figure 8.
Results of the parametric sensitivity analysis—compaction.
The obtained results are consistent with the works of Clayton and Symons [30] and with the tests carried out by Sharma [16].
In Figure 8 the closest values to the validation test are identified as FEM-u1-Cu-Verified and FEM-u2-Cu-Verified.
2.2.2. Model Length
The sensitivity analysis evaluates the model lengths of 0.3 m, 0.6 m, 1.5 m and 3 m for the validation experimental test [16]. The results obtained are shown in Figure 9.
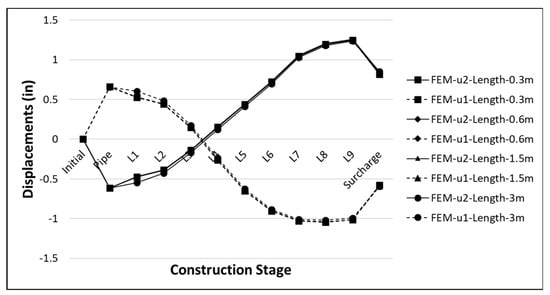
Figure 9.
Parametric sensitivity analysis results—model length.
For model lengths varying from 0.3 m to 3 m, the deflection variation is 4% for vertical displacements and 2% for horizontal displacements. The computational cost of an analysis of a 3 m long model is 50 times greater than that of a 0.3 m model. Therefore, and based on the results obtained, the simulation was performed in a 0.3 m length model.
2.2.3. Contact
According to the research of El Chazli et al. [31], the friction coefficient between soil materials and steel pipes takes values between 0.2 and 0.5. On the other hand, Shaurav Alam et al. [32] establish, for clay soils with an internal friction angle of 22.2° and cohesion of 87 kPa (12.5 psi), values between 0.3 to 0.96 for the friction angles and depending on the burial depth of the pipe. Taking these investigations into account, this study performs a sensitivity analysis in the range of 0.2 to 0.5 in steps of 0.1.
The Figure 10 shows the results obtained in this sensitivity analysis. It is observed that, for the coefficients analysed, the vertical and horizontal displacements vary by 10% and 14%, respectively. It is also observed that the variation in displacement values is not linear. A friction coefficient of 0.3 is used in the finite element model, both for the pipe–soil and for the soil–soil.
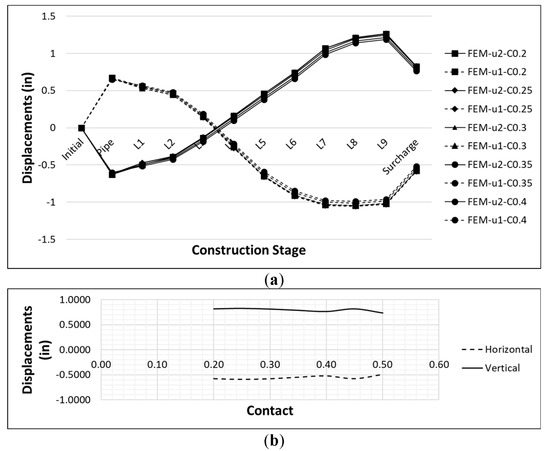
Figure 10.
Parametric sensitivity analysis results—(a) friction coefficient; (b) displacements in the last stage of construction vs. friction coefficient.
2.2.4. Mesh Size
The sensitivity analysis was developed for mesh sizes of 40 mm, 45 mm, 50 mm and 70 mm. The computational cost used for the densest mesh was 7 times higher than that of the least dense.
The results shown in Figure 11 indicate that the variation in displacement results in the last construction stage varies between 5% and 30% for vertical and horizontal displacements, respectively. To reduce these percentages denser meshes should be used. Based on the results a mesh density of 50 mm is used in the finite element model.
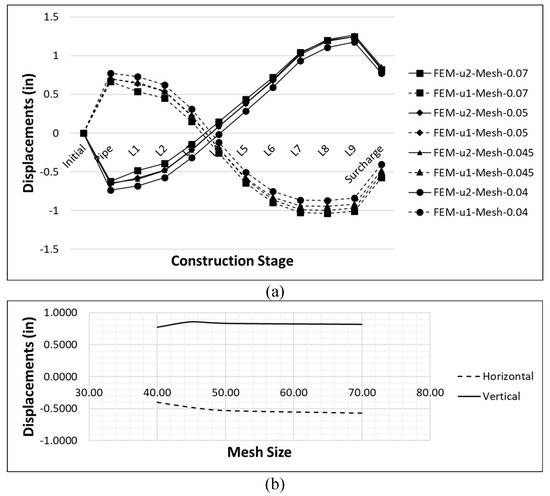
Figure 11.
Results of parametric sensitivity analysis—(a) mesh size of the model from Test 1a; (b) displacements in the last stage of construction vs. mesh size (mm).
2.3. Results of Validation of Model Finite Element
The finite element model proposed in this study has been developed using Abaqus/CAE 2019 software [33]. To define the characteristics of the three-dimensional model, a sensitivity analysis was carried out as described in previous section.
The results of the finite element analysis are compared with those obtained experimentally by Sharma [16]. The surcharge is applied on the trench surface and furthermore, the deflections during the construction process in layers and the deformations just at the end of the construction are compared. It is considered as 0° at the top of the pipe or crown and 180° at the base of the pipe or Invert. Validations results are shown in Figure 12 and Figure 13.
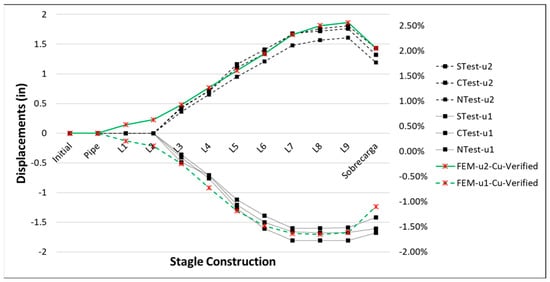
Figure 12.
Validation results: horizontal and vertical deflection. FEM vs. experimental test.
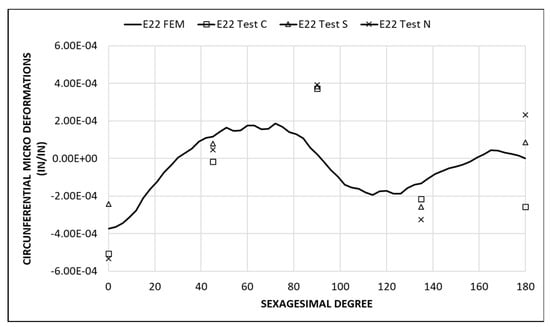
Figure 13.
Validation results: circumferential deformations. FEM vs. experimental test (final stage of construction).
Regarding Figure 12, the following results were obtained in deflection at the surcharge construction step. In the vertical diameter deflection (u2) there is a variation of 9.13% between FEM and test results, and in the horizontal diameter deflection (u1) there is a variation of 12.9% between FEM and test results. Based on these results authors consider that the results of the finite element analyses are fairly closed to the experimental test results.
Figure 13 compares FEM simulation with the deformation values measured during the test using strain gauges in the final construction stage (surcharge). There is a variation between FEM and test of 12.58% in the vertical deformation and 71.18% in the horizontal deformation. As expected, the variation values between FEM and test results are greater in deformation than in the deflection since the finite element models first approximate the displacements and then the deformations. However, in the case of horizontal deformations, the discrepancy is significant. Authors consider that this discrepancy may be due to the fact that the soil modulus of elasticity is not constant with depth, as stated by Hartley et al. [4]. Since the limiting deformation is the vertical deformation, and in this case the finite element approximation is acceptable, the model is considered validated.
3. External Loads over Haul Roads
The vehicles considered in this article, shown in Table 1, are mining trucks that transport the material to the primary crushing area. The road along which they circulate, called a mining haul road (see Figure 14), is normally an exclusive road built with highly resistant materials [34]. Several layers of crushed gravel, pit-run gravel and sand are arranged. An example of a haul road section in shown in Figure 15.
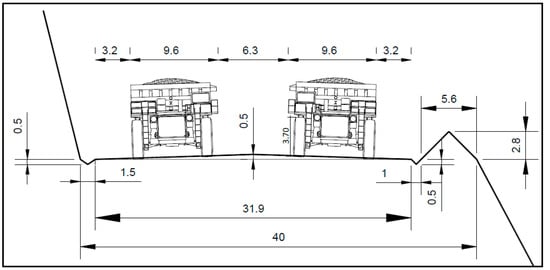
Figure 14.
Haul road design profile (Komatsu 980 t truck), (dimensions in meters).
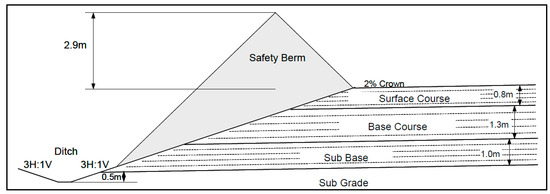
Figure 15.
Typical section of a section of a haul road for 320 t trucks [4].
Currently, international standards and recommendations for calculation and design of buried steel pipelines only consider the effects of live loads on the pipe for HS-20 type vehicles whose load does not exceed 35 tons [1,2]. One of the main contributions of this study is to analyse vehicles with a weight much higher than the weight contemplated in the standards. Therefore, this article evaluates the behaviour of a group of pipes subjected to higher magnitude loads. The finite element calculation procedure described in Section 2 has been used for the study.
Construction materials for haul road pavement require high durability. The determination of the height of the road layer depends on the vehicles that circulate on it. The elasticity modulus on the top layer (surface) is approximately 500 MPa, on the second layer (base) is in the range of 150 to 350 MPa and in the layer below the base (subbase) the value ranges between 100 to 150 MPa (Table 2). To simplify the parametric analysis, all layers with an elasticity modulus of 150 MPa are considered. This hypothesis is consistent with the fact that the thickness of the top layer is very small.

Table 2.
Minimum bearing capacity and Young’s modulus of haul road construction materials [34].
The tire print has an elliptical shape. The model has been simulated according to the work developed by several researchers [35,36,37,38]. Other authors, in order to simplify the calculation of the contact area, consider a circumference whose equivalent radius is half the real width of the tire [34].
To simplify the analysis, the tire print has been considered to be rectangular with a width equal to the width of the wheel and length (tire contact length). Its calculation is carried out using Equation (7), where:
- is the equivalent area of the tire print on the trench. It is determined using the equivalent radius (which is half the width of the wheel);
- the width of the wheel is .
The Figure 16 shows the representation of the tire prints of the vehicle. For the vehicles used in this article, the front axles are single and the rear axles double. According to the manufacturers’ technical sheets, the greatest load is exerted on the rear axle. Therefore, the contact pressure under the rear wheel area is taken into account.
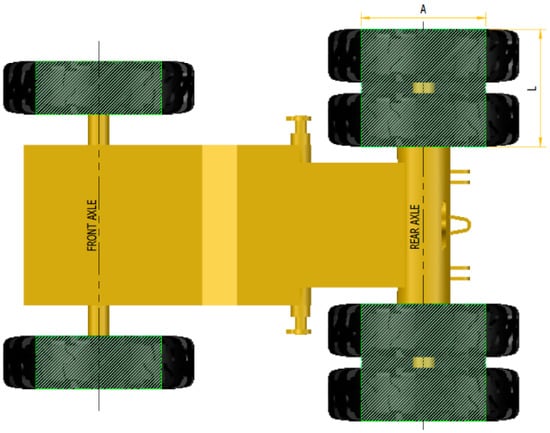
Figure 16.
Diagram of tracks of a vehicle on the surface.
As described in Section 1 of this article, there are equations that estimate the surface loads of rectangular sections. These loads are applied on the buried pipe and that are a function of the burial height. Helwany [39] has validated, through finite element models, the Spangler equation, which does not depend on the soil properties, but only on the burial height of the pipe.
The Table 3 shows the weights of the heavy-duty vehicles considered in Table 1. The surface pressures applied on these vehicles’ tire prints are shown in Table 4.

Table 3.
Weights of mining trucks.

Table 4.
Surface pressures of mining trucks.
As shown in Table 4, vehicles with different gross weights apply similar pressures on the tire prints, since their tires have different dimensions for each model. Therefore, only the highest-pressure value was used for this article, which corresponds to the CATERPILLAR truck model 797 F, whose pressure is approximately 1250 kPa, whereas a value of 2 is considered as a conservative impact factor to take into account road irregularities.
4. Parametric Study FEM Buried Pipe under Haul Road
This study analyses 36″, 42″ and 48″ steel pipes with standard wall thickness (0.375 in) [40] of ASTM A53-B material, buried under a haul road and with different installation conditions. A parametric analysis is performed on 108 trench–pipe interaction models that have been obtained by modifying the variables listed in the third figure in Section 4.1. The selected variables were those that showed a greater impact on the results of the analytical equations indicated in the introduction section. For the parametric study the finite element calculation procedure described in Section 2 was employed. The validation of the FEM model was carried out with experimental test data [16]. In the validation study a concrete box was used as the boundary of the trench walls. However, in the parametric study the walls of the haul road pavement are contemplated, to estimate more accurately the behaviour of the pipe–soil interaction.
4.1. Parametric Study
The trench cross section schematic used for the parametric analysis is shown in Figure 17.
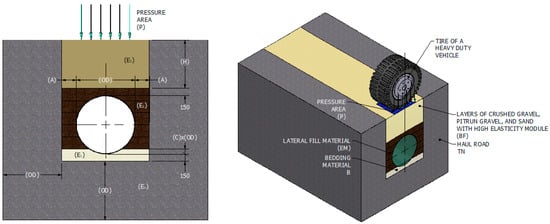
Figure 17.
Parameterized diagram of pipe installation section in trench (dimensions in mm, unscaled).
The nomenclature used for the parametric study is shown in Figure 18.
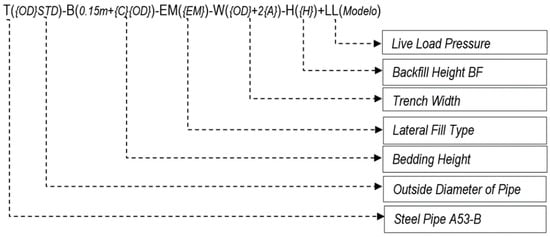
Figure 18.
Nomenclature of parametric models based on the analysed variables.
Lastly, Figure 19 shows a summary of the data flow for the parametric study of the behaviour of a steel pipe installed under a haul road using the finite element method.
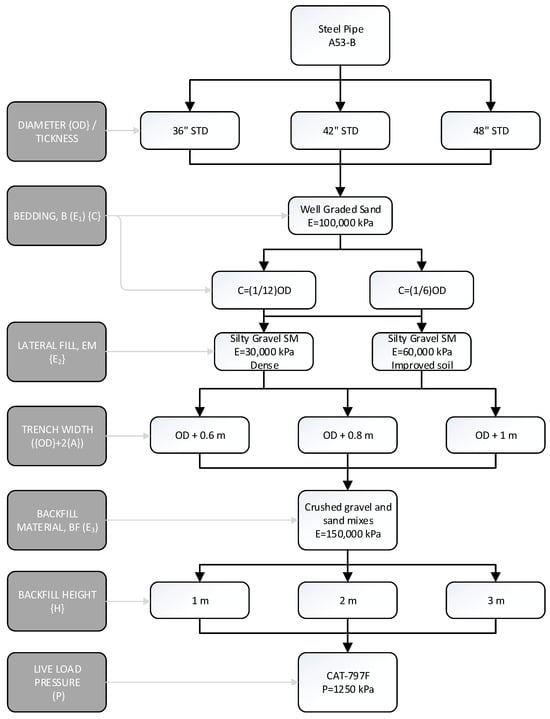
Figure 19.
Data flow for parametric calculation using the finite element method.
Table 5 shows the constitutive properties of the used materials.

Table 5.
Properties of trench materials used in parametric study.
4.2. General Considerations
The most important considerations taken into account for the development of the parametric analysis are described below:
- It is considered that the contact walls of the trench are made of natural soil in order to more accurately estimate the behaviour of the pipe (see Figure 17). Additionally, it is considered that the trench walls do not require external control measures due to possible instability during its construction.
- For the calculation of the residual lateral pressure of the lateral backfill on the pipe, the stiffness of the trench is taken into account.
- The model considers longitudinal and transverse symmetry to reduce computational costs (see Figure 20).
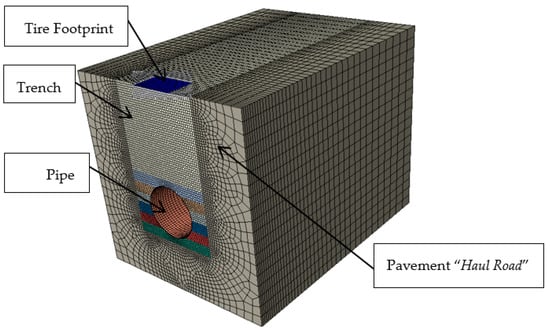 Figure 20. Section of three-dimensional finite element model, including trench sidewalls (transversal symmetric model).
Figure 20. Section of three-dimensional finite element model, including trench sidewalls (transversal symmetric model). - The surface load applied on the pipe is located in the central area of one of the rear wheel prints and the pipe is considered to be unaffected by the pressure of the front axle tire of the mining truck or the lateral rear wheel.
- According to the model boundary conditions, a restriction on the longitudinal displacement of the soil and the pipe is considered. A qualitative analysis of the effect of the model length on the variation in the vertical stress results produced by a surface load was carried out for model lengths of 3 m, 6 m, 9 m, 12 m and 15 m, for mesh sizes of 0.12 m. According to the results, it is concluded that the longer the pipe length, the less affected by this restriction are the results. Thus, for the parametric analysis, a model with a total length of 12 m and a minimum and maximum mesh density of 0.05 m and 0.5 m, respectively, was considered (longitudinal and transversal symmetrical model). Even when the results of vertical pressures on the pipe are slightly affected, the trends of stresses and deformations in the pipe will remain basically the same.
- To ensure that the pipe does not fail and to suggest design recommendations, the admissible stresses of the ASTM A53 Grade B material pipe will be considered in the analysis of the results.
4.3. Analysis of Results
For the analysis, 108 models were generated with the Abaqus/CAE 2019 software [33] with variation in parameters. The results were postprocessed in MS Excel spread sheets to have the data sorted and compare each of the solved cases. Figure 21 shows one of the simulated cases.

Figure 21.
Example of one of the FEM cases run for the parametric model: soil and pipe stress results for a pipe installation with 48″ + 0.8 m width, lateral backfill type EM1, bedding height 1/12 of 48″ buried 2 m high under a tire pressure load of a CAT-797F truck (Stress in kPa).
Haul roads are designed to withstand high pressures such as those produced by the wheels of high-tonnage haulage mining vehicles. The compacted soil layers typically operate within their elastic range, designed to achieve deformations of approximately 2000 microns [34]. For this reason, it is important that the pipe backfill receives the same treatment as the haul road design, so that the only load on the pipe will be that transmitted by the surface pressure applied by the truck tires, and there is no need to consider the failure of the soil with large vertical displacements.
4.3.1. Surface Pressure
It is important to note that the pressure applied on the surface dissipates with respect to depth, so the pressure that the pipe will assume will depends on the height of the top backfill of the trench. As shown in Figure 22, the pressure of 1250 kPa, applied on the surface, decreases as the measurement is deeper; hence, pipes installed at 1 m depth will receive much greater load than those installed at 3 m depth. Therefore, it will be important to evaluate the pipe and verify if the deflection and stresses applied on it are within acceptable limits.
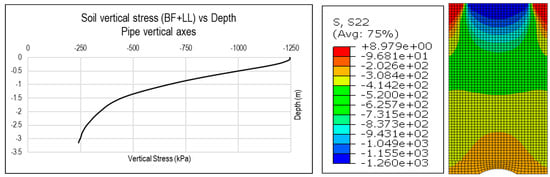
Figure 22.
Curve of vertical forces applied by a CAT-797F truck and the weight of the upper backfill, with respect to depth (Stress in kPa).
For example, for a 48″ pipe with standard wall thickness (0.375″) and with an allowable stress of 138 MPa installed at 1 m depth, the pressure produced by a CAT 797F truck with a weight of 600 tons generates maximum stresses under the von Mises pipe failure criteria of 79 Mpa at the crown of pipe. Considering a design safety factor of 2, the design limit stress is 69 Mpa, and hence the installation condition at a depth of 1 m is not recommended, because it exceeds the design limits at the pipe crown (See Figure 23).
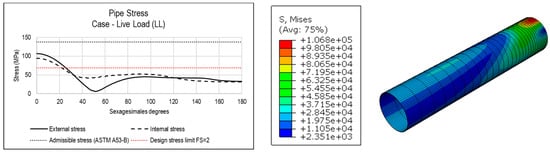
Figure 23.
Stresses of a 48″ STD A53-B pipe, buried at 1 m with a trench width of 48″ + 0.8 m and a bedding height of 1/12 of 48″ (Stress in kPa).
4.3.2. Trench Width and Pipe Bedding Height
On the other hand, it is important to point out that there are other parameters which can increase the stresses on the pipe: the width of the trench and the height of the pipe bedding.
Diagrams of the circumferential displacements on a 36″ pipe are shown in Figure 24 with an amplification factor of 5. It is observed that, when the trench width parameter is modified, the deflection increases as its width increases and, therefore, the stresses also increase, becoming closer to the allowable stress on the pipe. It is thus important to consider trenches with the minimal possible width, which also benefits the costs. However, it should be considered that it is necessary to compact the layers of the lateral backfill of the pipe with a compaction equipment, so that a suggested minimal adequate width, from the lateral wall of the pipe to the lateral wall of the trench, could be 300 mm.
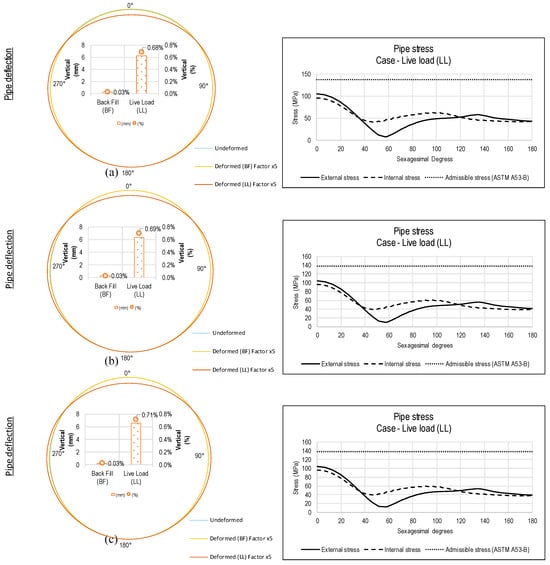
Figure 24.
Deflections and stresses of a 36″ STD A53-B pipe buried at 1 m under a CAT 979 F truck load with EM1 lateral soil material, for (a) 36″ + 0.6 m, (b) 36″ + 0.8 m h and (c) 36″ + 1 m trench width.
On the other hand, bedding heights of 1/12 OD and 1/6 OD has been considered in the model. The results show that increasing the bedding height reduces the deflection pipe. Figure 25 shows the effect of the bedding height. This effect is not very relevant, so one of the conclusions of this study is that is not necessary to increase more than 1/12 OD the bedding height.
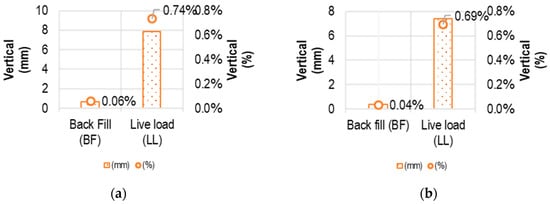
Figure 25.
Deflections of 42″ STD A53-B pipe buried at 1 m under a CAT 979 F truck load for 42″ + 1 m trench width with (a) bedding height of 1/12 of 42″ and (b) bedding height of 1/6 of 42″.
It is important to note that the bedding height of the pipe is relevant during pipe installation only if the pipe is installed with internal wooden supports (struts) that prevent the pipe from deflecting due to its own weight. This fact is more significant for pipes with a very high diameter/thickness ratio.
4.3.3. Lateral Backfill Material
Next analysed parameter is the pipe lateral backfill material. These materials are usually selected sand or fine gravel and have a high soil modulus of elasticity. However, these materials can sometimes be replaced by treated or improved soils to lower costs, in which case the soil obtains a modulus similar to those of the sand or fine gravel, as explained in “Development of a Model for Estimation of Buried Large Diameter Thin-Walled Steel Pipe Deflection due to External Loads” [16].
The study analyses soils with modulus of elasticity of 30,000 kPa and 60,000 kPa, with the same degree of compaction. The results show that the higher the modulus of soil elasticity, the lower the pipe deflection. An example is displayed in Figure 26, where analysing the 42″ STD A53-B pipe buried at 1 m and subjected to a surface load of a CAT 797F vehicle, with a 42″ + 0.6 m of trench width, the deflection varies by 15.6%, having the most favourable material an elasticity modulus of 60,000 kPa. Nevertheless, the costs of these materials increase the project budget, and hence it is necessary to evaluate the choice of material considering both its cost and if the pipe is within the allowable deflections and stresses.
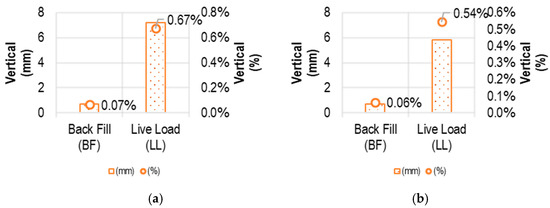
Figure 26.
Deflections of 42″ STD A53-B pipe buried at 1 m under a CAT 979 F truck load for 42″ + 0.6 m trench width with (a) lateral soil elasticity modulus E1 = 30,000 kPa and (b) lateral soil elasticity modulus E2 = 60,000 kPa.
4.3.4. Backfill Height
The results show that the maximum stresses on the pipe while the wheel load is passing over the buried pipe are located at the crown position (0° in Figure 27). The results also show that the increase in the backfill height reduces significantly the maximum pipe stresses and makes more uniform the stress distribution along the pipe perimeter.
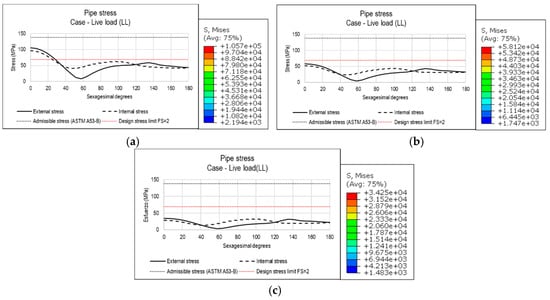
Figure 27.
Stresses on a 36″ STD A53-B pipe under a CAT 979 F truck load for 36″ + 0.6 m trench width; Installed: (a) at a height of 1 m; (b) at a height of 2 m; (c) at a height of 3 m (Stress S in kPa).
4.4. Trends—Parametric Analysis
The objective of this section is to show the trends produced by the changing of the analysed variables and to identify the variables with more impact in the pipe structural behaviour.
The analysis started from a base case identified as Case 1 in Figure 28. This base case presents the condition of minimum stress on the pipe, which implies a higher backfill height (H = 3 m), a lateral fill with a higher modulus of elasticity (E = 60,000 kPa), a higher bed height (1/6 OD) and a tighter trench width (OD + 0.6 m).
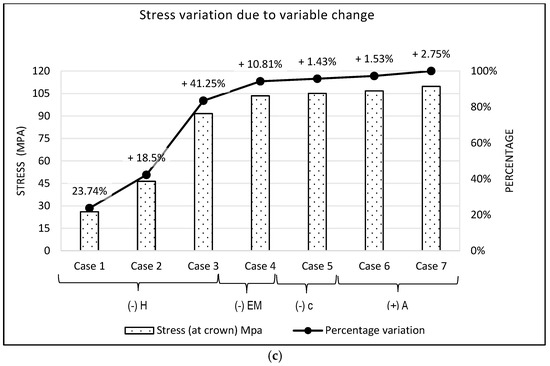
Figure 28.
Increase in pipe stress at crown due to change in variables (a) pipe 36″ STD A53 Gr. B; (b) pipe 42″ STD A53 Gr. B; (c) pipe 48″ STD A53 Gr. B.
The trend graphics for the three analysed pipes (36″, 42″, 48″/STD A53-Gr.B) are shown in the Figure 28.
Figure 28a shows that when the backfill height is reduced from 3 to 2 m, the stresses increase around 19%, whereas when reduced to 1 m, the stresses increase by about 40%. This variable has the greatest influence on the results.
Likewise, by reducing the elasticity modulus of the lateral fill (EM) from 60,000 kPa to 30,000 kPa, the stresses increase around 13%. This variable has the second greatest influence on the results.
On the other hand, by decreasing the pipe bedding height (C) from 1/6 OD to 1/12 of OD, the stresses only increase around 1.8%, which means that this variable does not affect significantly the results. As mentioned in Section 4.3, the pipe bedding height is important during the installation process, preventing the pipe from deflecting due to the pipe’s own weight.
When analysing the increase in the trench width (A), it is observed that the impact is almost negligible. If anything, it highlights that the trend for the three pipe diameters is different. For the 36″ pipe, the value of the stresses decreases slightly, while for the 42″ and 48″ it increases.
5. Conclusions
The following conclusions are drawn from this study:
- A calculation procedure has been developed to analyse pipes buried under haulage roads bearing a surface pressure of 1250 kPa using the finite element method and taking into account the residual lateral pressure due to the compaction of the fill. The model has been validated with experimental data. Likewise, a sensitivity analysis has been carried out to evaluate the following variables: model length, mesh size, contact and residual lateral load.
- A parametric study has been carried out with 108 models, varying the diameter of the pipe, the width and height of the trench, the height of the pipe bed and the type of lateral filling. The trend in the behaviour of the forces acting on the pipe when the selected variables are modified has been estimated. The results indicate that the most influential variables on the pipe deflection and stress are the height of the backfill and the elasticity modulus of the lateral fill.
- Changing the top fill height (H) from 3 m to 1 m increases stresses by approximately 60%. Likewise, changing the side fill material (EM) from 60,000 kPa to 30,000 kPa increases stresses by approximately 11%.
- Pipe bedding height (C) does not significantly affect stresses under mining truck loads. This variable is more important during the construction stage, where the higher the bed height (C) in the first installation stage, the better the pipe is supported, reducing initial deflections.
- The width of the trench does not significantly affect the stresses on the pipe. However, when the width increases, the results show that the stresses increase. Likewise, it is observed that if the width of the tire print is smaller than the pipe diameter, the efforts tend to increase; on the contrary, if the width of the tire print is greater than the pipe diameter, the efforts tend to be reduced.
- The variables that most influence installation costs are the height and width of the trench, along with the quality of the filling materials. The greater the trench height, the lower the stresses that the pipe bears, but on the other hand the excavation costs are higher. Likewise, the better the material quality with respect to the elasticity modulus, the lower the stresses that the pipe bears, but in the same way it increases the costs of the installation. Lastly, a reduction in the trench width implies both a reduction in stress on the pipe and a reduction in installation costs.
Author Contributions
Conceptualization, J.J.J.d.C.F.; methodology, J.J.J.d.C.F. and N.S.V.; validation, J.J.J.d.C.F., A.M.G.-A. and N.S.V.; formal analysis, N.S.V. and A.M.G.-A.; resources, J.J.J.d.C.F. and A.M.G.-A. and writing—review and editing, N.S.V. and A.M.G.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Horizontal pipe deflection (m) | |
| Outside pipe diameter (m) | |
| Buried pipe bedding constant | |
| α | Pipe bedding angle |
| Deflection lag factor (30% 40 years = 1.5) (1–1.5) | |
| Backfill load over pipe per pipe length unit (kN/m) | |
| External load over pipe per pipe length unit (kN/m) | |
| Mean radius of pipe shell (m) | |
| Pipe elasticity modulus (kPa) | |
| Transverse moment of inertia per length unit of pipe wall, ~ t3/12 (m3) | |
| t | Pipe thickness (m) |
| Modulus of soil reaction (kPa) | |
| Constrained Modulus (kPa) | |
| Backfill elasticity modulus (kPa) | |
| Poisson’s ratio of soil | |
| Impact factor | |
| Backfill height over pipe (m) | |
| Tire equivalent contact area (m2) | |
| Limit Bucking pressure (kPa) | |
| Water buoyancy factor | |
| Temperature variation | |
| Normal stress on the plane of soil failure | |
| Lateral stress of soil proportional to lateral fill cohesion (un-drained shear strength, Cu) | |
| Transversal area of soil layer (m2) | |
| Length of soil layer (m) | |
| Pipe young modulus x pipe thickness (kN/m) | |
| Lateral soil young modulus x Lateral soil length (kN/m) | |
| Lateral soil young modulus (kPa) | |
| Mohr–Coulomb yield function | |
| Friction angle | |
| Material cohesion | |
| Cu | Undrained cohesion |
| Tire contact length (m) | |
| Width contact, equivalent tire width (m) | |
| Equivalent radius | |
| Trench width | |
| Lateral fill elasticity modulus | |
| Pipe bedding height |
References
- AWWA M11. AWWA-M11 Steel Pipe-A Guide for Design and Installation; Edition, F(C); AWWA: Washington, DC, USA, 2017. [Google Scholar]
- AASHTO: American Association of State Highway and Transportation Officials. Standard Specifications for Highway Bridges, 17th ed.; AASHTO: Washington, DC, USA, 2002; ISBN 1560511710. [Google Scholar]
- Spangler, M.G. Underground Conduits—An Appraisal of Modern Research. Trans. Am. Soc. Civ. Eng. 1948, 113, 316–345. [Google Scholar] [CrossRef]
- Hartley, B.J.D.; Asce, A.M.; Duncan, J.M.; Asce, F. E’ and its variation with depth. J. Transp. Eng. 1988, 113, 538–553. [Google Scholar] [CrossRef]
- Krizek, R.J.; Parmelee, R.A.; Kay, J.; Elnaggar, H.A. Structural Analysis and Design of Pipe Culverts; NCHRP Report; NCHRP: Washington, DC, USA, 1971. [Google Scholar]
- Katona, M.G. Improved Methods for Simulating Live Loads for Two-Dimensional Structural Analysis of Buried Culverts. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 036119811984646. [Google Scholar] [CrossRef]
- Warman, D.J.; Hart, J.D.; Francini, R.B. Final Report Development of a Pipeline Surface Loading Screening Process & Assessment of Surface Load Dispersing Methods; Kiefner & Associates, Inc.: Worthington, OH, USA, 2009; p. 75. [Google Scholar]
- Turner, M.J.; Clough, R.W.; Martin, H.C.; Topp, L.J. Stiffness and Deflection Analysis of Complex Structures. J. Aeronaut. Sci. 1956, 23, 805–823. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J. Finite element analysis on mechanical behavior of semi-exposed pipeline subjected to debris flows. Eng. Fail. Anal. 2019, 105, 781–797. [Google Scholar] [CrossRef]
- Dezfooli, M.S.; Abolmaali, A.; Park, Y.; Razavi, M.; Bellaver, F. Staged Construction Modeling of Steel Pipes Buried in Controlled Low-Strength Material Using 3D Nonlinear Finite-Element Analysis. Int. J. Geomech. 2015, 15, 04014088. [Google Scholar] [CrossRef]
- Gálvez, D. Cálculo Estructural de Tuberías Enterradas por el Método de Elementos Finitos, con Base en el Informe Técnico Cen/Tr 1295-3 (Universidad Politécnica de Madrid). 2011. Available online: http://oa.upm.es/7753/1/DANIEL_GALVEZ_CRUZ.pdf (accessed on 24 October 2022).
- Liu, P.F.; Zheng, J.Y.; Zhang, B.J.; Shi, P. Failure analysis of natural gas buried X65 steel pipeline under deflection load using finite element method. Mater. Des. 2010, 31, 1384–1391. [Google Scholar] [CrossRef]
- Sharma, J.R.; Najafi, M.; Marshall, D.; Jain, A.; Rahjoo, S. Testing and Evaluation of Statically-Loaded Large Diameter Steel Pipe with Native Backfill Soils; ASCE Library: Lawrence, Kansas, 2011. [Google Scholar]
- Webb, M.C.; Trebicki DD, P.; Smulders, P.A. Field testing and buckling strength of buried large-diameter thin-walled steel pipes. Pipelines 2002-Beneath Our Feet: Challengers and Solutions. In Proceedings of the Pipeline Division Specialty Conference, Cleveland, OH, USA, 4–7 August 2002; p. 69. [Google Scholar] [CrossRef]
- Watkins, R.K.; Anderson, L.R. Structural Mechanics of Buried Pipes; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Sharma, J.R. Development of a Model for Estimation of Buried Large Diameter Thin-Walled Steel Pipe Deflection due to External Loads; University of Texas at Arlington: Arlington, TX, USA, 2013. [Google Scholar]
- Li, Z.; Xu, L.; Wang, W. A method for vehicle–track–soil interaction analysis considering soil deformation. Arch. Civ. Mech. Eng. 2022, 22, 1–21. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, H.; Jiang, X.; Yu, R. Analysis of stress and deformation of a positive buried pipe using the improved Spangler model. Soils Found. 2015, 55, 485–492. [Google Scholar] [CrossRef]
- Ai, Z.Y.; Cai, J.B. Static interaction analysis between a Timoshenko beam and layered soils by analytical layer element/boundary element method coupling. Appl. Math. Model. 2016, 40, 9485–9499. [Google Scholar] [CrossRef]
- Pilvin, P. Continuum Mechanics. In Mechanics-Microstructure-Corrosion Coupling; Elsevier: Amsterdam, The Netherlands, 2019; pp. 49–63. [Google Scholar] [CrossRef]
- Saberi, M.; Annan, C.D.; Konrad, J. On the mechanics and modeling of interfaces between granular soils and structural materials. Arch. Civ. Mech. Eng. 2018, 18, 1562–1579. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Quart. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Thurairajah, A. Yielding of clays in states wetter than critical. Géotechnique 1963, 13, 211–240. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Burland, J.B. On the generalized stress–Strain behavior of ‘wet clay. In Engineering Plasticity; Heyman, J., Leckie, F.A., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Duncan, J.M.; Byrne, P.; Wong, K.S.; Marby, P. Strength, Stress-Strain and Bulk Modulus Parameters for Finite Element Analysis of Stresses and Movements in Soil Masses; Rep. No. UCB/GT/801; University of California: Berkeley, CA, USA, 1980. [Google Scholar]
- Vermeer, P. A five constant model unifying well established concepts. In Constitutive Behavior of Soils; Balkema: Roterdam, The Netherlands, 1982; pp. 175–197. [Google Scholar]
- Schanz, T.; Vermeer, P.A.; Bonnier, P.G. The hardening soil model: Formulation and Verification. In Beyond 2000 in Computational Geotechnics–10 Years of PLAXIS; Balkema: Rotterdam, The Netherlands, 1999. [Google Scholar]
- Hsieh, P.G.; Ou, C.Y.; Lim, A. Use of the total stress un-drained model to the analysis of deep excavation. In Proceedings of the 17th Southeast Asian Geotechnical Conference, Taipei, Taiwan, 10–13 May 2010; Taipei International Convention Center: Taipei, Taiwan, 2010. [Google Scholar]
- Katona, M.G. Influence of Soil Models on Structural Performance of Buried Culverts. Int. J. Geomech. 2017, 17. [Google Scholar] [CrossRef]
- Clayton, C.R.I.; Symons, I.F. The pressure of compacted fill on retaining walls. Geotechnique 1992, 42, 127–130. [Google Scholar] [CrossRef]
- El Chazli, G. Experimental Investigation of Friction Factors in Horizontal Directional Drilling Installations. Master’s Thesis, University of Western Ontario, London, ON, Canada, 2005. [Google Scholar]
- Alam, S.; Alloinche, E.N.; Bartlett, C.; Sherpa, A.; Keil, B. Experimental Evaluation of Soil-Pipe Friction Coefficients. In Proceedings of the Pipeline Division Specialty Conference, Forth Worth, TX, USA, 23–26 June 2013; pp. 360–371. [Google Scholar]
- Abaqus. Analysis User’s Manual; (Version 6); Dassault Systemes Simulia, Inc.: Johnston, RI, USA, 2013; p. 11. [Google Scholar]
- Tannant, D.D.; Regensburg, B. Guide Lines for Mine Haul Road Design; Faculty of Engineering, School of Okanagan: Kelowna, BC, Canada, 2001. [Google Scholar] [CrossRef]
- Nehdi, M.L.; Mohamed, N.; Soliman, A.M. Investigation of Buried Full-Scale SFRC Pipes under Live Loads. Constr. Build. Mater. 2016, 102, 733–742. [Google Scholar] [CrossRef]
- Behroozinia, P.; Khaleghian, S.; Taheri, S.; Mirzaeifar, R. An investigation towards intelligent tyres using finite element analysis. Int. J. Pavement Eng. 2002, 21, 311–321. [Google Scholar] [CrossRef]
- Park, D.-W. Prediction of pavement fatigue and rutting life using different tire types. KSCE J. Civ. Eng. 2008, 12, 297–303. [Google Scholar] [CrossRef]
- Rao, G.V.; Dutta, R.K. Compressibility and strength behaviour of sand-tyre chip mixtures. Geotech. Geol. Eng. 2006, 24, 711–724. [Google Scholar] [CrossRef]
- Helwany, S. Applied Soil Mechanics: With ABAQUS Applications. In Applied Soil Mechanics: With ABAQUS Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- ASME: American Society of Mechanical Engineers. ASME B36.10M Welded and Seamless Wrought Steel Pipe; ASME: New York, NY, USA, 2018; p. 32. [Google Scholar]
- Diab, Y.G. Mechanical method to evaluate safety factors in buried pipes. J. Transp. Eng. 1995, 121, 94–101. [Google Scholar] [CrossRef]
- Obrzud, R.F.; Truty, A. The Hardening Soil Model—A Practical Guidebook; Zace Services Ltd., Software Engineering: Preverenges, Switzerland, 2018; Volume 5, p. 205. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).