Optimization of Construction Process and Determination of Intermediate Cable Forces for Composite Beam Cable-Stayed Bridge

Featured Application

In this paper, a fast construction method for a composite girder cable-stayed bridge is proposed. The method is used on the Xiangsizhou Bridge, and it complies with all bridge rules while reducing the entire construction time of the bridge by 4 months.

Abstract

This paper presents a comprehensive study of the Xiangsizhou Bridge, a double-tower double-cable steel–concrete composite girder cable-stayed bridge located in Pingnan, Guangxi, China. A finite element model of the full-bridge spatial truss system was established using a dual main beam simulation of the steel–concrete composite girder. To obtain the initial reasonable bridge state, the minimum bending energy method was employed, followed by optimization of the state using the unknown load coefficient method to attain the final reasonable completion state. This paper proposes an innovative construction scheme for the erection of the main girders, which is designed to address the issue of excessive tensile stresses in the bridge deck slabs that can arise in conventional construction schemes. This scheme can save about 4 months of construction time and shorten the construction cycle of main beam erection by 60%. Furthermore, the study derived and verified a formula for the intermediate cable force during the construction process, which demonstrated its effectiveness. This study provides practical value for the design and construction of similar bridges.

1. Introduction

The composite girder cable-stayed bridge is a structure that combines the upper concrete bridge deck panel with the lower steel main beam through shear connectors, fully utilizing the compressive performance of the concrete structure and the tensile performance of the steel beam [1,2]. When compared to an orthotropic plate that is under compression on the upper part of the steel beam, utilizing a concrete bridge deck panel has the potential to not only save costs but to also enhance the overall performance of the bridge deck [3,4]. Composite girder cable-stayed bridges typically use a single-segment cyclic construction sequence, which involves first hoisting the main beam segment and then hanging the stay cable and first tensioning, then pouring the wet joint, and finally, the stay cable second tensioning. However, this construction method has low efficiency and a long construction period. Now, there is a more efficient double-segment cyclic construction method. Different construction sequences will affect the stress distribution of the steel main beam and bridge deck panels of the composite girder cable-stayed bridge. Multiple-segment cyclic construction may cause cracks in the concrete bridge deck panels and affect the cable force during the bridge’s construction and operation, thereby affecting the safety and durability of the structure. Therefore, under the premise of a tight construction schedule, determining the reasonable completion state and reasonable construction state [5] corresponding to the multiple-segment cyclic construction plan while ensuring the safety of the composite girder cable-stayed bridge during the construction and operation period is a key technical issue for this type of bridge [6].

The stress state of a composite girder cable-stayed bridge is influenced by the main girder construction sequence, and optimizing the main girder erection process also requires corresponding adjustments to the construction cable forces of the cable-stayed bridge. Adjusting the cable forces during construction has an important impact on the reasonable completion state of the cable-stayed bridge [7,8,9]. Specifically, the timing of the composite of the bridge deck and steel main girders, as well as the pouring and curing time of the wet joint during construction, will affect the stress distribution and completion state of the composite girder cable-stayed bridge. Therefore, it is necessary to optimize the main girder erection process during construction and determine the intermediate cable force values according to the actual situation to ensure the safety and durability of the cable-stayed bridge during the construction and operation phases.

Scholars have conducted numerous studies on the effects of construction optimization on the structural stress of composite beam cable-stayed bridges. Wang et al. [10] employed four methods to analyze the impact of preloading on the deformation and stress of bridge structures. Chen et al. [11] proposed the force equilibrium method to determine the initial cable tension of the cable-stayed bridge under constant load, resulting in a more reasonable distribution of bridge deck bending moments. Hassan et al. [12] put forth a new method to determine the optimal post-tension cable tension of the bridge structure in the completed state, which effectively reduced the vertical defects of the deck and the horizontal deflection of the tower. Barbaros et al. [13] studied the influence of cable tension and different cable arrangement forms on structural stress performance. Huang et al. [14] studied the long-term performance of bridge decks affected by concrete shrinkage and creep at the back-pouring strip of steel–concrete composite beams. Hu et al. [15] studied the impact of different lagged pouring procedures for concrete bridge decks on structural stress. Ruan et al. [16] conducted a feasibility analysis of the overall structural stress of the bridge using the single-section, double-section, and three-section cyclic construction methods. In summary, previous studies have primarily focused on the effects of cable-staying forces on structural stresses in cable-stayed bridges and the impact of improved wet joint casting processes on bridge deck slabs. This paper addresses the issue of excessive tensile stresses in the concrete deck slab that may occur during the three-segment cyclic construction scheme by improving the construction process scheme. Based on previous research and using the Xiangsizhou Bridge of the Liyu Expressway in Guangxi, China, as the engineering basis, the revised construction process was successfully applied to an actual bridge project for the first time, resulting in improved on-site construction efficiency and a significantly shortened bridge construction period. Furthermore, the paper investigates the mechanical characteristics of the cantilever assembly construction of the combined girder cable-stayed bridge and derives the corresponding intermediate cable force formula based on the three-segment cyclic construction process of the cable-stayed bridge. According to this formula, the exact value of the intermediate cable force tension can be found, avoiding the use of valuation and artificial experience coefficients and reducing the uncertainty caused by human factors during the bridge construction process. This research shortened the construction period of the main girder of the Xiangsizhou Bridge by four months and can be applied to future bridges of the same type. Moreover, it provides a reference for other types of bridges, demonstrating its significant practical and economic importance.

2. The Xiangsizhou Bridge

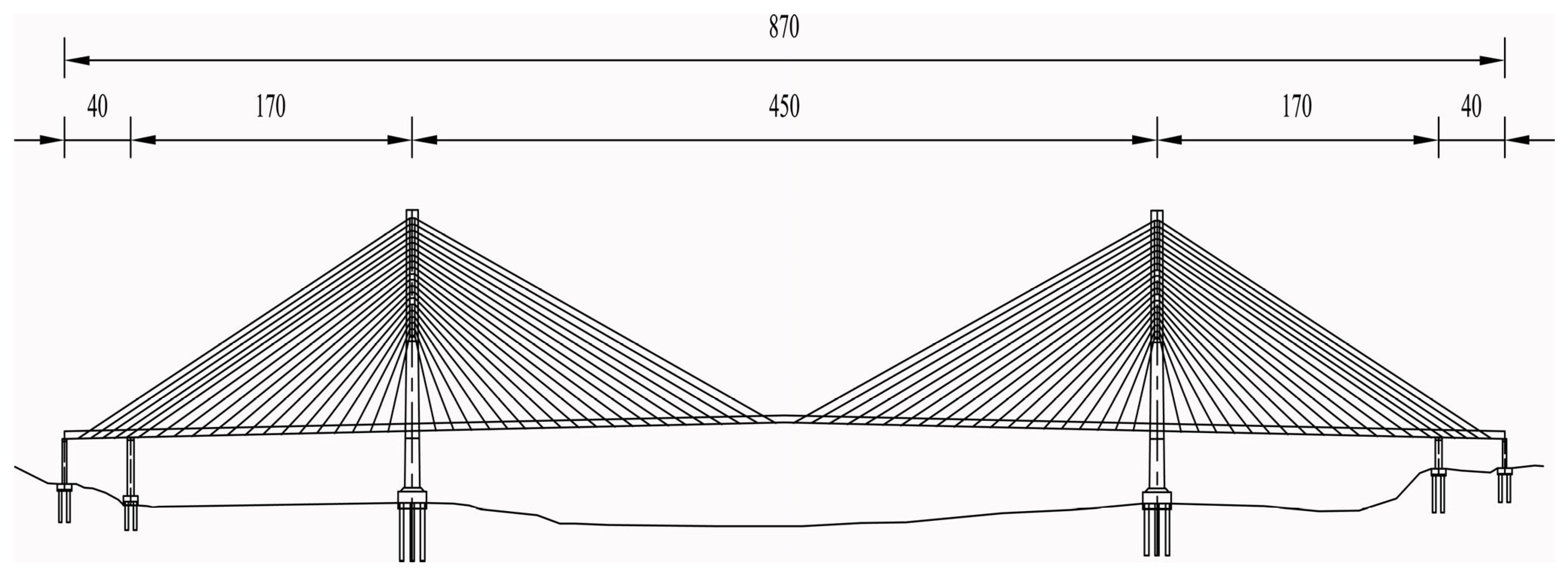
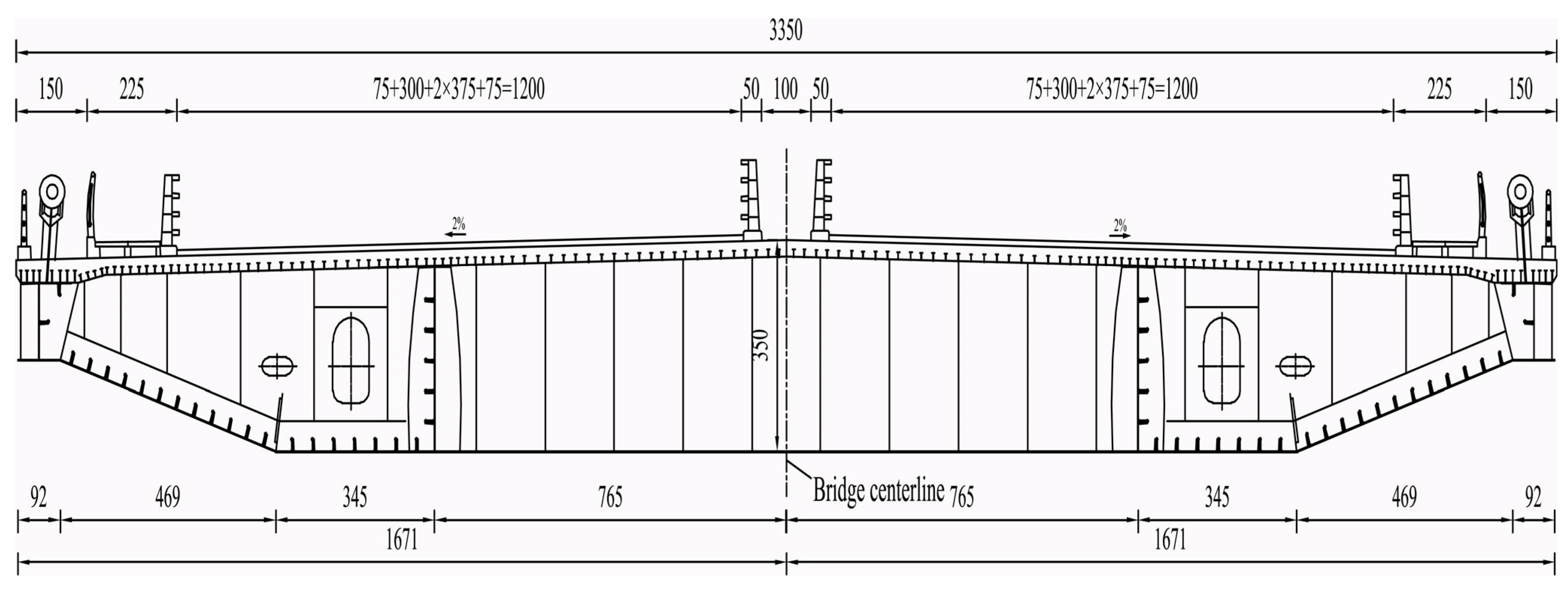
The semi-floating composite beam cable-stayed bridge structure with double towers and double-cable planes was adopted for the main bridge of Xiangsizhou Bridge. The main span is 450 m, and its span arrangement is (40 + 170 + 450 + 170 + 40) meters. The bridge profile layout is shown in Figure 1. The main beam adopts a separated double-box section with a beam height of 3.5 m, and the top slab is set with a bidirectional 2% cross slope. The bridge deck has a full width of 33.5 m, and the main beam cross-section is shown in Figure 2. An overview of the project is shown in

Table 1. Project overview.

Components	Description
Main beam	Beam Segments: 89 segments in total. Beam Lifting: Near cable tower and auxiliary pier: lifted by floating crane. Standard segments: lifted by bridge deck crane. Steel Material: Q345GJ (Similar to ‘ASTM A572 Grade 50’). Concrete Material: C55 high-performance concrete.
Stay cable	Material: 160 low-relaxation high-strength prestressed steel strands. Tensile Strength: 1860 MPa. Fatigue Stress Amplitude: Not less than 200 MPa. Specifications: 15.2–37, 15.2–43, 15.2–55, 15.2–61, 15.2–73, and 15.2–85. Anchorage points: Longitudinal distance of 19 × 10.8 m on the main span and a longitudinal distance of 14 × 10.8 m + 5 × 7.2 m on the side span.
Main tower	Structure: Diamond-shaped cable-stayed tower. Total Height: 147.3 m above the tower base for both cable-stayed towers. Crossbeam: Middle crossbeam set at a distance of about 51.4 m from the lower crossbeam. Top Crossbeam: Set at the tower top. Material: C55 high-performance concrete.
Bridge deck	Construction: Steel beams are prefabricated and directly poured to form composite beams. A 500 mm gap is left at both ends of each section as a post-pouring joint, which is subsequently filled with C55 slightly expanding concrete. Storage Time: At least two months to reduce the impact of concrete shrinkage and creep on the structure.

.

3. Determination of Reasonable Completion State

3.1. Finite Element Model

This paper presents a finite element model of the spatial truss system of the Xiangsizhou Bridge using MIDAS CIVIL commercial software (version 8.9.5) [17]. The element size is based on the design drawings, with an element size of approximately 0.5 m at the wet joints of the main beam element section, and an element size of approximately 3 m for equal section elements in the middle part of the main beam section. The main tower element size is approximately 1 m. The entire bridge consists of 1884 elements, including 1724 beam elements and 160 cable elements, as illustrated in Figure 3 and Figure 4. Figure 5 depicts the Xiangsizhou Bridge after its construction. The steel–concrete composite beam is simulated using a double main beam, where the steel main beam and the bridge deck are modeled separately as beam elements, and the shear connection between them is simulated using a rigid connection in an elastic link. The main tower, auxiliary pier, and transition pier are all modeled using spatial beam elements, while the cable-stayed bridge is simulated using cable elements. The main material parameters of the entire bridge model are shown in

Table 2. Main material parameters.

Structure	Materials	Elastic Modulus (MPa)	Unit Weight (kN/m3)
Steel beam	Q345GJ	2.06 × 105	78.5
Tower	C50	3.45 × 104	26.5
Bridge deck	C55	3.55 × 104	26.5
Cable	Steel strand *	1.95 × 105	91

* Low-relaxation high-strength prestressing steel strand with a tensile strength of 1860 MPa (similar to ASTM A416/A416M).

.

3.2. Reasonable Completion State

There are several methods to determine the reasonable completion state [18], and for the Xiangsizhou Bridge, this paper adopts a comprehensive method, combining the minimum bending energy method [19] with the unknown load coefficient method [20,21]. Specifically, the bending stiffness of the main beam and main tower is reduced by 10,000-times for the first-stage analysis, and the preliminary results of the cable-stayed bridge state are obtained through static analysis. Then, the cable forces are iteratively modified through the unknown load coefficient method to achieve a reasonable completion state. Considering the most unfavorable load combination, the bending moment and stress of the entire bridge and main beam in a reasonable bridge state are shown in Figure 6 and Figure 7.

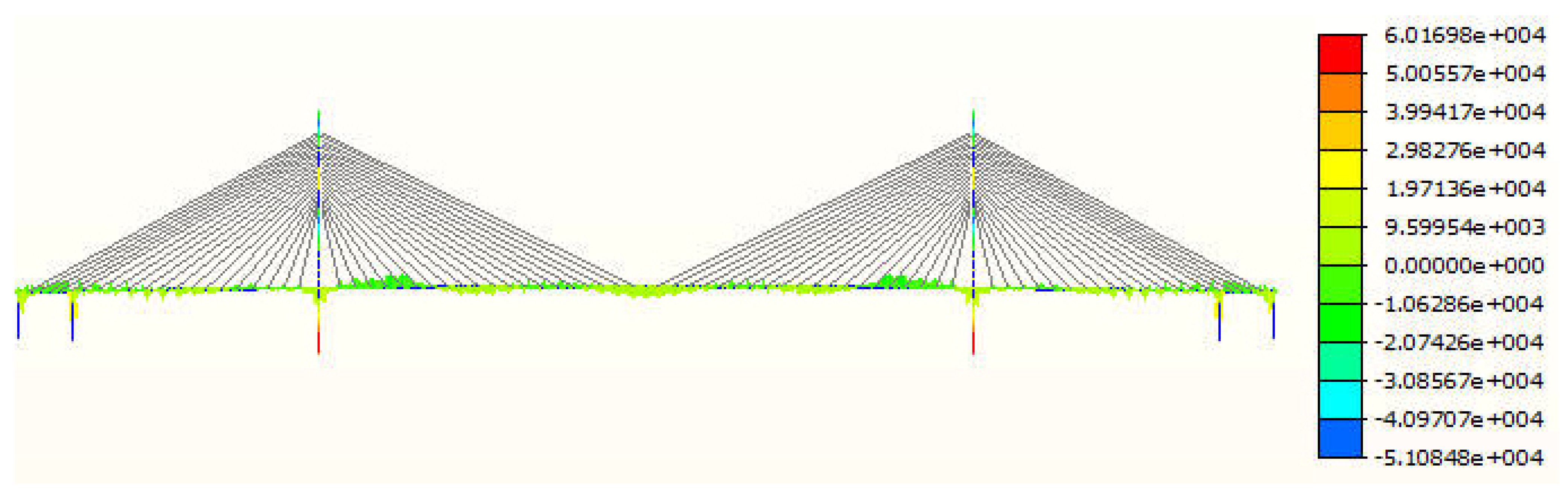
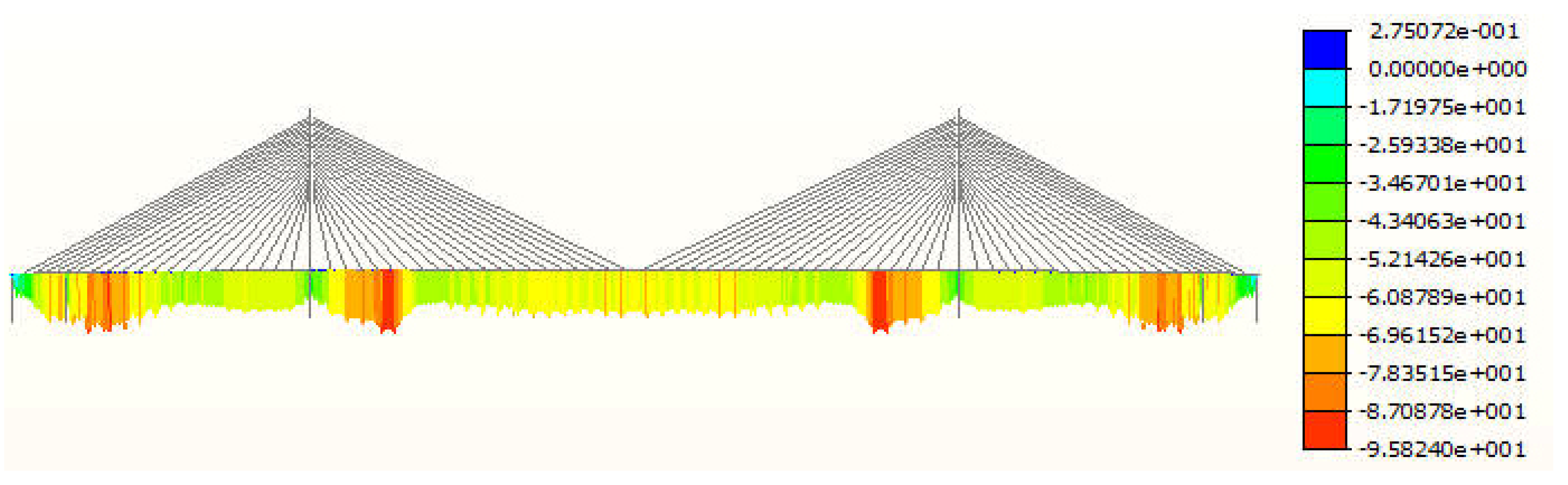
According to Figure 6 and Figure 7, the combined method used in this paper yields a relatively uniform distribution of bending moments in the main tower and main beam. The maximum bending moment in the main tower is located at the base of the tower and is 6.02 × 10⁴ kN·m, while the maximum bending moment in the main beam is located at the transition pier and is 2.69 × 10⁴ kN·m. The transmission of weight load from the main girder to the main tower in a cable-stayed bridge occurs through the anchorage relationship between the cable and the main girder, which ultimately transfers the load to the foundation. The cable stay’s action on the main girder structure distributes the bending moment in a wave-like cycle, ensuring even distribution of the bending moment throughout the bridge and preventing an excessive bending moment on any section of the main girder. Under the reasonable completion state, the bridge deck and steel main beam are subjected to compressive stress. The maximum compressive stress in the bridge deck is −18.30 MPa, which is located in the 13th section of the main beam. The maximum compressive stress in the steel main beam is −95.82 MPa, which is located in the 5th section of the main beam. During the bridge formation phase, both the deck slab and steel main girders experience compressive stresses only, which is advantageous for the structural stresses of the bridge. The compressive capacity of a concrete deck slab is much greater than its tensile capacity. Therefore, ensuring that the bridge is kept under compressive stress can prevent the deck slab from cracking under tensile stress. 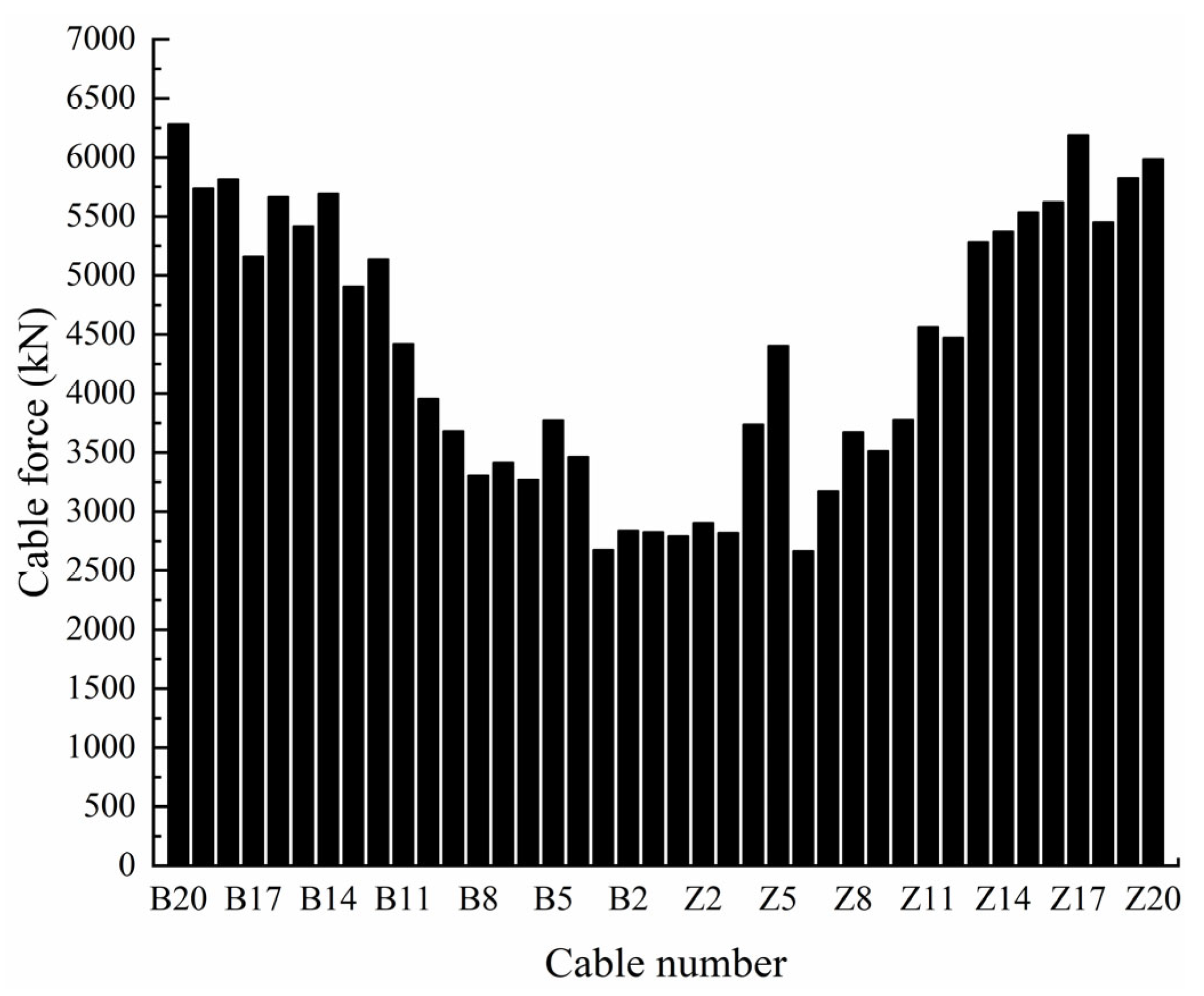The overall distribution of cable forces is shown in Figure 8, which is basically consistent with the pattern of increasing force from the main tower to the far end. In the diagram, B1 to B20 indicate the cable numbers of the side span from the main tower to the bank, while Z1 to Z20 indicate the cable numbers of the main span from the main tower to the main span. The maximum cable force is 6283.3 kN, located at the anchorage point of the B20 tail cable, and the maximum cable force for each cable under load combinations corresponds to a safety factor that is generally close.

4. Three-Segment Cycle Construction Scheme

The construction process of a composite beam cable-stayed bridge has significant impacts on the overall structural forces, construction duration, and material usage. In the engineering practice of the Xiangsizhou Bridge, factors, such as geographical location, hydrogeological conditions, time to open for traffic, and project economics, have imposed limitations on the construction. With a tight construction schedule, the installation period of the main beam determines the overall duration of the bridge project. Therefore, optimizing the construction process to shorten the duration while ensuring construction quality and structural safety is a critical issue that must be addressed for the Xiangsizhou Bridge.

To expedite the construction progress of composite beam cable-stayed bridges, scholars have proposed three approaches. The first method aims to reduce the tensioning frequency of cable-stayed ropes. The second method aims to shorten the maintenance time of the bridge deck wet joint, and the third method is to use a double- or multi-segment cyclic construction mode. However, each method has its drawbacks. The first approach involves tensioning the cable-stayed ropes to the final position in one go, which can cause cracks in the bridge deck due to excessive tensile stress. This can negatively impact the structural stress and durability of the bridge. The second approach aims to shorten the maintenance time of the bridge deck wet joint. However, this may result in concrete cracking, which can affect the overall stress of the bridge deck and steel main beam. The third approach involves the adoption of a double- or multi-segment cyclic construction mode. Although the double-segment cyclic construction has been used in several large-span composite beam cable-stayed bridges in China, further three-segment cyclic construction may lead to excessive tensile and compressive stresses on the bridge deck and high stress on the steel main beam in the joint area. Therefore, necessary measures must be taken to reduce the stress on the bridge deck and steel main beam.

According to the design requirements of the Xiangsizhou Bridge, the wet joint of the bridge deck panel adopts C55 concrete, and the strength of the wet joint concrete should reach 90% or more before proceeding to subsequent construction steps. Based on the analysis of the construction cycle of the main beam segment, the conventional single-segment construction cycle requires a duration of 10 days, of which 5–7 days are needed for curing the wet joint of the bridge deck panel, and during this curing period, no other operations are allowed on the bridge deck. Through comprehensive consideration and a large number of finite element simulation analyses and optimizations, a three-segment cycle construction of the bridge deck panel wet joint is adopted, as shown in Figure 9. For every three consecutive beam segments, the three-segment cycle scheme (simultaneous setting of three wet joints between four segments of the bridge deck panel, reinforcement binding, concrete pouring, and curing) is compared with the single-segment cycle scheme (one wet joint between two segments of the bridge deck panel, reinforcement binding, concrete pouring, and curing, usually requiring 10 days). The three-segment cycle scheme can save two segments of the wet joint construction time compared with the single-segment cycle scheme, which means at least 20 days of the construction period can be saved. Six rounds of three-segment cycle construction of the 20 beam segments can save 120 days of the construction period, which is of great significance for completing the main bridge closure plan on time.

To ensure that the bridge deck and the tensile and compressive stresses of the steel main beam in the completed beam segments during the three-segment cycle construction of the steel–concrete composite girder cable-stayed bridge do not exceed the standard, it is necessary to carry out a third tensioning of the diagonal cable on the n + 2# beam segment after the first tensioning of the n + 3# cable. The purpose of this tensioning is to increase the positive bending moment of the corresponding beam segment, increase the compressive stress reserve of the corresponding beam segment’s bridge deck, and avoid the tensile stress of the n + 2# beam segment’s bridge deck exceeding the limit value when hoisting the n + 4# beam segment. This adjustment is a critical step in determining the completed state of the steel–concrete composite girder cable-stayed bridge during the three-segment cycle construction.

5. Determination of Intermediate Cable Force Formula

In order to ensure that the internal forces of the structure during the construction of a cable-stayed bridge are not too great, and to ensure the safety of construction, a reasonable and efficient cable-tensioning plan must be designed to achieve a reasonable completed bridge state. In the cable-tensioning plan for construction, convenience should not be pursued blindly by attempting to tension the cables in one go, but rather a phased cable-tensioning plan should be designed to increase the safety reserve of the internal forces of the structure during the construction of the cable-stayed bridge, thus ensuring the safety of the construction process. Therefore, determining the appropriate intermediate cable-tensioning force during cable-stayed bridge construction is a key technical issue.

5.1. Basic Assumptions

To derive the formula for the intermediate cable tension in subsequent calculations, it is necessary to make a basic assumption: after the adjacent steel beams of the main beam are connected, but before the wet joint concrete is poured, the rigid connection between the steel beams can be simulated as hinged support. The following is a validation of this basic assumption:

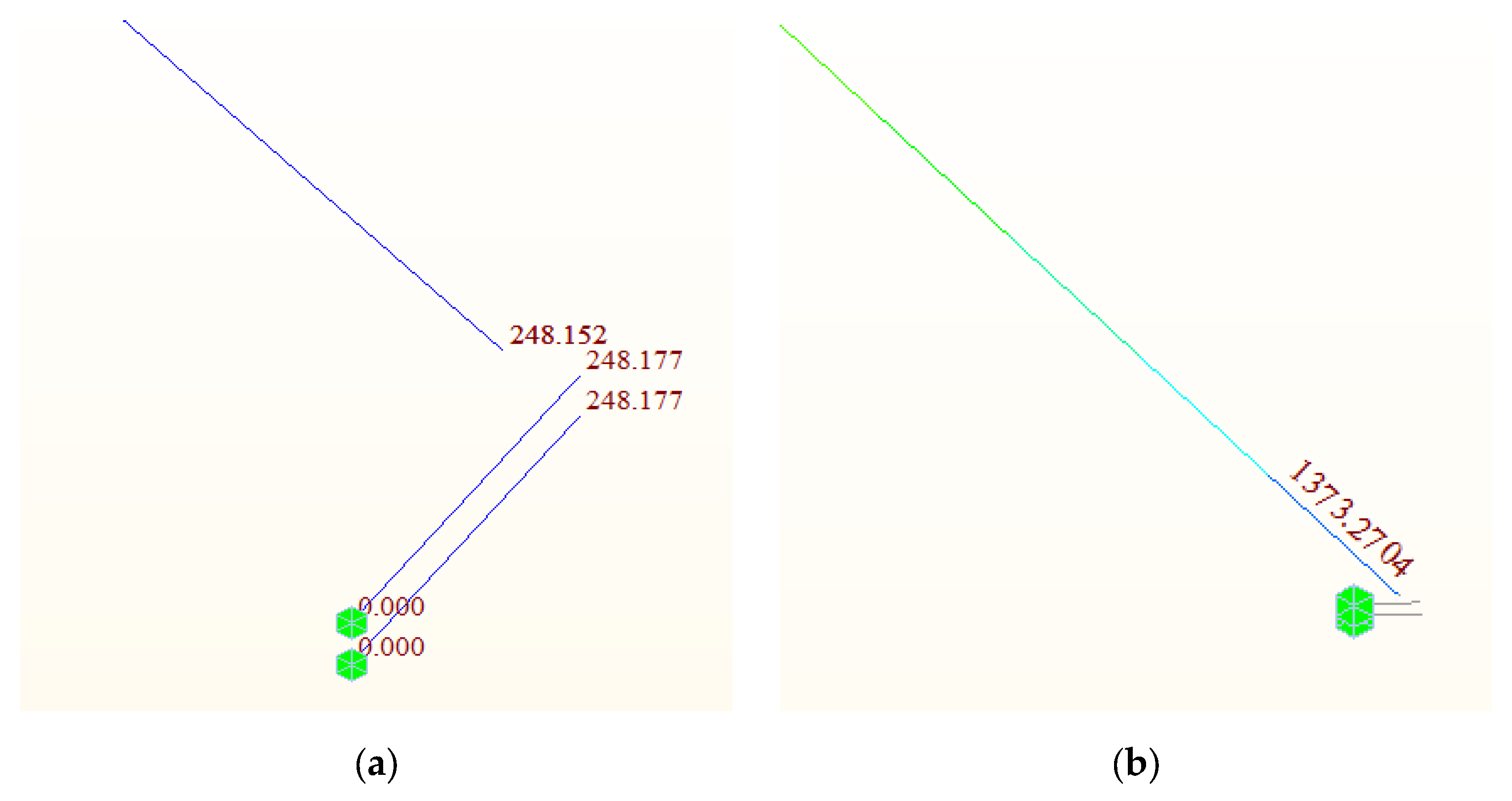
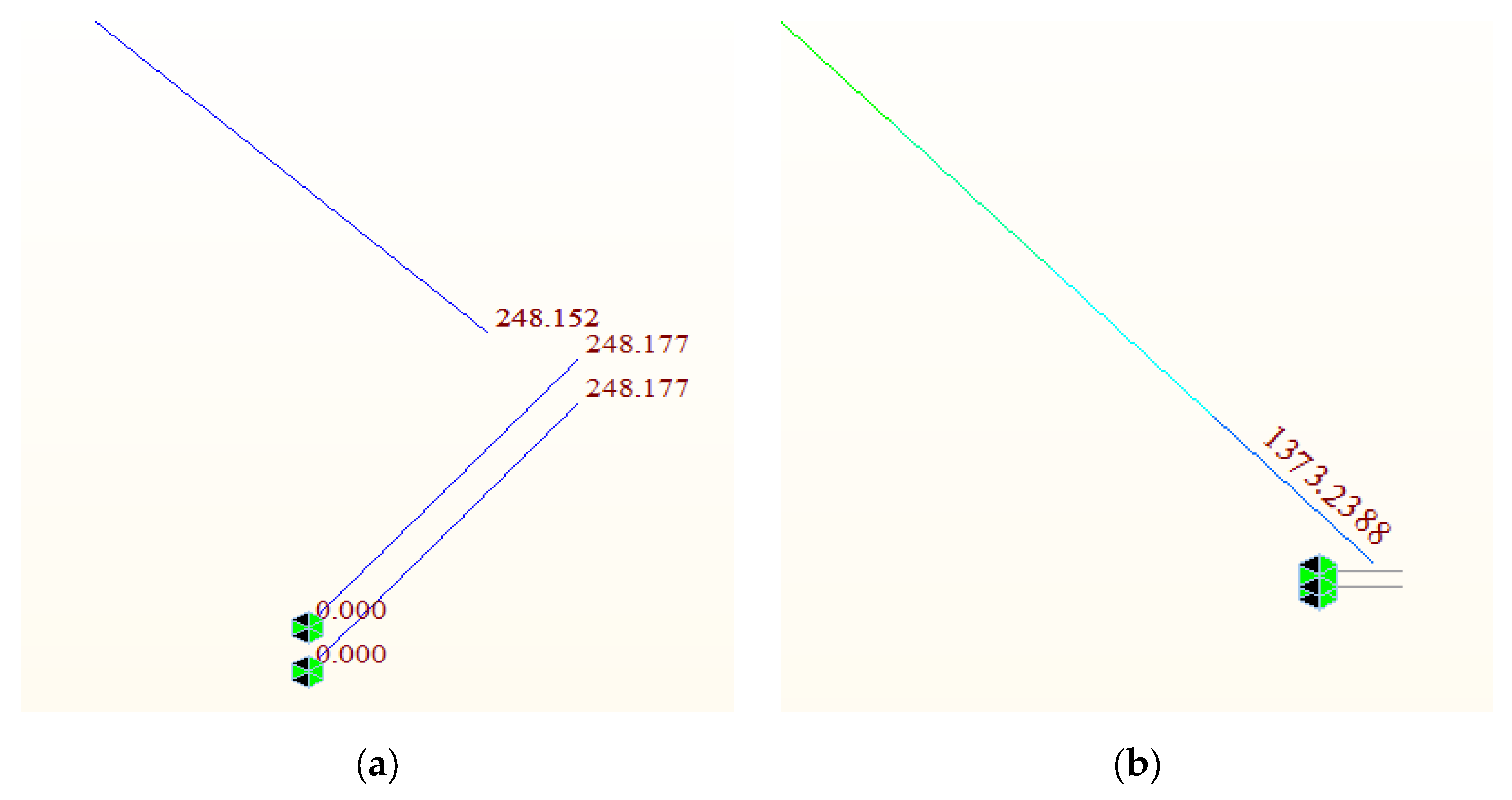
The finite element model of Xiangsizhou Bridge separately extracted the standard beam segment of the main span for simulated analysis of the supports. The influence of vertical displacement and cable tension under both rigid and hinged connections at the steel beam joints was simulated by applying boundary constraints. The results are shown in Figure 10 and Figure 11.

According to Figure 10 and Figure 11, it can be seen that the simulated vertical displacement between the steel beams for both rigid and hinged connections is identical at 248.177 mm. The cable tension only differs by 0.03 kN. Additionally, the vertical bending stiffness of the steel beam section is only 2.5511 m⁴, which makes simulating the steel beam connections as hinged supports before pouring the wet joint concrete between adjacent steel beam segments during lifting completely reasonable and feasible.

5.2. Derivation of Intermediate Cable Force Formula

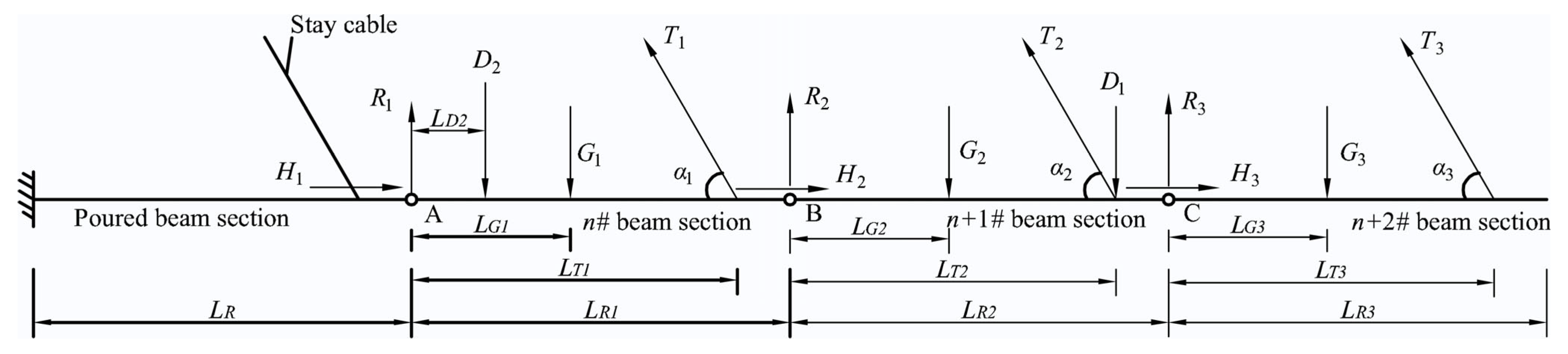
The tension value of the cable-stayed cable is not only related to the initial tension of the cable-stayed cable and the tension of the bridge cables, but also closely related to the construction process and the main beam construction plan. Different main beam erection plans will result in different tension values for the cable-stayed cables. Therefore, the tension values during the cable-stayed cable construction process should be adjusted according to the on-site construction plan to achieve the optimal internal force of the bridge structure. In order to better control the construction of the Xiangsizhou Bridge, it is necessary to simulate and calculate the intermediate cable tension of the cable-stayed bridge during the construction process. A force diagram of the three-segment cyclic structure is shown in Figure 12.

In Figure 12, the three-segment cyclic construction involves lifting three main beam segments on the basis of the already poured beam segment. Point A is the connection between the n# beam segment lifted and the steel beam of the poured beam segment, point B is the connection between the n + 1# beam segment and the n# beam segment steel beam, and point C is the connection between the n + 2# beam segment and the n + 1# beam segment steel beam. The simplified simulation of the steel beam connection after lifting the main beam segment is modeled as a hinged support connection. At this time, the hinged supports at points A, B, and C each receive a horizontal force H_i and a vertical force R_i. G_i is the weight of the lifted main beam segment, T_i is the tension force of the cable-stayed cable, and α_i is the angle between the cable-stayed cable and the horizontal direction. D₁ and D₂ are the forces acting on the front support point and rear anchor point of the bridge deck crane, respectively; L_Gi is the horizontal distance between the weight action point of the beam segment and the hinged support; L_Ti is the horizontal distance between the cable-stayed cable anchor point at the beam end and the hinged support; L_Ri is the length of the lifted beam segment. It should be noted that the above formula symbols i = 1, 2, 3.

To facilitate the structural analysis of the three-span continuous construction, it can be considered as a main structure and a sub-structure. As the sub-structure affects the main structure, while the main structure does not affect the sub-structure, it is necessary to divide them into three parts in the calculation of the structural force diagram. Specifically, in Figure 12, the completed beam section of the cable-stayed bridge can be regarded as the main structure, while the subsequent suspended beam sections can be viewed as sub-structures applied to the main structure. Therefore, the forces of the n + 2# sub-structure can be calculated first, followed by the forces of the n + 1# sub-structure, and finally the forces of the n# sub-structure. The balance equation for the first part can be written as:

$$H_3=T_{3}cos{\alpha }_3$$

(1)

$$R_3+T_{3}sin{\alpha }_3=G_3$$

(2)

The moment of the hinge support at point C is obtained as

$$G_3·L_{G3}=T_{3}sin{\alpha }_3·L_{T3}$$

(3)

The above equation can be solved to obtain

$$\left\{\begin{array}{c}{H}_3=\frac{G_3·L_{G3}}{tan{\alpha }_3·L_{T3}}\\ R_3=\frac{G_3·\left(L_{T3}-L_{G3}\right)}{L_{T3}}\\ T_3=\frac{G_3·L_{G3}}{sin{\alpha }_3·L_{T3}}\end{array}\right.$$

(4)

Once the horizontal force H₃ and vertical force R₃ in the first part of the n + 2# auxiliary structure are determined, the mechanical balance equations can be set up for the second part of the n + 1# auxiliary structure.

$$H_2+H_3=T_{2}cos{\alpha }_2$$

(5)

$$R_2+R_3+T_{2}sin{\alpha }_2=G_2+D_1$$

(6)

The moment of the hinge support at point B is obtained as

$$G_2·L_{G2}+D_1·L_{T2}=T_{2}sin{\alpha }_2·L_{T2}+R_3·L_{R2}$$

(7)

The above equation can be solved to obtain

$$\left\{\begin{array}{c}{H}_2=\frac{G_2·L_{G2}+D_1·L_{T2}-R_3·L_{R2}}{tan{\alpha }_2·L_{T2}}-H_3\\ R_2=\frac{G_2·\left(L_{T2}-L_{G2}\right)+R_3·\left(L_{R2}-L_{T2}\right)}{L_{T2}}\\ T_2=\frac{G_2·L_{G2}+D_1·L_{T2}-R_3·L_{R2}}{sin{\alpha }_2·L_{T2}}\end{array}\right.$$

(8)

After obtaining the horizontal force H₂ and vertical force R₂ in the second part of the n + 1# auxiliary structure, the mechanical equilibrium equation can be established for the first part of the n# basic structure.

$$H_1+H_2=T_{1}cos{\alpha }_1$$

(9)

$$R_1+R_2+T_{1}sin{\alpha }_1=D_2+G_1$$

(10)

The moment of the hinge support at point A is obtained as

$$D_2·L_{D2}+G_1·L_{G1}=T_{1}sin{\alpha }_1·L_{T1}+R_2·L_{R1}$$

(11)

$$T_1=\frac{D_2·L_{D2}+G_1·L_{G1}-R_2·L_{R1}}{sin{\alpha }_1·L_{T1}}$$

(12)

Substituting Equation (12) into Equations (9) and (10) yields

$$H_1=\frac{D_2·L_{D2}+G_1·L_{G1}-R_2·L_{R1}}{tan{\alpha }_1·L_{T1}}-H_2$$

(13)

$$R_1=\frac{D_2·\left(L_{T1}-L_{D2}\right)+G_1·\left(L_{T1}-L_{G1}\right)+R_2·\left(L_{R1}-L_{T1}\right)}{L_{T1}}$$

(14)

According to the above formulas, the intermediate cable forces of the three beam segments can be obtained, as shown in Equations (4), (8), and (12). Using these formulas, the specific tension values of the cables during construction can be determined, avoiding the use of artificial assumptions and empirical coefficients to determine the intermediate cable forces, ensuring the stability and safety of the structure from construction to completion.

6. Structural Force Analysis of Composite Girder Cable-Stayed Bridge

6.1. Structural Forces during the Construction Phase

A large-span cable-stayed bridge is usually constructed using the method of double-cantilever symmetrical construction. In the construction process of the main beam section, in order to ensure that the cable force reaches a reasonable state for the completion of the bridge, it is necessary to perform multiple tensioning and system conversion of the cables. This paper derives a formula for the intermediate cable force of the cable-stayed bridge and calculates the tensioning force of the cables during construction based on the weight of the main beam section. Then, this set of cable forces is used as the initial tensioning force and input into the model for positive mounting calculations [22,23]. The difference between the obtained result and the target value is corrected by the least squares method [24]. Then, the obtained cable forces are input into the model for positive mounting calculation, and the iteration is continued until the model converges. 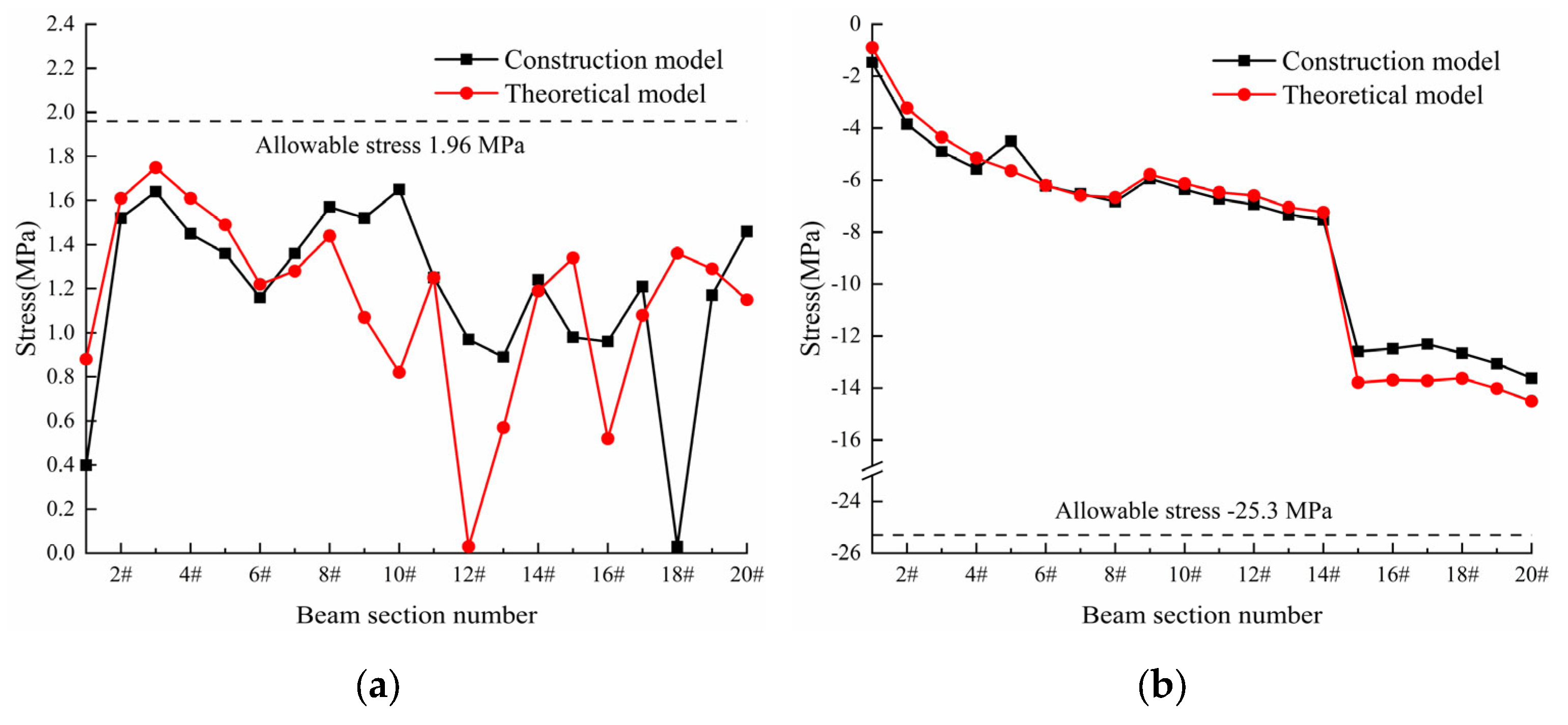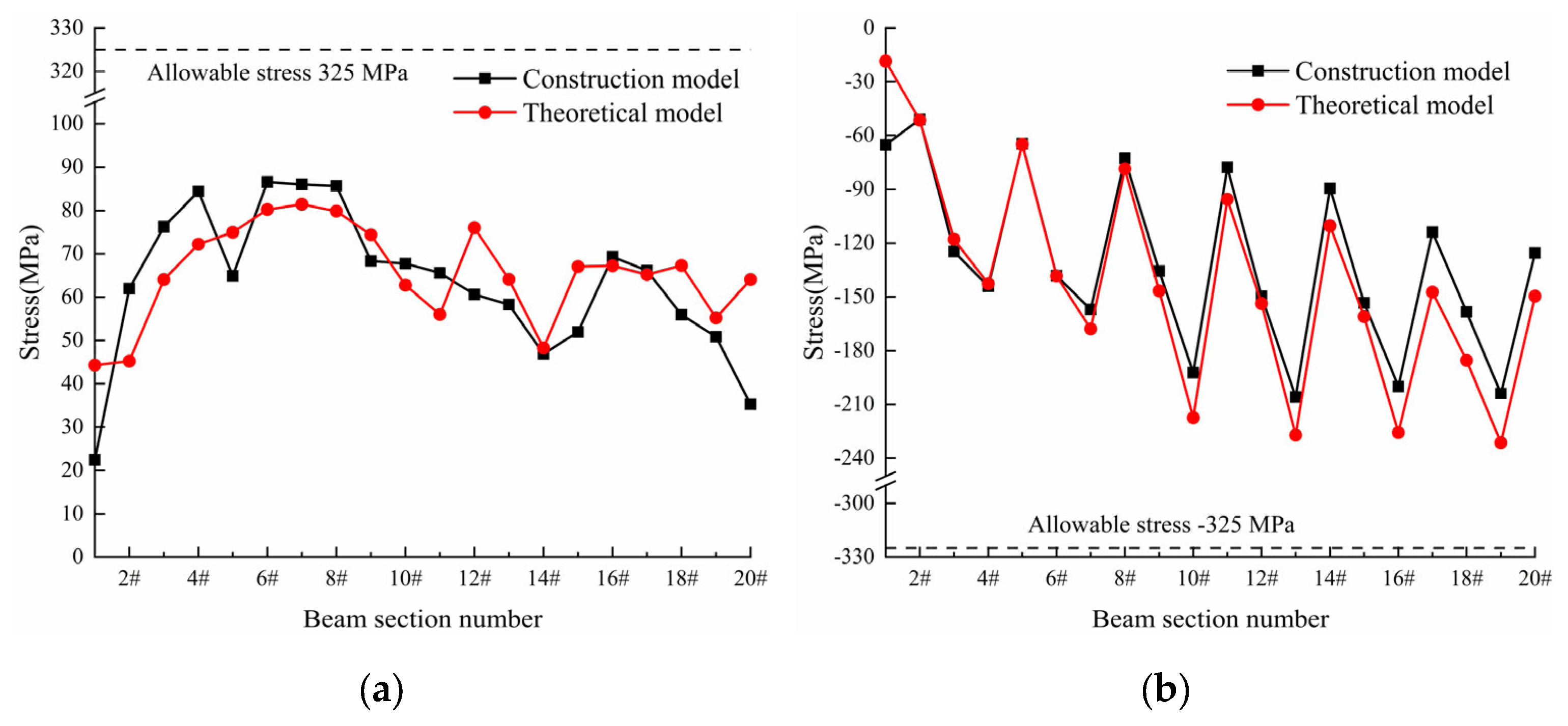It is worth noting that the last tensioning of each cable is not controlled by tensioning force but by the control of non-stress cable length [25]. Finally, the numerical values obtained using the formula for the intermediate cable force are input into the finite element model for the positive mounting simulation and compared and analyzed with the actual construction monitoring model data of the bridge. During the bridge construction phase, ensuring the safety of the main girder construction process is of the utmost importance. Therefore, particular attention should be paid to ensuring that the tensile stress on the deck slab does not exceed the limit value during the construction process. This is necessary to prevent excessive tensile stress on the deck structure, which may result in cracking. The maximum tensile and compressive stresses of the steel main beam and bridge deck panel in each beam section during the construction phase can be obtained, as shown in Figure 13 and Figure 14.

According to Figure 13 and Figure 14, the tensile and compressive stresses of the steel main girders and the bridge deck panels in each beam segment during the construction phase do not exceed the allowable values specified in the standards. The structural stresses obtained using the intermediate tension formula are generally consistent with the distribution and trend of the stresses obtained from the bridge construction monitoring model. The maximum tensile stress of the steel main girders obtained using the intermediate tension value method is 81.46 MPa, the maximum compressive stress is 231.35 MPa; the maximum tensile stress of the bridge deck panel is 1.75 MPa, and the maximum compressive stress is 14.51 MPa. The compressive stress of the bridge deck panel increases with the increase in the cantilever length of the main girder segment during construction and eventually reaches the maximum compressive stress before the main span closure. The compressive stress of the steel main girders during the construction phase exhibits periodic changes as the diagonal cables are tensioned.

6.2. Structural Forces during the Bridge Completion Stage

To optimize the structural stress in the bridge completion state, the main beam structure should only be subjected to compressive stress, not tensile stress. This is particularly important for the concrete bridge panels in composite beams, as their inferior tensile properties compared to compressive properties make them susceptible to cracking under excessive tensile stress. Thus, it is crucial to ensure that the compression performance of the bridge panel is fully utilized to increase its compressive stress reserve and prevent any adverse effects of tensile stress. The maximum stress values of the steel girder and the bridge deck at various stages of the main beam erection process were obtained. The specific results are shown in

Table 3. Maximum compressive stresses in each section of the steel girders and bridge deck at bridge completion stage.

Beam Section Number	Bridge Deck Compressive Stress (MPa)	Steel Beam Compressive Stress (MPa)
1	−5.27	−136.14
2	−5.16	−149.21
3	−4.92	−153.06
4	−4.64	−152.28
5	−4.26	−177.53
6	−3.99	−166.60
7	−3.80	−137.57
8	−3.50	−162.81
9	−5.29	−163.59
10	−7.65	−122.19
11	−8.41	−181.91
12	−8.27	−182.68
13	−9.63	−132.87
14	−5.56	−161.84
15	−4.21	−163.40
16	−2.71	−121.93
17	−3.26	−156.47
18	−3.79	−158.47
19	−5.93	−126.50
20	−4.49	−189.73

.

According to Table 3, it can be seen that in the completed bridge state, both the bridge deck and steel main girder only bear compressive stress. The maximum compressive stress of the bridge deck is 9.63 MPa, located at the 13th girder section, and the maximum compressive stress of the steel main girder is 189.73 MPa, located at the 20th girder section, which both meet the specification requirements. Considering the load combinations during the completion stage and the most unfavorable load combinations during operation, the maximum tensile and compressive stresses of the bridge deck and steel main girder also meet the specification requirements. A comparison of the difference between the tension values during the construction and the reasonable tension values during the completion stage is shown in

Table 4. Difference between reasonable completion state and construction stage cable force comparison.

Cable Number at Side Span	Reasonable Completion State Cable Force (kN)	Construction Stage Cable Force (kN)	Differences (%)	Cable Number at Main Span	Reasonable Completion State Cable Force (kN)	Construction Stage Cable Force (kN)	Differences (%)
B1 *	2826.71	2818.18	0.30	Z1	2793.49	2820.95	−0.98
B2	2838.46	2832.90	0.20	Z2	2903.02	2938.89	−1.24
B3	2676.58	2675.34	0.05	Z3	2820.68	2860.79	−1.42
B4	3463.52	3466.69	−0.09	Z4	3738.49	3781.52	−1.15
B5	3773.72	3780.18	−0.17	Z5	4404.27	4438.03	−0.77
B6	3265.97	3274.62	−0.26	Z6	2666.30	2687.98	−0.81
B7	3414.27	3424.41	−0.30	Z7	3173.88	3183.60	−0.31
B8	3304.18	3318.70	−0.44	Z8	3672.86	3672.53	0.01
B9	3680.29	3696.24	−0.43	Z9	3513.87	3504.05	0.28
B10	3954.56	3971.91	−0.44	Z10	3777.32	3761.75	0.41
B11	4421.20	4441.88	−0.47	Z11	4563.95	4543.96	0.44
B12	5136.19	5162.38	−0.51	Z12	4472.48	4452.65	0.44
B13	4905.55	4932.81	−0.56	Z13	5282.34	5264.66	0.33
B14	5694.06	5726.54	−0.57	Z14	5373.30	5356.12	0.32
B15	5416.82	5444.92	−0.52	Z15	5535.90	5523.17	0.23
B16	5665.77	5693.99	−0.50	Z16	5619.22	5610.69	0.15
B17	5161.80	5190.05	−0.55	Z17	6187.87	6182.76	0.08
B18	5814.35	5847.14	−0.56	Z18	5452.20	5449.41	0.05
B19	5737.61	5770.19	−0.57	Z19	5825.14	5823.43	0.03
B20	6283.33	6315.66	−0.51	Z20	5987.37	5985.52	0.03

* B1 to B20 indicate the cable numbers of the side span from the main tower to the bank, while Z1 to Z20 indicate the cable numbers of the main span from the main tower to the main span.

.

According to Table 4, the difference between the reasonable cable force values and the cable force values calculated using the forward iteration method for the completed bridge state is compared. The cable forces are distributed evenly between the two, and the pattern of cable force change is consistent. The cables located near the tower–beam intersection have a shorter length and, consequently, a smaller cable force, while those situated farther away from the intersection have a longer length and experience a gradual increase in cable force. This pattern of cable force distribution follows the standard rule. The maximum difference in cable force is 40.11 kN, located in the Z3 inclined cable, and the difference in the cable force is only −1.42%, which meets the standard requirements.

7. Conclusions

The construction process for a combined girder cable-stayed bridge is complex and technically challenging. The stress state of the bridge during the construction process is closely related to the construction procedure. This study employs finite element simulation using the commercial finite element software MIDAS CIVIL (version 8.9.5) to analyze the entire bridge structure, using the Xiangsizhou Bridge, a twin-tower, double-rope deck combination girder cable-stayed bridge in Pingnan, Guangxi, China, as a case study. The study proposes a rapid solution for the erection of the main girders, called the three-segment cyclic construction scheme, which saves construction and maintenance time and accelerates the construction schedule by casting three wet joints simultaneously. The main difference between the three-segment cyclic construction scheme and the single-segment cyclic construction scheme and the two-segment cyclic construction scheme lies in the tensioning steps of the diagonal cables. The three-segment cyclic solution requires three tensions on some sections of the beam, and the timing of the third tensioning of the cable and specific force values are crucial to ensuring the program runs smoothly. Improvements to the construction process during the construction of cable-stayed bridges will not only resolve construction issues but also significantly enhance construction efficiency, thereby generating enormous social and economic benefits.

During the construction process of cable-stayed bridges, multiple tensioning is often required. However, there is no clear formula available for determining the specific tensioning of an intermediate cable force in cable-stayed bridges. Therefore, the determination of the intermediate cable force is often based on a valuation or artificial empirical coefficients, which increases the uncertainty and risks in the bridge structure construction process. In this paper, a formula for calculating the intermediate cable force of the cable-stayed bridge is derived based on the mechanical characteristics of the cantilever assembly construction of a combined girder cable-stayed bridge. The intermediate cable force values calculated using this formula are input into a finite element model for analysis. The simulation results obtained from the model show that the stress distribution and change trends are basically the same as those obtained from the construction monitoring model of the Xiangsizhou Bridge, which proves the validity of the formula. This provides a significant reference value for building similar bridges in the future and reduces the uncertainty of human influence in the bridge construction process.

The cable forces play a crucial role in determining the internal forces of a bridge structure. To ensure an optimal structural stress state of the bridge, the cable force needs to be maintained at a reasonable level. In this study, the structural forces of a cable-stayed bridge are analyzed in both the construction and finished states. The bending moments are found to be distributed evenly throughout the bridge. During the construction stage, the stresses in the deck slab and steel girders are within the code limits. In the completed state, the main girders are subjected only to compressive stresses, which are more favorable to the structural forces. The cable force increases gradually with the cable length, consistent with the cable force distribution rule.

The research findings presented in this paper were successfully implemented for the first time in an actual bridge project, namely the Xiangsizhou Bridge in Pingnan, Guangxi. The construction of the Xiangsizhou Bridge was carried out on site, following the three-segment cyclic construction scheme proposed in this paper, which resulted in a four-month reduction in the construction period for the main girder erection. The bridge was completed and opened to traffic, and all of its performance indicators met the required specifications. The measured shape and internal force state of the bridge were found to be in high agreement with the theoretical values. The results of this study can be applied to similar bridge projects, as well as providing a valuable reference for other types of bridges.