Optimization of a Twistable Hovering Flapping Wing Inspired by Giant Hummingbirds Using the Unsteady Blade Element Theory
Abstract
1. Introduction
2. Materials and Methods
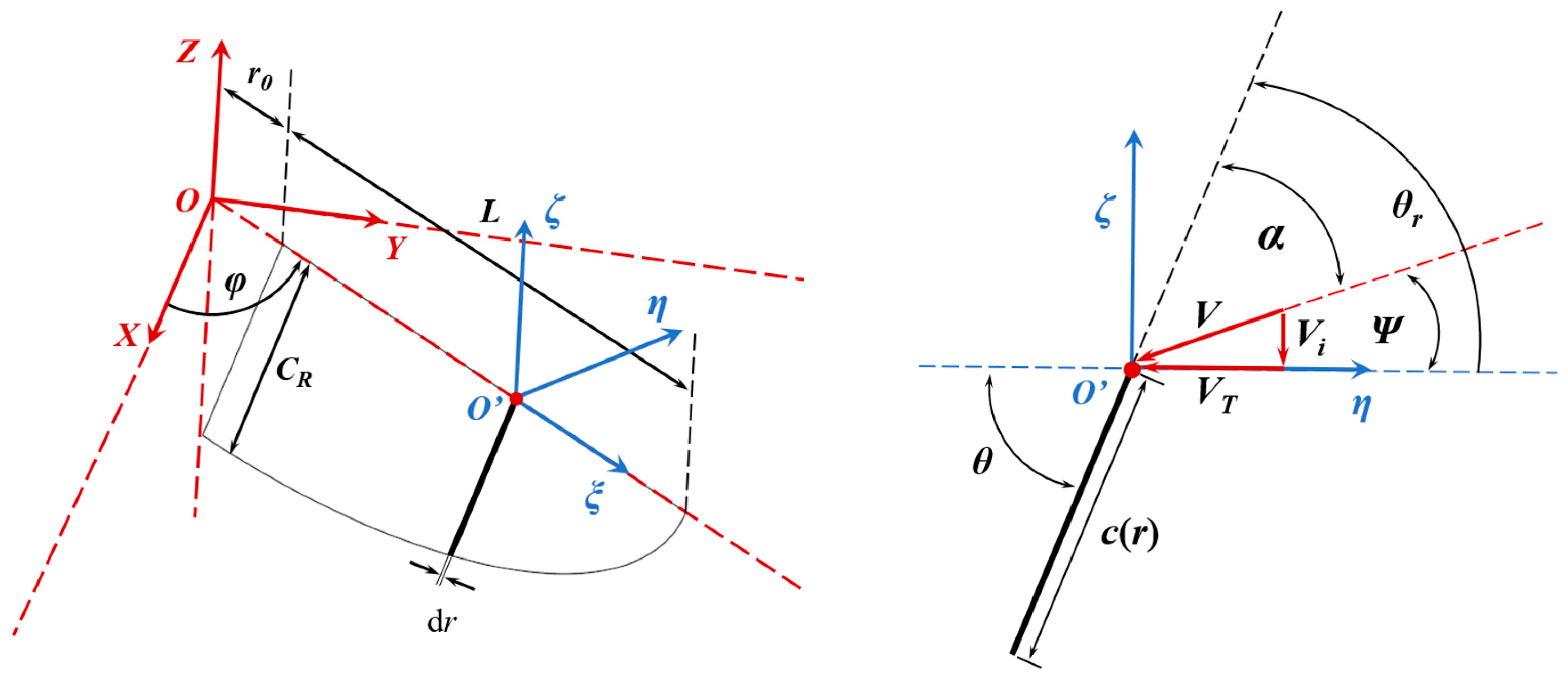
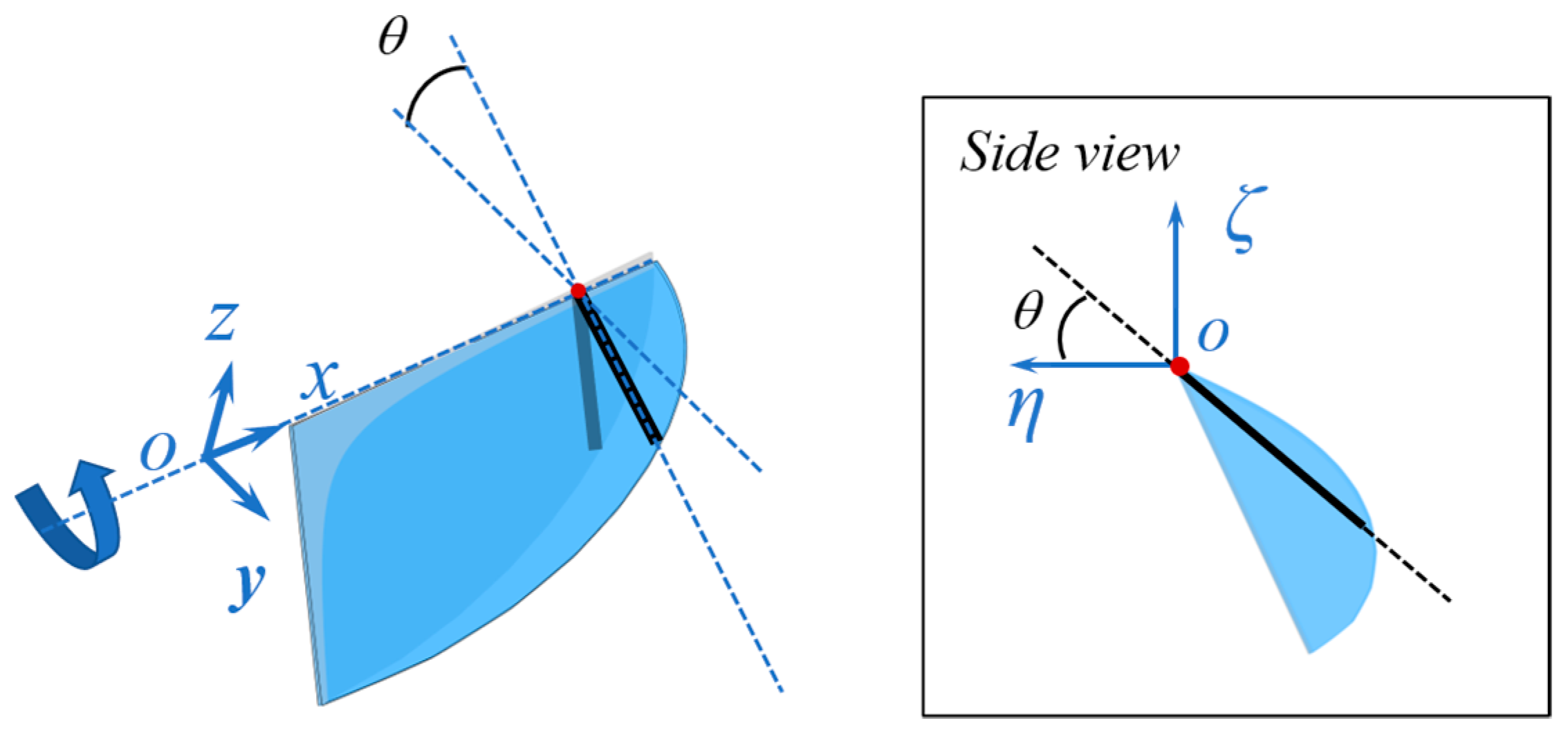
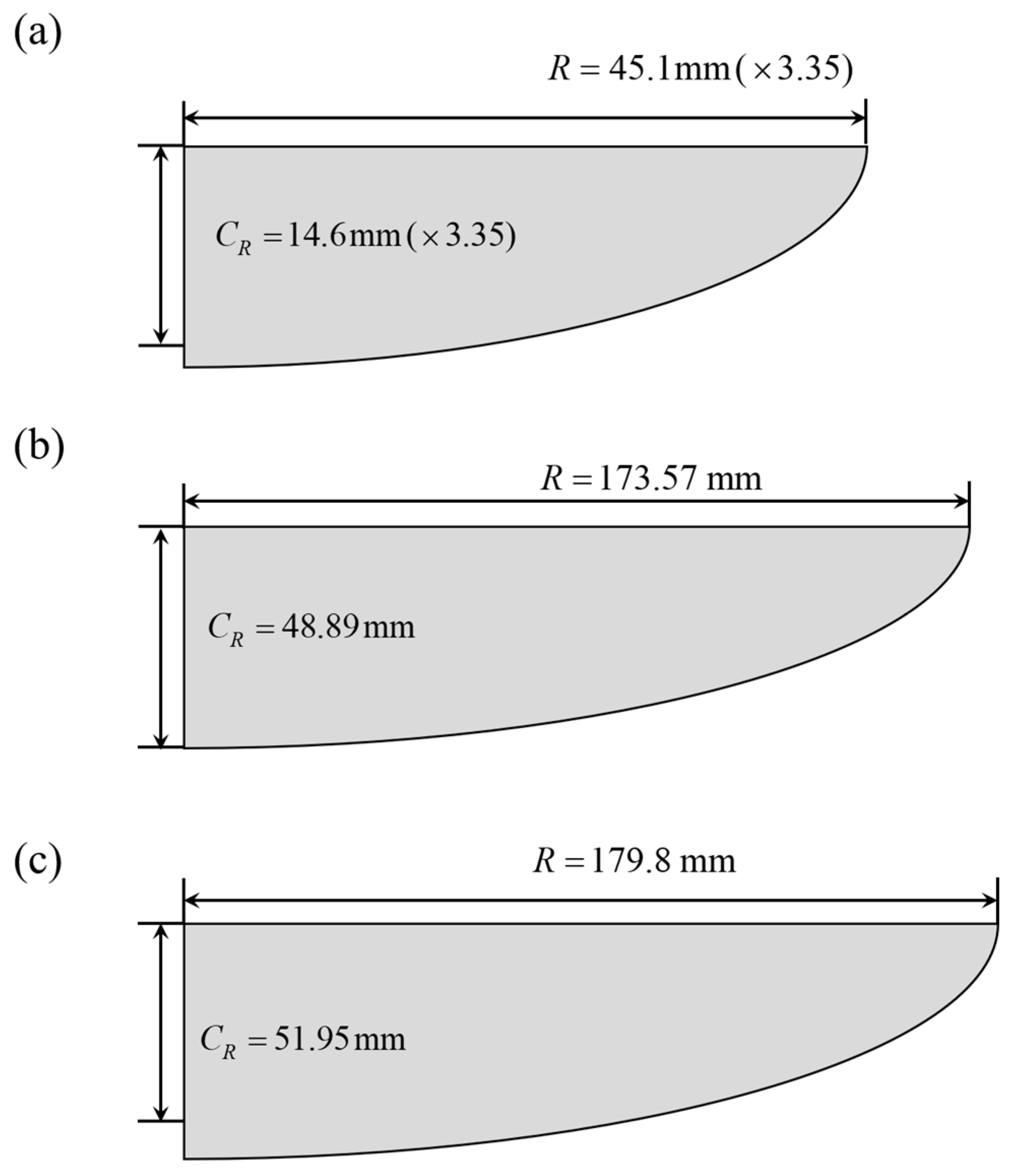
2.1. Morphological and Kinematic Parameterization of a Wing
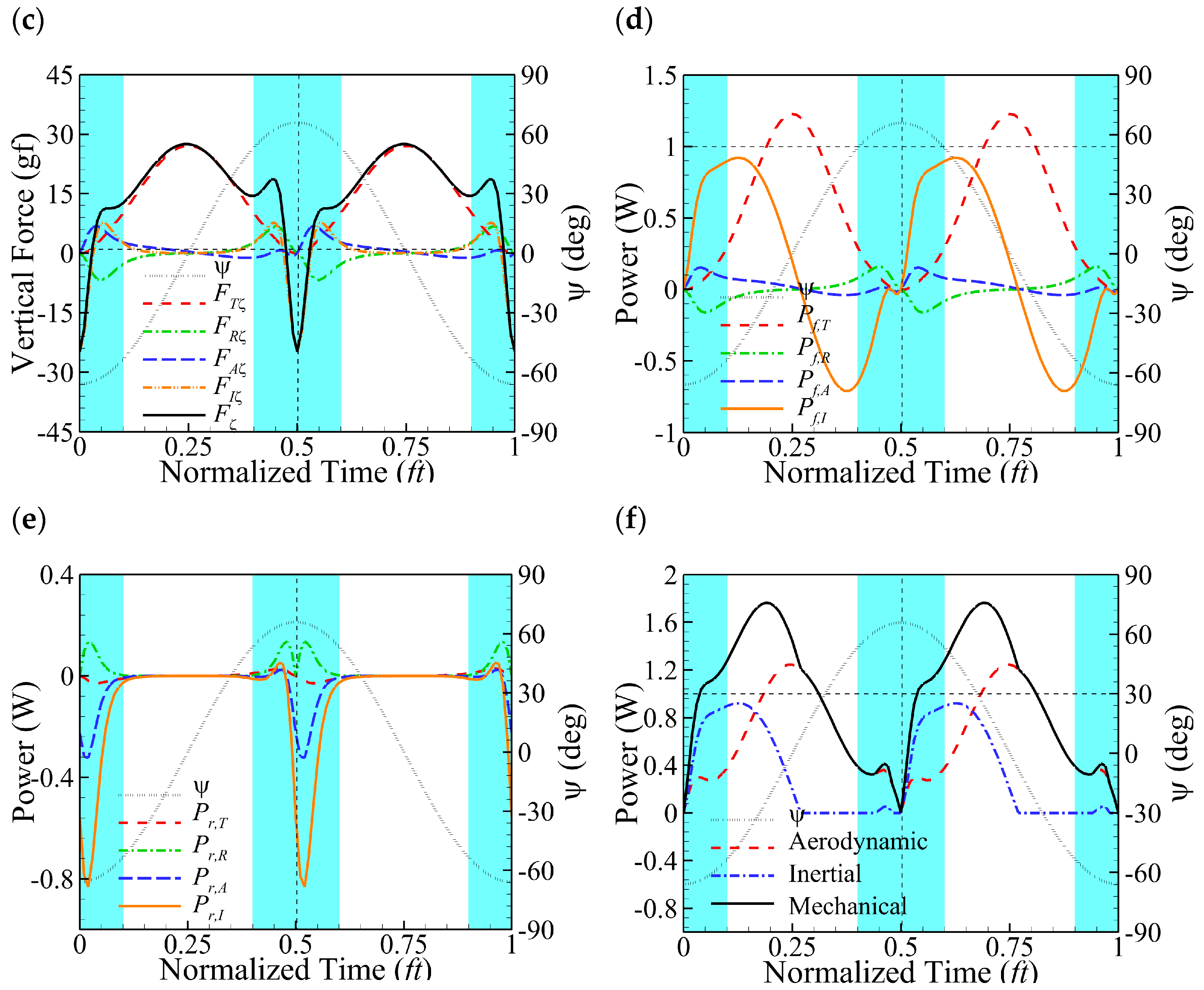
2.2. Estimation of Force and Power Consumption
2.3. Establishment of the Optimization Problem
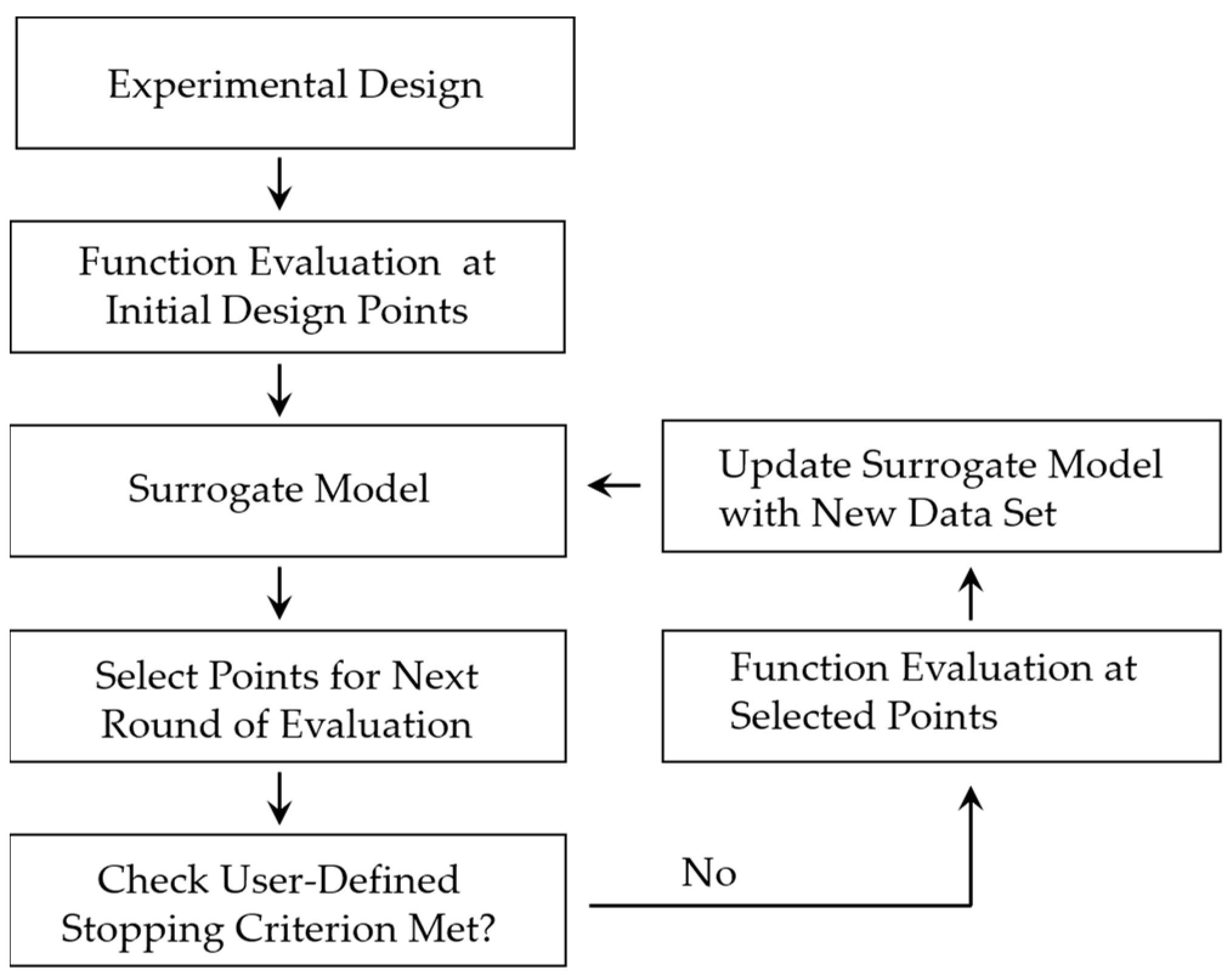
2.4. Optimization Techniques
3. Results and Discussion
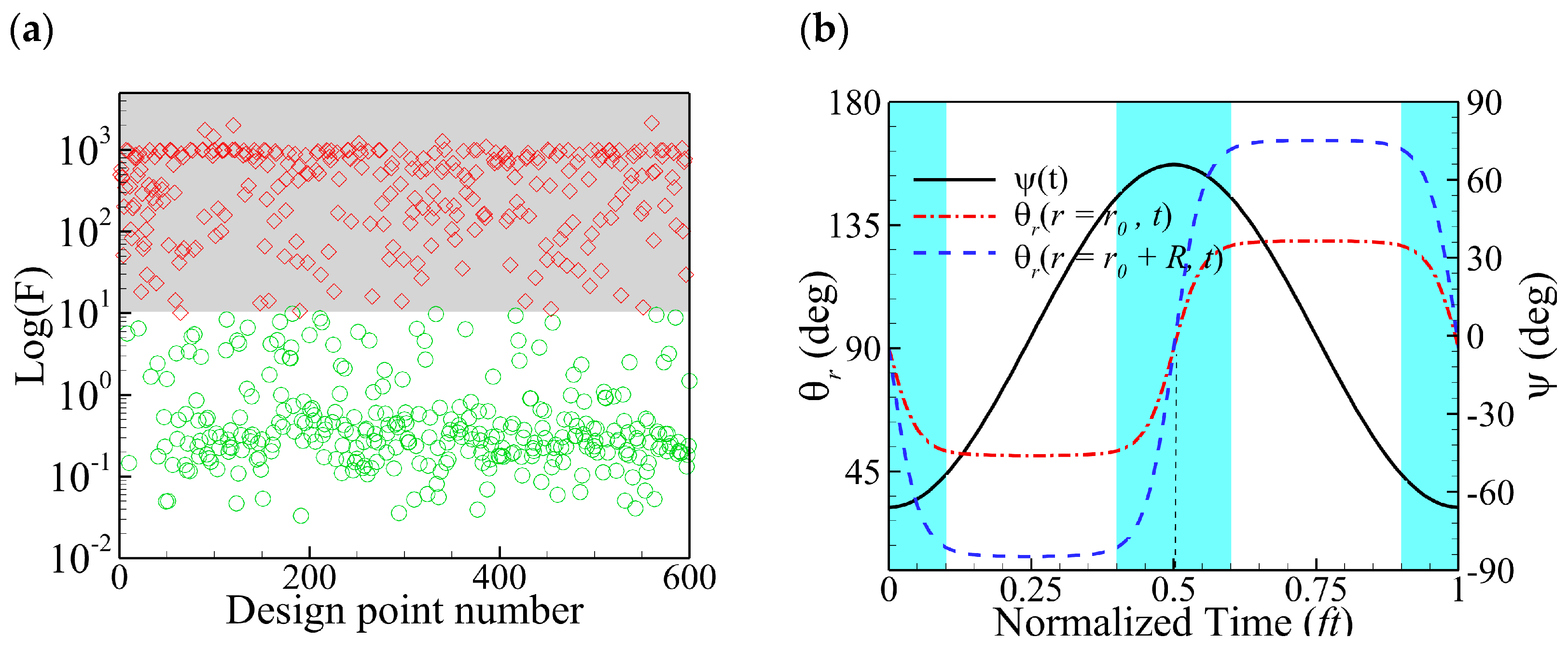
3.1. Optimization Results and Optimal Wing Performance
3.2. Sensitivity Analysis of Design Parameters
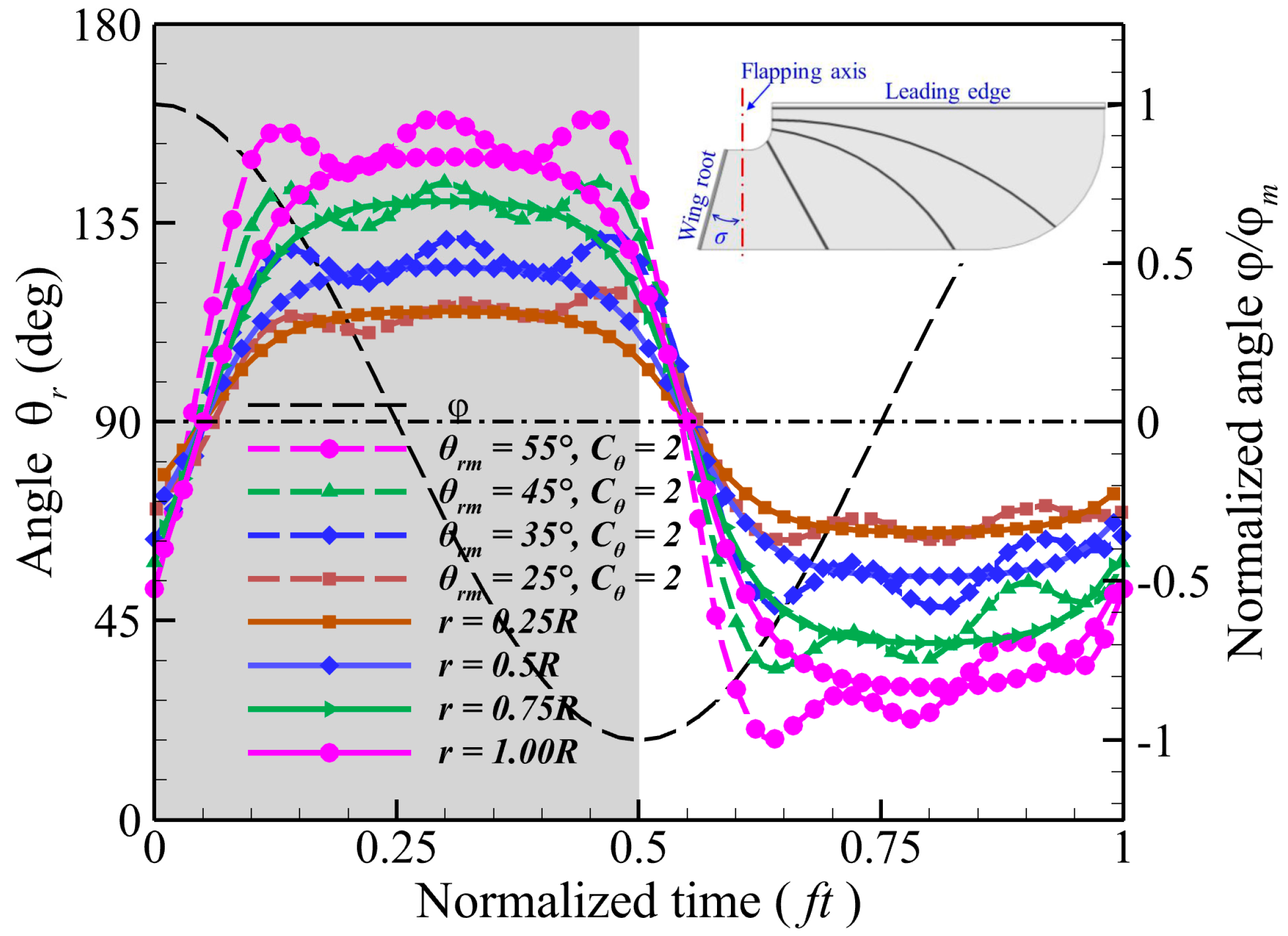
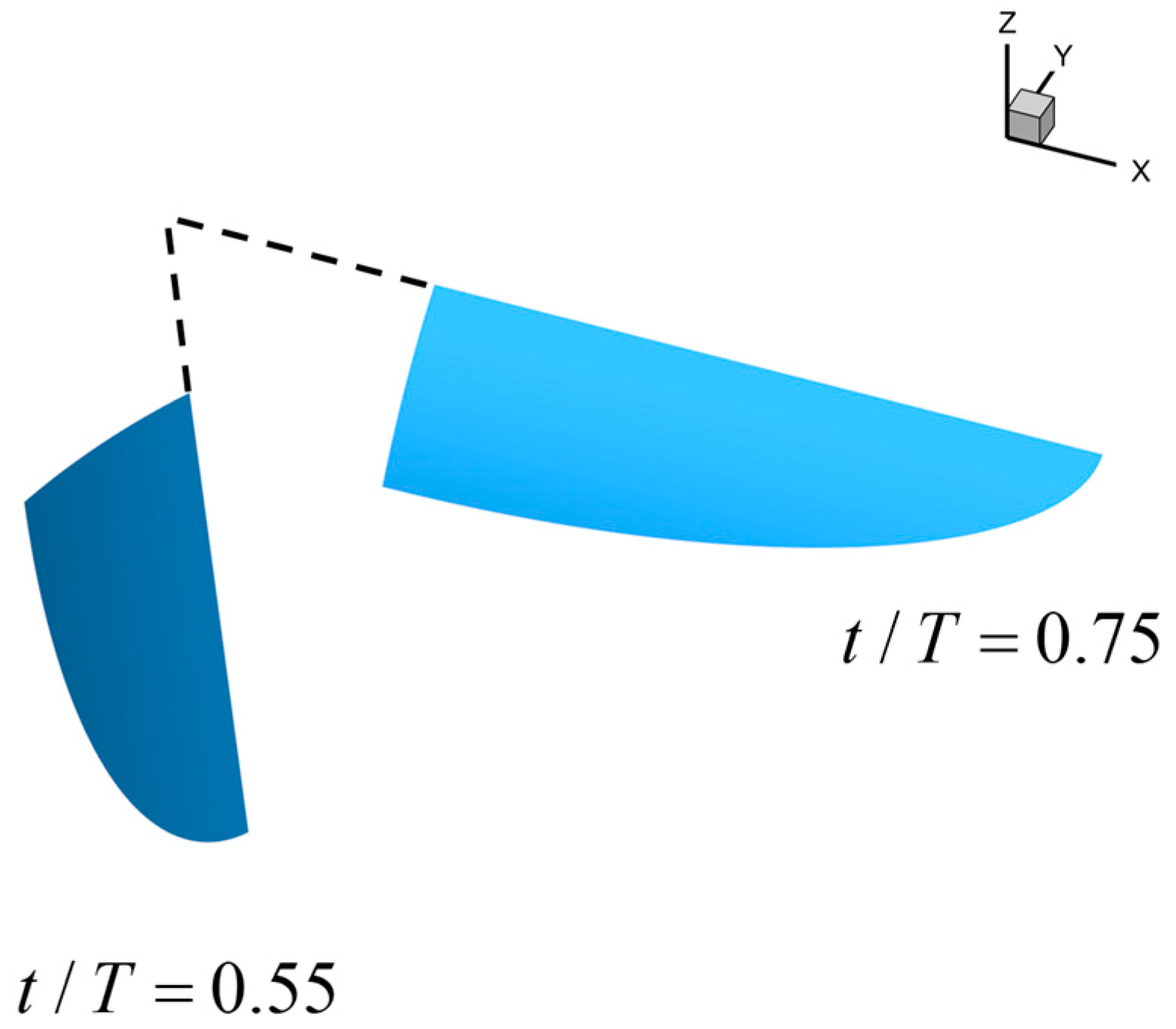
3.3. Effect of Wing Rotation Angle Distribution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chin, D.D.; Lentink, D. Flapping wing aerodynamics: From insects to vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Phan, H.V.; Park, H.C. Insect-inspired, tailless, hover-capable flapping-wing robots: Recent progress, challenges, and future directions. Prog. Aerosp. Sci. 2019, 111, 21. [Google Scholar] [CrossRef]
- Reid, H.E.; Schwab, R.K.; Maxcer, M.; Peterson, R.K.D.; Johnson, E.L.; Jankauski, M. Wing flexibility reduces the energetic requirements of insect flight. Bioinspir. Biomim. 2019, 14, 056007. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.; Fei, F.; Zhang, J.; Deng, X.Y. An At-Scale Tailless Flapping-Wing Hummingbird Robot. I. Design, Optimization, and Experimental Validation. IEEE Trans. Robot. 2020, 36, 1511–1525. [Google Scholar] [CrossRef]
- Coleman, D.; Benedict, M.; Hrishikeshavan, V.; Chopra, I. Design, Development and Flight-Testing of a Robotic Hummingbird. In Proceedings of the American Helicopter Society 71st Annual Forum, Virginia Beach, VA, USA, 5–7 May 2015. [Google Scholar]
- Roshanbin, A.; Abad, F.; Preumont, A. Kinematic and Aerodynamic Enhancement of a Robotic Hummingbird. Aiaa J. 2019, 57, 4599–4607. [Google Scholar] [CrossRef]
- Roshanbin, A.; Altartouri, H.; Karasek, M.; Preumont, A. COLIBRI: A hovering flapping twin-wing robot. Int. J. Micro Air Veh. 2017, 9, 270–282. [Google Scholar] [CrossRef]
- Nan, Y.H.; Karasek, M.; Lalami, M.E.; Preumont, A. Experimental optimization of wing shape for a hummingbird-like flapping wing micro air vehicle. Bioinspir. Biomim. 2017, 12, 026010. [Google Scholar] [CrossRef]
- Preumont, A.; Wang, H.; Kang, S.Z.; Wang, K.N.; Roshanbin, A. A Note on the Electromechanical Design of a Robotic Hummingbird. Actuators 2021, 10, 52. [Google Scholar] [CrossRef]
- Ingersoll, R.; Lentink, D. How the hummingbird wingbeat is tuned for efficient hovering. J. Exp. Biol. 2018, 221, jeb178228. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. Aero-optimum hovering kinematics. Bioinspir. Biomim. 2015, 10, 044002. [Google Scholar] [CrossRef]
- Shahzad, A.; Tian, F.B.; Young, J.; Lai, J.C.S. Effects of wing shape, aspect ratio and deviation angle on aerodynamic performance of flapping wings in hover. Phys. Fluids 2016, 28, 111901. [Google Scholar] [CrossRef]
- Gehrke, A.; Mulleners, K. Phenomenology and scaling of optimal flapping wing kinematics. Bioinspir. Biomim. 2020, 16, 026016. [Google Scholar] [CrossRef] [PubMed]
- Kurdi, M.; Stanford, B.; Beran, P. Optimal Kinematics of Hovering Insect Flight for Minimum Mechanical Power. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Coleman, D.; Gakhar, K.; Benedict, M.; Tran, J.; Siroh, J. Aeromechanics Analysis of a Hummingbird-Like Flapping Wing in Hover. J. Aircr. 2018, 55, 2282–2297. [Google Scholar] [CrossRef]
- Shahzad, A.; Tian, F.B.; Young, J.; Lai, J.C.S. Effects of flexibility on the hovering performance of flapping wings with different shapes and aspect ratios. J. Fluids Struct. 2018, 81, 69–96. [Google Scholar] [CrossRef]
- Addo-Akoto, R.; Han, J.-S.; Han, J.-H. Roles of wing flexibility and kinematics in flapping wing aerodynamics. J. Fluids Struct. 2021, 104, 103317. [Google Scholar] [CrossRef]
- Nan, Y.H.; Peng, B.; Chen, Y.; Feng, Z.Y.; McGlinchey, D. Can Scalable Design of Wings for Flapping Wing Micro Air Vehicle Be Inspired by Natural Flyers? Int. J. Aerosp. Eng. 2018, 2018, 9538328. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Chichester, UK, 2008. [Google Scholar]
- Lee, Y.J.; Lua, K.B.; Lim, T.T.; Yeo, K.S. A quasi-steady aerodynamic model for flapping flight with improved adaptability. Bioinspir. Biomim. 2016, 11, 036005, Corrected by Bioinspir. Biomim. 2016, 11, 049501. [Google Scholar] [CrossRef]
- Nakata, T.; Liu, H.; Bomphrey, R.J. A CFD-informed quasi-steady model of flapping-wing aerodynamics. J. Fluid Mech. 2015, 783, 323–343. [Google Scholar] [CrossRef]
- Truong, Q.T.; Nguyen, Q.V.; Truong, V.T.; Park, H.C.; Byun, D.Y.; Goo, N.S. A modified blade element theory for estimation of forces generated by a beetle-mimicking flapping wing system. Bioinspir. Biomim. 2011, 6, 036008. [Google Scholar] [CrossRef]
- Xuan, H.; Hu, J.; Yu, Y.; Zhang, J. Recent progress in aerodynamic modeling methods for flapping flight. AIP Adv. 2020, 10, 020701. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Tay, W.B.; van Oudheusden, B.W.; Bijl, H. Numerical simulation of a flapping four-wing micro-aerial vehicle. J. Fluids Struct. 2015, 55, 237–261. [Google Scholar] [CrossRef]
- Tay, W.B.; de Baar, J.H.S.; Percin, M.; Deng, S.; van Oudheusden, B.W. Numerical Simulation of a Flapping Micro Aerial Vehicle Through Wing Deformation Capture. Aiaa J. 2018, 56, 3257–3270. [Google Scholar] [CrossRef]
- Berman, G.J.; Wang, Z.J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Pesavento, U.; Wang, Z.J. Flapping Wing Flight Can Save Aerodynamic Power Compared to Steady Flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef]
- Wang, Z.J. Aerodynamic efficiency of flapping flight: Analysis of a two-stroke model. J. Exp. Biol. 2008, 211, 234–238. [Google Scholar] [CrossRef]
- Ke, X.J.; Zhang, W.P. Wing Geometry and Kinematic Parameters Optimization of Flapping Wing Hovering Flight. Appl. Sci. 2016, 6, 390. [Google Scholar] [CrossRef]
- Phan, H.V.; Truong, Q.T.; Au, T.K.L.; Park, H.C. Optimal flapping wing for maximum vertical aerodynamic force in hover: Twisted or flat? Bioinspir. Biomim. 2016, 11, 046007. [Google Scholar] [CrossRef]
- Phan, H.V.; Truong, Q.T.; Park, H.C. An experimental comparative study of the efficiency of twisted and flat flapping wings during hovering flight. Bioinspir. Biomim. 2017, 12, 036009. [Google Scholar] [CrossRef]
- Wang, Q.; Goosen, J.F.L.; van Keulen, F. A predictive quasi-steady model of aerodynamic loads on flapping wings. J. Fluid Mech. 2016, 800, 688–719. [Google Scholar] [CrossRef]
- Whitney, J.P.; Wood, R.J. Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 2010, 660, 197–220. [Google Scholar] [CrossRef]
- Wang, Q.; Goosen, J.F.L.; van Keulen, F. An efficient fluid–structure interaction model for optimizing twistable flapping wings. J. Fluids Struct. 2017, 73, 82–99. [Google Scholar] [CrossRef]
- Blasques, J.P.; Bitsche, R.D.; Fedorov, V.; Lazarov, B.S. Accuracy of an efficient framework for structural analysis of wind turbine blades. Wind. Energy 2016, 19, 1603–1621. [Google Scholar] [CrossRef]
- Tüfekci, M.; Genel, E.; Tatar, A.; Tüfekci, E. Dynamic Analysis of Composite Wind Turbine Blades as Beams: An Analytical and Numerical Study. Vibration 2020, 4, 1–15. [Google Scholar] [CrossRef]
- Meng, H.; Jin, D.Y.; Li, L.; Liu, Y.Q. Analytical and numerical study on centrifugal stiffening effect for large rotating wind turbine blade based on NREL 5 MW and WindPACT 1.5 MW models. Renew. Engergy 2022, 183, 321–329. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, X.; Wu, Y. Energy-efficient wing design for flapping wing micro aerial vehicles. J. Mech. Sci. Technol. 2019, 33, 4093–4104. [Google Scholar] [CrossRef]
- Chen, L.; Yang, F.L.; Wang, Y.Q. Analysis of nonlinear aerodynamic performance and passive deformation of a flexible flapping wing in hover flight. J. Fluids Struct. 2022, 108, 103458. [Google Scholar] [CrossRef]
- Phan, H.V.; Park, H.C. Design and evaluation of a deformable wing configuration for economical hovering flight of an insect-like tailless flying robot. Bioinspir. Biomim. 2018, 13, 036009. [Google Scholar] [CrossRef]
- Phan, H.V.; Aurecianus, S.; Au, T.K.L.; Kang, T.; Park, H.C. Towards the Long-Endurance Flight of an Insect-Inspired, Tailless, Two-Winged, Flapping-Wing Flying Robot. IEEE Robot. Autom. Lett. 2020, 5, 5059–5066. [Google Scholar] [CrossRef]
- Phan, H.V.; Truong, Q.T.; Park, H.C. Extremely large sweep amplitude enables high wing loading in giant hovering insects. Bioinspir. Biomim. 2019, 14, 066006. [Google Scholar] [CrossRef]
- Au, L.T.K.; Phan, H.V.; Park, H.C. Optimal Wing Rotation Angle by the Unsteady Blade Element Theory for Maximum Translational Force Generation in Insect-mimicking Flapping-wing Micro Air Vehicle. J. Bionic Eng. 2016, 13, 261–270. [Google Scholar] [CrossRef]
- Nan, Y.H.; Peng, B.; Chen, Y.; McGlinchey, D. From Studying Real Hummingbirds to Designing Hummingbird-Like Robots-A Literature Review. IEEE Access 2019, 7, 131785–131804. [Google Scholar] [CrossRef]
- Yan, Z.M.; Taha, H.E.; Hajj, M.R. Effects of aerodynamic modeling on the optimal wing kinematics for hovering MAVs. Aerosp. Sci. Technol. 2015, 45, 39–49. [Google Scholar] [CrossRef]
- Ke, X.J.; Zhang, W.P.; Cai, X.F.; Chen, W.Y. Wing geometry and kinematic parameters optimization of flapping wing hovering flight for minimum energy. Aerosp. Sci. Technol. 2017, 64, 192–203. [Google Scholar] [CrossRef]
- Lionetti, S.; Hedrick, T.L.; Li, C.Y. Aerodynamic explanation of flight speed limits in hawkmoth-like flapping-wing insects. Phys. Rev. Fluids 2022, 7, 093104. [Google Scholar] [CrossRef]
- Ye, K.Q.; Li, W.; Sudjianto, A. Algorithmic construction of optimal symmetric Latin hypercube designs. J. Stat. Plan. Inference 2000, 90, 145–159. [Google Scholar] [CrossRef]
- Wright, G.B. Radial Basis Function Interpolation: Numerical and Analytical Developments; University of Colorado at Boulder: Boulder, CO, USA, 2003. [Google Scholar]
- Friedman, J.H.; Roosen, C.B. An introduction to multivariate adaptive regression splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. A stochastic radial basis function method for the global optimization of expensive functions. INFORMS J. Comput. 2007, 19, 497–509. [Google Scholar] [CrossRef]
- Julie. Surrogate Model Optimization Toolbox. MATLAB Central File Exchange. 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/38530-surrogate-model-optimization-toolbox (accessed on 1 October 2022).
- Song, J.; Tobalske, B.W.; Powers, D.R.; Hedrick, T.L.; Luo, H. Three-dimensional simulation for fast forward flight of a calliope hummingbird. R. Soc. Open sci. 2016, 3, 160230. [Google Scholar] [CrossRef]


| Variables | Description | Min | Max |
|---|---|---|---|
| Wing root offset | 0.0 mm | 100 mm | |
| Wing length | 78.9 mm | 188.3 mm | |
| Root chord | 39.1 mm | 58.7 mm | |
| Frequency | 0.0 Hz | 30.0 Hz | |
| Flapping Amplitude | 0.0 deg | 90.0 deg | |
| Pitching Amplitude at the root | 0.0 deg | 90.0 deg | |
| Pitching Amplitude at the wingtip | 0.0 deg | 90.0 deg | |
| Regulating parameter of rotation angles | 0.0 deg | 5.0 |
| Variables | Description | Value |
|---|---|---|
| Wing root offset | 72.27 mm | |
| Wing length | 179.81 mm | |
| Root chord | 51.95 mm | |
| Frequency | 6.54 Hz | |
| Flapping Amplitude | 65.88 deg | |
| Pitching Amplitude at the root | 39.01 deg | |
| Pitching Amplitude at the wingtip | 75.96 deg | |
| Regulating parameter of rotation angles | 3.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Song, B.; Yang, W.; Xue, D. Optimization of a Twistable Hovering Flapping Wing Inspired by Giant Hummingbirds Using the Unsteady Blade Element Theory. Appl. Sci. 2023, 13, 5704. https://doi.org/10.3390/app13095704
Dong Y, Song B, Yang W, Xue D. Optimization of a Twistable Hovering Flapping Wing Inspired by Giant Hummingbirds Using the Unsteady Blade Element Theory. Applied Sciences. 2023; 13(9):5704. https://doi.org/10.3390/app13095704
Chicago/Turabian StyleDong, Yuanbo, Bifeng Song, Wenqing Yang, and Dong Xue. 2023. "Optimization of a Twistable Hovering Flapping Wing Inspired by Giant Hummingbirds Using the Unsteady Blade Element Theory" Applied Sciences 13, no. 9: 5704. https://doi.org/10.3390/app13095704
APA StyleDong, Y., Song, B., Yang, W., & Xue, D. (2023). Optimization of a Twistable Hovering Flapping Wing Inspired by Giant Hummingbirds Using the Unsteady Blade Element Theory. Applied Sciences, 13(9), 5704. https://doi.org/10.3390/app13095704







