Numerical Simulation of the Taylor Impact Test for Laser Powder Bed Fusion Parts Based on Microstructural Internal State Variables
Abstract
1. Introduction
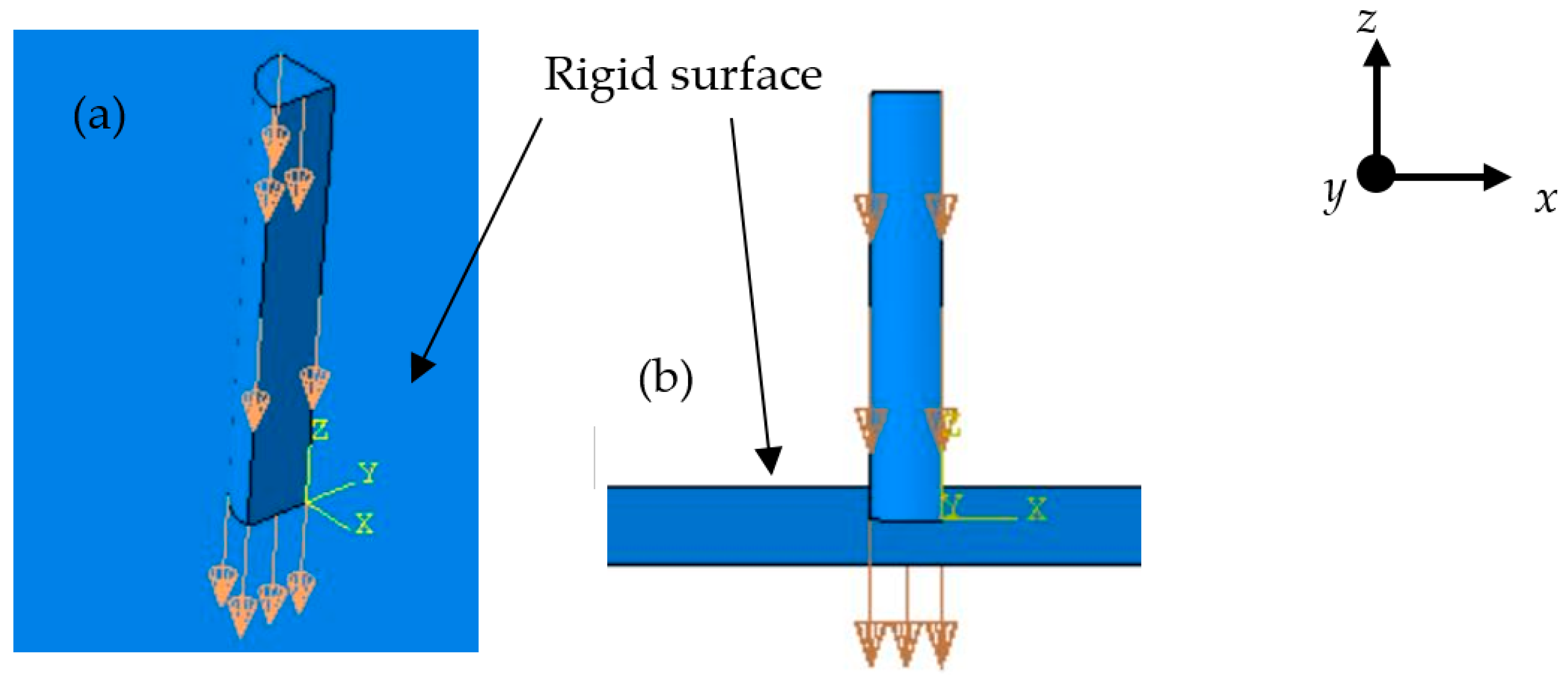
2. Finite Element Model of the Taylor Impact Test
3. Results and Discussion
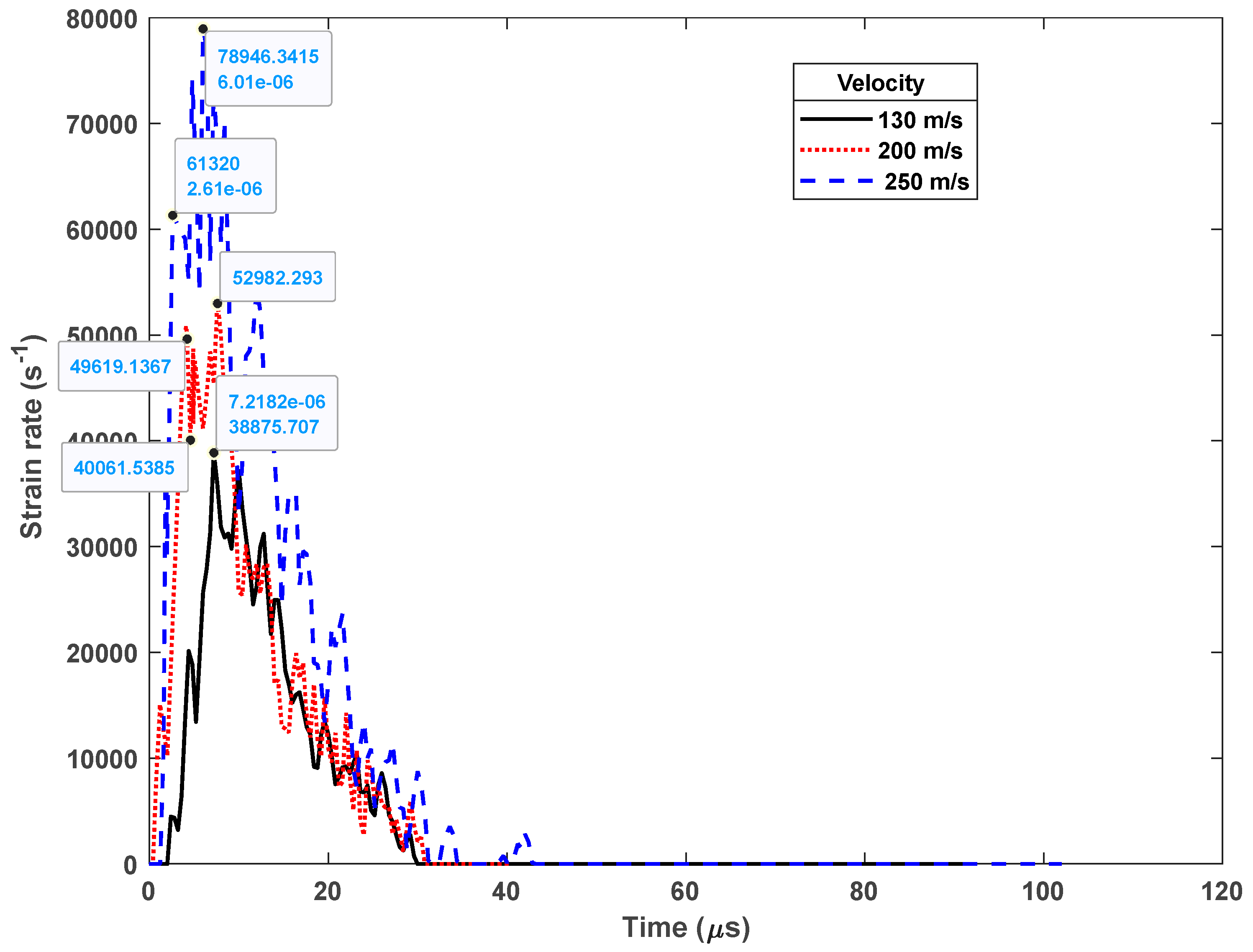
3.1. Strain Rate-Time Graph
3.2. Numerical Model at Different Prescribed Velocities
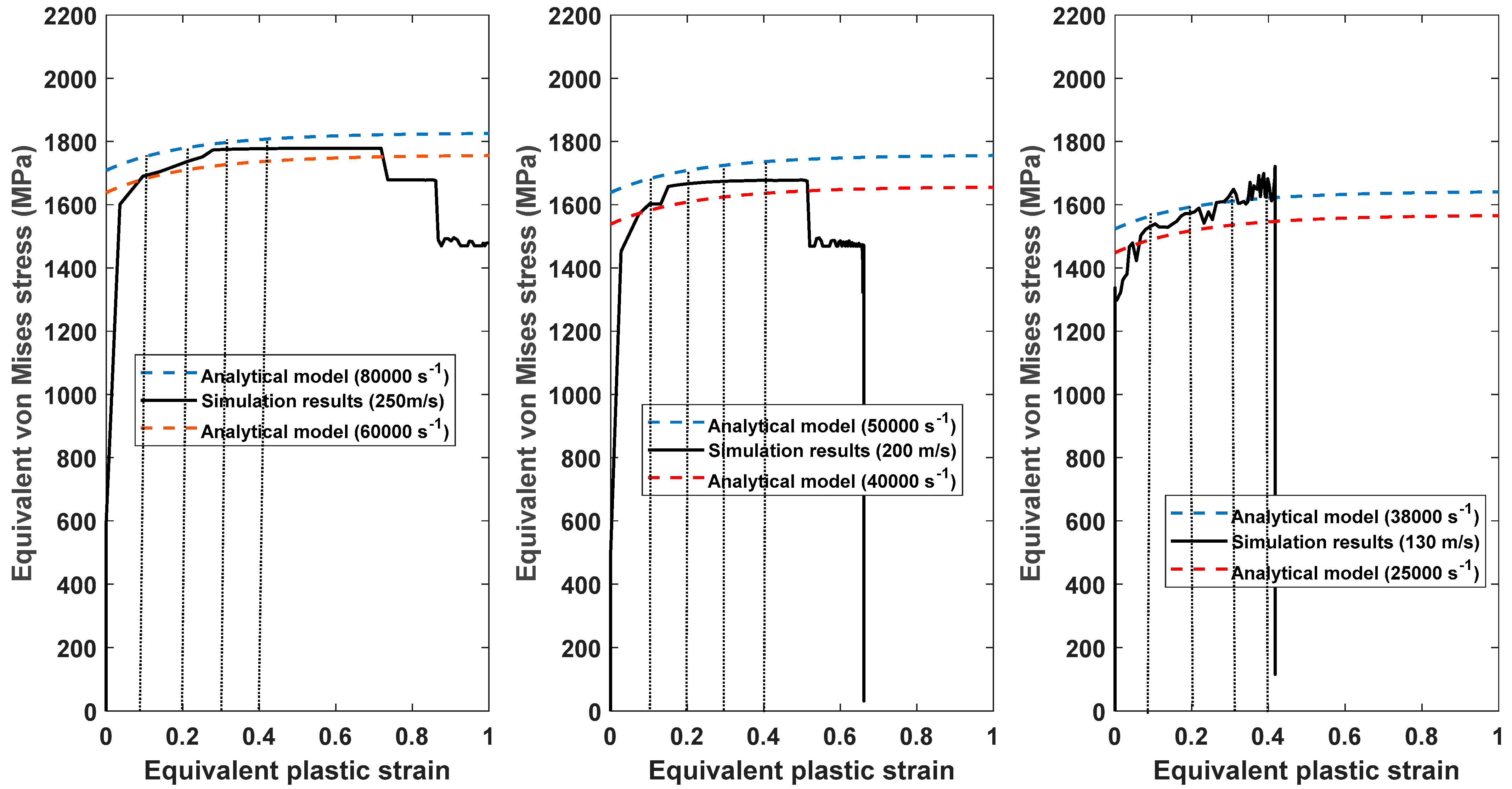
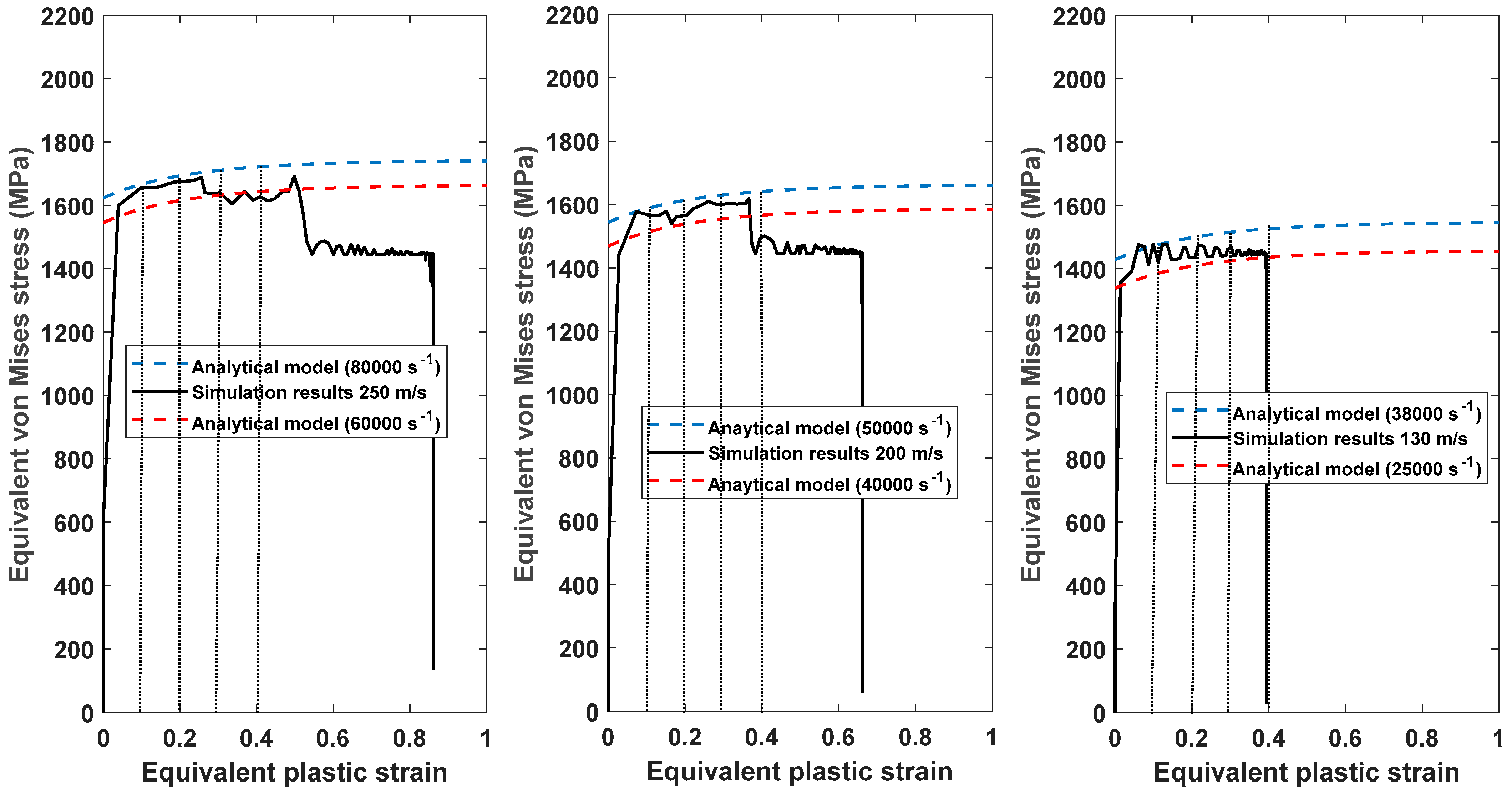
3.3. Equivalent Stress—Equivalent Plastic Strain Behaviour
4. Conclusions
- The initial peak strain rates for the Taylor impact model were lower at higher imposed velocities and vice versa.
- Remarkable deformation near the impact region was observed, whose magnitude increased with an increase in prescribed velocity.
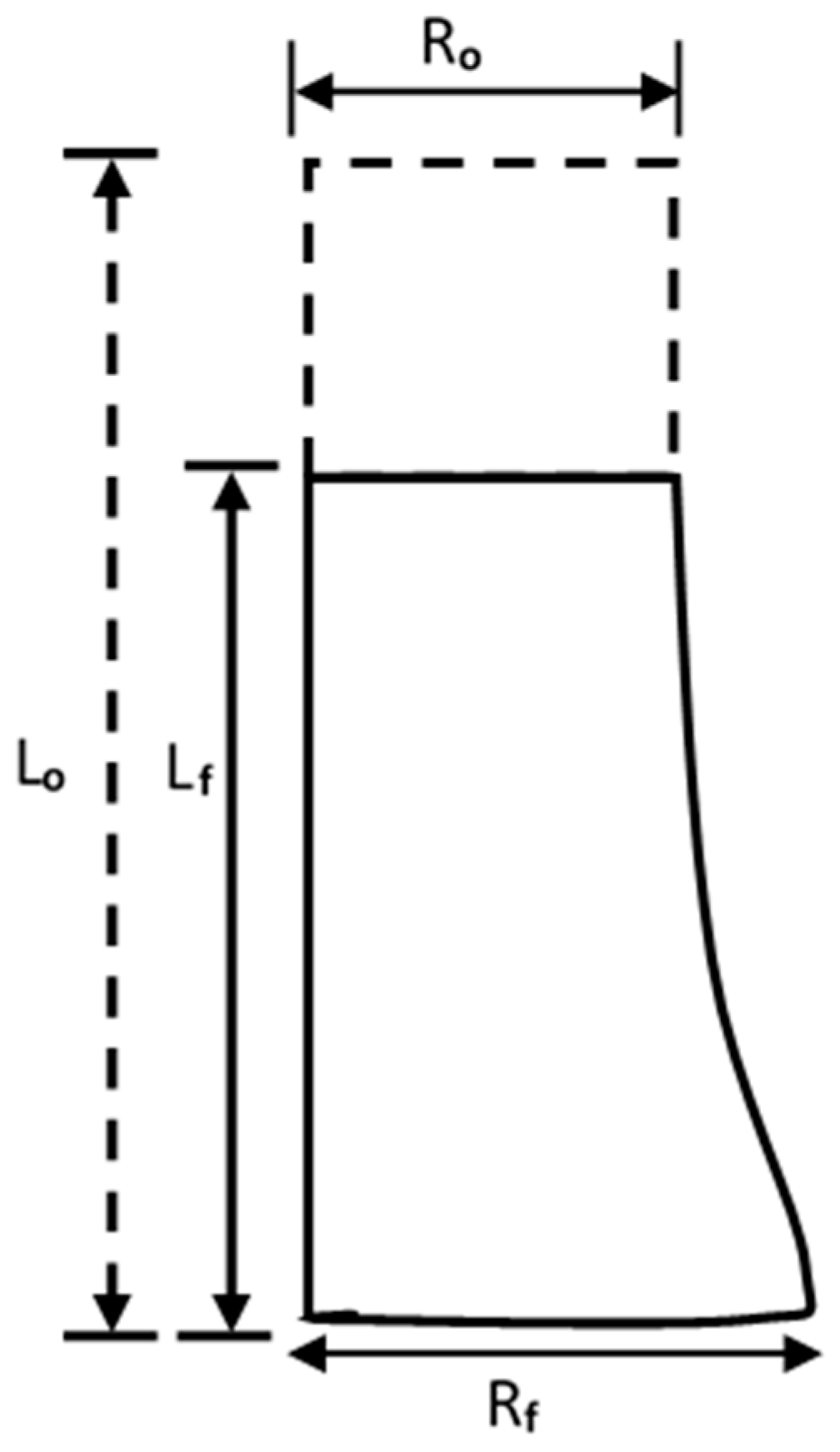
- The Rf/Ro ratio increased as the velocity imposed on the model increased and, conversely, the Lf/Lo ratio decreased as the imposed velocity increased.
- The instantaneous and average absolute errors between the numerical values and analytical values of the two models were generally less than 6%, indicating that the VUHARD subroutine is adequate for numerical simulation of the Taylor impact test of LPBF Ti6Al4V (ELI) alloy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seifi, M.; Salem, A.; Beuth, J.; Lewandowski, J. Overview of Materials Qualification Needs for Metal Additive Manufacturing. JOM 2016, 68, 747–764. [Google Scholar] [CrossRef]
- Muiruri, A.; Maringa, M.; du Preez, W. Numerical Simulation of High Strain Rate and Temperature Properties of Laser Powder Bed Fusion Ti6Al4V (ELI) Determined Using a Split Hopkinson Pressure Bar. Materials 2022, 15, 1872. [Google Scholar] [CrossRef] [PubMed]
- Muiruri, A.; Maringa, M.; du Preez, W. Validation of a Microstructure-Based Model for Predicting the High Strain Rate Flow Properties of Various Forms of Additively Manufactured Ti6Al4V (ELI) Alloy. Metals 2021, 11, 1628. [Google Scholar] [CrossRef]
- Nasiri, S.; Khosravani, M. Applications of data-driven approaches in prediction of fatigue and fracture. Mater. Today Commun. 2022, 33, 104437. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, D.; Lei, G. Experimental study on multiphase flow in fracture –vug medium using 3D printing technology and visualization techniques. J. Pet. Sci. Eng. 2020, 193, 107394. [Google Scholar] [CrossRef]
- Shunyu, L.; Yung, S. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Veiga, C.; Davim, J.P.; Loureiro, A.J. Review on machinability of titanium alloys: The process perspective. Rev. Adv. Mater. Sci. 2013, 34, 148–164. [Google Scholar]
- Saha, R.; Jacob, K. Casting of Titanium and its Alloys. Def. Sci. J. 2014, 36, 121–141. [Google Scholar] [CrossRef]
- Gaytan, S.M.; Murr, L.E.; Medina, F.; Martinez, E.; Lopez, M.I.; Wicker, R.B. Advanced metal powder-based manufacturing of complex components by electron beam melting. Mater. Technol. 2009, 24, 180–190. [Google Scholar] [CrossRef]
- Frazier, W. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Seifi, M. Metal additive manufacturing: A review of mechanical properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Muiruri, A.; Maringa, M.; du Preez, W. Development of VUMAT and VUHARD Subroutines for Simulating the Dynamic Mechanical Properties of Additively Manufactured Parts. Materials 2022, 15, 372. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.E.; Drinkard, J.A.; Rule, W.K.; Wilson, L.L. An elementary theory for the Taylor impact test. Int. J. Impact Eng. 1998, 21, 1–13. [Google Scholar] [CrossRef]
- Hawkyard, J.B.; Eaton, D.; Johnson, W. The mean dynamic yield strength of copper and low carbon steel at elevated temperatures from measurements of the “mushrooming” of flat-ended projectiles. Int. J. Impact Eng. 1968, 10, 929–930. [Google Scholar] [CrossRef]
- BS EN ISO 6892-1; Metallic Materials. Tensile Testing. Methods of Test at Room Temperature. The British Standards Institution: London, UK, 2019. [CrossRef]
- ASTM E8/E8M-13a; Standard Test Methods Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2013.
- Lee, S.; Huh, H. Shear stress hardening curves of AISI 4130 steel at ultra-high strain rates with Taylor impact tests. Int. J. Impact Eng. 2021, 149, 103789. [Google Scholar] [CrossRef]
- Brunig, M.; Larissa, D. Numerical simulation of Taylor impact tests. Int. J. Plast. 2007, 23, 1979–2003. [Google Scholar] [CrossRef]
- Rakvag, K.; Børvik, T.; Hopperstad, O.S. A numerical study on the deformation and fracture modes of steel projectiles during Taylor bar impacts tests. Int. J. Solids Struct. 2014, 51, 808–821. [Google Scholar] [CrossRef]
- AZO Materials. Grade 23 Ti6Al4V (ELI) Alloy (UNS R56401). Available online: https://www.azom.com/article.aspx?ArticleID=9365 (accessed on 12 June 2020).
- Picu, P.C.; Majorell, A. Mechanical behaviour of Ti6Al4V at high and moderate temperatures–Part II: Constitutive modelling. Mater. Sci. Eng. A 2002, 326, 306–316. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D.J. Introduction to Dislocations, 5th ed.; Elsevier: Oxford, UK, 2011; pp. 205–217. [Google Scholar]
- Cáceres, C.H.; Lukac, P. Strain hardening behaviour and the Taylor factor of pure magnesium. Philos. Mag. 2008, 88, 977–989. [Google Scholar] [CrossRef]
- Galindo, M.A.; Mumtaz, K.; Rivera, P.E.; Galindo-Nava, E.I.; Ghadbeigi, H. A microstructure sensitive model for deformation of Ti6Al4V describing cast-and-wrought and additive manufacturing morphologies. Mater. Des. 2018, 160, 350–362. [Google Scholar] [CrossRef]
- Kohn, D.H.; Ducheyne, P. Tensile and fatigue strength of hydrogen-treated Ti6Al4V alloy. J. Mater. Sci. 1991, 26, 328–334. [Google Scholar] [CrossRef]
- Ming, L.; Pantalé, O. An efficient and robust VUMAT implementation of elastoplastic constitutive laws in ABAQUS/explicit finite element code. Mech. Ind. 2018, 19, 308. [Google Scholar] [CrossRef]
- ABAQUS Documentation Version 6.6. Available online: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt03ch06s03at07.html#usb-anl-aexpdynamic (accessed on 12 November 2020).
- Muiruri, A.; Maringa, M.; du Preez, W. Evaluation of Dislocation Densities in Various Microstructures of Additively Manufactured Ti6Al4V (Eli) by the Method of X-ray Diffraction. Materials 2020, 13, 5355. [Google Scholar] [CrossRef] [PubMed]
- Muiruri, A.; Maringa, M.; du Preez, W. Crystallographic Texture Analysis of As-Built and Heat-Treated Ti6Al4V (ELI) Produced by Direct Metal Laser Sintering. Crystals 2020, 10, 699. [Google Scholar] [CrossRef]


| Symbol | Parameters Description | Value and Units | Ref |
|---|---|---|---|
| Boltzmann constant | 1.38 × 10−23 m2·kg·s−2. K−1 | - | |
| Shear modulus at absolute zero temperature | K | ||
| Shear modulus | GPa | [21] | |
| b | Burgers vector | m | [22] |
| Reference strain rate | 107 s−1 | [21] | |
| Test strain rate | s−1 | ||
| Threshold stress | 1063.2 MPa | Calibrated | |
| Normalised activation energy | 0.25 | Calibrated | |
| Dislocation accumulation coefficient | 8.3 × 1015 m−2 | Calibrated | |
| Dislocation annihilation coefficient | 10 | Calibrated | |
| p | Fitting constant | 1 | [21] |
| q | Fitting constant | 2 | [21] |
| M | Taylor factor | 3 | [23] |
| Geometrical factor | 0.2 | [24] | |
| Hall–Petch constant | 0.328 MPa.m1/2 | [25] | |
| T | Temperature | K | |
| ζ | Material constant | Calibrated for different microstructures | |
| χ | Effective damping coefficient | Calibrated for different microstructures | |
| Initial dislocation density | Measured in different microstructures | ||
| d | Average grain size | Measured in different microstructures | |
| Variable | Measured Value | ||
|---|---|---|---|
| Samples C | Samples D | Samples E | |
| Average grain size | 2.5 µm | 6.0 µm | 9.0 µm |
| Initial dislocation density (m−2) | 5.73 × 1014 | 5.09 × 1014 | 7.00 × 1014 |
| Material constant (ζ) | 207 | 210 | 210 |
| Effective damping coefficient (χ) | 0.00032 | 0.00030 | 0.00020 |
| Samples | C | D | E | |||
|---|---|---|---|---|---|---|
| Prescribed velocity | Rf/Ro | Lf/Lo | Rf/Ro | Lf/Lo | Rf/Ro | Lf/Lo |
| 130 m/s | 1.356 | 0.843 | 1.371 | 0.782 | 1.362 | 0.801 |
| 200 m/s | 1.630 | 0.710 | 1.662 | 0.667 | 1.647 | 0.664 |
| 250 m/s | 1.874 | 0.612 | 1.897 | 0.581 | 1.878 | 0.600 |
| Imposed Velocity | Approximate Range of Plastic Strain Rate Obtained from Figure 3 |
|---|---|
| 130 m/s | 25,000–38,000 s−1 |
| 200 m/s | 40,000–50,000 s−1 |
| 250 m/s | 60,000–80,000 s−1 |
| Samples C | ||||||
|---|---|---|---|---|---|---|
| ) | ) | |||||
| Velocity | Strain | 0.1 | 0.2 | 0.3 | 0.4 | |
| 130 m/s | 0.03 | 0.01 | 0.02 | 0.01 | 0.02 0.009 | |
| 0.01 | 0.03 | 0.02 | 0.03 | |||
| 200 m/s | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 0.016 | |
| 0.05 | 0.01 | 0.05 | 0.01 | |||
| 250 m/s | 0.01 | <0.01 | 0.01 | 0.03 | 0.015 0.009 | |
| <0.01 | 0.03 | <0.01 | <0.01 | |||
| Samples D | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | |||
| 130 m/s | 0.004 | 0.02 | 0.03 | 0.02 | 0.021 0.011 | |
| 0.04 | 0.02 | 0.01 | 0.02 | |||
| 200 m/s | 0.02 | 0.01 | 0.03 | 0.03 | 0.031 0.014 | |
| 0.05 | 0.05 | 0.03 | 0.03 | |||
| 250 m/s | 0.03 | 0.04 | 0.06 | 0.06 | 0.035 0.021 | |
| 0.02 | 0.01 | 0.01 | 0.05 | |||
| Samples E | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | |||
| 130 m/s | 0.04 | 0.04 | 0.02 | 0.02 | 0.030 0.018 | |
| 0.01 | 0.01 | 0.04 | 0.06 | |||
| 200 m/s | 0.09 | 0.02 | 0.02 | 0.05 | 0.029 0.0281 | |
| 0.02 | 0.02 | 0.01 | 0.003 | |||
| 250 m/s | 0.04 | 0.04 | 0.05 | 0.06 | 0.039 0.0181 | |
| 0.03 | 0.02 | 0.06 | 0.01 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muiruri, A.; Maringa, M.; du Preez, W. Numerical Simulation of the Taylor Impact Test for Laser Powder Bed Fusion Parts Based on Microstructural Internal State Variables. Appl. Sci. 2023, 13, 5372. https://doi.org/10.3390/app13095372
Muiruri A, Maringa M, du Preez W. Numerical Simulation of the Taylor Impact Test for Laser Powder Bed Fusion Parts Based on Microstructural Internal State Variables. Applied Sciences. 2023; 13(9):5372. https://doi.org/10.3390/app13095372
Chicago/Turabian StyleMuiruri, Amos, Maina Maringa, and Willie du Preez. 2023. "Numerical Simulation of the Taylor Impact Test for Laser Powder Bed Fusion Parts Based on Microstructural Internal State Variables" Applied Sciences 13, no. 9: 5372. https://doi.org/10.3390/app13095372
APA StyleMuiruri, A., Maringa, M., & du Preez, W. (2023). Numerical Simulation of the Taylor Impact Test for Laser Powder Bed Fusion Parts Based on Microstructural Internal State Variables. Applied Sciences, 13(9), 5372. https://doi.org/10.3390/app13095372








