Abstract
In the existing research on time-series event prediction (TSEP) methods, most of the work is focused on improving the algorithm for classifying subsequence sets (sets composed of multiple adjacent subsequences). However, these prediction methods ignore the timing dependence between the subsequence sets, nor do they capture the mutual transition relationship between events, the prediction effect on a small sample data set is very poor. Meanwhile, the sequence labeling problem is one of the common problems in natural language processing and image segmentation. To solve this problem, this paper proposed a new framework for time-series event prediction, which transforms the event prediction problem into a labeling problem, to better capture the timing relationship between the subsequence sets. Specifically, the framework used a sequence clustering algorithm for the first time to identify representative patterns in the time series, then represented the set of subsequences as a weighted combination of patterns, and used the eXtreme gradient boosting algorithm (XGBoost) for feature selection. After that, the selected pattern feature was used as the input of the long-term short-term memory model (LSTM) to obtain the preliminary prediction value. Furthermore, the fully-linked conditional random field (CRF) was used to smooth and refine the preliminary prediction value to obtain the final prediction result. Finally, the experimental results of event prediction on five real data sets show that the CX-LC method has a certain improvement in prediction accuracy compared with the other six models.
1. Introduction
Mining useful information from time-series data is an active research field that has attracted increasing attention in the last decades due to the rich application scenarios of TSEP, including mine hazard detection [1], nuclear power plants abnormal event detection [2], medical diagnosis [3], river level [4], temperature [5], stock price [6], and so on. Using the prediction of time series events, it is possible to predict the development trend of time series in the future and, in practical applications, it can help people to analyze and make decisions. Traditional time series forecasting methods use historical data to predict future values, which are not suitable for solving the problem of event forecasting in time series data. Because the events in the time series usually span a certain time range and show a certain trend or regularity through a continuous value, this is essentially different from a single value. In contrast to numerical forecasting in time series data, event forecasting in time series data has not been deeply studied. Due to the high dimensionality and noise of time series data, how to mine useful information from sequence data is still a big challenge.
Traditional TSEP methods use historical data to predict future time series values, and then classify the predicted subsequence to obtain event predictions. Such a framework mainly involves four tasks [7]: preprocessing, model derivation, time-series prediction, and event detection. The main methods of time-series prediction are traditional forecasting models such as ARIMA, SARIMA and GARCH. The main methods of event detection include decision trees (DT), artificial neural networks (ANN), and support vector machines (SVM). However, since time series events usually span a certain time range, these traditional forecasting models predict a single value and then classify it, are susceptible to small disturbances in the training data, and have a high degree of instability [8]. This type of method ignores the characteristics of each subsequence itself, and its predictive ability is limited.
In recent years, the new event prediction method represented by the graph model Time2Graph [9] has received widespread attention. Based on Time2Graph, the EvoNet model [10] has more successfully captured the time-varying relationship between time series. The specific steps are: representing and identifying representative patterns of subsequences, capturing the transitional relationship between the patterns, using pattern features as the input of the classifier and the classification result as the prediction of future events, so as to predict the event. The key to this prediction method is how to extract the characteristics of time subsequences. The above two methods extract the characteristics by establishing state diagrams. In addition, the time series can also be interpreted as a new state sequence and model their sequential dependencies. The literature provides a new method, X-HMM (XGBoost-HMM) [11], which takes the hidden state as the input of the classifier. Compared with the traditional framework, this kind of method omits the step of time series forecasting, thus avoiding the deviation caused by time series forecasting, but this method classifies each subsequence set separately, ignoring the remote dependencies between the various subsequence sets.
Inspired by the sequence labeling method, the use of depth models and probabilistic graph models for sequence labeling can well capture the dependencies between subsequence sets [12] and transfer the idea of sequence labeling to event prediction, which can greatly improve forecasting accuracy. As a classic sequence data processing model, LSTM has a solid theoretical foundation [13]. Using the LSTM model for event labeling prediction, and then using conditional random field (CRF) to smooth the prediction results, is expected to further improve the accuracy of event prediction to help solve various application problems in this field.
There are shape similarities and change similarities between different subsequences, so the method of pattern recognition can be used to extract representative patterns in the sequence and then express the subsequences as a combination of patterns. Studies have shown [10] that the clustering method (cluster) is superior to other pattern recognition methods such as SAX-VSM [14] and Fast shapelets [15] when extracting sequence patterns for relationship modeling. The cluster method is easy to realize and has other advantages, such as high classification accuracy [16], so this paper mainly uses the cluster method for pattern recognition to obtain the transitional relationship between the patterns. However, after expressing the subsequence as a combination of patterns, problems such as excessive data dimensions and redundant information will occur. The XGBoost algorithm [17] has the advantages of parallelization, high scalability, and fast speed, so this article chooses this algorithm for feature selection and obtains the soft classification probability value of the subsequence sets to assist LSTM-CRF in event prediction. Thus, a novel prediction model based on Cluster-XGBoost-LSTM-CRF is constructed. Compared with previous models, this model can capture the dependency between subsequence sets well and take the interaction of different events into account in the model.
In order to verify the effectiveness of CX-LC, this article conducted experiments on five real data sets. The prediction results show that CX-LC is superior to several other models in event prediction. The main contributions of this research are:
- This paper transformed the problem of event prediction into a problem of sequence labeling and captures the dependency between subsequence sets;
- The CX-LC model developed in this paper can well extract the features in the original data set and smoothly optimize the prediction results;
- This paper conducted experiments on five data sets to prove that the CX-LC model has more accurate predictions.
The main content of this paper is structured as follows:
2. Definitions and Methods
2.1. Definitions
Definition 1 (Time-Series).
is a panel data set, which contains the N time series with length (i.e., N samples), for any sample , there are K subsequences divided in chronological order, denoted as , where is the k-th subsequence of , which can be expressed as , where L is a hyperparameter, which has different values in different data sets (e.g., there is days in a week), is a D-dimensional observation value of the time series at time l, and is the observation event of the k-th subsequence [18] (e.g., if abnormality occurs, the value is 1). For the convenience of understanding this article, the definition set table is attached in the Appendix A Table A1.
Definition 2 (Time-Series Event Prediction).
Taking the i-th sample as an example, use the sliding window method to obtain M data sets containing τ subsequences from , denoted as , where ; this paper refers to as “Subsequence Set” . Time series event prediction is to predict the event of the subsequence based on the subsequence set [19], where τ is called the prediction history length, and . For the prediction problem solved in this paper, there are the following assumptions:
- Each time series is independent and evenly distributed;
- The past of the event will continue into the future;
- The divided subsequence is appropriate for the description of the event.
Definition 3 (Pattern and Pattern Recognition).
The representative subsequence pattern in the time series is represented by the symbol [20]. Use the sequence clustering method to identify all patterns from the data set, the pattern set is , and the number of patterns V is a hyperparameter.
Definition 4 (Classification Event Prediction Method).
In this paper, the following two traditional time series time prediction methods are called classification event prediction methods. (1) The first method is to predict the subsequence value in the time period based on the subsequence set , and then classify to obtain the event prediction result ; (2) The second method is to take the subsequence set as an independent individual, extract the numerical features in the as the input of the classifier, and use the event prediction result as the output of the classifier. It can be seen that these two methods are classification algorithms that do not consider the time factor between the subsequence sets .
Definition 5 (Sequence Labeling Problem).
The sequence labeling problem is one of the most common problems in Natural Language Processing (NLP) [21]. The so-called “sequence labeling” means that for a linear observation sequence , each element in the sequence is labeled with a certain label in the label set to obtain the output. The sequence , that is, the m-th observation value , is labeled as , .
Definition 6 (Labeling Event Prediction Method).
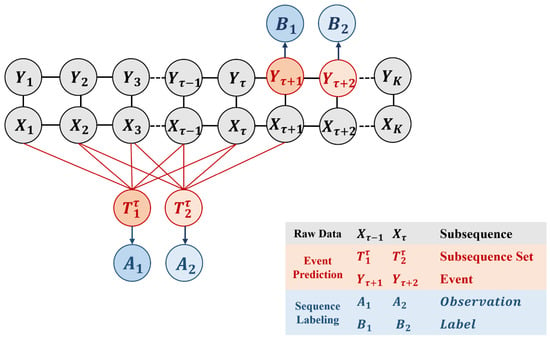
Sequence labeling is a classification method that takes into account the time factor. Inspired by this, the m-th subsequence set is regarded as the observation , and the to-be-predicted value is regarded as the label , so the event prediction problem can be converted into a sequence tagging problem. Figure 1 shows the specific conversion process.

Figure 1.
Labeling Prediction Method. As shown in the figure, the first subsequence set is regarded as the observation , the to-be-predicted value is regarded as annotated label , and the second subsequence set is the same. The problem conversion is carried out in turn, and the event prediction problem can be converted into a sequence labeling problem.
2.2. CX-LC Framework
Aiming at the shortcomings of the traditional classification prediction method, which does not consider the timing between subsequence sets, and has a too-high complexity, this paper proposes a new framework for time-series event prediction, the Cluster-XGBoost-LSTM-CRF model (CX-LC). Because it converts the time prediction problem into a labeled problem, this model can also be called a “labeling” prediction method.
2.2.1. Patterns Recognition
One of the key problems of sequence marking is how to extract the features of sub-segments as the input of the model. In the existing literature, the original data of the subsequence set are used as input, which ignores the conversion relationship between various patterns in the subsequence set, and is easily affected by noise such as outliers in the original data. Using representative patterns in time series, effective and interpretable time series modeling can be carried out. In this paper, the subsequence is recognized as a weighted combination of multiple patterns, and then the characteristics of the patterns are used as the model input, which can improve the robustness of the model.
First, identify V sequence patterns from the original data set . Experiments show that [10], as V increases, the prediction accuracy rate may not necessarily increase, so V is an empirically determined value. This paper uses the cluster algorithm to recognize patterns. Taking Kmeans [22] as an example, the purpose of the algorithm is to divide the segment into classes—the set of classes is —and then extract the representative model of each class by minimizing the sum of squares within the cluster. The specific formula is as follows:
where is the average value of all segments in . Thus, the pattern set of the data set is obtained.
After obtaining the mode set as Θ, the subsequence can be expressed as a weighted combination of modes. For a given state and a subsequence , the distance between the two can be normalized to the identification weight. In this article, Euclidean distance and the linear function normalization method (Min-Max scaling) are used:
is the probability of recognizing the subsequence as the state , that is, the weight of in the pattern combination of . Each subsequence can be calculated to obtain V identification weights, expressed as ; so, based on the pattern representation, the feature set of the subsequence set can be obtained as .
In order to illustrate how pattern recognition reveals the evolution of time series and helps predict events, this paper conducted an observational study on the PM2.5 data set (see Section 3.1 for details on the data set). Take the data of a certain air detection station as an example, the detection station can obtain an observation value of PM2.5 every day (i.e., ) and divide the data with one week as a subsequence (i.e., ). If the mean value of PM2.5 in a week is greater than one standard deviation of the overall mean value, it is determined that the air quality of the week is abnormal. Intercept the data of the first six weeks and draw the line chart shown in Figure 2. There were abnormal fluctuations in the PM2.5 value in the first and fourth weeks (red line), and it was normal in the other weeks (blue line). Each week can be identified as a combination of different states. As shown in the figure, the first week has a high similarity with pattern 4 (black broken line), so pattern 4 occupies a higher weight in , and pattern 4 belongs to the representative mode of the abnormal sequence. It can be seen that the weight value of the pattern can well reflect whether the subsequence is abnormal. The fourth week and pattern 16, and the sixth week and pattern 9 can all illustrate this point.
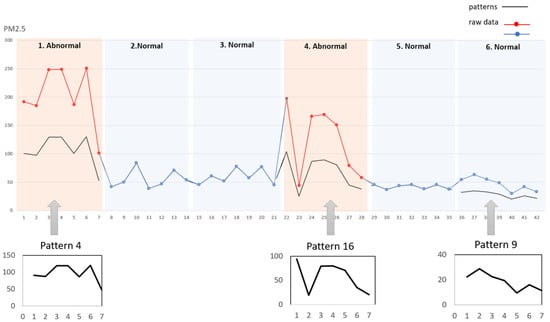
Figure 2.
Representation of subsequences to states: pattern 4, pattern 9, and pattern 16 (black broken line) are three patterns of the V patterns identified from the time series data set, pattern 4 and pattern 16 are the patterns with abnormal fluctuations, pattern 9 is a normal pattern. In the original sequence, the first week and the second week are the time series (red broken line) where abnormalities were detected. It can be seen from the figure that these two weeks have a high degree of coincidence with the abnormal representative pattern. Therefore, it is interpretable to express the subsequence as a combination of patterns.
2.2.2. Feature Extraction
In Section 3.1, the pattern characteristics of each subsequence set have been obtained ,, . It can be seen that the data dimension increases with the increase of the history length τ and the number of states V, but in the features, there is information redundancy. If all the pattern features are used as the input of LSTM, it will not only greatly increase the calculation time, it will also affect the prediction effect. This paper used the XGBoost model to perform feature selection, extract important features from high-dimensional data and remove redundant features. XGBoost is a powerful machine learning algorithm for structured data. It can improve the speed and performance of calculation based on the implementation of gradient boosting decision tree (GBDT). This article uses the characteristics of its tree model as a basis for quantifying the importance of each feature [23]. In the process of building the tree model, each layer greedily selects a feature as a leaf node to maximize the gain of the entire tree after segmentation. This means that the more a feature is segmented, the more the feature will bring to the entire tree, and the greater the benefit, the more important this feature is. In the process of segmentation, the weight of each leaf node can be expressed as , and are, respectively:
where l is the loss function, used to measure the distance between the true value and the predicted value . and are the first derivative and the second derivative of the loss function, respectively. In order to minimize the cost of the split tree, according to the weights of all leaf nodes, consider the gain generated when each feature is used as the split point, as follows:
It shows that, for each split point, its gain can be expressed as the total weight after splitting (the sum of the total weight of the left subtree of the leaf node and the total weight of the right subtree) minus the total weight of the leaf node before the split total weight. The importance measurement index is a measure to evaluate the importance of each feature in its own feature set. This paper selected the feature average gain value AverageGain (Equation (7)) as the basis for constructing the decision tree in order to accurately complete the classification task.
where indicates that the feature is classified into the j-th leaf node and F is the set of . The eigenvalues are sorted in descending order according to the size of the comparison AverageGain, and the first few most representative features are selected. At the same time, the XGBoost model obtained by fitting can be used to softly classify each sub-sequence set and obtain the probability value of each input under different classification results. The probability value only considers the internal information transfer of the subsequence set and can also be used as subsequence set characteristics. Therefore, the pattern feature of the filtered subsequence set is reduced to a Q-dimensional variable and there is .
2.2.3. Event Prediction
Unlike most existing work on modeling individual subsequence sets, this paper introduced the idea of sequence annotation, which not only classifies subsequence sets according to their respective characteristics but also treats all subsequence sets as a whole, taking into account the interaction and coherence between events. RNN is a series of powerful correlation models, which capture the dynamics of time through the loops in the graph, and is often used in the problem of sequence annotation. In practice, it is difficult for RNN to capture the long-term dependence of timing due to the problem of gradient disappearance or gradient explosion [24]. The long short term memory model (LSTM) [25] is a variant of RNN, which aims to solve these vanishing gradient problems. An LSTM unit consists of four multiplication gates, which control the proportion of the forgotten information and the information passed to the next time step. Figure 3 is a comparison diagram of the basic structure of RNN and LSTM units.
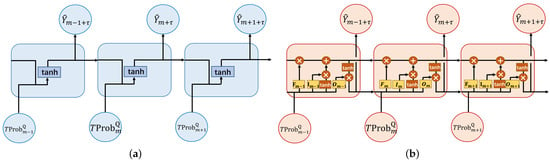
Figure 3.
Comparison of the basic structure of RNN and LSTM units. (a) Basic structure of RNN unit and (b) basic structure of LSTM unit.
In Section 3.2, the pattern features of the subsequence set () have been extracted and the pattern features in turn as the input of the LSTM model, the prediction result of the event is obtained. The specific formula is as follows:
among them, F, I, O, and C are forget gate, input gate, output gate, and memory gate, respectively; a is the intermediate output of the hidden layer, used to store all useful information of time m (and before), and is activation functions, “∘” is the element-wise product symbol, is the weight matrix, is the bias matrix, and are both learnable parameters. Using the LSTM model to perform recursive operations, the preliminary predicted value of the event is obtained. Because the Adam optimizer [26] has the advantages of simple implementation, efficient calculation, and fewer memory requirements, this article used the Adam optimizer to adjust the learnable parameters in LSTM. The true event has a value range of , so the following formula for minimizing the cross-entropy loss can be obtained:
Because LSTM can construct high-dimensional and dense nonlinear features, it has very powerful feature extraction capabilities. However, if we only use LSTM to mark a sequence, the transfer relationship cannot be explicitly modeled. LSTM can only extract complex features by simulating the emission function, but cannot simulate the transfer function, so sometimes it is too tolerant to unreasonable parts. Take the labeling problem of sentence structure as an example; B stands for the beginning of the word, E stands for the end of the word. Logically speaking, the marking result of a complete sentence has a structure similar to BB and EB, which is absolutely wrong, but LSTM pays more attention to the overall loss minimization and does not explicitly model the neighbor transition relationship, so such structural errors are always unavoidable. The linear chain conditional random field (linear-CRF) model brings a transition matrix parameter, which can very effectively solve this problem. That is, LSTM is responsible for feature extraction and linear-CRF is responsible for neighboring transition relationship management, and smoothly refines the prediction results of LSTM.
2.2.4. Smooth Prediction
Probabilistic graphical models are a type of model with a sound theoretical foundation and good application effects in machine learning. Especially the Markov Random Field (MRF) and its variant CRF have been developed as an effective method to improve the accuracy of sequence labeling. Since the time-series are arranged in a linear chain, the linear chain conditional random field (linear-CRF) is often used for sequence labeling. In the problem of time-series event prediction, the subsequence set is the observation sequence, and the event value is the output tag sequence; according to the definition of CRF, under the condition given by , the conditional distribution of Y satisfies the Markov property:
Therefore, according to the Hammesley theorem [27], the joint probability can be decomposed into the product of multiple potential functions based on the maximal clique:
where Z is the normalization factor, the subset of nodes with edges connected between any two nodes is a “clique” , the set of all cliques is C. is called the potential function, and each potential function is only related to one clique, is a non-negative real function defined on a subset of variables, usually constructed as an exponential function, used to define the probability distribution function. Due to the linear chain structure of linear-CRF (as shown in Figure 4), the two adjacent events and form a maximal clique, and the parameterized form of linear-CRF can be obtained:
where is the transition characteristic function defined on the edge, which depends on the current and previous positions (also called binary score), and is the state characteristic function defined on the point, which depends on the current position (also called the unary score).
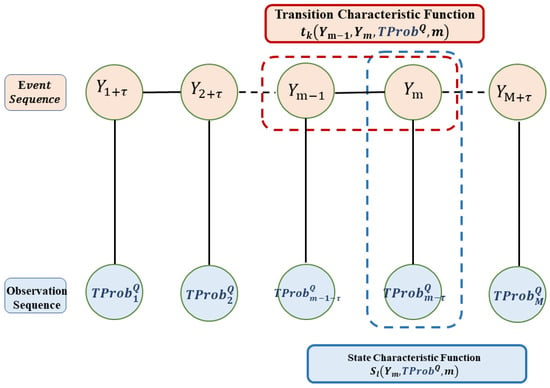
Figure 4.
Graphical linear-CRF.
In the combination of LSTM-CRF, the value of is the output of LSTM (i.e., the preliminary prediction value ) and is the label transition matrix obtained by training CRF. When calculating , the logarithm is usually taken to obtain and then the forward algorithm [28] is used to calculate. Similarly, the LSTM-CER model can use the Adam optimizer for parameter optimization and use the negative log-likelihood function as the loss function:
So far, the LSTM-CRF model has been trained. It is beneficial to the Viterbi algorithm [29] to decode the event’s final predicted value . The model training process is summarized in Algorithm 1 and Figure 5 shows the flow chart of the CX-LC model.
| Algorithm 1 The learning procedure of CX-LC. |
|
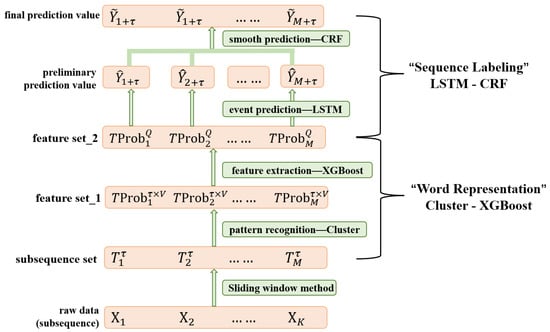
Figure 5.
CX-LC model framework.
3. Experiment
This article applied the CX-LC model to the prediction of time-series events and aimed to explore and answer the following two questions:
- Q1: Compared with other advanced classification event prediction methods, how does CX-LC perform on the same prediction task?
- Q2: Do the pattern recognition, feature selection, and smoothing refinement parts of the CX-LC framework really improve the prediction results?
3.1. Introduction to Data Sets and Prediction Tasks
This article used five real-world data sets for experimental exploration. All five data sets are public data from Kaggle:
- 1.
- DJIA 30 Stock Time Series;
- 2.
- Web Traffic Time Series Forecasting;
- 3.
- Air Quality Data in India (2015–2020);
- 4.
- Daily Climate time series data.
Except for the WebTraffic data set, the rest are small sample data. Table 1 shows the relevant information of these data sets.

Table 1.
Data set statistics.
DJIA30: This data set is a stock time-series. It contains the stock price data set of 30 DJIA companies in the past 13 years (518 weeks in total). It contains five trading days each week, and each trading day records four observations: opening price, trading volume, highest price, and lowest price reached on the day. If the slope of one of the four observations of a stock in a week is greater than 1, it is determined that the price of the week fluctuates abnormally. The prediction task is to predict whether there will be abnormal price fluctuations in the next week, based on the observed values in the past year (50 weeks).
WebTraffic(Web): This data set is a time-series of network traffic. It contains the number of views of 50,000 Wikipedia articles in the past 2 years (26 months in total), 30 days each month, and one observation per day is recorded. When the slope of the observed value curve of an article in a month is greater than 1.0, it is determined that the reading volume of the article has increased rapidly this month. The prediction task is to predict whether there will be a rapid increase in reading volume in the next month, based on the observations in the past year (12 months).
PM2.5: This data set is a time-series of air quality. It contains the PM2.5 detection concentrations of 38 air detection stations in the past 3 years (130 weeks in total), 7 days a week, and one observation value is recorded every day. If the observed mean value of a testing station in a week is too large (two variances exceeding the overall mean value), it is determined that there is an abnormality in the PM2.5 concentration in that week. The prediction task is to predict whether there will be an abnormal change in concentration in the next week, based on the observed values in the past five months (20 weeks).
CO: This data set is a time-series of air quality. It contains the CO detection concentrations of 24 Italian cities in the past 4 months (2664 h in total), 24 h a day, and an observation value is recorded every hour. If the difference between the maximum value and the minimum value observed in a city in a day is too large, it is determined that there is an abnormality in the CO concentration of that city on that day. The prediction task is to predict whether there will be an abnormal change in concentration in the next day, based on the observed values in the past three weeks (20 days).
Temperature(Temp): This data set is a temperature time-series. It contains the temperature of 100 representative cities in the world in the past 4 years (222 weeks in total), 7 days a week, and one observation value is recorded every day. If the difference between the maximum value and the minimum value observed in a city in a week is too large, it is determined that the temperature of the city on that day is abnormal. The prediction task is to predict whether there will be an abnormal temperature change in the next week based on the observed value in the past year (50 weeks).
3.2. Baseline Method
This article compares the proposed CX-LC model with eight other models:
Classification event prediction method. For the prediction of time series events, most of the current research is to take each subsequence set as an independent individual, extract the information in the subsequence set as the input of the classifier, and use the event prediction result as the output of the classifier. This article uses the most advanced sets of frameworks as the baseline model. X-HMM [11] is a sequential model, XGBoost can capture the relationship between different observation features, and then HMM can find the most likely hidden state sequence of a given observation sequence, so as to make event prediction. Time2Graph [9] adopts shapelet to extract states; it aggregates the graphs at different times as a static graph and conduct DeepWalk to learn graph’s representations, which then serve as features for event predictions. Evolutionary State Graph Network models (EvoNet) [10] both the node-level (state-to-state) and graph-level (segment-to-segment) propagation, and captures the node-graph (state-to-segment) interactions over time, and then uses it as a function of event prediction. Since the original EvoNet model combines and scrambles the subsequences of different samples before training the classifier, in order to highlight the comparison effect, this article added the model ( ), which trains different samples separately. Call the original model (). These four methods are all classification algorithms that do not consider the time factor between the subsequence sets .
Labeling event prediction method. The CX-LC model proposed in this paper first uses the cluster algorithm for pattern recognition, uses XGBoost for feature selection, then uses the LSTM algorithm for event prediction, and finally uses the CRF model to improve the continuity of the prediction results. In order to explore whether the first, second, and last steps have an effect on improving the prediction accuracy, this article used the XGBoost-LSTM-CRF (X-LC) model with the pattern recognition step removed, the cluster-LSTM-CRF (C-LC) model without the step of feature selection, and the cluster-XGBoost-LSTM (CX-L) model without smoothing are tested on five data sets. As we expected, the complete CX-LC model has better forecast results.
3.3. Implementation Details
This article conducted experiments on five data sets, applied the time series missing value filling algorithm based on matrix decomposition to interpolate [30]. When dividing the data set, the data set was divided into a training set and a test set at a ratio of 8:2, the training set was used for training the model, and the test set was used for model evaluation. When the model was optimized, each model went through 100 iterations. When selecting the activation function of the neural network, the selection was made by traversal, using the tanh activation function in the fully linked layer of LSTM. Similarly, other hyperparameters were determined by empirical judgment and traversal debugging.
3.4. Performance Comparison and Discussion
3.4.1. Performance Comparison
In this section, the performance of CX-LC and other models were compared. Because the ratio of positive and negative samples was not balanced, Recallratio, Precisionratio, and F1-score were used as evaluation indicators at the same time. All reports were the average results of five repeated experiments and were run in the same environment. Table 2 shows the prediction results.

Table 2.
Comparison of prediction Recallratio, Precisionratio and F1-score(%). Bold text is the best performance, while underlined text represents the second best performance.
By comparing the results of labeling and classification prediction methods, Q1 can be answered. The results in Table 2 show that, in addition to the Webtraffic and Djia30 data sets, the labeling prediction results of the other three data sets are basically better than the classification prediction results, converting the event prediction problem into a sequence labeling problem can greatly improve the prediction effect. There is still valuable information transfer between the subsequence sets, and the labeling prediction method predicts the events of the subsequence sets in chronological order; the prediction at each moment is related to the prediction at the previous moment. The algorithmic process of event prediction on the subsequence set, in turn, can well capture the important correlations in the time propagation process.
Comparing the classification and prediction methods, EvoNet and Time2Graph has a better classification effect than the sequential model X-HMM. Time2Graph models the aggregated static graph, and the EvoNet model performs node-graph interaction during the time graph propagation, making it more suitable for the time modeling of an evolutionary state graph. This indicates that, in future research, we can try to build a graph model to capture the characteristic information of the subsequence, and then carry out label prediction.
Vertical comparison of classification results shows that the Precisionratio of each model is higher than the Recallratio, except for the Djia30 data set, which indicates that the model has a low misjudgment rate for positive events, but it can not comprehensively detect positive events.
By comparing the results of the four labeling prediction methods, Q2 can be answered. The results in Table 2 show that, on all data sets, the prediction performance of the CX-LC model is better than the other three models.
Comparing CX-LC and X-LC, the prediction performance of CX-LC is much higher than that of the X-LC model, which means that, when making labeling predictions, the prediction performance of the model is easily affected by input features. The original data of as input ignore the influence of each subsequence itself on the event, and the mode is the most direct response to the occurrence of the event. Expressing the subsequence as a weighted combination of each mode can effectively extract the important information in the subsequence.
Comparing CX-LC and C-LC, it can be seen that the prediction performance of CX-LC is higher than that of the C-LC model, and feature extraction does improve the prediction accuracy, avoiding the influence of redundant information on the prediction model.
Comparing CX-LC and CX-L, it can be seen that the prediction performance of CX-LC is slightly higher than that of the CX-L model, indicating that considering the transition relationship between events can effectively correct the prediction results of LSTM.
In summary, CX-LC has almost the best performance on different data sets, which also makes CX-LC universally applicable.
3.4.2. Discussion
It is not difficult to find that CX-LC is sometimes better than EvoNet, sometimes worse, but sometimes very similar. In order to further discuss the predictive performance of the two models and analyze their classification ability for different samples, this article discussed the misclassification samples of the two models using PM2.5 data and Djia30 data.
For the prediction task of PM2.5, among the negative samples predicted by CX-LC as positive samples, the top 20 samples with the highest frequency of occurrence are shown in Figure 6. According to this figure, each historical data point used as a prediction sample contains 140 days (20 weeks) of PM2.5 data, with significant fluctuations in the overall sample. Regardless of which stage of the data, there is a high weekly mean. When CX-LC predicts such historical data, it is easy to predict negative samples as positive samples. According to the definition in Section 3.1, positive samples mean a high level of PM2.5. Under the long-term high PM2.5 indicators, relevant departments may control the air, so as to quickly reduce the PM2.5 value in a short time. In this case, the model CX-LC often does not have good strain energy, and how to better predict this sudden change is the focus of future research. Similarly, for the PM2.5 dataset, among the positive samples predicted by CX-LC as negative samples, the top 20 samples with the highest frequency of occurrence are shown in Figure 7. Observing these 20 samples, it can be found that the 140 day long historical data only have significant fluctuations in the middle stage (such as the 19th, 26th, 57th, 101st week, etc.), or is generally relatively flat, with periodic fluctuations and no obvious trend (such as the 171st, 180th, 182nd, 632nd week, etc.). CX-LC has a poor prediction performance for samples with stable fluctuations and low mean values. Compared to predicting negative cases as positive cases, CX-LC is less likely to predict positive cases as negative cases; because the increase in PM2.5 value often takes a certain amount of time, it is rare for the air to suddenly deteriorate, such as an increase in vehicles traveling during holidays and an increase in vehicle exhaust emissions.
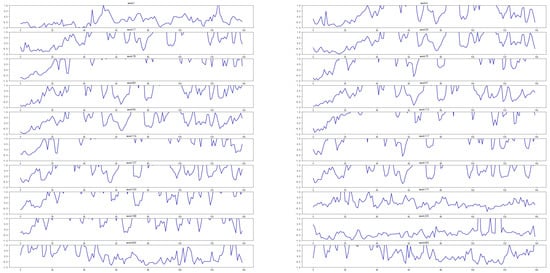
Figure 6.
PM2.5 dataset, negative samples predicted by CX-LC as positive samples.
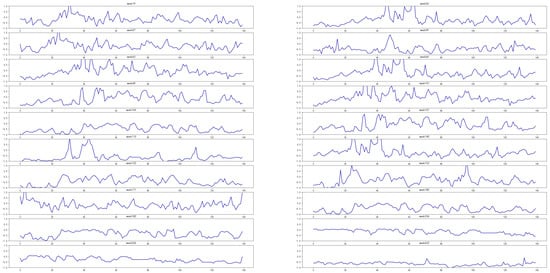
Figure 7.
PM2.5 dataset, positive samples predicted by CX-LC as negative samples.
As shown in Table 2, as a classification model, EvoNet also has a good classification performance on the PM2.5 dataset. To compare with CX-LC, Figure 8 and Figure 9 show EvoNet’s two types of classification errors.
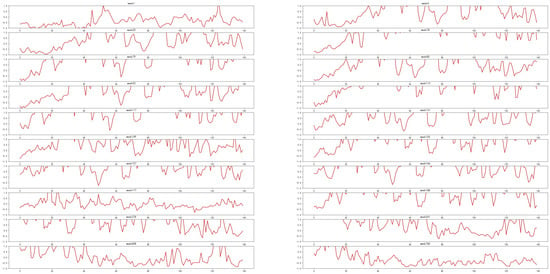
Figure 8.
PM2.5 dataset, negative samples predicted by EvoNet as positive samples.
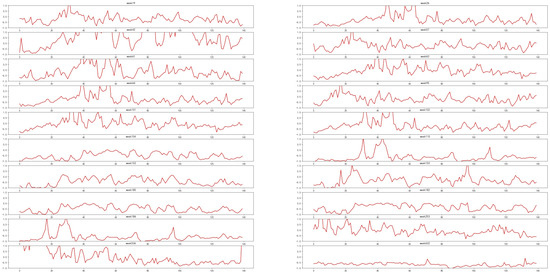
Figure 9.
PM2.5 dataset, positive samples predicted by EvoNet as negative samples.
Observing Figure 6 and Figure 8, it can be seen that both types of models have more difficulty predicting sudden decreases in PM2.5 values. However, compared to EvoNet, CX-LC has a better predictive performance for samples with a slow upward trend (such as weeks 17, 84, 96, 127, 325, etc.). Observing Figure 7 and Figure 9, it can be seen that both types of models have certain shortcomings in predicting sudden increases in PM2.5 values. However, compared to EvoNet, CX-LC has a better predictive performance for samples with smoother fluctuations (such as week 59, week 69, week 336, week 526, etc.). Because CX-LC considers the more remote dependencies of data, when predicting each sample, it not only considers the sample itself, but also considers all previous data. For samples with no obvious or slow trends, CX-LC can make correct predictions based on earlier history.
For small-scale datasets, CX-LC can often achieve better prediction results, but for large-scale datasets, EvoNet has a better prediction performance. To analyze CX-LC’s shortcomings, this article uses the djia30 dataset to discuss sample features. As shown in Table 2, when predicting the djia30 dataset, EvoNet has a higher Precisionratio than CX-LC. Based on this result, the classification performance of the two models for positive cases is discussed. As shown in Figure 10, there are 40 typical positive samples in the djia30 dataset that were misclassified by CX-LC but correctly classified by EvoNet. These samples were misclassified as negative by CX-LC and correctly classified as positive by EvoNet. As shown in the figure, the weekly historical data of this type of sample have significant fluctuations. Due to the length of the historical data being 50, each sample contains a sufficiently rich weekly slope, while the EvoNet model focuses on extracting feature transformations within the sample and training the classifier based on an unordered subsequence set. Therefore, when the sample size is large and the prediction history length is long, it can achieve better results than CX-LC.
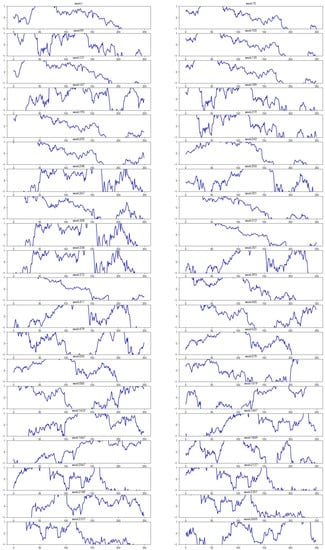
Figure 10.
Forty typical positive samples in the djia30 dataset that were misclassified by CX-LC but correctly classified by EvoNet.
4. Conclusions and Future Work
Based on the idea of sequence labeling, this paper proposed a novel time-series event prediction framework, namely cluster-XGBoost-LSTM-CRF. This model captured the pattern information of subsequences through pattern recognition, and the state of the pattern is the key to determining the occurrence of an event. The labeling prediction of LSTM can capture the interaction between the set of subsequences and the long-term dependencies between events. In order to verify the effectiveness of CX-LC, we conducted extensive experiments on five real-world data sets. Experimental results show that our model is better than other popular benchmarking methods. Based on this, the time-series event prediction problem was transformed into a labeling problem, which can complete the prediction task well. In the five data sets, the CX-LC model has a good prediction effect on the change trend of temperature and air quality, indicating that the model is more suitable for data sets with less human intervention and is relatively stable, so it can be used to provide a relevant basis for atmospheric environmental impact assessment, planning, management, and decision-making. However, for more complex and larger data sets, the prediction effect of such models is poor. How to capture more complex time series patterns and how to solve the problem of uneven samples still needs to be studied.
The CX-LC model is only a preliminary exploration of applying the idea of sequence labeling to the problem of event prediction. The model still has shortcomings, and there are directions that can continue to be explored:
- 1.
- When performing feature extraction of subsequence sets, we can consider the pattern changes between subsequences, construct the pattern evolution diagram, and enrich the feature information;
- 2.
- The LSTM model is a relatively simple and conventional sequence labeling algorithm; only the sequence structure is considered in the calculation process, if the pattern is successfully constructed for the evolution diagram, we can try a more comprehensive network structure, such as GNN, GCN, etc.;
- 3.
- In the event prediction, the periodicity and seasonality of the original data were not considered, although such characteristics can be captured when fitting the CX-LC model. However, if these effects are directly reflected in the structure of the model, it may be able to improve the forecasting progress of the model;
- 4.
- The results of 4.4 show that the performance of CX-LC on small-sample data sets is better than other models, but the prediction effect on large data sets still needs to be improved.
There is still a lot of work to be carried out on how to improve the framework based on sequence annotation to be more suitable for event prediction. In the future, we will also look for better event prediction methods for different types of time data sets.
Author Contributions
Conceptualization, S.L. and Z.Z.; methodology, S.L.; validation, S.L., K.S. and Z.Z.; formal analysis, S.L.; investigation, Z.Z.; resources, S.L. and K.S.; writing—original draft preparation, Z.Z.; writing—review and editing S.L. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some data presented in this study are available in [10].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Variable Description.
Table A1.
Variable Description.
| Variable Symbol | Description |
|---|---|
| The i-th time series sample, which can be expressed as . | |
| is the k-th subsequence of , which can be expressed as . | |
| is the observation event of the k-th subsequence of . | |
| is a D-dimensional observation value of the time-series at time l. | |
| For , use the sliding window method to obtain M data sets containing subsequences from , denoted as . | |
| The m-th subsequence set of , . | |
| Based on subsequence set to predict the event of subsequence . | |
| The representative subsequence pattern in the time-series. | |
| Euclidean distance between states and subsequences . | |
| The probability of recognizing the subsequence as the state . | |
| Each subsequence can be calculated to obtain V identification weights, expressed as . | |
| The feature set of the subsequence set . | |
| The pattern feature of the filtered sub-sequence set is reduced to a Q-dimensional variable, and there is . |
References
- Theunissen, C.D.; Bradshaw, S.M.; Auret, L.; Louw, T.M. One-Dimensional Convolutional Auto-Encoder for Predicting Furnace Blowback Events from Multivariate Time Series Process Data—A Case Study. Minerals 2021, 11, 1106. [Google Scholar] [CrossRef]
- Wang, M.-D.; Lin, T.-H.; Jhan, K.-C.; Wu, S.-C. Abnormal event detection, identification and isolation in nuclear power plants using lstm networks. Prog. Nucl. Energy 2021, 140, 103928. [Google Scholar] [CrossRef]
- Soni, J.; Ansari, U.; Sharma, D.; Soni, S. Predictive data mining for medical diagnosis: An overview of heart disease prediction. Int. J. Comput. Appl. 2011, 17, 43–48. [Google Scholar]
- Arbian, S.; Wibowo, A. Time series methods for water level forecasting of dungun river in terengganu malayzia. Int. J. Eng. Sci. Technol. 2012, 4, 1803–1811. [Google Scholar]
- Asklany, S.A.; Elhelow, K.; Youssef, I.K.; Abd El-Wahab, M. Rainfall events prediction using rule-based fuzzy inference system. Atmos. Res. 2011, 101, 228–236. [Google Scholar] [CrossRef]
- Lai, R.K.; Fan, C.-Y.; Huang, W.-H.; Chang, P.-C. Evolving and clustering fuzzy decision tree for financial time series data forecasting. Expert Syst. Appl. 2009, 36, 3761–3773. [Google Scholar] [CrossRef]
- Molaei, S.M.; Keyvanpour, M.R. An analytical review for event prediction system on time series. In Proceedings of the 2015 2nd International Conference on Pattern Recognition and Image Analysis (IPRIA), Rasht, Iran, 11–12 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Anderson, O.D. The box-jenkins approach to time series analysis. Rairo Oper. Res. 1977, 11, 3–29. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, Y.; Wang, W.; Hu, W.; Zhuang, Y.; Song, G. Time2graph: Revisiting time series modeling with dynamic shapelets. arXiv 2019. [Google Scholar] [CrossRef]
- Hu, W.; Yang, Y.; Cheng, Z.; Yang, C.; Ren, X. Time-series event prediction with evolutionary state graph. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event, 8–12 March 2021; pp. 580–588. [Google Scholar]
- Liu, M.; Huo, J.; Wu, Y. Stock Market Trend Analysis Using Hidden Markov Model and Long Short Term Memory. arXiv 2021. [Google Scholar] [CrossRef]
- Ma, X.; Hovy, E. End-to-end sequence labeling via bi-directional lstm-cnns-crf. arXiv 2016, arXiv:1603.01354. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short term memory networks for anomaly detection in time series. In Proceedings of the 23rd European Symposium on Artifical Neural Networks, Computational Intelligence and Macine Learning, Bruges, Belgium, 22–24 April 2015; Volume 89, pp. 89–94. [Google Scholar]
- Senin, P.; Malinchik, S. Sax-vsm: Interpretable time series classification using sax and vector space model. In Proceedings of the 2013 IEEE 13th International Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1175–1180. [Google Scholar]
- Rakthanmanon, T.; Keogh, E. Fast shapelets: A scalable algorithm for discovering time series shapelets. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; SIAM: Philadelphia, PA, USA, 2013; pp. 668–676. [Google Scholar]
- Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [CrossRef] [PubMed]
- Ailliot, P.; Monbet, V. Markov-switching autoregressive models for wind time series. Environ. Model. Softw. 2012, 30, 92–101. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, J. Hmm-based hybrid meta-clustering ensemble for temporal data. Knowl.-Based Syst. 2014, 56, 299–310. [Google Scholar] [CrossRef]
- Neogi, S.; Dauwels, J. Factored latent-dynamic conditional random fields for single and multi-label sequence modeling. Pattern Recognit. 2022, 122, 108236. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Q.; Yu, B.; Yu, Z.; Lawrence, P.; Ma, Q.; Zhang, Y. Improving protein-protein interactions prediction accuracy using xgboost feature selection and stacked ensemble classifier. Comput. Biol. Med. 2020, 123, 103899. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. A method for stochastic optimization. arXiv 2015. [Google Scholar] [CrossRef]
- Lafferty, J.; McCallum, A.; Pereira, F.C.N. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data; Penn Libraries: Philadelphia, PA, USA, 2001. [Google Scholar]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P. Conditional random fields as recurrent neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1529–1537. [Google Scholar]
- Roth, D.; Yih, W. Integer linear programming inference for conditional random fields. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 736–743. [Google Scholar]
- Chen, X.; Chen, Y.; Saunier, N.; Sun, L. Scalable low-rank tensor learning for spatiotemporal traffic data imputation. Transp. Res. Part C Emerg. Technol. 2021, 129, 103226. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).