1. Introduction
With the continuous increase in people’s requirements for computing power, traditional single-processor systems cannot satisfy the needs of users. Real-time systems are applied on performance asymmetric multiprocessor platforms to meet the high computing needs of users effectively [
1]. A performance asymmetric multiprocessor architecture allows the system to allocate computing resources according to demand and make full use of available fast and slow cores to handle dynamic workload demands; hence, it can improve the performance and reduce the power consumption [
2]. Moreover, it has shown strong performance advantages in some specific applications, such as smartphones, high-end digital cameras, and other electronic devices [
3]. All these high-level products can boost our lives in different aspects. This has also led to the emergence of services such as the Internet of Things, intelligent transportation, and health monitoring, and people’s high computing needs continue to increase. Researchers have conducted a lot of research on this. Irtija et al. proposed an efficient edge computing solution to meet the computing needs of Internet of Things nodes [
4]. Experiments show that the number of satisfied users increases by
with only a
drop in maximum accuracy.
Ensuring the real-time performance of tasks is the most important goal in real-time systems. For real-time systems, optimizing resources and power consumption is important. However, the most important aspect is to ensure the real-time nature of the task. However, current research is still unable to guarantee real-time requirements. This means that the performance asymmetric multiprocessors cannot make full use of the performance in the real-time system [
5].
To track this challenge, researchers have proposed some works. The earliest deadline first (EDF) scheduling algorithm was proposed by Liu et al. [
6]. It is optimal on a single processor. EDF’s computable schedulability test was demonstrated by Baker et al. on homogeneous multiprocessors [
7]. On symmetric multiprocessors, an algorithm that improves the schedulability of non-preemptive tasks was proposed by Lee et al. [
8]. For the global EDF, Zhou et al. obtained a more accurate response time analysis method [
9]. Jiang et al. improved the schedulability of the DAG task system [
10]. Their new approach combines federated scheduling and global EDF.
Now, the field of unmanned vehicle research is very popular, and many large companies have also invested a lot of energy in the research of unmanned vehicles. The Linux kernel is used in many companies’ unmanned vehicle operating systems, such as Tesla’s operating system. The scheduling strategy of the Linux kernel has used scheduling algorithms such as Completely Fair Scheduling (CFS) and EDF. Thus, the study of EDF is very important.
The processor allocation strategy used in previous EDF scheduling algorithms studies on performance asymmetric multiprocessors aims to assign the high-priority tasks to the fastest processors. However, few researchers take the allocation of processors into consideration. To address this issue, we believe that it is possible to assign the high-priority tasks to a suitable or slow-speed processor.
In this paper, we study the different processor allocation strategies of EDF in performance asymmetric multiprocessor platforms. The EDF scheduling algorithm assigns priority according to the deadline of the task, and assigns the processor according to the priority. The fastest speed fit earliest deadline first (FSF-EDF) scheduling algorithm assigns high-priority tasks to the fastest processors. The best speed fit earliest deadline first (BSF-EDF) scheduling algorithm seeks to assign high-priority tasks to the most suitable speed processor. The slowest speed fit earliest deadline first (SSF-EDF) scheduling algorithm seeks to assign high-priority tasks to the slowest speed processor first. Thus, we propose a schedulability test for SSF-EDF. Below are the main contributions of this paper.
We place three EDF scheduling algorithms with different processor allocation strategies together and propose a novel schedulability test strategy for the SSF-EDF algorithm.
Extensive experiments are described to fully explore the performance of these three EDF scheduling algorithms.
The rest of this paper is organized as follows.
Section 2 illustrates the system model and related definitions.
Section 3 describes the schedulability tests for the SSF-EDF.
Section 4 compares EDF scheduling algorithms with three different processor allocation strategies.
Section 5 draws conclusions about the proposed strategy.
2. System Models and Definitions
2.1. Sporadic Task Systems
Let denote sporadic real-time tasks. The execution time of on the slowest processor is denoted as . The relative deadline of is denoted as . The minimum interval time between two task requests is denoted as . Let the set of n tasks be denoted as . If the task satisfies the conditions of , then is considered a restricted set. The job of task is denoted as , and its arrival time is denoted as .
Note that an understanding of the relationship between the execution time and processor speed is critical. The worst execution time is the execution time required by on the processor with speed , which is a fixed value. Since we conduct research on performance asymmetric multiprocessor platforms, different processors do not have the same speed. Processors with different speeds perform differently at the same time. Therefore, the actual execution time required by on different processors is not the same. In the following, we need to take into account the effect of processor speed when calculating the execution time.
The processor utilization of task
is defined as
.
represents the maximum utilization among all tasks:
The density of task
is defined as
.
represents the maximum density among all tasks:
is used to represent the upper limit of the maximum cumulative processing time required for task
’s job to arrive at and within a time interval of length
. Among them, the size of
can be arbitrary. This has been proven by Baruah [
11]:
The load parameters based on the DBF function are defined as follows [
12]:
2.2. Performance Asymmetric Multiprocessor Platform
Let
be a performance asymmetric multiprocessor platform. The processing speed of the processors increases from small to large; that is, the processing speed of
is equal to or slower than that of
. The processor speed of the processor is denoted by
. For ease of understanding, the slowest processor speed is set to 1, which is
. The other, faster processors
are multiples of
, such as
. The sum of the speeds of the first
k processors in
is denoted as
, i.e.,
The “lambda” parameter was defined by Funk et al. in their research on a uniform multiprocessor [
13,
14]:
The value range of is . When all processors are the same, takes the maximum value .
The main symbols used in this article and their meanings are summarized in
Table 1.
2.3. SSF-EDF Scheduling
SSF-EDF assigns high priority to tasks with early deadlines. We also chose a global scheduling strategy. We establish a global ready task queue and extract tasks for scheduling according to demand. Our algorithm allows the preemption of tasks and allows tasks to be migrated between processors of different speeds. In reality, this migration introduces additional overhead. We measure this overhead by considering the number of task migrations in our experiments. The time complexity of the SSF-EDF scheduling algorithm is O(mn), where n is the number of tasks and m is the number of processors. According to the time complexity, it can be seen that SSF-EDF is used in real-time systems.
The SSF-EDF scheduling algorithm operates on a performance asymmetric multiprocessor as follows: (1) when there is an active job waiting to be executed, no processor is idle; (2) fast processors are idled when the number of processors is greater than the number of active jobs; (3) we execute higher-priority jobs on slower processors.
A given set of sporadic tasks is SSF-EDF schedulable if SSF-EDF scheduling is able to meet the deadlines of all jobs for the given set of sporadic tasks on a given platform. We will derive a schedulability test for SSF-EDF in
Section 3. This can guarantee the schedulability of SSF-EDF.
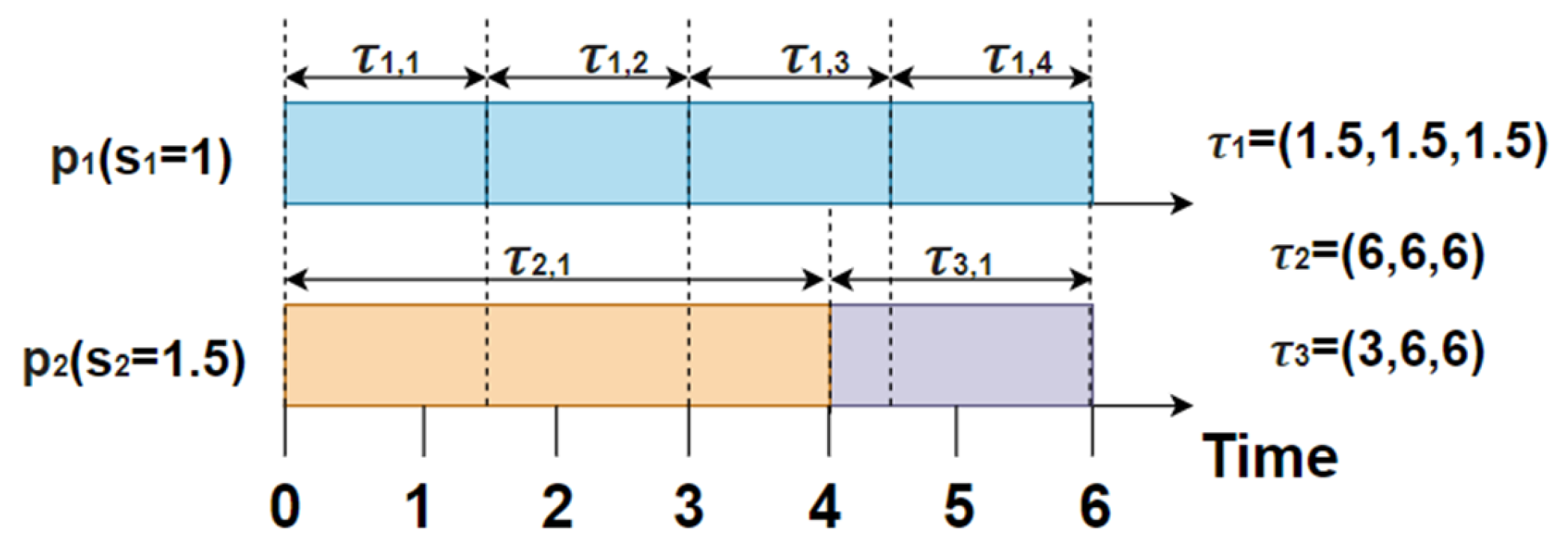
Example 1. Figure 1 is an example of SSF-EDF on the performance asymmetric multiprocessors. Task is represented by a triple . Consider and . Different colors indicate different tasks. First, obtains the highest priority, executes on the slowest processor , and executes on . At , job is done. However, makes another request, which is still executed on . Up to time , job is done. Since does not have a higher priority than , is assigned to processor for execution until the job is done. It is easy to see that under the framework of SSF-EDF, all tasks will meet their deadlines and the processor will reach utilization. 3. SSF-EDF Schedulability Analysis
We derive a schedulability test for SSF-EDF scheduling. Our derivation process follows the following idea: under SSF-EDF scheduling, the necessary conditions for task missed deadlines are derived. In negating this condition, the sufficient schedulability condition is obtained.
Suppose that job
of task
first misses the deadline at
(see
Figure 2). Under SSF-EDF scheduling, jobs with late deadlines will not affect jobs with early deadlines. Therefore, we give up the legitimate job sequence whose deadline is later than
, and only consider the SSF-EDF scheduling of the job request of the remaining legitimate sequence. Thus,
missed deadline occurs at time
(which is the earliest task missed deadline to occur).
For a given task set , let be the amount of processor time required within , and let be the amount of work done in .
Our derivation process has the following three steps: (1) to derive the lower bound of in , (2) to derive the upper bound of in , (3) combining (1) and (2) yields the necessary condition. in the figure is a special time point, which we will explain later.
3.1. Lower Bound
Consider that first misses the deadline at . Assume that under SSF-EDF scheduling, there are exactly v processors in whose execution time is denoted by , . For example, represents the time at which only one processor is executing, and represents the time at which two processors are executing. Please note that the value of is not necessarily zero, because there are situations where all processors are idle. However, this work has already assumed that missed the deadline. Thus, within , at least one processor will be processing . In this case, the value of must be zero.
Above, we have mentioned the need to consider the effects of processors of different speeds. Let the execution time
of the
v processors being executed be multiplied by the sum
of the speeds of these processors. We have obtained the actual workload performed by
v processors through
. For example, there are two tasks assigned to the processors
and
, respectively. Let the execution time
, and then the actual workload is
. Then, we can write
Because of
and
, we obtain
As defined by
in
Section 2.2, when
, it is obvious that
From (8) and (9) above, we can draw a conclusion
Due to the nature of SSF-EDF, except when all processors are busy, during time interval
,
will be assigned to a processor with speed
,
. Then, the worst execution time
of
. Moreover, since
missed the deadline, it cannot receive more execution time than
; otherwise,
can finish before the deadline, which contradicts the previous assumption. Therefore, we obtain
Combining (10) and (11) gives
From (12) and (13), it follows that
We can find many time points
t that satisfy condition
.
is the earliest one among all time points
t that satisfy the condition. At
,
still holds. This leads to
. Hence, the lower bound of
has been deduced. Let
. Then, we obtain
According to the previous assumption, job
misses the deadline
. That is, the total workload
W is less than or equal to the time requirement
Q. It can be concluded
Now, we find that the lower bound of is .
3.2. Upper Bound
Before derivation, we need to classify the job. Carry-in jobs are jobs that arrive before and are not completed before . The total processor time requirement caused by these jobs is denoted by . Other jobs are regular jobs. The total processor time requirement caused by this job is denoted by . The sum of these two time demands is the that we need.
The study of Baruah et al. shows that
can calculate the upper bound of
[
11,
12]. LOAD and DBF are defined as follows:
Let us calculate the upper bound of again.
Lemma 1. The remaining execution requirement at time for any carry-in job is lower than .
Proof. Let us analyze the carry-in job
whose arrival time is
and whose execution is not completed at time
(see
Figure 2). Let
. Let
be the execution time of
within time interval
.
continues to use the same definition as in
Section 3.1.
can be calculated from
. Since job
did not complete execution at time
, we can conclude
Since
, there is
It is given by (18) and (19)
According to the definition of
(see (15)), it must satisfy
Since
is the earliest time
t satisfying such conditions, any time
t before
does not satisfy the above formula, i.e.,
This is given by (20) and (23)
By combining (6), we have
With the exception of the case wherein all processors are busy, the carry-in job
must be executed on one of the processors. Since
is not completed before
, the worst execution time of
is not less than the execution time in
. Among them, the execution time of
in
is at least
. Thus, we have
It is given by (25) and (26) that
It is also given by (13) and (27) that
Since
, there is
Because
missed the deadline at
,
’s absolute deadline is no greater than
. We can write
. Thus, we have
□
Therefore, any carry-in job contributes no more to than .
Lemma 2. The number of carry-in jobs depends on Proof. Suppose that an arbitrarily small positive number is represented by
, as shown by (21) and (22),
Infer from the definition of . Thus, we obtain the conclusion of . Therefore, some processors are idle during . All the carry-in jobs are being executed. Thus, the number of carry-in jobs does not exceed . □
Consequently, the upper bound of is .
Therefore, the upper bound of
can be expressed as
3.3. SSF-EDF Schedulability Test
Theorem 1. Sporadic task set Λ
is SSF-EDF schedulable on a performance asymmetric multiprocessor platform π, provided thatwhere μ and β are defined in (13) and (31), respectively. Proof. A sufficient condition for SSF-EDF schedulability arises by negating the necessary condition for missing the deadline.
From the previous discussion, the bounds for
are as follows:
From this, the necessary conditions for
to miss the deadline are as follows:
Therefore, negation of (36) gives
This is Theorem 1. □
4. Experimental Evaluation
In this section, we implement several schedulability tests and compare their performance through extensive simulations. In the first set of experiments, we demonstrate that BSF-EDF has the best schedulability. Then, we further verify that BSF-EDF schedules more task sets than the other two processor assignment strategies. Then, we find that as the proportion of fast processors increases, so does the proportion of the task set that the algorithm can schedule. We also compare the number of task migrations and effective processor utilization (EPU), where SSF-EDF performs best.
We randomly generate various parameters on a performance asymmetric multiprocessor platform
. The total number
m of processors is randomly selected from a range of
. While satisfying
, the number
q of the slowest processors is also selected from the same range. The speed of the processor is randomly generated within
.
Table 2 is the parameter range for each task. We generated
task sets, and each task set contained
tasks.
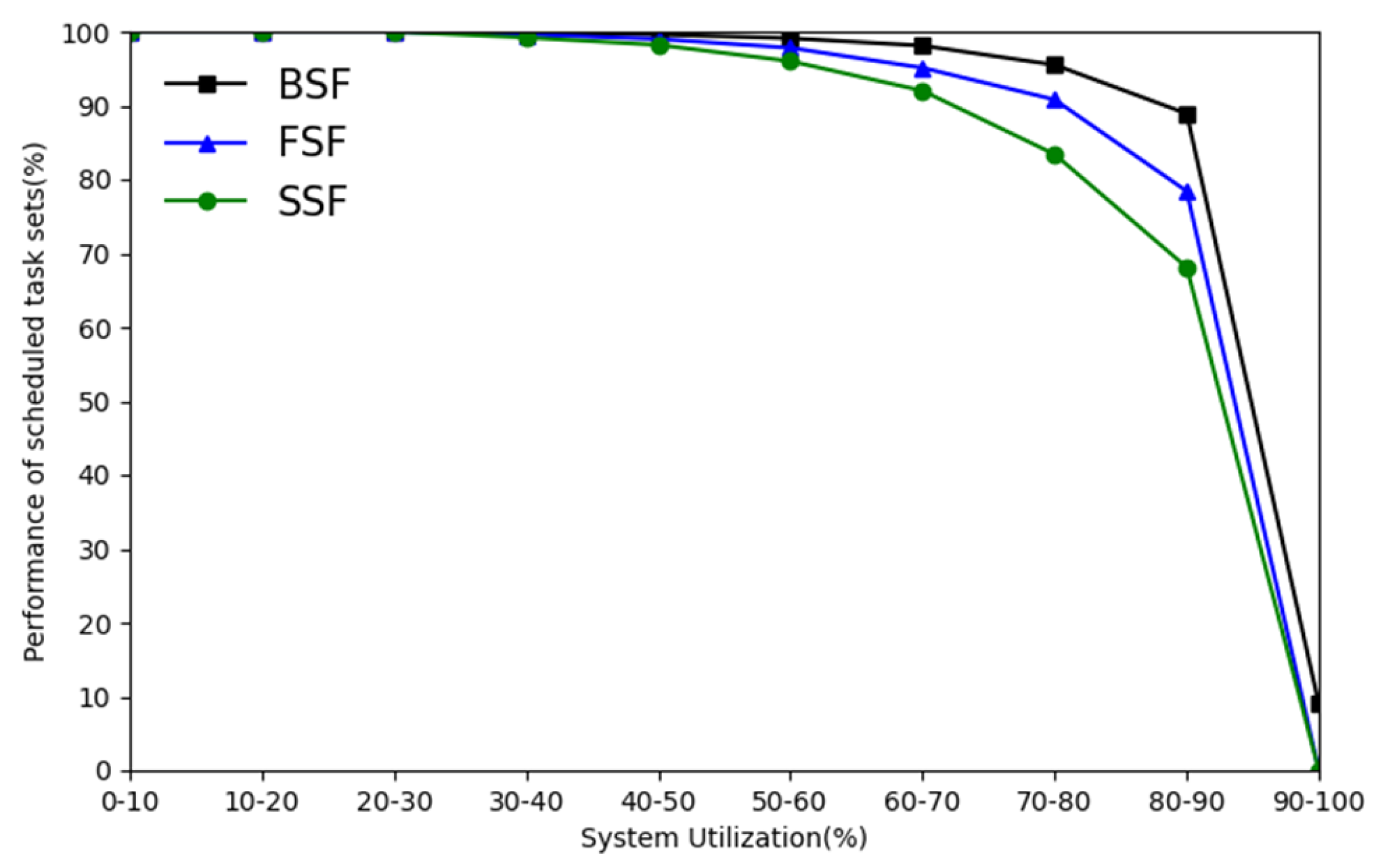
Figure 3 shows that BSF-EDF performs better than FSF-EDF and SSF-EDF on four-core performance asymmetric multiprocessors. The results show that the schedulability of BSF-EDF is the highest for different system utilization cases. The
X-axis represents the system utilization rate, and the system utilization rate is defined as
. When the system utilization rate reaches 40–50%, the task set that can be scheduled by the three processor allocation strategies begins to decrease. When the system utilization reaches 80–90%, BSF-EDF can still schedule up to
task sets, while the other two processor allocation strategies can only schedule
and
task sets. After this, the proportion that the algorithm can schedule decreases rapidly. When the system utilization reaches 90–100%, the three processor allocation strategies can only schedule
,
, and
task sets.
Figure 4 shows the experimental results on seven-core performance asymmetric multiprocessors. When the system utilization is low, the three algorithms perform well. BSF-EDF performs better than the other two processor allocation strategies at high system utilization. When the system utilization reaches 80–90%, the BSF-EDF can schedule up to
of the task set, which is lower than the performance on four-core processors. However, it still schedules
and
more task sets than the other two processor allocation strategies. When the system utilization reaches 90–100%, the three processor allocation strategies can only schedule
,
, and
task sets.
When
, the experiment further verifies the leading position of BSF-EDF. In
Figure 5, BSF-EDF outperforms the other two processor allocation strategies at high system utilization. When the system utilization reaches 80–90%, the BSF-EDF can schedule
of the task set, which is lower than the performance on seven-core processors. However, it still schedules
and
more task sets than the other two processor allocation strategies. When the system utilization reaches 90–100%, the three processor allocation strategies can only schedule
,
, and
task sets.
In the first set of simulation experiments, we did not limit the number of high-utilization tasks in the task set, and the data were generated randomly. Now, we limit the proportion of high-utilization tasks in the task set, in which we define high-utilization tasks as a utilization rate of 80–100%. When the proportion of high-utilization tasks is high, the range of system utilization is bound to be limited by its definition. It is difficult to compare the performance of the three different processor allocation strategies under different system utilization values. Therefore, we choose
of high-utilization tasks to conduct experiments on 10-core performance asymmetric multiprocessors. In
Figure 6, the performance of the three different processor allocation strategies is again degraded, but BSF-EDF still schedules more task sets than the other two processor allocation strategies. When the system utilization reaches 80–90%, the three processor allocation strategies can only schedule
,
, and
task sets. When the system utilization reaches 90–100%, the three processor allocation strategies can only schedule
,
, and
task sets.
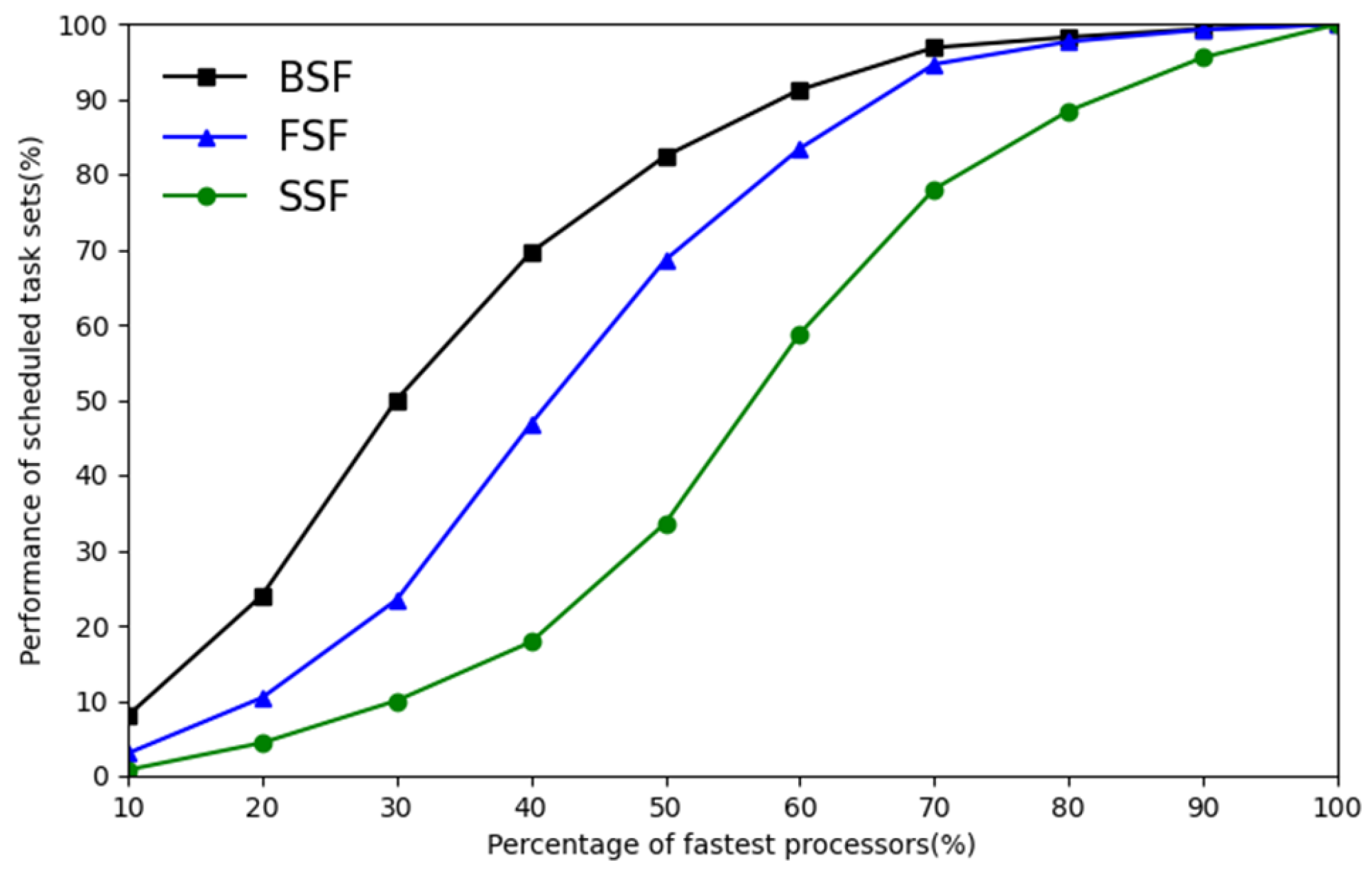
We compare the three processor allocation strategies by modifying the proportion of fast processors on a 10-core performance asymmetric multiprocessor. In
Figure 7, with the increasing proportion of fast processors, the schedulable task set ratio of the three processor allocation strategies also increases, among which BSF-EDF increases the fastest. When the fast processor ratio reaches
, all processors are at the same speed. In this case, the scheduling process of the three different processor allocation strategies is not different, so the three algorithms can schedule
of the task set.
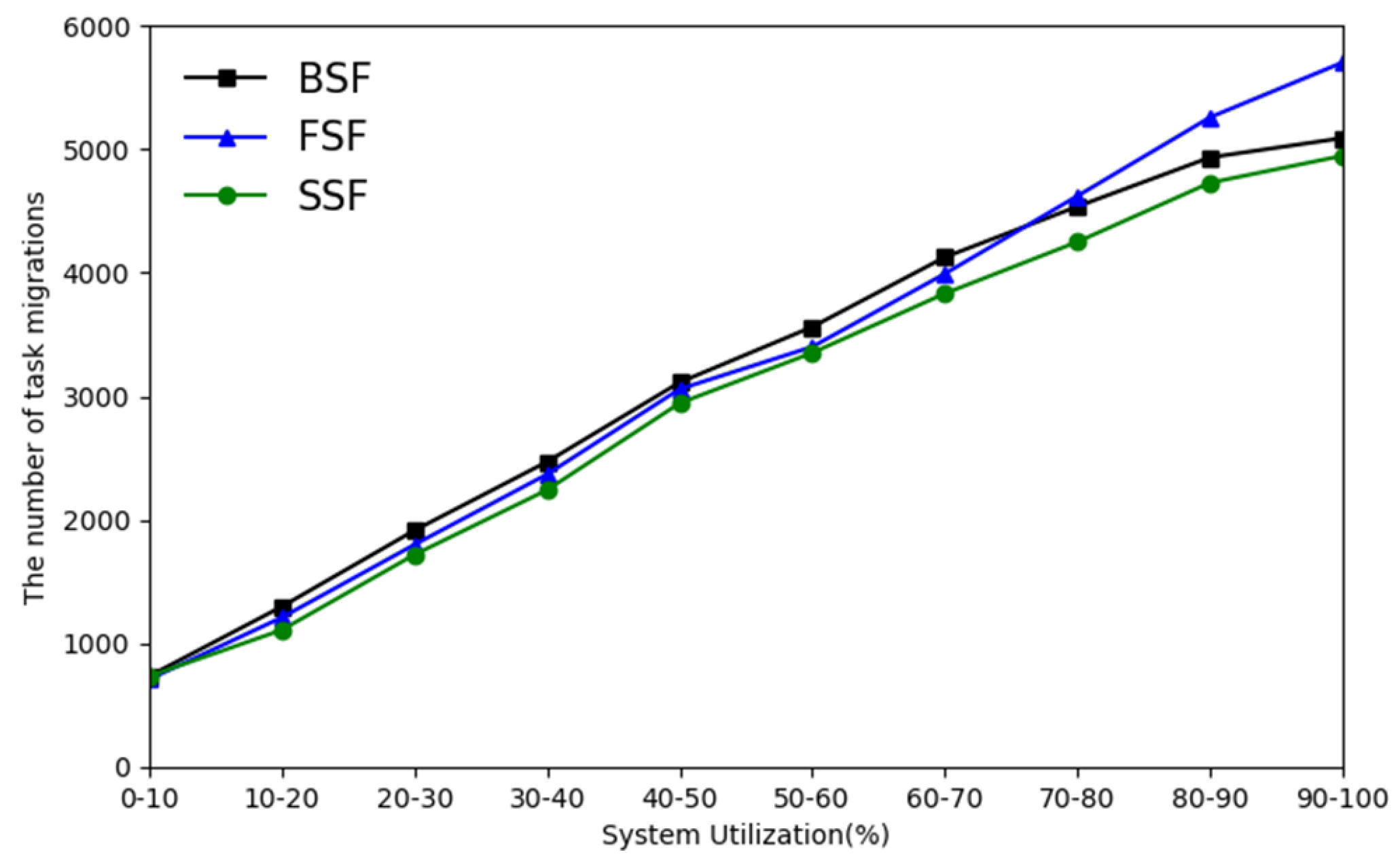
Since we allow the preemption of tasks, it is important to consider the overhead of task migration. We measure this overhead by the number of task migrations. We conduct experiments on a 10-core performance asymmetric multiprocessor. In
Figure 8, the number of migrations of SSF-EDF is the least for different system utilization cases. BSF-EDF has the most migrations when the system utilization is low. When the system utilization exceeds 70–80%, FSF-EDF has the most migrations.
Effective processor utilization (EPU) is defined as
[
15]. If the job is completed within its deadline, the value of
V is equal to the execution time of the job; if the job misses the deadline,
.
is the set of tasks that the processor executes.
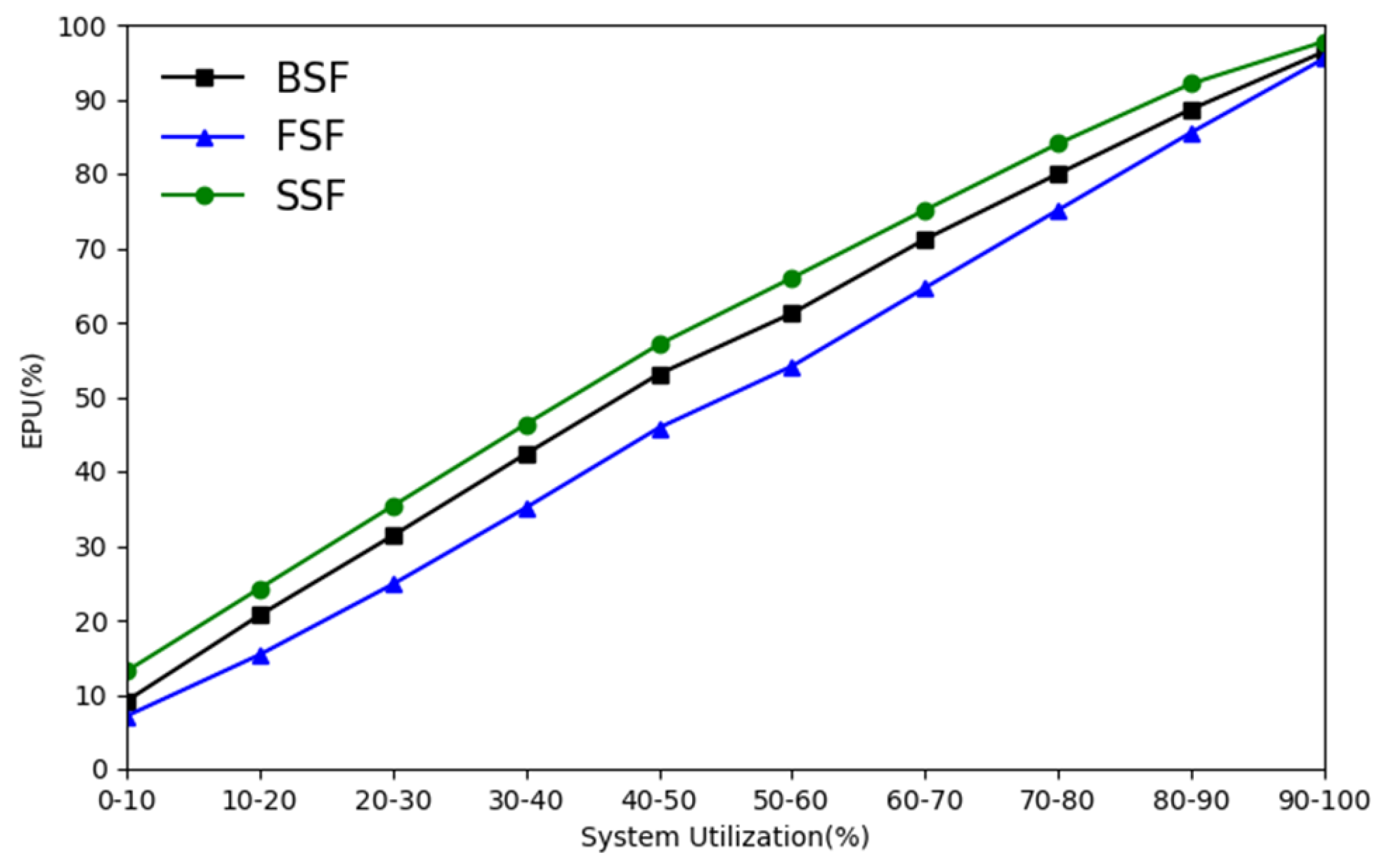
P is the total time of execution. The level of EPU reflects the level of effective utilization of the processor by the scheduling algorithm. In
Figure 9, for different system utilization rates, the EPU of SSF-EDF is the highest. This means that SSF-EDF is more efficient for processor utilization.