Abstract
A time-scale varying finite difference method (TSFDM) was proposed to analyze the influence of rainfall infiltration and water level fluctuation on the stability of a bank slope in the Yunnan Pulang tailings pond. The stability of the slope obtained by the TSFDM and the limit equilibrium method (LEM) were compared. The result indicates that the TSFDM can obtain reliable spatiotemporal variation features of geotechnical parameters of the bank slope under different conditions. The water level fluctuation has a greater impact on the stability than rainfall infiltration. In addition, the safety factor decreases as the shear strain rate increases on the weathering interface. The safety factors under all conditions are smaller than one, so corresponding measures should be taken. The research provides references for preventing disasters caused by bank slope failure.
1. Introduction
Many methods have been proposed to evaluate the stability of bank slope, such as limit equilibrium method (LEM) and limit difference method (LDM). A stability analysis based on LEM cannot constrain the evolution characteristics of the slope stress and strain during slope failure [1] (Chen, 2014). A time-varying analysis method was proposed to analyze the temporal and spatial changes of the mechanical properties of engineer objects [2]. This method focuses on the change of pore water pressure over time, but pays little attention to the change of safety factors. Zhang et al. [3] established a time-varying analysis model for slope stability on the basis of Geostuido, and replaced the traditional independent safety factors with the safety factor curve, but using the safety factor alone can hardly assess the accuracy of the results. Jiang et al. [4] improved the FISH function in the FLAC3D software, and studied the three-dimensional evolution features of the seepage field of the unsaturated slope under rainfall infiltration, but little on the slope mechanism. At present, many secondary developments have been added to FLAC3D software, and they concentrate on establishing constitutive models of rock-soil mass [5,6,7], but rarely consider the time series analysis of slope safety factors. These related studies either use LEM to explore the time-varying characteristics of slopes, or use the finite difference method to calculate the safety factor of the slope at a single time. However, the finite difference method is rarely used to analyze the stability in a long time span and with a small time interval, especially for tailing pond bank slopes.
In this study, a time-varying analysis method (TSFDM) is proposed for analyzing slope stability based on the finite difference method. We use Python to improve the FISH function in the TSFDM. The improved FISH function can analyze the temporal change features of the unsaturated slope seepage and numerically simulate the slope under rainfall, water level changes and a combination of the two conditions.
2. Method
2.1. Shear Strength Theory of Unsaturated Soil
This paper adopted the shear strength formula based on the dual stress variable strength theory from [8], as follows:
is the soil shear strength; and are the effective cohesion and effective friction angle, respectively; is the void water pressure; is the void air pressure; and is the matrix suction internal friction angle.
When the soil becomes saturated, the pore water pressure and pore gas pressure are similar, that is, − tends to be 0. In such case, the matrix suction term in Formula (1) is equal to 0, and the shear strength formula of unsaturated soil is the same as that of saturated soil.
2.2. Principle of TSFDM
In the TSFDM, Darcy’s law is used for analyzing the changes of the seepage field. Formula (2) describes the relationship among saturation, fluid pressure and fluid volume change [9]:
where is the Biot modulus; is the porosity of the porous medium; is time; represents the fluid volume change in the porous media per unit volume. From Formula (2), we can derive the formula describing the pore water pressure of saturated soil, by setting the saturation degree as 1.0 (FLAC3D, 2012), which is:
For calculating the saturation degree of the unsaturated soil, the pore water pressure on the node is set as 0, so the node saturation degree is
As Formulas (3) and (4) show, obtaining the relationship between saturation degree and negative pressure is important for calculating the permeability of unsaturated soil. The saturation degree can be used to obtain the permeability coefficient in the unsaturated zone. In the calculation, we adjusted the unit permeability coefficient to analyze the seepage process in the unsaturated zone.
2.3. Strength Reduction Method
The strength reduction method assumes that the slope failure shows as the shear failure of rock mass if the external load remains the same. So the geotechnical parameters are adjusted as follows:
where and are the initial cohesion and internal friction angle of rock mass, respectively; and are those with the reduction coefficient . The implementation of strength reduction method varies over software, and its implementation process in TSFDM can be found in Song et al. [10].
2.4. Improvement of FISH Function
For pores with negative pore water pressure (matrix suction) above the infiltration line, the TSFDM automatically sets their pore water pressure as 0. Then the permeability coefficient is a constant. However, this is unreasonable, as the permeability coefficient of the rock-soil mass in the slope is not a constant, but changes with the saturation degree and porosity. The permeability coefficient can be expressed by the Van Genuchten model that describes the soil water characteristic curve and the permeability of unsaturated slope [11].
where θ, and are the corrected, residual and saturated volumetric water content, respectively; represents the corrected saturation degree, is the residual saturation degree, , and are the fitting parameters. Formula (8) expresses the relationship between the relative permeability coefficient and saturation degree, from which we can derive Formula (9). , and are the saturated, relative and corrected permeability coefficients, respectively. The following analysis is based on Formulas (6)–(9).
The shear strength parameters of saturated and unsaturated soil are quite different, so we improved the FISH function to analyze the shear strength changes in the saturated and unsaturated slope separately. The function can adjust the shear strength parameters automatically according to the pore water pressure [12].
The specific improvements are as follows:
(1) Set the fluid tensile strength threshold, which allows the nodal flow outflow and forms a negative pressure zone during the seepage calculation.
(2) The pore water pressure changes with the hydraulic boundary. Use the built-in variable zone.pp (xcz) to obtain the unit negative pore water pressure, and then calculate the unit saturation degree by Formula (7). Distribute one constitutive model and the initial shear strength parameters to each unit.
(3) Substitute the obtained unit saturation to Formula (8) to calculate the unit relative to permeability coefficient, and then arrive at the corrected unit permeability coefficient by Formula (9). Meanwhile, adjust the unit shear strength parameters according to the pore water pressure.
Figure 1 shows the flowchart using the FISH function to calculate the unit permeability coefficient and shear strength parameters of the unsaturated soil.
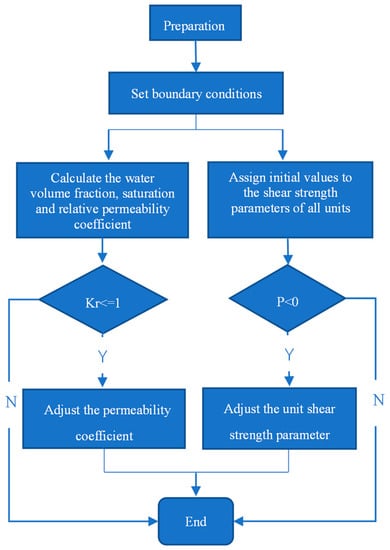
Figure 1.
Flowchart for calculating the unit permeability coefficient and shear strength parameters of the unsaturated slope using the FISH function.
2.5. Development of the FISH Program
In the time-varying analysis of the tailings pond slope stability, when setting the boundary conditions we should consider their changes over time. According to the improved FISH function, the hydraulic boundary conditions change over time, and the TSFDM generates a seepage field file every two steps [13]. If the time interval is small and the time span is large, the generated seepage field files are abundant. These seepage field files are input to the stress field module for analysis. The obtained stress-strain field is then adopted in strength reduction to calculate the safety factor with Formula (5). To obtain the safety factor for each period, the seepage field file should be restored repeatedly, but the original FISH function cannot restore the seepage field file by batch, so we improved the FISH function by Python programming.
We used Python to realize the slope stability analysis in TSFDM as follows (Figure 2):
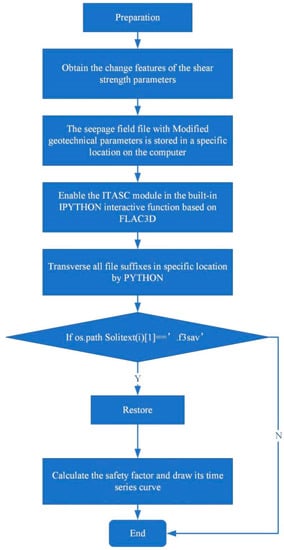
Figure 2.
Flowchart for analyzing the bank slope stability.
(1) Use the improved FISH function to obtain the seepage field changes in each unit time under the condition of the pond water level change and rainfall, and store it in a specific location.
(2) Traverse all seepage field files (.f3sav) in a specific location on Python, which are called into the ITASC module in the Ipython console. Restore all seepage field files in batches and input the pore water pressure field.
(3) Set the mechanical boundary. Use the FDSRM to calculate the safety factor corresponding to the seepage field at each unit time. Finally, the safety factor curve is used to analyze the slope stability of the tailing pond.
2.6. Establish a Finite Difference Model
This study analyzed the bank slope of a tailing pond in Yunnan Pulang mine. The slope is 160 m high, 368 m wide, and 10 m thick (Figure 3a). We established a numerical simulation model for the slope (Figure 3b). The model is composed of hexahedral mesh elements, with 8867 nodes and 11,018 units. The slope has 3 stratum layers (Ⅰ: Gravel soil (GS), Ⅱ: Strongly weathered carbonaceous slate (SWCS), and Ⅲ: Weathered carbonaceous slate (WCS). The geological parameters from survey data are shown in Table 1. The Mohr Coulomb criterion was adopted as the material failure criterion. The bank slope stability was calculated by the TSFDM and the Morganston-Price based LEM method, separately [14].
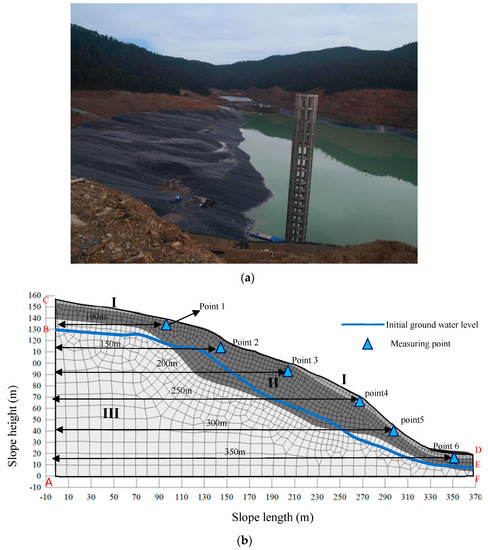
Figure 3.
Actual photos and numerical model of the trailing pond slope. (a) Actual photos. (b) Numerical simulation model.

Table 1.
Geological parameters of the pond bank slope.
As Figure 3 shows, AB and FE are the fixed water level boundaries, which are 130 m and 10 m high, respectively. The initial groundwater level was determined according to the survey data. CD is the rainfall infiltration interface, AF is the impervious boundary, and BC and DE are the pervious boundaries. To study the seepage characteristics, we selected 6 measuring points (points 1–6) 10 m below the surface.
We focused on the seepage changes under the impacts of rainfall infiltration and pond water level fluctuation [14]. The boundary conditions of the slope surface should be adjusted timely to simulate the seepage field changes and slope seepage. In Figure 4, we simulate the separate and coupled influences of hourly rainfall and groundwater level changes on the slope stability from 0:00 on 1 April to 0:00 on 27 July 2019.
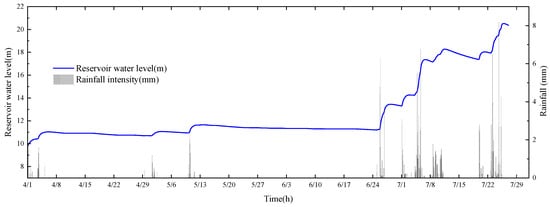
Figure 4.
Rainfall and reservoir water level of the trailing pond during 1 April 2019 and 29 July 2019.
3. Results
3.1. Temporal Changes of the Seepage in the Saturated and Unsaturated Slopes
Figure 5a shows the seepage field of the bank slope on 1 April. Negative pore water pressure appears in the area above the initial water level. The shear strength parameters above and below the water level are different. As all strength parameters are stored in one unit, only the distribution of gravity is shown in Figure 5a. Figure 5b is the seepage field of the slope on 27 July. We adjust the strength parameters of saturated and unsaturated slopes to obtain the gravity distribution in Figure 5b. After the rainy season the seepage change continues, resulting in a variation of shear strength parameters [15].
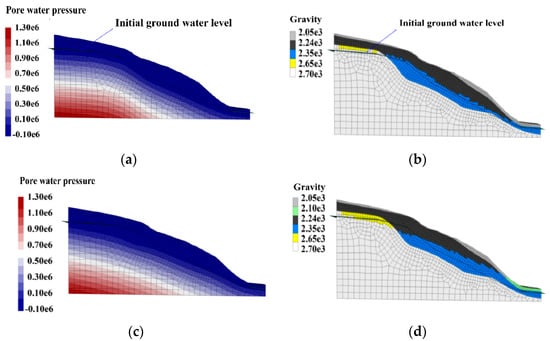
Figure 5.
Variation of pore water pressure and gravity distribution on (a,b) 1 April and (c,d) 27 July 2019.
3.2. Impacts of Real Rainfall and Pond Water Level Changes on Slope Stability
We analyzed the impacts of real rainfall, pond water level changes, and the combined impacts on the slope stability [16]. The results are shown in Figure 6, Figure 7 and Figure 8. In these figures, “by FDSRM” means the results obtained by the improved FISH function and the FDSRM, and “by LEM” means the results obtained by the Morgenston-Price based LEM method. If the two results are close, the stability analysis procedure is reliable.
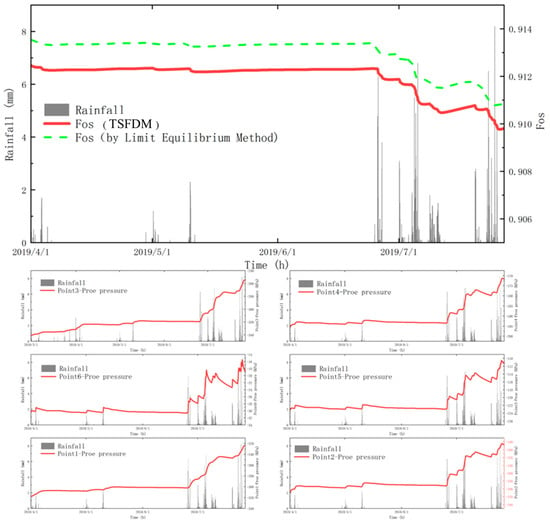
Figure 6.
The impact of rainfall on slope safety factor and pore water pressure at the monitoring points. FOS stands for factor of safety.
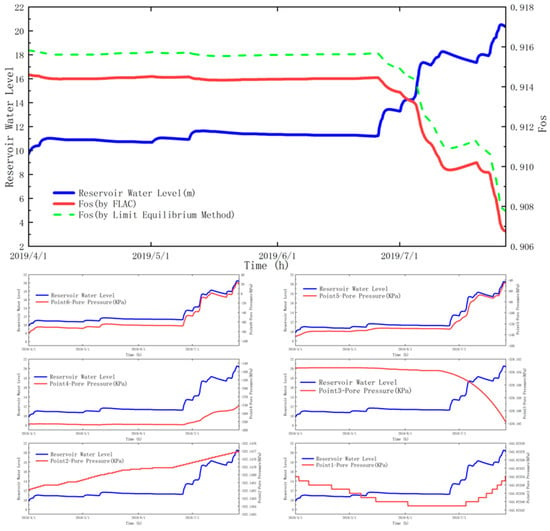
Figure 7.
The impact of the pond water level on the safety factor and the pore water pressure at the monitoring points.
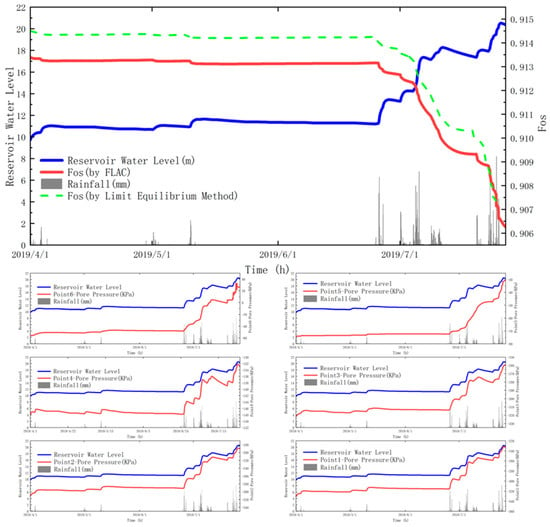
Figure 8.
The coupled impacts of rainfall and pond water level on the safety factor and the pore water pressure at the monitoring points.
Figure 6 shows the slope safety factor and the pore water pressure at the monitoring points under the real rainfall data. The slope safety factor is negatively related with the rainfall, that is, it decreases with the increasing rainfall and goes up when the rain stops, but the pore water pressure of the six monitoring points is related to the rainfall infiltration. Point 5 and Point 6 at the slope toe near the gravel pile are sensitive to the pore water pressure. After penetrating the slope body, the water will flow to the toe, which will increase the pore water pressure.
Figure 7 reflects impacts of water level change on the slope stability. The pore water pressure at Points 4–6 at the slope toe correlates to the pond water level. The closer the point to the water, the stronger the correlation. Points 1–3 are far away from the water, so their pore water pressure changes slightly (≤0.01%) with the water level.
Figure 8 shows the combined impacts of rainfall and water level on the slope stability. The increase of water level enhances rainfall infiltration and further reduces the bank slope safety factor. In addition, the rainfall infiltration raises the water level. The changes of water level have greater impacts on the safety factor than that of rainfall, as the pore pressure changes at Points 1–3 under the coupled condition are similar to that under only the water level change.
4. Discussion
Using the proposed time-scale varying finite difference method (TSFDM), we calculated the safety factor of the bank slope of a tailing pond from 1 April to 27 July 2019, considering the rainfall and pond water level change (Figure 9). On 1 April 2019, under the impacts of both rainfall and water level changes, the safety factor was 0.914, and the potential sliding surface was in the middle and lower part of the slope, across the strongly weathered carbonaceous slate and gravel soil (Figure 9a).
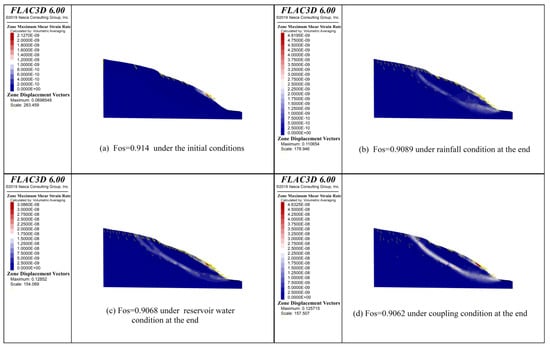
Figure 9.
The bank slope safety factor calculated by the TSFDM and the displacement vector (a) under the initial conditions, (b) under the rainfall impact alone at the end of the observation, (c) under the pond water level change impact alone at the end of the observation, and (d) under the impacts of both conditions at the end of the observation.
On 27 July 2019, affected by rainfall alone, the safety factor was 0.9089 (Figure 9b). A new shear strain surface was formed on the weathering interface of carbonaceous slate. The rear part of the slope was in tension [17]. The strongly weathered carbonaceous slate and gravel soil front above the weathering zone have an obvious downward trend. This is because the rock and soil above the weathering zone were deformed under the effects of rainwater seepage, softening, and suspension. The safety factor is smaller than that in April, which requires attention [18].
On 27 July 2019, impacted by the pond water level change alone, the safety factor of the bank slope was 0.9068 (Figure 9c). The water level changes softened the rock-soil mass on the weathering zone. The shear strain rate of the weathering zone increased, and some parts of the front edge of the bank slope became unstable [19,20].
As Figure 9d shows, at the end of the observation period, under the combined impacts of rainfall and water level change, the slope safety factor was 0.9062. The weathering zone had softened seriously, and the shear strain rate of the weathering zone increased significantly. Some parts of the front edge of the bank slope became unstable, requiring treatments [21].
The safety factor calculated by TSFDM was generally smaller than that calculated by LEM. This is because the TSFDM underestimates the shear strength parameters of the saturated slope, which is in line with reality, but the LEM uses the parameters of unsaturated slope, generating larger shear strength parameters, and a higher safety factor. The program automatically reads the slope seepage field file by batch, performs finite difference calculation, and realizes the intelligent calculation of the geological model. Using TSFDM to study the slope stability of a tailings pond under heavy rainfall and water level fluctuations obtains the evolution features of the stress and strain of the weathering zone and gravel belt [22].
5. Conclusions
This paper proposed a time-scale varying finite difference method (TSFDM) to analyze the influence of rainfall infiltration and water level fluctuation on the stability of the bank slope in the Yunnan Pulang tailings pond. We used Python programming to improve the FISH function in FLAC3D. The improved function can adjust the shear strength parameters of rock-soil mass according to pore pressure, and also solve the restoration failure in the old FISH function. Using the improved FISH function for the numerical simulation of the tailing pond slope can greatly reduce the code operation time and achieve long-time and high frequency stability monitoring.
The TSFDM was compared with the LEM in calculating the safety factor of the tailing pond slope. The results are similar, so the TSFDM is reliable. The TSFDM gets a smaller result, which is in line with reality and can better reflect the stress and strain evolution of the slope.
Compared with rainfall, water level fluctuation has a greater impact on the safety factor. The safety factor decreases with the increase in the shear strain rate of the weathering zone. The potential sliding surface goes through the bottom of the gravel soil and the weathering zone of carbonaceous slate. The safety factors under different conditions are all smaller than 1, so corresponding measures should be taken. For example, spraying waterproof concrete on the slope surface to reduce the infiltration of water on the one hand and strengthen the stability of the slope on the other.
Author Contributions
Conceptualization, G.Z. and G.L.; formal analysis, C.X. and T.L.; writing—original draft, D.B. and G.L.; writing—review and editing, G.Z. and T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China under Grant No. 41974148 and Grant No. 52004327; Hunan Provincial Key Research and Development Program, Grant No. 2020SK2135; Natural Resources Research Project of Hunan Province, Grant No. 2021-15; and Science and Technology Project of Hunan Provincial Department of Transportation Grant No. 202012.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source data can be obtained in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, G.Q.; Huang, R.Q.; Shi, Y.C.; Xu, Q. Stability Analysis of Slope Based on Dynamic and Whole Strength Reduction Methods. Chin. J. Rock Mech. Eng. 2014, 33, 243–256. [Google Scholar]
- Cao, Z.Y. Construction mechanics and time-varying mechanics in civil engineering. China Civ. Eng. J. 2001, 34, 41–46. [Google Scholar]
- Zhang, D.; Jian, W.B.; Ye, Q.; Lin, W. A time-varying analytic model of tailings slope and its application. Rock Soil Mech. 2014, 35, 835–840. [Google Scholar]
- Jiang, Z.M.; Xiong, X.H.; Zeng, L. Unsaturated seepage analysis of slope under rainfall condition based on FLAC3D. Rock Soil Mech. 2014, 35, 855–861. [Google Scholar]
- Chu, W.J.; Xu, W.Y.; Yang, S.Q.; Zhou, W.Y. Secondary development of a viscoelasto-plastic rheological constitutive model of rock based on FLAC3D. Rock Soil Mech. 2006, 27, 2005–2010. [Google Scholar]
- He, Z.; Dai, B. Secondary Development of a Nonlinear Creep Model Based on Fractional Derivative in FLAC3D. In Proceedings of the 2018 11th International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 22–23 September 2018. [Google Scholar]
- Wang, C.B.; Ding, W.Q.; Qiao, Y.F. Development and application of hardening soil constitutive model in FLAC(3D). Chin. J. Rock Mech. Eng. 2014, 33, 199–208. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Ou, X.P.; Bai, K.; Zhu, Y.S.; Yuan, C.; Wang, J.; Liu, D.T.; Liu, H.J. The Strength Reduction Method for Stability Analysis of Slope Based on FLAC-3D. J. Wuhan Univ. Technol. 2009, 31, 59–61. [Google Scholar]
- Song, Y.S.; Chae, B.G.; Lee, J. A method for evaluating the stability of an unsaturated slope in natural terrain during rainfall. Eng. Geol. 2016, 210, 84–92. [Google Scholar] [CrossRef]
- Genuchten, M.V. A Closed-form Equation for Predicting Hydraulic Conductivity for Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Chen, X.; Fu, J.J.; Zhao, H.B.; Huang, T.P.; Shi, K. Analysis of Slope Reliability by Finite-Difference Strength-Reduction Method Considering the Thought of Monte Carlo Method. J. Yangtze River Sci. Res. Inst. 2011, 28, 36–40. [Google Scholar]
- Jiang, X.L.; Yang, H.; Cao, P. FLAC(3D) analysis of interaction between goaf and opencut mining slope with 3D geological model using SURPAC. Rock Soil Mech. 2011, 32, 1234–1240. [Google Scholar]
- Liu, C.H.; Chen, C.X.; Feng, X.T.; Xiao, G.F. Effect of groundwater on stability of slopes at reservoir bank. Rock Soil Mech. 2005, 26, 419–422. [Google Scholar]
- Liu, J.X.; Liu, Y.T.; Hu, Q.J. Stability of embankment slope subjected to rainfall infiltration considering both runoff-underground seepage and fluid-solid coupling. Rock Soil Mech. 2010, 31, 903–910. [Google Scholar]
- Koner, R.; Chakravarty, D. Numerical analysis of rainfall effects in external overburden dump. Int. J. Min. Sci. Technol. 2016, 26, 825–831. [Google Scholar] [CrossRef]
- Mousavi, S.M. Landslide Susceptibility in Cemented Volcanic Soils, Ask Region, Iran. Indian Geotech. J. 2016, 47, 115–130. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Borgesson, L.; Chijimatsu, M.; Rutqvist, J.; Fujita, T.; Hernelind, J.; Kobayashi, A.; Ohnishi, Y.; Tanaka, M.; Jing, L. Hydro-mechanical response of a fractured granitic rock mass to excavation of a test pit—The Kamaishi Mine experiment in Japan. Int. J. Rock Mech. Min. Sci. 2001, 38, 79–94. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, Z.; Chen, W. Lower bound analysis of soil slope stability using finite elements subjected to pore water pressure. Rock Soil Mech. 2005, 16, 1258–1262+1268. [Google Scholar]
- Wang, L.F.; Li, L.G.; Yang, X. Instability initiation mechanism of gravel soil slope in Three Gorges Reservoir: Case study of Hongyanzi landslide in Wushan county. Chin. J. Geot. Eng. 2018, 40, 209–214. [Google Scholar]
- Wang, M.H.; Yan, E.C. Study on influence of reservoir water impounding on reservoir landslide. Rock Soil Mech. 2007, 28, 2722–2725. [Google Scholar]
- Zhang, W.; Goh, A.T. Reliability assessment on ultimate and serviceability limit states and determination of critical factor of safety for underground rock caverns. Tunn. Undergr. Space Technol. 2012, 32, 221–230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).