Abstract
Solar generation has become increasingly important in grid applications. In order to improve the energy efficiency of the photovoltaic array (PV), factors such as temperature, nonlinear characteristics, and partial shadow conditions (PSCs) of the PV must be fully considered. An excellent maximum power point tracking (MPPT) control strategy can effectively improve the energy utilization efficiency of photovoltaic cells and provide strong support for the construction of smart campuses in terms of environmental protection and energy saving. A traditional method such as Perturb & Observe (P&O) and incremental conductance (INC) will fall into the local maximum power point (LMPP). In the past decade, researchers have proposed many MPPT methods to solve the difficulties of the PV system. However, they have failed to fully consider dynamic changes in irradiance conditions. Changes in the irradiance of photovoltaic arrays can lead to an extension of the convergence time and an increase in the oscillation amplitude. Many current MPPT methods have shortcomings such as requiring a long convergence time, large oscillation amplitude, and being prone to falling into LMPP. In order to reduce the oscillation amplitude and improve the convergence speed, a novel Multi-strategy Improved Tuna Swarm Optimization hybrid INC (ITSO-INC) method is introduced in this article. This strategy involves improving the Tuna Swarm Optimization (TSO) through Levy Flight and a linear weight coefficient. In addition, the INC method is added in the later stage to improve the accuracy of MPPT tracking. The proposed algorithm can extract the global maximum power point under different partial shading. In order to verify the effectiveness of the proposed method, the proposed method was compared with other metaheuristic algorithms such as Cuckoo Search (CS) and TSO. The proposed ITSO-INC technique was tested over four different patterns of partial shading conditions. Modulation was performed by tracking the sudden change in the shadow pattern of the MPP. These simulation results confirm that the proposed method has fast convergence, high accuracy, zero steady state oscillation, and a rapid response to dynamic change.
1. Introduction
Large amounts of greenhouse gas emissions have a great negative impact on global environmental issues. The development and utilization of renewable energy is an urgent issue. Solar energy as a sustainable energy source has the advantages of high conversion efficiency, abundant reserves, and low pollution [1]. The development and utilization of solar energy are of great concern to governments of all countries, and photovoltaic power generation is considered to be the most promising technology in the field of renewable energy. Solar energy has been widely developed and used in recent years, and it occupies a very important position in the global energy structure [2]. In the construction of a smart campus, energy conservation and the use of green energy are the key points.
An analysis of the output characteristics of PV cells shows that changes in light intensity and temperature can cause changes in the maximum power point (MPP), but there is always a GMPP for a particular light intensity and temperature [3]. The task of MPPT is to find that point and keep the PV cell in that state for continuous operation and maximum external power output to improve PV cell utilization.
Traditional MPPT methods have good optimization finding characteristics under stable conditions such as constant illumination and constant temperature. However, local shadows, for example from birds and trees, often disturb PV modules when they are arranged [4]. These partial shadow conditions (PSCs) can lead to different levels of solar irradiance for each part of the PV module. These methods often suffer from the continuous oscillation of the P-U characteristic curve and tend to fall into local power maxima when dealing with complex shading changes, thus reducing the PV system output power and affecting the system efficiency. A metaheuristic algorithm ensures that the PV module operates at the GMPP, minimizing the effect of shadows on the PV cells. At the same time, the algorithm has good adaptability in dealing with multi-peak and non-linear function-seeking problems, and has been widely studied and applied by many scholars in the MPPT control of photovoltaic power generation [5].
Traditional MPPT methods include perturbation observations (P&O) and conductance increment algorithms (INC), which are widely used because of their simple design and easy implementation. However, P&O generates large oscillations near the MPP, and the solution accuracy is poor. The INC method does not easily converge to a stable MPP, generating continuous oscillations when disturbed [6].
In recent years, researchers have proposed many new metaheuristic algorithms to solve the problem of parameter identification, which are similar to the Tuna Swarm Optimization (TSO) [7], Flower Pollination Algorithm, (FPA) [8], Bat Algorithm (BA) [9], Harmony Search (HS) [10], Squirrel Search Algorithm (SSA). All of these algorithms have been added to the MPPT application. Ref. [11] combined an optimized neural network trained through Deep Reinforcement Learning (DRL) with a classical closed-loop control and proved that this method can effectively improve the performance of MPPT. Literature [12] applied the FPA method to MPPT and achieved good results. In addition, there is a new trend in improving metaheuristic algorithms to solve the problem of multimodal objective functions. For example, [13] proposes to improve the performance of MPPT by reducing the random number in the CS. An MPPT algorithm for fast-changing shadows was proposed by [14], which showed good performance in reducing the algorithm oscillation frequency. Ref. [15] proposed to improve the Grey Wolf Algorithm by adding a Levy flight strategy. Ref. [16] proposed the Tunicate Swarm Algorithm (TSA) in an MPPT Control. Ref. [17] proposed the novel Musical Chairs Algorithm (MCA), which performs well in convergence time and reducing steady-state oscillations. In the study [18], by improving the tracking method of the CS algorithm, the tracking accuracy of the MPPT was effectively improved and the oscillation amplitude was reduced.
Another noteworthy method is to mix different algorithms to improve the efficiency of MPPT. Literature [19] proposed a new hybrid TSA-PSO algorithm that combines the Tunicate Swarm Algorithm (TSA) with the particle swarm optimization (PSO) technique for efficient maximum power in PSCs. Ref. [20] combined the Cuckoo Algorithm with Grey Wolf Optimization, and the tracking accuracy of the MPPT was improved successfully. Ref. [21] presents a new hybrid MPPT technique by combining the Artificial Bee Colony (ABC) and P&O algorithms. This technique accelerates the convergence speed of the algorithm. In the article [22], Considering the Sliding mode control structure, the improved PSO (MPSO) algorithm is combined with P&O to effectively improve the convergence speed and stability of the tracking process. Research in [23] combines an improved Artificial Bee Colony algorithm with the Multiple Heat Transfer Search algorithm, greatly improving the accuracy of algorithm tracking. The noteworthy MPPT algorithm features found in a literature review are shown in Table 1.

Table 1.
Research summary of published MPPT algorithms.
TSO, as a new metaheuristic algorithm with a fast dynamic response, has been used in MPPT. The TSO algorithm has the advantages of good stability and relatively few algorithm parameters. Moreover, the algorithm has great potential for improvement in tracking speed and convergence time. Improving the TSO algorithm has the potential to effectively reduce the oscillation amplitude and improve the algorithm convergence speed. The TSO algorithm also has the potential to further optimize the dynamic response speed. In this paper, the Levy flight strategy was added to the TSO algorithm to improve the ability of the algorithm to jump out of the previous LMPP. Due to the fixed weight coefficient of the TSO algorithm, the global stable convergence cannot be considered. The introduction of an adaptive weight coefficient can effectively improve the local convergence performance of the TSO algorithm. During the algorithm initialization stage, the search agents were initialized by equally dividing them to increase the probability of the initial position being near the MPP. In the later stage, a variable step formula was added to improve the convergence speed of the algorithm. Combining the improved ITSO algorithm with INC can effectively overcome the problem of conventional MPPT algorithms falling into LMPP and further accelerate the convergence speed of the algorithm. The ITSO-INC algorithm runs in two stages. The first stage uses the ITSO algorithm because the improved TSO algorithm has a large search range and the ability to jump out of LMPP. The algorithm transitions to the next stage when the number of iterations meets the specified conditions. This second stage uses the INC algorithm for accurate tracking. ITSO is used over a large search range in the early stage, and INC is used for small step tracking over a small range. This two-stage approach can effectively prevent the algorithm from falling into sustained oscillations. The proposed algorithm improves tracking accuracy and search efficiency in the later stage, ensuring that the algorithm can effectively track changes in irradiance by setting algorithm restart conditions. When the irradiance of the photovoltaic array changes significantly, the algorithm is restarted.
The main contributions of the article are:
- In this paper, the author introduces a novel multi-strategy method to improve the TSO algorithm for MPPT tracking.
- A simulated battery model was established, and the effectiveness of the proposed method was verified using three different shadow conditions. To verify the effectiveness of the algorithm under changing shadow conditions, the photovoltaic array irradiance was set to suddenly change from pattern2, pattern3 to pattern4.
- During the sudden change of radiation conditions, the robustness of the algorithm in tracking GMPP was evaluated.
- By comparing the new algorithm with the basic TSO algorithm and CS algorithm, the superiority of the new algorithm in fitness convergence performance was verified.
- The simulation experiment of MPPT was carried out using a photovoltaic cell model. Compared with the basic TSO, CS, and INC, the results show that the new algorithm has more advantages in MPPT’s fast response and anti-interference.
2. Distributed PV System and Proposed MPPT Algorithm
In this section, the distributed PV system and the proposed algorithm will be explained in detail, including the patterns and characteristic curves of PV cells. The specific steps of the ITSO-INC method in MPPT application will also be introduced.
2.1. Distributed PV System
The system in the current investigation is shown in Figure 1. The system consists of one PV module, one Module-level power electronics (MLPE), and a DC-DC boost converter connected to a resistive load. The MPPT algorithm controls the duty ratio of the MLPE. The described models in the system are presented as follows.
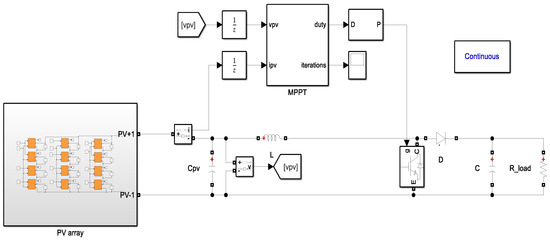
Figure 1.
MATLAB Simulink Photovoltaic system model.
2.1.1. PV Module
The equivalent model of a photovoltaic cell is shown in Figure 2. The photovoltaic module consists of an ideal current source (Iph), two internal resistors (Rsh, Rs), and a diode (D).
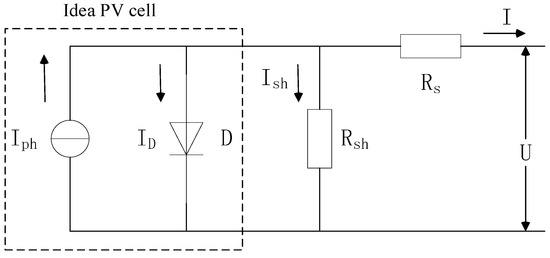
Figure 2.
Equivalent circuit of a photovoltaic cell.
The equivalent circuit of photovoltaic cells and Kirchhoff’s law, as well as the output current equation can be written as shown in in Equation (1):
The current flowing through the diode can be written as shown in Equation (2):
The total current generated by the PV module can be estimated by applying KCL to the circuit, and the final current equation can be written as shown in Equation (3):
In order to further calculate the total current of the PV module under partial shading, the formula in Equation (3) can be rewritten as [24]:
where and represent the number of parallel and series-connected PV modules, respectively.
is the output current of the photovoltaic cell, is the photocurrent, is the reverse saturation current, is the unit charge, IRs is the equivalent series resistance, Rsh is parallel resistance, is the Boltzmann constant, is the quality factor of the diode, and is the absolute temperature [25].
The characteristic curves of the photovoltaic module drawn according to Equation (4) are shown in Figure 3. These curves have several variables worthy of attention, including The short-circuit current (ISC), open-circuit voltage (VOC), maximum power point (MPP), voltage at MPP (VMPP), current at MPP (IMPP), and power at MPP.
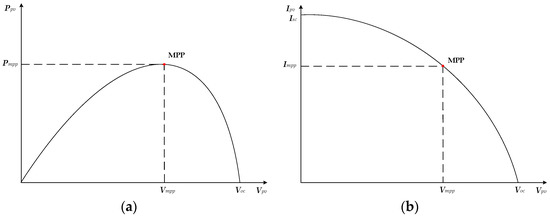
Figure 3.
The characteristic curve of PV module. (a) Current–voltage characteristic curve; (b) power–voltage characteristic curve.
2.1.2. Description of DC–DC Boost Converter
This article uses a boost circuit, as shown in Figure 4.
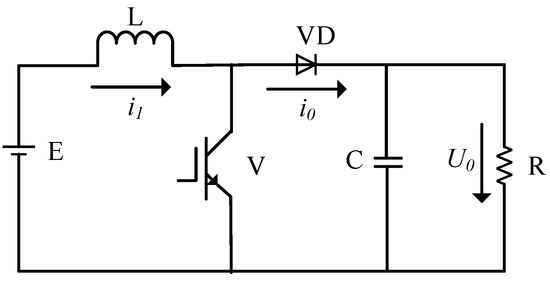
Figure 4.
Boost circuit diagram.
When the circuit operates stably, the energy stored by the inductor, L in one cycle T, is equal to the energy released by it. This relationship can be represented by the following equation:
The output voltage is:
From Equation (7), it can be determined that:
where, is the duty ratio, .
According to Equations (7) and (8), the equivalent internal resistance of the boost circuit is:
The output capacitance equivalent formula is:
where is output resistance, is the output voltage ripple factor, and is the switching frequency.
A DC/DC boost converter was applied to the MPPT system, and the corresponding data are presented in Table 2.

Table 2.
DC/DC boost converter parameters.
2.1.3. Partial Shading and Its Effects
Under ideal operating conditions, the characteristic curve of photovoltaic cells is shown in Figure 3a. However, the operation of photovoltaic cells under actual working conditions will be affected by various external factors. PV cells are usually partially or completely covered by adjacent buildings, trees, and clouds. Under PSCs, the PV curve of photovoltaic cells will become very complex and have multiple peaks. One peak is called the global MPP (GMPP), while the other peaks are called local MPPs (LMPP) [26]. The photovoltaic cell JY-210-A parameters are shown in Table 3.

Table 3.
PV cell JY-210-A parameters.
In this simulation, a PV consisting of four rows and three columns is built, and each PV module is composed of four PV cells. The PV model and P-V curves are shown in Figure 5. PV model temperature is set to either 25 °C or 30 °C. Each photovoltaic module is inserted into the anti-counterattack diode to ensure the stable operation of the battery.
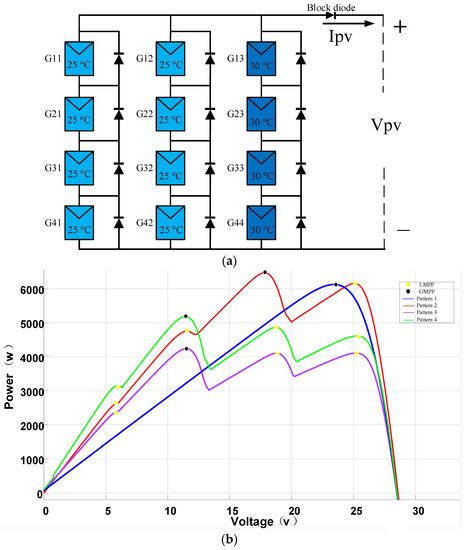
Figure 5.
Partial shading analysis of the model PV system. (a) Shading patterns, (b) P−V curves under PSC.
In order to verify the proposed method, constant irradiance (pattern 1) and variable PSCs (pattern 2, pattern 3, and pattern 4) were set. The irradiance settings for three patterns are shown in Table 4. By setting different irradiance levels for each photovoltaic module (G11, G12, G13, etc.), sudden changes in irradiance were controlled through step functions.

Table 4.
Photovoltaic array irradiance settings.
Pattern 1 has only one GMPP and no LMPP. It is worth noting that there are three LMPPs and one GMPP in pattern 2, three LMPPs and one GMPP in pattern 3, and three LMPPs and one GMPP in pattern 4.
2.2. Multi-Strategy Improved Tuna Swarm Optimization (ITSO)
Tuna Swarm Optimization was proposed by Lei Xie et al. in 2021. The Tuna Swarm Optimization algorithm has a large search range and high accuracy in solving single-objective problems, and it is an efficient meta-heuristic algorithm. The algorithm was inspired by the cooperative foraging behavior of tuna, and it includes two strategies: spiral foraging and parabolic foraging [27].
2.2.1. Initializing
The ITSO algorithm randomly and uniformly generates the initial population in the search space. The initialization is represented mathematically as shown in Equation (12):
where is the first initial individual, and the upper and lower boundaries of search space are the tuna population.
In this study, the initialization conditions for CS and TSO algorithms were improved by equally dividing the search agents, as shown in Equation (13) [20]:
where is the swarm-size and is the initial individual (duty cycle).
2.2.2. Spiral Foraging
According to the standard TSO, the weight coefficients α1 and α2 control the global exploration and local development ability of the algorithm. Basic weight coefficients are represented mathematically as shown in Equations (14) and (15).
A larger weight coefficient is beneficial to the algorithm in obtaining a larger search space in the pre-iteration and mid-iteration. When the weight coefficient is smaller, the algorithm can better carry out local development in the later iteration and accelerate the convergence of the algorithm. The linearly changing weight coefficient will easily lead to the algorithm falling into the local optimum at the early stage of iteration, and the slow decline at the later stage will make the local development ability of tuna individuals insufficient.
To balance the global and local search capabilities of TSO, α1, and α2 make nonlinear improvements, and the weight coefficient after improvement is shown in Formulas (16) and (17). The trend in the original weight coefficient and the improved weight coefficient with the number of iterations is shown in Figure 6. It can be seen in Figure 6 that the improved weight coefficient changes nonlinearly with α1 and α2. The range of change in the first half of α2 enhances the global exploration ability of the algorithm. When the iteration reaches the later stage, α1 and α2 rapidly change to a stable value, making the individual quickly approach the optimal individual and fully complete the local development. Therefore, the improved weight coefficient can further balance the global and local search process [7].
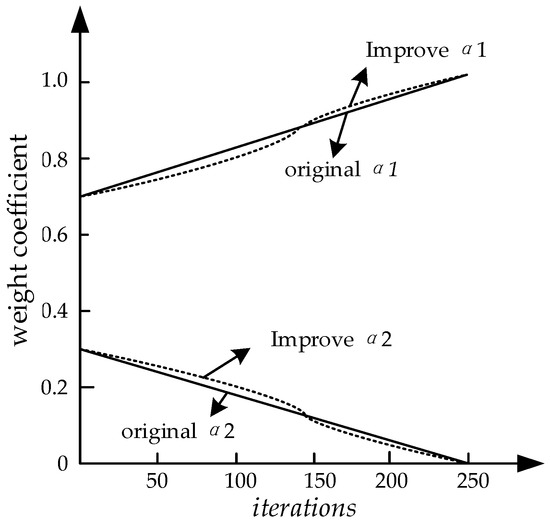
Figure 6.
A comparison of weight coefficient improvements.
The mathematical equation of the final spiral feeding is as follows:
where is a randomly generated reference point in the search space, is the position after iteration, is the maximum number of iterations, is the current number of iterations, and is the current best location.
2.2.3. Parabolic Foraging
The basic TSO parabolic foraging behavior is shown in Equation (19).
where is a random number, ranging from −1 to 1.
For basic TSO, the most critical issue is how to eliminate the attraction of the local best. The introduction of the Levy flight strategy into the parabolic foraging strategy can enhance the global search ability of the algorithm. Therefore, this article introduces the Levy flight strategy to modify the TSO’s group update strategy. Equation (19) is updated to (20),
where u and v obey normal distribution.
2.2.4. Step Length and Restart
The improved algorithm can consider the global search efficiency. In order to ensure the convergence speed of the later algorithm, the MPPT late step formula is changed to Equation (24):
where the current step size of the algorithm, D is the step amplification factor, is the maximum step length, is the current number of iterations, and is the maximum number of iterations.
The algorithm control restart conditions are:
The flowchart of ITSO implementation in problem-solving is demonstrated in Figure 7.
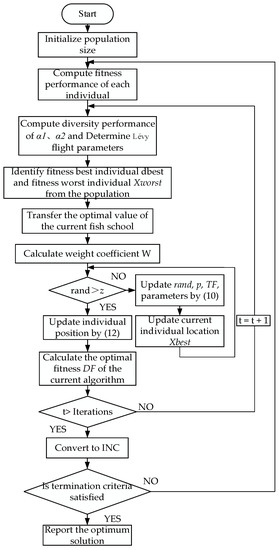
Figure 7.
Flow chart of the ITSO-INC algorithm.
2.2.5. Algorithm Test
Four groups of classical test functions were selected for testing to verify that the improved algorithm had improved performance. The functions used for testing are shown in Table 5. And the function image is shown in Figure 8. The ITSO algorithm was compared with the basic TSO and CS. To avoid accidental interference, all algorithms were repeated 30 times, and the maximum number of iterations was limited to 500. The experimental results are shown in Table 6.

Table 5.
Benchmark functions.
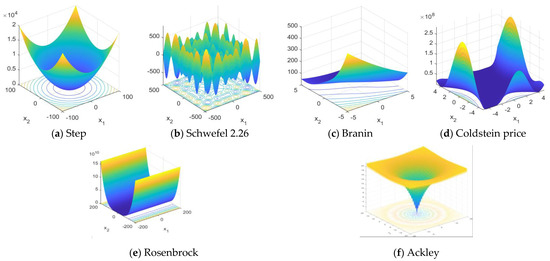
Figure 8.
Three-dimensional visualization of two-dimensional benchmark functions.

Table 6.
Experimental results in 30 dimensions.
3. Simulation Results
In this section, the main content is to apply the proposed ITSO to MPPT for simulation experiments, and to compare and analyze the performance of four methods: ITSO-INC, TSO, CS, and INC in MPPT. The swarm size for all metaheuristic algorithms is six. The parameters used in these optimization techniques shown in Table 7 have been frequently used in previous studies; therefore, they have good performance in MPPT applications.

Table 7.
The parameters used in this study.
3.1. Result of Pattern 1
The ITSO-INC performance in solving MPPT problems was evaluated for pattern 1. The results of ITSO-INC were also compared with CS, TSO, and INC. The PV power curves obtained using the TSO, ITSO-INC, CS, and INC are shown in Figure 9. Pattern 1 had a peak power of 6166.24 w. Obviously, the steady-state fluctuation of MPPT based on ITSO-INC was very low, reaching a maximum power of 6166.72 w. Compared with INC, TSO, and CS, ITSO-INC reached the maximum power point at an extremely fast speed, with a tracking efficiency of 99.95%. The peak power of TSO, CS, and INC MPPT methods in pattern 1 were 6165.51 w, 6153.07 w, and 6145.29 w, and the tracking efficiency was 99.95%, 99.75%, and 99.58%, respectively. In terms of tracking efficiency, these three basic methods required 0.34 s, 0.275 s, and 0.41 s, respectively. ITSO-INC only needed 0.048 s to reach GMPP, which was the fastest speed of the four methods. As shown in Table 8, ITSO-INC had a higher accuracy and tracking efficiency in MPPT than CS, INC, and TSO.
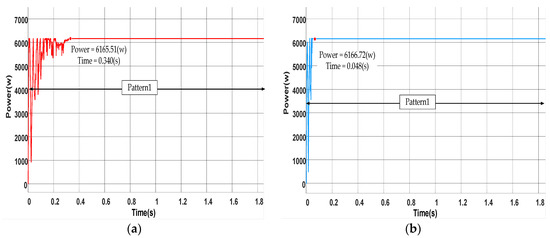
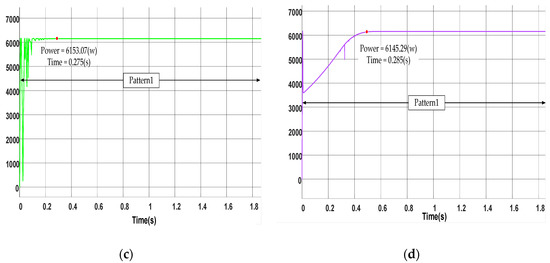
Figure 9.
The obtained power by the algorithms in constant irradiance condition from pattern 1. (a) TSO; (b) ITSO-INC; (c) CS; (d) INC.

Table 8.
Numerical results of TSO, ITSO-INC, CS, and INC methods in pattern 1.
The PV duty cycle curves obtained using TSO, ITSO-INC, CS, and INC are shown in Figure 10. It can be seen in the figure that the four methods can maintain zero stable state occupation after a certain period of time. Compared with TSO and CS, the new method can quickly maintain stability after small frequency shocks and converge to the maximum power point. It is proved that the stability of the ITSO-INC algorithm was better than CS and TSO algorithms in the case of pattern 1.
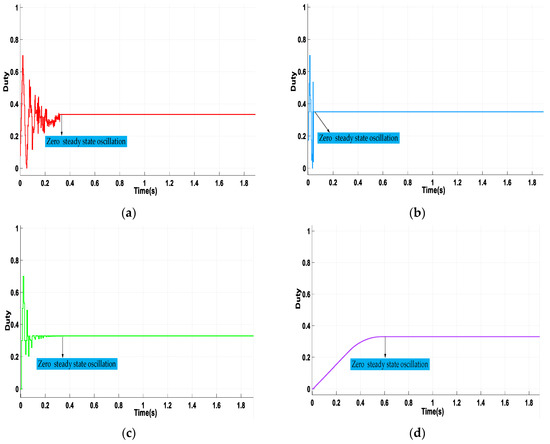
Figure 10.
The obtained duty cycle by the algorithms in constant irradiance condition from pattern 1. (a) TSO; (b) ITSO; (c) CS; (d) INC.
3.2. Result of Pattern 2, Pattern 3 and Pattern 4
In this section, the design of the PV system to accommodate dynamic changes in irradiation (from pattern 2 to pattern 3 to pattern 4) is discussed. The comparison results of the four algorithms are described below.
For pattern 2, it can be seen in Figure 11 that CS, TSO, and ITSO-INC were able to reach the maximum power of the PV system and maintain a zero state occupation, with maximum power values of 6468.86 w, 6470.66 w, and 6265.27 w, respectively. INC failed to maintain GMPP due to the large amplitude of oscillation, resulting in an average power value of 6044.33 w. These results indicate that the efficiency of INC was the lowest. In terms of algorithm optimization time, the minimum time of INC was 0.022 s, but under PSCs, INC could not maintain zero steady-state optimization.
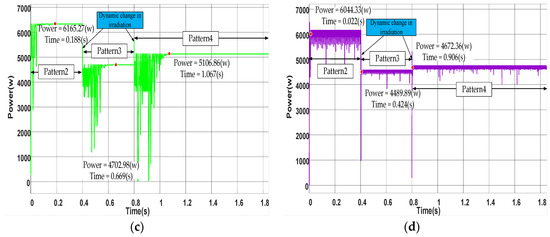
Figure 11.
The obtained power by the algorithms over the step changes from pattern 3 and pattern 4. (a) TSO; (b) ITSO-INC; (c) CS; (d) INC.
The time of TSO, ITSO-INC, and CS algorithms was 0.272 s, 0.095 s, and 0.188 s, respectively. On the premise of ensuring the efficiency of the algorithm, the ITSO-INC method took the shortest time and had a small frequency of oscillation, which could ensure stable operation in GMPP.
In the case of dynamic change in irradiation in pattern 3, when irradiance suddenly changed at 0.4 s, INC fell into LMPP with a value of 4489.89 w. TSO, ITSO-INC, and CS reached GMPP again after the disturbance. The recovery time of ITSO-INC after the disturbance was 0.054 s, which shows that the improved algorithm has better robustness. In terms of algorithm efficiency, the maximum power of the four methods in pattern 3 were 4352.33 w, 4701.45 w, 4702.89 w, and 4489.89 w.
When the irradiance suddenly changed at 0.8s, TSO, CS, and INC all exhibited significant oscillations. The ITSO-INC method proposed in this study had a lower oscillation amplitude and frequency, resulting in better performance. In terms of tracking efficiency, the proposed algorithm outperformed the other two metaheuristic algorithms. The INC ethod could not be maintained near MPP. Compared with TSO and CS, the ITSO-INC method improved tracking time by 26.89% and 60.29%.
It can be concluded from Table 9 that ITSO-INC has better robustness, algorithm efficiency, and algorithm tracking speed.

Table 9.
Numerical results of TSO, ITSO-INC, CS, and INC methods in pattern 3 and pattern 4.
As can be seen from Figure 12, TSO, ITSO-INC, and CS could maintain zero steady-state dispersion before and after disturbance in the four comparison algorithms. Although the INC algorithm had fast tracking speed, it could not maintain stable operation, and the curve continued to oscillate in constant amplitude. The ITSO-INC algorithm had the fastest tracking speed and the highest algorithm efficiency among the algorithms that could estimate zero steady state.
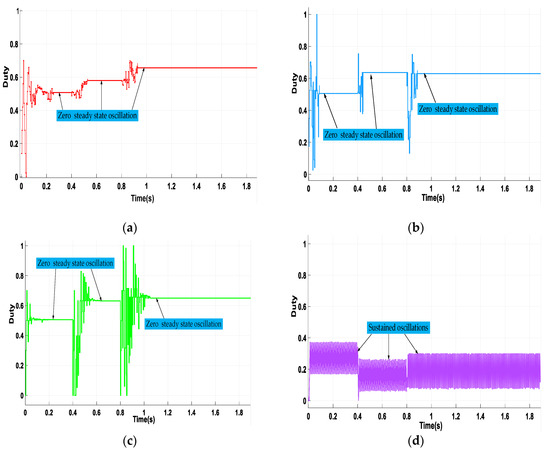
Figure 12.
The obtained duty cycle by the algorithms over the step changes from pattern 3 and pattern 4. (a) TSO; (b) ITSO; (c) CS; (d) INC.
4. Conclusions
This article proposes a new method that combines the multi-strategy improved TSO and INC methods to track the GMPP of a PV system. The proposed new method performs MPPT tracking by optimizing the converter duty cycle. In the simulation, the PV system was composed of PV array, boost converter, and an MPPT control module. The results were obtained by comparing the proposed ITSO-INC with INC, CS, and TSO through the MATLAB simulation platform. Under three different shadow conditions, ITSO-INC had good tracking speed, robustness, and tracking efficiency. ITSO-INC had good performance under constant and variable PSCs. Compared with TSO and INC, the tracking efficiency of the new method increased by 7.39% and 4.48% under pattern 4. In terms of MPPT tracking rate, ITSO-INC was greatly improved compared with the other three methods. Under the condition of variable PSCs, the new method increased the tracking rate by 26.89% and 60.29%. These results show that ITSO-INC is a competitive and robust high-speed tracking method. Therefore, it can be concluded that ITSO-INC gives the best solution to track MPP for any sort of irradiation changes.
Author Contributions
Conceptualization, Y.L.; methodology, L.L.; validation, Y.J., J.Z., Y.G. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by key projects of the East University of Heilongjiang (HDFKY200104) and general projects of the East University of Heilongjiang (HDFKY210106).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| PV | Photovoltaic |
| PSCs | Partial Shadow Conditions |
| MPPT | Maximum Power Point Tracking |
| P&O | Perturb & Observe |
| INC | Incremental Conductance |
| LMPP | Local Maximum Power Point |
| TSO | Tuna Swarm Optimization |
| ITSO-INC | Multi-strategy Improved Tuna Swarm Optimization hybrid INC |
| GMPP | Global Maximum Power Point |
| MPP | Maximum Power Point |
| CS | Cuckoo Search |
| FPA | Flower Pollination Algorithm |
| BA | Bat Algorithm |
| HS | Harmony Search |
| SSA | Squirrel Search Algorithm |
| DRL | Deep Reinforcement Learning |
| MCA | Musical Chairs Algorithm |
| PSO | Particle Swarm Optimization |
| ABC | Artificial Bee Colony |
| TSA | Tunicate Swarm Algorithm |
| TSA-PSO | Artificial Bee Colony Artificial Hybrid Particle Swarm Optimization |
| CS-GWO | Cuckoo Search Hybrid Gray Wolf Optimization |
| ABC-P&O | Artificial Bee Colony Hybrid Perturb & Observe |
| MPSO-MP&O | Modified Particle Swarm Optimization and Modified Perturb & Observe |
| IABC-SHTS | Improved artificial bee colony and simultaneous heat transfer search algorithm |
| MLPE | Module-level power electronics |
References
- Kusch-Brandt, S. Urban Renewable Energy on the Upswing: A Spotlight on Renewable Energy in Cities in REN21’s “Renewables 2019 Global Status Report. Resources 2019, 8, 139. [Google Scholar] [CrossRef]
- Fraunhofer. Photovoltaics Report 2021; Fraunhofer Institute for Solar Energy Systems: Freiburg, Germany, 2021. [Google Scholar]
- Huixiu, L.; Lina, Z.; Shuo, T. Research on photovoltaic MPPT control Strategy based on improved sliding mode control. J. Phys. Conf. Ser. 2022, 2310, 012039. [Google Scholar]
- Saba, J.; Kashif, I. A comprehensive analyses with new findings of different PSO variants for MPPT problem under partial shading. Ain Shams Eng. J. 2022, 13, 101680. [Google Scholar]
- Subramanian, A.; Jayaparvathy, R. Performance comparison of modified elephant herding optimization tuned MPPT for PV based solar energy systems. Circuit World 2022, 48, 309–321. [Google Scholar] [CrossRef]
- Harrison, A.; Nfah, E.M.; de Dieu Nguimfack Ndongmo, J.; Alombah, N.H. An Enhanced P&O MPPT Algorithm for PV Systems with Fast Dynamic and Steady-State Response under Real Irradiance and Temperature Conditions. Int. J. Photoenergy 2022, 2022, 6009632. [Google Scholar]
- Wentao, W.; Jun, T. An Improved Nonlinear Tuna Swarm Optimization Algorithm Based on Circle Chaos Map and Levy Flight Operator. Electronics 2022, 11, 3678. [Google Scholar]
- Diab, A.A.Z.; Rezk, H. Global MPPT based on flower pollination and differential evolution algorithms to mitigate partial shading in building integrated PV system. Sol. Energy 2017, 157, 171–186. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Kok Soon, T.; Jamei, E.; Thirunavukkarasu, G.S.; Horan, B.; Mekhilef, S.; Stojcevski, A. Maximum Power Point Tracking for Photovoltaic Systems under Partial Shading Conditions Using Bat Algorithm. Sustainability 2018, 10, 1347. [Google Scholar] [CrossRef]
- Geem, Z.W. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2018, 44, 148–175. [Google Scholar]
- Yousri, D.; Babu, T.S.; Allam, D.; Ramachandaramurthy, V.K.; Beshr, E.; Eteiba, M.B. Fractional Chaos Maps with Flower Pollination Algorithm for Partial Shading Mitigation of Photovoltaic Systems. Energies 2019, 12, 3548. [Google Scholar] [CrossRef]
- Ali, E.M.; Abdelsalam, A.K.; Youssef, K.H.; Hossam-Eldin, A.A. An Enhanced Cuckoo Search Algorithm Fitting for Photovoltaic Systems’ Global Maximum Power Point Tracking under Partial Shading Conditions. Energies 2021, 14, 7210. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. A novel flower pollination based global maximum power point method for solar maximum power point tracking. IEEE Trans. Power Electron. 2017, 32, 8486–8499. [Google Scholar]
- Su, W.; Wencheng, C.; Liang, Z. Research on MPPT Based on Gray Wolf Algorithm improved by Levy Flight. J. Phys. Conf. Ser. 2021, 1865, 042089. [Google Scholar]
- Majad, M.; Feroz, M.A.; Fei, L.; Qiang, L. An Intelligent Tunicate Swarm Algorithm Based MPPT Control Strategy for Multiple Configurations of PV Systems under Partial Shading Conditions. Adv. Theory Simul. 2021, 4, 2100246. [Google Scholar]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Jately, V.; Averbukh, M.; Rajput, S.; Azzopardi, B. A Novel TSA-PSO Based Hybrid Algorithm for GMPP Tracking under Partial Shading Conditions. Energies 2022, 15, 3164. [Google Scholar] [CrossRef]
- Salim, J.A.; Albaker, B.M.; Alwan, M.S.; Hasanuzzaman, M. Hybrid MPPT approach using Cuckoo Search and Grey Wolf Optimizer for PV systems under variant operating conditions. Glob. Energy Interconnect. 2022, 5, 627–644. [Google Scholar] [CrossRef]
- Restrepo, C.; Yanẽz-Monsalvez, N.; González-Castaño, C.; Kouro, S.; Rodriguez, J. A Fast Converging Hybrid MPPT Algorithm Based on ABC and P&O Techniques for a Partially Shaded PV System. Mathematics 2021, 9, 2228. [Google Scholar]
- Rajamand, S. A novel sliding mode control and modified PSO-modified P&O algorithms for peak power control of PV. ISA Trans. 2022, 130, 533–552. [Google Scholar]
- Gong, L.; Hou, G.; Huang, C. A two-stage MPPT controller for PV system based on the improved artificial bee colony and simultaneous heat transfer search algorithm. ISA Trans. 2022, 132, 428–443. [Google Scholar] [CrossRef] [PubMed]
- Aly, M.; Mohamed, E.A.; Rezk, H.; Nassef, A.M.; Elhosseini, M.A.; Shawky, A. An Improved Optimally Designed Fuzzy Logic-Based MPPT Method for Maximizing Energy Extraction of PEMFC in Green Buildings. Energies 2023, 16, 1197. [Google Scholar] [CrossRef]
- Başoğlu, M.E. Comprehensive review on distributed maximum power point tracking: Submodule level and module level MPPT strategies. Sol. Energy 2022, 241, 85–108. [Google Scholar]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [PubMed]
- Shishavan, S.T.; Gharehchopogh, F.S. An improved cuckoo search optimization algorithm with genetic algorithm for community detection in complex networks. Multimed. Tools Appl. 2022, 81, 25205–25231. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).