Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch
Abstract
:1. Introduction
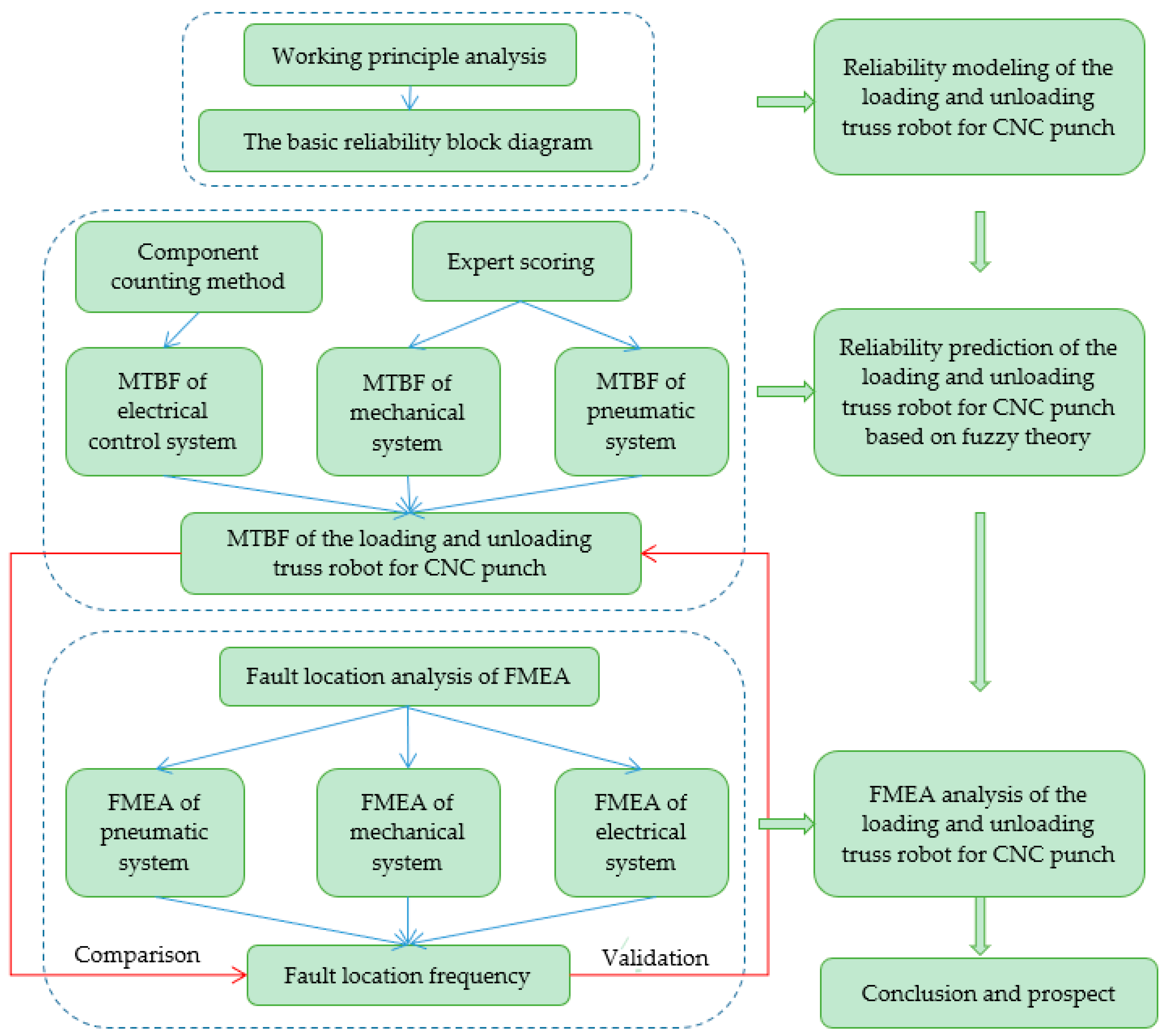
2. Materials and Methods
2.1. Reliability Prediction
- (1)
- Evaluate whether each system of the loading and unloading truss robot for CNC punch can reach the specified reliability index;
- (2)
- Lay the foundation for reliability distribution of the loading and unloading truss robot for CNC punch;
- (3)
- According to the reliability prediction results, the weak links of the loading and unloading truss robot for CNC punch are discovered in advance to reduce the research and development cost and time;
- (4)
- Develop preventive maintenance plan, parts reserve and update plan for the loading and unloading truss robot for CNC punch.
2.2. Failure Modes and Effects Analysis
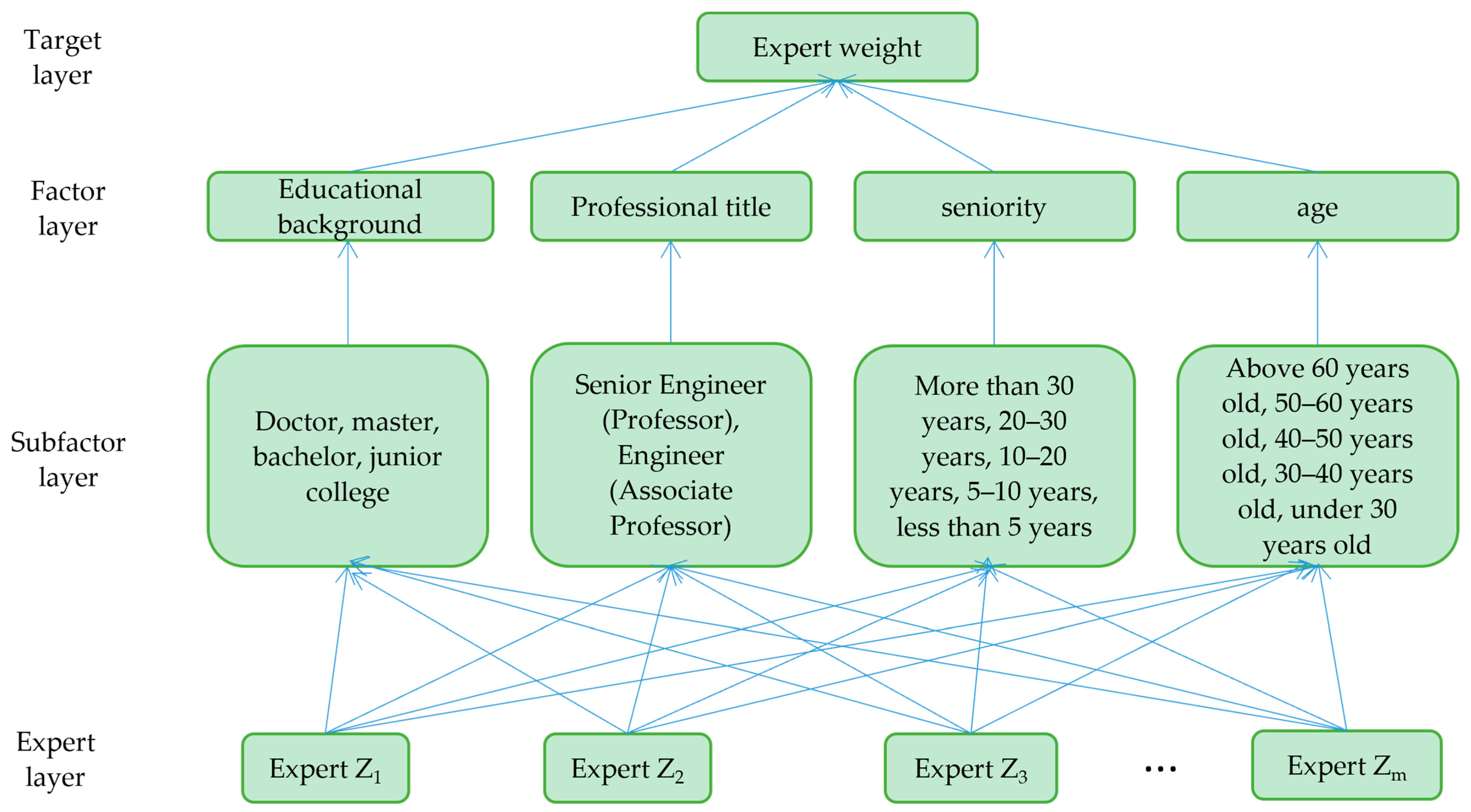
2.3. Combination of Reliability Prediction and FMEA
3. Results
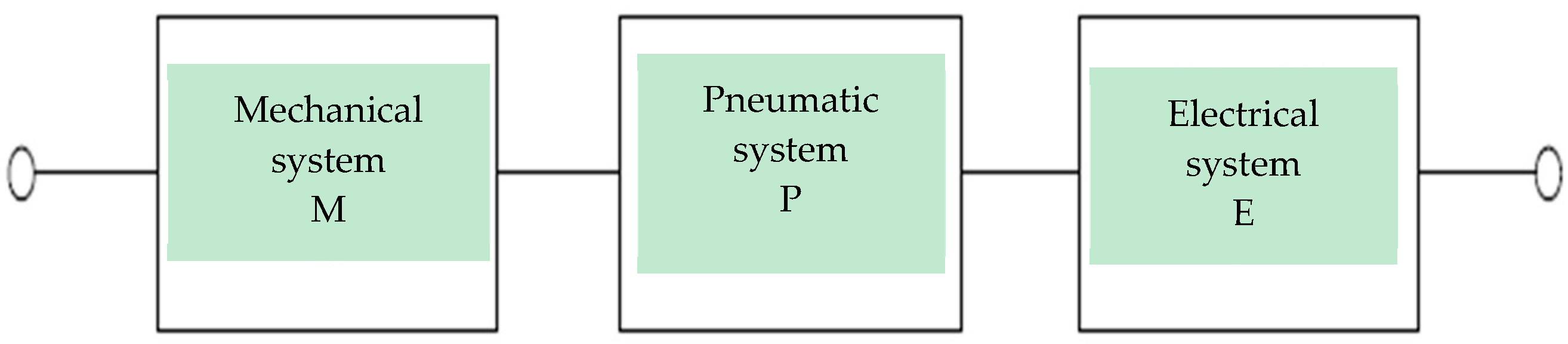
3.1. Establishment of Reliability Model
3.2. Reliability Prediction
3.2.1. Reliability Prediction of Electrical Control System
3.2.2. Reliability Prediction of Mechanical System and Pneumatic System
- —λ cut set of global fuzzy evaluation of system complexity ;
- —λ cut set of global fuzzy evaluation of system technical level ;
- —λ cut set of global fuzzy evaluation of system working time ;
- —λ cut set of global fuzzy evaluation of system environmental condition ;
- —λ cut set of complexity fuzzy weights given by experts ;
- —λ cut set of fuzzy weights of technical level given by experts ;
- —λ cut set of fuzzy weight of working time given by experts ;
- —λ cut-off set of fuzzy weights of environmental conditions given by experts .
3.3. Fault Location Analysis of FMEA
4. Discussion
5. Conclusions and Prospect
5.1. Conclusions
- (1)
- Using reliability engineering and fuzzy theory, the reliability of the loading and unloading truss robot for CNC punch is studied, and a new reliability prediction method is proposed. Firstly, the failure rate of existing components is used, and the failure rate of an electrical control system is estimated to be 3.146 × 10−4 (1/h) by the component counting method. Secondly, based on the predicted results of electrical control system, the failure rates of the mechanical system and pneumatic system are estimated to be 3.628 × 10−4 (1/h) and 3.715 × 10−4 (1/h), respectively, by using fuzzy theory. Finally, it is estimated that the failure rate of the loading and unloading truss robot for CNC punch is 1.0489 × 10−3 (1/h), and the weak link is the pneumatic system. Therefore, the reliability prediction method proposed in this paper not only makes effective use of the existing reliability data of electrical control system, but also fully considers the actual characteristics of the lack of data of the mechanical system and pneumatic system. Combined with the project experience of relevant experts on the loading and unloading truss robot for CNC punch, the accuracy and operability of reliability prediction are improved;
- (2)
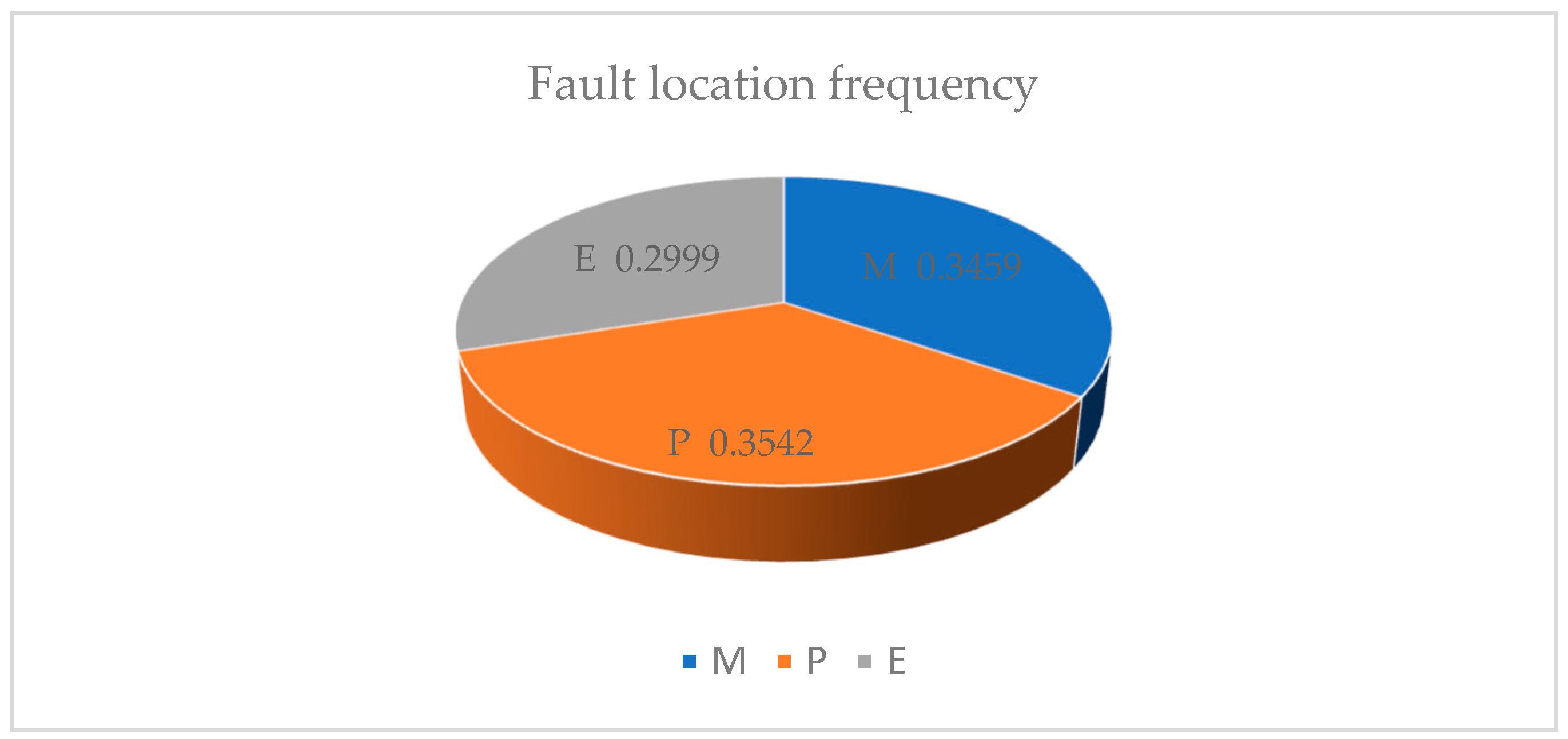
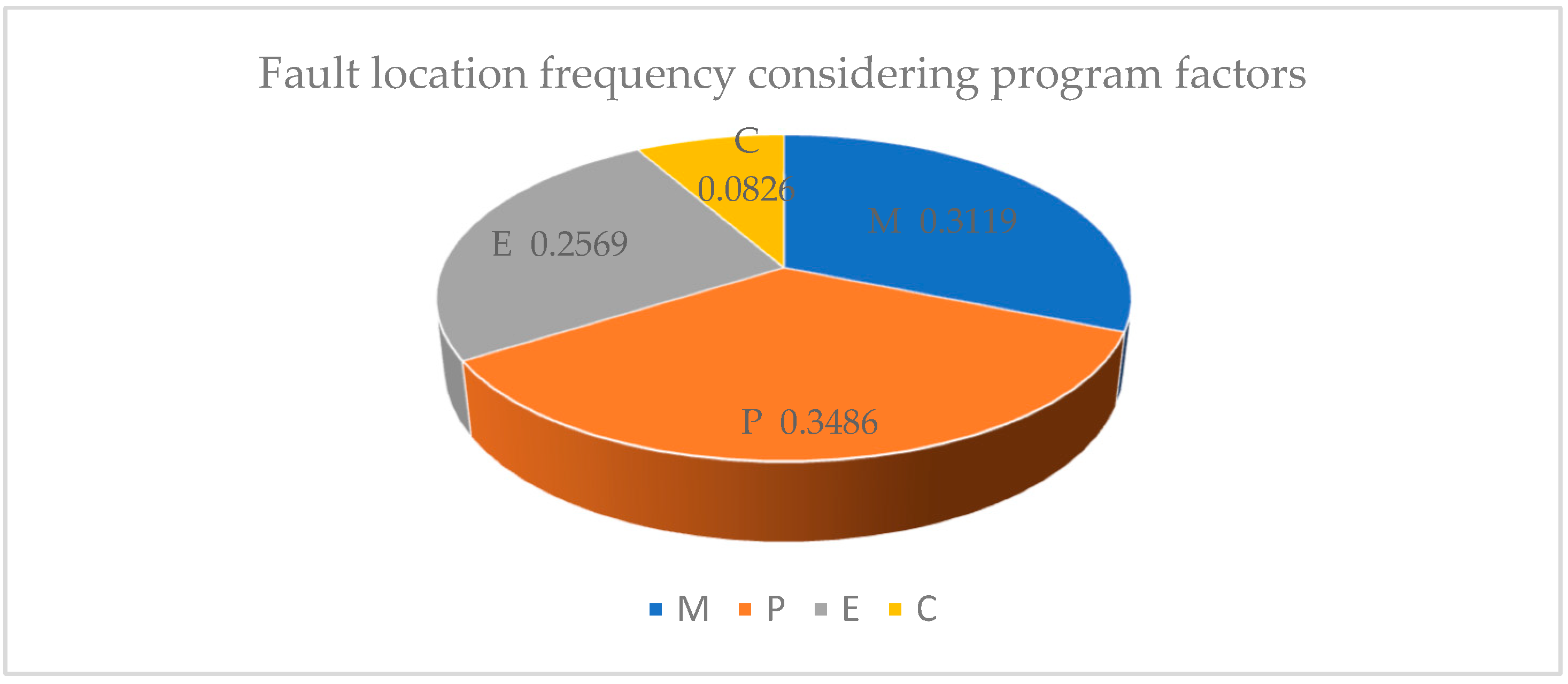
- Due to the influence of human factors in the proposed reliability prediction method, the failure frequency, failure mode and main failure causes of each system of the loading and unloading truss robot for CNC punch are calculated through FMEA analysis on the collected fault record data of the loading and unloading truss robot for CNC punch. Among them, the pneumatic system is the most frequent failure system of the loading and unloading truss robot for CNC punch, accounting for 34.86%. Therefore, it is concluded that the pneumatic system is the weak link of the loading and unloading truss robot for CNC punch, which verifies the effectiveness of the reliability prediction method and the accuracy of the predicted results;
- (3)
- The reliability prediction method proposed in this paper is consistent with the results of FMEA analysis based on actual maintenance fault record data, which indicates that FMEA analysis can be used to verify the reliability prediction results and provides a new research idea for the combination of reliability prediction and FMEA method.
5.2. Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Z.L. Design and Study of Gantry Robot System for Loading and Unloading of CNC Lathe; Dalian University of Technology: Dalian, China, 2019. [Google Scholar]
- Li, W. Design and Research of Loading and Unloading Pneumatic Manipulator for Stamping Head Based on PLC Control; South China University of Technology: Guangzhou, China, 2017. [Google Scholar]
- Pang, N.; Jia, P.; Liu, P.L.; Yin, F.; Zhou, L.; Wang, L.Q.; Yun, F.H.; Wang, X.Y. A fuzzy Markov model for risk and reliability prediction of engineering systems: A case study of a subsea wellhead connector. Appl. Sci. 2020, 10, 6902. [Google Scholar] [CrossRef]
- Kumar, R.S.; Madhusmita, S.; Prasad, D.S.; Kishoro, B.S.; Mangal, S. A Comparative Analysis of SVM and ELM Classification on Software Reliability Prediction Model. Electronics 2022, 11, 2707. [Google Scholar]
- Hao, Q.B.; Yang, Z.J.; Chen, C.H.; Chen, F.; Li, G.F. Reliability prediction for NC Machine tool based on interval AHP. J. Jilin Univ. (Eng. Technol. Ed.) 2012, 42, 845–850. [Google Scholar]
- Luan, J.H.; Tong, Y.F.; Li, D.B. Reliability prediction of PR1400 welding robot system based on fuzzy theory. Mach. Des. Manuf. Eng. 2017, 46, 38–41. [Google Scholar]
- Zhang, G.B.; Xu, F.W.; Ran, Y.; Zhang, X.G. Research on similarity evaluation and reliability prediction of mechanical structure. Chin. J. Eng. Des. 2017, 24, 264–272. [Google Scholar]
- Shenvi, A.A. Software FMEA: A learning experience. In Proceedings of the 4th India Software Engineering Conference, Thiruvananthapuram Kerala, India, 24–27 February 2011; pp. 111–114. [Google Scholar]
- Hu, T.; Yu, J.; Wang, S. Research on complex system FMEA method based on functional modeling. In Proceedings of the 2009 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009; pp. 63–66. [Google Scholar]
- Sun, L.P.; Pan, J.W.; Hu, D.W. Risk decision for FPSO oil tanks based on improved fuzzy gray relational degree. J. Harbin Eng. Univ. 2018, 39, 1760–1766. [Google Scholar]
- Wang, D.S.; Jia, Z.X.; Bi, W.H.; Pan, X.W. Reliability analysis of power and transmission system of bending robot based on FMEA. Manuf. Technol. Mach. Tool 2019, 3, 13–16. [Google Scholar] [CrossRef]
- Li, Y.F.; Huang, H.Z.; Huang, Y.X. Failure Mode and Effects Analysis and Time Varying Reliability of Solar Array Drive Assembly. J. Mech. Eng. 2020, 56, 108–115. [Google Scholar]
- Chen, C.H.; Yang, Z.J.; Chen, F.; Hao, Q.B.; Xu, B.B.; Kan, Y.N. Failure mode analysis of compute numerical control machine tools based on fuzzy-DEA. J. Jilin Univ. (Eng. Technol. Ed.) 2013, 43, 1523–1528. [Google Scholar]
- Yang, P.L.; Xu, K.; Xue, C.C.; Jia, H.R. Study on FMEA for Electromechanical Systems Based on Model Checking. J. Mech. Eng. 2016, 52, 162–168. [Google Scholar] [CrossRef]
- Prerita, O.; Apel, D.B.; Robert, H.; Brett, Z.; Krzysztof, S. A Review of Reliability and Fault Analysis Methods for Heavy Equipment and Their Components Used in Mining. Energies 2022, 15, 6263. [Google Scholar]
- Wang, Z.L.; Liu, J.; Yu, S. Time-variant reliability prediction for dynamic systems using partial information. Reliab. Eng. Syst. Saf. 2020, 195, 106756. [Google Scholar] [CrossRef]
- Hu, X.Y.; Wang, R.P.; Wang, X.; Fu, Y.T. Recent development of safety and reliability analysis technology for model-based complex system. Acta Aeronaut. Astronaut. Sincia 2020, 41, 523436. [Google Scholar]
- Xu, Z.G.; Dang, Y.Z.; Munro, P.; Wang, Y.H. A data-driven approach for constructing the component-failure mode matrix for FMEA. J. Intell. Manuf. 2020, 31, 249–265. [Google Scholar] [CrossRef]
- Chang, K.H.; Chang, Y.C.; Lai, P.T. Applying the concept of exponential approach to enhance the assessment capability of FMEA. J. Intell. Manuf. 2014, 25, 1413–1427. [Google Scholar] [CrossRef]
- GB/T 37963-2019; Handbook of Reliability Prediction Model and Data for Electronic Equipment. State Administration for Market Regulation, Standardization Administration of the People’s Republic of China; Standards Press of China: Beijing, China, 2019.
- Fan, S.H. Reliability Allocation of NC Lathe Based on Fuzzy Theory; Jilin University: Changchun, China, 2011; pp. 12–33. [Google Scholar]
- Wang, Y.M.; Chin, K.S.; Poon, G.K.K.; Yang, J.B. Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean. Expert Syst. Appl. 2009, 36, 1195–1207. [Google Scholar] [CrossRef]
- Bian, R.P. Research on Reliability of Material-Cutting Truss Robot on CNC Punch; School of Mechanical Engineering, University of Science and Technology Beijing: Beijing, China, 2020. [Google Scholar]

| Serial Number | Name | Quantity | Failure Rate (1/h) | Cumulative Failure Rate (1/h) |
|---|---|---|---|---|
| 1 | Sensor | 34 | 3.858 × 10−6 | 1.312 × 10−4 |
| 2 | Connector | 500 | 7.890 × 10−8 | 3.945 × 10−5 |
| 3 | Digital module | 6 | 5.787 × 10−6 | 3.472 × 10−5 |
| 4 | Circuit breaker | 7 | 2.894 × 10−6 | 2.026 × 10−5 |
| 5 | AC contactor | 3 | 6.705 × 10−6 | 2.012 × 10−5 |
| 6 | Light curtain | 2 | 5.787 × 10−6 | 1.157 × 10−5 |
| 7 | Intermediate relay | 5 | 2.251 × 10−6 | 1.126 × 10−5 |
| 8 | Touch screen | 1 | 9.645 × 10−6 | 9.645 × 10−6 |
| 9 | PLC | 1 | 8.267 × 10−6 | 8.267 × 10−6 |
| 10 | Communication module | 1 | 7.716 × 10−6 | 7.716 × 10−6 |
| 11 | Switch | 1 | 6.430 × 10−6 | 6.430 × 10−6 |
| 12 | Analog module | 1 | 5.787 × 10−6 | 5.787 × 10−6 |
| 13 | Servo drive | 3 | 9.873 × 10−7 | 2.962 × 10−6 |
| 14 | Switching power supply | 2 | 1.250 × 10−6 | 2.500 × 10−6 |
| 15 | Tricolor lights | 1 | 9.690 × 10−7 | 9.690 × 10−7 |
| 16 | Breakout connector | 8 | 6.903 × 10−8 | 5.522 × 10−7 |
| 17 | Isolating switch | 1 | 3.041 × 10−7 | 3.041 × 10−7 |
| 18 | Operating handle | 1 | 3.041 × 10−7 | 3.041 × 10−7 |
| 19 | Switch | 1 | 3.041 × 10−7 | 3.041 × 10−7 |
| 20 | Button | 3 | 7.180 × 10−8 | 2.154 × 10−7 |
| 21 | Frequency converter | 2 | 2.355 × 10−8 | 4.709 × 10−8 |
| Statistics | 3.146 × 10−4 |
| Evaluation Factor Language Fuzzy Variable | Level | Fuzzy Number |
|---|---|---|
| Exceptionally High (VH) | 9–10 | (8, 9, 10), (9, 10, 10) |
| High (H) | 7–8 | (6, 7, 8), (7, 8, 9) |
| Medium (M) | 5–6 | (4, 5, 6), (5, 6, 7) |
| Low | 3–4 | (2, 3, 4), (3, 4, 5) |
| Extra Low (VL) | 1–2 | (1, 1, 2), (1, 2, 3) |
| Evaluation Factors | Expert | M | P | E |
|---|---|---|---|---|
| Complexity | Z1 | (8, 9, 10) | (1, 2, 3) | (6, 7, 8) |
| Z2 | (7, 8, 9) | (2, 3, 4) | (7, 8, 9) | |
| Z3 | (8, 9, 10) | (1, 2, 3) | (6, 7, 8) | |
| Z4 | (8, 9, 10) | (3, 4, 5) | (8, 9, 10) | |
| Z5 | (7, 8, 9) | (2, 3, 4) | (6, 7, 8) | |
| Technical level | Z1 | (1, 2, 3) | (2, 3, 4) | (5, 6, 7) |
| Z2 | (1, 1, 2) | (3, 4, 5) | (4, 5, 6) | |
| Z3 | (1, 1, 2) | (2, 3, 4) | (6, 7, 8) | |
| Z4 | (2, 3, 4) | (2, 3, 4) | (5, 6, 7) | |
| Z5 | (1, 1, 2) | (4, 5, 6) | (7, 8, 9) | |
| Working hours | Z1 | (5, 6, 7) | (8, 9, 10) | (8, 9, 10) |
| Z2 | (7, 8, 9) | (9, 10, 10) | (9, 10, 10) | |
| Z3 | (6, 7, 8) | (7, 8, 9) | (9, 10, 10) | |
| Z4 | (6, 7, 8) | (8, 9, 10) | (8, 9, 10) | |
| Z5 | (7, 8, 9) | (8, 9, 10) | (8, 9, 10) | |
| Environmental conditions | Z1 | (5, 6, 7) | (6, 7, 8) | (1, 1, 2) |
| Z2 | (2, 3, 4) | (5, 6, 7) | (1, 1, 2) | |
| Z3 | (5, 6, 7) | (7, 8, 9) | (1, 2, 3) | |
| Z4 | (4, 5, 6) | (7, 8, 9) | (1, 2, 3) | |
| Z5 | (4, 5, 6) | (6, 7, 8) | (1, 1, 2) |
| Expert | Expert Weight | Complexity Weight | Technical Level Weight | Work Time Weight | Environmental Condition Weight |
|---|---|---|---|---|---|
| Z1 | 0.23 | (3, 4, 5) | (2, 3, 4) | (1, 1, 2) | (1, 1, 2) |
| Z2 | 0.19 | (2, 3, 4) | (2, 3, 4) | (2, 3, 4) | (1, 2, 3) |
| Z3 | 0.14 | (4, 5, 6) | (3, 4, 5) | (1, 2, 3) | (1, 2, 3) |
| Z4 | 0.13 | (2, 3, 4) | (2, 3, 4) | (2, 3, 4) | (2, 3, 4) |
| Z5 | 0.31 | (3, 4, 5) | (3, 4, 5) | (1, 2, 3) | (1, 1, 2) |
| System | Complexity | Technical Level | Working Hours | Environmental Conditions |
|---|---|---|---|---|
| M | (7.50, 8.50, 9.50) | (1.13, 1.49, 2.49) | (6.27, 7.27, 8.27) | (3.99, 4.99, 5.99) |
| P | (1.76, 2.76, 3.76) | (2.81, 3.81, 4.81) | (8.05, 9.05,9.86) | (6.08, 7.08, 8.08) |
| E | (6.45, 7.45, 8.45) | (5.57, 6.57, 7.57) | (8.33, 9.33, 10.00) | (1.00, 1.27, 2.27) |
| Factor weight | (2.82, 3.82, 4.82) | (2.45, 3.45, 4.45) | (1.32, 2.09, 3.09) | (1.13, 1.59, 2.59) |
| System | Cut Set | Complexity | Technical Level | Working Hours | Environmental Conditions |
|---|---|---|---|---|---|
| M | 0 | (7.50, 9.50) | (1.13, 2.49) | (6.27, 8.27) | (3.99, 5.99) |
| 0.2 | (7.70, 9.30) | (1.20, 2.29) | (6.47, 8.07) | (4.19, 5.79) | |
| 0.4 | (7.90, 9.10) | (1.27, 2.09) | (6.67, 7.87) | (4.39, 5.59) | |
| 0.6 | (8.10, 8.90) | (1.35, 1.89) | (6.87, 7.67) | (4.59, 5.39) | |
| 0.8 | (8.30, 8.70) | (1.42, 1.69) | (7.07, 7.47) | (4.79, 5.19) | |
| 1 | (8.50, 8.50) | (1.49, 1.49) | (7.27, 7.27) | (4.99, 4.99) | |
| P | 0 | (1.76, 3.76) | (2.81, 4.81) | (8.05, 9.86) | (6.08, 8.08) |
| 0.2 | (1.96, 3.56) | (3.01, 4.61) | (8.25, 9.70) | (6.28, 7.88) | |
| 0.4 | (2.16, 3.36) | (3.21, 4.41) | (8.45, 9.54) | (6.48, 7.68) | |
| 0.6 | (2.36, 3.16) | (3.41, 4.21) | (8.65, 9.37) | (6.68, 7.48) | |
| 0.8 | (2.56, 2.96) | (3.61, 4.01) | (8.85, 9.21) | (6.88, 7.28) | |
| 1 | (2.76, 2.76) | (3.81, 3.81) | (9.05, 9.05) | (7.08, 7.08) | |
| E | 0 | (6.45, 8.45) | (5.57, 7.57) | (8.33, 10.00) | (1.00, 2.27) |
| 0.2 | (6.65, 8.25) | (5.77, 7.37) | (8.53, 9.87) | (1.05, 2.07) | |
| 0.4 | (6.85, 8.05) | (5,97, 7,17) | (8.73, 9.73) | (1.11, 1.87) | |
| 0.6 | (7.05, 7.85) | (6.17, 6.97) | (8.93, 9.60) | (1.16, 1.67) | |
| 0.8 | (7.25, 7.65) | (6.37, 6.77) | (9.13, 9.46) | (1.22, 1.47) | |
| 1 | (7.45, 7.45) | (6.57, 6.57) | (9.33, 9.33) | (1.27, 1.27) |
| Cut Set | ||||
|---|---|---|---|---|
| 0 | (0.189, 0.624) | (0.164, 0.576) | (0.088, 0.400) | (0.076, 0.336) |
| 0.2 | (0.228, 0.569) | (0.194, 0.524) | (0.109, 0.358) | (0.090, 0.297) |
| 0.4 | (0.267, 0.514) | (0.224, 0.472) | (0.129, 0.317) | (0.103, 0.259) |
| 0.6 | (0.306, 0.459) | (0.255, 0.420) | (0.150, 0.275) | (0.117, 0.221) |
| 0.8 | (0.346, 0.404) | (0.285, 0.367) | (0.170, 0.233) | (0.131, 0.183) |
| 1 | (0.349, 0.349) | (0.315, 0.315) | (0.191, 0.191) | (0.145, 0.145) |
| System | Score Centroid Value | Scoring Factor | MTBF Value (h) | Failure Rate (1/h) |
|---|---|---|---|---|
| Mechanical system | 1.840 | 0.867 | 2756.319 | 3.628 × 10−4 |
| Pneumatic system | 1.797 | 0.847 | 2691.464 | 3.715 × 10−4 |
| Electrical control system | 2.122 | 1.000 | 3179.145 | 3.146 × 10−4 |
| Fault Location Code | Fault Location | Fault Record | Number of Failures | Total System Failures | Failure Frequency |
|---|---|---|---|---|---|
| M | Mechanical system | The frame of the raw material car is deformed | 1 | 34 | 0.3119 |
| X-axis chain is disconnected | 1 | ||||
| U-axis drag chain collision parts | 1 | ||||
| Clamp interferes with locating plate | 1 | ||||
| Brush table slider damaged | 1 | ||||
| X-axis motor is damaged | 1 | ||||
| X-axis slider is damaged | 1 | ||||
| Motor damage of raw material car | 1 | ||||
| The brush machine motor is crushed by the panel | 1 | ||||
| X-axis chain slot is damaged | 1 | ||||
| Hydraulic elevator reducer oil leakage | 1 | ||||
| The motor of the brush stand is burnt out | 1 | ||||
| U-shaft unloading clamp reducer is damaged | 1 | ||||
| U-shaft unloading clamp reducer does not turn | 1 | ||||
| Z-axis reducer oil leakage | 1 | ||||
| Z-axis is disconnected from the gear shaft connected with the reducer | 1 | ||||
| Unloading reducer oil leakage | 1 | ||||
| The wheel of the raw material car slipped | 1 | ||||
| Fence deformation | 1 | ||||
| U-shaft reducer oil leakage | 1 | ||||
| The chain of X-axis is loose | 1 | ||||
| U-axis chain is disconnected | 1 | ||||
| X-axis chain groove deformation | 1 | ||||
| Cylinder leakage | 1 | ||||
| X-axis reducer oil leakage | 1 | ||||
| The key between the U-axis motor and the reducer slips out | 1 | ||||
| X-axis motor is burnt out | 1 | ||||
| X-axis chain deformation | |||||
| The roller bearing of the raw material car is broken | 1 | ||||
| Brush table roller slip | 1 | ||||
| Raw material car motor abnormal sound | 1 | ||||
| The U shaft interferes with the tooling cylinder during unloading | 1 | ||||
| Brush table slip when full load | 1 | ||||
| Motor coupling of raw material car falls off | 1 | ||||
| P | Pneumatic system | Individual tooling sucker does not inhale | 1 | 38 | 0.3486 |
| The tooling cylinder rod is broken | 8 | ||||
| Vacuum generator failure | 3 | ||||
| Individual sucker cannot absorb the sheet material | 1 | ||||
| The tooling cylinder broke the sucker | 1 | ||||
| The reducing valve is damaged | 2 | ||||
| Sucker failure | 2 | ||||
| Tooling cylinder damage | 4 | ||||
| Vacuum pump damage | 2 | ||||
| Three-way pilot solenoid valve is damaged | 2 | ||||
| The vacuum generator is damaged by oil | 1 | ||||
| The vacuum generator is damaged by oil | 1 | ||||
| The sucker has no suction | 1 | ||||
| The tooling sucker is knocked off | 1 | ||||
| Tooling cylinder positioning plate is not accurate | 1 | ||||
| The gear cylinder does not move | 1 | ||||
| The tooling sucker is damaged | 1 | ||||
| Sucker with plate | 1 | ||||
| Right-angle gas pipe joint leaks | 1 | ||||
| Three-way gas pipe joint leakage damage | 1 | ||||
| The tooling cylinder does not pop out sensitively | 1 | ||||
| The tooling cylinder does not operate | 1 | ||||
| E | Electrical control system | The curtain of light flickers frequently | 1 | 28 | 0.2569 |
| Proximity switch failure | 1 | ||||
| Breaker damage | 1 | ||||
| Displacement sensor failure | 1 | ||||
| The emergency stop button is damaged | 1 | ||||
| PLC controller damaged | 1 | ||||
| Z-axis motor line is disconnected | 1 | ||||
| Inverter damage | 3 | ||||
| Hydraulic lifting platform towing chain line disconnected | 1 | ||||
| Motor line of raw material car is disconnected | 1 | ||||
| X-axis servo motor drive burned out | 1 | ||||
| The indicator light of the electric cabinet is not on | 1 | ||||
| The outer wiring of the light curtain is burnt by short circuit | 1 | ||||
| The fan of the electric cabinet is damaged | 1 | ||||
| Curtain failure | 1 | ||||
| Inspection proximity switch is damaged | 1 | ||||
| X-axis servo drive is damaged | 1 | ||||
| The fan of the electric cabinet does not work | 1 | ||||
| The loading drag chain is disconnected | 1 | ||||
| Z-axis servo motor drive is damaged | 2 | ||||
| Proximity switch failure | 1 | ||||
| Full load proximity switch of hydraulic lifting platform is damaged | 1 | ||||
| Access switch of U-axis retaking clamp is damaged | 1 | ||||
| Unloading tow line is damaged | 1 | ||||
| The light curtain line is broken by the groove cover | 1 | ||||
| C | Program | The sucker failed to pick up the sheet | 1 | 9 | 0.0826 |
| Tooling cylinder interference plate | 1 | ||||
| Sucker with plate | 1 | ||||
| When loading, the sucker cannot absorb the sheet material alarm | 1 | ||||
| Misalignment of loading material | 1 | ||||
| U-shaft motor will alarm when unloading | 1 | ||||
| Loading position is unstable | 1 | ||||
| Loading rebound causes abnormal positioning | 1 | ||||
| Z-axis motor often alarms | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Jia, Z.; Bian, R.; He, K.; Jia, Z. Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch. Appl. Sci. 2023, 13, 4951. https://doi.org/10.3390/app13084951
Zhang K, Jia Z, Bian R, He K, Jia Z. Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch. Applied Sciences. 2023; 13(8):4951. https://doi.org/10.3390/app13084951
Chicago/Turabian StyleZhang, Kaiyue, Zhixin Jia, Renpeng Bian, Ketai He, and Zhicheng Jia. 2023. "Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch" Applied Sciences 13, no. 8: 4951. https://doi.org/10.3390/app13084951
APA StyleZhang, K., Jia, Z., Bian, R., He, K., & Jia, Z. (2023). Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch. Applied Sciences, 13(8), 4951. https://doi.org/10.3390/app13084951






