A New Method of Investigation of the Orientation of Galaxies in Clusters in the Absence of Information on Their Morphological Types
Abstract
1. Introduction
2. Observational Data
3. Method of the Investigation
3.1. Statistical Methods
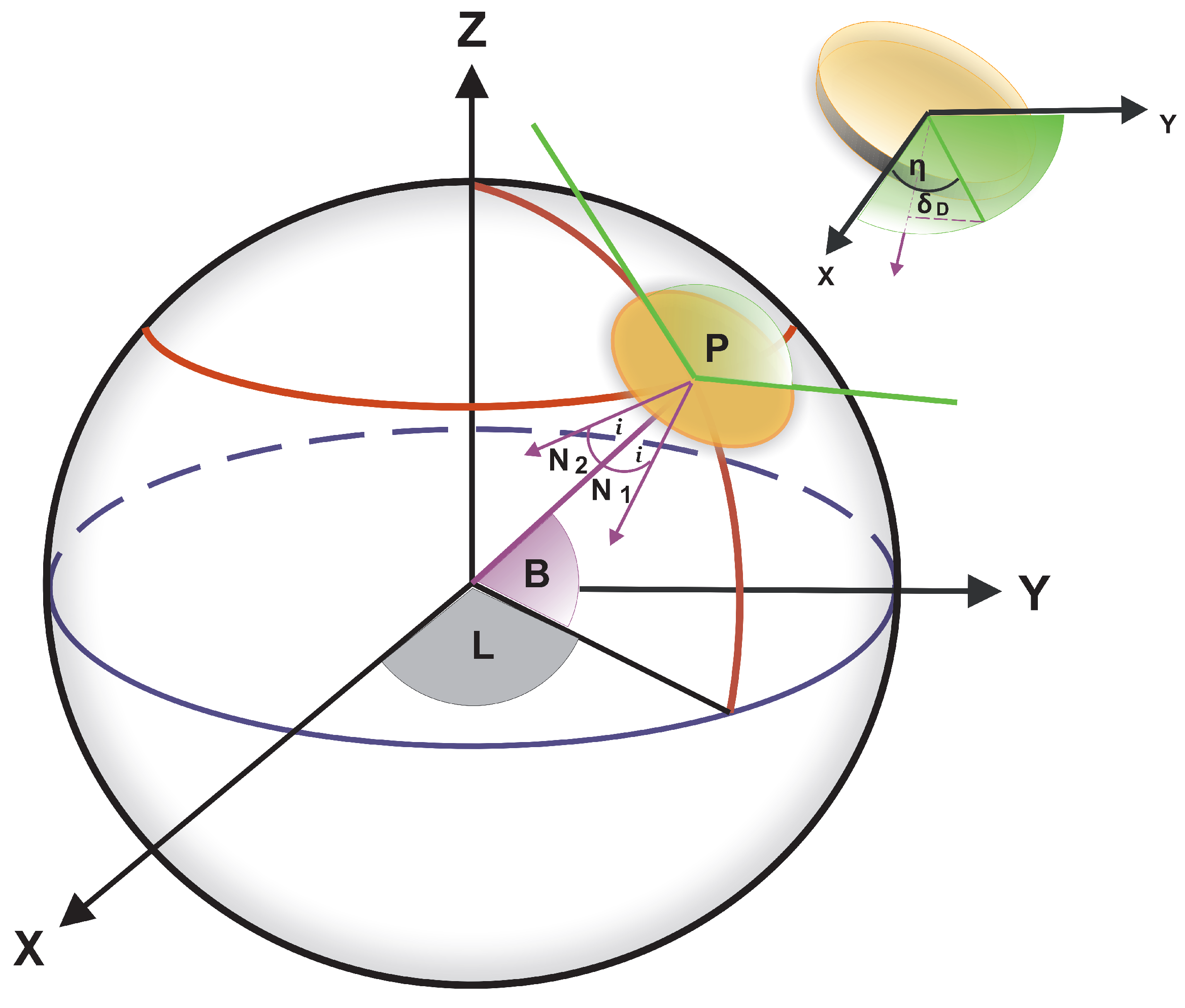
3.2. Assumptions of a New Method of Investigation
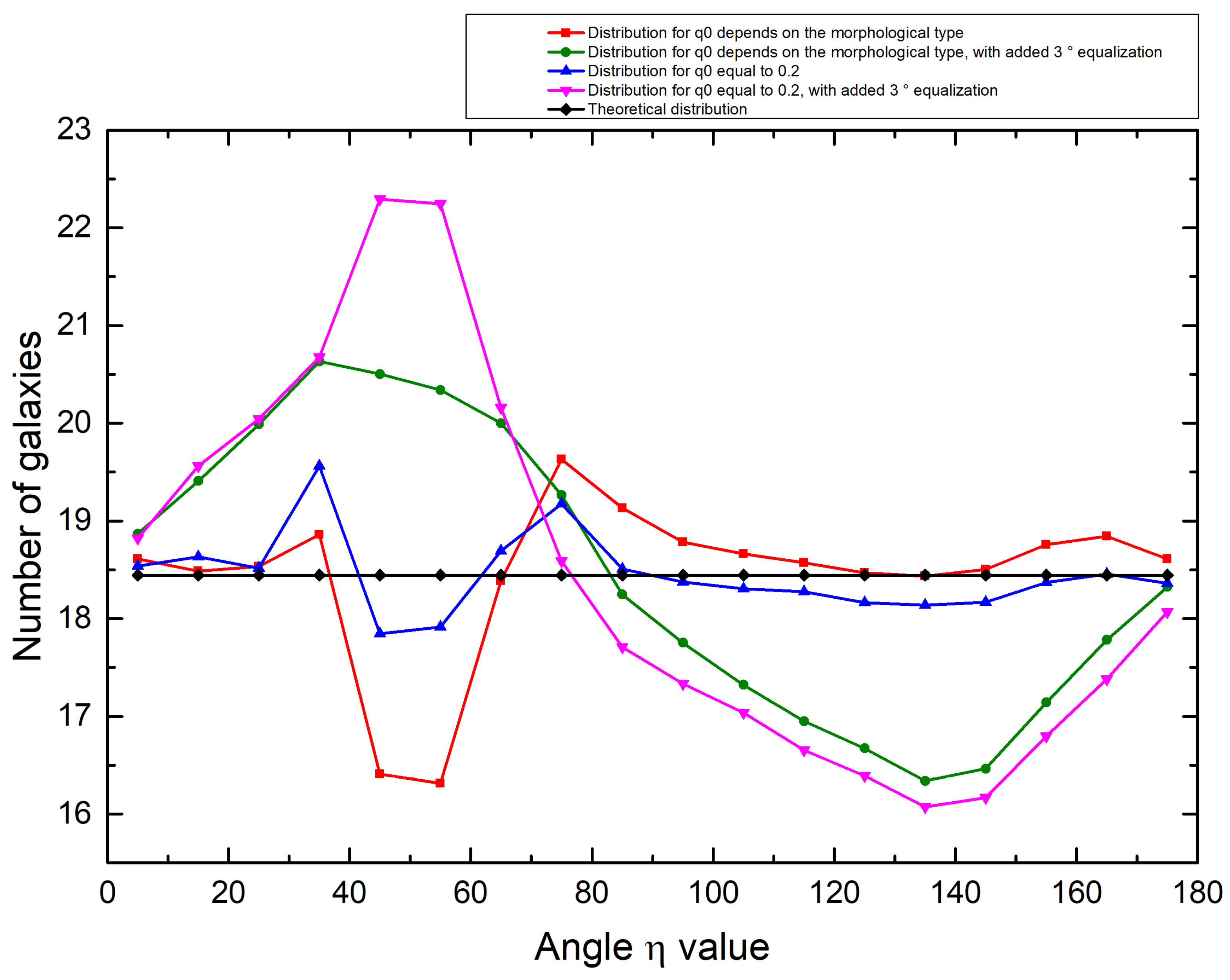
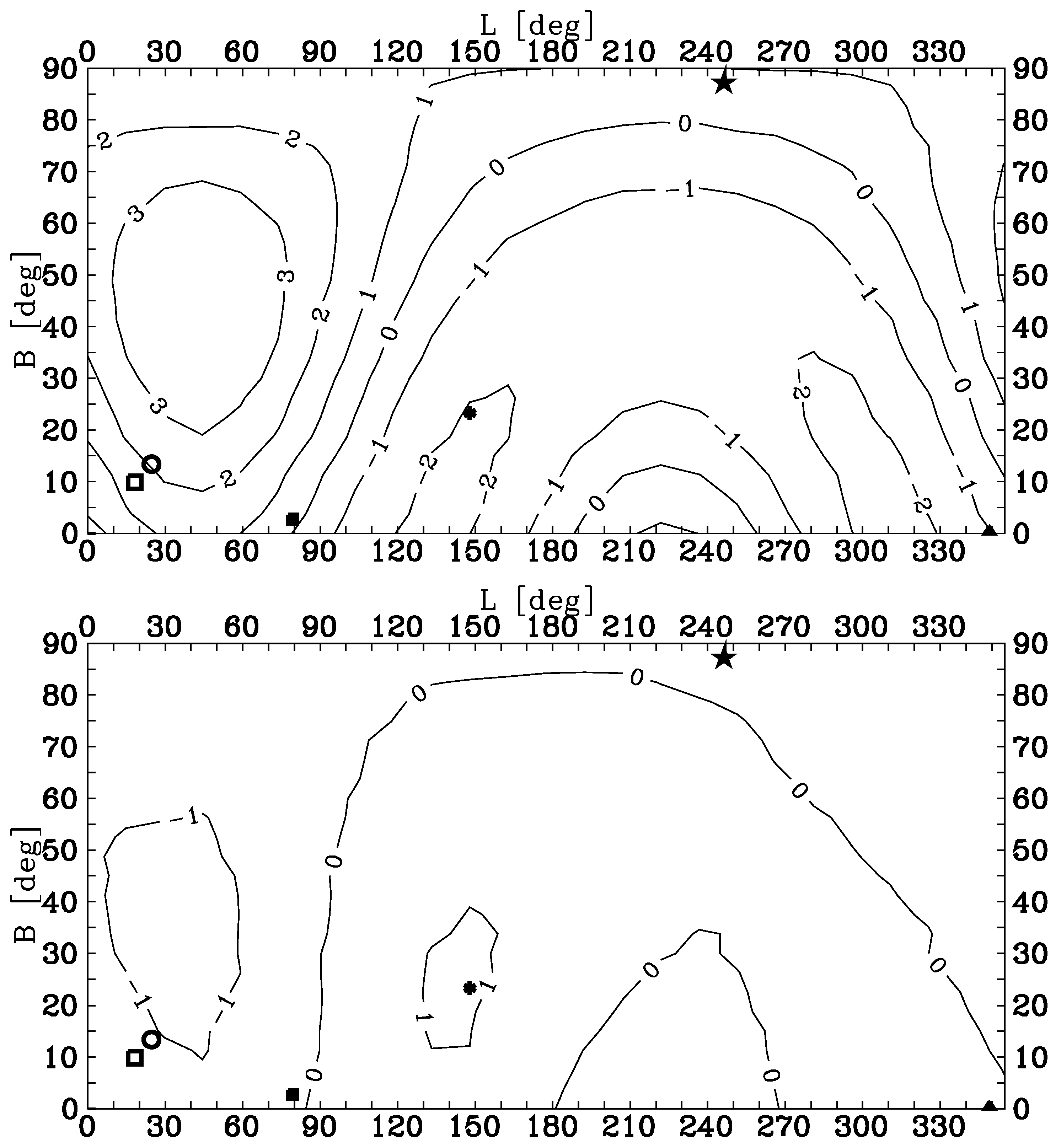
4. The Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fourier Test
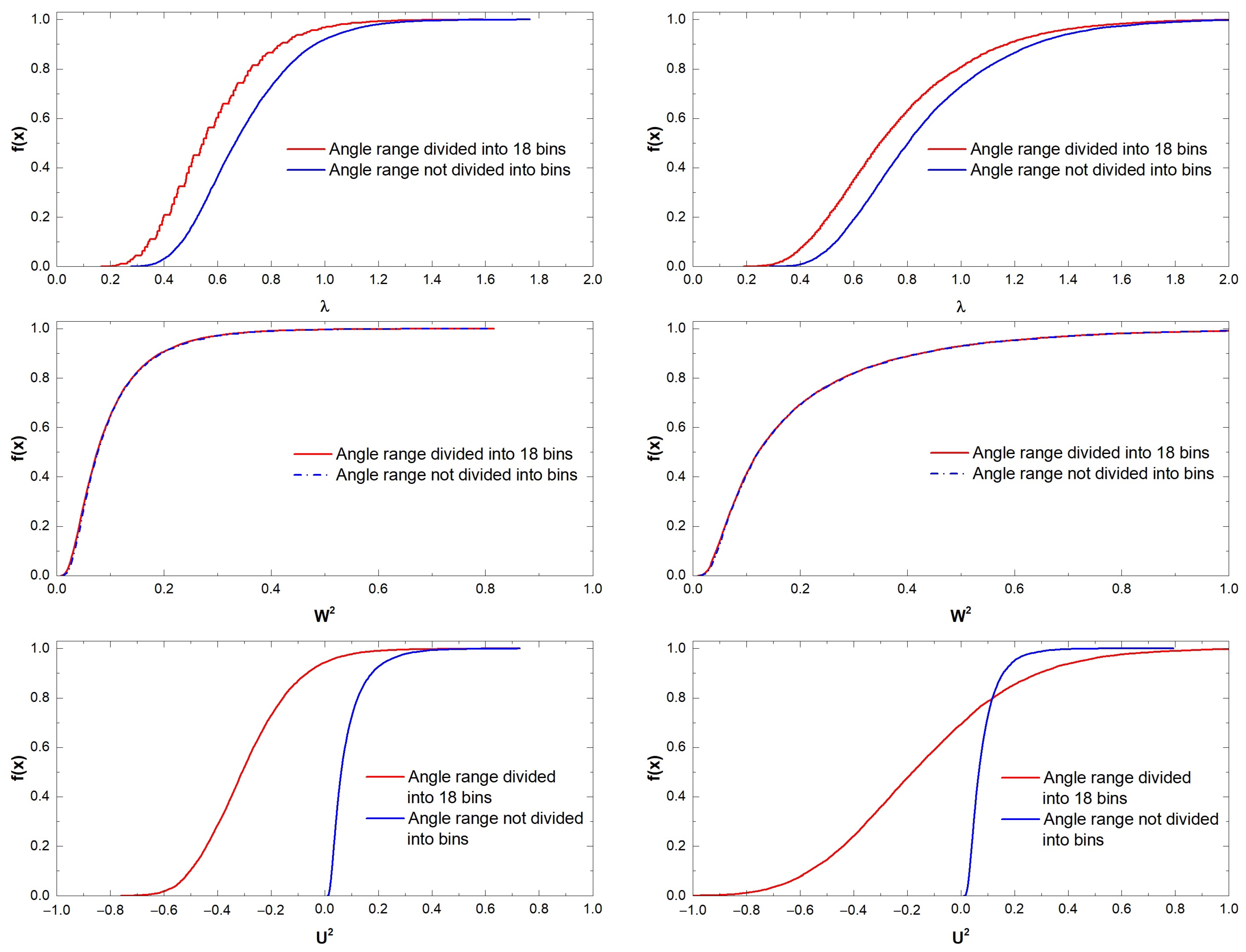
Appendix B. Influence of Division into Bins on the Values of the Obtained Statistical Tests
| Group | Angle Range Not Divided into Bins | Angle Range Divided into 18 Bins | ||||||
|---|---|---|---|---|---|---|---|---|
| 11 | 1.332 | 0.6221 | 0.5021 | 0.6193 | 1.197 | 0.6769 | 0.5367 | −0.1641 |
| 12 | 0.792 | 0.1445 | 0.5041 | 0.1388 | 0.549 | 0.1183 | 0.5374 | −0.3470 |
| 13 | 0.645 | 0.0515 | 0.5023 | 0.0509 | 0.621 | 0.0726 | 0.5357 | −0.0905 |
| 14 | 0.852 | 0.2021 | 0.5123 | 0.1376 | 0.779 | 0.1772 | 0.5493 | −0.8586 |
| 15 | 0.619 | 0.0478 | 0.4889 | 0.0318 | 0.589 | 0.0612 | 0.5223 | −0.0036 |
| 17 | 0.882 | 0.1242 | 0.4680 | 0.0421 | 0.818 | 0.1604 | 0.5002 | 0.1604 |
| 21 | 1.280 | 0.4832 | 0.4610 | 0.1051 | 1.143 | 0.4859 | 0.4947 | 0.4789 |
| 22 | 0.849 | 0.1455 | 0.5278 | 0.0481 | 0.618 | 0.1290 | 0.5568 | −0.2775 |
| 23 | 0.657 | 0.0624 | 0.4944 | 0.0592 | 0.468 | 0.0670 | 0.5286 | −0.0148 |
| 31 | 1.982 | 1.3491 | 0.4321 | 0.3796 | 1.794 | 1.3340 | 0.4656 | 1.0848 |
| 41 | 1.473 | 0.5381 | 0.5365 | 0.2828 | 1.371 | 0.5135 | 0.5710 | −0.4546 |
| 42 | 0.915 | 0.2320 | 0.5265 | 0.0705 | 0.747 | 0.2420 | 0.5604 | −0.5970 |
| 44 | 1.273 | 0.4698 | 0.5518 | 0.2551 | 1.336 | 0.4800 | 0.5885 | −0.1473 |
| 51 | 1.508 | 0.5760 | 0.4644 | 0.2862 | 1.443 | 0.5956 | 0.4990 | 0.5954 |
| 52 | 1.528 | 0.6346 | 0.4547 | 0.2816 | 1.417 | 0.6913 | 0.4897 | 0.6731 |
| 53 | 0.723 | 0.1024 | 0.4888 | 0.0698 | 0.620 | 0.0862 | 0.5241 | −0.0647 |
| 61 | 0.728 | 0.0932 | 0.4993 | 0.0930 | 0.615 | 0.0900 | 0.5320 | −0.1735 |
| 64 | 1.007 | 0.2512 | 0.5375 | 0.1075 | 0.836 | 0.2517 | 0.5696 | −0.2426 |
| Group | Angle Range Not Divided into Bins | Angle Range Divided into 18 Bins | ||||||
|---|---|---|---|---|---|---|---|---|
| 11 | 2.089 | 1.2378 | 0.4744 | 0.8272 | 2.003 | 1.2774 | 0.5020 | 1.2750 |
| 12 | 1.810 | 1.0361 | 0.5449 | 0.3667 | 1.756 | 0.9940 | 0.5723 | −0.7409 |
| 13 | 0.914 | 0.1862 | 0.5132 | 0.1638 | 0.766 | 0.2142 | 0.5430 | −0.0221 |
| 14 | 1.142 | 0.3100 | 0.5177 | 0.1769 | 1.001 | 0.2964 | 0.5455 | −0.5861 |
| 15 | 1.020 | 0.2726 | 0.4606 | 0.0707 | 0.906 | 0.2649 | 0.4910 | 0.2545 |
| 17 | 0.548 | 0.0570 | 0.4946 | 0.0546 | 0.460 | 0.0467 | 0.5236 | 0.0021 |
| 21 | 1.274 | 0.3330 | 0.5241 | 0.1894 | 1.228 | 0.2912 | 0.5515 | −0.3671 |
| 22 | 1.004 | 0.1719 | 0.4771 | 0.1058 | 0.980 | 0.1935 | 0.5040 | 0.1915 |
| 23 | 1.163 | 0.3179 | 0.4610 | 0.1660 | 1.089 | 0.2968 | 0.4900 | 0.2868 |
| 31 | 1.744 | 0.6451 | 0.4533 | 0.1865 | 1.564 | 0.6733 | 0.4820 | 0.6054 |
| 41 | 1.967 | 0.8206 | 0.4525 | 0.3880 | 1.949 | 0.8840 | 0.4800 | 0.8075 |
| 42 | 1.231 | 0.5851 | 0.5403 | 0.2119 | 1.238 | 0.5716 | 0.5679 | −0.4880 |
| 44 | 0.731 | 0.1182 | 0.5119 | 0.1068 | 0.783 | 0.1229 | 0.5424 | −0.0206 |
| 51 | 1.187 | 0.3431 | 0.4732 | 0.1790 | 1.148 | 0.3636 | 0.5012 | 0.3633 |
| 52 | 1.927 | 1.0018 | 0.4408 | 0.3992 | 1.923 | 1.1189 | 0.4671 | 0.9322 |
| 53 | 0.434 | 0.0278 | 0.4999 | 0.0278 | 0.338 | 0.0229 | 0.5286 | −0.1903 |
| 61 | 0.775 | 0.0735 | 0.4956 | 0.0685 | 0.643 | 0.0716 | 0.5243 | −0.0812 |
| 64 | 2.056 | 1.1930 | 0.4116 | 0.3966 | 1.881 | 1.4348 | 0.4368 | 1.0276 |
| Group | Angle Range Not Divided into Bins | Angle Range Divided into 18 Bins | ||||||
|---|---|---|---|---|---|---|---|---|
| 11 | 0.713 | 0.0803 | 0.4983 | 0.0784 | 0.677 | 0.0710 | 0.5325 | −0.5891 |
| 12 | 0.593 | 0.0551 | 0.4997 | 0.0550 | 0.384 | 0.0455 | 0.5351 | −0.3625 |
| 13 | 0.830 | 0.1985 | 0.5056 | 0.1945 | 0.786 | 0.2241 | 0.5389 | 0.0307 |
| 14 | 0.731 | 0.0988 | 0.5089 | 0.0651 | 0.623 | 0.1024 | 0.5444 | −0.7387 |
| 15 | 0.771 | 0.0949 | 0.5131 | 0.0726 | 0.789 | 0.0932 | 0.5482 | −0.2091 |
| 17 | 0.622 | 0.1100 | 0.4664 | 0.0197 | 0.559 | 0.0890 | 0.4999 | 0.0890 |
| 21 | 0.928 | 0.1562 | 0.4786 | 0.0421 | 0.889 | 0.1671 | 0.5118 | 0.1328 |
| 22 | 0.938 | 0.1272 | 0.5157 | 0.0962 | 0.707 | 0.1110 | 0.5488 | −0.1888 |
| 23 | 0.762 | 0.1337 | 0.5162 | 0.1074 | 0.614 | 0.1435 | 0.5487 | −0.0934 |
| 31 | 1.140 | 0.2597 | 0.4738 | 0.1159 | 0.966 | 0.2677 | 0.5075 | 0.2560 |
| 41 | 0.834 | 0.2486 | 0.5301 | 0.0751 | 0.722 | 0.2679 | 0.5628 | −0.4889 |
| 42 | 0.992 | 0.2092 | 0.5212 | 0.1054 | 0.786 | 0.1954 | 0.5525 | −0.4389 |
| 44 | 1.004 | 0.2639 | 0.5419 | 0.1233 | 0.900 | 0.2598 | 0.5777 | −0.2228 |
| 51 | 0.638 | 0.0958 | 0.4838 | 0.0362 | 0.552 | 0.0833 | 0.5185 | 0.0054 |
| 52 | 1.580 | 0.7954 | 0.4434 | 0.2440 | 1.454 | 0.7803 | 0.4799 | 0.7109 |
| 53 | 0.621 | 0.0842 | 0.5130 | 0.0401 | 0.523 | 0.0901 | 0.5479 | −0.5060 |
| 61 | 0.989 | 0.1736 | 0.4810 | 0.0804 | 0.802 | 0.1902 | 0.5125 | 0.1498 |
| 64 | 0.686 | 0.0856 | 0.5184 | 0.0510 | 0.594 | 0.0868 | 0.5513 | −0.1816 |
| Group | Angle Range Not Divided into Bins | Angle Range Divided into 18 Bins | ||||||
|---|---|---|---|---|---|---|---|---|
| 11 | 1.182 | 0.4085 | 0.4981 | 0.4062 | 1.101 | 0.4450 | 0.5249 | 0.0557 |
| 12 | 1.015 | 0.2816 | 0.5238 | 0.0936 | 0.860 | 0.2365 | 0.5490 | −0.5615 |
| 13 | 1.303 | 0.2504 | 0.4681 | 0.1204 | 1.110 | 0.2416 | 0.4970 | 0.2405 |
| 14 | 0.939 | 0.1626 | 0.5122 | 0.0997 | 0.775 | 0.1649 | 0.5406 | −0.5359 |
| 15 | 0.841 | 0.2022 | 0.4684 | 0.0725 | 0.643 | 0.1576 | 0.4991 | 0.1575 |
| 17 | 0.824 | 0.1234 | 0.4678 | 0.0403 | 0.683 | 0.1061 | 0.4965 | 0.1052 |
| 21 | 0.678 | 0.0876 | 0.4859 | 0.0381 | 0.564 | 0.0917 | 0.5139 | 0.0438 |
| 22 | 0.452 | 0.0394 | 0.4997 | 0.0394 | 0.535 | 0.0286 | 0.5273 | −0.0656 |
| 23 | 0.537 | 0.0514 | 0.5009 | 0.0513 | 0.444 | 0.0477 | 0.5278 | −0.0294 |
| 31 | 1.292 | 0.2844 | 0.4694 | 0.0877 | 1.104 | 0.3029 | 0.4966 | 0.3005 |
| 41 | 1.209 | 0.2698 | 0.4883 | 0.2434 | 0.962 | 0.2555 | 0.5174 | 0.1976 |
| 42 | 0.900 | 0.2695 | 0.5276 | 0.0943 | 0.879 | 0.2468 | 0.5543 | −0.4326 |
| 44 | 0.592 | 0.0703 | 0.4838 | 0.0492 | 0.472 | 0.0678 | 0.5139 | 0.0524 |
| 51 | 1.423 | 0.3883 | 0.4668 | 0.1367 | 1.214 | 0.4058 | 0.4946 | 0.3993 |
| 52 | 1.362 | 0.5905 | 0.4536 | 0.2205 | 1.339 | 0.6194 | 0.4793 | 0.5459 |
| 53 | 0.788 | 0.0917 | 0.4900 | 0.0657 | 0.675 | 0.0943 | 0.5167 | 0.0221 |
| 61 | 1.087 | 0.2415 | 0.4748 | 0.0781 | 0.955 | 0.2249 | 0.5039 | 0.2211 |
| 64 | 0.779 | 0.1157 | 0.4940 | 0.1120 | 0.627 | 0.1198 | 0.5218 | 0.0714 |
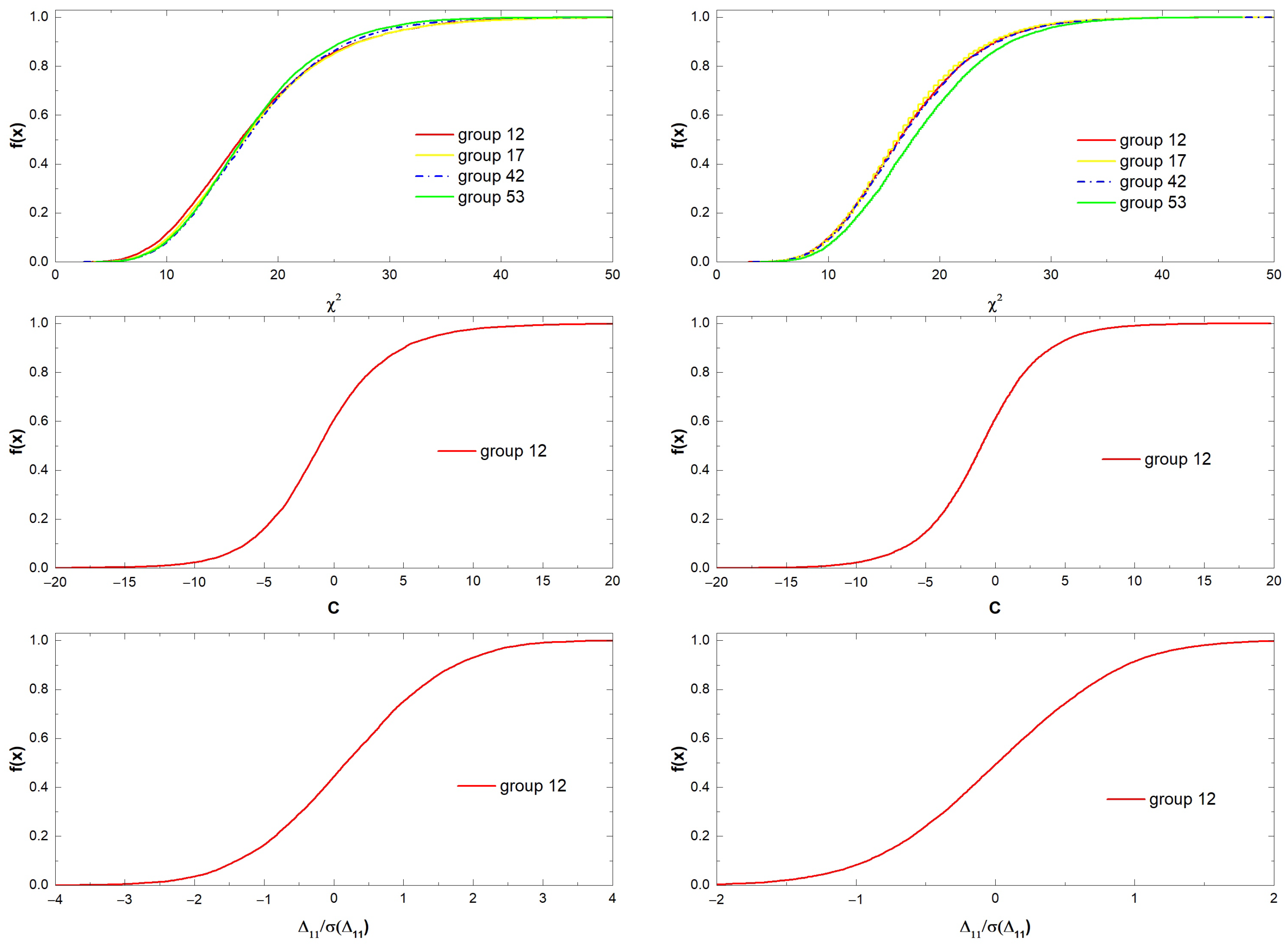
References
- Romanowsky, A.J.; Fall, S.M. Angular Momentum and Galaxy Formation Revisited. Astrophys. J. Suppl. 2015, 203, 17. [Google Scholar] [CrossRef]
- Joachimi, B.; Cacciato, M.; Kitching, T.D.; Leonard, A.; Mandelbaum, R.; Schäfer, B.M.; Sifón, C.; Hoekstra, H.; Kiessling, A.; Kirk, D. Rassat A Galaxy Alignments: An Overview. Space Sci. Rev. 2015, 193, 1. [Google Scholar] [CrossRef]
- Kiessling, A.; Cacciato, M.; Joachimi, B.; Kirk, D.; Kitching, T.D.; Leonard, A.; Mandelbaum, R.; Schäfer, B.M.; Sifón, C.; Brown, M.L.; et al. Galaxy Alignments: Theory, Modelling & Simulations. Space Sci. Rev. 2015, 193, 67. [Google Scholar]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Silk, J. Cosmic Black-Body Radiation and Galaxy Formation. Astrophys. J. 1968, 151, 459. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. Small-Scale Fluctuations of Relic Radiation. Astrophys. Space Sci. 1970, 7, 3–19. [Google Scholar] [CrossRef]
- Stephanovich, V.A.; Godłowski, W. The Distribution of Galaxies’ Gravitational Field Stemming from Their Tidal Interaction. Astrophys. J. 2015, 810, 14. [Google Scholar] [CrossRef]
- Godłowski, W.; Flin, P. The Orientations of Galaxy Groups and Formation of the Local Supercluster. Astrophys. J. 2010, 708, 920. [Google Scholar] [CrossRef]
- Pajowska, P.; Godłowski, W.; Zhu, Z.-H.; Popiela, J.; Panko, E.; Flin, P. Investigation of the orientation of galaxies in clusters: The importance, methods and results of research. J. Cosmol. Astropart. Phys. 2019, 2, 5. [Google Scholar] [CrossRef]
- Wang, P.; Libeskind, N.I.; Tempel, E.; Pawlowski, M.S.; Kang, X.; Guo, Q. The Alignment of Satellite Systems with Cosmic Filaments in the SDSS DR12. Astrophys. J. 2020, 900, 8. [Google Scholar] [CrossRef]
- Moon, J.S.; An, S.H.; Yoon, S.J. Living with Neighbors. III. The Origin of the Spin-Orbit Alignment of Galaxy Pairs: A Neighbor versus the Large-scale Structure. Astrophys. J. 2021, 909, 15. [Google Scholar] [CrossRef]
- Tovmassian, H.M. On the Problem of the Galaxy Alignment with Groups and Clusters. Astrophysics 2021, 64, 141. [Google Scholar] [CrossRef]
- Yuan, Z.S.; Wen, Z.L. The alignment between brightest cluster galaxies and host clusters. Mon. Not. R. Astr. Soc. 2022, 516, 3159. [Google Scholar] [CrossRef]
- Petit, Q.; Ducourant, C.; Slezak, E.; Sluse, D.; Delchambre, L. Shape, alignment, and mass distribution of baryonic and dark-matter halos in one EAGLE simulation. Astron. Astrophys. 2023, 669, 18. [Google Scholar] [CrossRef]
- Trujillo, I.; Carretero, C.; Patri, G. Detection of the effect of cosmological large-scale structure on the orientation of galaxies. Astrophys. J. 2006, 640, L111. [Google Scholar] [CrossRef]
- Varela, J.; Betancort-Rijo, J.; Trujillo, I.; Ricciardelli, E. The orientation of disk galaxies around large cosmic voids. Astrophys. J. 2012, 744, 82. [Google Scholar] [CrossRef]
- Okabe, T.; Nishimichi, T.; Oguri, M.; Peirani, S.; Kitayama, T.; Sasaki, S.; Suto, Y. Projected alignment of non-sphericities of stellar, gas and dark matter distributions in galaxy clusters: Analysis of the Horizon-AGN simulation. Mon. Not. R. Astr. Soc. 2018, 478, 1141. [Google Scholar] [CrossRef]
- Codis, S.; Jindal, A.; Chisari, N.E.; Vibert, D.; Dubois, Y.; Pichon, C.; Devriendt, J. Galaxy orientation with the cosmic web across cosmic time. Mon. Not. R. Astr. Soc. 2018, 481, 4753. [Google Scholar] [CrossRef]
- Ciotti, L.; Dutta, S.N. Alignment and morphology of elliptical galaxies: The influence of thecluster tidal field. Mon. Not. R. Astr. Soc. 1994, 270, 390. [Google Scholar] [CrossRef]
- Ciotti, L.; Giampieri, G. Motion of a Rigid Body in a Tidal Field: An application to elliptical galaxies in clusters. Cel. Mec. 1997, 68, 313. [Google Scholar] [CrossRef]
- Thompson, L.A. The Angular Momentum Properties of Galaxies in Rich Clusters. Astron. J. 1976, 209, 22–34. [Google Scholar] [CrossRef]
- Godłowski, W.; Piwowarska, P.; Panko, E.; Flin, P. The Orientation of Galaxies in Galaxy Clusters. Astrophys. J. 2010, 723, 985–992. [Google Scholar] [CrossRef]
- Hutsemekers, D. Evidence for Very Large-Scale Coherent Orientations of Quasar Polarization Vectors. Astron. Astrophys. 1998, 332, 410. [Google Scholar]
- Hutsemekers, D.; Cabanac, R.; Lamy, H.; Sluse, D. Mapping extreme-scale alignments of Quasar Polarization Vectors. Astron. Astrophys. 2005, 441, 915. [Google Scholar] [CrossRef]
- Migkas, K.; Pacaud, F.; Schellenberger, G.; Erler, J.; Nguyen-Dang, N.T.; Reiprich, T.H.; Ramos-Ceja, M.E.; Lovisari, L. Cosmological implications of the anisotropy of ten galaxy cluster scaling relations. Astron. Astrophys. 2021, 649, 115. [Google Scholar] [CrossRef]
- Hawley, D.L.; Peebles, P.J.E. Distribution of observed orientations of galaxies. Astron. J. 1975, 80, 477–491. [Google Scholar] [CrossRef]
- Godłowski, W. Remarks on the Methods of Investigations of Alignment of Galaxies. Astrophys. J. 2012, 747, 7. [Google Scholar] [CrossRef]
- Öpik, E.J. Preferential Orientation of Galaxies: On the Possibility of Detection. Ir. Astron. J. 1970, 9, 211. [Google Scholar]
- Jaaniste, J. The accretion spiral. Tartu Obs. 1977, 50–67. [Google Scholar]
- Jaaniste, J.; Saar, E. Orientation of Spiral Galaxies as a Test of Theories of Galaxy Formation. In The Large Scale Structures of the Universe, Proceedings of the Symposium, Tallin, Estonian, 12–16 September 1977; Longair, M.S., Einasto, J., Eds.; IAU Symposium, No. 79; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1978; p. 488. [Google Scholar]
- Flin, P.; Godłowski, W. The orientation of galaxies in the Local Supercluster. Mon. Not. R. Astr. Soc. 1986, 222, 525–541. [Google Scholar] [CrossRef]
- Holmberg, E. On the Apparent Diameters and the Orientation in Space of Extragalactic Nebulae. Medd. Fran Lunds Astron. Obs. Ser. II 1946, 117, 3–82. [Google Scholar]
- Holmberg, E. On the A photographic photometry of extragalactic nebulae. Medd. Lund. Astron. Obs. Ser. II 1958, 136, 1. [Google Scholar]
- Holmberg, E. Magnitudes, Colors, Surface Brightness, Intensity Distributions Absolute Luminosities, and Diameters of Galaxies. In Galaxies and the Universe; Sandage, A., Sandage, M., Kristian, J., Eds.; University of Chicago Press: Chicago, IL, USA, 1975; p. 123. [Google Scholar]
- Fouque, P.; Paturel, G. Standard photometric diameters of galaxies. II. Reduction of the ESO, UGC, MCG catalogues. Astron. Astroph. 1985, 150, 192–204. [Google Scholar]
- Tully, R.B. Nearby Galaxies Catalogue (NBG), 2nd ed.; Cambridge University Press: Cambridge, UK, 1988; Available online: https://vizier.cds.unistra.fr/viz-bin/VizieR?-source=VII/145 (accessed on 7 April 2023).
- Dressler, A. A catalog of morphological types in 55 rich clusters of galaxies. Astrophys. J. Suppl. Ser. 1980, 42, 565–609. [Google Scholar] [CrossRef]
- Calvi, R.; Poggianti, B.M.; Fasano, G.; Vulcani, B. The distribution of galaxy morphological types and the morphology-mass relation in different environments at low redshift. Mon. Not. R. Astr. Soc. 2012, 419, L14–L18. [Google Scholar] [CrossRef]
- Coenda, V.; Muriel, H.; Martinez, H.J. Comparing galaxy populations in compact and loose groups of galaxies. Astron. Astrophys. 2012, 543, 12. [Google Scholar] [CrossRef]
- Hoyle, B.; Masters, K.L.; Nichol, R.C.; Jimenez, R.; Bamford, S.P. The fraction of early-type galaxies in low-redshift groups and clusters of galaxies. Mon. Not. R. Astr. Soc. 2012, 423, 3478–3485. [Google Scholar] [CrossRef]
- Tully, R.B. Nearby Groups of Galaxies. II. an All-Sky Survey within 3000 Kilometers per Second. Astrophys. J. 1987, 321, 280. [Google Scholar] [CrossRef]
- Lauberts, A. ESO/Uppsala Survey of the ESO B Atlas, 1st ed.; European Southern Observatory: Garching, Germany, 1982. [Google Scholar]
- Lauberts, A.; Valentijn, E. The Surface Photometry Catalogue of the ESO-Uppsala Galaxies, 1st ed.; European Southern Observatory: Garching, Germany, 1989. [Google Scholar]
- Nilson, P. Uppsala General Catalogue of Galaxies; Uppsala Astronomiska Observatoriums Annaler; Astronomiska Observatorium: Uppsala, Sweden, 1973; Volume 1. [Google Scholar]
- Nilson, P. Catalogue of Selected Non-UGC Galaxies; Uppsala Astronomical Observatory Reports 5; Astronomiska Observatorium: Uppsala, Sweden, 1974. [Google Scholar]
- Tully, R.B.; Shaya, E.J. Infall of galaxies into the virgo cluster and some cosmological constraints. Astrophys. J. 1984, 281, 31. [Google Scholar] [CrossRef]
- Godłowski, W.; Ostrowski, M. Investigation of galactic alignment in Local Supercluster galaxy clusters. Mon. Not. R. Astr. Soc. 1999, 303, 50–64. [Google Scholar] [CrossRef][Green Version]
- Godłowski, W. Some observational aspects of the orientation of galaxies. Acta Phys. Pol. B 2011, 42, 2323–2334. [Google Scholar] [CrossRef]
- Pajowska, P.; Godlowski, W.; Panko, E.; Flin, P. Some aspects of the orientation of galaxies in clusters. J. Phys. Stud. 2012, 16, 4901. [Google Scholar] [CrossRef]
- Aryal, B.; Kafle, P.R.; Saurer, W. Radial velocity dependence in the spatial orientations of galaxies in and around the local supercluster. Mon. Not. R. Astr. Soc. 2006, 389, 471. [Google Scholar] [CrossRef]
- Feigelson, E.D.; Babu, G.J. Modern Statistical Methods for Astronomy with R Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- von Mises, R. Wahrscheinlichkeit Statistic Und Wahrheit, 1st ed.; Verlag von Julius Springer: Vienna, Austria, 1928. [Google Scholar]
- Cramér, H. On the composition of elementary errors. Scand. Actuar. J. 1928, 1928, 13–74. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-of-Fit Tests on a Circle. Biometrika 1961, 48, 109–114. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-of-Fit Tests on a Circle. II. Biometrika 1962, 49, 57–63. [Google Scholar] [CrossRef]
- Heidmann, J.; Heidmann, N.; de Vaucouleurs, G. Inclination and absorption effects on the apparent diameters, optical luminosities and neutral hydrogen radiation of galaxies. Mem. R. Astron. Soc. 1972, 75, 85. [Google Scholar]
- Chernoff, H.; Lehmann, E.L. The Use of Maximum Likelihood Estimates in χ2 Tests for Goodness of Fit. Ann. Math. Statist. 1954, 25, 579. [Google Scholar] [CrossRef]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods; Iowa Univ. Press: Iowa City, IA, USA, 1967. [Google Scholar]
- Krysicki, W.; Bartos, J.; Dyczka, W.; Królikowska, K.; Wasilewski, M. The Probability Calculus and Mathematical Statistics in Exercises (in Polish Rachunek Prawdopodobieństwa i Statystyka Matematyczna w Zadaniach II); Warszawa PWN: Warsaw, Poland, 1998. [Google Scholar]
- Percival, B.D.; Walden, A.T. Spectral Analysis for Physical Applications; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Yu, J.T.; Peebles, P.J.E. Superclusters of Galaxies? Astrophys. J. 1969, 158, 103. [Google Scholar] [CrossRef]
- Newman, W.I.; Haynes, M.P.; Terzian, Y. Redshift Data and Statistical Inference. Astrophys. J. 1994, 431, 147. [Google Scholar] [CrossRef]
- Godłowski, W.; Bajan, K.; Flin, P. Weak redshift discretisation in the Local Group of galaxies? Astron. Nachrichten 2006, 327, 103. [Google Scholar] [CrossRef][Green Version]
- Smirnow, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Origin of the Angular Momentum of Galaxies. Astrophys. J. 1969, 155, 393. [Google Scholar] [CrossRef]
- Efstathiou, G.A.; Silk, J. The Formation of Galaxies. Fundam. Cosm. Phys. 1983, 9, 1. [Google Scholar]
- Shandarin, S.F.; Habib, S.; Heitmann, K. Cosmic web, multistream flows, and tessellations. Phys. Rev. D 2012, 85, 083005. [Google Scholar] [CrossRef]
- Catelan, P.; Theuns, T. Evolution of the angular momentum of protogalaxies from tidal torques: Zel’dovich approximation. Mon. Not. R. Astr. Soc. 1996, 282, 436. [Google Scholar] [CrossRef]
- Li, L.X. Effect of the global rotation of the universe on the formation of galaxies. Gen. Rel. Grav. 1998, 30, 497. [Google Scholar] [CrossRef]
- Banerjee, P.; Szabo, T.; Pierpaoli, E.; Franco, G.; Ortiz, M.; Oramas, A.; Tornello, B. An optical catalog of galaxy clusters obtained from an adaptive matched filter finder applied to SDSS DR9 data. New Astron. 2018, 58, 61. [Google Scholar] [CrossRef]
- Wen, Z.L.; Han, J.L. Calibration of the Optical Mass Proxy for Clusters of Galaxies and an Update of the WHL12 Cluster Catalog. Astrophys. J. 2015, 807, 178. [Google Scholar] [CrossRef]
- Zou, H.; Gao, J.; Xu, X.; Zhou, X.; Ma, J.; Zhou, Z.; Zhang, T.; Nie, J.; Wang, J.; Xue, S. Galaxy Clusters from the DESI Legacy Imaging Surveys. I. Cluster Detection. Astrophys. J. Suppl. Ser. 2021, 253, 56. [Google Scholar] [CrossRef]
- Bisigello, L.; Conselice, C.J.; Baes, M.; Bolzonella, M.; Brescia, M.; Cavuoti, S.; Cucciati, O.; Humphrey, A.; Hunt, L.K.; Maraston, C. Euclid preparation—XXIII. Derivation of galaxy physical properties with deep machine learning using mock fluxes and H-band images. Mon. Not. R. Astr. Soc. 2023, 520, 3529–3548. [Google Scholar]
- Brandt, S. Data Analysis: Statistical and Computational Methods for Scientists and Engineers, 4th ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]

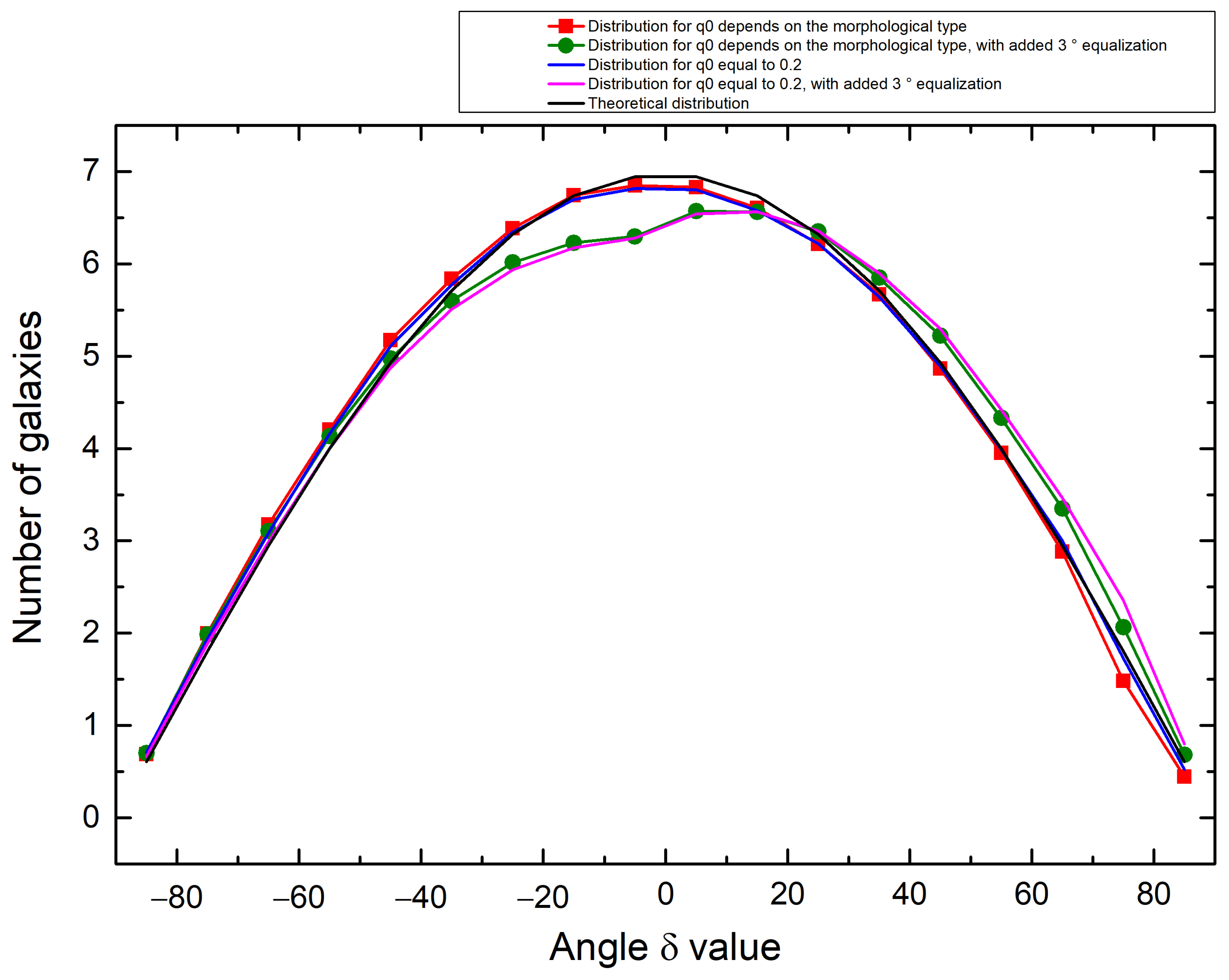
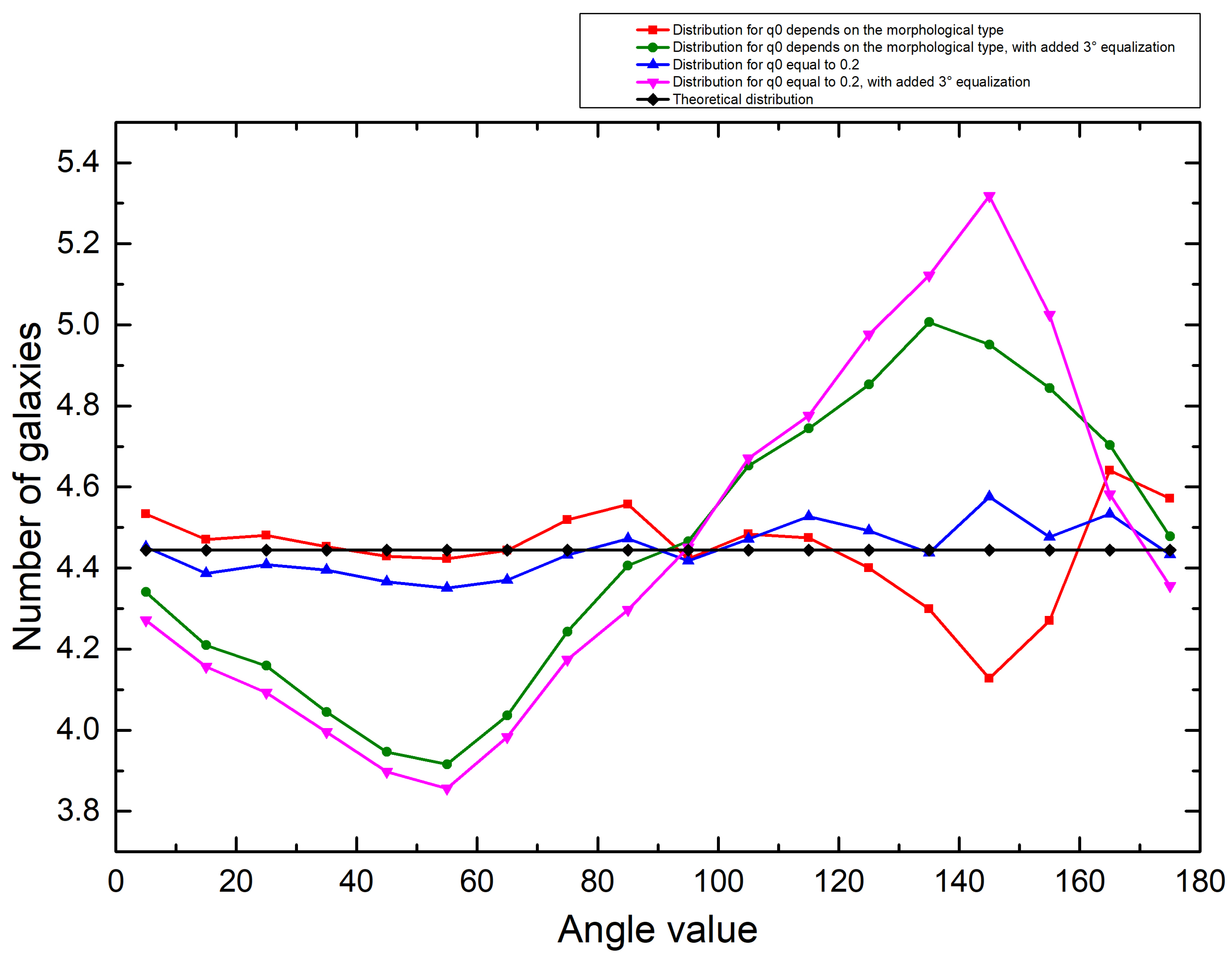
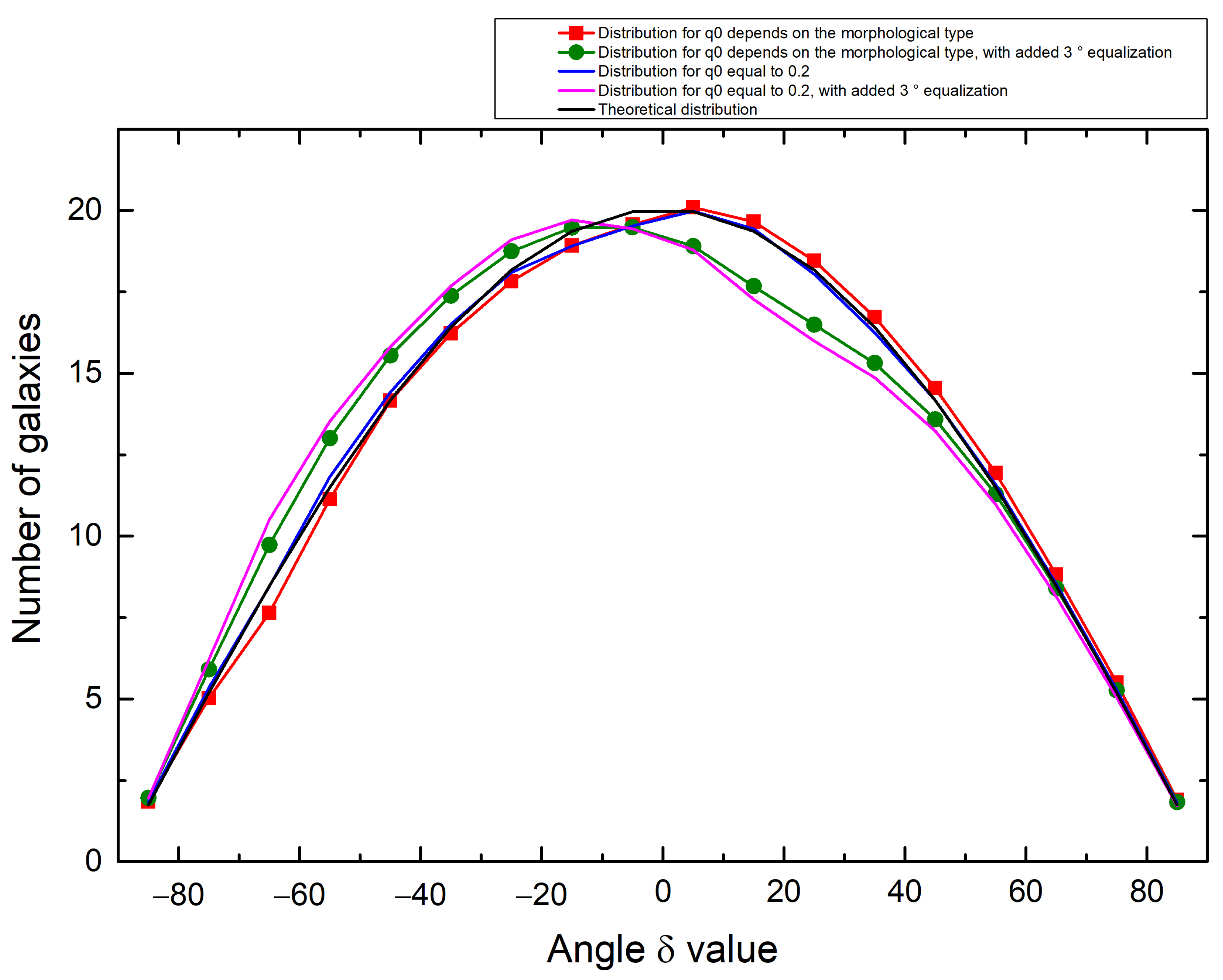
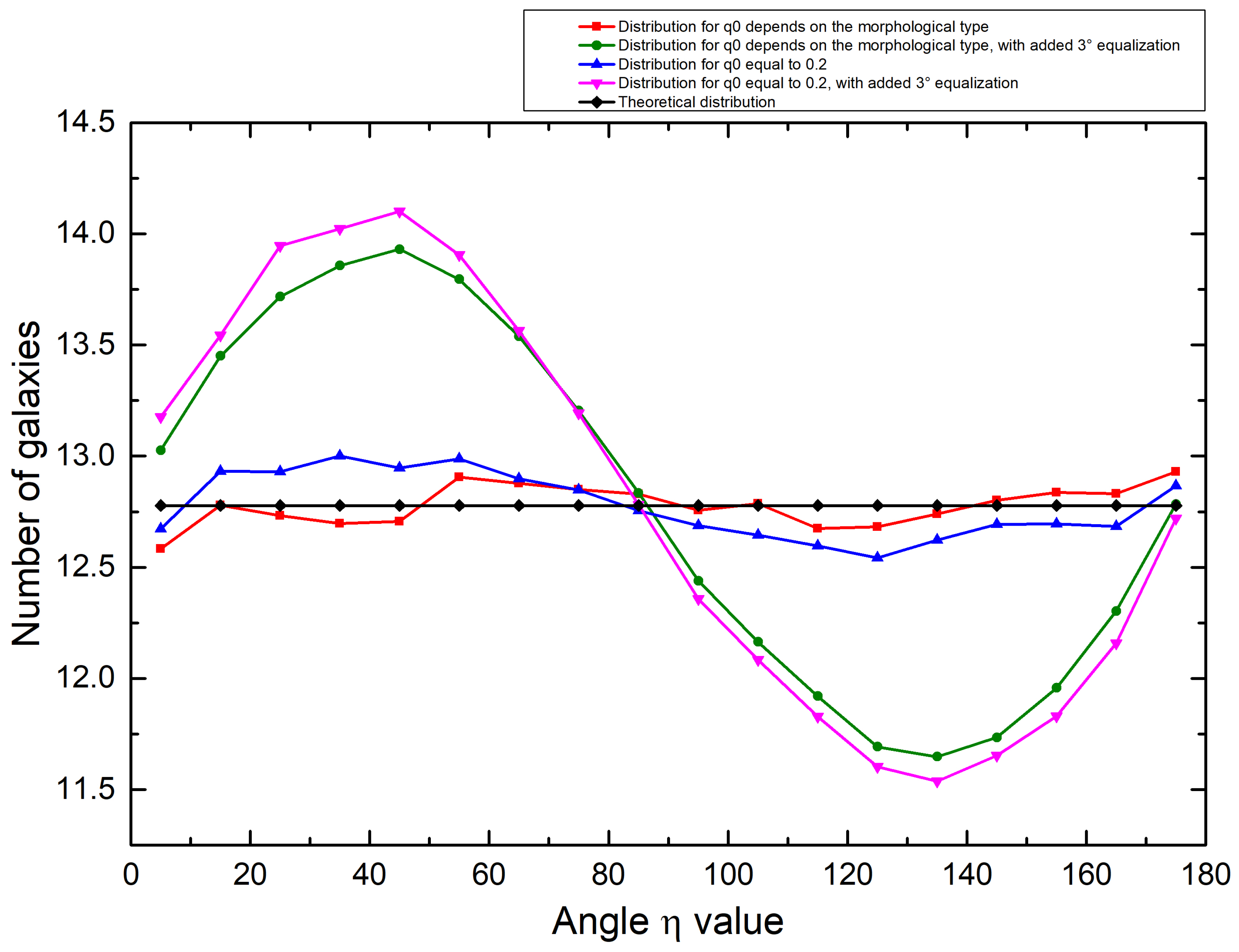
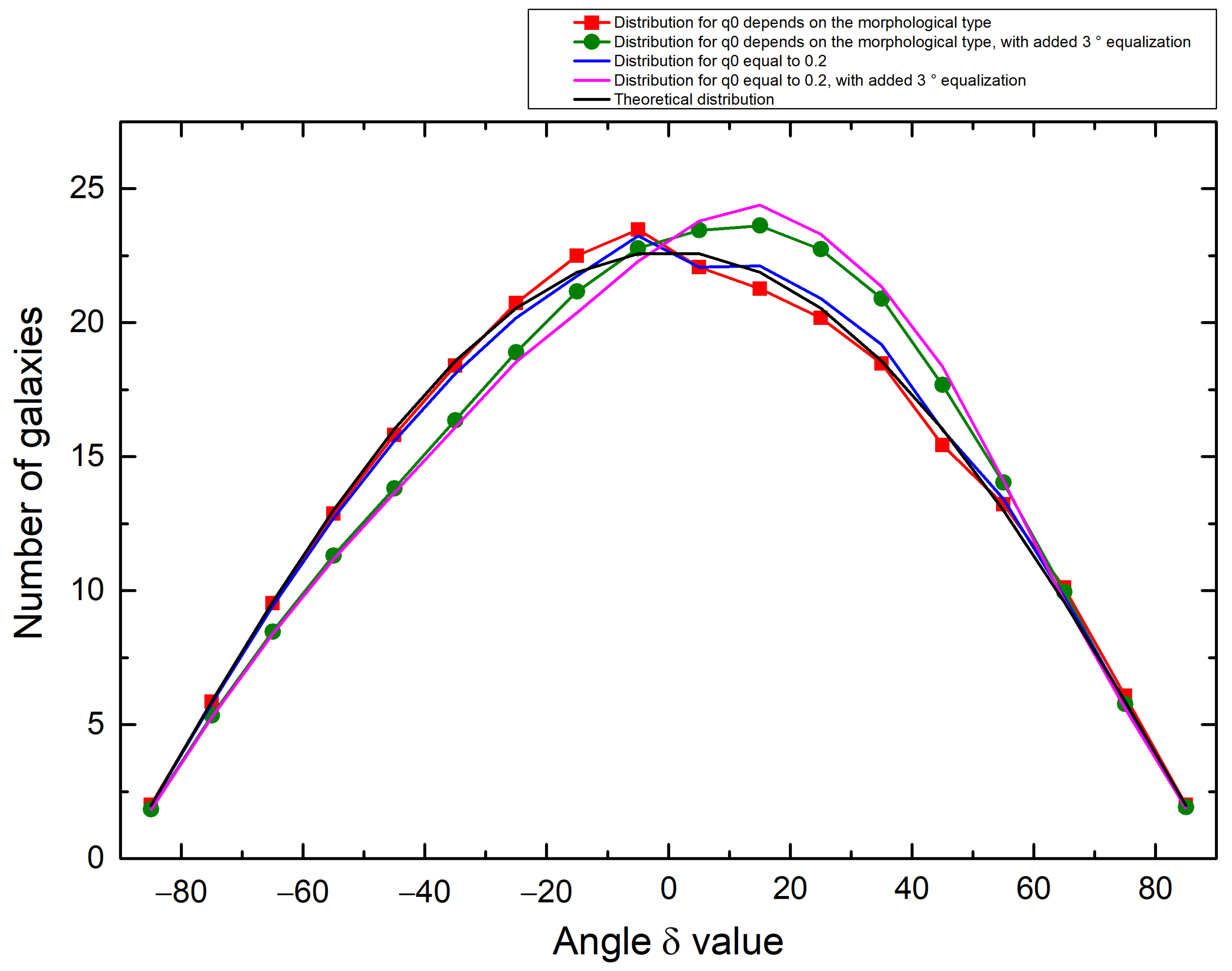
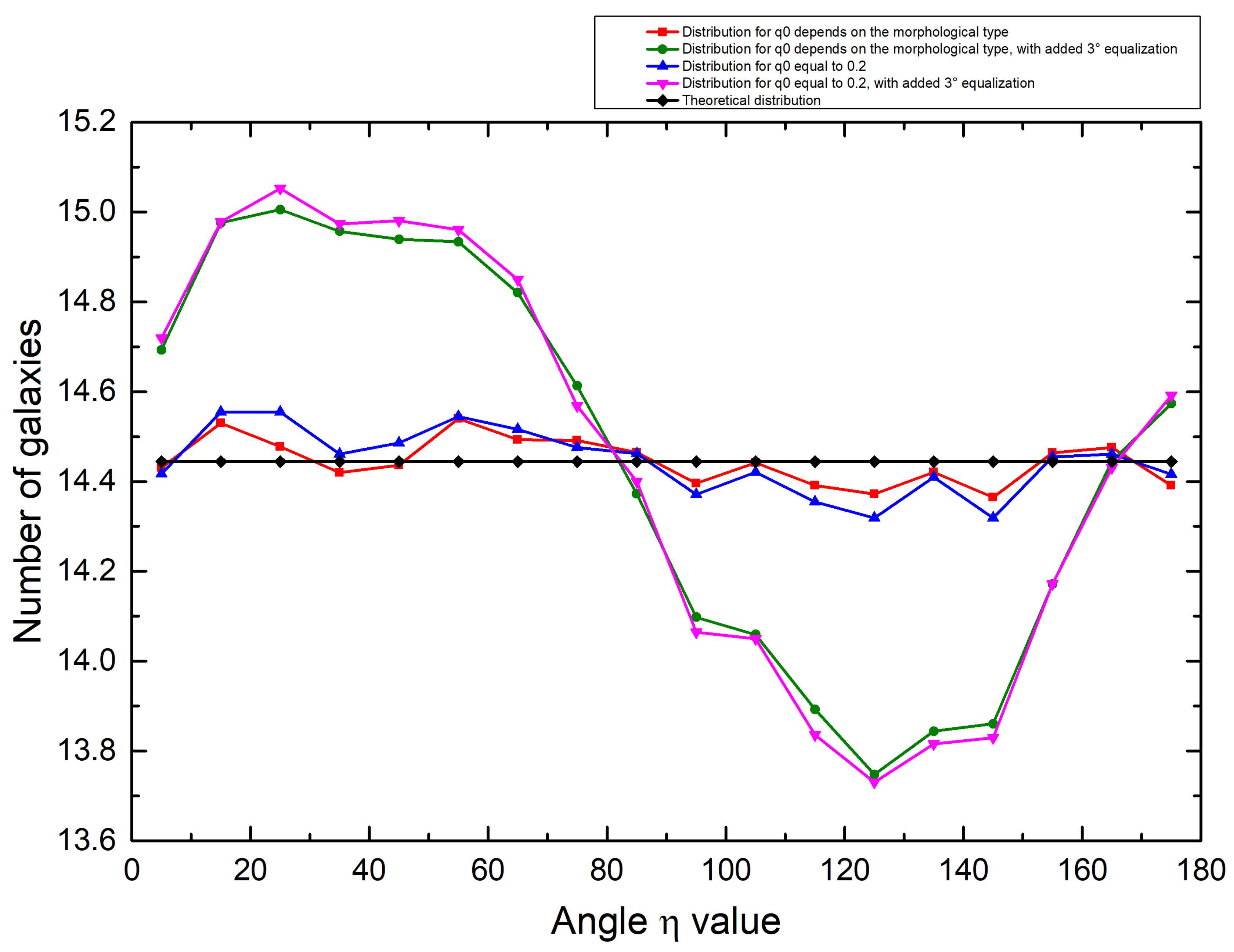
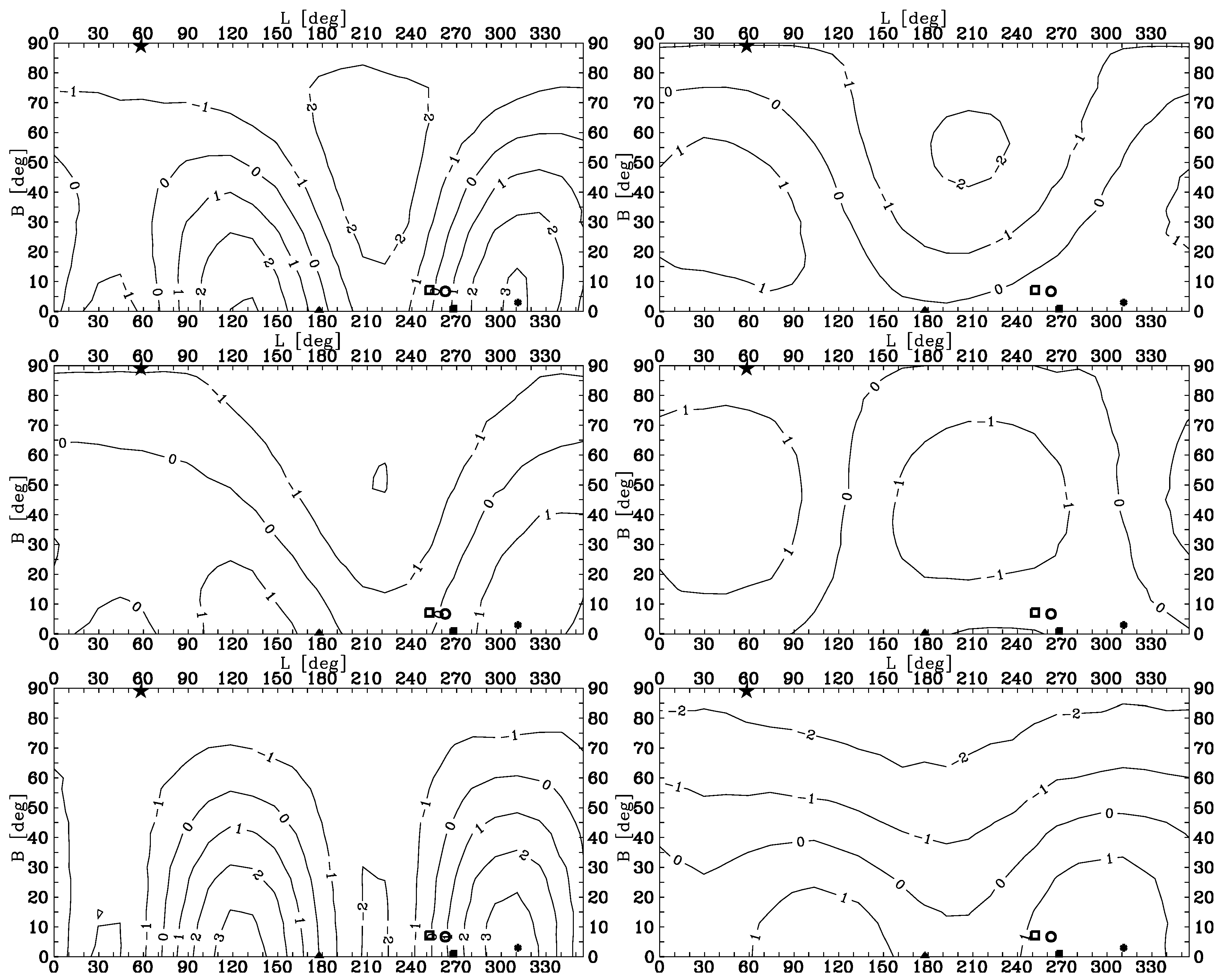
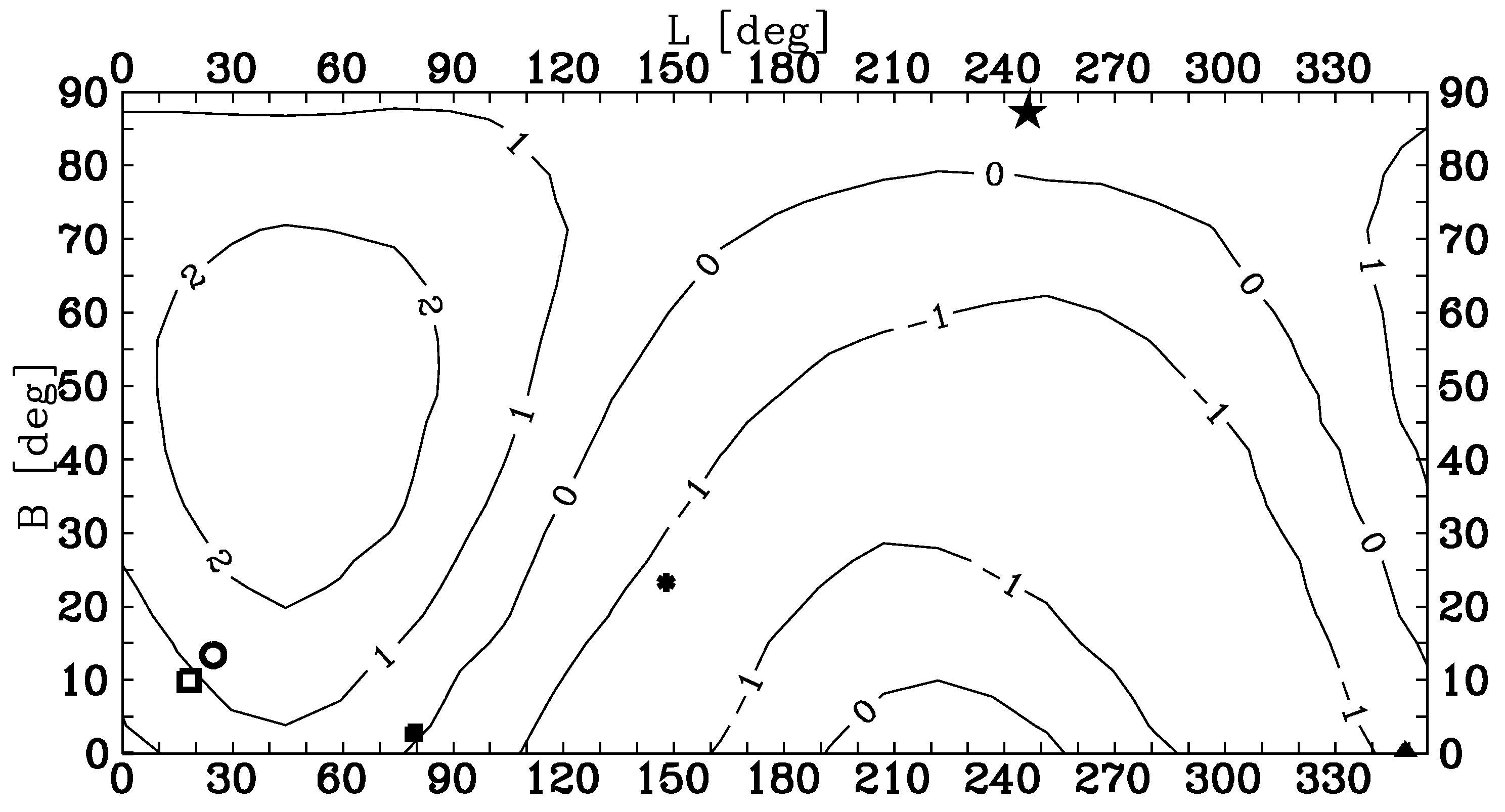
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 62.79 | 9.505 | 0.0002 | 0.0004 | −0.2365 | 0.0585 | −4.0459 | 1.197 | 0.6769 | −0.1641 |
| 12 | 332 | 25.67 | −11.484 | 0.2992 | 0.6338 | −0.1247 | 0.0803 | −1.5534 | 0.549 | 0.1183 | −0.3470 |
| 13 | 128 | 29.72 | −6.939 | 0.9148 | 0.9438 | 0.0022 | 0.1293 | 0.0174 | 0.621 | 0.0726 | −0.0905 |
| 14 | 426 | 23.96 | 3.524 | 0.1700 | 0.2538 | −0.1201 | 0.0709 | −1.6941 | 0.779 | 0.1772 | −0.8586 |
| 15 | 130 | 13.07 | −1.876 | 0.7906 | 0.7285 | −0.0036 | 0.1283 | −0.0283 | 0.589 | 0.0612 | −0.0036 |
| 17 | 80 | 13.81 | −5.502 | 0.6210 | 0.7426 | −0.0996 | 0.1635 | −0.6093 | 0.818 | 0.1604 | 0.1604 |
| 21 | 248 | 14.17 | 0.237 | 0.1196 | 0.2995 | −0.0351 | 0.0929 | −0.3780 | 1.143 | 0.4859 | 0.4789 |
| 22 | 126 | 7.03 | 0.680 | 0.5463 | 0.8569 | 0.0979 | 0.1303 | 0.7514 | 0.618 | 0.1290 | −0.2775 |
| 23 | 100 | 17.05 | −1.818 | 0.6127 | 0.7009 | 0.1398 | 0.1463 | 0.9560 | 0.468 | 0.0670 | −0.0148 |
| 31 | 210 | 33.70 | 15.978 | 0.0004 | 0.0022 | 0.1371 | 0.1009 | 1.3586 | 1.794 | 1.3340 | 1.0848 |
| 41 | 192 | 22.78 | 6.538 | 0.0495 | 0.0119 | −0.0040 | 0.1056 | −0.0381 | 1.371 | 0.5135 | −0.4546 |
| 42 | 230 | 24.65 | −3.775 | 0.4007 | 0.4443 | 0.0556 | 0.0965 | 0.5768 | 0.747 | 0.2420 | −0.5970 |
| 44 | 80 | 26.72 | 7.946 | 0.0472 | 0.0498 | −0.2000 | 0.1635 | −1.2230 | 1.336 | 0.4800 | −0.1473 |
| 51 | 228 | 29.64 | −0.409 | 0.0245 | 0.0184 | 0.0928 | 0.0969 | 0.9574 | 1.443 | 0.5956 | 0.5954 |
| 52 | 172 | 21.61 | 3.039 | 0.0107 | 0.0399 | −0.2028 | 0.1115 | −1.8187 | 1.417 | 0.6913 | 0.6731 |
| 53 | 260 | 13.32 | −3.290 | 0.5558 | 0.8212 | −0.0549 | 0.0907 | −0.6048 | 0.620 | 0.0862 | −0.0647 |
| 61 | 258 | 19.85 | −3.128 | 0.8344 | 0.1754 | −0.0487 | 0.0911 | −0.5352 | 0.615 | 0.0900 | −0.1735 |
| 64 | 102 | 28.73 | −7.542 | 0.1803 | 0.4877 | 0.0804 | 0.1448 | 0.5551 | 0.836 | 0.2517 | −0.2426 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 60.01 | 5.955 | 0.0000 | 0.0000 | 0.3040 | 0.0565 | 5.3782 | 2.003 | 1.2774 | 1.2750 |
| 12 | 332 | 29.30 | 7.669 | 0.0013 | 0.0092 | −0.0686 | 0.0776 | −0.8836 | 1.756 | 0.9940 | −0.7409 |
| 13 | 128 | 25.56 | 2.781 | 0.0791 | 0.1048 | 0.2416 | 0.1250 | 1.9332 | 0.766 | 0.2142 | −0.0221 |
| 14 | 426 | 27.38 | 6.634 | 0.0904 | 0.1476 | 0.0551 | 0.0685 | 0.8046 | 1.001 | 0.2964 | −0.5861 |
| 15 | 130 | 22.86 | 2.508 | 0.7643 | 0.2086 | 0.0362 | 0.1240 | 0.2918 | 0.906 | 0.2649 | 0.2545 |
| 17 | 80 | 13.15 | −5.975 | 0.4703 | 0.8201 | −0.0590 | 0.1581 | −0.3732 | 0.460 | 0.0467 | 0.0021 |
| 21 | 248 | 26.94 | −3.548 | 0.0539 | 0.2016 | 0.0584 | 0.0898 | 0.6509 | 1.228 | 0.2912 | −0.3671 |
| 22 | 126 | 11.71 | 5.571 | 0.1768 | 0.2239 | 0.1938 | 0.1260 | 1.5381 | 0.980 | 0.1935 | 0.1915 |
| 23 | 100 | 20.24 | −0.100 | 0.0811 | 0.2323 | −0.1644 | 0.1414 | −1.1623 | 1.089 | 0.2968 | 0.2868 |
| 31 | 210 | 24.00 | 0.429 | 0.0455 | 0.0363 | 0.1940 | 0.0976 | 1.9882 | 1.564 | 0.6733 | 0.6054 |
| 41 | 192 | 27.19 | 10.219 | 0.0009 | 0.0022 | 0.3001 | 0.1021 | 2.9406 | 1.949 | 0.8840 | 0.8075 |
| 42 | 230 | 15.90 | 3.296 | 0.0335 | 0.0690 | 0.0363 | 0.0933 | 0.3890 | 1.238 | 0.5716 | −0.4880 |
| 44 | 80 | 20.35 | −3.050 | 0.2264 | 0.1385 | 0.1482 | 0.1581 | 0.9370 | 0.783 | 0.1229 | −0.0206 |
| 51 | 228 | 30.63 | −5.368 | 0.0416 | 0.1250 | 0.2175 | 0.0937 | 2.3223 | 1.148 | 0.3636 | 0.3633 |
| 52 | 172 | 38.14 | 12.291 | 0.0012 | 0.0013 | 0.2118 | 0.1078 | 1.9644 | 1.923 | 1.1189 | 0.9322 |
| 53 | 260 | 12.22 | −8.277 | 0.8159 | 0.9486 | 0.0075 | 0.0877 | 0.0856 | 0.338 | 0.0229 | −0.1903 |
| 61 | 258 | 23.72 | −12.558 | 0.5492 | 0.5111 | 0.0912 | 0.0880 | 1.0362 | 0.643 | 0.0716 | −0.0812 |
| 64 | 102 | 50.12 | −3.529 | 0.0024 | 0.0004 | 0.4016 | 0.1400 | 2.8681 | 1.881 | 1.4348 | 1.0276 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 57.92 | 23.719 | 0.0000 | 0.0000 | −0.2933 | 0.0585 | −5.0172 | 1.677 | 1.0639 | 0.7595 |
| 12 | 332 | 19.86 | 4.313 | 0.0214 | 0.0845 | −0.2191 | 0.0803 | −2.7296 | 0.933 | 0.2848 | −0.3688 |
| 13 | 128 | 21.74 | −1.985 | 0.9017 | 0.7291 | −0.0366 | 0.1293 | −0.2831 | 0.533 | 0.0713 | 0.0309 |
| 14 | 426 | 32.58 | 5.004 | 0.0400 | 0.0967 | −0.1722 | 0.0709 | −2.4297 | 0.848 | 0.2398 | −0.7484 |
| 15 | 130 | 11.19 | −0.758 | 0.5857 | 0.7867 | −0.0287 | 0.1283 | −0.2235 | 0.676 | 0.1626 | 0.1623 |
| 17 | 80 | 9.12 | −0.995 | 0.3735 | 0.6282 | −0.1663 | 0.1635 | −1.0171 | 0.818 | 0.1892 | 0.1871 |
| 21 | 248 | 23.79 | 7.660 | 0.0141 | 0.0136 | −0.0726 | 0.0929 | −0.7816 | 1.479 | 1.0499 | 0.9137 |
| 22 | 126 | 10.84 | 0.657 | 0.6402 | 0.7832 | 0.0186 | 0.1303 | 0.1425 | 0.668 | 0.1539 | 0.1539 |
| 23 | 100 | 12.33 | −0.395 | 0.7644 | 0.8413 | 0.0620 | 0.1463 | 0.4238 | 0.768 | 0.1197 | 0.1174 |
| 31 | 210 | 44.38 | 25.404 | 0.0000 | 0.0000 | 0.1639 | 0.1009 | 1.6236 | 2.346 | 2.5927 | 1.7750 |
| 41 | 192 | 27.61 | 8.682 | 0.0068 | 0.0031 | −0.0286 | 0.1056 | −0.2714 | 1.756 | 0.9233 | −0.6765 |
| 42 | 230 | 32.77 | 9.035 | 0.0333 | 0.0111 | −0.0440 | 0.0965 | −0.4559 | 1.615 | 1.0730 | −1.1977 |
| 44 | 80 | 26.92 | 6.010 | 0.0843 | 0.0494 | −0.1695 | 0.1635 | −1.0366 | 1.336 | 0.3753 | −0.1509 |
| 51 | 228 | 25.02 | 8.541 | 0.0031 | 0.0036 | 0.1017 | 0.0969 | 1.0493 | 1.841 | 1.1469 | 1.0003 |
| 52 | 172 | 34.29 | 13.770 | 0.0001 | 0.0004 | −0.2716 | 0.1115 | −2.4355 | 2.059 | 1.3897 | 1.2726 |
| 53 | 260 | 24.59 | −8.649 | 0.1497 | 0.3568 | −0.0173 | 0.0907 | −0.1910 | 1.116 | 0.3326 | 0.3127 |
| 61 | 258 | 15.34 | 2.191 | 0.4203 | 0.2260 | −0.0692 | 0.0911 | −0.7596 | 0.778 | 0.2029 | −0.5779 |
| 64 | 102 | 16.20 | 3.880 | 0.0686 | 0.2525 | 0.0967 | 0.1448 | 0.6675 | 1.174 | 0.5700 | −0.3663 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 56.85 | 36.319 | 0.0000 | 0.0000 | 0.3537 | 0.0565 | 6.2568 | 2.243 | 1.6620 | 1.6619 |
| 12 | 332 | 42.75 | 21.169 | 0.0000 | 0.0000 | −0.0827 | 0.0776 | −1.0655 | 2.525 | 2.3969 | −0.9833 |
| 13 | 128 | 11.78 | 3.062 | 0.4461 | 0.2028 | 0.0761 | 0.1250 | 0.6086 | 0.687 | 0.0881 | 0.0152 |
| 14 | 426 | 37.01 | 6.169 | 0.0028 | 0.0184 | 0.1192 | 0.0685 | 1.7393 | 2.003 | 0.8524 | −0.9157 |
| 15 | 130 | 15.11 | 1.538 | 0.9386 | 0.5245 | 0.0362 | 0.1240 | 0.2918 | 0.819 | 0.1946 | 0.1892 |
| 17 | 80 | 27.55 | −4.175 | 0.0331 | 0.1025 | −0.0693 | 0.1581 | −0.4384 | 1.242 | 0.4029 | 0.3807 |
| 21 | 248 | 32.74 | 2.911 | 0.0233 | 0.0766 | 0.1423 | 0.0898 | 1.5846 | 1.672 | 0.5100 | −0.5151 |
| 22 | 126 | 18.57 | 4.857 | 0.0283 | 0.0446 | 0.2867 | 0.1260 | 2.2756 | 1.336 | 0.4646 | 0.4329 |
| 23 | 100 | 30.32 | 1.880 | 0.0028 | 0.0129 | −0.2230 | 0.1414 | −1.5770 | 1.500 | 0.5953 | 0.5530 |
| 31 | 210 | 19.71 | 4.714 | 0.1124 | 0.0604 | 0.1546 | 0.0976 | 1.5847 | 1.426 | 0.6460 | 0.5611 |
| 41 | 192 | 30.19 | 18.000 | 0.0001 | 0.0001 | 0.3337 | 0.1021 | 3.2692 | 2.165 | 1.3420 | 1.1144 |
| 42 | 230 | 29.20 | 8.774 | 0.0011 | 0.0023 | 0.0056 | 0.0933 | 0.0601 | 1.568 | 1.0667 | −0.4937 |
| 44 | 80 | 20.35 | −3.500 | 0.1931 | 0.1889 | −0.0166 | 0.1581 | −0.1051 | 1.230 | 0.2769 | −0.1731 |
| 51 | 228 | 27.32 | −5.526 | 0.0152 | 0.0749 | 0.2658 | 0.0937 | 2.8376 | 1.038 | 0.3010 | 0.2699 |
| 52 | 172 | 42.95 | 14.384 | 0.0001 | 0.0001 | 0.2723 | 0.1078 | 2.5252 | 1.999 | 1.4852 | 1.1819 |
| 53 | 260 | 17.20 | −8.346 | 0.8463 | 0.9801 | 0.0506 | 0.0877 | 0.5765 | 0.331 | 0.0288 | −0.1908 |
| 61 | 258 | 14.23 | 1.395 | 0.0624 | 0.2010 | 0.0777 | 0.0880 | 0.8823 | 1.038 | 0.2738 | −0.3536 |
| 64 | 102 | 49.41 | 7.059 | 0.0004 | 0.0001 | 0.4467 | 0.1400 | 3.1898 | 2.145 | 1.5728 | 1.1656 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 40.50 | 9.005 | 0.0010 | 0.0029 | −0.2162 | 0.0585 | −3.6976 | 1.117 | 0.5127 | −0.2190 |
| 12 | 332 | 26.26 | −10.374 | 0.2806 | 0.6207 | −0.1266 | 0.0803 | −1.5776 | 0.659 | 0.1273 | −0.4848 |
| 13 | 128 | 30.23 | −4.625 | 0.9468 | 0.6984 | 0.0284 | 0.1293 | 0.2196 | 0.709 | 0.0777 | −0.0391 |
| 14 | 426 | 23.06 | 2.429 | 0.2470 | 0.2648 | −0.1030 | 0.0709 | −1.4527 | 0.671 | 0.1606 | −0.8602 |
| 15 | 130 | 13.03 | −2.190 | 0.9535 | 0.9219 | 0.0182 | 0.1283 | 0.1419 | 0.413 | 0.0334 | −0.0864 |
| 17 | 80 | 11.69 | −3.653 | 0.5899 | 0.7242 | −0.1028 | 0.1635 | −0.6288 | 0.818 | 0.1568 | 0.1567 |
| 21 | 248 | 14.35 | −0.545 | 0.2296 | 0.3445 | −0.0367 | 0.0929 | −0.3949 | 0.953 | 0.3753 | 0.3751 |
| 22 | 126 | 7.19 | 1.262 | 0.5879 | 0.8853 | 0.0890 | 0.1303 | 0.6831 | 0.618 | 0.1265 | −0.2792 |
| 23 | 100 | 9.84 | 1.101 | 0.6842 | 0.7517 | 0.1274 | 0.1463 | 0.8712 | 0.468 | 0.0590 | 0.0039 |
| 31 | 210 | 35.10 | 12.811 | 0.0011 | 0.0050 | 0.1452 | 0.1009 | 1.4387 | 1.794 | 1.1787 | 0.9978 |
| 41 | 192 | 19.23 | 10.133 | 0.0976 | 0.0101 | 0.0186 | 0.1056 | 0.1765 | 1.227 | 0.3955 | −0.3974 |
| 42 | 230 | 22.75 | −2.786 | 0.4480 | 0.4779 | 0.0426 | 0.0965 | 0.4414 | 0.731 | 0.2791 | −0.6753 |
| 44 | 80 | 16.97 | 3.285 | 0.2003 | 0.2551 | −0.1580 | 0.1635 | −0.9659 | 0.894 | 0.2674 | −0.1486 |
| 51 | 228 | 28.26 | −0.982 | 0.0717 | 0.0408 | 0.0878 | 0.0969 | 0.9067 | 1.245 | 0.4125 | 0.4042 |
| 52 | 172 | 24.44 | 1.966 | 0.0078 | 0.0299 | −0.2071 | 0.1115 | −1.8568 | 1.417 | 0.7238 | 0.7047 |
| 53 | 260 | 13.23 | −5.424 | 0.5904 | 0.7270 | −0.0768 | 0.0907 | −0.8468 | 0.496 | 0.0673 | −0.1603 |
| 61 | 258 | 17.20 | −6.559 | 0.9514 | 0.5678 | −0.0125 | 0.0911 | −0.1378 | 0.491 | 0.0480 | −0.1855 |
| 64 | 102 | 23.89 | −7.883 | 0.3004 | 0.6505 | 0.1192 | 0.1448 | 0.8232 | 0.737 | 0.1460 | −0.1888 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 40.46 | 3.137 | 0.0001 | 0.0005 | 0.2435 | 0.0565 | 4.3073 | 1.603 | 0.7477 | 0.6802 |
| 12 | 332 | 21.71 | 7.235 | 0.0041 | 0.0255 | −0.0555 | 0.0776 | −0.7154 | 1.592 | 0.8543 | −0.7237 |
| 13 | 128 | 12.91 | −0.313 | 0.8080 | 0.4251 | 0.0813 | 0.1250 | 0.6504 | 0.756 | 0.0885 | 0.0746 |
| 14 | 426 | 19.52 | 6.972 | 0.0690 | 0.1265 | 0.0727 | 0.0685 | 1.0616 | 1.034 | 0.3047 | −0.5727 |
| 15 | 130 | 17.88 | 2.508 | 0.5804 | 0.2758 | −0.0232 | 0.1240 | −0.1871 | 0.906 | 0.3805 | 0.3258 |
| 17 | 80 | 13.60 | −5.975 | 0.5065 | 0.8224 | −0.0249 | 0.1581 | −0.1577 | 0.460 | 0.0461 | 0.0041 |
| 21 | 248 | 24.61 | −6.016 | 0.2029 | 0.5005 | 0.0590 | 0.0898 | 0.6565 | 1.101 | 0.2125 | −0.4175 |
| 22 | 126 | 12.57 | 2.714 | 0.1768 | 0.2631 | 0.1849 | 0.1260 | 1.4675 | 0.980 | 0.1725 | 0.1670 |
| 23 | 100 | 17.36 | 1.880 | 0.0814 | 0.2286 | −0.1751 | 0.1414 | −1.2384 | 1.089 | 0.3724 | 0.3302 |
| 31 | 210 | 20.23 | 0.343 | 0.1140 | 0.0630 | 0.1528 | 0.0976 | 1.5657 | 1.426 | 0.5653 | 0.5141 |
| 41 | 192 | 27.94 | 9.750 | 0.0016 | 0.0030 | 0.3032 | 0.1021 | 2.9706 | 1.732 | 0.6493 | 0.6384 |
| 42 | 230 | 15.90 | 6.191 | 0.0283 | 0.0396 | 0.0266 | 0.0933 | 0.2854 | 1.172 | 0.6226 | −0.4905 |
| 44 | 80 | 15.40 | 1.900 | 0.4251 | 0.1171 | 0.0399 | 0.1581 | 0.2524 | 0.671 | 0.0897 | 0.0080 |
| 51 | 228 | 21.63 | −2.368 | 0.0611 | 0.2111 | 0.2101 | 0.0937 | 2.2437 | 1.148 | 0.3162 | 0.3148 |
| 52 | 172 | 36.67 | 14.802 | 0.0015 | 0.0015 | 0.2082 | 0.1078 | 1.9304 | 1.847 | 1.0693 | 0.8969 |
| 53 | 260 | 11.80 | −2.600 | 0.5311 | 0.7438 | 0.0522 | 0.0877 | 0.5953 | 0.531 | 0.0563 | −0.0874 |
| 61 | 258 | 18.98 | −10.116 | 0.5731 | 0.8244 | 0.0469 | 0.0880 | 0.5328 | 0.664 | 0.0420 | −0.2271 |
| 64 | 102 | 45.88 | 5.471 | 0.0023 | 0.0001 | 0.3941 | 0.1400 | 2.8144 | 1.980 | 1.4383 | 1.0381 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 17.88 | 7.01 | −0.410 | 4.756 | 0.646 | 0.202 | 0.1210 | 0.0820 | −0.3606 | 0.1580 |
| 12 | 332 | 17.04 | 6.78 | −0.634 | 4.557 | 0.612 | 0.192 | 0.1091 | 0.0747 | −0.4693 | 0.1320 |
| 13 | 128 | 17.62 | 6.97 | −0.851 | 4.627 | 0.648 | 0.208 | 0.1252 | 0.0892 | 0.0487 | 0.1291 |
| 14 | 426 | 16.97 | 6.26 | −0.758 | 4.276 | 0.638 | 0.211 | 0.1216 | 0.0864 | −0.5227 | 0.2569 |
| 15 | 130 | 17.45 | 6.39 | −0.593 | 4.385 | 0.732 | 0.285 | 0.1835 | 0.1776 | −0.0160 | 0.2446 |
| 17 | 80 | 17.24 | 6.58 | −0.961 | 4.410 | 0.629 | 0.211 | 0.1183 | 0.0894 | 0.0492 | 0.1213 |
| 21 | 248 | 17.40 | 6.24 | −0.617 | 4.404 | 0.728 | 0.286 | 0.1830 | 0.1790 | −0.1209 | 0.3277 |
| 22 | 126 | 17.52 | 6.46 | −0.476 | 4.477 | 0.713 | 0.269 | 0.1695 | 0.1553 | 0.0001 | 0.2211 |
| 23 | 100 | 17.22 | 6.41 | −0.698 | 4.310 | 0.649 | 0.217 | 0.1266 | 0.0959 | 0.0334 | 0.1419 |
| 31 | 210 | 17.21 | 6.10 | −0.646 | 4.178 | 0.768 | 0.316 | 0.2143 | 0.2262 | −0.1733 | 0.3613 |
| 41 | 192 | 17.56 | 6.37 | −0.590 | 4.447 | 0.739 | 0.292 | 0.1837 | 0.1747 | −0.1945 | 0.2968 |
| 42 | 230 | 17.59 | 6.34 | −0.560 | 4.433 | 0.718 | 0.267 | 0.1676 | 0.1466 | −0.2908 | 0.2841 |
| 44 | 80 | 17.31 | 6.29 | −0.692 | 4.271 | 0.759 | 0.313 | 0.2052 | 0.2111 | −0.0070 | 0.2206 |
| 51 | 228 | 17.26 | 6.19 | −0.614 | 4.238 | 0.770 | 0.326 | 0.2193 | 0.2307 | −0.1817 | 0.3801 |
| 52 | 172 | 17.31 | 6.23 | −0.655 | 4.401 | 0.705 | 0.253 | 0.1608 | 0.1381 | −0.0247 | 0.2365 |
| 53 | 260 | 17.34 | 6.12 | −0.588 | 4.192 | 0.769 | 0.314 | 0.2142 | 0.2209 | −0.2262 | 0.3967 |
| 61 | 258 | 17.34 | 6.19 | −0.644 | 4.291 | 0.679 | 0.234 | 0.1424 | 0.1097 | −0.3296 | 0.2494 |
| 64 | 102 | 17.29 | 6.29 | −0.549 | 4.293 | 0.751 | 0.294 | 0.1944 | 0.1885 | −0.0508 | 0.2340 |
| Group | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 0.5730 | 0.2938 | 0.5587 | 0.3181 | 0.0068 | 0.0717 | 0.1156 | 1.2271 |
| 12 | 332 | 0.5877 | 0.2976 | 0.5748 | 0.3117 | 0.0049 | 0.0981 | 0.0605 | 1.2217 |
| 13 | 128 | 0.5716 | 0.2900 | 0.5597 | 0.3086 | 0.0082 | 0.1533 | 0.0636 | 1.1860 |
| 14 | 426 | 0.5612 | 0.2868 | 0.5538 | 0.2953 | 0.0064 | 0.0807 | 0.0905 | 1.1389 |
| 15 | 130 | 0.5205 | 0.2952 | 0.5104 | 0.2987 | 0.0072 | 0.1239 | 0.0560 | 0.9657 |
| 17 | 80 | 0.5787 | 0.2937 | 0.5678 | 0.3035 | 0.0057 | 0.1910 | 0.0347 | 1.1681 |
| 21 | 248 | 0.5286 | 0.2963 | 0.5156 | 0.3004 | 0.0053 | 0.0873 | 0.0566 | 0.9404 |
| 22 | 126 | 0.5343 | 0.2968 | 0.5171 | 0.3034 | 0.0077 | 0.1357 | 0.0594 | 1.0417 |
| 23 | 100 | 0.5691 | 0.2914 | 0.5491 | 0.3007 | 0.0048 | 0.1686 | 0.0331 | 1.1527 |
| 31 | 210 | 0.5009 | 0.2962 | 0.4995 | 0.2920 | 0.0037 | 0.0722 | 0.0371 | 0.7149 |
| 41 | 192 | 0.5200 | 0.2973 | 0.5088 | 0.3005 | 0.0044 | 0.0997 | 0.0413 | 0.9448 |
| 42 | 230 | 0.5272 | 0.2929 | 0.5152 | 0.2988 | 0.0070 | 0.1004 | 0.0721 | 1.0406 |
| 44 | 80 | 0.5060 | 0.2982 | 0.5060 | 0.2969 | 0.0050 | 0.1289 | 0.0303 | 0.7884 |
| 51 | 228 | 0.5042 | 0.299 | 0.5061 | 0.2967 | 0.0030 | 0.0661 | 0.0309 | 0.6821 |
| 52 | 172 | 0.5294 | 0.2914 | 0.5185 | 0.2954 | 0.0053 | 0.1183 | 0.0477 | 1.0609 |
| 53 | 260 | 0.4989 | 0.2971 | 0.4938 | 0.2972 | 0.0034 | 0.0674 | 0.0375 | 0.7428 |
| 61 | 258 | 0.5467 | 0.2902 | 0.5287 | 0.2953 | 0.0049 | 0.1008 | 0.0536 | 1.1066 |
| 64 | 102 | 0.5076 | 0.2944 | 0.5045 | 0.2968 | 0.0072 | 0.1260 | 0.0497 | 0.8699 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 18.11 | 6.38 | −0.449 | 4.335 | 0.706 | 0.237 | 0.1424 | 0.1113 | −0.3902 | 0.3356 |
| 12 | 332 | 17.22 | 6.01 | −0.861 | 4.145 | 0.760 | 0.299 | 0.1882 | 0.1900 | −0.2306 | 0.3157 |
| 13 | 128 | 16.65 | 5.81 | −1.055 | 3.987 | 0.748 | 0.290 | 0.1839 | 0.1832 | −0.0250 | 0.2040 |
| 14 | 426 | 16.98 | 5.96 | −0.898 | 4.061 | 0.741 | 0.275 | 0.1732 | 0.1653 | −0.2386 | 0.3469 |
| 15 | 130 | 16.72 | 5.73 | −0.932 | 3.968 | 0.732 | 0.264 | 0.1686 | 0.1572 | −0.0175 | 0.1935 |
| 17 | 80 | 16.51 | 5.69 | −1.013 | 3.919 | 0.745 | 0.291 | 0.1834 | 0.1859 | 0.0247 | 0.1751 |
| 21 | 248 | 16.86 | 5.74 | −1.020 | 4.049 | 0.735 | 0.266 | 0.1701 | 0.1567 | −0.0984 | 0.2643 |
| 22 | 126 | 16.73 | 5.77 | −1.025 | 4.045 | 0.740 | 0.285 | 0.1789 | 0.1762 | −0.0223 | 0.2019 |
| 23 | 100 | 17.07 | 6.13 | −1.197 | 4.301 | 0.745 | 0.306 | 0.1855 | 0.1958 | 0.0225 | 0.1988 |
| 31 | 210 | 17.75 | 6.08 | −0.295 | 4.342 | 0.791 | 0.296 | 0.2027 | 0.1921 | −0.0656 | 0.2705 |
| 41 | 192 | 16.60 | 5.71 | −0.926 | 4.046 | 0.734 | 0.273 | 0.1718 | 0.1635 | −0.0693 | 0.2363 |
| 42 | 230 | 16.65 | 5.89 | −1.093 | 3.999 | 0.741 | 0.281 | 0.1768 | 0.1719 | −0.1016 | 0.2667 |
| 44 | 80 | 17.12 | 5.81 | −0.700 | 4.100 | 0.763 | 0.283 | 0.1855 | 0.1769 | 0.0295 | 0.1686 |
| 51 | 228 | 17.31 | 5.92 | −0.524 | 4.253 | 0.759 | 0.275 | 0.1842 | 0.1683 | −0.0867 | 0.2620 |
| 52 | 172 | 16.65 | 5.71 | −1.027 | 4.028 | 0.722 | 0.265 | 0.1635 | 0.1534 | −0.0560 | 0.2190 |
| 53 | 260 | 17.65 | 6.00 | −0.305 | 4.291 | 0.786 | 0.288 | 0.1960 | 0.1801 | −0.0954 | 0.2919 |
| 61 | 258 | 16.64 | 5.62 | −1.062 | 3.925 | 0.735 | 0.271 | 0.1728 | 0.1629 | −0.1203 | 0.2733 |
| 64 | 102 | 16.92 | 5.84 | −0.793 | 4.011 | 0.747 | 0.275 | 0.1788 | 0.1676 | 0.0102 | 0.1832 |
| Group | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 0.5127 | 0.3044 | 0.4647 | 0.3027 | 0.0226 | 0.0676 | 0.4004 | 1.1968 |
| 12 | 332 | 0.5164 | 0.2935 | 0.5019 | 0.2957 | −0.0021 | 0.0552 | −0.0276 | 0.7107 |
| 13 | 128 | 0.5108 | 0.2902 | 0.5137 | 0.2896 | 0.0040 | 0.0980 | 0.0321 | 0.7841 |
| 14 | 426 | 0.5100 | 0.2928 | 0.5013 | 0.2942 | 0.0054 | 0.0660 | 0.0795 | 0.9630 |
| 15 | 130 | 0.4947 | 0.2886 | 0.4992 | 0.2878 | 0.0002 | 0.1217 | 0.0013 | 0.9810 |
| 17 | 80 | 0.5218 | 0.2918 | 0.5218 | 0.2911 | 0.0009 | 0.1131 | 0.0059 | 0.7154 |
| 21 | 248 | 0.4954 | 0.2921 | 0.5029 | 0.2906 | −0.0026 | 0.0924 | −0.0284 | 1.0285 |
| 22 | 126 | 0.5071 | 0.2942 | 0.5077 | 0.2927 | 0.0003 | 0.1212 | 0.0025 | 0.9624 |
| 23 | 100 | 0.5432 | 0.3079 | 0.5252 | 0.3054 | −0.0065 | 0.1084 | −0.0462 | 0.7668 |
| 31 | 210 | 0.4386 | 0.2948 | 0.4384 | 0.2931 | 0.0021 | 0.1064 | 0.0220 | 1.0905 |
| 41 | 192 | 0.5026 | 0.2914 | 0.5044 | 0.2908 | −0.0024 | 0.1046 | −0.0239 | 1.0251 |
| 42 | 230 | 0.5010 | 0.2897 | 0.5097 | 0.2883 | −0.0013 | 0.0826 | −0.0140 | 0.8856 |
| 44 | 80 | 0.4679 | 0.2942 | 0.4725 | 0.2887 | 0.0013 | 0.1565 | 0.0079 | 0.9900 |
| 51 | 228 | 0.4623 | 0.2966 | 0.4635 | 0.2949 | −0.0053 | 0.1083 | −0.0561 | 1.1565 |
| 52 | 172 | 0.5159 | 0.2943 | 0.5147 | 0.2925 | −0.0002 | 0.1134 | −0.0018 | 1.0520 |
| 53 | 260 | 0.4369 | 0.2941 | 0.4410 | 0.2937 | −0.0013 | 0.0968 | −0.0143 | 1.1042 |
| 61 | 258 | 0.5017 | 0.2887 | 0.5100 | 0.2884 | 0.0060 | 0.0788 | 0.0681 | 0.8944 |
| 64 | 102 | 0.4858 | 0.2958 | 0.4876 | 0.2923 | −0.0024 | 0.1505 | −0.0175 | 1.0747 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 59.24 | 23.837 | 0.0000 | 0.0000 | −0.3015 | 0.0588 | −5.1272 | 1.340 | 0.9076 | 0.0284 |
| 12 | 332 | 23.51 | 0.701 | 0.0346 | 0.1072 | −0.2091 | 0.0807 | −2.5897 | 0.879 | 0.2563 | −0.2613 |
| 13 | 128 | 22.40 | −2.716 | 0.9304 | 0.8442 | −0.0388 | 0.1300 | −0.2988 | 0.405 | 0.0473 | −0.1276 |
| 14 | 426 | 26.87 | 6.327 | 0.0358 | 0.1166 | −0.1767 | 0.0712 | −2.4833 | 0.900 | 0.2252 | −0.6374 |
| 15 | 130 | 9.52 | −1.566 | 0.7928 | 0.8999 | −0.0054 | 0.1283 | −0.0421 | 0.603 | 0.0975 | 0.0884 |
| 17 | 80 | 8.26 | −2.106 | 0.5284 | 0.6738 | −0.1596 | 0.1644 | −0.9710 | 0.722 | 0.1157 | 0.1095 |
| 21 | 248 | 20.46 | 1.613 | 0.0446 | 0.0695 | −0.0705 | 0.0928 | −0.7591 | 1.267 | 0.7711 | 0.7104 |
| 22 | 126 | 6.81 | −2.527 | 0.9384 | 0.9975 | 0.0267 | 0.1305 | 0.2046 | 0.224 | 0.0095 | −0.1159 |
| 23 | 100 | 10.41 | 1.246 | 0.8812 | 0.8719 | 0.0692 | 0.1468 | 0.4713 | 0.438 | 0.0418 | −0.0487 |
| 31 | 210 | 36.41 | 19.094 | 0.0000 | 0.0001 | 0.1678 | 0.1007 | 1.6666 | 2.163 | 2.0593 | 1.5171 |
| 41 | 192 | 27.75 | 11.562 | 0.0069 | 0.0017 | −0.0289 | 0.1055 | −0.2741 | 1.804 | 0.9063 | −0.6480 |
| 42 | 230 | 30.49 | 3.900 | 0.1172 | 0.0522 | −0.0416 | 0.0966 | −0.4311 | 1.269 | 0.6391 | −0.9776 |
| 44 | 80 | 23.95 | 5.304 | 0.1277 | 0.1055 | −0.1613 | 0.1629 | −0.9902 | 1.213 | 0.3297 | −0.1475 |
| 51 | 228 | 30.51 | 7.548 | 0.0021 | 0.0013 | 0.0899 | 0.0964 | 0.9328 | 1.901 | 1.3166 | 1.0980 |
| 52 | 172 | 32.83 | 9.707 | 0.0006 | 0.0019 | −0.2640 | 0.1117 | −2.3634 | 1.841 | 1.0431 | 1.0122 |
| 53 | 260 | 21.10 | −8.961 | 0.2312 | 0.5331 | −0.0388 | 0.0904 | −0.4288 | 0.715 | 0.2149 | 0.1665 |
| 61 | 258 | 14.47 | 1.584 | 0.6123 | 0.3232 | −0.0641 | 0.0913 | −0.7016 | 0.638 | 0.1630 | −0.5230 |
| 64 | 102 | 15.93 | 0.741 | 0.2564 | 0.6032 | 0.0964 | 0.1446 | 0.6663 | 0.904 | 0.2979 | −0.3018 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 51.09 | 34.516 | 0.0000 | 0.0000 | 0.3406 | 0.0570 | 5.9768 | 2.083 | 1.4864 | 1.4824 |
| 12 | 332 | 38.26 | 14.673 | 0.0000 | 0.0002 | −0.0708 | 0.0770 | −0.9197 | 2.096 | 1.5317 | −0.7605 |
| 13 | 128 | 14.28 | −3.196 | 0.5306 | 0.2900 | 0.0919 | 0.1244 | 0.7387 | 0.482 | 0.0908 | −0.0924 |
| 14 | 426 | 30.46 | 2.379 | 0.0113 | 0.0521 | 0.1018 | 0.0685 | 1.4850 | 1.801 | 0.8471 | −0.9937 |
| 15 | 130 | 14.22 | −0.256 | 0.8737 | 0.6347 | 0.0559 | 0.1239 | 0.4512 | 0.723 | 0.1404 | 0.1404 |
| 17 | 80 | 34.01 | −15.640 | 0.1415 | 0.4103 | −0.0651 | 0.1572 | −0.4143 | 0.990 | 0.2576 | 0.2576 |
| 21 | 248 | 33.80 | 3.921 | 0.0289 | 0.1073 | 0.1186 | 0.0898 | 1.3207 | 1.630 | 0.5451 | −0.5519 |
| 22 | 126 | 18.46 | 7.166 | 0.0417 | 0.0353 | 0.2560 | 0.1260 | 2.0310 | 1.357 | 0.4754 | 0.4349 |
| 23 | 100 | 27.23 | 5.659 | 0.0041 | 0.0111 | −0.1985 | 0.1409 | −1.4084 | 1.571 | 0.7560 | 0.6315 |
| 31 | 210 | 18.66 | 4.842 | 0.1164 | 0.0629 | 0.1541 | 0.0975 | 1.5796 | 1.289 | 0.4804 | 0.4539 |
| 41 | 192 | 30.01 | 18.142 | 0.0001 | 0.0002 | 0.3595 | 0.1021 | 3.5205 | 2.036 | 1.0864 | 0.9845 |
| 42 | 230 | 32.96 | 6.630 | 0.0015 | 0.0015 | −0.0162 | 0.0932 | −0.1739 | 1.603 | 1.0393 | −0.5294 |
| 44 | 80 | 19.60 | −1.483 | 0.2254 | 0.1314 | 0.0048 | 0.1581 | 0.0304 | 1.120 | 0.1952 | −0.1201 |
| 51 | 228 | 26.59 | −2.132 | 0.0070 | 0.0381 | 0.2885 | 0.0937 | 3.0789 | 1.184 | 0.3519 | 0.3292 |
| 52 | 172 | 42.00 | 16.865 | 0.0001 | 0.0002 | 0.2685 | 0.1078 | 2.4900 | 2.021 | 1.4674 | 1.1505 |
| 53 | 260 | 11.53 | −5.162 | 0.8673 | 0.9880 | 0.0456 | 0.0877 | 0.5196 | 0.266 | 0.0230 | −0.1978 |
| 61 | 258 | 10.94 | 2.142 | 0.1072 | 0.3355 | 0.0747 | 0.0880 | 0.8492 | 1.012 | 0.2731 | −0.4037 |
| 64 | 102 | 52.33 | 2.005 | 0.0009 | 0.0001 | 0.4370 | 0.1401 | 3.1199 | 2.149 | 1.5422 | 1.1508 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 29.10 | −5.254 | 0.3443 | 0.4907 | −0.0761 | 0.0585 | −1.3019 | 0.677 | 0.0710 | −0.5891 |
| 12 | 332 | 12.72 | −4.261 | 0.6408 | 0.9215 | −0.0751 | 0.0803 | −0.9354 | 0.384 | 0.0455 | −0.3625 |
| 13 | 128 | 27.84 | 2.881 | 0.1580 | 0.0280 | 0.2268 | 0.1293 | 1.7539 | 0.786 | 0.2241 | 0.0307 |
| 14 | 426 | 19.25 | 6.103 | 0.9108 | 0.0589 | 0.0000 | 0.0709 | 0.0004 | 0.623 | 0.1024 | −0.7387 |
| 15 | 130 | 23.10 | −7.212 | 0.5977 | 0.6819 | 0.1024 | 0.1283 | 0.7986 | 0.789 | 0.0932 | −0.2091 |
| 17 | 80 | 5.58 | 0.524 | 0.8311 | 0.7163 | 0.0242 | 0.1635 | 0.1480 | 0.559 | 0.0890 | 0.0890 |
| 21 | 248 | 19.39 | −6.411 | 0.6978 | 0.4134 | 0.0265 | 0.0929 | 0.2852 | 0.889 | 0.1671 | 0.1328 |
| 22 | 126 | 14.82 | 3.054 | 0.6707 | 0.7872 | 0.0879 | 0.1303 | 0.6748 | 0.707 | 0.1110 | −0.1888 |
| 23 | 100 | 17.97 | −1.012 | 0.2056 | 0.3434 | 0.2343 | 0.1463 | 1.6021 | 0.614 | 0.1435 | −0.0934 |
| 31 | 210 | 31.90 | −0.093 | 0.0887 | 0.1243 | 0.1252 | 0.1009 | 1.2399 | 0.966 | 0.2677 | 0.2560 |
| 41 | 192 | 11.74 | 5.787 | 0.2636 | 0.1864 | 0.1102 | 0.1056 | 1.0443 | 0.722 | 0.2679 | −0.4889 |
| 42 | 230 | 17.49 | 4.119 | 0.4208 | 0.0946 | 0.1201 | 0.0965 | 1.2447 | 0.786 | 0.1954 | −0.4389 |
| 44 | 80 | 12.06 | 0.588 | 0.1610 | 0.4258 | −0.1710 | 0.1635 | −1.0457 | 0.900 | 0.2598 | −0.2228 |
| 51 | 228 | 17.44 | −4.402 | 0.6561 | 0.8442 | 0.0662 | 0.0969 | 0.6832 | 0.552 | 0.0833 | 0.0054 |
| 52 | 172 | 17.94 | 5.950 | 0.0082 | 0.0450 | −0.1677 | 0.1115 | −1.5040 | 1.454 | 0.7803 | 0.7109 |
| 53 | 260 | 9.79 | −0.320 | 0.7056 | 0.8484 | −0.0633 | 0.0907 | −0.6983 | 0.523 | 0.0901 | −0.5060 |
| 61 | 258 | 15.76 | 0.848 | 0.3385 | 0.2690 | 0.0710 | 0.0911 | 0.7796 | 0.802 | 0.1902 | 0.1498 |
| 64 | 102 | 19.78 | −0.098 | 0.5297 | 0.6798 | 0.0697 | 0.1448 | 0.4813 | 0.594 | 0.0868 | −0.1816 |
| Group | N | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 626 | 36.84 | 14.121 | 0.0009 | 0.0001 | 0.2020 | 0.0565 | 3.5736 | 1.101 | 0.4450 | 0.0557 |
| 12 | 332 | 17.37 | 2.464 | 0.4599 | 0.4165 | −0.0462 | 0.0776 | −0.5950 | 0.860 | 0.2365 | −0.5615 |
| 13 | 128 | 17.12 | 6.297 | 0.4194 | 0.0529 | 0.1510 | 0.1250 | 1.2083 | 1.110 | 0.2416 | 0.2405 |
| 14 | 426 | 14.96 | 0.338 | 0.2655 | 0.3551 | 0.0321 | 0.0685 | 0.4685 | 0.775 | 0.1649 | −0.5359 |
| 15 | 130 | 13.72 | 2.092 | 0.6530 | 0.2863 | 0.0164 | 0.1240 | 0.1324 | 0.643 | 0.1576 | 0.1575 |
| 17 | 80 | 9.10 | 0.550 | 0.7567 | 0.7188 | −0.0213 | 0.1581 | −0.1347 | 0.683 | 0.1061 | 0.1052 |
| 21 | 248 | 17.35 | −4.710 | 0.7749 | 0.7616 | −0.0028 | 0.0898 | −0.0306 | 0.564 | 0.0917 | 0.0438 |
| 22 | 126 | 16.57 | −2.571 | 0.9707 | 0.4506 | 0.0216 | 0.1260 | 0.1717 | 0.535 | 0.0286 | −0.0656 |
| 23 | 100 | 10.16 | −0.820 | 0.5729 | 0.8232 | −0.1210 | 0.1414 | −0.8555 | 0.444 | 0.0477 | −0.0294 |
| 31 | 210 | 17.31 | −0.514 | 0.3238 | 0.2418 | 0.1239 | 0.0976 | 1.2698 | 1.104 | 0.3029 | 0.3005 |
| 41 | 192 | 24.38 | 0.375 | 0.0181 | 0.0228 | 0.2685 | 0.1021 | 2.6307 | 0.962 | 0.2555 | 0.1976 |
| 42 | 230 | 16.05 | 0.478 | 0.4551 | 0.2283 | −0.0077 | 0.0933 | −0.0830 | 0.879 | 0.2468 | −0.4326 |
| 44 | 80 | 14.05 | 1.000 | 0.8306 | 0.1871 | 0.0644 | 0.1581 | 0.4073 | 0.472 | 0.0678 | 0.0524 |
| 51 | 228 | 28.58 | 0.158 | 0.2769 | 0.1317 | 0.1375 | 0.0937 | 1.4683 | 1.214 | 0.4058 | 0.3993 |
| 52 | 172 | 17.63 | 4.651 | 0.0161 | 0.0758 | 0.1180 | 0.1078 | 1.0947 | 1.339 | 0.6194 | 0.5459 |
| 53 | 260 | 14.85 | −4.192 | 0.3857 | 0.6592 | 0.0099 | 0.0877 | 0.1130 | 0.675 | 0.0943 | 0.0221 |
| 61 | 258 | 11.86 | 0.977 | 0.3174 | 0.2960 | 0.1159 | 0.0880 | 1.3159 | 0.955 | 0.2249 | 0.2211 |
| 64 | 102 | 12.71 | 2.118 | 0.1482 | 0.4019 | 0.2528 | 0.1400 | 1.8053 | 0.627 | 0.1198 | 0.0714 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godłowski, W.; Mrzygłód, B. A New Method of Investigation of the Orientation of Galaxies in Clusters in the Absence of Information on Their Morphological Types. Appl. Sci. 2023, 13, 4845. https://doi.org/10.3390/app13084845
Godłowski W, Mrzygłód B. A New Method of Investigation of the Orientation of Galaxies in Clusters in the Absence of Information on Their Morphological Types. Applied Sciences. 2023; 13(8):4845. https://doi.org/10.3390/app13084845
Chicago/Turabian StyleGodłowski, Włodzimierz, and Błażej Mrzygłód. 2023. "A New Method of Investigation of the Orientation of Galaxies in Clusters in the Absence of Information on Their Morphological Types" Applied Sciences 13, no. 8: 4845. https://doi.org/10.3390/app13084845
APA StyleGodłowski, W., & Mrzygłód, B. (2023). A New Method of Investigation of the Orientation of Galaxies in Clusters in the Absence of Information on Their Morphological Types. Applied Sciences, 13(8), 4845. https://doi.org/10.3390/app13084845





