Equivalent Stress Intensity Factor: The Consequences of the Lack of a Unique Definition

Abstract

The concept of an equivalent stress intensity factor K_eq is used in the study of fatigue crack growth in mixed-mode situations. A problem seldom discussed in the research literature are the consequences of the coexistence of several alternative definitions of mixed mode K_eq, leading to rather different results associated with the alternative K_eq definitions. This note highlights the problem, considering several K_eq definitions hitherto not analyzed simultaneously. Values of K_eq calculated according to several criteria were compared through the determination of K_eq/K_I over a wide range of values of K_I/K_II or K_II/K_I. In earlier work on Al alloy AA6082 T6, the fatigue crack path and growth rate were measured in 4-point bend specimens subjected to asymmetrical loading and in compact tension specimens modified with holes. The presentation of the fatigue crack growth data was made using a Paris law based on K_eq. Important differences are found in the Paris laws, corresponding to the alternative definitions of K_eq considered, and the requirements for candidate K_eq definitions are discussed. A perspective for overcoming the shortcomings may consist in developing a data-driven modelling methodology, supported by material characterization and structure monitoring during its life cycle.

1. Introduction

The application of Fracture Mechanics to fatigue crack growth phenomena seeks two main goals: i—to quantitatively characterize a material as regards crack growth (path, rate, etc.); and ii—to model fatigue crack propagation in real structural components, starting from existing or assumed cracks that progress under a cyclic load until reaching a larger size or final rupture.

The first goal involves measuring the crack growth rate, path and other relevant properties as the crack grows under diverse loading conditions, including the stress ratio, eventually mixed mode, and environmental effects, such as corrosion, aging and thermal effects. By understanding how cracks propagate in different materials and under different conditions, more accurate models for predicting the life of structural components subject to fatigue can be developed and employed to design and assess structural behavior.

The second goal aims to model and evaluate the propagation of cracks in real structural components. This involves starting with either existing or assumed cracks or microcracks, and modelling their growth under cyclic loading until a given size or final rupture is reached. This type of modelling is critical for assessing the safety and reliability of components subject to fatigue conditions, as it allows one to predict the component’s behavior over time under different loading conditions and to design and maintain safety-critical structures—such as aeronautical or nuclear structures—with a high reliability. Many specialized treatises present the relevant methodologies, e.g., [1,2].

Fatigue crack growth (FCG) modelling relies upon relationships between the fatigue crack growth rate and stress intensity factor K, as in the Paris law applied to mode I situations [3]:

$$\frac{da}{dN}=C{\left(\Delta K_I\right)}^m$$

(1)

where a is the crack length, N is the number of cycles, and the empirical constants C and m depend upon the material and particular testing conditions, e.g., load ratio R (R = K_min/K_max). Following the findings of Paris [4], it has been noted that ‘Fracture Mechanics approach applied to life prediction has often been misused, or has ignored obvious characteristics which effect the precision and relevance of the predictions’. This warning might be taken into account in mixed-mode situations, where instead of the mode I stress intensity factor K_I, the concept of equivalent stress intensity factor K_eq is commonly used, and the Paris law is rewritten as:

$$\frac{da}{dN}=C{\left(\Delta K_{eq}\right)}^m$$

(2)

where the constants C and m are generally different from those relevant for mode I.

Several alternative definitions of mixed mode K_eq coexist, raising the question of what the consequences of that variety of definitions are—are the consequences noteworthy, or are they negligible? An alternative way of formulating the research question is: in the general K_I, K_II domain, how do different definitions of K_eq compare?

This note considers a number of K_eq definitions hitherto not analyzed simultaneously. Experimental and modelling aspects of the mixed-mode-I-II fatigue crack growth problem are revisited, and the values of K_eq according to several criteria were compared through the determination of K_eq/K_I over a wide range of K_I/K_II or K_II/K_I values.

Mixed-mode situations are found in planar geometries, e.g., biaxially loaded plates, asymmetrically loaded 3- or 4-point bending specimens, or cylindrical specimens subjected to torsion combined with uniaxial tensile or compressive loading. This note concentrates on planar specimens, with crack path predictions based on 2D finite element method (FEM) analysis and a consideration of K_I and K_II in the frame of suitable K_eq criteria.

Experimental FCG results were available for Al alloy AA6082 T6 [5,6]. Four-point bend specimens subjected to asymmetrical loading and compact tension (CT) specimens modified with holes were subjected to fatigue crack growth tests, where the fatigue crack path and fatigue crack growth rate were measured. The presentation of the FCG data was made using a Paris law based upon K_eq, and the tests were modelled using the extended finite element method (XFEM) implemented in ABAQUS [7]. The present note builds upon that earlier work, expanding the number of K_eq definitions considered and quantifying the important differences found in the Paris laws corresponding to the alternative definitions of K_eq. While considering a wide range of mixity values, it was found that seven different definitions for K_eq led to different results. A data-driven modelling methodology (see e.g., [8]) is suggested as a perspective to overcome this unsatisfactory situation, following encouraging applications to mode I FCG, e.g., [9,10,11,12].

2. The Equivalent Stress Intensity Factor K_eq

Several approaches are available to define the equivalent stress intensity factor K_eq for a mixed-mode-I–II situation. For a given situation characterized by the pair K_I, K_II, the proposed equations for the calculation of K_eq provide different values; the question of how different K_eq values compare may be relevant in engineering practice and is not readily apparent from a quick perusal of the relevant equations.

With the support of Matlab scripting, a systematic comparison of the various approaches for calculating K_eq was performed and led to graphical presentations of K_eq/K_I vs. K_I/K_II or K_II/K_I. The literature sources for definitions of K_eq include research involving monotonic and fatigue loading. In the context of monotonic loading and unstable crack propagation, K_eq = f(K_I, K_II) = K_Ic. In the context of FCG, the stress intensity factor range ΔK_eq is used. In both cases (unstable crack propagation or fatigue crack propagation), the concept of K_eq plays the same role of substituting one single value (K_eq) for the original two (K_I and K_II).

2.1. Energy Approach

Irwin’s pioneering work [13] leads to the energy approach, Equation (3), where self-similar crack propagation is assumed (see e.g., [14,15,16,17,18]). This equation is found to be written as a function of the strain energy release rate G, e.g., [6,16], or of the J integral, e.g., [9,19]:

$$K_{eq}={\left(K_I^2+K_{II}^2\right)}^{\frac{1}{2}}$$

(3)

2.2. Tanaka’s Approach

Tanaka [20] proposed a definition used or mentioned, e.g., in [15,21,22,23]:

$$K_{eq}={\left(K_I^4+8K_{II}^4\right)}^{\frac{1}{4}}$$

(4)

Tanaka assumes that FCG occurs when a critical displacement value is attained in a plastic strip. For mixed-mode situations, no interaction between mode I and mode II deformations is assumed.

2.3. Lardner’s Approach

Lardner’s contribution concerns the use of dislocation theory to assess fatigue crack growth [24]. As discussed by Tanaka [20], a first Lardner approach (given by Equation (24) of reference [20]) is:

$$K_{eq}={\left(K_I^2+2K_{II}^2\right)}^{\frac{1}{2}}$$

(5)

Tanaka [20] also discusses a different interpretation of Lardner’s results, (in the following called Lardner B, given by Equation (25) of reference [20]):

$$K_{eq}={\left(K_I^4+4K_{II}^4\right)}^{\frac{1}{4}}$$

(6)

2.4. Chen and Keer Approach

FCG was related to the accumulated crack opening and sliding plastic displacements by Chen and Keer. Their approach was originally presented in [25] and is used, e.g., in [21] or [22]:

$$K_{eq}={\left[{\left(K_I^2+3K_{II}^2\right)}^3\left(K_I^2+K_{II}^2\right)\right]}^{\frac{1}{8}}$$

(7)

2.5. Pook’s Approach

As presented, e.g., in [26], Pook proposes the empirical relation:

$$K_{eq}=\frac{0.83K_I+{\left(0.4489K_I^2+3K_{II}^2\right)}^{\frac{1}{2}}}{1.5}$$

(8)

2.6. Demir’s Approach

For the ranges of the K_I and K_II values considered [27,28], the following empirical equation was found suitable for CTS (compact tension shear specimen) and for a new type of specimen, labelled T-specimen:

$$K_{eq}={\left(1.0519K_I^4-0.035K_{II}^4+2.3056K_I^2{K}_{II}^2\right)}^{\frac{1}{2}}$$

(9)

2.7. Richard/Henn Approach

According to Richard [29]:

$$K_{eq}=\frac{K_I}{2}+\frac{1}{2}{\left(K_I^2+6K_{II}^2\right)}^{\frac{1}{2}}$$

(10)

Equation (10) is designated the Richard/Henn approach in [30] and is found, e.g., in [31,32,33]. This was originally presented as a function of the mode I/mode II ratio of fracture toughness α₁:

$$K_{eq}=\frac{K_I}{2}+\frac{1}{2}{\left[K_I^2+4\left({\alpha }_1{K}_{II}^2\right)\right]}^{\frac{1}{2}} ; {\alpha }_I=\frac{K_{Ic}}{K_{IIc}}$$

(11)

The formulation of Equation (11), proposed in [34], is found in [23,35,36,37] and generalized in [36,38] to include K_III. Using the value α₁ = 1.155, Richard et al. also propose, as a good approximation:

$$K_{eq}=\frac{K_I}{2}+\frac{1}{2}{\left(K_I^2+5.336K_{II}^2\right)}^{\frac{1}{2}}$$

(12)

See, e.g., [39,40,41].

There are, however, other definitions of the equivalent stress intensity factor for mixed-mode situations, including expressions where parameters are fitted to the experimental data, e.g., [42]. The selection presented above, however, is deemed sufficient to check the consequences of diversity, as follows.

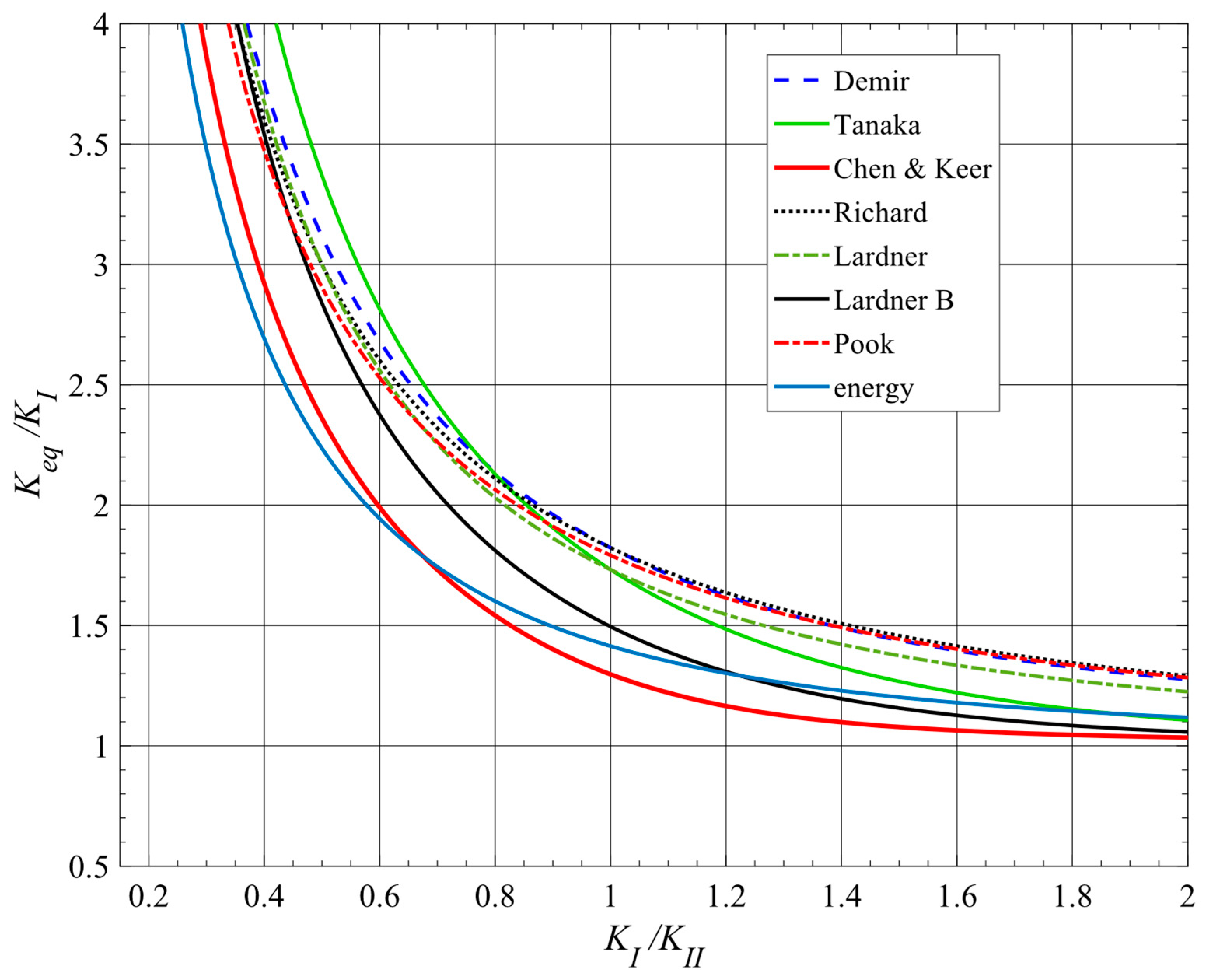
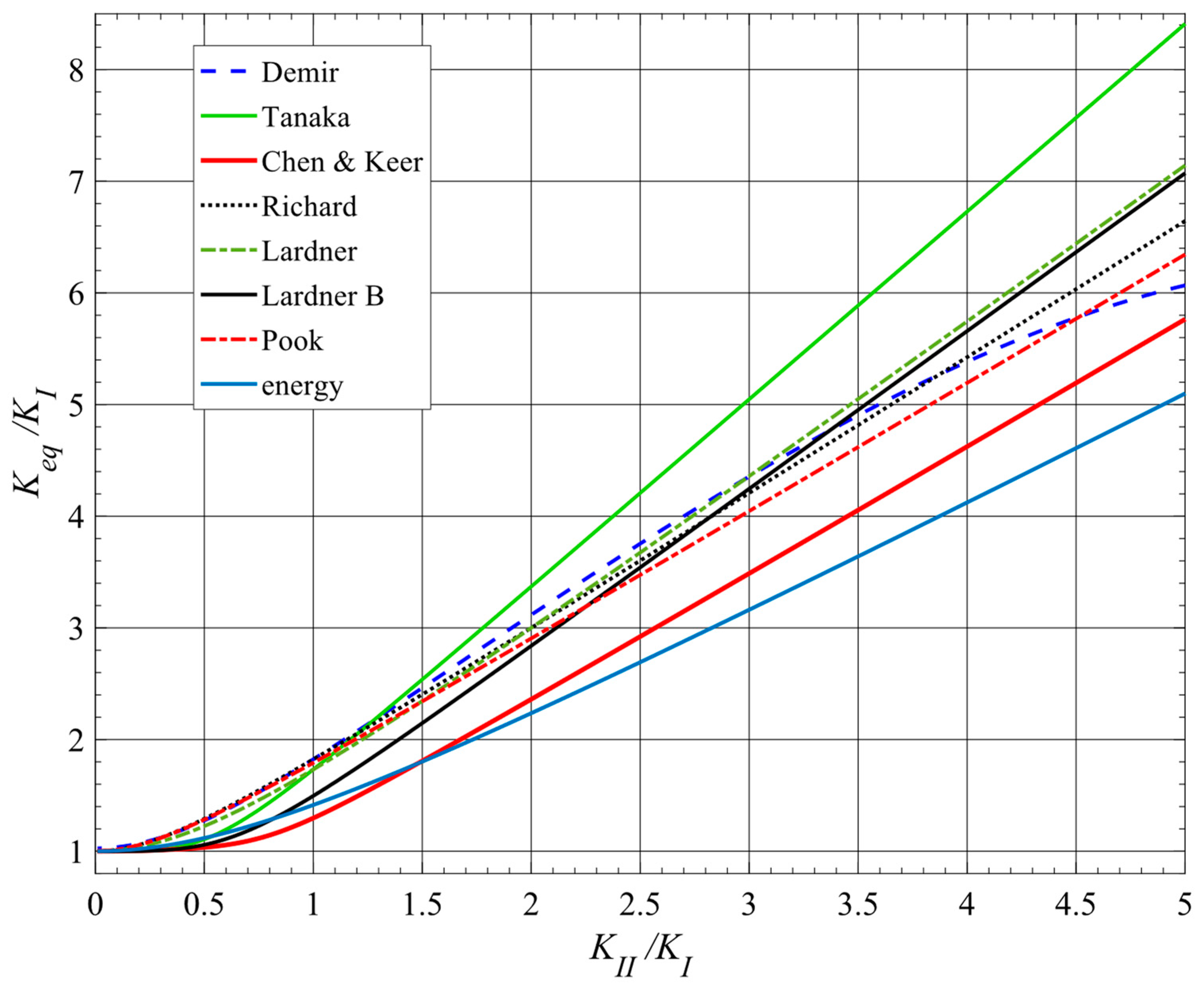
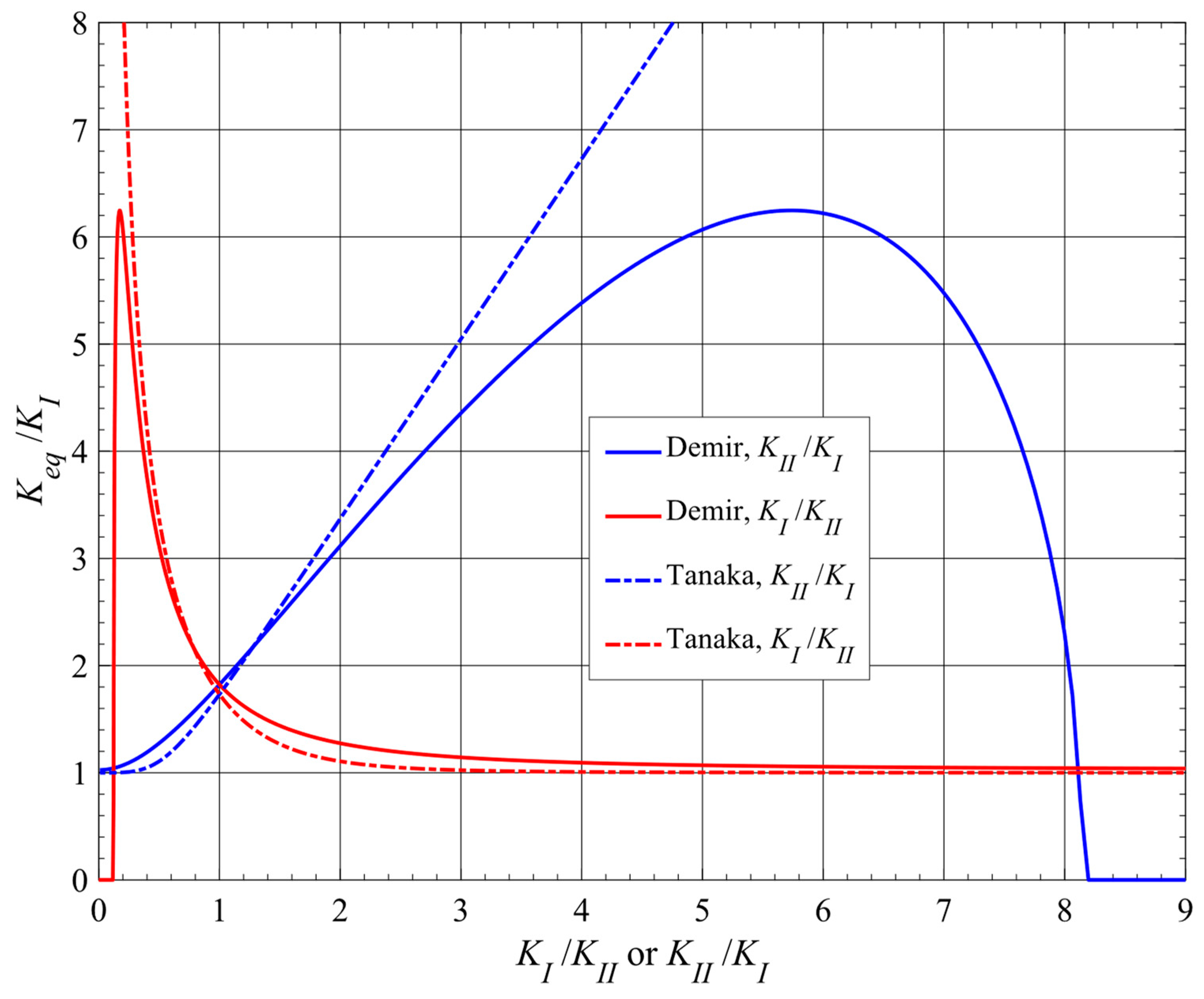
3. Comparisons

For the purpose of a comparison, K_eq/K_I was plotted as a function of K_I/K_II and of K_II/K_I. Equation (10) was adopted as representative of the Richard approach, and the previous Equations (3)–(10) were rewritten as follows:

Energy:

$$\frac{K_{eq}}{K_I}={\left[1+{\left(\frac{K_{II}}{K_I}\right)}^2\right]}^{\frac{1}{2}}$$

(13)

Tanaka:

$$\frac{K_{eq}}{K_I}={\left[1+8{\left(\frac{K_{II}}{K_I}\right)}^4\right]}^{\frac{1}{4}}$$

(14)

Lardner:

$$\frac{K_{eq}}{K_I}={\left[1+2{\left(\frac{K_{II}}{K_I}\right)}^2\right]}^{\frac{1}{2}}$$

(15)

Lardner B:

$$\frac{K_{eq}}{K_I}={\left[1+4{\left(\frac{K_{II}}{K_I}\right)}^4\right]}^{\frac{1}{4}}$$

(16)

Chen and Keer:

$$\frac{K_{eq}}{K_I}={\left\{{\left[1+3{\left(\frac{K_{II}}{K_I}\right)}^2\right]}^3\left[1+{\left(\frac{K_{II}}{K_I}\right)}^2\right]\right\}}^{\frac{1}{8}}$$

(17)

Pook:

$$\frac{K_{eq}}{K_I}={\left\{{\left[1+3{\left(\frac{K_{II}}{K_I}\right)}^2\right]}^3\left[1+{\left(\frac{K_{II}}{K_I}\right)}^2\right]\right\}}^{\frac{1}{8}}$$

(18)

Demir:

$$\frac{K_{eq}}{K_I}=\frac{K_{II}}{K_I}{\left(1.0519{\left(\frac{K_I}{K_{II}}\right)}^2-0.035{\left(\frac{K_{II}}{K_I}\right)}^2+2.3056\right)}^{\frac{1}{2}}$$

(19)

Richard:

$$\frac{K_{eq}}{K_I}=\frac{1}{2}+\frac{1}{2}{\left[1+6{\left(\frac{K_{II}}{K_I}\right)}^2\right]}^{\frac{1}{2}}$$

(20)

Figure 1 plots the non-dimensional K_eq/K_I as a function of K_I/K_II for the approaches considered, in a region K_I/K_II < 2. Figure 2 plots the non-dimensional K_eq/K_I as a function of K_II/K_I for the approaches considered, in the region K_II/K_I < 5.

Within the range of K_I and K_II values of Figure 1 and Figure 2, Demir’s approach [27,28] leads to K_eq values that approximately follow the trend of other K_eq approaches. Nevertheless, the format of Equation (19) and its resulting curve in Figure 2 raised an interest in analyzing its behavior over a wider range of K_I and K_II values. Notice that, unlike the others, Demir’s curve shows a noticeable decrease of the derivative as K_II/K_I increases. Indeed, Equation (19) shows K_eq/K_I = 0 for K_I/K_II = 0.178, which results from:

$$\begin{array}{l}1.0519{\left(\frac{K_I}{K_{II}}\right)}^2-0.035{\left(\frac{K_{II}}{K_I}\right)}^2+2.3056=0\\ 1.0519{\left(\frac{K_I}{K_{II}}\right)}^2-\frac{0.035}{{\left(\frac{K_I}{K_{II}}\right)}^2}+2.3056=0\end{array}$$

(21)

Discarding the complex region (square root of a negative number), Figure 3 shows K_eq/K_I as a function of K_I/K_II and of K_II/K_I. Clearly, Equation (19) does not apply to all domains of K_I and K_II; it presents zeroes for K_I/K_II = 0.178 and K_II/K_I = 8.144. Nevertheless, it follows the expected trend of the solution for K_I/K_II > ~0.4 and for K_II/K_I < ~4, as shown in Figure 3, where for comparison it is plotted together with Tanaka’s equation.

Two conditions that candidate definitions of K_eq should satisfy are:

$$\begin{array}{l}{K}_{eq}/K_I\to 1 \mathrm{for} K_I/K_{II}\to \infty \\ K_{eq}/K_I\to \infty \mathrm{for} K_I/K_{II}\to 0\end{array}$$

(22)

Since the present analyses are concerned with solutions that are as general as possible, the K_eq definition of Equations (9) and (19) was no longer used, given its limited application.

4. Experimental Data and Discussion

Data from [43,44] using Tanaka’s definition of K_eq (Equation (4)) indicate that, for the test conditions and structural steels considered, the experimentally measured da/dN vs. ΔK_I and da/dN vs. ΔK_eq were approximately similar, a trend also found by Akama using Richard’s K_eq definition and testing biaxially loaded plates [45]. Using CTS specimens and Richard’s K_eq definition of Equations (11) and (12), [46] notes that C and m in Equation (2) depend on the angle of load direction and initial pre-crack, i.e., on the initial values of K_II/K_I. Such a dependence is also shown in [33]; that is a weak dependence, which is not surprising given that in CTS specimens, after the initial shift in the crack path, most of the FCG takes place in near-mode-I conditions. Similar conclusions were obtained by Hong et al. [47].

As shown in Section 2, substantial differences between K_eq definitions are found. What are the consequences of that diversity?

The mixed-mode fatigue crack propagation tests may be performed using a travelling microscope measuring horizontal and vertical coordinates. Preferably, to monitor both surfaces of the specimen, two travelling microscopes may be used. The measurement of the crack path’s x, y coordinates in a mixed-mode fatigue crack propagation test is a tedious and time-consuming task. It involves the identification of the number of cycles needed for the crack tip to move from location x₁, y₁ to x₂, y₂. As a simplification, the distance between points 1 and 2 is assumed to be a straight line and therefore:

$$\Delta a\approx \frac{\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}}{\Delta N}$$

(23)

A higher accuracy is obtained if more points are used to define the path, implying more frequent measurements of coordinates associated with lower values of $\Delta a$, which can be achieved with automatic systems and high-resolution digital cameras. The crack growth rate $da/dN$ is then defined as:

$$\frac{da}{dN}\approx \frac{\Delta a}{\Delta N}$$

(24)

In tests reported in [5,6], Al alloy AA6082 T6 CT specimens modified with holes, along with cracked 4-point bend specimens subjected to asymmetrical loading promoting mixed-mode situations, were subjected to FCG tests where the crack path and crack growth rate were measured. As in [48,49,50], for the CT specimens with holes, K_eq values were not far from K_I, and da/dN vs. ΔK_eq data were close to da/dN vs. ΔK_I data. Figure 4 shows the crack path in a CT specimen modified with a hole [51].

Research showing a good predictability of FCG was also presented by Alshoaibi in [52,53], where, again, the values of KII were typically smaller or much smaller than the values of K_I. However, for the 4-point bend specimens, a great diversity of mixity values was achieved in [5], and substantial differences between mode-I and mixed-mode FCG could be identified. The difference between da/dN vs. ΔK_eq and da/dN vs. ΔK_I data increases with the mixity value.

According to a suitable choice of loading points, 4-point bend tests may produce pure mode II situations. As an example, Figure 5 shows a 4-point bend specimen, tested under initial pure mode II. Of interest here is the initial direction of the crack growth, starting from the precrack—in this test, the crack growth takes place at an angle of approx. 90°. Details of the experiments may be found in [5].

The present note highlights the need for data clarifying what is the best definition for K_eq. This is illustrated by the Paris laws obtained from the dataset of

Table 1. Tests at R = 0.1, maximum values of K_I and K_II per cycle, and FCG rate [5].

	da/dN [mm/cycle]	KI, max [MPamm−1/2]	KII, max [MPamm−1/2]
spec. #1	0.00015	172.3	512.9
	5.9 × 10−5	738.6	9.6
	0.001	834.6	51
	0.01	1.08 × 103	83.7
spec. #3	9.70 × 10−5	344,7	258.9
	0.0014	574.9	100.5
	0.00041	840	50.6
	0.006	919.4	183.5
	0.019	1169.8	132.3

, using the present enlarged set of definitions of K_eq.

The corresponding Paris law representation, in terms of different K_eq definitions, is provided in Figure 6.

One example of the consequences of the presented analysis is the expected FCG rate for a given ΔK_eq value, considering different definitions for K_eq. For the dataset used, and as shown in Figure 4, the ranking of growth rates is not constant along the values of ΔK_eq. Indeed, above ~700 MPamm^−1/2, the ranking of the FCG rates would be different. With data for K_eq = 400 MPamm^−1/2 and for K_eq = 800 MPamm^−1/2, one such example is provided in

Table 2. FCG rate for 6082 T6 for K_eq = 400 MPamm^−1/2 and for K_eq = 800 MPamm^−1/2 (mm/cycle).

	Keq = 400 MPamm−1/2	Keq = 800 MPamm−1/2
Chen & Keer	3.16 × 10−5	5.12 × 10−3
Pook	3.40 × 10−5	4.75 × 10−3
Richard	4.15 × 10−5	4.52 × 10−3
Lardner	5.62 × 10−5	4.14 × 10−3
Tanaka	8.76 × 10−5	4.27 × 10−3
Energy/Irwin	1.54 × 10−4	3.78 × 10−3

.

As mentioned in the introduction section, one aim of the application of Fracture Mechanics to fatigue is to model fatigue crack propagation in real structural components, starting from existing or assumed cracks that progress under a cyclic load up to a larger size or final rupture. Clearly, those applications are successful in mode I, where no doubts exist concerning the transformation of the stress state of the cracked component or structure into a value of K_I. However, as seen above, for mixed-mode situations, a variety of K_eq definitions are currently in use, and they may lead to rather different FCG predictions.

Recent work by Sajith et al. illustrates the point in several structures and specimen geometries. The work of these authors evaluates the FCG predictability performance of different K_eq criteria, using CTS specimens with various precrack inclination values [54]. The experimental a vs. N curve was compared with the predictions. In the region just after the precrack, the differences found were more important, and they diminished as the crack grew. This is consistent with the fact that in CTS specimens, after the initial shift from the precrack direction, most of the FCG takes place under the approximate mode I condition. Interestingly, in [55], the same authors examined plates with an inclined central precrack and found a similar trend of larger errors near the initial precrack. It is worth recalling that the inclined central crack in a plate tends to grow into a mode I situation.

Furthermore, using a single definition of K_eq, the same value of K_eq may be achieved via an infinity of different combinations of K_I and K_II, and it is clear that different combinations imply different FCG rates. The still unanswered question is therefore: what could be a definition of K_eq that aims at a wide and universal applicability?

A perspective to counteract the shortcomings presented would be to address the modelling methodology in a data-driven fashion. Unsupervised learning may help to reveal hidden patterns that will potentially support our understanding of the material’s behavior. Data-driven modelling and machine learning was already successfully applied, e.g., to materials science [8,56,57], failure of concrete [58] or geology [59]. Using numerical data, Baptista et al. [60] showed that artificial neural networks can be trained to predict an FCG’s path and life, and they reckon that experimental data is required to improve training. Considering that FCG can be described with physical laws, physics-informed data-driven approaches [61,62] can be exploited in analyses involving mixed-mode FCG; however, those approaches require significant experimental data for model training, which is not yet widely available.

5. Concluding Remarks

This article compared several definitions of the equivalent stress intensity factor in mixed-mode situations, currently in use among researchers.

Requirements for candidate definitions were the trends of K_eq/K_I when K_I/K_II tends to infinity or to zero. One definition of K_eq found in the literature was shown to fail the requirements.

Values of K_eq for the different definitions were compared through a determination of K_eq/K_I over a wide range of values of K_I/K_II or K_II/K_I. It was found that the different approaches converged to the same value as K_I/K_II increased. For large K_II/K_I, differences between values of K_eq persisted, and in the regions 0 < K_I/K_II < 2 and 0 < K_II/K_I < 2, no stable result trend could be defined.

The present note aimed at highlighting the difficulties of modelling FCG in mixed-mode situations, created by the coexistence of different K_eq definitions. The same set of experimental mixed-mode FCG data leads to different constants C and m of the Paris law equation; consequently, when integrating the law, different lives are found. For the FCG dataset used, it was found that the ranking of different definitions as regarded the FCG rate depended on the ΔK_eq value considered—for lower values of ΔK_eq, the Chen and Keer definition provided the lower FCG rate, whereas for the higher values of ΔK_eq, the lower values of the FCG rate corresponded to the ‘energy’ definition of K_eq.

Data-driven modelling, and in particular physics-informed data-driven methodologies, are possible perspectives for overcoming the present shortcomings of mixed-mode FCG modelling. Integrating data-driven approaches such as machine learning or neural networks with FCG equations and with the structural and material behavior of a structural component can create more reliable and accurate models for predicting FCG behavior. However, this approach demands a significant amount of data and an individualized calibration for each structural component, in order to capture the particular material behavior and environmental conditions of that component.