Shock Wave Formation and Cloaking in Hyperelastic Rods
Abstract
1. Introduction
1.1. An Overview
1.2. Problem Statement
2. Yeoh Equation of State
2.1. Basic Relations
2.2. Hyperelastic Potential
2.3. Stress–Strain Relation
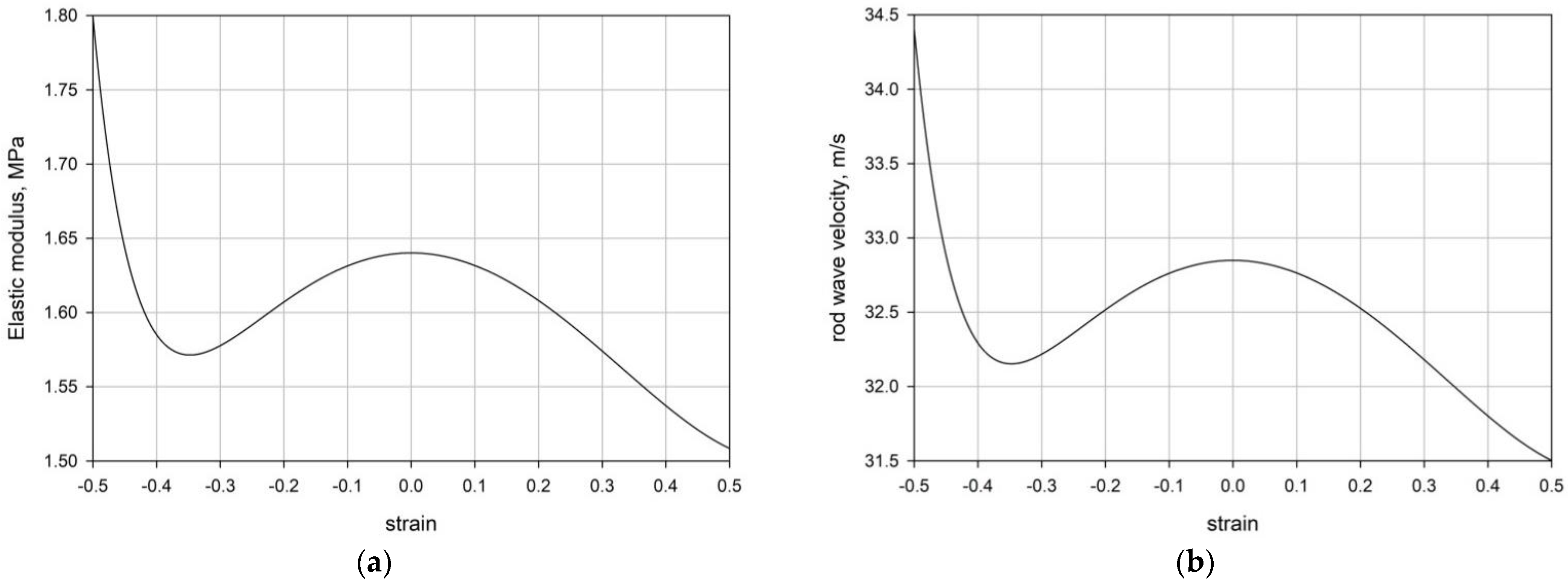
2.4. Tangent Elastic Modulus
2.5. Rod Velocity
3. Secular Equations
3.1. Equation of Motion
3.2. Boundary and Initial Conditions
3.3. Energy Balance
3.4. FE Formulation
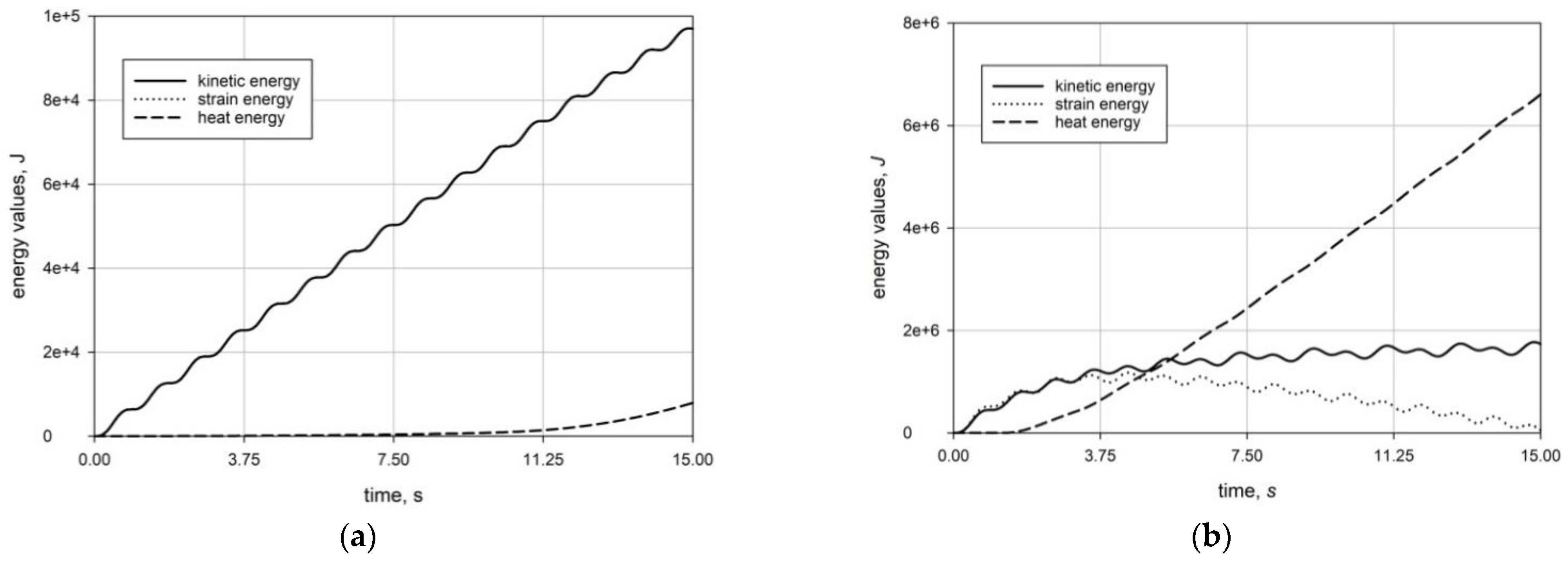
4. Numerical Analyses
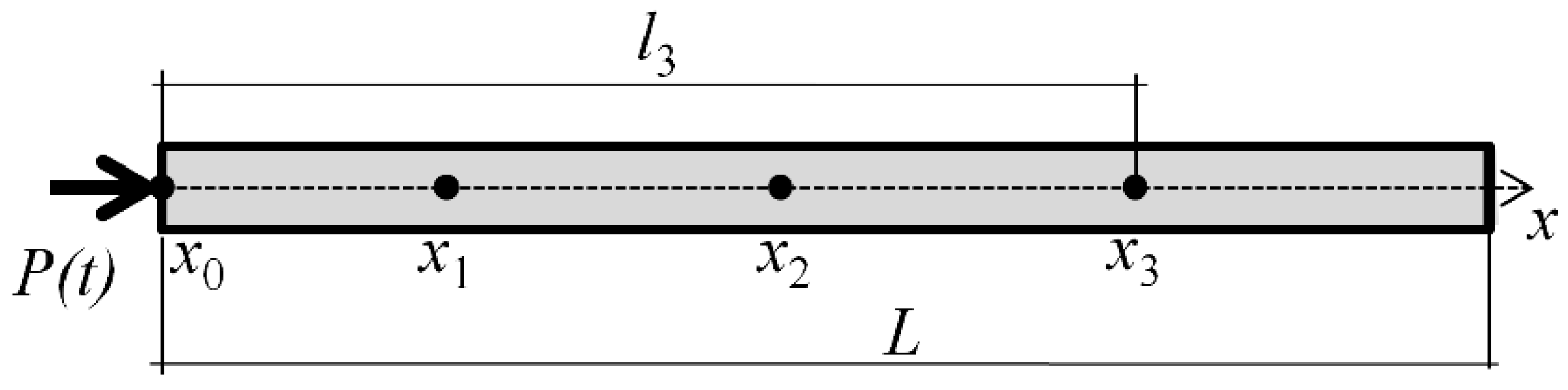
4.1. The Model
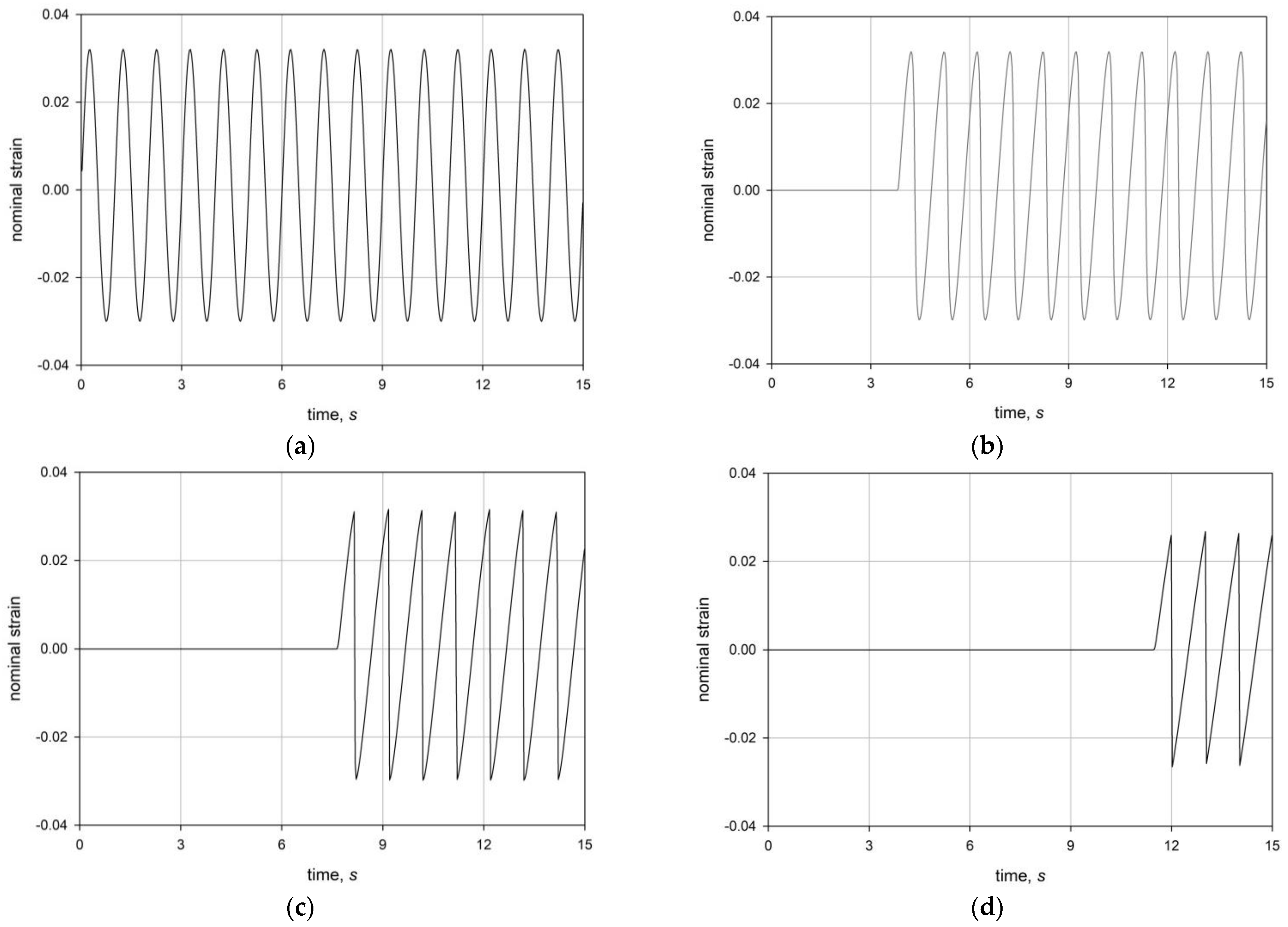
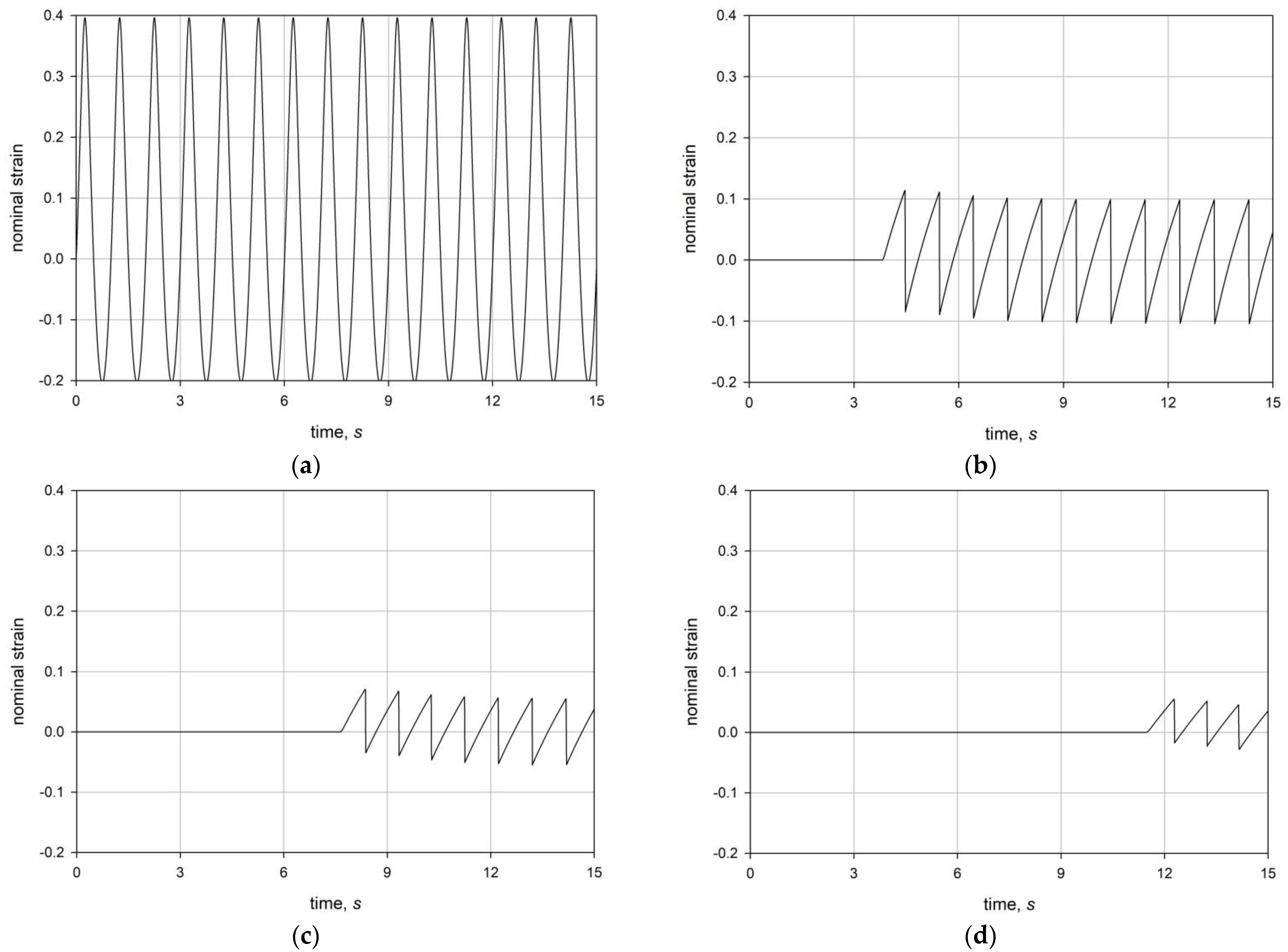
4.2. Harmonic Excitations
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rankine, W.J.M. On the thermodynamic theory of waves of finite longitudinal disturbances. Phil. Trans. Roy. Soc. London 1870, 160, 277–286. [Google Scholar]
- Vieille, P. Etude sur le role des discontinuites dans les phenomenes de propagation. Meml. Poudres Salpetres 1900, 10, 177–260. [Google Scholar] [CrossRef]
- Anile, A.M. Propagation of weak shock waves. Wave Motion 1984, 6, 571–578. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.O. Supersonic Flow and Shock Waves; Interscience Inc.: New York, NY, USA, 1948. [Google Scholar]
- Landau, L.D. Shock waves at large distances from their place of formation. Sov. Phys. J. 1945, 9, 496–500. [Google Scholar]
- Lighthill, M.J. The diffraction of blast. I. Proc. Roy. Soc. Ser. A 1949, 198, 454–470. [Google Scholar]
- Maslov, V.P. Propagation of shock waves in an isentropic non-viscous gas. J. Math. Sci. 1980, 13, 119–163. [Google Scholar] [CrossRef]
- Maslov, V.P.; Mosolov, P.P. General theory of the solutions of the equations of motion of an elastic medium of different moduli. J. Appl. Math. Mech. 1985, 49, 322–336. [Google Scholar] [CrossRef]
- McCarthy, M.F. Singular surfaces and waves. In Continuum Physics; Eringen, A.C., Ed.; Academic Press: London, UK, 1975; Volume 2, pp. 449–521. [Google Scholar]
- Resler, E.L.; Lin, S.C.; Kantrowitz, A. The production of high temperatures in shock tubes. J. App. Phys. 1952, 23, 1390–1399. [Google Scholar] [CrossRef]
- Thomas, T.Y. The fundamental hydrodynamical equations and shock conditions for gases. Math. Mag. 1949, 22, 169–189. [Google Scholar] [CrossRef]
- Thomas, T.Y. The growth and decay of sonic discontinuities in ideal gases. J. Math. Mech. 1957, 6, 455–469. [Google Scholar] [CrossRef]
- Thomas, T.Y. Extended compatibility conditions for the study of surface discontinuity in continuum mechanics. J. Math. Mech. 1957, 6, 311–322. [Google Scholar]
- Whitham, G.B. On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 1958, 4, 337–360. [Google Scholar] [CrossRef]
- Whitham, G.B. A new approach to problems of shock dynamics. Part II. Three-dimensional problems. J. Fluid Mech. 1959, 5, 369–386. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley & Sons: New York, NY, USA, 1974. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 2nd ed.; Springer-Verlag: Berlin, Germany, 1999. [Google Scholar]
- Mortell, M.P.; Seymour, B.R. Nonlinearization and waves in bounded media: Old wine in a new bottle. J. Phys. Conf. Ser. 2017, 811, 012006. [Google Scholar] [CrossRef]
- Neumann, J.V.; Richtmyer, R. A method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 1950, 21, 232–237. [Google Scholar] [CrossRef]
- Jordan, P.M.; Christov, C.I. A simple finite difference scheme for modeling the finite-time blow-up of acoustic acceleration waves. J. Sound Vibr. 2005, 281, 1207–1216. [Google Scholar] [CrossRef]
- Woodward, P.; Colella, P. The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comp. Phys. 1984, 54, 115–173. [Google Scholar] [CrossRef]
- Yassein, S.M.; Ashwad, A.A. Efficient iterative method for solving Korteweg-de-Vries equations. Iraqi J. Sci. 2019, 60, 1575–1583. [Google Scholar] [CrossRef]
- Hartmann, R.; Houston, P. Adaptive discontinuous Galerkin finite element methods for the compressible Euler equations. J. Comp. Phys. 2002, 183, 508–532. [Google Scholar] [CrossRef]
- Menina, R.; Saurel, R. Modelling gas dynamics in 1D ducts with abrupt area change. Shock. Waves 2011, 21, 451–466. [Google Scholar] [CrossRef]
- Jin, H.; Wang, H.; Wu, Z.; Ge, Z.; Chen, Y. Numerical investigation of the effect of surface roughness on flow and heat transfer characteristics of single sphere particle in supercritical water. Comput. Math. Appl. 2019, 81, 562–572. [Google Scholar] [CrossRef]
- Lu, L.; Xu, J.; Ge, W.; Yue, Y. EMMS-based discrete particle method (EMMS–DPM) for simulation of gas–solid flows. Chem. Eng. Sci. 2014, 120, 67–87. [Google Scholar] [CrossRef]
- Zhou, L.; Lv, W.; Bai, L.; Han, Y.; Wang, J.; Shi, W.; Huang, G. CFD–DEM study of gas–solid flow characteristics in a fluidized bed with different diameter of coarse particles. Energy Rep. 2022, 8, 2376–2388. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Karman, T.; Duwez, P. The propagation of plastic deformation in solids. J. Appl. Phys. 1950, 21, 987–994. [Google Scholar] [CrossRef]
- Howell, P.; Ockendon, H.; Ockendon, J.R. Mathematical modelling of elastoplasticity at high stress. Proc. R. Soc. A 2012, 468, 3842–3868. [Google Scholar] [CrossRef]
- Johnson, J.N.; Barker, L.M. Dislocation dynamics and steady plastic wave profiles in 6061 T6 aluminum. J. Appl. Phys. 1969, 40, 4321–4334. [Google Scholar] [CrossRef]
- Davison, L.; Graham, R. Shock compression of solids. Phys. Rep. 1979, 55, 255–379. [Google Scholar] [CrossRef]
- Cohen, T.; Durban, D. Longitudinal shock waves in solids: The piston shock analogue. Proc. R. Soc. A 2014, 470, 2164. [Google Scholar] [CrossRef]
- Grady, D.E. Shock-wave compression of brittle solids. Mech. Mater. 1998, 29, 181–203. [Google Scholar] [CrossRef]
- Graziani, F.; Moldabekov, Z.; Olson, B.; Bonitz, M. Shock physics in warm dense matter: A quantum hydrodynamics perspective. Contrib. Plasma Phys. 2021, 62, e202100170. [Google Scholar] [CrossRef]
- Molinari, A.; Ravichandran, G. Fundamental structure of steady plastic shock waves in metals. J. Appl. Phys. 2004, 95, 1718–1732. [Google Scholar] [CrossRef]
- Pack, D.C.; Evans, W.M.; James, H.J. The propagation of shock waves in steel and lead. Proc. Phys. Soc. 1948, 60, 1–8. [Google Scholar] [CrossRef]
- Taylor, G.I. The testing of materials at high rates of loading. J. Inst. Civ. Eng. 1946, 26, 486–519. [Google Scholar] [CrossRef]
- Hill, R. Acceleration waves in solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Bland, D.R. On shock structure in a solid. J. Inst. Math. Appl. 1965, 1, 56–75. [Google Scholar] [CrossRef]
- Truesdell, C. General and exact theory of waves in finite elastic strain. Arch. Rat. Mech. Anal. 1961, 8, 263–296. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Dequiedt, J.L.; Stolz, C. Propagation of a shock discontinuity in an elasto-plastic material: Constitutive relations. Arch. Mech. 2004, 56, 391–410. [Google Scholar]
- Gavrilov, S.N.; Herman, G.C. Wave propagation in a semi-infinite heteromodular elastic bar subjected to a harmonic loading. J. Sound Vib. 2012, 331, 4464–4480. [Google Scholar] [CrossRef]
- Kuznetsova, M.; Khudyakov, M.; Sadovskii, V. Wave propagation in continuous bimodular media. Mech. Adv. Mater. Struct. 2021, 29, 3147–3162. [Google Scholar] [CrossRef]
- Lax, P.D.; Wendroff, B. Difference schemes for hyperbolic equations with high order of accuracy. Commun. Pure Appl. Math. 1964, 17, 381–398. [Google Scholar] [CrossRef]
- Lucchesi, M.; Pagni, A. Longitudinal oscillations of bimodular rods. Int. J. Struct. Stab. Dynam. 2005, 5, 37–54. [Google Scholar] [CrossRef]
- Ostrovsky, L.A. Wave processes in media with strong acoustic nonlinearity. J. Acoust. Soc. Am. 1991, 90, 3332–3337. [Google Scholar] [CrossRef]
- Radostin, A.; Nazarov, V.; Kiyashko, S. Propagation of nonlinear acoustic waves in bimodular media with linear dissipation. Wave Motion 2013, 50, 191–196. [Google Scholar] [CrossRef]
- Dudchenko, A.V.; Dias, D.; Kuznetsov, S.V. Vertical wave barriers for vibration reduction. Arch. Appl. Mech. 2021, 91, 257–276. [Google Scholar] [CrossRef]
- Zigoneanu, L.; Popa, B.I.; Cummer, S. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 13, 352–355. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. A new method for solving dynamic problems of fractional derivative viscoelasticity. Int. J. Eng. Sci. 2001, 39, 149–176. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Kandu, V.V.; Krusser, A.I. On nonlinear vibrations of an elastic plate on a fractional viscoelastic foundation in a viscoelastic medium in the presence of the one-to-one internal resonance. J. Sound Vibr. 2023, 549, 117564. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Tech. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Gajewski, M.; Szczerba, R.; Jemioło, S. Modelling of elastomeric bearings with application of Yeoh hyperelastic material model. Procedia Eng. 2015, 111, 220–227. [Google Scholar] [CrossRef]
- Knowles, J. Impact-induced tensile waves in a rubberlike material. J. Appl. Math. 2002, 62, 1153–1175. [Google Scholar] [CrossRef]
- Cardone, D.; Gesualdi, G. Experimental evaluation of the mechanical behaviour of elastomeric materials for seismic applications at different air temperatures. Int. J. Mech. Sci. 2012, 64, 127–143. [Google Scholar] [CrossRef]
- Reuter, T.; Ponomarev, I. Biomechanical parameter determination of scaffold-free cartilage constructs (SFCCs) with the hyperelastic material models Yeoh, Ogden and Demiray. Curr. Direc. Biomed. Eng. 2015, 1, 442–445. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Dudchenko, A.V.; Kuznetsov, S.V. The modified Cam-Clay (MCC) model: Cyclic kinematic deviatoric loading. Arch. Appl. Mech. 2016, 86, 2021–2031. [Google Scholar] [CrossRef]
- Kuznetsov, S. Fundamental and singular solutions of Lame equations for media with arbitrary elastic anisotropy. Q. Appl. Math. 2005, 63, 455–467. [Google Scholar] [CrossRef]
- Kuznetsov, S. Lamb waves in stratified and functionally graded plates: Discrepancy, similarity, and convergence. Waves Random Complex Media 2019, 31, 1540–1549. [Google Scholar] [CrossRef]
- Kuznetsov, S. Abnormal dispersion of flexural Lamb waves in functionally graded plates. Z. Angew. Math. Phys. 2019, 70, 89. [Google Scholar] [CrossRef]
- Scovazzi, G.; Song, T.; Zeng, X. A velocity/stress mixed stabilized nodal finite element for elastodynamics: Analysis and computations with strongly and weakly enforced boundary conditions. Comp. Meth. Appl. Mech. Eng. 2017, 325, 532–576. [Google Scholar] [CrossRef]
- Winnicki, I.; Jasinski, J.; Pietrek, S. New approach to the Lax-Wendroff modified differential equation for linear and nonlinear advection. Numer. Meth. Part. Dif. Eq. 2019, 35, 2275–2304. [Google Scholar] [CrossRef]
- Simon Portillo, F.J.; Cuadrado Sempere, Ó.; Marques, E.A.; Sánchez Lozano, M.; Da Silva, L.F. Mechanical characterisation and comparison of hyperelastic adhesives: Modelling and experimental validation. J. Appl. Comput. Mech. 2022, 8, 359–369. [Google Scholar]
- Pence, T.J.; Gou, K. On compressible versions of the incompressible neo-Hookean material. Math. Mech. Solids 2015, 20, 157–182. [Google Scholar] [CrossRef]
- Ilyashenko, A.V.; Kuznetsov, S. Theoretical aspects of applying Lamb waves in nondestructive testing of anisotropic media. Russ. J. Nondestruct. Test. 2017, 53, 243–259. [Google Scholar] [CrossRef]
- Ilyashenko, A.V.; Kuznetsov, S.V. Pochhammer–Chree waves: Polarization of the axially symmetric modes. Arch. Appl. Mech. 2018, 88, 1385–1394. [Google Scholar] [CrossRef]
- Zemanek, J. An experimental and theoretical investigation of elastic wave propagation in a cylinder. J. Acoust. Soc. Am. 1972, 51, 265–283. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Williams, W.O. On the first law of thermodynamics. Arch. Ration. Mech. Anal. 1971, 42, 77–92. [Google Scholar] [CrossRef]
- Zohuri, B.; McDaniel, P. First law of thermodynamics. In Thermodynamics In Nuclear Power Plant Systems; Springer: Berlin, Germany, 2015. [Google Scholar]
- Djeran-Maigre, I.; Kuznetsov, S.V. Velocities, dispersion, and energy of SH-waves in anisotropic laminated plates. Acoust. Phys. 2014, 60, 200–207. [Google Scholar] [CrossRef]
- Burtscher, S.L.; Dorfmann, A. Compression and shear tests of anisotropic high damping rubber bearings. Eng. Struct. 2004, 26, 1979–1991. [Google Scholar] [CrossRef]
- Davison, L. Fundamentals of Shock Wave Propagation in Solids; Springer: Berlin, Germany, 2008. [Google Scholar]
- Goldstein, R.V.; Kuznetsov, S.V. Long-wave asymptotics of Lamb waves. Mech. Solids 2017, 52, 700–707. [Google Scholar] [CrossRef]
- Li, S.; Brun, M.; Djeran-Maigre, I.; Kuznetsov, S. Hybrid asynchronous absorbing layers based on Kosloff damping for seismic wave propagation in unbounded domains. Comp. Geotech. 2019, 109, 69–81. [Google Scholar] [CrossRef]
- Zubeldia, M. Energy concentration and explicit Sommerfeld radiation condition for the electromagnetic Helmholtz equation. J. Func. Anal. 2012, 263, 2832–2862. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, S.V. Shock Wave Formation and Cloaking in Hyperelastic Rods. Appl. Sci. 2023, 13, 4740. https://doi.org/10.3390/app13084740
Kuznetsov SV. Shock Wave Formation and Cloaking in Hyperelastic Rods. Applied Sciences. 2023; 13(8):4740. https://doi.org/10.3390/app13084740
Chicago/Turabian StyleKuznetsov, Sergey V. 2023. "Shock Wave Formation and Cloaking in Hyperelastic Rods" Applied Sciences 13, no. 8: 4740. https://doi.org/10.3390/app13084740
APA StyleKuznetsov, S. V. (2023). Shock Wave Formation and Cloaking in Hyperelastic Rods. Applied Sciences, 13(8), 4740. https://doi.org/10.3390/app13084740





