Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
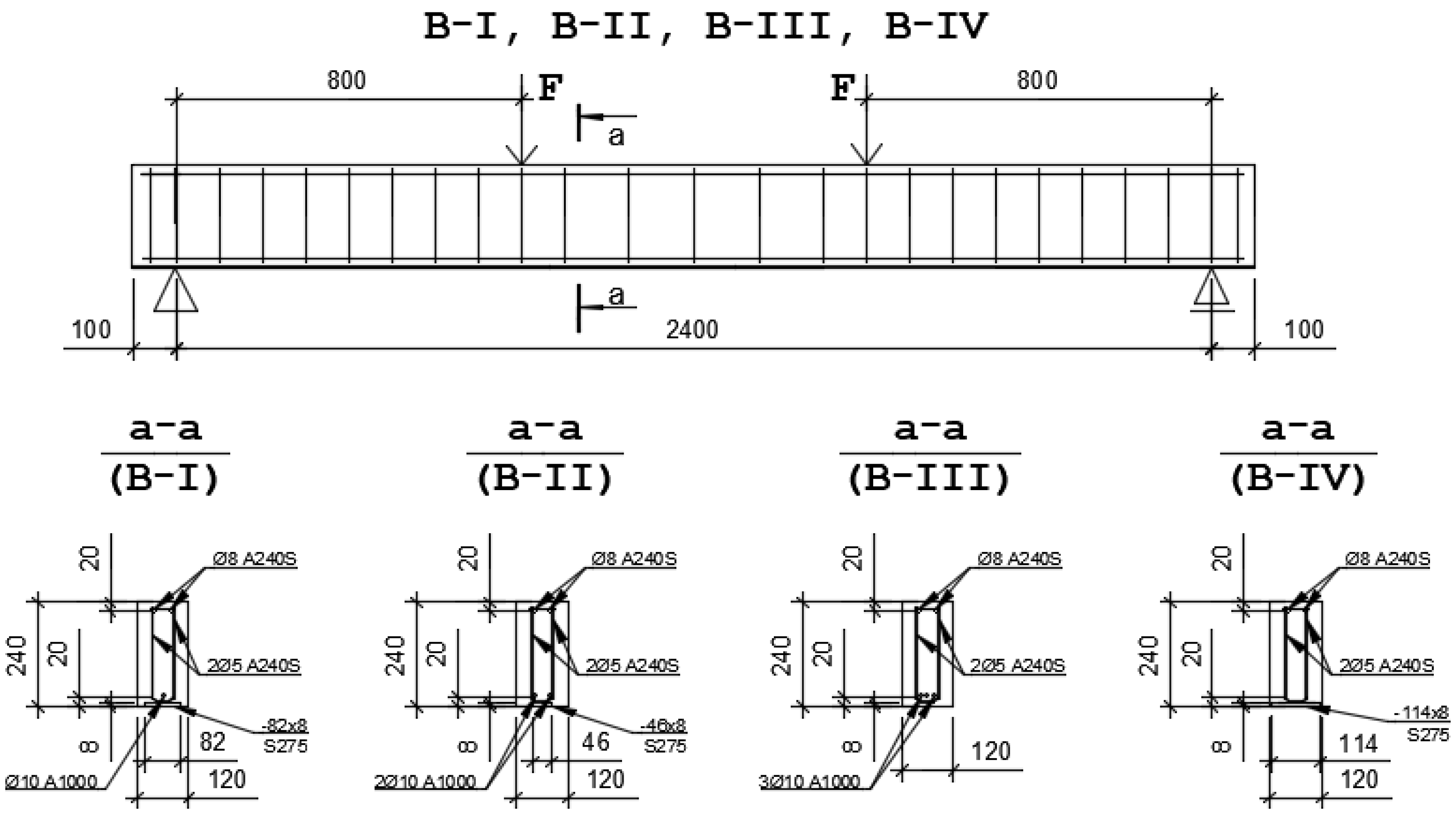
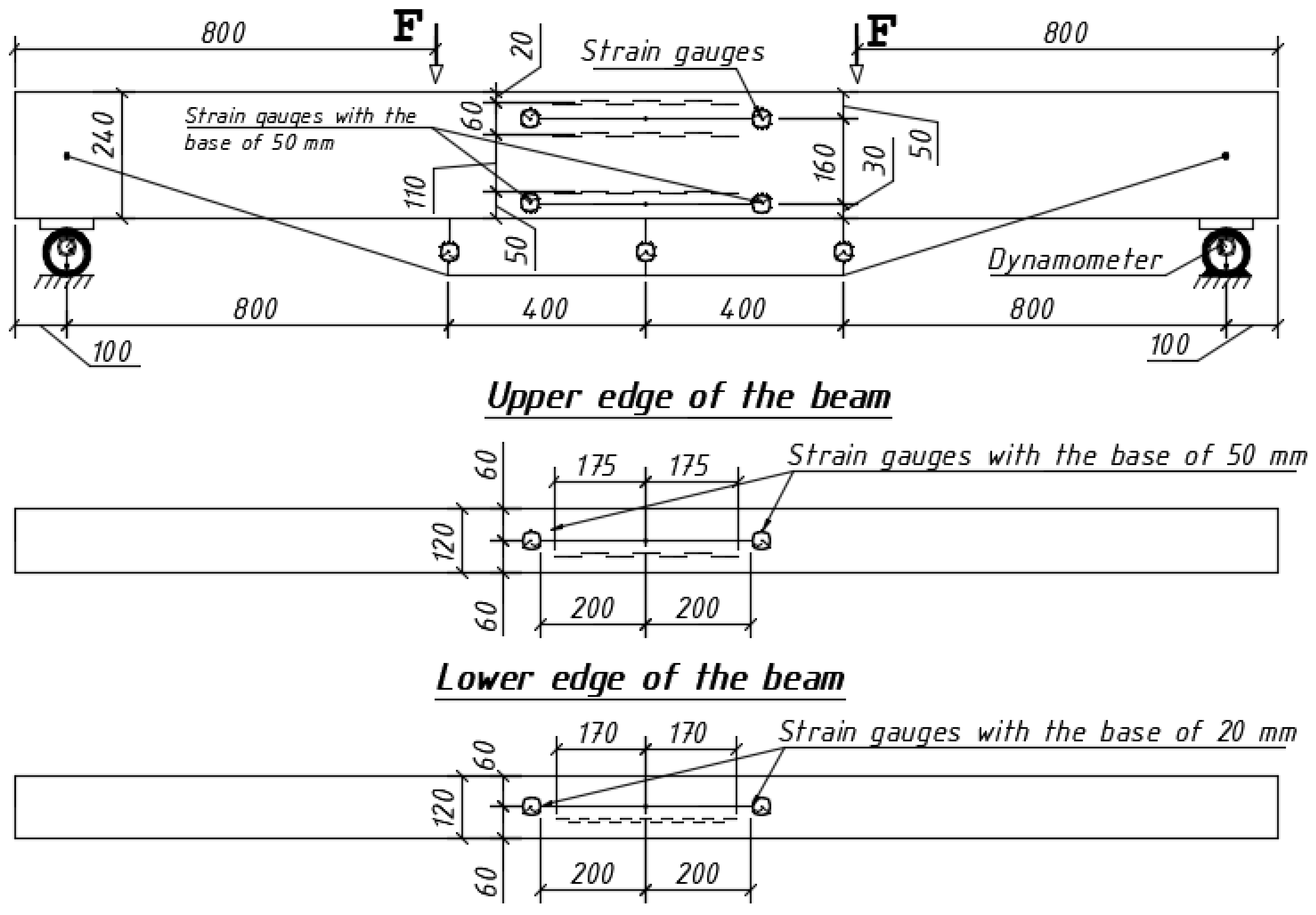
2.1. Experimental Investigation
2.2. Analytical Investigation
3. Results and Discussion
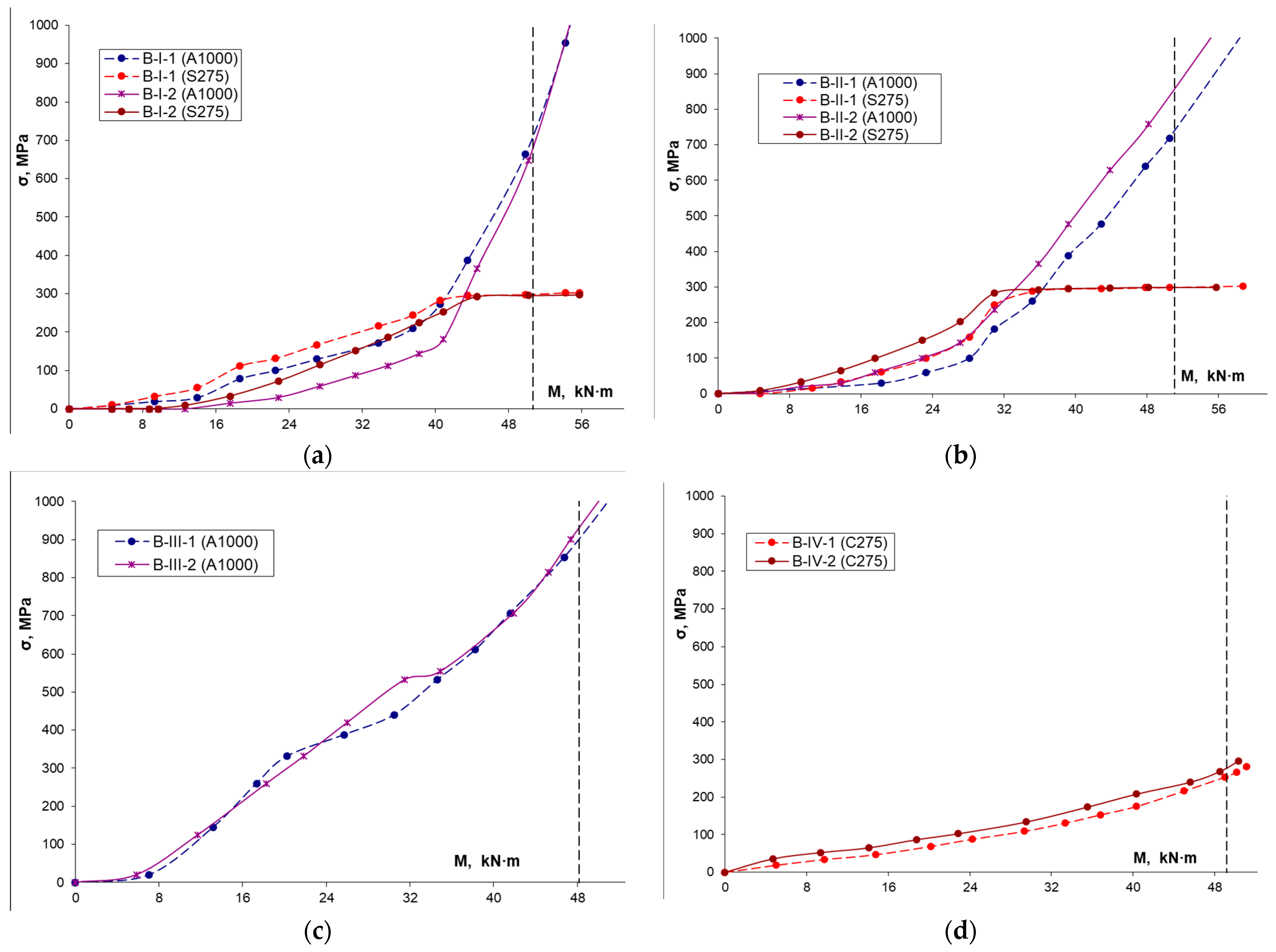
3.1. The Work of the Test Samples until the Moment of the Formation of Cracks
3.2. Process of Cracking
3.3. Deformability or Research Sample with Cracks in Stretched Zone
3.4. Destruction Stages of Research Beams
3.5. Curvature and Deflections of Test Beams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Notation of the Beams | B-I-1, B-I-2 | B-II-1, B-II-2 | B-III-1, B-III-2 | B-IV-1, B-IV-2 | |
|---|---|---|---|---|---|
| Parameters of beam’s cross-section | Width b, mm | 120 | 120 | 120 | 120 |
| Height h, mm | 240 | 240 | 240 | 240 | |
| Area A, cm2 | 288 | 288 | 288 | 288 | |
| Tape reinforcement of S275 class (stretched zone) | Width bs, mm | 82 | 46 | - | 114 |
| Thickness ts, mm | 8 | 8 | - | 8 | |
| Area As, cm2 | 6.56 | 3.68 | - | 9.12 | |
| Longitudinal steel bars of (stretched zone) | Number and diameter of steel bars øs, mm. Strength class | 1ø10 A1000 | 2ø10 A1000 | 3ø10 A1000 | - |
| Area As, cm2 | 0.785 | 1.570 | 2.355 | - | |
| Rs(fyk) × As, steel bar Rs(fyk) × As, tape | 31.2% 68.8% | 61.9% 38.1% | 100% 0% | 0% 100% | |
| The total reinforcement ratio | 2.77% | 1.97% | 0.89% | 3.45% | |
| Longitudinal steel bars (compressed zone) | Number and diameter of steel bars øs, mm | 2ø8 A400S | 2ø8 A400S | 2ø8 A400S | 2ø8 A400S |
| Area As′, cm2 | 1.005 | 1.005 | 1.005 | 1.005 | |
| Transverse steel bars | Number and diameter of steel bars øsw, mm | 2ø5 A240S | 2ø5 A240S | 2ø5 A240S | 2ø5 A240S |
| Area Asw, cm2 | 0.392 | 0.392 | 0.392 | 0.392 | |
| spacing S, mm | 70 | 70 | 70 | 70 | |
| Notation of the Beams | B-I-1, B-I-2 | B-II-1, B-II-2 | B-III-1, B-III-2 | B-IV-1, B-IV-2 | |
|---|---|---|---|---|---|
| Concrete | Characteristic value of strength, fck,cube/fck,prism, MPa | 48.7/29.6 | 46.3/28.1 | 46.3/28.1 | 49.2/29.9 |
| Design value of strength, fcd, MPa | 22.8 | 21.6 | 21.6 | 23.0 | |
| Modulus of elasticity, Ecm × 103, MPa | 38.00 | 37.76 | 38.04 | 38.50 | |
| Tape reinforcement (stretched zone) | Width×thickness, Bs × ts, mm | 82 × 8 | 46 × 8 | - | 114 × 8 |
| Characteristic value of strength, fyk, MPa | 287 | 287 | - | 287 | |
| Design value of strength, fyd, MPa | 273 | 273 | - | 273 | |
| Modulus of elasticity, Ep × 105, MPa | 2.05 | 2.05 | - | 2.05 | |
| Strength class | S275 | S275 | - | S275 | |
| Longitudinal steel bars of (stretched zone) | Diameter, ∅, mm | 1ø10 | 2ø10 | 3ø10 | - |
| Characteristic value of strength, fyk, MPa | 1080 | 1080 | 1080 | - | |
| Design value of strength, fyd, MPa | 900 | 900 | 900 | - | |
| Modulus of elasticity, Ep × 105, MPa | 1.85 | 1.85 | 1.85 | - | |
| Strength class | A1000 | A1000 | A1000 | - | |
| Longitudinal steel bars (compressed zone) | Diameter, ∅′, mm | 8 | 8 | 8 | 8 |
| Characteristic value of strength, fyk′, MPa | 594.5 | 594.5 | 594.5 | 594.5 | |
| Design value of strength, fyd′, MPa | 495 | 495 | 495 | 495 | |
| Modulus of elasticity, Ep′ × 105, MPa | 2.05 | 2.05 | 2.05 | 2.05 | |
| Strength class | A400S | A400S | A400S | A400S | |
| Transverse steel bars | Diameter, ∅, mm | 5 | 5 | 5 | 5 |
| Design value of strength, fywd, MPa | 296 | 296 | 296 | 296 | |
| Modulus of elasticity, Ep × 105, MPa | 2.05 | 2.05 | 2.05 | 2.05 | |
| Strength class | A240S | A240S | A240S | A240S | |
Appendix B
References
- Dorofeyev, V.; Pushkar, N.; Zinchenko, H. The Influence of Concrete Structure on the Destruction of Reinforced Concrete Bended Elements. Lect. Notes Civ. Eng. 2021, 100, 243839. [Google Scholar] [CrossRef]
- Jin, M.; Ma, Y.; Zeng, H.; Liu, J.; Jiang, L.; Yang, G.; Gu, Y. Developing a Multi-Element Sensor to Non-Destructively Monitor Several Fundamental Parameters Related to Concrete Durability. Sensors 2020, 20, 5607. [Google Scholar] [CrossRef]
- Adamczak-Bugno, A.; Lipiec, S.; Vavruš, M.; Koteš, P. Non-Destructive Methods and Numerical Analysis Used for Monitoring and Analysis of Fibre Concrete Deformations. Materials 2022, 15, 7268. [Google Scholar] [CrossRef]
- Koteš, P.; Kotula, P.; Odrobiňák, J.; Prokop, J. Diagnostics and Evaluation of Two Atypical Girder Bridges on Railway Line. Key Eng. Mater. 2022, 930, 211–216. [Google Scholar] [CrossRef]
- Kos, Z.; Klymenko, Y.; Karpiuk, I.; Grynyova, I. Bearing Capacity near Support Areas of Continuous Reinforced Concrete Beams and High Grillages. Appl. Sci. 2022, 12, 685. [Google Scholar] [CrossRef]
- Pawłowicz, J.A. Computer-aided design in the construction industry—BIM technology as a modern design tool. Constr. Optim. Energy Potential CoOEP 2020, 9, 89–96. [Google Scholar] [CrossRef]
- Kramarchuk, A.; Ilnytskyy, B.; Kopiika, N. Ensuring the Load-Bearing Capacity of Monolithic Reinforced Concrete Slab Damaged by Cracks in the Compressed Zone. In Proceedings of EcoComfort 2022, Lviv, Ukraine, 14–16 September 2022; Lecture Notes in Civil Engineering; Blikharskyy, Z., Ed.; Springer: Cham, Switzerland, 2023; Volume 290, pp. 217–229. [Google Scholar] [CrossRef]
- Zeng, H.; Lu, C.; Zhang, L.; Yang, T.; Jin, M.; Ma, Y.; Liu, J. Prediction of Temperature Distribution in Concrete under Variable Environmental Factors through a Three-Dimensional Heat Transfer Model. Materials 2022, 15, 1510. [Google Scholar] [CrossRef] [PubMed]
- Kos, Z.; Klymenko, Y.; Polianskyi, K.; Crnoja, A. Research of the Residual Bearing Capacity and the Work of Damaged Reinforced Concrete Beams’ Inclined Sections. Tech. J. 2020, 14, 466–472. [Google Scholar] [CrossRef]
- Blikharskyy, Y.; Selejdak, J. Influence of the percentage of reinforcement damage on the bearing capacity of RC beams. Constr. Optim. Energy Potential CoOEP 2021, 10, 145–150. [Google Scholar] [CrossRef]
- Kopiika, N.; Vegera, P.; Vashkevych, R.; Blikharskyy, Z. Stress-strain state of damaged reinforced concrete bended elements at operational load level. Prod. Eng. Arch. 2021, 27, 242–247. [Google Scholar] [CrossRef]
- Blikharskyy, Y.; Vashkevych, R.; Kopiika, N.; Bobalo, T.; Blikharskyy, Z. Calculation residual strength of reinforced concrete beams with damages, which occured during loading. In IOP Conference Series: Materials Science and Engineering, Proceedings of the International Scientific Conference Energy Efficiency in Transport (EET 2020), 1021, Kharkiv, Ukraine, 18–20 November 2021; IOP Publishing: Bristol, UK, 2021. [Google Scholar] [CrossRef]
- Helbrych, P. Effect of dosing with propylene fibers on the mechanical properties of concretes. Constr. Optim. Energy Potential CoOEP 2021, 10, 39–44. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Hu, W. Fatigue Analysis of CFRP-Reinforced Concrete Ribbed Girder Bridge Deck Slabs. Polymers 2022, 14, 3814. [Google Scholar] [CrossRef] [PubMed]
- Blikharskyy, Y.; Kopiika, N.; Volynets, M.; Bobalo, T. Theoretical analysis of RC beams reinforced with high strength rebar’s and steel plate. In Proceedings of CEE 2019: Advances in Resource-Saving Technologies and Materials in Civil and Environmental Engineering, Proceedings of the 8th International Scientific Conference «Reliability and Durability of Railway Transport Engineering Structures and Buildings» (TransBud 2019), 708(1), Kharkiv, Ukraine, 20–22 November 2019; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Jing, Z.N.; Liu, R.G.; Xie, G.H.; Liu, D. Shear strengthening of deep T-section RC beams with CFRP bars. Materials 2021, 14, 6103. [Google Scholar] [CrossRef] [PubMed]
- Jahami, A.; Temsah, Y.; Khatib, J.; Baalbaki, O.; Kenai, S. The behavior of CFRP strengthened RC beams subjected to blast loading. Mag. Civ. Engi. 2021, 103, 10309. [Google Scholar] [CrossRef]
- Dalyan, I.; Doran, B. An investigation on the flexural behaviour of RC beams wrapped with CFRP. Int. Adv. Res. Eng. J. 2021, 5, 97–105. [Google Scholar] [CrossRef]
- Rahul Raja, S.; Victor Sagaya Raj, U.; Sriram, K.; Rahul, P.S.; Vedhanayaghi, V.J. Retrofitting of RC beams using CFRP. Int. J. Emerg. Technol. Adv. Eng. 2018, 8, 112–114. [Google Scholar]
- Vatulia, G.; Rezunenko, M.; Petrenko, D.; Rezunenko, S. Evaluation of the carrying capacity of rectangular steel-concrete columns. Civ. Environ. Eng. 2018, 14, 76–83. [Google Scholar] [CrossRef]
- Szewczak, I.; Rzeszut, K.; Rozylo, P. Structural behaviour of steel cold-formed sigma beams strengthened with bonded steel tapes. Thin-Walled Struct. 2021, 159, 107295. [Google Scholar] [CrossRef]
- Karpiuk, I.; Danilenko, D.; Karpiuk, V.; Danilenko, A.; Lyashenko, T. Bearing capacity of damaged reinforced concrete beams strengthened with metal casing. Acta Polytech. 2021, 61, 703–721. [Google Scholar] [CrossRef]
- Araújo, D.d.L.; Nunes, F.G.T.; Filho, R.D.T.; Araújo, M.A.S. Shear strength of steel fiber-reinforced concrete beams. Acta Scientiarum. Technol. Mar. 2014, 36, 389–397. [Google Scholar] [CrossRef]
- Sarhat, S.R.; Abdul-Ahad, R.B. The combined use of steel fibers and stirrups as shear reinforcement in reinforced concrete beams. Spec. Publ. 2006, 235, 269–282. [Google Scholar]
- Eklou, R.J.; Yani, M.B.; Saifullah, H.A.; Sangadji, S.; Kristiawan, S.A. Experimental study: Shear behaviour of reinforced concrete beams using steel plate strips as shear reinforcement. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1144, 012040. [Google Scholar] [CrossRef]
- Zedong, L. Experimental Research on Flexural Behavior of Steel Reinforced Concrete Slabs Combination Strengthened with Enlarging Section and Gluing Steel Plates. Master’s Thesis, Hebei Institute of Civil Engineering and Architecture, Beijing, China, 2017. [Google Scholar]
- Blikharskyy, Y.; Selejdak, J.; Kopiika, N. Corrosion fatigue damages of rebars under loading in time. Materials 2021, 14, 3416. [Google Scholar] [CrossRef] [PubMed]
- Lipiński, T. Investigation of corrosion rate of X55CrMo14 stainless steel at 65% nitrate acid at 348 K. Prod. Eng. Arch. 2021, 27, 108–111. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, J.; Yu, L. Evaluation on Reinforcement Effect of Steel-UHPC Composite Deck with Steel Strip. J. Highw. Transp. Res. Dev. 2022, 39, 74–84. [Google Scholar] [CrossRef]
- Yin, X.; Lin, Q.; Li, K. Calculation of flexural capacity of reinforced concrete slab strengthened with profiled steel sheeting and concrete. Sichuan Build. Sci. 2020, 46, 1–7. [Google Scholar]
- Zhang, Q.; Cao, W. Application of structure strengthening with steel plate and concrete in construction engineering. Sichuan Build. Sci. 2022, 48, 30–35. [Google Scholar]
- Bobalo, T.; Blikharskyy, Y.; Kopiika, N.; Volynets, M. Influence of the percentage of reinforcement on the compressive forces loss in pre-stressed RC beams strengthened with a package of steel bars. Lecture Notes in Civil Engineering. In Proceedings of the 2nd International Scientific Conference on EcoComfort and Current Issues of Civil Engineering EcoComfort 100, Lviv, Ukraine, 16–18 September 2020. [Google Scholar] [CrossRef]
- Wang, W. Research on Flexural Capacity of Reinforced Concrete Beam Strengthened with Bolted Bottom Steel Plate. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2018. [Google Scholar]
- Liu, L.; Wang, L.F.; Xiao, Z.W. Flexural bearing capacity of RC hollow slab beam strengthened by steel plates of different thicknesses. Int. J. Struct. Integr. 2021, 12, 613–628. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Zhu, T.; Li, S.; Zhang, H.J. Numerical analysis of load bearing capacity for RC two-way slab strengthened with well-shaped CFRP—Steel strips. J. Basic Sci. Eng. 2018, 26, 337–345. [Google Scholar]
- Dung, D.T.M.; Khai, L.T.Q. Nonlinear analysis of multi-layer steel fiber reinforced concrete beams. J. Constr. 2021, 4, 58–63. [Google Scholar]
- Vavruš, M.; Koteš, P. Methods of Modeling Contact between Concrete and Fiber Concrete. Solid State Phenom. 2022, 329, 87–92. [Google Scholar] [CrossRef]
- Szewczak, I.; Rozylo, P.; Rzeszut, K. Influence of Mechanical Properties of Steel and CFRP Tapes on the Effectiveness of Strengthening Thin-Walled Beams. Materials 2021, 14, 2388. [Google Scholar] [CrossRef] [PubMed]
- Vatulia, G.L.; Smolyanyuk, N.V.; Shevchenko, A.A.; Orel, Y.F.; Kovalov, O.M. Evaluation of the load-bearing capacity of variously shaped steel-concrete slabs under short term loading. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1002, 012007. [Google Scholar] [CrossRef]
- Kinasz, R.; Bilozir, V.; Shmyh, R.; Bidenko, I. Deformability of Steel-Fiber Beams with External Tape Reinforcement. IOP Conf. Ser. Mater. Sci. Eng. 2020, 960, 022046. [Google Scholar] [CrossRef]
- da Rocha Almeida, M.M.; de Souza, A.S.C.; de Albuquerque, A.T. Experimental study of prestressed steel-concrete composite beams with profiled steel decking. J. Constr. Steel Res. 2022, 194, 107331. [Google Scholar] [CrossRef]
- Bobalo, T.; Blikharskyy, Y.; Kopiika, N.; Volynets, M. Serviceability of RC beams reinforced with high strength rebar’s and steel plate. Lect. Notes Civ. Eng. 2020, 47, 25–33. [Google Scholar] [CrossRef]
- DSTU B V.2.6-156:2010; Constructions of Buildings and Structures. Concrete and Reinforced Concrete Structures Made of Heavy Concrete. Design Rules. Ministry of Regional Construction of Ukraine: Kyiv, Ukraine, 2011.
- EN 1992-1-1; Eurocode 2: Design of concrete structures—Part 1-1: General Rules and Rules for Buildings. Management Centre: Brussels, Belgium, 2004.
- DSTU B V.2.6-7-95; Construction of Buildings and Structures. Precast Concrete and Reinforced Concrete Construction Products. Load Test Methods. Rules for Assessing Strength, Stiffness and Crack Resistance. SE “State Research Institute of Building Structures” (NDIBK), Ministry of Regional Construction of Ukraine: Kyiv, Ukraine, 1995.
- DBN B.2.6-98:2009; Constructions of Buildings and Structures. Concrete and Reinforced Concrete Structures. Main Principles. SE “State Research Institute of Building Structures” (NDIBK), Ministry of Regional Construction of Ukraine: Kyiv, Ukraine, 2009.






| Notation of the Beams | M, kN × m | εs × 105 | εs tape × 105 | εbt × 105 | εb × 105 | Deflection fmax, mm |
|---|---|---|---|---|---|---|
| B-I-1 | 7 | 8 | 11 | 10 | 14 | 0.58 |
| B-I-2 | 7 | 7 | 10 | 9 | 15 | 0.65 |
| B-II-1 | 7 | 10 | 12 | 11 | 15 | 0.72 |
| B-II-2 | 7 | 11 | 14 | 15 | 17 | 0.78 |
| B-III-1 | 7 | 21 | - | 24 | 20 | 1.15 |
| B-III-2 | 7 | 24 | - | 28 | 24 | 1.36 |
| B-IV-1 | 7 | - | 9 | 8.5 | 12 | 0.61 |
| B-IV-2 | 7 | - | 10 | 11 | 14 | 0.65 |
| Notation of the Beams | Beginning of Crack Formation | ||
|---|---|---|---|
| Experimental Mexpcrc, kN × m | According to DBN V.2.6-98:2009 MDBN, mm | (Mexpcrc − MDBN)/Mexpcrc, % | |
| B-I-1 | 6.9 | 5.92 | 14.2 |
| B-I-2 | 7.15 | 17.2 | |
| B-II-1 | 8.00 | 6.12 | 23.5 |
| B-II-2 | 7.46 | 18.0 | |
| B-III-1 | 6.42 | 5.26 | 18.1 |
| B-III-2 | 5.6 | 6.1 | |
| B-IV-1 | 8.08 | 7.12 | 11.9 |
| B-IV-2 | 7.92 | 10.1 | |
| Notation of the Beams | M, kN×m | εs × 105 | εs tape × 105 | εB t × 105 | εB × 105 | Deflection f, mm |
|---|---|---|---|---|---|---|
| B-I-1 | 6.9 | 7 | 10 | 16 | 9 | 0.60 |
| B-I-2 | 7.15 | 9 | 12 | 17 | 10 | 0.68 |
| B-II-1 | 8.00 | 16 | 18 | 19 | 25 | 1.08 |
| B-II-2 | 7.46 | 12 | 16 | 18 | 31 | 1.11 |
| B-III-1 | 6.42 | 18 | - | 20 | 16 | 1.09 |
| B-III-2 | 5.6 | 15 | - | 17 | 11 | 0.83 |
| B-IV-1 | 8.08 | - | 16 | 15 | 22 | 0.93 |
| B-IV-2 | 7.92 | - | 14 | 13 | 19 | 0.82 |
| Notation of the Beams | Maximum Crack Opening | |||
|---|---|---|---|---|
| Normative Width wMax, mm | Experimental Mexp, kN × m | DBN B.2.6-98:2009 MDBN0.3 | (Mexp − MDBN0.3)/Mexp, % | |
| B-I-1 | 0.3 | 28.35 | 24.37 | 14.0 |
| B-I-2 | 0.3 | 28.06 | 13.2 | |
| B-II-1 | 0.3 | 27.30 | 26.87 | 1.6 |
| B-II-2 | 0.3 | 30.70 | 12.5 | |
| B-III-1 | 0.3 | 33.45 | 32.90 | 1.6 |
| B-III-2 | 0.3 | 36.79 | 10.6 | |
| B-IV-1 | 0.3 | 43.26 | 41.75 | 3.5 |
| B-IV-2 | 0.3 | 42.97 | 2.8 | |
| Notation of the Beams | 0.7 Mdr2, кH | εs ×105 | εs tape ×105 | εB t ×105 | εB ×105 | Deflection fdr2, mm |
|---|---|---|---|---|---|---|
| B-I-1 | 44.93 | 105 | 127 | 124 | 94 | 4.55 |
| B-I-2 | 46.06 | 117 | 144 | 139 | 102 | 5.08 |
| B-II-1 | 48.10 | 259 | 304 | 298 | 147 | 9.44 |
| B-II-2 | 47.90 | 251 | 292 | 287 | 135 | 9.56 |
| B-III-1 | 49.38 | 439 | - | 498 | 221 | 20.32 |
| B-III-2 | 49.25 | 445 | - | 517 | 227 | 21.57 |
| B-IV-1 | 42.18 | - | 92 | 90 | 90 | 4.15 |
| B-IV-2 | 42.18 | - | 98 | 94 | 93 | 4.55 |
| Notation of the Beams | Experimental Value of Mdr1 at Yielding of Steel Tape | Deflection of Beam before the Yielding of Tape, fdr1, mm | Load Bearing Capacity (Yield Point of High-Strength Rebar, Crashing of the Compressed Concrete) | Deflection fdr2, mm at M = 0.7 MDBN, | ||||
|---|---|---|---|---|---|---|---|---|
| Experimental Value Mdr2, kNm | According to DBN V.2.6-98:2009 MDBN, kNm | (Mdr2 – MDBN)/Mdr2, % | Experimental Value fdr2, mm | According to DBN V.2.6-98:2009 fDBN, mm | (fdr2 – fDBN)/fdr2, % | |||
| B-I-1 | 42.70 | 6.87 | 51.52 | 51.38 | 0.3 | 4.55 | 5.5 | 20.9 |
| B-I-2 | 43.60 | 11.98 | 52.64 | 2.4 | 5.08 | 8.3 | ||
| B-II-1 | 31.10 | 8.01 | 55.20 | 52.10 | 5.6 | 9.44 | 10.4 | 10.2 |
| B-II-2 | 31.10 | 7.36 | 52.40 | 0.6 | 9.56 | 8.8 | ||
| B-III-1 | - | - | 55.36 | 52.85 | 4.5 | 20.32 | 21.8 | 7.3 |
| B-III-2 | - | - | 57.04 | 7.3 | 21.57 | 1.1 | ||
| B-IV-1 | 51.49 | 7.91 | 51.49 | 50.25 | 2.4 | 4.15 | 4.4 | 6.0 |
| B-IV-2 | 50.57 | 10.72 | 50.57 | 0.6 | 4.55 | −3.3 | ||
| Notation of the Beams | 0.4 Mdr2 | 0.7 Mdr2 | ||||
|---|---|---|---|---|---|---|
| Experimental fexp1, mm | DBN B.2.6:2009 fDBN 1 mm | (fDBN 1 – fexp1)/fexp1, % | Experimental fexp2 mm | DBN B.2.6:2009 fDBN 2 mm | (fDBN 2 – fexp2)/fexp2 % | |
| B-I-1 | 2.21 | 2.15 | −2.7 | 4.55 | 5.5 | 20.9 |
| B-I-2 | 2.35 | −8.5 | 5.08 | 8.3 | ||
| B-II-1 | 4.81 | 4.5 | −6.4 | 9.44 | 10.4 | 10.2 |
| B-II-2 | 3.98 | 13.1 | 9.56 | 8.8 | ||
| B-III-1 | 8.25 | 8.9 | 7.9 | 20.32 | 21.8 | 7.3 |
| B-III-2 | 9.64 | −7.7 | 21.57 | 1.1 | ||
| B-IV-1 | 1.94 | 2.12 | 9.3 | 4.15 | 4.4 | 6.0 |
| B-IV-2 | 2.08 | 1.9 | 4.55 | −3.3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobalo, T.; Blikharskyy, Y.; Selejdak, J.; Kopiika, N.; Blikharskyy, Z. Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape. Appl. Sci. 2023, 13, 4528. https://doi.org/10.3390/app13074528
Bobalo T, Blikharskyy Y, Selejdak J, Kopiika N, Blikharskyy Z. Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape. Applied Sciences. 2023; 13(7):4528. https://doi.org/10.3390/app13074528
Chicago/Turabian StyleBobalo, Taras, Yaroslav Blikharskyy, Jacek Selejdak, Nadiia Kopiika, and Zinoviy Blikharskyy. 2023. "Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape" Applied Sciences 13, no. 7: 4528. https://doi.org/10.3390/app13074528
APA StyleBobalo, T., Blikharskyy, Y., Selejdak, J., Kopiika, N., & Blikharskyy, Z. (2023). Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape. Applied Sciences, 13(7), 4528. https://doi.org/10.3390/app13074528






