Abstract
Achievements in the field of high-speed spatial modulation electrooptic components provide the possibility to create perspective optical-digital diffractive systems for information storage and processing that outperform modern electronic counterparts by utilizing throughput, energy efficiency, and reliability. This work presents a study of computer-generated holography methods that allow the formation of spatially-modulated information signals (data pages) with high accuracy using phase-only spatial light modulators. Computer-generated Fourier hologram fringe patterns were formed using bipolar intensity and double-phase coding. Numerical and experimental results of both methods’ implementation are compared. It was determined that bipolar intensity holograms provide higher data density on the data page if complex digital modulation methods such as multilevel amplitude and phase or quadrature modulation are used to represent data points. Double-phase coding can offer perspective for multilevel amplitude or multilevel intensity modulated data page reconstruction; however, exact control of phase modulation characteristics is required to obtain high reconstruction quality.
1. Introduction
Holographic data storage systems [1,2,3,4,5], coherent diffractive image correlators [6,7,8,9], optical encryption schemes [10,11,12,13], optical-digital Fourier processors [14], and diffractive neuroprocessors [15,16,17,18,19] require the formation of coherent optical fields with a given complex amplitude distribution in space. These systems provide optical-digital processing of analyzed digital signals. The signal is optically transformed, registered by a digital camera, and subsequently digitally post-processed using a computer. In the case of coherent diffractive image correlators, an input digital encoded image or a complex invariant filter [9] can be considered as such a signal. In the case of optical holographic memory systems, the signal is a data page [1,2], which can be either amplitude or complex-modulated [20]. For optical encryption, this is the key image [10]. In the case of diffractive neuroprocessors, the signal is the weight matrix of the convolutional layer of the neural network [21,22]. In contrast to the images for visual observation, these images have increased requirements for the accuracy of their formation. This is because their distortion leads to the loss of encoded information and the incorrect performance of the optical-digital system.
Electro-optical spatial light modulators are widely applied for information signal generation [23,24,25,26,27]. They provide high-speed input of digital information into the optical system. However, current devices cannot independently control both the amplitude and the phase of the optical field in space. The maximum spatial resolution of 10 megapixels can be obtained using phase-only liquid crystal on silicon (LCoS) spatial light modulators [28]. These types of spatial light modulators (SLMs) are widely applied to form a complex impulse response using computer-generated holography methods [29]. Another practical example of phase computer-generated holograms (CGH) of data page implementation is the HDS system, which uses a data recorder device based on a single beam incoherent projection scheme [30,31]. Fourier CGH fringe patterns are displayed on a screen of amplitude LCoS SLM and projected onto a photosensitive carrier. Using phase medium and anamorphotic optics allowed us to record and reconstruct binary data pages from multiplexed holograms using a reader device based on a coherent optical scheme [31,32].
The throughput of optoelectronic information processing systems mentioned above is defined not only by the frame rate of SLM used for CGH introduction into the optical scheme but also by the speed of CGH calculation. Therefore, the problem of fast-calculating the CGH fringe pattern is relevant. Fourier CGHs are attractive for application along with phase-only SLMs, as this type of CGH requires only one fast Fourier transformation in object beam calculation algorithms and provides a high space-bandwidth product limited to one-half of the total number of SLM pixels. Different methods allow the encoding of a complex wavefront of the object beam onto a phase of the CGH fringe pattern. Well-known iterative methods, such as those that are based on the Gerchberg-Saxton algorithm [33], or optimization methods, such as optimal projection [34] or direct search with random trajectory [35], are not capable of satisfying the requirement of high-speed CGH calculation. The most promising methods for fast synthesis of the phase Fourier CGH fringe pattern are bipolar intensity [29] and double-phase coding methods [36,37,38]. The advantage of both methods is the direct analytical calculation of a hologram. A large number of iterations and solutions to optimization tasks are not required. Though both methods require only several matrices of element-wise addition or multiplication, the calculation complexity of these methods linearly depends on the number of elements in the matrices. There is no information about the advantages of using one or another method for holographic memory data page reconstruction purposes. Therefore, in this work, we compared these methods.
The article structure is organized as follows. Section 2 represents the typical image used in optical-digital systems, a data page, and an equation for bit error rate estimation. In Section 3, the methods of CGH fringe pattern calculation are considered with an emphasis on two of the fastest methods: bipolar intensity and double-phase coding. At the end of this section, the result of numeric modeling of both methods implementation for reconstructing the complex modulated data page is presented, and a comparative analysis of numeric results is given. Section 4 is dedicated to the experimental setup used for the two methods under consideration investigation. In Section 5, the results of experimental data analysis and common conclusions about the pros and cons of both methods’ implementation for data page reconstruction are presented. The main results are provided in the Conclusions.
2. Data Page
Holographic data storage systems theoretically allow recording information with a density of up to 1 Tb/cm3 [1,2]. The absence of contact with the storage medium during its data recovery significantly increases the service life of such devices. A holographic data writer records information in parallel and not bitwise. Therefore, the high speed of data writing and access can be achieved with more than 20 MB/s [28]. The data page is the main signal in the holographic memory system. Figure 1 shows an image of a binary amplitude data page with a size of 84 × 240 pixels.

Figure 1.
Binary data page of archival holographic memory.
The peculiarity of such pages is that one byte is encoded using a track of 16 elements. Three elements correspond to “1,” and thirteen ones correspond to “0”. The format of the data page was adapted from the well-known ECMA-377 standard, the first standard for a holographic disk cartridge. The considered format provides equality of diffraction efficiencies for holograms containing different information. In addition, bits corresponding to “1” cannot be located on the track in neighboring cells. This provides an increase in the quality of the reconstructed data page and a decrease in bit errors.
Random or pseudo-random phase masks can be added to achieve high diffraction efficiency of holograms that form images of binary or multilevel amplitude data pages [39]. Modern holographic data storage systems use multilevel complex light modulation methods to represent digital information in the form of a data page, which allows for increasing the recording density. For example, multilevel amplitude [40], ternary [41], multilevel phase, and multilevel amplitude-phase (quadrature) [20] modulation methods can be used to represent digital information with data page pixels. There are several methods available to reconstruct complex or bipolar amplitude data pages, which include the interferometric method [42], digital holography method [43], transport-of-intensity equation method [44], embedded phase shift method [45], etc.
Analysis of data page images is usually performed by calculating the signal-to-noise ratio (SNR) for measured in-phase and quadrature components of the complex amplitude. As a result, the bit error rate (BER) value can be determined. For binary intensity or amplitude-modulated data pages, such as those shown in Figure 1, the BER value can be found as follows:
where Erf(x) is the complementary error function. For quadrature-modulated data pages with M complex symbols, the bit error rate value can be found as:
3. Methods for Synthesizing Phase Fourier CGH of Data Page
The impulse response of an optoelectronic coherent system can be formed by modulation of different types. Phase modulation has the following advantages:
- Holograms implemented with the phase medium can have high diffraction efficiency values [46];
- The most perspective SLMs with high spatial resolution and short response time (for example, ferroelectric SLM [28]) are purely phase devices;
- Phase holograms can be realized using different holographic materials such as photopolymers and photo-thermo-refractive glasses or printed as surface reflective or transmissive holograms.
The first step in the Fourier CGH synthesis process is calculating the object beam model in the hologram plane [29]. Direct calculation using a point-cloud model is a standard in the field of 3D objects and 3D scene visualization [47]. However, this approach requires either a lot of calculations or an extension of system random access memory (RAM). In the case of plane objects, such as holographic data storage pages, implementing scalar diffraction theory integral transformations using fast Fourier transformation algorithms can significantly speed up the calculation process. In the case of Fourier CGH object beam model can be obtained using a simple equation:
where are the coordinates in the data page plane, are the coordinates in the hologram plane, which is the Fraunhofer plane for the plane, —data page model function, —object beam model function, —Fourier transformation operator from the to plane. In the common case and are complex functions of spatial coordinates. While the object beam function is modeled numerically, there is no problem with object model complex function implementation. The main problem is the encoding of object beam function in the hologram plane onto the phase-only fringe pattern function.
The next step in the CGH obtaining process is diffraction pattern synthesis, the process aimed at converting the object beam complex model onto the fringe pattern model with the a priori specified modulation characteristic of a holographic medium. Within the variety of methods for calculating the phase Fourier CGH fringe pattern, the bipolar intensity and double-phase coding methods are among the fastest. Further, the mathematical descriptions of these methods’ implementation are presented.
3.1. Bipolar Intensity Method
The bipolar intensity method is based on the modeling of holographic recording of complex light fields in the off-axis Leith-Upatnieks scheme [48]. Firstly, an interference pattern between the object and reference beams should be simulated. Let Γ be the hologram of object O, and let R be the reference beam. Then the transmission function of the calculated hologram can be described mathematically as:
where and are complex amplitudes of the reference and object beams in the hologram plane correspondingly, * is a sign of the complex conjugation.
Since the calculation is performed numerically, and can be excluded. Then the transmission function of the obtained hologram takes the form:
where Γ(ξ, η) is a real sign-variable function, and is a function of calculating the real part of the complex numbers. It can only be implemented using a medium with bipolar amplitude modulation, which is real-axis amplitude modulation with a variable sign. However, a hologram can be implemented on a medium with unipolar modulation by adding an amplitude bias:
where C is the amplitude bias. It is usually a positive value defined as:
The fringe pattern model (Equation (6)) can be displayed by phase-only SLM. This procedure is similar to the well-known technique of hologram bleaching. The expression for the CGH model, in this case, can be written as:
where ζ is the modulation depth coefficient. This hologram can be implemented on a device with a unipolar phase modulation type. An example of fringe patterns obtained using the bipolar intensity method is shown in Figure 2a. The fragment size is 128 × 128 pixels. The number of phase levels is 256. The black pixels correspond to the 0 phase shift. White pixels provide a 2п phase shift. We can see that the majority of pixels are gray. They correspond to intermediate phase levels.

Figure 2.
Fragments of holograms generated by bipolar intensity (a) and double-phase coding (b) methods.
Three diffraction orders can typically be obtained in the light field reconstructed by bipolar intensity hologram: zero-order—a bright point at the center of the light field; −1 order, which is the object image itself; and +1 order, which is a conjugate image. The main drawback of this type of CGH is the impossibility of reconstructing the object image located on the optical axis of the read-out scheme.
3.2. Double-Phase Coding Method
Double-phase coding method implements complex values of the object beam model. It is based on the vector addition of two elements with a pure-phase modulation characteristic. An arbitrary complex number can be described as a sum of two phasors:
where are coordinates (pixel positions) of the concrete value.
Two neighboring pixels of phase-only SLM can act as two phasors [11], representing a single value of the object beam complex field. This is an example of an element-wise representation of the hologram fringe pattern.
Any complex number can be presented using and according to Equation (9). Phasor values can be found in the following form [28]:
where angle difference can be determined from the modulus of the complex number:
The hologram is displayed onto phase SLM. Therefore, the hologram pixels are equal to:
where is a new coordinates count.
There are ways to improve the accuracy of image reconstruction by using 4 pixels. Two pixels correspond to the phasor , and two others correspond to the phasor . Pixels corresponding to one phasor must be arranged in a checkerboard pattern [34]. An example of the CGH fragment synthesized by the double-phase coding method is shown in Figure 2b. The fragment size is 128 × 128 pixels. The number of phase levels is 256. The black pixels correspond to the 0 phase shift. White pixels provide a 2п phase shift. The method provides sharper phase value changes between pixels than the bipolar intensity method (see Figure 2a).
In the case of a double-phase hologram, the reconstructed light field contains only the object image and its spatially separated second-order non-inverted copy. If the phase modulation characteristic of the holographic carrier is strictly linear within the modulation depth of 2π radians, there is no central zero order presented at the output field, and an undistorted on-axis object image can be obtained.
3.3. Numerical Modeling
Image formation of a complex-modulated data page was numerically simulated with the application of both methods of phase-only fringe pattern synthesis under consideration. To demonstrate the quality of reconstructed complex values, the constellation diagram is useful for quadrature amplitude modulation (QAM). The diagram points are usually arranged in a square grid. The 16-QAM digital format was used in numeric modeling. This modulation format allows representing 4 bits of a binary code using one element of the data page. The dimension of the simulated data page was 200 × 200 pixels. The Fourier CGH of the holographic data page images was calculated using the two investigated methods. The hologram size was equal to 1024 × 1024 pixels. The Fourier CGH has 256 phase shift levels at a 2π phase modulation depth. Images of complex-modulated data pages were numerically reconstructed. These images are matrices of values of the complex amplitude distribution function of the light field in space. After the numeric reconstruction, the in-phase and quadrature components were demodulated and normalized. The SNR values for these components were estimated, and the obtained constellation diagrams for both methods are shown in Figure 3. Red dots correspond to ideal constellation points. Blue dots correspond to reconstructed constellation points.
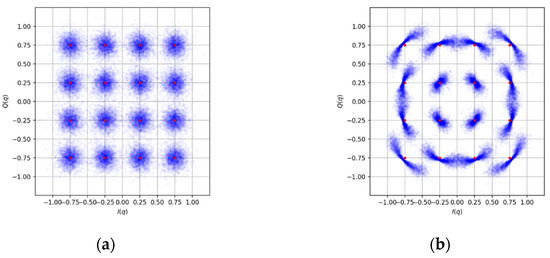
Figure 3.
Numerical simulation: the reconstructed data pages using phase Fourier CGH for bipolar intensity (a) and double-phase (b) methods.
It can be seen that data page images for the bipolar intensity method have a normal error distribution. The dispersion values (normalized rooted mean square error, NRMSE) in both in-phase and quadrature components of complex amplitude and amplitude modulus were obtained at about 0.12, corresponding to a BER of 0.001.
In the double-phase coding method, the distortions have a predominant phase noise. It leads to the variance of the in-phase and quadrature components at 0.16. Obtained BER value is 0.006. However, the variance of the normalized amplitude modulus was obtained at about 0.04. Additionally, it was observed that different parts of the data page produce different phase errors in the case of double-phase Fourier CGH. The larger the distance of the data page element from the vertical axis of the data page, the bigger the error obtained. The shift to the left from the vertical axis produces a negative phase error, while the shift to the right from the vertical axis produces a positive phase error. It is worth noting that the CGH superpixel was contained by two phasor subpixels aligned horizontally.
A numeric experiment with an enlarged data page was also carried out. Doubling the data page size resulted in the rise of NRMSE to 0.27 and 0.29 for bipolar intensity and double-phase cases, respectively. Such an error does not allow for the satisfactory reconstruction of the data page in a 16-QAM format. Even in the case of 4-level phase modulation, the value of BER was obtained at about 0.02. It should be added that the modulus-of-amplitude NRMSE in the case of double-phase CGH appeared to be 0.08, enough to reconstruct 8-level bipolar amplitude modulated data pages with BER value on the order of 10−7.
Thus, the bipolar intensity method allows the forming of quadrature-modulated data page images with better quality than the double-phase method. The reconstructed data pages for the double-phase coding method have higher phase noise. However, the amplitude noise is lower for the double-phase coding method. Therefore these holograms are promising for the multilevel amplitude modulation types of the data pages. Ternary, bipolar amplitude, and unipolar amplitude (intensity) modulation are examples of these modulation types.
4. Experiments on Reconstructing Binary Data Page Images
The data page shown in Figure 1 with an added two-level pseudo-random phase mask was used as an object of study. This format can be considered an analog to a complex ternary modulation. A single element of the data page can provide the values −1, 0 or +1 of the normalized complex amplitude of the light field. For simplicity, these data pages can be registered with a digital camera sensitive to the spatial intensity distribution. This method does not allow distinguishing elements with values −1 and +1. However, the amplitude modulus distribution (the square root of intensity) will allow the estimation of the complex amplitude noise.
Figure 4 shows a scheme for reconstructing the data page images using Fourier CGH. A Cobolt Samba (200 mW, 532 nm) laser was used as a light source. The coherent beam was collimated using lenses L1 and L2 and aperture M. The Fourier CGH was displayed onto phase LCoS SLM HoloEye PLUTO-2 (1920 × 1080 pixels; pixel size is 8 × 8 µm). Fourier CGH were calculated using bipolar intensity and double-phase coding methods. The modulation depth of the SLM was equal to 2π. The reconstructed data page was registered by Flare 48 M digital camera (7920 × 6004 pixels; pixel size is 4.6 × 4.6 µm) in the Fourier plane. The beam splitter BS allows for directing both the collimated beam into the SLM plane and the reflected beam from the SLM to the digital camera plane. An L3 lens (40 mm focal length) coupled the registration plane and the SLM far diffraction zone. The registered images of the data page were digitally processed. Processing algorithms included linearization of a sinc-shaped envelope caused by the square shape of SLM pixels. The width of the main maximum of the sinc envelope was estimated as 2λF/Δ where λ is the wavelength, F is the focal length of the Fourier objective, and Δ is pixel linear size. The informative area of the data page image was cropped, geometrically corrected, and spatially sampled. Examples of reconstructed light field intensity distributions registered in the experiments and data page enlarged images are shown in Figure 5. Both methods of Fourier CGH synthesis were used.
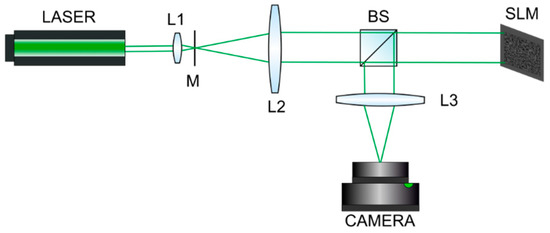
Figure 4.
The experimental scheme for reconstructing and registering binary data page images using phase Fourier CGH: laser, lenses L1, L2, and L3, beam splitter BS, spatial light modulator SLM, and digital camera.

Figure 5.
Registered images of a reconstructed data page (a,b) and its informative parts (b,d). Fourier CGHs were synthesized by the bipolar intensity (a,c) and double-phase coding (b,d) methods.
5. Analysis of Reconstructed Data Page Images
First, in the case of double-phase holograms, it appeared impossible to reconstruct the data page image in an on-axis configuration without being distorted by zero order. So, for the experiments, we decided to shift the data page image into the off-axis zone during CGH synthesis. In Figure 5b, the result of the registration of the output field formed by double-phase off-axis Fourier CGH is illustrated. One can see the presence of sharp zero order, and the image of the data page shifted from it to a certain distance great enough to avoid the cross-section.
The registered data page images were analyzed. The complex amplitude modulus (square root of intensity) of the images was subjected to analysis. The mathematical expectations M1 of the pixel values in the true locations of the bits corresponding to the units were determined. The mathematical expectation M0 for the zeros is equal to 0. The standard deviations σ1 and σ0 of units and zeros were also calculated. Two following cases were considered. Elements of the data page were decoded:
- Without taking into account the presence of zeros next to units;
- Taking into account the presence of zeros next to units.
Figure 6 shows histograms for the data page elements’ amplitude modulus. They correspond to the 0 and ±1 elements. Both mentioned cases taking features into account are given. Blue columns correspond to the pixel numbers of ±1 elements. Orange columns correspond to the 0 elements. Gray parts of columns correspond to pixel numbers of ±1 and zero elements.
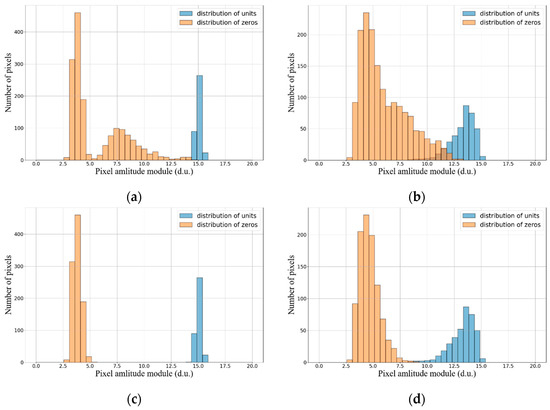
Figure 6.
Amplitude modulus histograms of zero and unit elements of the registered data pages. Fourier CGH were generated with the bipolar intensity (a,c) and double-phase coding (b,d) methods. The top row (a,b) does not consider the data page features. The bottom row (c,d) takes the data page features into account.
It can be seen that the double-phase coding method provides a lower quality of reconstructed images. Without taking features into account, this method gave a significant intersection of the zeros and ±1 elements (see Figure 6b). Herewith for the bipolar intensity method, the intersection is almost absent (see Figure 6a). Taking the features of data page representation into account improves the quality even more. For the double-phase coding method, the intersection almost disappears (see Figure 6d). There is no intersection for the bipolar intensity method (see Figure 6c). At the same time, there was even a clear range separation between zeros and ±1 elements. To access the improvement, signal-to-noise ratio and bit error rate values were determined. The SNR was calculated using the following equation:
The probability of BER value was estimated using Equation (1). Obtained values for both cases of data page consideration are shown in Table 1 and Table 2.

Table 1.
Obtained results for data page image analysis in the case of ignoring data page specificities.

Table 2.
Obtained results for data page image analysis in case of taking into account data page specificities.
It can be seen that all obtained results are better for the bipolar intensity method. The SNR value is higher at 1.3 (ignoring features; see Table 1) and 1.7 times (taking features into account; see Table 2). The BER values for the bipolar intensity method are more than ten times higher than that for the double-phase method. One of the possible reasons for the low accuracy of the double-phase coding method is the high sensitivity of such holograms to the spatial phase error. This error occurs in the reconstruction system due to the aberrations and spatial phase shift non-uniformity of the used SLM. This issue requires further research and will be investigated in the future.
The coding features can be taken into account for the reconstruction accuracy increase. However, the information capacity of the data page decreases. In our experiments, 16 elements correspond to 8 characters of information. Therefore, the capacity of the data page decreases by 2 times for each coordinate. Thus we can find a compromise between reconstruction accuracy and the information capacity by using coding features.
6. Conclusions
In this work, a problem of complex data page image reconstruction in holographic memory was investigated. Phase Fourier computer-generated holograms of data pages were synthesized using bipolar intensity and double-phase coding methods. The quality of reconstructed images was analyzed in numerical and optical experiments.
The bipolar intensity method implemented with a 2π phase modulation depth appeared most suitable for data page reconstruction. It allows the formation of data page images represented by multilevel complex modulation (for example, quadrature modulation) with better quality. The reconstructed data pages for the double-phase coding method have high phase noise. However, in numerical experiments, the amplitude noise of double-phase holograms was lower than in the case of bipolar intensity holograms. Therefore double-phase holograms are promising for creating data pages in the form of multilevel amplitude modulation types. Selection of data page size and proper modulation format appeared to be the major challenge in designing of optoelectronic information processing and storage system providing a suitable reconstruction of embedded information on one hand and high throughput of a system on another.
In the experiment, the reconstruction accuracy for a ternary modulation was higher in the case of the bipolar intensity method. One of the possible reasons for the low accuracy of the double-phase coding method is the high sensitivity of such holograms to the spatial phase error. A highly linear representation of phase modulation within the modulation depth of 2π radians is required to obtain high-quality images in the reconstructed light field.
The obtained results can be used in optoelectronic data storage and processing systems, which use spatial phase light modulation to form and manipulate information signals.
Author Contributions
Conceptualization, E.Y.Z. and R.S.S.; methodology, E.Y.Z. and T.Z.M.; software, T.Z.M.; validation, T.Z.M. and E.Y.Z.; formal analysis, P.A.C.; investigation, T.Z.M., P.A.C., and E.Y.Z.; resources, R.S.S. and N.N.E.; data curation, T.Z.M.; writing—original draft preparation, T.Z.M. and P.A.C.; writing—review and editing, T.Z.M. and P.A.C.; visualization, T.Z.M.; supervision, N.N.E.; project administration, R.S.S.; funding acquisition, P.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation (RSF), Grant No. 22-79-10340.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Curtis, K.; Dhar, L.; Hill, A.; Wilson, W.; Ayres, M. Holographic Data Storage; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9780470975787. [Google Scholar]
- Yoneda, N.; Saita, Y.; Nomura, T. Binary Computer-Generated-Hologram-Based Holographic Data Storage. Appl. Opt. 2019, 58, 3083–3090. [Google Scholar] [CrossRef] [PubMed]
- Makowski, M.; Bomba, J.; Frej, A.; Kolodziejczyk, M.; Sypek, M.; Shimobaba, T.; Ito, T.; Kirilyuk, A.; Stupakiewicz, A. Dynamic Complex Opto-Magnetic Holography. Nat. Commun. 2022, 13, 7286. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Wang, K.; Lin, X.; Hao, J.; Lin, D.; Zheng, Q.; Chen, R.; Wang, S.; Tan, X. Combination Compensation Method to Improve the Tolerance of Recording Medium Shrinkage in Collinear Holographic Storage. Photonics 2022, 9, 149. [Google Scholar] [CrossRef]
- Hong, J.; Li, J.; Chu, D. Efficient Dynamic Control Method of Light Polarization Using Single Phase-Only Liquid Crystal on Silicon Spatial Light Modulators for Optical Data Storage. Appl. Opt. 2021, 61, B34–B42. [Google Scholar] [CrossRef]
- Drăgulinescu, A. Optical Correlators for Cryptosystems and Image Recognition: A Review. Sensors 2023, 23, 907. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shen, X.; Zhou, B.; Liu, J.; Cai, J.; Liu, X.; Cheng, Y. Optical Asymmetric JTC Cryptosystem Based on Binary Phase Modulation and Image Superposition–Subtraction Operation. Appl. Opt. 2022, 61, 8711–8729. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, X.; Liu, J.; Peng, K. Optical Asymmetric JTC Cryptosystem Based on Multiplication-Division Operation and RSA Algorithm. Opt. Laser Technol. 2023, 160, 109042. [Google Scholar] [CrossRef]
- Shaulskiy, D.V.; Evtikhiev, N.N.; Starikov, R.S.; Starikov, S.N.; Zlokazov, E.Y. MINACE Filter: Variants of Realization in 4-f Correlator. SPIE Proc. 2014, 9094, 90940K. [Google Scholar] [CrossRef]
- Nishchal, N.K. Optical Cryptosystems; IOP Publishing Ltd.: Philadelphia, PA, USA, 2019; ISBN 9780750322188. [Google Scholar] [CrossRef]
- Alfalou, A.; Brosseau, C. Optical Image Compression and Encryption Methods. Adv. Opt. Photonics 2009, 1, 589–636. [Google Scholar] [CrossRef]
- Yu, N.; Xi, S.; Wang, X.; Lang, L.; Wang, X.; Zhang, L.; Han, H.; Dong, Z.; Jiao, X.; Wang, H.; et al. Optical Implementation of Image Encryption Based on Digital Holography and Computer Generated Hologram. J. Opt. 2020, 22, 075702. [Google Scholar] [CrossRef]
- Qu, G.; Meng, X.; Yin, Y.; Wu, H.; Yang, X.; Peng, X.; He, W. Optical Color Image Encryption Based on Hadamard Single-Pixel Imaging and Arnold Transformation. Opt. Lasers Eng. 2021, 137, 106392. [Google Scholar] [CrossRef]
- Macfaden, A.J.; Gordon, G.S.D.; Wilkinson, T.D. An Optical Fourier Transform Coprocessor with Direct Phase Determination. Sci. Rep. 2017, 7, 13667. [Google Scholar] [CrossRef] [PubMed]
- Zuo, Y.; Li, B.; Zhao, Y.; Jiang, Y.; Chen, Y.-C.; Chen, P.; Jo, G.-B.; Liu, J.; Du, S. All-Optical Neural Network with Nonlinear Activation Functions. Optica 2019, 6, 1132–1137. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, X.; Wu, J.; Chen, Y.; Xie, H.; Li, Y.; Fan, J.; Wu, H.; Fang, L.; Dai, Q. Large-Scale Neuromorphic Optoelectronic Computing with a Reconfigurable Diffractive Processing Unit. Nat. Photonics 2021, 15, 367–373. [Google Scholar] [CrossRef]
- Zhang, D.; Tan, Z. A Review of Optical Neural Networks. Appl. Sci. 2022, 12, 5338. [Google Scholar] [CrossRef]
- Panda, S.S.; Hegde, R.S. Fault Tolerance and Noise Immunity in Freespace Diffractive Optical Neural Networks. Eng. Res. Express 2022, 4, 011301. [Google Scholar] [CrossRef]
- Dong, C.; Cai, Y.; Dai, S.; Wu, J.; Tong, G.; Wang, W.; Wu, Z.; Zhang, H.; Xia, J. An Optimized Optical Diffractive Deep Neural Network with OReLU Function Based on Genetic Algorithm. Opt. Laser Technol. 2023, 160, 109104. [Google Scholar] [CrossRef]
- Honma, S.; Sekiguchi, T. Multilevel Phase and Amplitude Modulation Method for Holographic Memories with Programmable Phase Modulator. Opt. Rev. 2014, 21, 597–598. [Google Scholar] [CrossRef]
- Sui, X.; Wu, Q.; Liu, J.; Chen, Q.; Gu, G. A Review of Optical Neural Networks. IEEE Access 2020, 8, 70773–70783. [Google Scholar] [CrossRef]
- Xu, R.; Lv, P.; Xu, F.; Shi, Y. A Survey of Approaches for Implementing Optical Neural Networks. Opt. Laser Technol. 2021, 136, 106787. [Google Scholar] [CrossRef]
- Yin, K.; Hsiang, E.-L.; Zou, J.; Li, Y.; Yang, Z.; Yang, Q.; Lai, P.-C.; Lin, C.-L.; Wu, S.-T. Advanced Liquid Crystal Devices for Augmented Reality and Virtual Reality Displays: Principles and Applications. Light Sci. Appl. 2022, 11, 161. [Google Scholar] [CrossRef]
- Kukołowicz, R.; Chlipala, M.; Martinez-Carranza, J.; Idicula, M.S.; Kozacki, T. Fast 3D Content Update for Wide-Angle Holographic Near-Eye Display. Appl. Sci. 2021, 12, 293. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Butt, M.A.; Grakhova, E.P.; Kutluyarov, R.V.; Stepanov, I.V.; Kazanskiy, N.L.; Khonina, S.N.; Lyubopytov, V.S.; Sultanov, A.K. Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review. Sensors 2021, 21, 4988. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Adachi, Y.; Kinashi, K.; Tsutsumi, N.; Sakai, W.; Jackin, B.J. Tailoring Large Asymmetric Laguerre–Gaussian Beam Array Using Computer-Generated Holography. Photonics 2023, 10, 247. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Li, P.; Zhang, Y.; Wen, Y.; Qiu, Y.; Liu, Z.; Li, Y.; Liu, L. Femtosecond Laser-Based Processing Methods and Their Applications in Optical Device Manufacturing: A Review. Opt. Laser Technol. 2021, 135, 106687. [Google Scholar] [CrossRef]
- Zlokazov, E.Y. Methods and Algorithms for Computer Synthesis of Holographic Elements to Obtain a Complex Impulse Response of Optical Information Processing Systems Based on Modern Spatial Light Modulators. Quantum Electron. 2020, 50, 643–652. [Google Scholar] [CrossRef]
- Matsushima, K. Introduction to Computer Holography: Creating Computer-Generated Holograms as the Ultimate 3D Image; Springer: Cham, Switzerland, 2020; ISBN 9783030384357. [Google Scholar] [CrossRef]
- Betin, A.Y.; Bobrinev, V.I.; Odinokov, S.B.; Evtikhiev, N.N.; Starikov, R.S.; Starikov, S.N.; Zlokazov, E.Y. Holographic Memory Optical System Based on Computer-Generated Fourier Holograms. Appl. Opt. 2013, 52, 8142–8145. [Google Scholar] [CrossRef] [PubMed]
- Odinokov, S.; Zlokazov, E.; Donchenko, S.; Verenikina, N. Optical Memory System Based on Incoherent Recorder and Coherent Reader of Multiplexed Computer Generated One-Dimensional Fourier Transform Holograms. Jpn. J. Appl. Phys. 2017, 56, 09NA02. [Google Scholar] [CrossRef]
- Betin, A.Y.; Bobrinev, V.I.; Donchenko, S.S.; Odinokov, S.B.; Evtikhiev, N.N.; Starikov, R.S.; Starikov, S.N.; Zlokazov, E.Y. Holographic Memory System Based on Projection Recording of Computer-Generated 1D Fourier Holograms. Appl. Opt. 2014, 53, 6591–6597. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik 1971, 2, 237–246. [Google Scholar] [CrossRef]
- Laude, V.; Réfrégier, P. Multicriteria Characterization of Coding Domains with Optimal Fourier Spatial Light Modulator Filters. Appl. Opt. 1994, 33, 4465. [Google Scholar] [CrossRef]
- Cheremkhin, P.A.; Evtikhiev, N.N.; Krasnov, V.V.; Starikov, R.S.; Zlokazov, E.Y. Iterative synthesis of binary inline Fresnel holograms for high-quality reconstruction in divergent beams with DMD. Opt. Lasers Eng. 2022, 150, 106859. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Mínguez-Vega, G.; Lancis, J. Encoding Complex Fields by Using a Phase-Only Optical Element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef]
- Hsueh, C.K.; Sawchuk, A.A. Computer-Generated Double-Phase Holograms. Appl. Opt. 1978, 17, 3874–3883. [Google Scholar] [CrossRef]
- Arrizón, V.; Sánchez-de-la-Llave, D. Double-Phase Holograms Implemented with Phase-Only Spatial Light Modulators: Performance Evaluation and Improvement. Appl. Opt. 2002, 41, 3436–3447. [Google Scholar] [CrossRef] [PubMed]
- Evtikhiev, N.N.; Zlokazov, E.Y.; Starikov, R.S.; Starikov, S.N.; Bobrinev, V.I.; Odinokov, S.B. Specificities of Data Page Representation in Projection Type Optical Holographic Memory System. Opt. Mem. Neural Netw. 2015, 24, 272–278. [Google Scholar] [CrossRef]
- King, B.M.; Burr, G.W.; Neifeld, M.A. Experimental Demonstration of Gray-Scale Sparse Modulation Codes in Volume Holographic Storage. Appl. Opt. 2003, 42, 2546–2559. [Google Scholar] [CrossRef]
- Berger, G.; Dietz, M.; Denz, C. Hybrid Multinary Modulation Codes for Page-Oriented Holographic Data Storage. J. Opt. A: Pure Appl. Opt. 2008, 10, 115305. [Google Scholar] [CrossRef]
- Joseph, J.; Waldman, D.A. Homogenized Fourier Transform Holographic Data Storage Using Phase Spatial Light Modulators and Methods for Recovery of Data from the Phase Image. Appl. Opt. 2006, 45, 6374. [Google Scholar] [CrossRef]
- Zukeran, K.; Okamoto, A.; Takabayashi, M.; Shibukawa, A.; Sato, K.; Tomita, A. Double-Referential Holography and Spatial Quadrature Amplitude Modulation. Jpn. J. Appl. Phys. 2013, 52, 09LD13. [Google Scholar] [CrossRef]
- Yoneda, N.; Saita, Y.; Komuro, K.; Nobukawa, T.; Nomura, T. Transport-of-Intensity Holographic Data Storage Based on a Computer-Generated Hologram. Appl. Opt. 2018, 57, 8836–8840. [Google Scholar] [CrossRef]
- Bunsen, M.; Umetsu, S.; Takabayashi, M.; Okamoto, A. Method of Phase and Amplitude Modulation/Demodulation Using Datapages with Embedded Phase-Shift for Holographic Data Storage. Jpn. J. Appl. Phys. 2013, 52, 09LD04. [Google Scholar] [CrossRef]
- Evtikhiev, N.N.; Starikov, S.N.; Cheremkhin, P.A.; Kurbatova, E.A. Evaluation of Diffraction Efficiency and Image Quality in Optical Reconstruction of Digital Fresnel Holograms. Radiophys. Quantum Electron. 2015, 57, 635–649. [Google Scholar] [CrossRef]
- Kim, S.-C.; Kim, E.-S. Effective Generation of Digital Holograms of Three-Dimensional Objects Using a Novel Look-up Table Method. Appl. Opt. 2008, 47, D55. [Google Scholar] [CrossRef] [PubMed]
- Leith, E.N.; Upatnieks, J. Wavefront Reconstruction with Diffused Illumination and Three-Dimensional Objects. J. Opt. Soc. Am. 1964, 54, 1295–1301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).