Comparative Study on Hot Metal Flow Behaviour of Virgin and Rejuvenated Heat Treatment Creep Exhausted P91 Steel
Abstract
1. Introduction
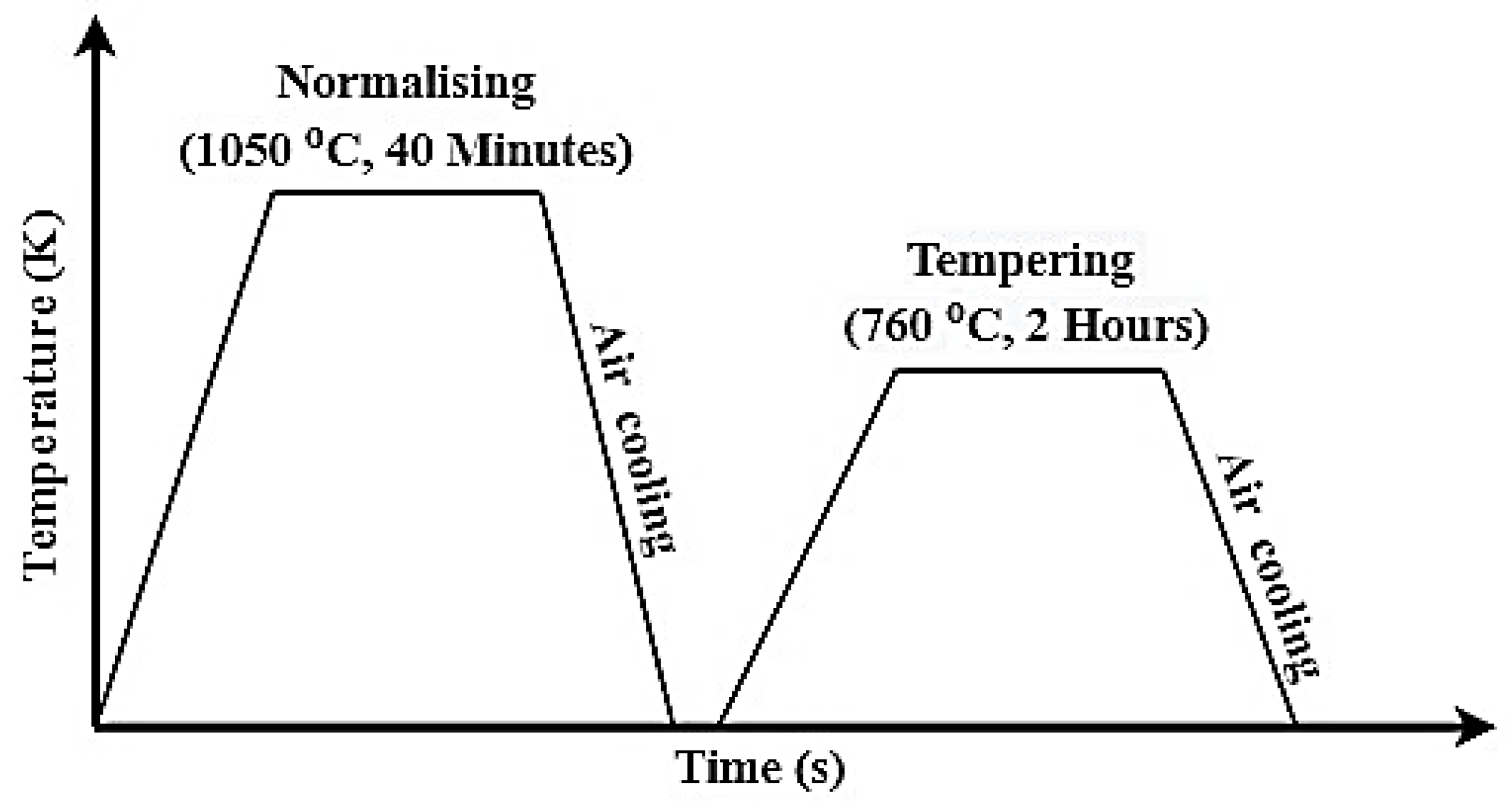
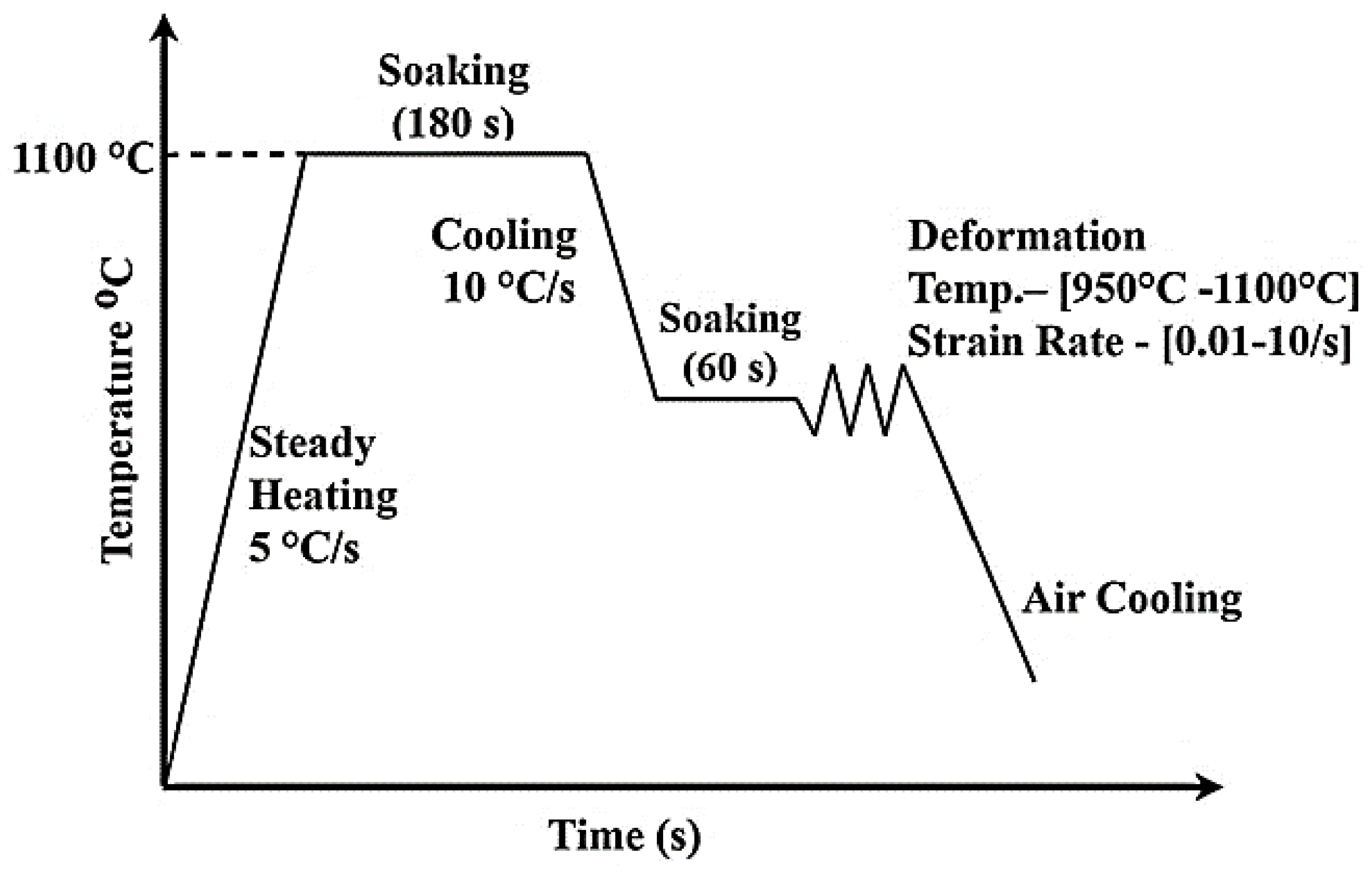
2. Materials and Methods
3. Results
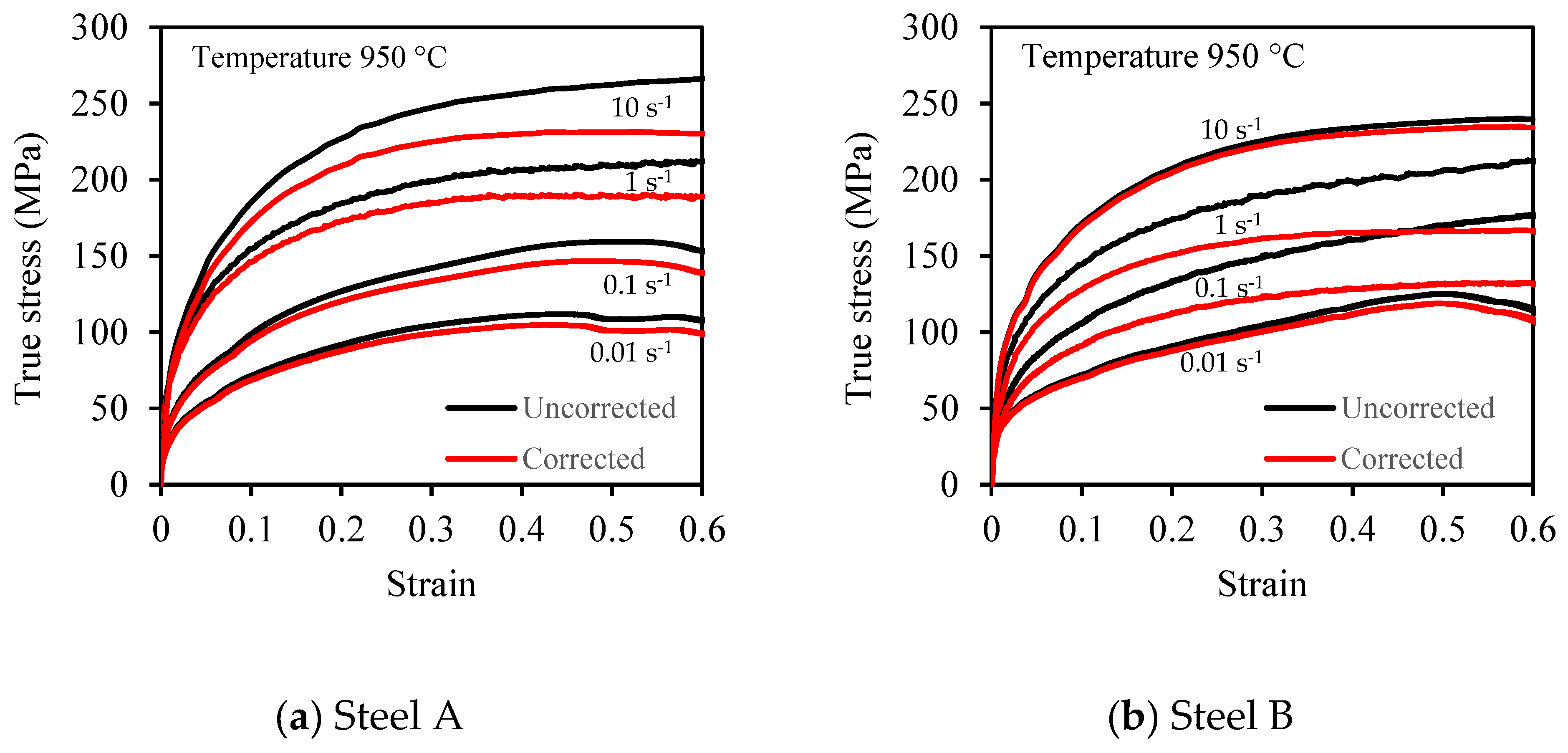
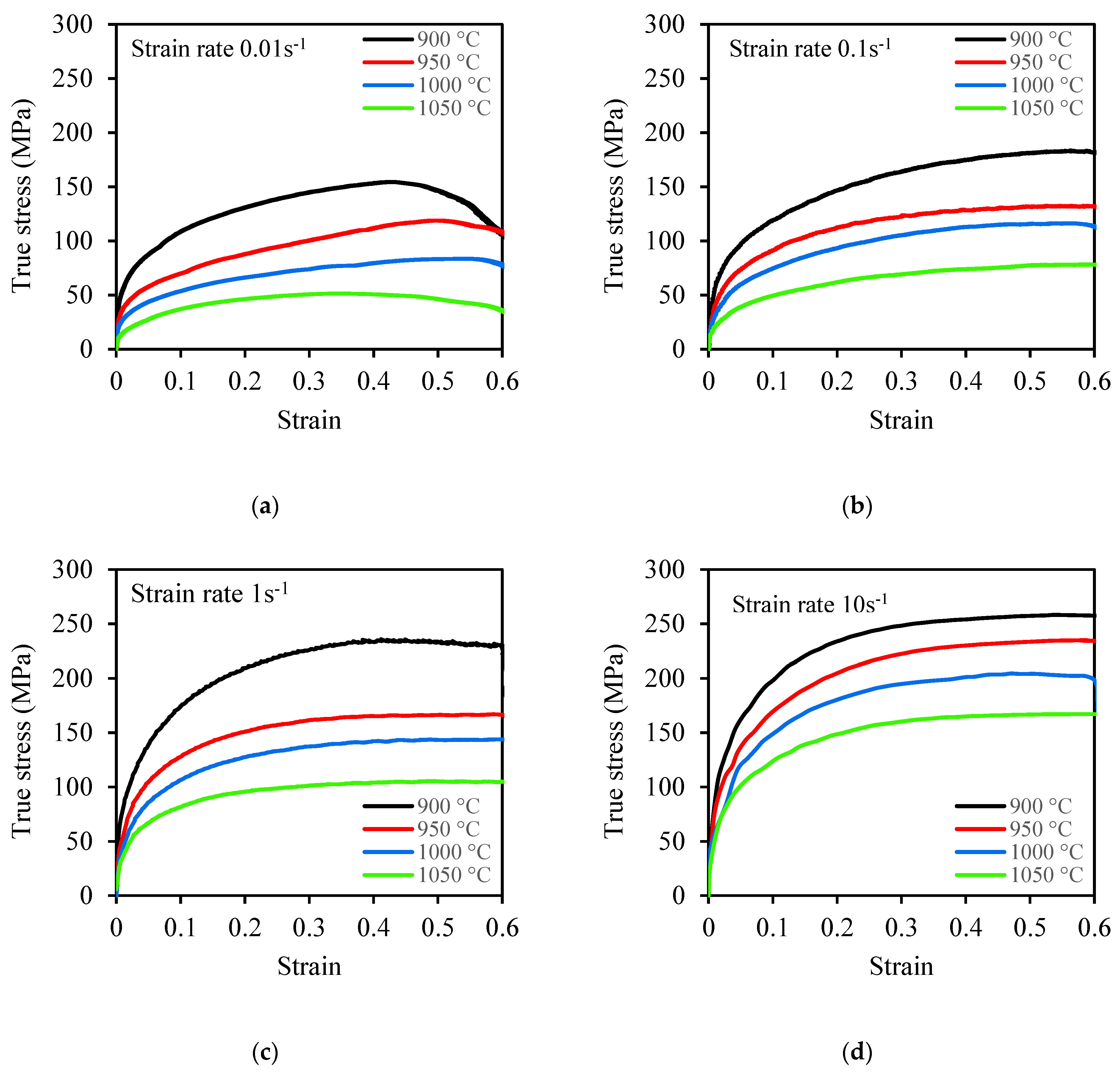
3.1. Flow Stress–Strain Curves
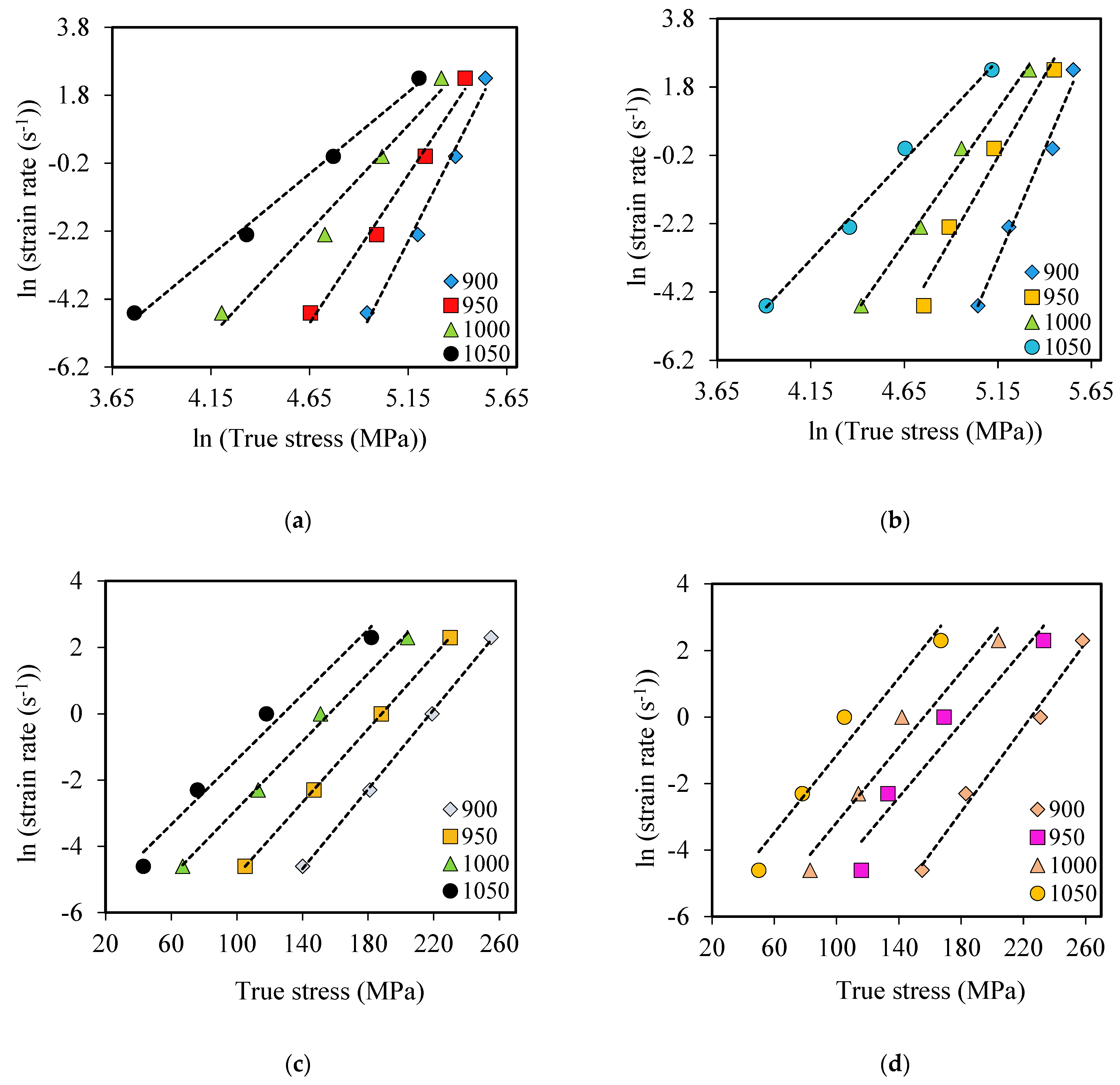
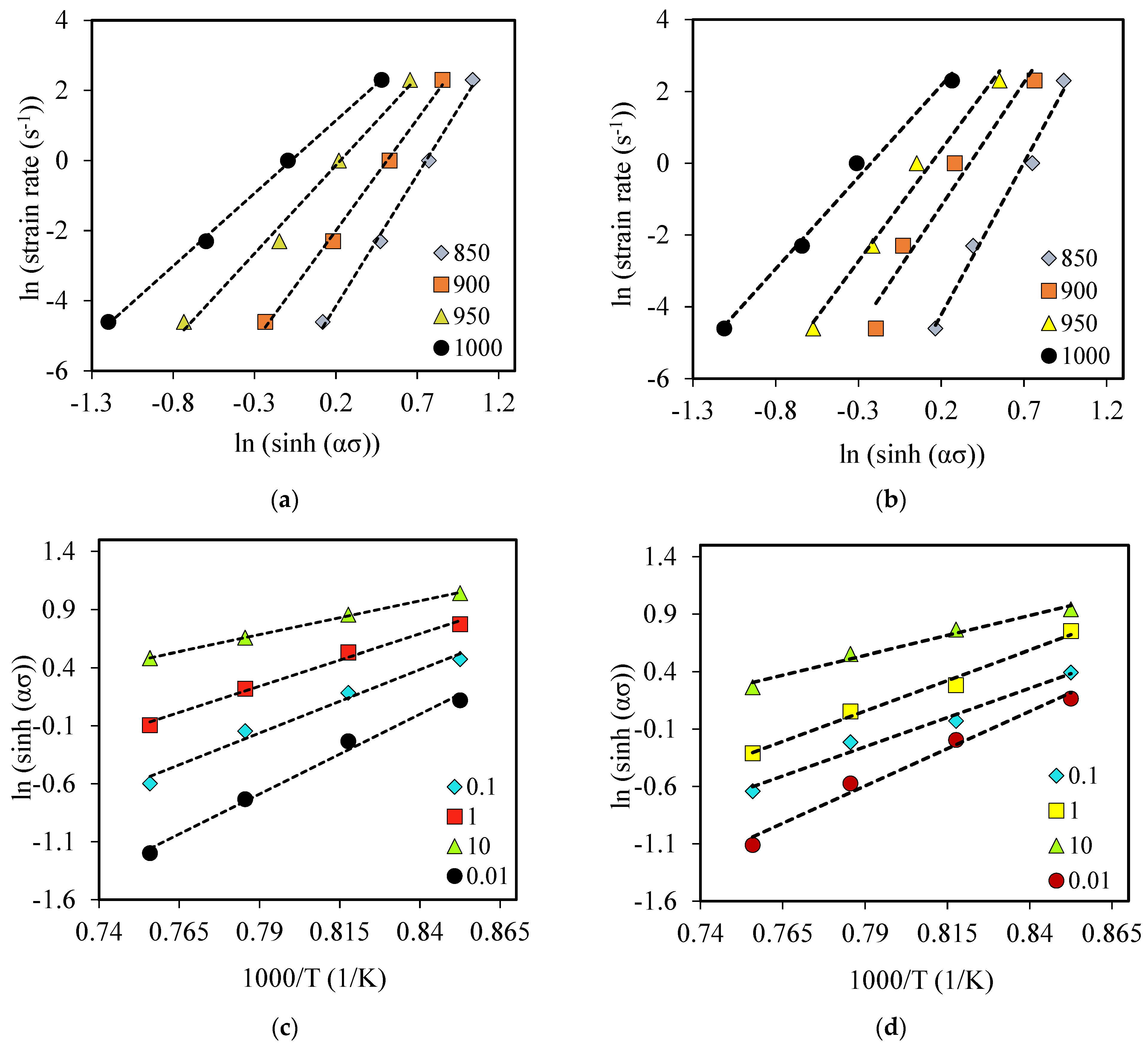
3.2. Constitutive Equation and Material Constants
3.3. Activation Energy and Stress Exponent
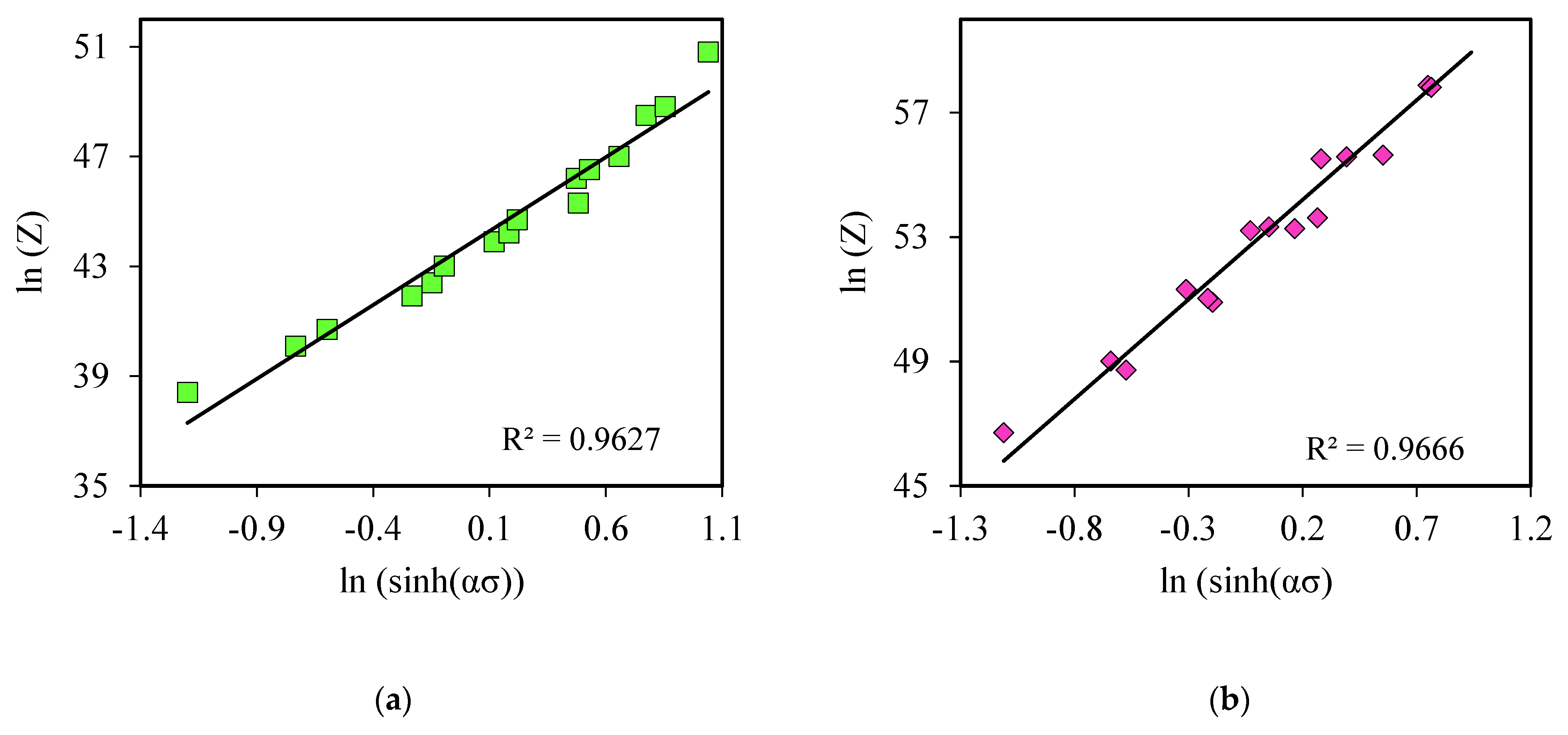
3.4. Constitutive Model of Flow Stresses
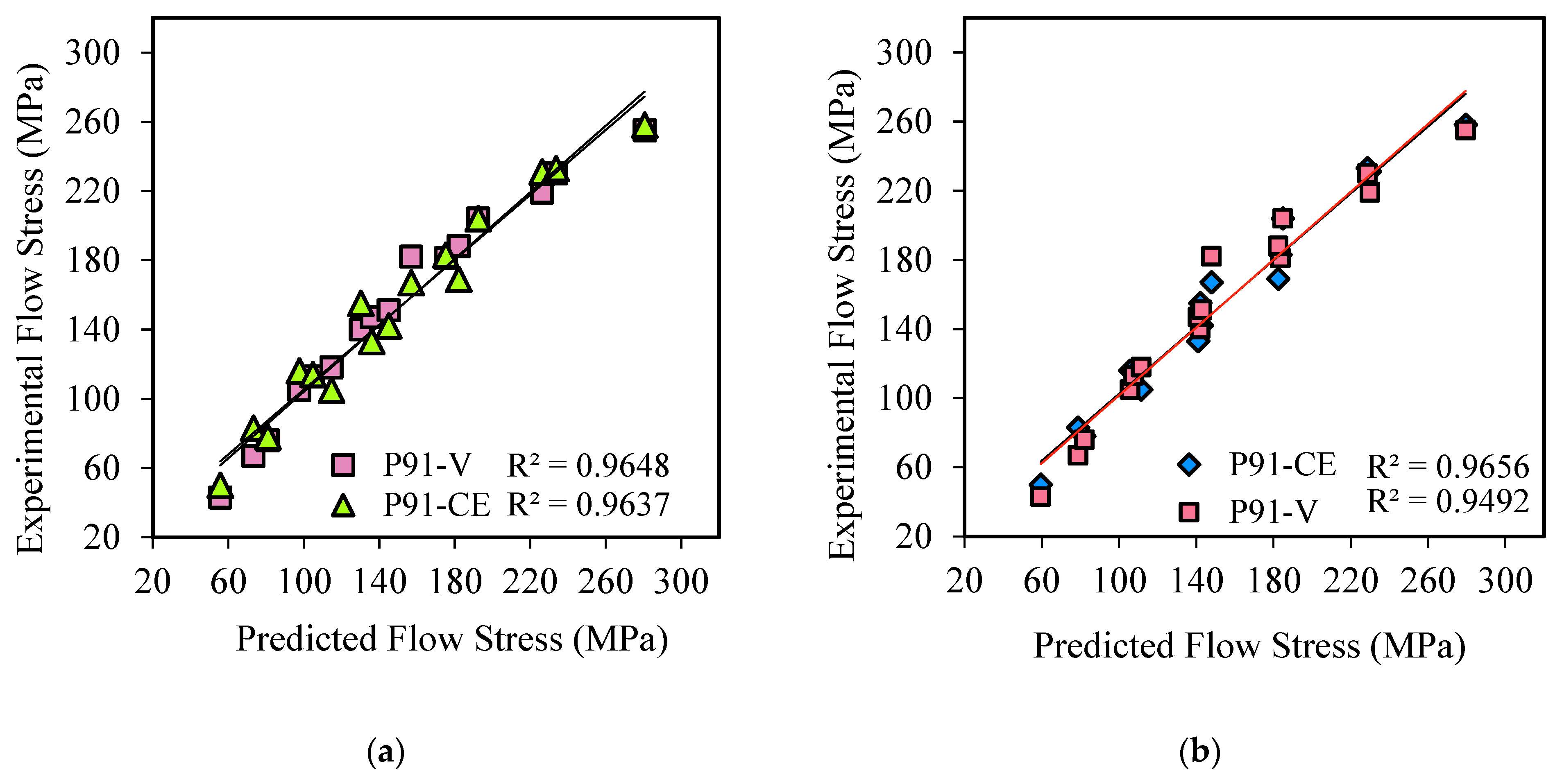
3.5. Verification of Constitutive Models
3.6. Comparison of Constitutive Equations
4. Conclusions
- The flow stress–strain curves show that the flow stress increased with an increase in strain rate (0.01 s−1 to 10 s−1) and decreased with an increase in temperature (900 °C to 1050 °C) for the two steels. The flow stress–strain curves exhibited a DRV+WH as the deformation mechanism.
- The apparent activation energy of steel A was 473.08 kJ/mol, and for steel B it was 564.48 kJ/mol. These Q-values were much higher compared to the self-diffusion energy of iron in austenite (270 kJmol−1)
- The mathematical constitutive models for steel A and steel B to a total strain of 0.6 are as given in Equations (22) and (23).
- The constitutive models were validated using Pearson’s correlation coefficient, R and the average absolute relative error, AARE. For steel A, R was 0.97, and AARE was 7.62%. For Steel B, R was 0.98, and AARE was 6.54%. The developed models were used interchangeably with acceptable accuracy. Using the model for steel A on steel B, R was 0.96, and AARE was 7.19%. Similarly, using the steel B model on steel A, the R was 0.95, and AARE was 8.36%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gutiérrez, N.Z.; Alvarado, J.V.; de Cicco, H.; Danón, A. Microstructural Study of Welded Joints in a High Temperature Martensitic-ferritic ASTM A335 P91 Steel. Procedia Mater. Sci. 2015, 8, 1140–1149. [Google Scholar] [CrossRef]
- Pandey, C.; Mahapatra, M.M.; Kumar, P.; Saini, N. Some studies on P91 steel and their weldments. J. Alloys Compd. 2018, 743, 332–364. [Google Scholar] [CrossRef]
- Sharma, A.; Verma, D.K.; Kumaran, S. Effect of post weld heat treatment on microstructure and mechanical properties of Hot Wire GTA welded joints of SA213 T91 steel. Mater. Today Proc. 2018, 5, 8049–8056. [Google Scholar] [CrossRef]
- Oñoro, J. Martensite microstructure of 9–12% Cr steels weld metals. J. Mater. Process. Technol. 2006, 180, 137–142. [Google Scholar] [CrossRef]
- Dak, G.; Pandey, C. A critical review on dissimilar welds joint between martensitic and austenitic steel for power plant application. J. Manuf. Process. 2020, 58, 377–406. [Google Scholar] [CrossRef]
- Danielsen, H.K. Review of Z phase precipitation in 9–12 wt-%Cr steels. Mater. Sci. Technol. 2016, 32, 126–137. [Google Scholar] [CrossRef]
- Li, H.; Mitchell, D. Microstructural Characterization of P91 Steel in the Virgin, Service Exposed and Post-Service Re-Normalized Conditions. Steel Res. Int. 2013, 84, 1302–1308. [Google Scholar] [CrossRef]
- Hurtado-Noreña, C.; Danón, C.; Luppo, M.; Bruzzoni, P. Evolution of Minor Phases in a P91 Steel Normalized and Tempered at Different Temperatures. Procedia Mater. Sci. 2015, 8, 1089–1098. [Google Scholar] [CrossRef]
- Falat, L.; Čiripová, L.; Homolová, V.; Džupon, M.; Džunda, R.; Kovaľ, K. The Effects of Various Conditions of Short-Term Rejuvenation Heat Treatment on Room-Temperature Mechanical Properties of Thermally Aged P92 Boiler Steel. Materials 2021, 14, 6076. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.S.; Nategh, S.; Ekrami, A.-A. Microstructural evolution in damaged IN738LC alloy during various steps of rejuvenation heat treatments. J. Alloys Compd. 2012, 512, 340–350. [Google Scholar] [CrossRef]
- Jamalpour, A.; Hajjari, E.; Baghal, S.M.L. Effect of rejuvenation heat treatment on microstructure and hot corrosion resistance of a service-exposed nickel-based gas turbine blade. Mater. Res. Express 2019, 6, 1265c6. [Google Scholar] [CrossRef]
- Subbiah, R.; Rahel; Sravika, A.; Ambika, R.; Srujana, A.; Navya, E. Investigation on Microstructure and Mechanical Properties of P91 Alloy Steel Treated With Normalizing Process—A Review. Mater. Today Proc. 2019, 18, 2265–2269. [Google Scholar] [CrossRef]
- Peng, N.G.; Ahmad, B.; Muhamad, M.R.; Ahadlin, M. Phase Transformation of P91 Steels upon Cooling after Short Term Overheating above Ac1 and Ac3 Temperature. Adv. Mater. Res. 2013, 634–638, 1756–1765. [Google Scholar] [CrossRef]
- Vimalan, G.; Ravichandran, G.; Muthupandi, V. Phase Transformation Behaviour in P91 During Post Weld Heat Treatment: A Gleeble Study. Trans. Indian Inst. Met. 2017, 70, 875–885. [Google Scholar] [CrossRef]
- Pandey, C.; Giri, A.; Mahapatra, M. Effect of normalizing temperature on microstructural stability and mechanical properties of creep strength enhanced ferritic P91 steel. Mater. Sci. Eng. A 2016, 657, 173–184. [Google Scholar] [CrossRef]
- Abe, F. Grade 91 Heat-Resistant Martensitic Steel; Woodhead Publishing Limited: Sawston, UK, 2014; Volume 91, pp. 3–51. [Google Scholar] [CrossRef]
- Yan, W.; Wang, W.; Shan, Y.-Y.; Yang, K. Microstructural stability of 9–12%Cr ferrite/martensite heat-resistant steels. Front. Mater. Sci. 2013, 7, 1–27. [Google Scholar] [CrossRef]
- Pandey, C.; Mahapatra, M.; Kumar, P.; Saini, N. Homogenization of P91 weldments using varying normalizing and tempering treatment. Mater. Sci. Eng. A 2018, 710, 86–101. [Google Scholar] [CrossRef]
- Hald, J. Microstructure and long-term creep properties of 9–12% Cr steels. Int. J. Press. Vessels Pip. 2008, 85, 30–37. [Google Scholar] [CrossRef]
- Pandey, C.; Giri, A.; Mahapatra, M. Evolution of phases in P91 steel in various heat treatment conditions and their effect on microstructure stability and mechanical properties. Mater. Sci. Eng. A 2016, 664, 58–74. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. Constitutive analysis to predict high-temperature flow stress in modified 9Cr–1Mo (P91) steel. Mater. Des. 2010, 31, 981–984. [Google Scholar] [CrossRef]
- Niu, X.; Shen, L.; Chen, C.; Zhou, J.; Chen, L. An Arrhenius-type constitutive model to predict the deformation behavior of Sn0.3Ag0.7Cu under different temperature. J. Mater. Sci. Mater. Electron. 2019, 30, 14611–14620. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Li, G.-S.; Wang, Y.; Lv, W.-Q.; Yu, C.-T.; Zhou, J. A characterization for the flow behavior of as-extruded 7075 aluminum alloy by the improved Arrhenius model with variable parameters. Mater. Res. 2013, 16, 19–27. [Google Scholar] [CrossRef]
- Yang, X.; Li, W. Flow Behavior and Processing Maps of a Low-Carbon Steel During Hot Deformation. Met. Mater. Trans. A Phys. Metall. Mater. Sci. 2015, 46, 6052–6064. [Google Scholar] [CrossRef]
- Obiko, J.; Chown, L.; Whitefield, D.; Bodunrin, M. Metal flow behaviour and processing maps of high heat resistant steel during hot compression. Int. J. Adv. Manuf. Technol. 2022, 121, 4153–4167. [Google Scholar] [CrossRef]
- Lakshmi, A.A.; Rao, C.S.; Gangadhar, J.; Srinivasu, C.; Singh, S.K. Review of Processing Maps and Development of Qualitative Processing Maps. Mater. Today Proc. 2017, 4, 946–956. [Google Scholar] [CrossRef]
- Prasad, Y.; Rao, K. Processing maps for hot deformation of rolled AZ31 magnesium alloy plate: Anisotropy of hot workability. Mater. Sci. Eng. A 2008, 487, 316–327. [Google Scholar] [CrossRef]
- Xiao, Z.-B.; Huang, Y.-C.; Liu, Y. Modeling of Flow Stress of 2026 Al Alloy under Hot Compression. Adv. Mater. Sci. Eng. 2016, 2016, 3803472. [Google Scholar] [CrossRef]
- Kumar, A.; Pandey, S.M.; Pandey, C. Dissimilar weldments of ferritic/martensitic grade P92 steel and Inconel 617 alloy: Role of groove geometry on mechanical properties and residual stresses. Arch. Civ. Mech. Eng. 2022, 23, 54. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Mishnev, R.; Fedoseeva, A.; Dudova, N. The Role of Microstructure in Creep Strength of 9–12% Cr Steels. Mater. Sci. Forum 2017, 879, 36–41. [Google Scholar] [CrossRef]
- Bhanu, V.; Pandey, S.M.; Gupta, A.; Pandey, C. Dissimilar weldments of P91 and Incoloy 800HT: Microstructure, mechanical properties, and residual stresses. Int. J. Press. Vessels Pip. 2022, 199, 104782. [Google Scholar] [CrossRef]
- Chatterjee, A.; Dutta, A.; Sk, B.; Mitra, R.; Bhaduri, A.K.; Chakrabarti, D. Effect of Microalloy Precipitates on the Microstructure and Texture of Hot-Deformed Modified 9Cr-1Mo Steel. Met. Mater. Trans. A Phys. Metall. Mater. Sci. 2017, 48, 2410–2424. [Google Scholar] [CrossRef]
- Obiko, J. Friction correction of flow stress-strain curve in the upsetting process. IOP SciNotes 2021, 2, 014401. [Google Scholar] [CrossRef]
- Li, Y.; Onodera, E.; Chiba, A. Friction Coefficient in Hot Compression of Cylindrical Sample. Mater. Trans. 2010, 51, 1210–1215. [Google Scholar] [CrossRef]
- Roebuck, B.; Lord, J.; Brooks, M.; Loveday, M.; Sellars, C.; Evans, R. Measurement of flow stress in hot axisymmetric compression tests. Mater. High Temp. 2006, 23, 59–83. [Google Scholar] [CrossRef]
- Ghosh, S.; Somani, M.C.; Setman, D.; Mula, S. Hot Deformation Characteristic and Strain Dependent Constitutive Flow Stress Modelling of Ti + Nb Stabilized Interstitial Free Steel. Met. Mater. Int. 2020, 27, 2481–2498. [Google Scholar] [CrossRef]
- Hu, M.; Dong, L.; Zhang, Z.; Lei, X.; Yang, R.; Sha, Y. Correction of Flow Curves and Constitutive Modelling of a Ti-6Al-4V Alloys. Metals 2018, 8, 256. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. Optimization of hot working parameters for thermo-mechanical processing of modified 9Cr–1Mo (P91) steel employing dynamic materials model. Mater. Sci. Eng. A 2011, 528, 5204–5211. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, É. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X.-M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Bodunrin, M.O.; Chown, L.H.; van der Merwe, J.W.; Alaneme, K.K. Hot working behaviour of experimental Ti-4.5Al-1 V-3Fe alloy with initial lamellar microstructure. Int. J. Adv. Manuf. Technol. 2020, 106, 1901–1916. [Google Scholar] [CrossRef]
- Obiko, J.; Chown, L.; Whitefield, D.; Bodunrin, M. Understanding hot workability of power plant P92 creep resistant steels using dynamic material modelling (DMM) and microstructural evolution. Int. J. Interact. Des. Manuf. 2022. [Google Scholar] [CrossRef]
- Obiko, J.O.; Chown, L.H.; Whitefield, D.J. Warm deformation behaviour of P92 steel. Mater. Res. Express 2019, 6, 1265j7. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Zhai, R.; Ma, R.; Zhao, J.; Mu, Z. Constitutive Equations for Describing the Warm and Hot Deformation Behavior of 20Cr2Ni4A Alloy Steel. Metals 2020, 10, 1169. [Google Scholar] [CrossRef]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.-M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef]
- He, J.; Zhang, D.; Zhang, W.; Qiu, C.; Zhang, W. Constitutive Equation and Hot Compression Deformation Behavior of Homogenized Al–7.5Zn–1.5Mg–0.2Cu–0.2Zr Alloys. Materials 2017, 10, 1193. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A. A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Constitutive relationships for hot deformation of austenite. Acta Mater. 2011, 59, 6441–6448. [Google Scholar] [CrossRef]
- Alsagabi, S. High Temperature Deformation Behavior of P92 Steel. Trans. Indian Inst. Met. 2015, 69, 1513–1518. [Google Scholar] [CrossRef]
- Bodunrin, M.O. Flow stress prediction using hyperbolic-sine Arrhenius constants optimised by simple generalised reduced gradient refinement. J. Mater. Res. Technol. 2020, 9, 2376–2386. [Google Scholar] [CrossRef]
- Sellars, C.; McTegart, W. On the mechanism of hot deformation. Acta Met. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Menapace, C.; Sartori, N.; Pellizzari, M.; Straffelini, G. Hot Deformation Behavior of Four Steels: A Comparative Study. J. Eng. Mater. Technol. 2018, 140, 021006. [Google Scholar] [CrossRef]
- Cabrera, J.M.; Jonas, J.J.; Prado, J.M. Flow behaviour of medium carbon microalloyed steel under hot working conditions. Mater. Sci. Technol. 1996, 12, 579–585. [Google Scholar] [CrossRef]
- Baktash, R.; Mirzadeh, H. A Simple Constitutive Model for Prediction of Single-Peak Flow Curves Under Hot Working Conditions. J. Eng. Mater. Technol. 2016, 138, 021004. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Babalola, S.A.; Bodunrin, M.O. On the prediction of hot deformation mechanisms and workability in Al6063/Ni and Al6063/steel composites using hyperbolic-sine constitutive equation. Mater. Today Proc. 2021, 38, 942–948. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Carsí, M.; Peñalba, F.; Rieiro, I.; Ruano, O.A. High temperature workability behaviour of a modified P92 steel. Int. J. Mater. Res. 2011, 102, 1378–1383. [Google Scholar] [CrossRef]
- Zhou, D.; Xu, X.; Mao, H.; Yan, Y.; Nieh, T.; Lu, Z. Plastic flow behaviour in an alumina-forming austenitic stainless steel at elevated temperatures. Mater. Sci. Eng. A 2014, 594, 246–252. [Google Scholar] [CrossRef]
- Mehtonen, S.; Karjalainen, L.; Porter, D. Hot deformation behavior and microstructure evolution of a stabilized high-Cr ferritic stainless steel. Mater. Sci. Eng. A 2013, 571, 1–12. [Google Scholar] [CrossRef]
- Obiko, J.O.; Mwema, F.M.; Shangwira, H. Forging optimisation process using numerical simulation and Taguchi method. SN Appl. Sci. 2020, 2, 713. [Google Scholar] [CrossRef]
- Mwema, F.; Obiko, J.; Mahamood, R.; Adediran, A.; Bodunrin, M.; Akinlabi, E.; Jen, T. Constitutive analysis of hot forming process of P91 steel: Finite element method approach. Adv. Mater. Process. Technol. 2021, 8, 1182–1193. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti–6Al–4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Z.; Misra, R.D.K.; Liu, H.; Yu, F. Constitutive modeling and dynamic softening mechanism during hot deformation of an ultra-pure 17%Cr ferritic stainless steel stabilized with Nb. Met. Mater. Int. 2014, 20, 939–951. [Google Scholar] [CrossRef]



| Cr | C | Mn | Mo | V | Nb | W | Ni | Si | Fe | P | Cu | Mg | Sn |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9.189 | 0.1 | 0.447 | 0.885 | 0.191 | 0.076 | ˂0.01 | 0.158 | 0.254 | 88.01 | 0.02 | 0.086 | 0.016 | 0.006 |
| P91 | ή | β | η | ɑ | S | Q (kJmol−1) | ln A |
|---|---|---|---|---|---|---|---|
| Steel A | 7.79 | 0.054 | 5.76 | 0.0069 | 9.89 | 473.08 | 9.98 × 1018 |
| Steel B | 9.03 | 0.058 | 6.67 | 0.0065 | 10.18 | 564.48 | 9.58 × 1022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maube, S.; Obiko, J.; Van der Merwe, J.; Mwema, F.; Klenam, D.; Bodunrin, M. Comparative Study on Hot Metal Flow Behaviour of Virgin and Rejuvenated Heat Treatment Creep Exhausted P91 Steel. Appl. Sci. 2023, 13, 4449. https://doi.org/10.3390/app13074449
Maube S, Obiko J, Van der Merwe J, Mwema F, Klenam D, Bodunrin M. Comparative Study on Hot Metal Flow Behaviour of Virgin and Rejuvenated Heat Treatment Creep Exhausted P91 Steel. Applied Sciences. 2023; 13(7):4449. https://doi.org/10.3390/app13074449
Chicago/Turabian StyleMaube, Shem, Japheth Obiko, Josias Van der Merwe, Fredrick Mwema, Desmond Klenam, and Michael Bodunrin. 2023. "Comparative Study on Hot Metal Flow Behaviour of Virgin and Rejuvenated Heat Treatment Creep Exhausted P91 Steel" Applied Sciences 13, no. 7: 4449. https://doi.org/10.3390/app13074449
APA StyleMaube, S., Obiko, J., Van der Merwe, J., Mwema, F., Klenam, D., & Bodunrin, M. (2023). Comparative Study on Hot Metal Flow Behaviour of Virgin and Rejuvenated Heat Treatment Creep Exhausted P91 Steel. Applied Sciences, 13(7), 4449. https://doi.org/10.3390/app13074449








