Strategic Development of Dielectric Strength Prediction Protocol for Perfluorocarbon and Nonperfluorocarbon Compounds
Abstract
1. Introduction
2. Methodology
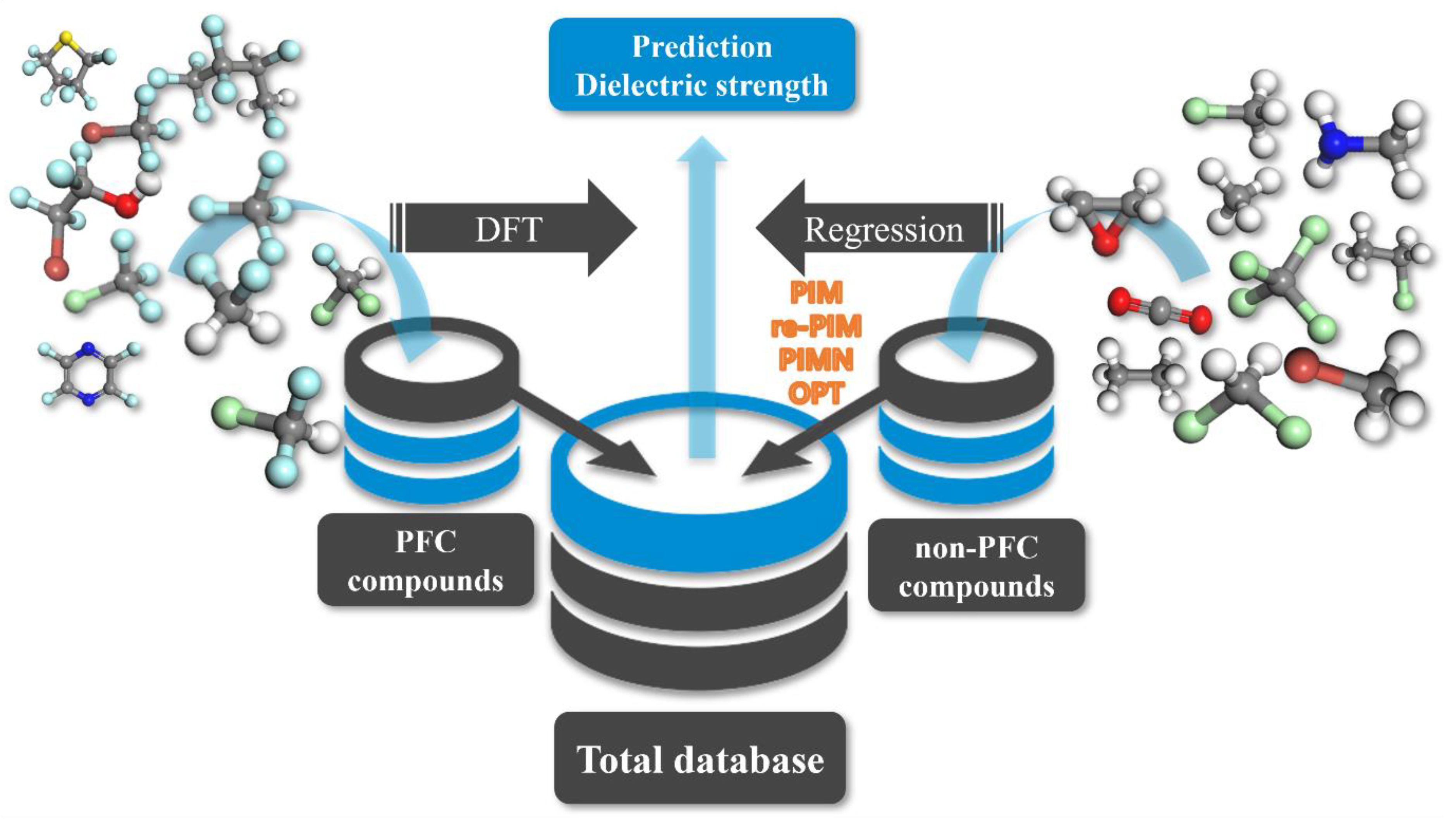
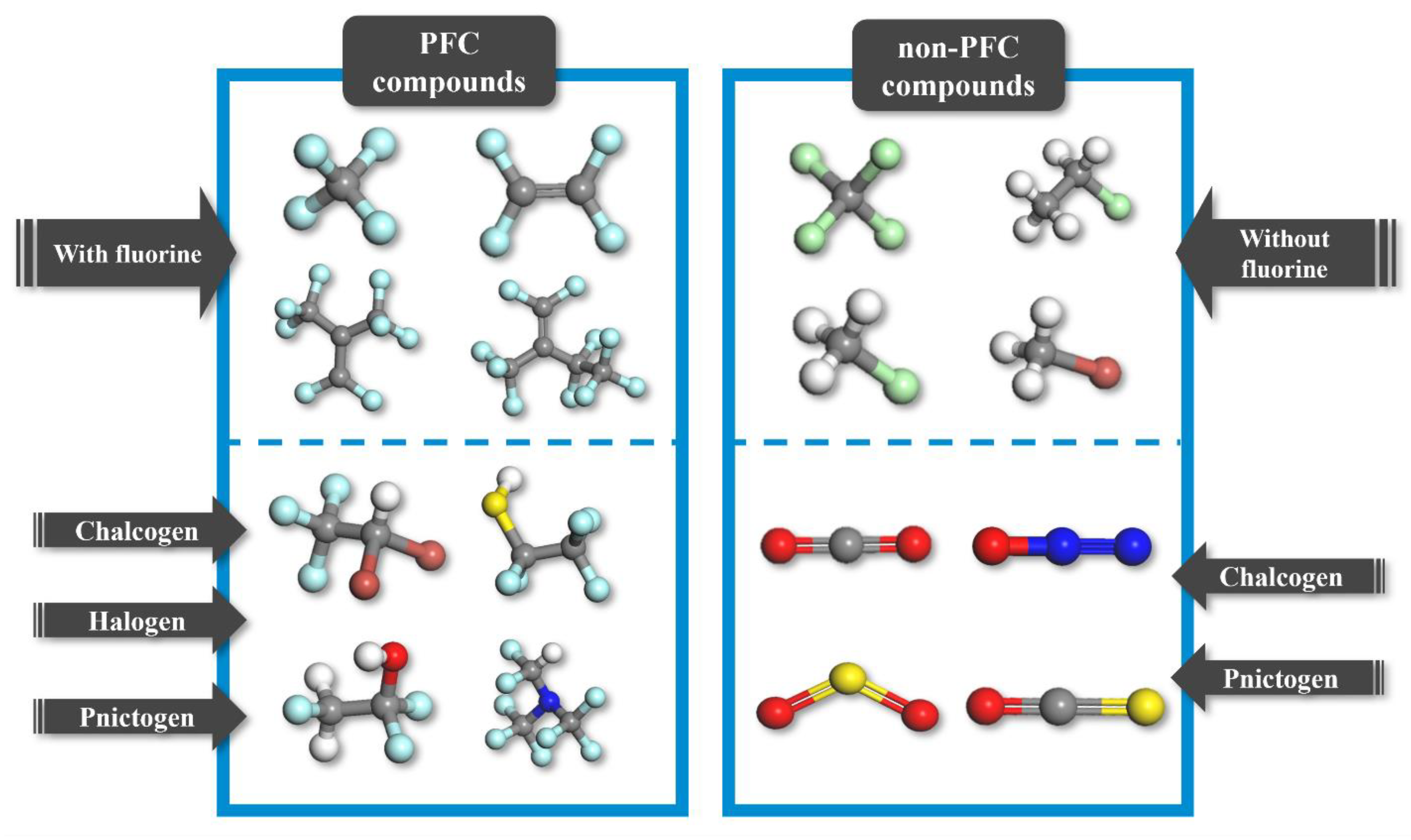
2.1. Overview of Strategy and Materials Database
2.2. Computational Protocols Employed to Predict Dielectric Strength
3. Results and Discussion
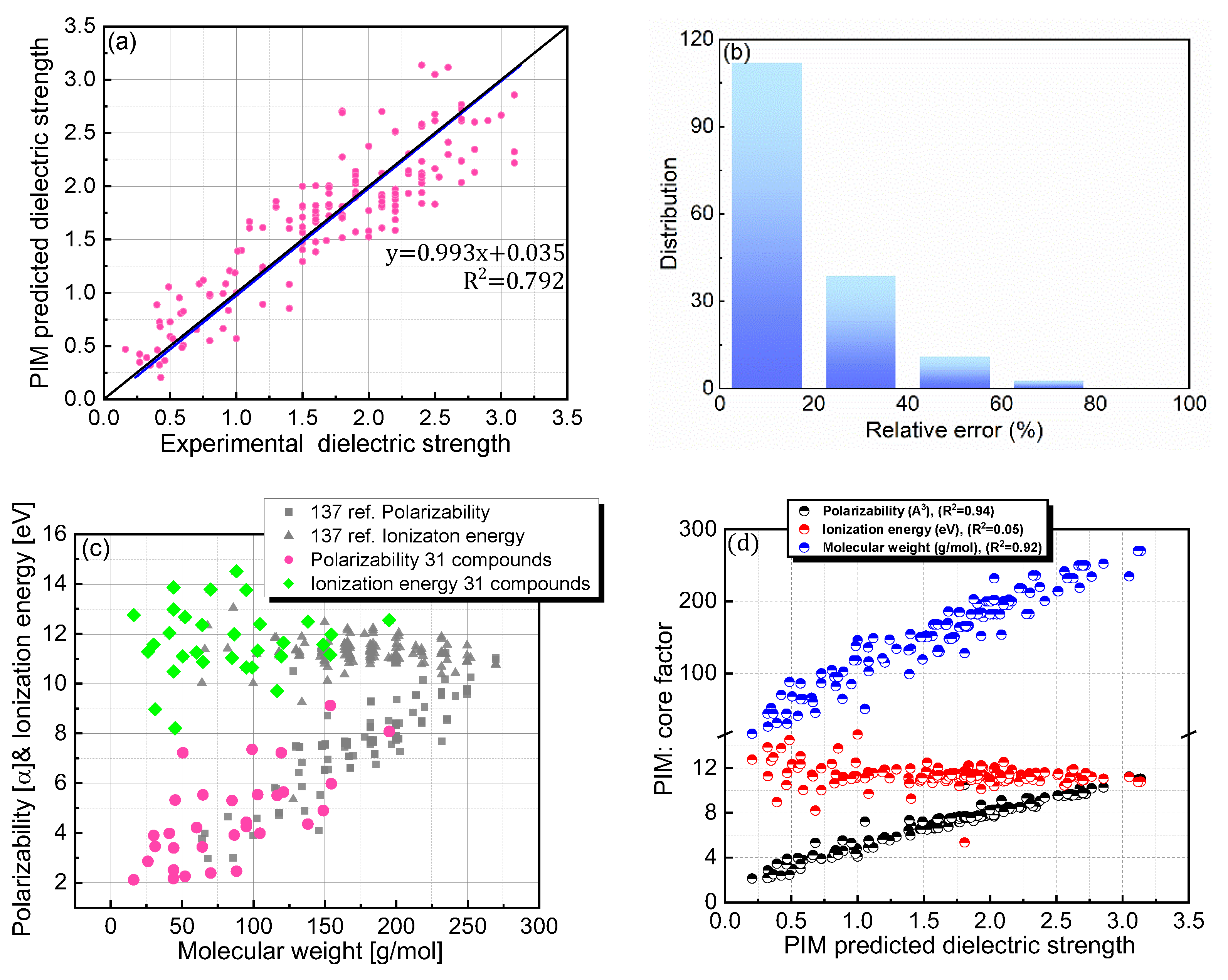
3.1. Universal Validity: Reliability of Previous Protocol for Predicting the Dielectric Strengths of Non-PFC Materials
3.2. Strategies for Upgrading the Dielectric Strength Prediction Protocol
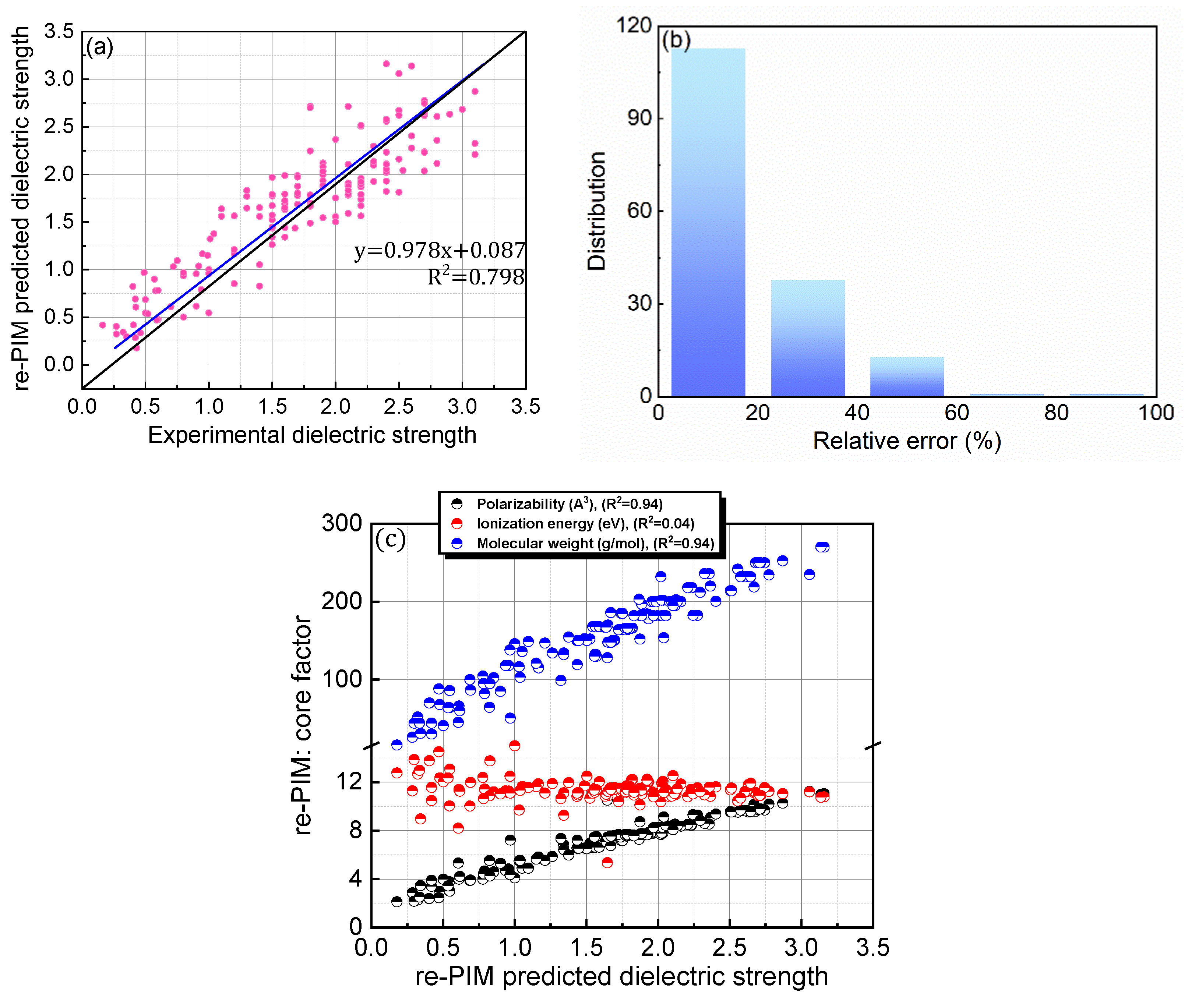
3.2.1. Strategy I: Reparameterization of Previous Protocol
3.2.2. Strategy II: Incorporation of a Novel Factor into the Previous Protocol
3.2.3. Strategy III: Importance of Original Factors in Dielectric Strength Predictions
3.3. In-Depth Analysis of Correlations between Dielectric Strength and Various Core Factors
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, B.; Wang, G.; Shi, H.; Shen, J.; Ji, H.-K.; Kil, G.-S. Green gas for grid as an eco-friendly alternative insulation gas to SF6: A review. Appl. Sci. 2020, 10, 2526. [Google Scholar] [CrossRef]
- Kieffel, Y.; Irwin, T.; Ponchon, P.; Owens, J. Green gas to replace SF6 in electrical grids. IEEE Power Electron. Mag. 2016, 14, 32–39. [Google Scholar] [CrossRef]
- Dervos, C.T.; Vassiliou, P.; Mergos, J.A. Thermal stability of SF6 associated with metallic conductors incorporated in gas insulated switchgear power substations. J. Phys. D Appl. Phys. 2007, 40, 6942–6952. [Google Scholar] [CrossRef]
- Zhong, L.; Rong, M.; Wang, X.; Wu, J.; Han, G.; Han, G.; Lu, Y.; Yang, A.; Wu, Y. Compositions, thermodynamic properties, and transport coefficients of hightemperature C5F10O mixed with CO2 and O2 as substitutes for SF6 to reduce global warming potential. AIP Adv. 2017, 7, 075003. [Google Scholar] [CrossRef]
- Rabie, M.; Franck, C.M. Assessment of eco-friendly gases for electrical insulation to replace the most potent industrial greenhouse gas SF6. Environ. Sci. Technol. 2018, 52, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Hou, H.; Wang, B. Prediction on dielectric strength and boiling point of gaseous molecules for replacement of SF6. J. Comput. Chem. 2017, 38, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Rabie, M.; Dahl, D.A.; Donald, S.M.A.; Reiher, M.; Franck, C. Predictors for gases of high electrical strength. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 856–863. [Google Scholar] [CrossRef]
- Franck, C.M.; Dahl, D.A.; Rabie, M.; Haefliger, P.; Koch, M. An efficient procedure to identify and quantify new molecules for insulating gas mixtures. Contrib. Plasma Phys. 2014, 54, 3–13. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Cressault, Y.; Hu, J.; Wang, B.; Xiao, S.; Li, Y.; Kabbaj, N. Research status of replacement gases for SF6 in power industry. AIP Adv. 2020, 10, 050702. [Google Scholar] [CrossRef]
- Beroual, A.; Haddad, A.M. Recent advances in the quest for a new insulation gas with a low impact on the environment to replace sulfur hexafluoride (SF6) gas in high-voltage power network applications. Energies 2017, 10, 1216. [Google Scholar] [CrossRef]
- Owens, J.; Xiao, A.; Bonk, J.; DeLorme, M.; Zhang, A. Recent development of two alternative gases to SF6 for high voltage electrical power applications. Energies 2021, 14, 5051. [Google Scholar] [CrossRef]
- Juntao, J.; Dengming, X.; Xiaoling, Z.; Yunkun, D. Analysis of the molecules structure and vertical electron affnity of organic gas impact on electric strength. Plasma Sci. Technol. 2016, 18, 554–559. [Google Scholar]
- Hu, S.; Wang, Y.; Zhou, W.; Qiu, R.; Luo, Y.; Wang, B. Dielectric properties of CF3SO2F/N2 and CF3SO2F/CO2 mixtures as a substitute to SF6. Ind. Eng. Chem. Res. 2020, 59, 15796–15804. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, S.; Han, Y.; Cressault, Y. Experimental studies on power frequency breakdown voltage of CF3I/N2 mixed gas under different electric fields. Appl. Phys. Lett. 2016, 108, 092901. [Google Scholar] [CrossRef]
- Pagliaro, J.L.; Linteris, G.T. Hydrocarbon flame inhibition by C6F12O (Novec 1230): Unstretched burning velocity measurements and predictions. Fire Saf. 2017, 87, 10–17. [Google Scholar] [CrossRef]
- Cooke, C.; Cookson, A. The nature and practice of gases as electrical insulators. IEEE Electr. Insul. Mag. 1978, 13, 239–248. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, H.; Cheng, L.; Zhao, K. First principles based computational scheme for designing new SF6 replacements. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2572–2578. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Tian, S.; Xiao, S.; Chen, D.; Tang, J.; Zhuo, R. Decomposition mechanism of the C5-PFK/CO2 gas mixture as an alternative gas for SF6. Chem. Eng. J. 2017, 336, 36–48. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, L.; Li, X.; Guo, Z.; Pu, Y.; Tang, N. Evaluating the dielectric strength of promising SF6 alternatives by DFT calculations and DC breakdown tests. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1187–1194. [Google Scholar] [CrossRef]
- Rabie, M.; Franck, C. Computational screening of new high voltage insulation gases with low global warming potential. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 296–302. [Google Scholar] [CrossRef]
- Jang, J.; Jung, K.H.; Kim, K.C. Development of computational design for reliable prediction of dielectric strengths of perfluorocarbon compounds. Sci. Rep. 2022, 12, 7027. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Hu, X.; Gao, Z. Study on relative electrical strength of SF6 substitute gas based on density functional theory. IEEE Access. 2022, 10, 75395–75403. [Google Scholar] [CrossRef]
- Go, C.Y.; Jang, S.S.; Kim, K.C. Tailored design of electrochemically degradable anthraquinone functionality toward organic cathodes. ACS Appl. Mater. Interfaces 2021, 13, 35729–35738. [Google Scholar] [CrossRef]
- Go, C.Y.; Lim, S.; Lee, J.; Kim, K.C. Toward coupling of electrochemical redox properties with electrostatic potential surfaces tailored by dopant architectures for pyrenetetrone. Energy Stor. Mater. 2021, 35, 610–619. [Google Scholar] [CrossRef]
- Jeong, G.S.; Lee, D.K.; Kim, K.C. Crucial role of cyanides for high-potential electrochemical reduction reaction. Energy Stor. Mater. 2020, 29, 140–148. [Google Scholar] [CrossRef]
- Jung, K.H.; Jeong, G.S.; Go, C.Y.; Kim, K.C. Conjugacy of organic cathode materials for high-potential lithium-ion batteries: Carbonitriles versus quinones. Energy Stor. Mater. 2020, 24, 237–246. [Google Scholar] [CrossRef]
- Jung, K.H.; Jeong, G.S.; Joo, J.B.; Kim, K.C. Improving the understanding of the redox properties of Fluoranil derivatives for cathodes in Sodium-ion batteries. ChemSusChem 2019, 12, 4968–4975. [Google Scholar] [CrossRef]
- Jung, K.H.; Lim, S.; Choi, S.; Kim, K.C. Unraveling three-stage discharging behaviors of bio-inspired organic cathode materials. Adv. Funct. Mater. 2021, 31, 2105285. [Google Scholar] [CrossRef]
- Kim, K.C. Design strategies for promising organic positive electrodes in Lithium-ion batteries: Quinones and carbon materials. Ind. Eng. Chem. Res. 2017, 56, 12009–12023. [Google Scholar] [CrossRef]
- Kim, K.C.; Liu, T.; Jung, K.H.; Lee, S.W.; Jang, S.S. Unveiled correlations between electron affinity and solvation in redox potential of quinone-based sodium-ion batteries. Energy Stor. Mater. 2019, 19, 242–250. [Google Scholar] [CrossRef]
- Kim, K.C.; Liu, T.; Lee, S.W.; Jang, S.S. First-principles density functional theory modeling of Li binding: Thermodynamics and redox properties of quinone derivatives for Lithium-ion batteries. J. Am. Chem. Soc. 2016, 138, 2374–2382. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Kim, K.C.; Kavian, R.; Jang, S.S.; Lee, S.W. High-density Lithium-ion energy storage utilizing the surface redox reactions in folded graphene films. Chem. Mater. 2015, 27, 3291–3298. [Google Scholar] [CrossRef]
- Liu, T.; Kim, K.C.; Lee, B.; Chen, Z.; Noda, S.; Jang, S.S.; Lee, S.W. Self-polymerized dopamine as an organic cathode for Li- and Na-ion batteries. Energy Environ. Sci. 2017, 10, 205–215. [Google Scholar] [CrossRef]
- Zhu, Y.; Kim, K.C.; Jang, S.S. Boron-doped coronenes with high redox potential for organic positive electrodes in lithium-ion batteries: A first-principles density functional theory modeling study. J. Mater. Chem. A 2018, 6, 10111–10120. [Google Scholar] [CrossRef]
| Prediction Protocol and Core Factor | Average Relative Error | RMSD | x | y | z | m | n | ||
|---|---|---|---|---|---|---|---|---|---|
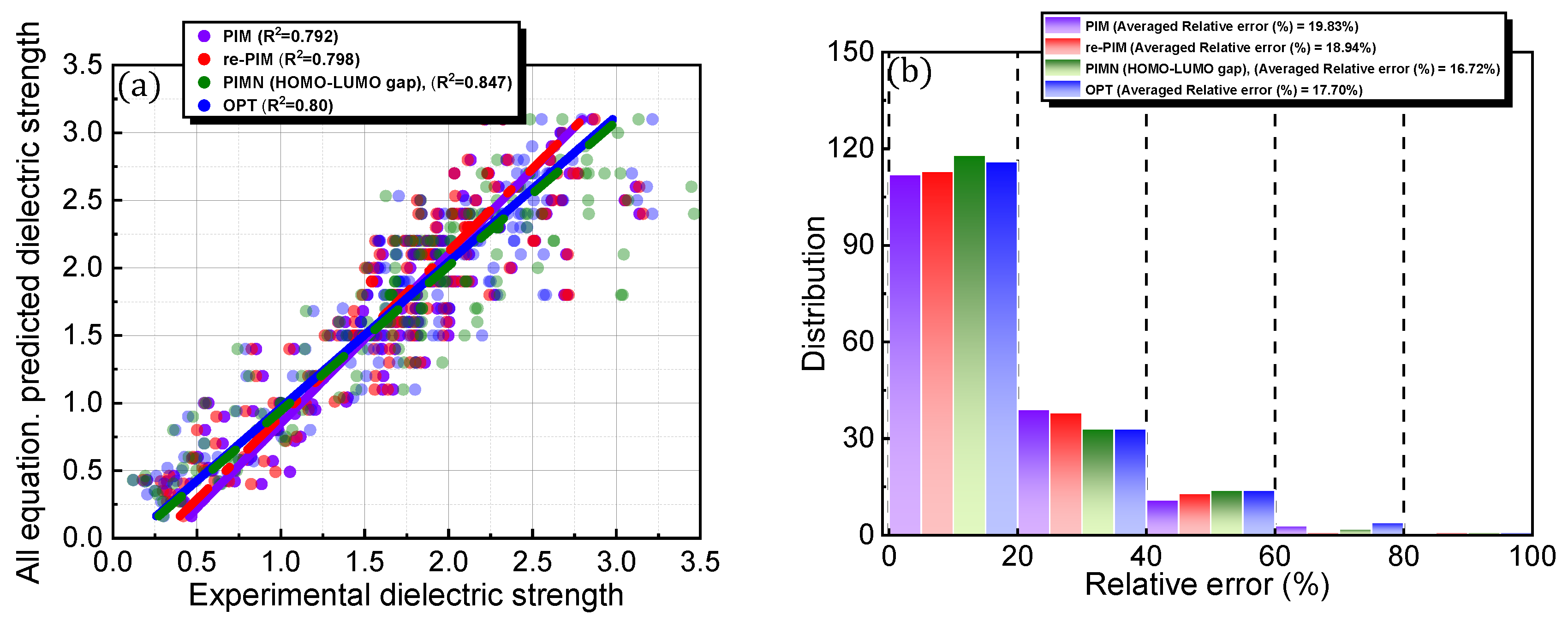
| Equation (1). PIM | 19.83% | 0.329 | 0.0012 | 1 | 0.288 | 0.401 | - | ||
| Equation (2). re-PIM | 18.94% | 0.328 | 1 | 1 | 0.327 | 0.457 | - | ||
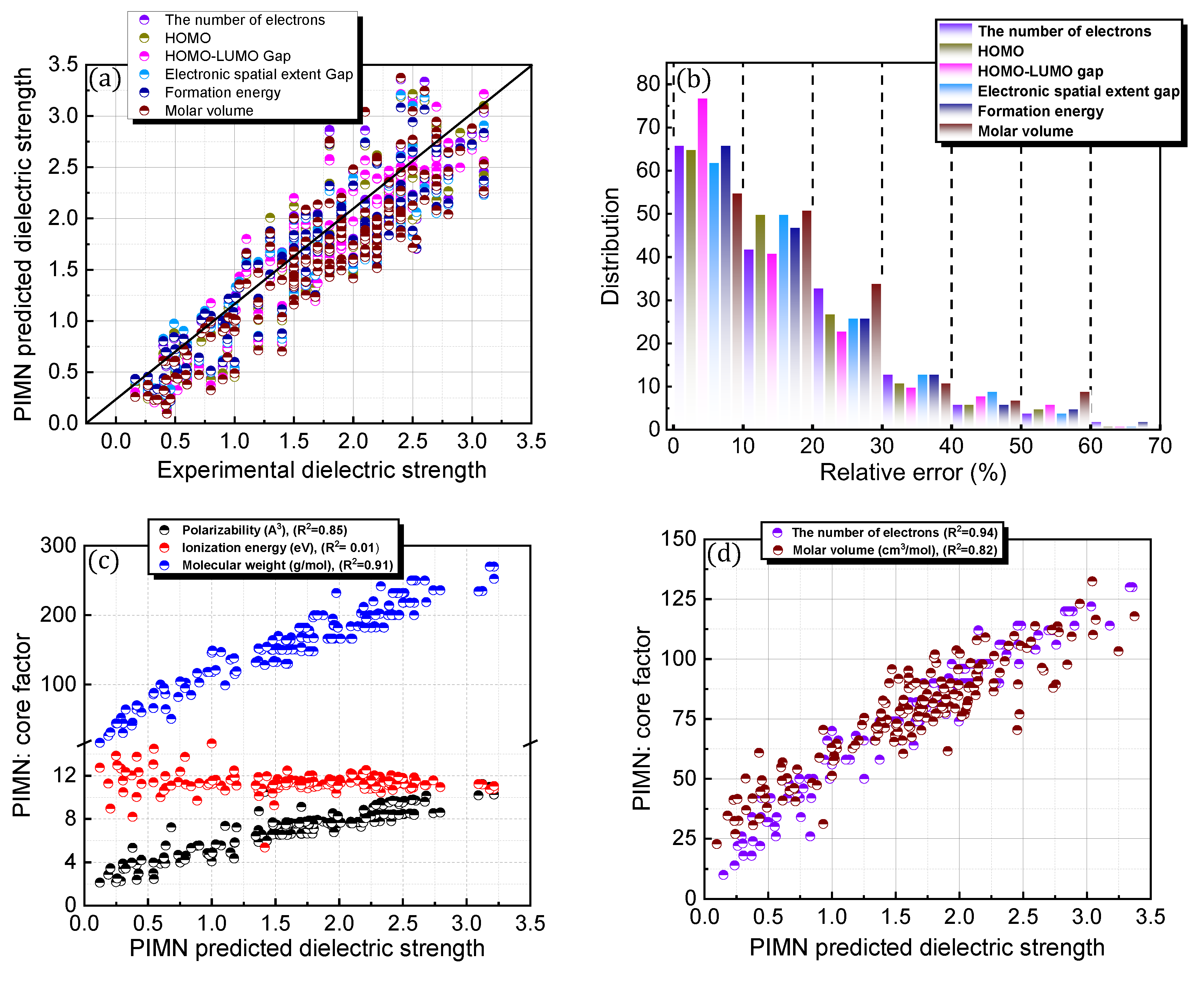
| Equation (3). PIMN | Number of electrons (Ne) | 18.20% | 0.329 | 1 | 0.94 | 0.32 | 0.1 | 0.522 | |
| HOMO [eV] | 17.59% | 0.313 | 0.98 | 1.275 | 0.005 | 0.408 | 1 | ||
| HOMO–LUMO gap [eV] | 16.72% | 0.289 | 1.21 | 0.916 | 0.217 | 0.732 | 0.65 | ||
| Electronic spatial extent gap [a.u.] | 18.96% | 0.328 | 0.65 | 1.012 | 0.37 | 0.459 | 0.001 | ||
| Formation energy [a.u.] | 18.45% | 0.320 | 0.38 | 0.83 | 0.48 | 0.461 | 0.106 | ||
| Molar volume [cm3 mol−1] | 17.89% | 0.346 | 1 | 0.638 | 0.281 | 0.757 | 0.253 | ||
| Prediction protocol and core factor | Average relative error | RMSD | x | y | z | m | n | l | |
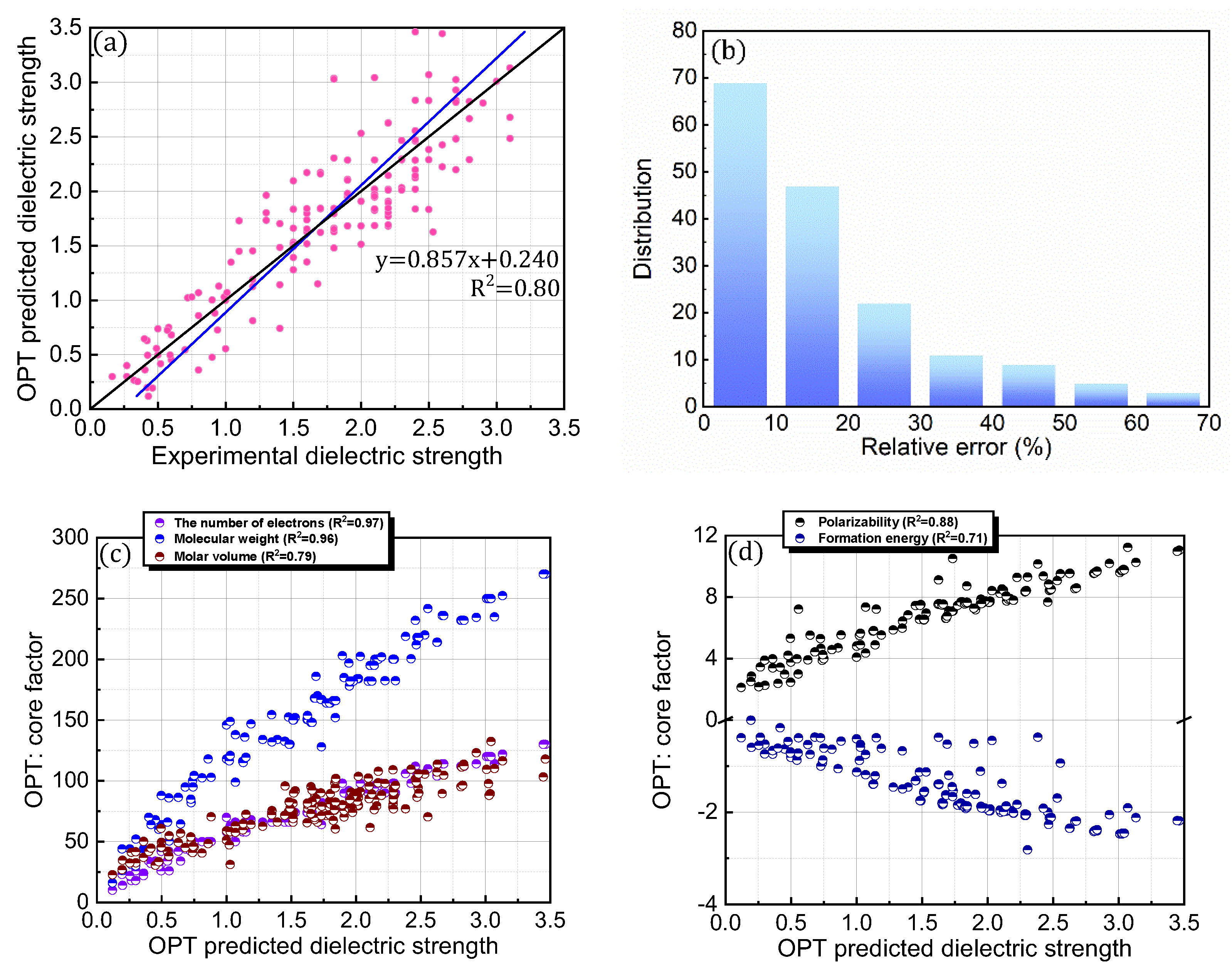
| Equation (4). OPT | 17.70% | 0.340 | 0.365 | 0.549 | 0.9 | 0.001 | 0.079 | 0.008 | |
| Prediction Protocol | Core Factor | Linear Regression Line | Correlation Coefficient (R2) | Corresponding Figure |
|---|---|---|---|---|
| Equation (1). PIM | Polarizability [Å3] | 0.94 | Figure 3d | |
| Ionization energy [eV] | 0.05 | |||
| Molecular weight [g mol−1] | 0.92 | |||
| Equation (2). re-PIM | Polarizability [Å3] | 0.94 | Figure 4c | |
| Ionization energy [eV] | 0.04 | |||
| Molecular weight [g mol−1] | 0.94 | |||
| Equation (3). PIMN | Polarizability [Å3] | 0.85 | Figure 5c | |
| Ionization energy [eV] | 0.01 | |||
| Molecular weight [g mol−1] | 0.91 | |||
| Number of electrons | 0.94 | Figure 5d | ||
| Molar volume [cm3 mol−1] | 0.82 | |||
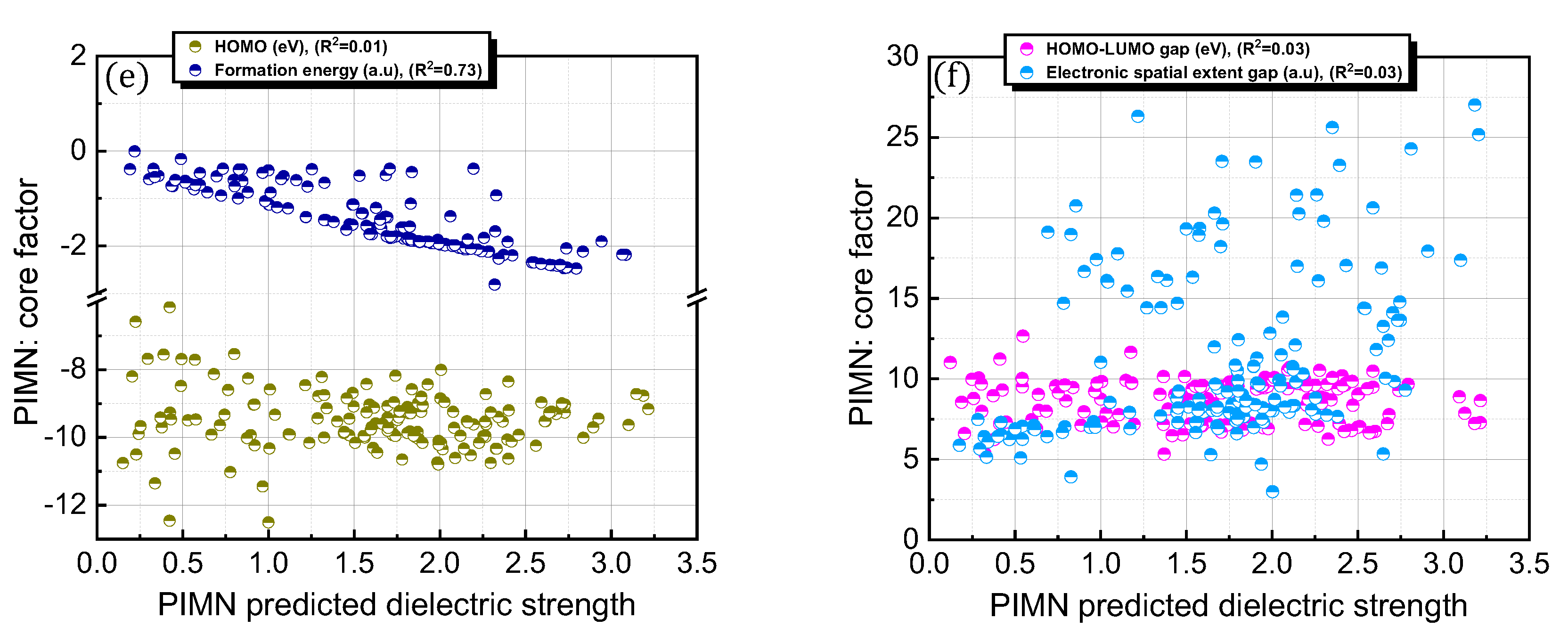
| HOMO [eV] | 0.01 | Figure 5e | ||
| Formation energy [a.u.] | 0.73 | |||
| HOMO–LUMO gap [eV] | 0.03 | Figure 5f | ||
| Electronic spatial extent gap [a.u.] | 0.03 | |||
| Equation (4). OPT | Number of electrons | 0.97 | Figure 6c | |
| Molecular weight [g mol−1] | 0.96 | |||
| Molar volume [cm3 mol−1] | 0.79 | |||
| Polarizability [Å3] | 0.88 | Figure 6d | ||
| Formation energy [a.u.] | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, M.K.; Kim, K.C. Strategic Development of Dielectric Strength Prediction Protocol for Perfluorocarbon and Nonperfluorocarbon Compounds. Appl. Sci. 2023, 13, 4318. https://doi.org/10.3390/app13074318
Choi MK, Kim KC. Strategic Development of Dielectric Strength Prediction Protocol for Perfluorocarbon and Nonperfluorocarbon Compounds. Applied Sciences. 2023; 13(7):4318. https://doi.org/10.3390/app13074318
Chicago/Turabian StyleChoi, Min Kyu, and Ki Chul Kim. 2023. "Strategic Development of Dielectric Strength Prediction Protocol for Perfluorocarbon and Nonperfluorocarbon Compounds" Applied Sciences 13, no. 7: 4318. https://doi.org/10.3390/app13074318
APA StyleChoi, M. K., & Kim, K. C. (2023). Strategic Development of Dielectric Strength Prediction Protocol for Perfluorocarbon and Nonperfluorocarbon Compounds. Applied Sciences, 13(7), 4318. https://doi.org/10.3390/app13074318






