Numerical Design and Optimisation of Self-Compacting High Early-Strength Cement-Based Mortars

Abstract

The use of SCC in Europe began in the 1990s and was mainly promoted by the precast industry. Precast companies generally prefer high early-strength concrete mixtures to accelerate their production rate, reducing the demoulding time. From a materials science point of view, self-compacting and high early-strength concrete mixes may be challenging because they present contradicting mixture design requirements. For example, a low water/binder ratio (w/b) is key to achieving high early strength. However, it may impact the self-compacting ability, which is very sensitive to Vw/Vp. As such, the mixture design can be complex. The design of the experimental approach is a powerful tool for designing, predicting, and optimising advanced cement-based materials when several constituent materials are employed and multi-performance requirements are targeted. The current work aimed at fitting models to mathematically describe the flow ability, viscosity, and mechanical strength properties of high-performance self-compacting cement-based mortars based on a central composite design. The statistical fitted models revealed that Vs/Vm exhibited the strongest (negative) effect on the slump-flow diameter and T-funnel time. Vw/Vp showed the most significant effect on mechanical strength. Models were then used for mortar optimisation. The proposed optimal mixture represents the best compromise between self-compacting ability—a flow diameter of 250 mm and funnel time equal to 10 s—and compressive strength higher than 50 MPa at 24 h without any special curing treatment.

1. Introduction

The building and construction industries have a heavy environmental impact. They account for 40% of natural resources, consume 70% of electrical power and 12% of potable water, and produce 45–65% of landfilled waste and 48% of GHG emissions [1]. In Europe, construction is the most significant economic sector, employing 18 million people directly and creating close to 10% of the European Union Gross Domestic Product. Thus, construction is an essential pillar in the context of the 2030 Agenda since it impacts the economic, environmental, and social spheres.

Concrete is a massively used construction material and the second most-consumed material worldwide, just after water [2]. This is mainly because the basic constituents, cement, aggregates, and water, are widely available worldwide; thus, concrete can be produced locally and consequently, it is inexpensive. Moreover, it hardens quickly and in all habitable environments, including underwater.

Over recent decades, efforts have been made to improve the behaviour of concrete materials. It took more than 150 years from the patenting of Portland cement (in 1824) until the discovery and development of self-compactable concrete (SCC) in the 1980s in Japan [3,4]. The development of superplasticisers allowed the efficient dispersal of cementitious particles and the emergence of SCC. According to the European standard EN 206-1 (specification, performance, production, and conformity of concrete), the constituent raw materials of SCC are similar to ordinary vibrated concrete (OVC). The main differences between OVC and SCC are due to the constituents’ proportions. Figure 1 presents the indicative volumetric proportions of SCC and OVC [5]. As can be seen, the main difference between SCC and OVC is a higher dosage of fine materials, i.e., cement and supplementary cementitious materials (SCM), and a smaller amount of coarse aggregate and smaller particle size distribution [6].

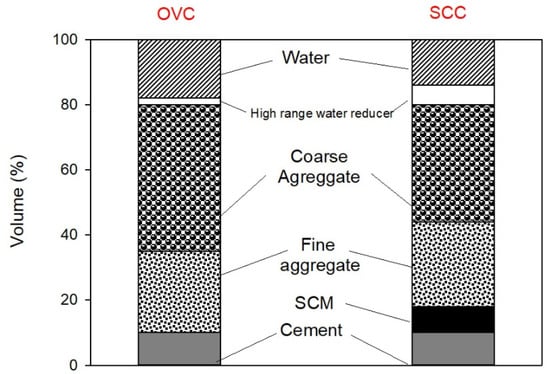
Figure 1. Mixture proportions of OVC and SCC (in % volume).

As such, the design of more advanced cement-based materials such as SCC can be complex since several requirements must co-exist, such as (i) engineering properties, (ii) architecture, (iii) cost, and (iv) eco-efficiency, among others. Even though the selection of the material should try to improve robustness, making the mixture more tolerant to raw material variability, for economic reasons, depends significantly on local availability; hence, there is no fixed rule for the amount/type of aggregates, cement, additions, and admixtures [6]. Therefore, a decisive factor for designing advanced cementitious materials, such as self-compacting concrete (SCC), is a clear understanding of each constituent raw material’s effect and interactions on the final product properties [7]. Additionally, the design and optimisation of such mixtures require intensive laboratory testing, particularly if new and unconventional supplementary cementitious materials or aggregates are incorporated [8], such as agricultural or industrial by-products [9]. Thus, a more scientific and multi-scale approach to mix-design is needed in which key mixture design variables can explain the composite properties [10].

The Design of Experiments (DoE) is a systematic approach to understanding how process and product parameters affect response variables, such as processability, physical properties, or product performance. DoE uses statistical methodology to analyse data and predict product property performance under all possible conditions within limits selected for the experimental design [10]. From a literature survey, the DoE approach [11] has shown promise for aiding the understanding of the effect of mixture parameters on key fresh and hardened SCC properties. It can also facilitate the test protocol required to optimise SCC [12] or quantify SCC mixtures’ robustness [6] to develop a more eco-friendly SCC that incorporates different types of SCM and meets multiple performance requirements [3,13,14,15,16,17,18,19,20,21].

Research Significance and Objectives

Previous research shows that statistical models and numerical optimisation techniques allow for finding the best combination of self-compacting high-strength concrete (SCHPC) constituents which (i) reduce the risk of cracking during the first days, ensuring a more impermeable concrete in the final structure [3]; (ii) study the influence of mixture parameters and their coupled effects on deformability, viscosity, compressive strength, resistivity and resistance to carbonation [15]; (iii) optimise chloride permeability and the strength of concrete containing metakaolin [22]; (iv) optimise the durability and service life of self-consolidating concrete containing metakaolin [19]; (v) optimise the mixture proportions and analyse the fresh and hardened properties [20]; and (vi) minimise the cost of the most unsustainable concrete components [21], including cost and sustainability indicators, in a reduced time [3,14,21,23]. These models and counterplot charts are beneficial for predicting and selecting the optimum mixture proportions for a given application simply and accurately.

From a materials science point of view, self-compacting and high early-strength concrete mixes may be challenging because they contradict mixture design requirements and fresh-state properties. For example, a low water/binder ratio (w/b) is key to achieving high early strength [24]. However, it may also impact self-compacting ability, which is very sensitive to Vw/Vp.

Maia [25] carried out a full central composite design on self-compacting high early-strength cement-based mortars (SCHSCM) based on key mixture design parameters and described the target engineering properties, namely, self-compacting ability and high early-age strength. The key five SCHSM mixture parameters chosen were [25]: (i) Vw/Vc—water to cement volume ratio; (ii) Sp/p—superplasticiser to powder mass ratio; (iii) Vw/Vp—water to powder volume ratio; (iv) Vs/Vm—sand to mortar volume ratio; and (v) Vfs/Vs—fine sand to total sand volume ratio to produce a total of 50 SCHSM mixtures. The current work aims at statistical analysis, model fitting, validation, and optimisation of the data experiments carried out by Maia [25]. As such, combining the statistical design methods and regression analysis allowed for creating a model to mathematically describe the flow ability, viscosity, and flexural and compressive strength of SCHSCM. The models obtained were validated and used to optimise self-compacting mixtures with additional high early-age strength. The goal was to develop SCHSM with a minimum slump flow of 250 mm, flow time of 10 s, and compressive strength of at least 50 MPa at 24 h without any special curing treatment.

The current work starts with a brief explanation of the data obtained by Maia [25] in Section 2. The model’s fitting and adequacy are detailed in Section 3, and Section 4 presents the optimisation of SCHSCM, considering the performance requirements established by the authors. Finally, Section 5 presents the main conclusions.

2. Central Composite Design

In general, the DoE involves the following key steps: (i) a choice of factors (mixture parameters), levels, and ranges; (ii) a selection of response variable(s); (iii) a choice of experimental design; (iv) performing the experiments; (v) a statistical analysis of the data (fitting a model); and (vi) other computations with response models. The current work focused on steps (iv) and (v). A brief explanation of the design adopted is presented in Section 2.1, and the output properties are discussed in Section 2.2.

2.1. Experiment Definition and Planning

The present work sought to analyse 50 mortar mixes published by Maia [25] using DoE, the statistical methodology to analyse data and predict properties. It was necessary to integrate simple and conventional statistical methods into the experimental design methodology to draw statistically sound conclusions from the experiment. Subsequently, the commercial software Design-Expert was employed in the current study to develop a polynomial regression model.

Maia’s data set [25] corresponds to a full central 2⁵ composite design augmented by 10 axial runs plus 8 central runs. It allows for the development of a polynomial regression model for each response variable as a function of the five design variables considered in that study (key factors): (i) Vw/Vc—water to cement volume ratio; (ii) Sp/p—superplasticiser to powder mass ratio; (iii) Vw/Vp—water to powder volume ratio; (iv) Vs/Vm—sand to mortar volume ratio; and (v) Vfs/Vs—fine sand to total sand volume ratio. In addition to the 50 mixes previously described, 14 extra mixes were produced to allow for comparing and validating the results of the response models. The effect of each key factor was evaluated at five levels −α, −1, 0, +1, and +α, as shown in Table 1. To make the design rotatable, the value of α was equal to n_F^1/4, where n_F is the number of points in the factorial part of the design. In the current study, this corresponds to α equal to 2.378.

Table 1. Correspondence between the coded values and actual values of the design variables.

Design Variables	−2.378	−1	0	+1	+2.378
X1: Vw/Vc	0.682	0.805	0.895	0.894	1.108
X2: Sp/p	0.019	0.022	0.024	0.025	0.029
X3: Vw/Vp	0.434	0.513	0.570	0.627	0.706
X4: Vs/Vm	0.366	0.432	0.480	0.528	0.594
X5: Vfs/Vs	0.043	0.250	0.400	0.550	0.757

The self-compacting mortars were produced with the following commercial materials available (in Portugal): (i) cement CEM I 42.5 R with a specific gravity of 3100 g/m³, (ii) limestone filler with a specific gravity of 2680 kg/m³, (iii) siliceous natural sands with a maximum particle size of 4 mm, specific gravity of 2620 kg/m³, and water absorption of 0.40%, (iv) fine siliceous sand with a maximum particle size of 2 mm, specific gravity of 2630 kg/m³, and water absorption of 0.20%, and (v) a polycarboxylate based superplasticiser with a specific gravity of 1080 kg/m³ and solid content of 40% [25].

Four dependent variables (i.e., response variables) were considered: (i) slump-flow diameter (D-flow); (ii) the time in the V-funnel (T-funnel); (iii) flexural strength at 24 h, determined by the three-point loading method (F,24 h); and (iv) uniaxial compressive strength at 24 h (Rc,24 h). Table 2 summarises the response variables and is followed by a brief explanation of the measurement procedures to access the dependent variables.

Table 2. Response variable summary.

Response Variables	Units	Measurement Method
Y1: D-flow	mm	EFNARC
Y2: T-funnel	s	EFNARC
Y3: F,24 h	MPa	EN 196-1
Y4: Rc,24 h	MPa	EN-196-1

Immediately after production, the (mini) slump flow was assessed following the procedures of EFNARC [26]. The procedure consists, in brief, in filling the mini cone with the fresh composite and then taking the cone off and observing the flow capacity on a plane surface. When the fresh composite stops moving, two perpendicular diameters are measured, and the average value is considered the flow diameter (D-flow) in mm.

Additionally, the V-funnel test was performed to assess the viscosity and passing ability using the mini funnel according to EFNARC [26]. In brief, the fresh composite was poured into the funnel after production. Then, the trap door was opened, allowing the fresh composite to flow out under gravity, and the time for the discharge to complete (the flow time), i.e., when light is seen from above through the funnel, was recorded. These results showed a typical trend of an increase in slump-flow diameter with a reduction in flow time. After fresh tests, three specimens 40 × 40 × 160 {mm³} were moulded. The specimens were demoulded at 24 h, and the mechanical strength was assessed following EN 196-1 [27].

2.2. Results

The experimental results obtained by Maia concerning the D-flow, T-funnel, F,24 h, and Rc,24 h response variables used for model fitting (Section 3.2) are presented in Table 3, as well as 14 validation points (Vi). The D-flow results presented in Table 3 correspond to the average of the two results obtained by Maia [25]. The F,24 h corresponds to an average of three results for each CCD mortar point, and the Rc,24 h is the average of six results, based on Maia [25].

Table 3. The mixture proportion (coded values) and experimental results obtained by Maia [25] and used for model fitting and validation points.

CCD Point	Coded Values					Results
	Vw/Vc	Sp/p	Vw/Vp	Vs/Vm	Vfs/Vs	D-Flow	T-Funnel	F,24 h	Rc,24 h
						(mm)	(s)	(MPa)	(MPa)
C1	0.00	0.00	0.00	0.00	0.00	346.50	14.98	11.77	59.89
C2	0.00	0.00	0.00	0.00	0.00	346.00	13.77	12.29	62.10
C3	0.00	0.00	0.00	0.00	0.00	339.50	14.15	11.28	59.31
C4	0.00	0.00	0.00	0.00	0.00	348.00	14.74	12.08	60.90
C5	0.00	0.00	0.00	0.00	0.00	339.50	14.53	11.96	60.00
C6	0.00	0.00	0.00	0.00	0.00	341.00	14.38	11.89	62.17
C7	0.00	0.00	0.00	0.00	0.00	345.00	13.56	11.05	60.18
C8	0.00	0.00	0.00	0.00	0.00	344.50	14.23	11.03	59.63
F1	−1.00	−1.00	−1.00	−1.00	−1.00	330.00	18.89	11.60	72.54
F2	1.00	−1.00	−1.00	−1.00	−1.00	349.00	12.26	11.05	57.80
F3	−1.00	1.00	−1.00	−1.00	−1.00	338.50	16.70	12.64	70.09
F4	1.00	1.00	−1.00	−1.00	−1.00	354.50	11.32	10.50	56.06
F5	−1.00	−1.00	1.00	−1.00	−1.00	375.00	9.24	11.26	67.05
F6	1.00	−1.00	1.00	−1.00	−1.00	369.50	7.08	9.43	55.72
F7	−1.00	1.00	1.00	−1.00	−1.00	376.00	7.80	10.60	68.47
F8	1.00	1.00	1.00	−1.00	−1.00	375.00	6.91	10.18	53.40
F9	−1.00	−1.00	−1.00	1.00	−1.00	253.00	114.06	11.68	73.13
F10	1.00	−1.00	−1.00	1.00	−1.00	289.50	38.91	11.64	58.49
F11	−1.00	1.00	−1.00	1.00	−1.00	260.50	74.32	10.48	71.81
F12	1.00	1.00	−1.00	1.00	−1.00	289.50	33.03	10.91	59.30
F13	−1.00	−1.00	1.00	1.00	−1.00	295.00	25.40	11.83	67.80
F14	1.00	−1.00	1.00	1.00	−1.00	313.50	17.53	11.41	55.93
F15	−1.00	1.00	1.00	1.00	−1.00	303.50	26.33	11.41	68.43
F16	1.00	1.00	1.00	1.00	−1.00	320.00	14.15	10.93	56.48
F17	−1.00	−1.00	−1.00	−1.00	1.00	300.00	28.43	11.06	66.54
F18	1.00	−1.00	−1.00	−1.00	1.00	351.50	12.89	10.69	55.93
F19	−1.00	1.00	−1.00	−1.00	1.00	334.50	17.67	11.57	69.59
F20	1.00	1.00	−1.00	−1.00	1.00	349.50	11.73	10.73	55.10
F21	−1.00	−1.00	1.00	−1.00	1.00	378.00	9.90	11.20	65.92
F22	1.00	−1.00	1.00	−1.00	1.00	379.50	7.16	9.93	54.52
F23	−1.00	1.00	1.00	−1.00	1.00	385.50	8.54	10.71	64.39
F24	1.00	1.00	1.00	−1.00	1.00	382.00	6.94	10.26	53.64
F25	−1.00	−1.00	−1.00	1.00	1.00	233.00	*	12.10	67.34
F26	1.00	−1.00	−1.00	1.00	1.00	275.00	52.64	11.42	55.30
F27	−1.00	1.00	−1.00	1.00	1.00	265.50	67.34	12.79	68.54
F28	1.00	1.00	−1.00	1.00	1.00	285.00	33.30	10.48	56.02
F29	−1.00	−1.00	1.00	1.00	1.00	289.50	26.20	11.98	65.12
F30	1.00	−1.00	1.00	1.00	1.00	315.00	16.51	10.98	53.39
F31	−1.00	1.00	1.00	1.00	1.00	309.00	18.57	11.88	60.96
F32	1.00	1.00	1.00	1.00	1.00	314.00	17.07	10.66	53.41
CC1	−2.38	0.00	0.00	0.00	0.00	168.00	*	11.91	78.42
CC2	2.38	0.00	0.00	0.00	0.00	342.00	11.55	10.25	48.92
CC3	0.00	−2.38	0.00	0.00	0.00	330.50	17.64	11.45	62.44
CC4	0.00	2.38	0.00	0.00	0.00	337.00	12.71	11.22	58.89
CC5	0.00	0.00	−2.38	0.00	0.00	295.00	79.63	12.11	64.13
CC6	0.00	0.00	2.38	0.00	0.00	368.50	7.27	10.18	63.04
CC7	0.00	0.00	0.00	−2.38	0.00	398.00	7.49	9.43	59.77
CC8	0.00	0.00	0.00	2.38	0.00	169.50	*	10.32	62.62
CC9	0.00	0.00	0.00	0.00	−2.38	338.00	16.55	Na	62.21
CC10	0.00	0.00	0.00	0.00	2.38	330.50	16.14	Na	57.75
V1	0.63	3.05	0.21	0.52	−2	16.17	320.50	11.70	58.45
V2	0.63	1.5	0.21	0.52	−2	16.58	327.00	11.09	60.53
V3	0.63	1.5	0.21	0.52	−2.67	18.33	310.50	11.17	61.54
V4	−0.13	0.21	−0.66	−0.62	0.00	12.96	353.00	12.02	61.33
V5	1.08	−0.42	−1.13	−0.62	0.00	14.09	337.50	11.47	56.70
V6	−1.34	0.52	−0.14	−0.62	0.00	14.15	347.00	10.35	70.59
V7	−0.82	0.58	−0.39	−0.62	0.00	13.64	338.50	9.68	65.96
V8	0.57	−0.15	−0.92	−0.62	0.00	13.02	335.00	11.16	59.11
V9	−0.13	−0.42	−0.66	−0.62	0.00	14.76	350.00	13.29	63.51
V10	−0.13	−0.42	−0.66	−0.62	0.00	15.01	344.50	11.14	65.16
V11	1.08	−0.42	−1.13	−0.62	0.00	14.32	346.50	11.76	57.25
V12	−1.34	0.52	−0.14	−0.62	0.00	15.65	344.50	13.97	72.63
V13	−0.82	0.58	−0.39	−0.62	0.00	15.26	345.50	13.12	68.96
V14	0.57	−0.15	−0.92	−0.62	0.00	15.08	347.50	Na	59.54

* impossible to measure; Na—non-available result.

3. Response Models

3.1. Test Results Analysis

Table 4 presents the statistical summaries of all the experimental results obtained (Table 3) and the eight central point’s results only. The perception of the coefficient of variation on the central points (Ci) and all CCD points (all Ci, Fi, and CCi) predicts a good fit for the D-flow, T-funnel, and Rc,24 h. On the other hand, good fits are not expected for F,24 h given that the coefficient of variation evaluated on the central points (4.16%) is close to the coefficient of variation assessed on the 50 points of the CCD (6.93%).

Table 4. The main statistics for all CCD points and central points.

	D-Flow (mm)	T-Funnel (s)	F,24 h (MPa)	Rc,24 h (MPa)
All 50 mixtures
Minimum	168.00	6.91	9.43	48.92
Maximum	398.00	114.06	12.79	78.42
Mean	323.31	22.39	11.17	61.61
Standard deviation	48.97	21.63	0.77	6.24
Coefficient of variation (%)	15.15	96.62	6.93	10.14
Central points (Ci)
Minimum	339.50	13.56	11.03	59.31
Maximum	348.00	14.98	12.29	62.17
Mean	343.75	14.29	11.67	60.52
Standard deviation	3.31	0.47	0.48	1.10
Coefficient of variation (%)	0.96	3.31	4.16	1.81

3.2. Model Fitting

Design-Expert software was used to assist in analysing the results for each response variable by examining summary plots of the data; fitting a model using regression analysis and ANOVA; validating the model by examining the residuals for trends and outliers, leverage points, autocorrelation, and violation of statistical assumptions, in general; and interpreting the model graphically. A significance level of 5% was used throughout. A detailed description of this procedure is presented in Section 3.2 to Section 3.5. The central composite design adopted allows for estimating a full quadratic model, as shown in Equation (1) [28,29].

$$Y={\beta }_0+{\displaystyle \sum }_{i=1}^k{\beta }_i{X}_i+{\displaystyle \sum }_{i=1}^k{\beta }_{ii}{X}_i^2+{\displaystyle \sum }_{i<j}{\displaystyle \sum }{\beta }_{ij}{X}_i{X}_j+\epsilon$$

(1)

where Y represents the response variable; X_i corresponds to the design variables considered; β is used for model parameters (β₀ is the independent term, β_i represents the linear effect of X_i, β_ii represents the quadratic effect of X_i, and β_ij represents the linear-by-linear interaction between X_i and X_j); and ε is the fitting error. The model parameters (β₀, β_i, and β_ij) can be estimated through multilinear regression analysis. In the course of the analysis, some of the terms in Equation (1) may not be significant. The results of the fitting procedure for the four response variables are summarised in Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12. The model generated with all observed values for D-flow and T-funnel resulted in a significant lack of fit. This fact led to the withdrawal of the axial runs for the D-flow results and also the inclusion of one term (Sp/p) × (Vfs/Vs) in the model because the term was considered the most significant among those excluded, due to its low p-value (0.0574). In the case of the T-funnel model, in addition to applying the inverse transformation as a recommended Box–Cox transformation to the response, one observation was removed (F15 = 26.33, see Table 3). The F,24 h and Rc,24 h fitting considered all runs and resulted in a non-significant lack of fit.

3.3. D-Flow Model

For the D-flow model, the authors decided not to include the axial points (CC1, CC2, CC3, CC4, CC5, CC6, CC7, CC8, CC9, and CC10) because the D-flow values contained a wide range of spread flow diameters, as presented in Section 2.2, from 168 to 398 mm. The attempt to fit a quadratic model led to a significant lack of fit when axial runs were included, due essentially to non-linearities that a quadratic model is not able to explain. Moreover, axial points are associated with high Cook’s distances and leverage points. Further research should be put into finding a non-linear model for D-flow response.

Table 5 presents the ANOVA for D-flow data considering the aforementioned conditions. The reduced quadratic model is significant. Examining the magnitude of the effects, it can be perceived that Vs/Vm (factor X₄) and Vw/Vp (factor X₃) are dominant compared to Sp/p (factor X₂), Vw/Vc (factor X₁), and Vfs/Vs (factor X₅). The analysis of variance confirms the previous interpretation. In this case, Vw/Vc, Sp/p, Vw/Vp, and Vs/Vm are significant terms of the model, i.e., the main effects Vw/Vc, Sp/p, Vw/Vp, and Vs/Vm, and the second order effects, (Vw/Vc) × (Vw/Vp), (Vw/Vp) × (Vfs/Vs), and (Vw/Vc)², are those that most significantly influence the response Y₁: D-flow. The predicted R² of 0.9683 is in reasonable agreement with the adjusted R² of 0.9802 (i.e., the difference is less than 0.2). The coefficients of the estimated regression model for D-flow (in coded values) are presented in the second column of Table 6. Since the second-order effect (Vw/Vp) × (Vfs/Vs) is considered a significant factor, Vfs/Vs was added to the model. Furthermore, (Sp/p) × (Vfs/Vs) was forced to enter the model to avoid a significant lack of fit. Table 6 presents the model’s coefficients’ standard error and confidence intervals.

Table 5. ANOVA for the D-flow response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	59,008.65	11	5364.42	176.44	<0.0001
	Residual	851.29	28	30.4
	Total	59,859.94	39
Lack of Fit	Lack of Fit	774.79	21	36.89	3.38	0.0523
	Pure Error	76.5	7	10.93
Partial significance of each predictor variable	Vw/Vc	2547.2	1	2547.2	83.78	<0.0001
	Sp/p	670.7	1	670.7	22.06	<0.0001
	Vw/Vp	12,070.7	1	12,070.7	397.02	<0.0001
	Vs/Vm	39,025.2	1	39,025.2	1283.59	<0.0001
	Vfs/Vs	64.7	1	64.7	2.13	0.1558
	(Vw/Vc) × (Sp/p)	267.38	1	267.38	8.79	0.0061
	(Vw/Vc) × (Vw/Vp)	919.13	1	919.13	30.23	<0.0001
	(Vw/Vc) × (Vs/Vm)	309.38	1	309.38	10.18	0.0035
	(Sp/p) × (Vfs/Vs)	114.38	1	114.38	3.76	0.0626
	(Vw/Vp) × (Vfs/Vs)	285.01	1	285.01	9.37	0.0048
	(Vw/Vc)2	2734.89	1	2734.89	89.95	<0.0001

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Table 5. ANOVA for the D-flow response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	59,008.65	11	5364.42	176.44	<0.0001
	Residual	851.29	28	30.4
	Total	59,859.94	39
Lack of Fit	Lack of Fit	774.79	21	36.89	3.38	0.0523
	Pure Error	76.5	7	10.93
Partial significance of each predictor variable	Vw/Vc	2547.2	1	2547.2	83.78	<0.0001
	Sp/p	670.7	1	670.7	22.06	<0.0001
	Vw/Vp	12,070.7	1	12,070.7	397.02	<0.0001
	Vs/Vm	39,025.2	1	39,025.2	1283.59	<0.0001
	Vfs/Vs	64.7	1	64.7	2.13	0.1558
	(Vw/Vc) × (Sp/p)	267.38	1	267.38	8.79	0.0061
	(Vw/Vc) × (Vw/Vp)	919.13	1	919.13	30.23	<0.0001
	(Vw/Vc) × (Vs/Vm)	309.38	1	309.38	10.18	0.0035
	(Sp/p) × (Vfs/Vs)	114.38	1	114.38	3.76	0.0626
	(Vw/Vp) × (Vfs/Vs)	285.01	1	285.01	9.37	0.0048
	(Vw/Vc)2	2734.89	1	2734.89	89.95	<0.0001

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Table 6. D-flow model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	343.75	1.95	339.76	347.74
Vw/Vc	8.92	0.9747	6.93	10.92
Sp/p	4.58	0.9747	2.58	6.57
Vw/Vp	19.42	0.9747	17.43	21.42
Vs/Vm	−34.92	0.9747	−36.92	−32.93
Vfs/Vs	−1.42	0.9747	−3.42	0.5748
Vw/Vc × Sp/p	−2.89	0.9747	−4.89	−0.894
Vw/Vc × Vw/Vp	−5.36	0.9747	−7.36	−3.36
Vw/Vc × Vs/Vm	3.11	0.9747	1.11	5.11
Sp/p × Vfs/Vs	1.89	0.9747	−0.106	3.89
Vw/Vp × Vfs/Vs	2.98	0.9747	0.9877	4.98
(Vw/Vc)2	−20.67	2.18	−25.14	−16.21

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Table 6. D-flow model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	343.75	1.95	339.76	347.74
Vw/Vc	8.92	0.9747	6.93	10.92
Sp/p	4.58	0.9747	2.58	6.57
Vw/Vp	19.42	0.9747	17.43	21.42
Vs/Vm	−34.92	0.9747	−36.92	−32.93
Vfs/Vs	−1.42	0.9747	−3.42	0.5748
Vw/Vc × Sp/p	−2.89	0.9747	−4.89	−0.894
Vw/Vc × Vw/Vp	−5.36	0.9747	−7.36	−3.36
Vw/Vc × Vs/Vm	3.11	0.9747	1.11	5.11
Sp/p × Vfs/Vs	1.89	0.9747	−0.106	3.89
Vw/Vp × Vfs/Vs	2.98	0.9747	0.9877	4.98
(Vw/Vc)2	−20.67	2.18	−25.14	−16.21

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Figure 2a presents the normal probability plot of the model’s residuals. It is reasonable to consider that there are no relevant normality issues in the data. The plot of externally studentised residuals is presented in Figure 2b. One can notice an observation falls outside the −2 to +2 band, corresponding to the spreading diameter measurement of F5 with a value of 375 mm. It was decided to keep this observation since it did not constitute a leverage point, and the Cook’s distance was well below 50%.

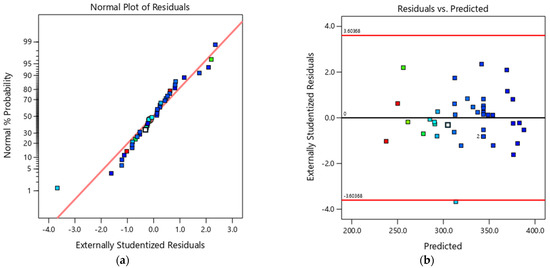
Figure 2. (a) Normal probability plot of the externally studentised residuals for the D-flow fitted model, and (b) plot of the externally studentised residuals versus D-flow predicted values.

3.4. T-Funnel Model

Regarding the T-funnel data, attempts to fit a quadratic model to all points lead to a severe lack of fit, potentially due to strong non-linearities. F15 exhibits an abnormal residual which compromises the fit; the following modelling steps exclude this point (see Figure 3).

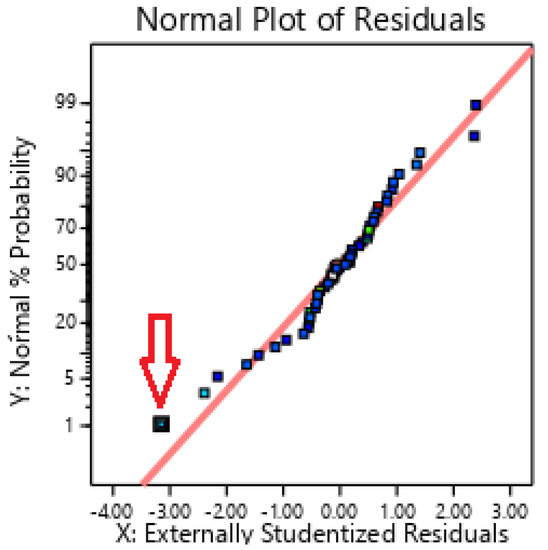
Figure 3. T-funnel results: F15 excluded (arrow).

The inverse transformation was applied to the T-funnel response, as found in previous works [3,14]. Examining the magnitude of the effects, it can be perceived that Vs/Vm (factor X₄) and Vw/Vp (factor X₃) are dominant compared to Sp/p (factor X₂), Vw/Vc (factor X₁), and Vfs/Vs (factor X₅), as obtained in the D-flow response (see Table 7). All five factors are significant, as well as three of the interactions and the other three s-order terms. The predicted R² of 0.9827 is in reasonable agreement with the adjusted R² of 0.9897, i.e., the difference is negligible.

Table 7. ANOVA results for the T-funnel response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	0.0640	11	0.0058	394.23	<0.0001
	Residual	0.0005	34	0
	Total	0.0645	45
Lack of Fit	Lack of Fit	0.0005	27	0	3.14	0.0607
	Pure Error	0	7	5.457 × 10−6
Partial significance of each predictor variable	Vw/Vc	0.0041	1	0.0039	305.22	<0.0001
	Sp/p	0.0010	1	0.0011	82.2	<0.0001
	Vw/Vp	0.0251	1	0.0243	1895.62	<0.0001
	Vs/Vm	0.0317	1	0.0271	2113.06	<0.0001
	Vfs/Vs	0.0001	1	0.0001	6.9	0.0131
	(Vw/Vc) × (Sp/p)	0.0001	1	0.0001	11.61	0.0018
	(Vw/Vc) × (Vs/Vm)	0.0004	1	0.0003	23.66	<0.0001
	(Vw/Vp) × (Vs/Vm)	0.0011	1	0.0009	73.86	<0.0001
	(Vw/Vc)2	0.0001	1	0.0001	6.79	0.0138
	(Vw/Vp)2	0.0001	1	0.0001	4.84	0.0351
	(Vfs/Vs)2	0.0001	1	0.0001	8.39	0.0067

The three most significant parameters are typed bold and the most significant term is also underlined.

Table 7. ANOVA results for the T-funnel response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	0.0640	11	0.0058	394.23	<0.0001
	Residual	0.0005	34	0
	Total	0.0645	45
Lack of Fit	Lack of Fit	0.0005	27	0	3.14	0.0607
	Pure Error	0	7	5.457 × 10−6
Partial significance of each predictor variable	Vw/Vc	0.0041	1	0.0039	305.22	<0.0001
	Sp/p	0.0010	1	0.0011	82.2	<0.0001
	Vw/Vp	0.0251	1	0.0243	1895.62	<0.0001
	Vs/Vm	0.0317	1	0.0271	2113.06	<0.0001
	Vfs/Vs	0.0001	1	0.0001	6.9	0.0131
	(Vw/Vc) × (Sp/p)	0.0001	1	0.0001	11.61	0.0018
	(Vw/Vc) × (Vs/Vm)	0.0004	1	0.0003	23.66	<0.0001
	(Vw/Vp) × (Vs/Vm)	0.0011	1	0.0009	73.86	<0.0001
	(Vw/Vc)2	0.0001	1	0.0001	6.79	0.0138
	(Vw/Vp)2	0.0001	1	0.0001	4.84	0.0351
	(Vfs/Vs)2	0.0001	1	0.0001	8.39	0.0067

The three most significant parameters are typed bold and the most significant term is also underlined.

The estimated coefficients of the regression model for the T-funnel (in coded values) are presented in the second column of Table 8. Additionally, Table 8 presents standard errors and confidence intervals. To check the regression assumptions on the residuals, a normal probability plot was examined in Figure 4a and other plots such as the one in Figure 4b. No outliers were detected, although F15 has been considered a leverage point. In the author’s view, this point does not considerably compromise the fitted model’s quality.

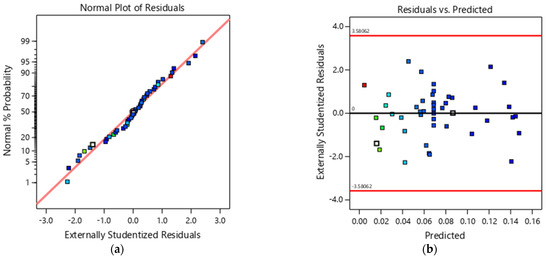
Figure 4. (a) Normal probability plot of the externally studentised residuals for the T-funnel fitted model, and (b) plot of the externally studentised residuals versus T-funnel fitted values.

Table 8. T-funnel model coefficients (coded values).

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	0.0688	0.0011	0.0667	0.071
Vw/Vc	0.0115	0.0007	0.0101	0.0129
Sp/p	0.005	0.0006	0.0038	0.0062
Vw/Vp	0.0248	0.0006	0.0236	0.026
Vs/Vm	−0.0302	0.0007	−0.0315	−0.0289
Vfs/Vs	−0.0016	0.0006	−0.0028	−0.0004
(Vw/Vc) × (Sp/p)	−0.002	0.0007	−0.0035	−0.0006
(Vw/Vc) × (Vs/Vm)	−0.0037	0.0007	−0.0051	−0.0022
(Vw/Vp) × (Vs/Vm)	−0.0061	0.0007	−0.0076	−0.0047
(Vw/Vc)2	−0.0017	0.0007	−0.0031	−0.0003
(Vw/Vp)2	0.0011	0.0005	0.0001	0.0021
(Vfs/Vs)2	−0.0014	0.0005	−0.0024	−0.0003

The three most significant parameters are typed bold and the most significant term is also underlined.

Table 8. T-funnel model coefficients (coded values).

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	0.0688	0.0011	0.0667	0.071
Vw/Vc	0.0115	0.0007	0.0101	0.0129
Sp/p	0.005	0.0006	0.0038	0.0062
Vw/Vp	0.0248	0.0006	0.0236	0.026
Vs/Vm	−0.0302	0.0007	−0.0315	−0.0289
Vfs/Vs	−0.0016	0.0006	−0.0028	−0.0004
(Vw/Vc) × (Sp/p)	−0.002	0.0007	−0.0035	−0.0006
(Vw/Vc) × (Vs/Vm)	−0.0037	0.0007	−0.0051	−0.0022
(Vw/Vp) × (Vs/Vm)	−0.0061	0.0007	−0.0076	−0.0047
(Vw/Vc)2	−0.0017	0.0007	−0.0031	−0.0003
(Vw/Vp)2	0.0011	0.0005	0.0001	0.0021
(Vfs/Vs)2	−0.0014	0.0005	−0.0024	−0.0003

The three most significant parameters are typed bold and the most significant term is also underlined.

3.5. Flexural Strength: F,24 h Model

No leverage points were found for the F,24 h model and the Cook’s distance was below 60%. Table 9 presents the ANOVA results for the F,24 h model. Examining the magnitude of the effects, it can be perceived that Vw/Vc (factor X₁), Vw/Vp (factor X₃), and Vs/Vm (factor X₄) are dominant compared to Sp/p (factor X₂) and Vfs/Vs (factor X₅). The analysis of variance confirms the previous interpretation. The quadratic model is significant. In this case, Vw/Vc, Vw/Vp, and Vs/Vm are significant terms of the model, i.e., the main effects Vw/Vc, Vw/Vp, and Vs/Vm, and the second order effects (Vw/Vp) × (Vs/Vm) and (Vs/Vm)² are those that most significantly influence the F,24 h response. The predicted R² of 0.5671 is in reasonable agreement with the adjusted R² of 0.6216 (i.e., the difference is less than 10%). Although R² did not reach a value close to 1, the model was considered useful for navigating the design space.

Table 9. ANOVA results for the F,24 h response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	18.65	5	3.73	16.44	<0.0008
	Residual	9.53	42	0.2269
	Total	28.18	47
Lack of Fit	Lack of Fit	7.88	35	0.2252	0.9574	0.5812
	Pure Error	1.65	7	0.2352
Partial significance of each predictor variable	Vw/Vc	7.11	1	7.11	31.36	<0.0001
	Vw/Vp	2.95	1	2.95	13.01	0.0008
	Vs/Vm	2.95	1	2.95	12.98	0.0008
	(Vw/Vp) × (Vs/Vm)	1.07	1	1.07	4.70	0.0358
	(Vs/Vm)2	4.57	1	4.57	20.16	<0.0001

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Table 9. ANOVA results for the F,24 h response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	18.65	5	3.73	16.44	<0.0008
	Residual	9.53	42	0.2269
	Total	28.18	47
Lack of Fit	Lack of Fit	7.88	35	0.2252	0.9574	0.5812
	Pure Error	1.65	7	0.2352
Partial significance of each predictor variable	Vw/Vc	7.11	1	7.11	31.36	<0.0001
	Vw/Vp	2.95	1	2.95	13.01	0.0008
	Vs/Vm	2.95	1	2.95	12.98	0.0008
	(Vw/Vp) × (Vs/Vm)	1.07	1	1.07	4.70	0.0358
	(Vs/Vm)2	4.57	1	4.57	20.16	<0.0001

The three most significant parameters are typed in bold, and the most significant term is also underlined.

The estimated values of the regression model coefficients in the coded values are presented in the second column of Table 10. Additionally, Table 10 presents standard errors and confidence intervals. Figure 5a presents the normal probability plot of the residuals of the observed values of flexural strength. The externally studentised residuals are presented in Figure 5b and show no strong evidence of violating the white noise assumptions of the remaining error in the regression model. It is reasonable to consider that there are no normality issues in the data.

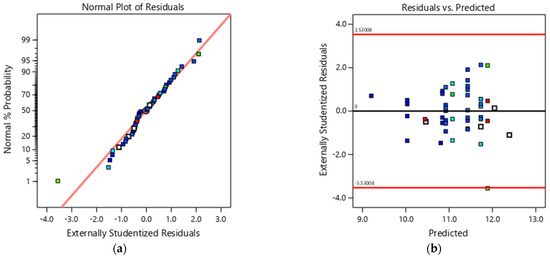
Figure 5. (a) Normal probability plot of the externally studentised residuals for the F,24 h fitted model, and (b) plot of the externally studentised residuals versus F,24 h fitted values.

Table 10. F,24 h model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	11.43	0.0893	11.25	11.61
Vw/Vc	−0.4053	0.0724	−0.5513	−0.2592
Vw/Vp	−0.261	0.0724	−0.4071	−0.115
Vs/Vm	0.2608	0.0724	0.1147	0.4068
(Vw/Vp) × (Vs/Vm)	0.1826	0.0842	0.0127	0.3525
(Vs/Vm)2	−0.2834	0.0631	−0.4108	−0.156

Table 10. F,24 h model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	11.43	0.0893	11.25	11.61
Vw/Vc	−0.4053	0.0724	−0.5513	−0.2592
Vw/Vp	−0.261	0.0724	−0.4071	−0.115
Vs/Vm	0.2608	0.0724	0.1147	0.4068
(Vw/Vp) × (Vs/Vm)	0.1826	0.0842	0.0127	0.3525
(Vs/Vm)2	−0.2834	0.0631	−0.4108	−0.156

3.6. Compressive Strength: Rc,24 h Model

Table 11 presents the ANOVA results for Rc,24 h. Examining the magnitude of the effects, it can be perceived that Vw/Vc (factor X₁), Vw/Vp (factor X₃), and Vfs/Vs (factor X₅) are dominant compared to Sp/p (factor X₂). The reduced quadratic model is significant (p < 0.0001) and there is no lack of fit. The analysis of variance confirms the previous interpretation: Vw/Vc, Vw/Vp, and Vfs/Vs are significant terms of the model, i.e., the main effects Vw/Vc, Vw/Vp, and Vfs/Vs, the second order effects (Vs/Vm) × (Vfs/Vs), (Vw/Vc)², and (Vw/Vp)², are those that most significantly influence the response Rc,24 h. In addition, the predicted R² of 0.9326 is reasonably close to the adjusted R².

Table 11. ANOVA results for the Rc,24 h response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	1850.32	10	185.03	119.74	<0.0001
	Residual	60.26	39	1.35
	Cor Total	1910.58	49
Lack of Fit	Lack of Fit	51.87	32	1.62	1.35	0.3599
	Pure Error	8.40	7	1.20
Partial significance of each predictor variable	Vw/Vc	1650.75	1	1650.75	879.84	<0.0001
	Sp/p	5.37	1	5.37	3.48	0.698
	Vw/Vp	61.35	1	61.35	39.70	<0.0001
	Vs/Vm	3.05	1	3.05	1.98	0.1677
	Vfs/Vs	76.06	1	76.06	49.22	<0.0001
	(Vw/Vc) × (Vw/Vp)	6.08	1	6.08	3.93	0.0545
	(Vw/Vc) × (Vfs/Vs)	7.09	1	7.09	4.59	0.0385
	(Vs/Vm) × (Vfs/Vs)	7.79	1	7.79	5.04	0.0305
	(Vw/Vc)2	18.43	1	18.43	11.93	0.0013
	(Vw/Vp)2	17.44	1	17.44	11.29	0.0018

The three most significant parameters are typed in bold, and the most significant term is also underlined.

Table 11. ANOVA results for the Rc,24 h response.

Test for	Source	Sum of Squares	Degrees of Freedom	Mean of Square	F-Value	p-Value
Significance of Regression	Model	1850.32	10	185.03	119.74	<0.0001
	Residual	60.26	39	1.35
	Cor Total	1910.58	49
Lack of Fit	Lack of Fit	51.87	32	1.62	1.35	0.3599
	Pure Error	8.40	7	1.20
Partial significance of each predictor variable	Vw/Vc	1650.75	1	1650.75	879.84	<0.0001
	Sp/p	5.37	1	5.37	3.48	0.698
	Vw/Vp	61.35	1	61.35	39.70	<0.0001
	Vs/Vm	3.05	1	3.05	1.98	0.1677
	Vfs/Vs	76.06	1	76.06	49.22	<0.0001
	(Vw/Vc) × (Vw/Vp)	6.08	1	6.08	3.93	0.0545
	(Vw/Vc) × (Vfs/Vs)	7.09	1	7.09	4.59	0.0385
	(Vs/Vm) × (Vfs/Vs)	7.79	1	7.79	5.04	0.0305
	(Vw/Vc)2	18.43	1	18.43	11.93	0.0013
	(Vw/Vp)2	17.44	1	17.44	11.29	0.0018

The three most significant parameters are typed in bold, and the most significant term is also underlined.

The estimated values of the coefficients of the regression model that will be used to predict Rc,24 h in the coded values are presented in the second column of Table 12. Additionally, Table 12 shows the standard errors and confidence intervals. Figure 6a illustrates the normal probability plot of the residuals of the observed compressive strength values. It is reasonable to consider that there are no normality issues in the data. An example plot of the residuals against the predicted values is presented in Figure 6b. There is no evidence of assumption violation regarding the regression model fit.

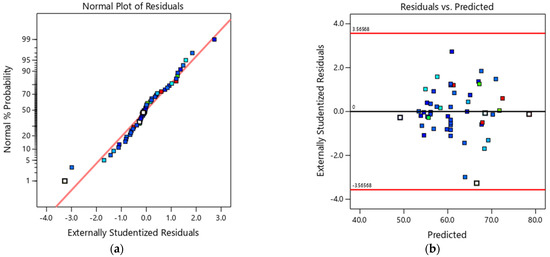
Figure 6. (a) Normal probability plot of the externally studentised residuals for the Rc,24 h fitted model, and (b) plot of the externally studentised residuals versus Rc,24 h fitted values.

The subsequent diagnostics include the identification of possible outliers in the regression or observations that could be leverage points. Points with a Cook’s distance higher than 1.0 or high leverage were not found (see Figure 7).

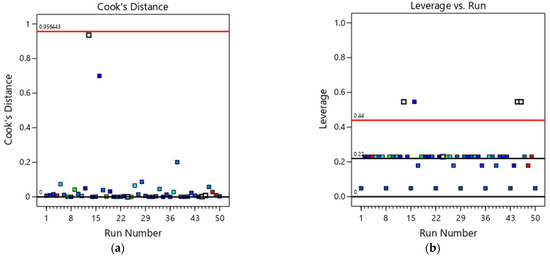
Figure 7. Rc,24 h: (a) Cook’s distance and (b) leverage.

Table 12. Rc,24 h model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	60.65	0.2733	60.09	61.2
Vw/Vc	−6.17	0.1889	−6.56	−5.79
Sp/p	−0.3522	0.1889	−0.7342	0.0299
Vw/Vp	−1.19	0.1889	−1.57	−0.8081
Vs/Vm	0.2655	0.1889	−0.1165	0.6476
Vfs/Vs	−1.33	0.1889	−1.71	−0.9431
(Vw/Vc) × (Vw/Vp)	0.4357	0.2197	−0.0088	0.8802
(Vw/Vc) × (Vfs/Vs)	0.4706	0.2197	0.0261	0.9151
(Vs/Vm) × (Vfs/Vs)	−0.4934	0.2197	−0.9379	−0.049
(Vw/Vc)2	0.5639	0.1633	0.2336	0.8941
(Vw/Vp)2	0.5486	0.1633	0.2183	0.8788

Table 12. Rc,24 h model coefficients in terms of coded values.

Factor	Coefficient Estimate	Standard Error	95% CI Low	95% CI High
Intercept	60.65	0.2733	60.09	61.2
Vw/Vc	−6.17	0.1889	−6.56	−5.79
Sp/p	−0.3522	0.1889	−0.7342	0.0299
Vw/Vp	−1.19	0.1889	−1.57	−0.8081
Vs/Vm	0.2655	0.1889	−0.1165	0.6476
Vfs/Vs	−1.33	0.1889	−1.71	−0.9431
(Vw/Vc) × (Vw/Vp)	0.4357	0.2197	−0.0088	0.8802
(Vw/Vc) × (Vfs/Vs)	0.4706	0.2197	0.0261	0.9151
(Vs/Vm) × (Vfs/Vs)	−0.4934	0.2197	−0.9379	−0.049
(Vw/Vc)2	0.5639	0.1633	0.2336	0.8941
(Vw/Vp)2	0.5486	0.1633	0.2183	0.8788

3.7. Significant Individual and Interaction Effects

The final models (in terms of coded factors) are illustrated in Figure 8 regarding the relative impact of each factor by comparing the corresponding coefficient with the remaining (higher values of the estimated coefficient indicate the higher influence of the design variable in the response). The sign (positive or negative) of the estimated coefficient is marked on each bar’s label. We recall that a positive coefficient means that the response (or transformed response) variable will increase if the given mixture parameter increases and vice-versa.

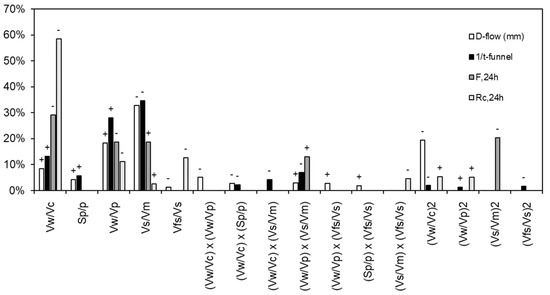
Figure 8. Influence of each factor on fresh state responses, in which (+) Positive effect in response models; (−) Negative effect in response model (see Table 13).

The response surfaces corresponding to the two main effects for each response of the mixtures are illustrated in Figure 9. For the D-flow and the T-funnel variation, the most significant factor is the volume of sand concerning the mortar (Vs/Vm) and the content of water/fines factors (Vw/Vp). In addition, it was possible to confirm the great influence of the water/cement factor (Vw/Vc) on the flexural (F,24 h) and compressive strength (Rc,24 h) of the mortars. In the order of inversely proportional influence, there is the fine sand concerning medium sand (Vfs/Vs) and the content of water/fines factors (Vw/Vp). The other factors have a smaller influence on the responses, exhibiting smaller estimated coded coefficients.

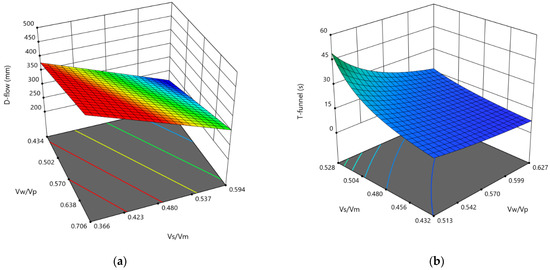
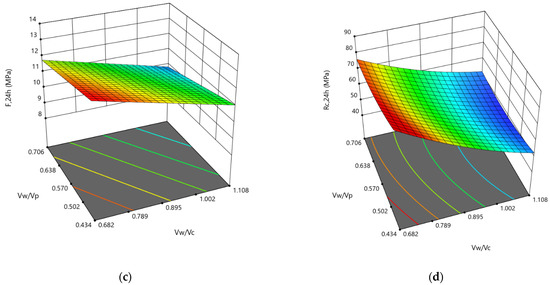
Figure 9. Effect of the Vs/Vm and Vw/Vp ratios on (a) D-flow and (b) T-funnel; effect of Vw/Vc and Vw/Vp on (c) F,24 h and (d) Rc,24 h.

The equations in terms of actual factors can be used to predict the response for the given levels of each factor (Table 13 and Figure 10). Uncertainty in the fitted models (confidence interval in Table 6, Table 8, Table 10 and Table 12) is provided for a 95% confidence level.

Table 13. Final equations in terms of actual factors: estimated coefficients.

Model Terms	D-Flow (mm)	1/(T-Funnel) (s)	F,24 h (MPa)	Rc,24 h (MPa)
Independent	−2154.81	−1.3582	5.400	293.77
Vw/Vc	5375.51	1.2092	−4.529	−257.75
Sp/p	15,060.05	13.4743	-	−186.47
Vw/Vp	1141.35	1.1255	−36.616	−289.80
Vs/Vm	−1375.32	1.4119	85.487	32.94
Vfs/Vs	−365.99	0.0374	-	−7.31
(Vw/Vc) × (Vw/Vp)	−1050.80	-	-	85.43
(Vw/Vc) × (Sp/p)	−17,105.24	−12.0954	-	-
(Vw/Vc) × (Vs/Vm)	723.96	−0.8550	-	-
(Vw/Vp) × (Vs/Vm)	-	−2.2390	66.741	-
(Vw/Vp) × (Vfs/Vs)	349.05	-	-	35.06
(Sp/p) × (Vfs/Vs)	6673.75	-	-	-
(Vs/Vm) × (Vfs/Vs)	-	-	-	−68.53
(Vw/Vc)2	−2581.92	−0.2148	-	70.43
(Vw/Vp)2	-	0.3375	-	168.84
(Vs/Vm)2	-	-	−123.018	-
(Vfs/Vs)2	-	−0.0602	-	-

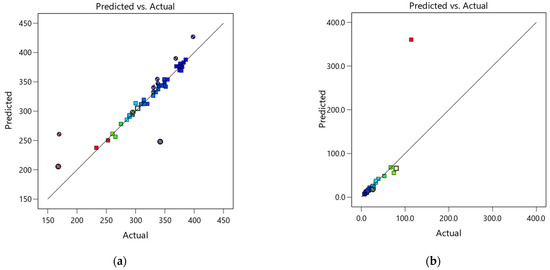
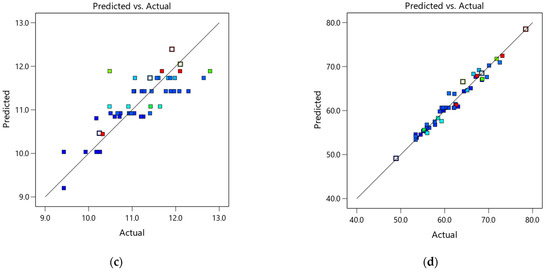
Figure 10. Predicted versus actual plan: (a) D-flow, (b) T-funnel, (c) F,24 h, and (d) Rc,24 h.

3.8. Models Validation

In order to validate the statistical models presented in Table 13, Maia [25] produced more than 14 SCHSCM mixtures and performed the experiments described in Section 2. The mixture proportion (in coded values) for these mixtures is presented in the last 14 lines of Table 3. The experimental results obtained and the estimated results given by the regression models are illustrated in Figure 11, including the x = y diagonals. The ratio between the predicted-to-measured values ranges from 0.84 to 1.20. The most accurate predictions are given by the Rc,24 h and D-flow models, where predicted-to-measured values range from 0.96 to 1.02 and 0.92 to 1.05, respectively. In addition, as expected, the flexural strength obtained results that exhibited higher dispersions when compared to the other results.

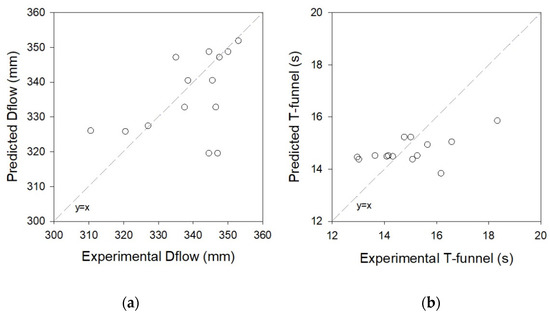
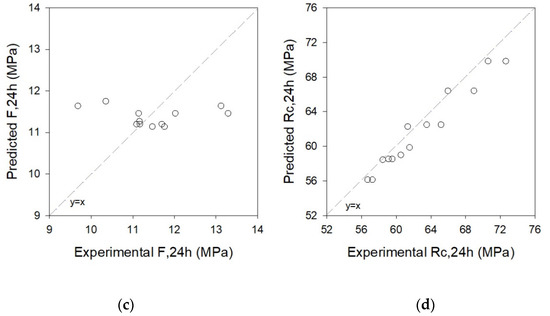
Figure 11. Predicted versus measured: (a) D-flow; (b) T-funnel; (c) F,24 h, and (d) Rc,24 h.

4. Optimisation

The empirical models obtained for modelling and predicting the relevant SCHSM properties were also used for mixture optimisation purposes. The optimisation module in Design-Expert studied in this paper searches for a combination of factor levels that simultaneously satisfy the goals established for each response and factor (see Table 14). The procedure uses the desirability function (D), and the solutions with D ≥ 0.995 were considered optimal. The optimisation was developed in two different scenarios, as follows in Section 4.1 and Section 4.2.

Table 14. Optimisation criteria.

	Self-Compacting Ability	Self-Compacting Ability and High Early Strength
Constraints for optimisation
Mixture parameters:
Vw/Vc	In CCD range	In CCD range
Sp/p	In CCD range	In CCD range
Vw/Vp	In CCD range	In CCD range
Vs/Vm	In CCD range	In CCD range
Vfs/Vs	In CCD range	In CCD range
Response Variables:
D-flow (mm)	Target 260	In range {259, 261}
T-funnel (s)	Target 10	In range {9.8, 10.2}
F,24 h (MPa)	None	None
Rc,24 h (MPa)	None	>50

4.1. Self-Compacting Ability

The first optimisation scenario was to find mortar mixtures with self-compacting ability. The self-compacting ability was translated by targeting optimisation restrictions of a D-flow = 260 mm and a T-funnel = 10 s. This optimisation problem is defined in the second column of Table 14 and is entitled “self-compacting ability”. The importance level for all constraints, both mixture parameters and response variables, was kept the same. The optimisation aimed only to obtain solutions within the CCD region. Thus, the constraint conditions for mixture parameters were “In CCD range”.

In total, 68 mixture SCHSM solutions were found with D ≥ 0.995 in the region $1.069 \le \mathrm{Vw}/\mathrm{Vc}\le 1.108$; $0.019 \le \mathrm{Sp}/\mathrm{p}\le 0.029$; $0.446\le \mathrm{Vs}/\mathrm{Vm}\le 0.525$; $0.540\le \mathrm{Vw}/\mathrm{Vp}\le 0.706$; and $0.088\le \mathrm{Vsf}/\mathrm{Vs}\le 0.731$.

4.2. SCC with High Early Strength

The second optimisation scenario was intended to discover self-compacting and high early strength mixtures simultaneously (see the third column of Table 14, entitled “self-compacting ability and high early strength”). For that, the optimisation conditions were: D-flow in the range from 259 to 261 mm, T-funnel in the range from 9.8 to 10.2 s, and compressive strength higher than 50 MPa at 24 h. The importance level for all constraints, both mixture parameters and response variables were kept the same. The optimisation aimed only to obtain solutions within the CCD region; thus, the constraint conditions for mixture parameters were “In CCD range”.

The best combination of SCHSM mixture parameters was: Vc/Vp = 1.098; sp/p = 0.0243; Vw/Vp = 0.607; Vs/Vm = 0.478; and Vfs/vs = 0.047. The corresponding estimated properties and their 95% confidence interval are presented in Table 15.

Table 15. Estimated SCHSM properties of the optimised mixture.

Response	Predicted Results	95% CI Low	95% CI High
D-flow	259.15	237.78	280.51
T-funnel	9.87	9.1	10.79
F,24 h	10.31	9.93	10.7
Rc,24 h	50.00	46.86	53.14

5. Conclusions

The current study investigates the effect of SCHSCM mixture design variables. It selects the best combination of powder materials (in a binary mixture of Portland cement + MTCK), water/binder ratio, superplasticiser dosage, and aggregates to reach optimum values of self-compactability and high early-age strength. As such, the DoE approach was followed to obtain regression models that could describe and predict the relevant engineering properties. In addition, regression models were used for optimisation purposes. The following main conclusions were drawn:

-

Regression models were found to be adequate to describe SCHSCM properties over the experimental region, namely, slump-flow diameter, T-funnel time, and flexural and compressive strength at 24 h;

-

The Vs/Vm factor exhibited the strongest (negative) effect on the slump-flow diameter and T-funnel time;

-

The Vw/Vp factor was found to have the most significant effect on mechanical strength, corresponding to response variables F,24 h and Rc,24 h;

-

Vw/Vc was the second most influencing factor, with a positive effect on the slump-flow diameter and T-funnel time and a negative effect on F,24 h and Rc,24 h;

-

The variation of Sp/p used in the current CCD was small compared to the remaining factors. As such, Sp/p exhibited the lowest influence on SCHSCM properties when compared to other mixture parameters;

-

The proposed optimal mixture represented the best compromise between self-compacting ability—a flow diameter of 250 mm and funnel time equal to 10 s—and a compressive strength higher than 50 MPa at 24 h without any special curing treatment and was found for Vc/Vp = 1.098; sp/p = 0.0243; Vw/Vp = 0.607; Vs/Vm = 0.478; and Vfs/vs = 0.047.

Even though transposing the mortar study into SCC is out of the scope of the manuscript, SCC mixtures can be obtained by fixing the mortar mix proportions given in Section 4.2 and adding a coarse aggregate. However, tests on the concrete level are needed to optimise the aggregate skeleton. Moreover, based on regression models, contour plots or interaction diagrams can be computed and simplify the test protocol required to optimise a given SCC mixture, namely, to select the combination of powder materials with admixtures. In particular, they can help to compare the efficiency of different admixtures and alternative SCM. Optimised mortar mixtures can serve as reference mixtures in a quality control plan to detect variations in different deliveries of constituent materials, such as cement, filler, or superplasticiser. The derived models can also be useful to predict mortar properties when the material properties change, such as the cement source.

The procedure presented in this work can easily be implemented in any concrete laboratory of a production centre since it involves mortar tests which are easy to carry out with simple tests and equipment.