Novel Incremental Conductance Feedback Method with Integral Compensator for Maximum Power Point Tracking: A Comparison Using Hardware in the Loop
Abstract
1. Introduction
2. Review of PV Model and MPPT Control Methods
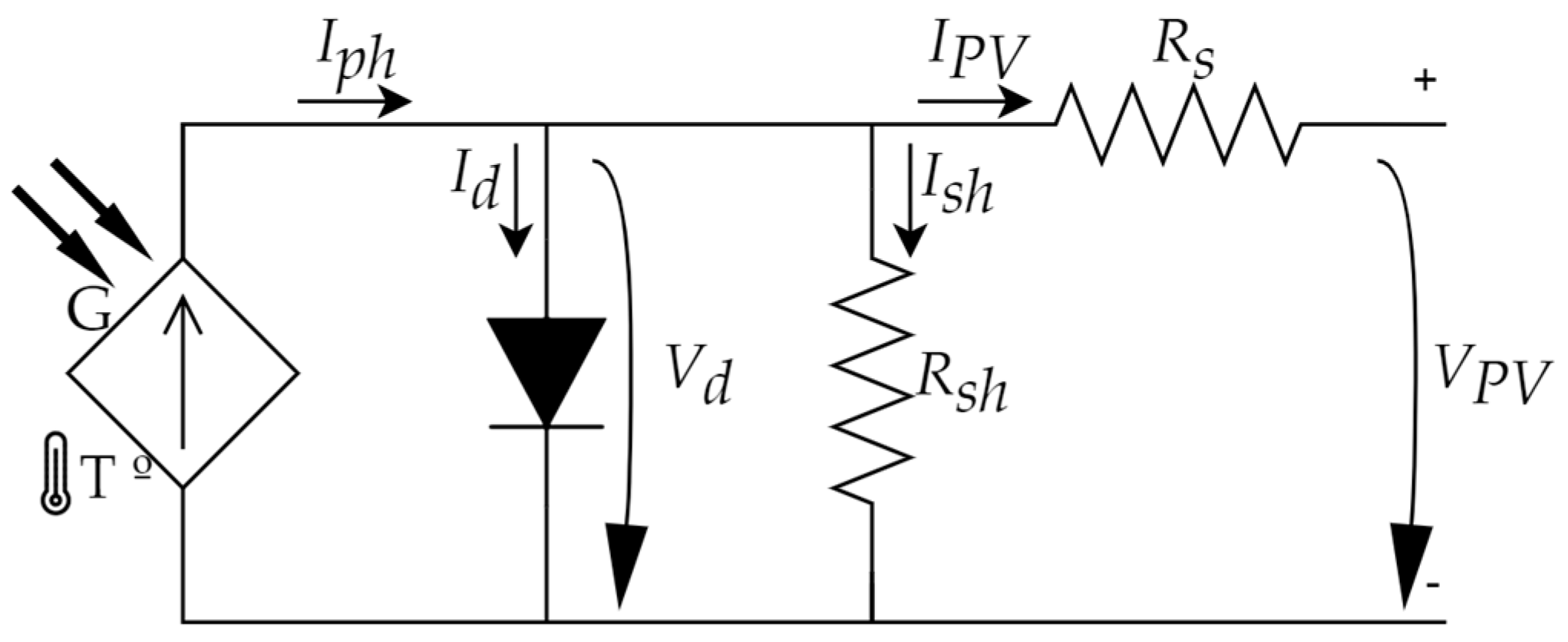
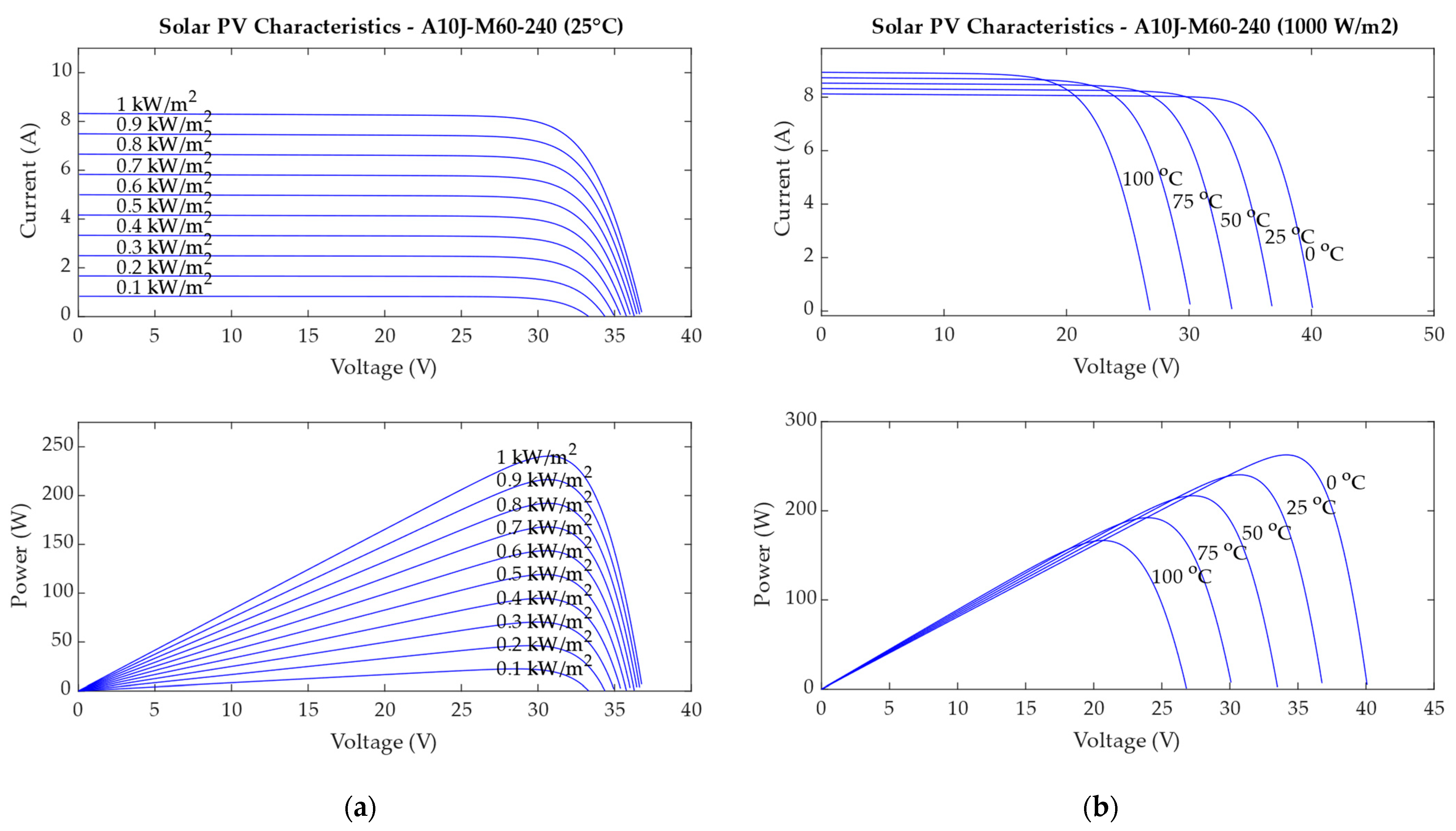
2.1. Mathematical Model of Solar Panels
- —the short circuit current under Standard Test Conditions (STC) (model first parameter)
- —the short circuit temperature coefficient
- —the cell temperature
- —the reference temperature (298.15 K)
- —solar irradiance
- —solar irradiance STC
- —the diode saturation current (second parameter of the model)
- —the electron charge constant ()
- —the diode voltage
- —the ideal factor of the diode (third parameter of the model)
- —Boltzmann’s constant ()
- —the photovoltaic cell voltage
- —the photovoltaic cell current
- —the series resistance of the solar panel (fourth model parameter)
- —the parallel or shunt resistance of the solar panel (fifth model parameter).
2.2. Review of MPPT Control Methods
2.2.1. Perturb and Observe (P&O)
2.2.2. Incremental Conductance (INC)
2.2.3. Fuzzy Logic (FL)
2.2.4. Artificial Neural Network (ANN)
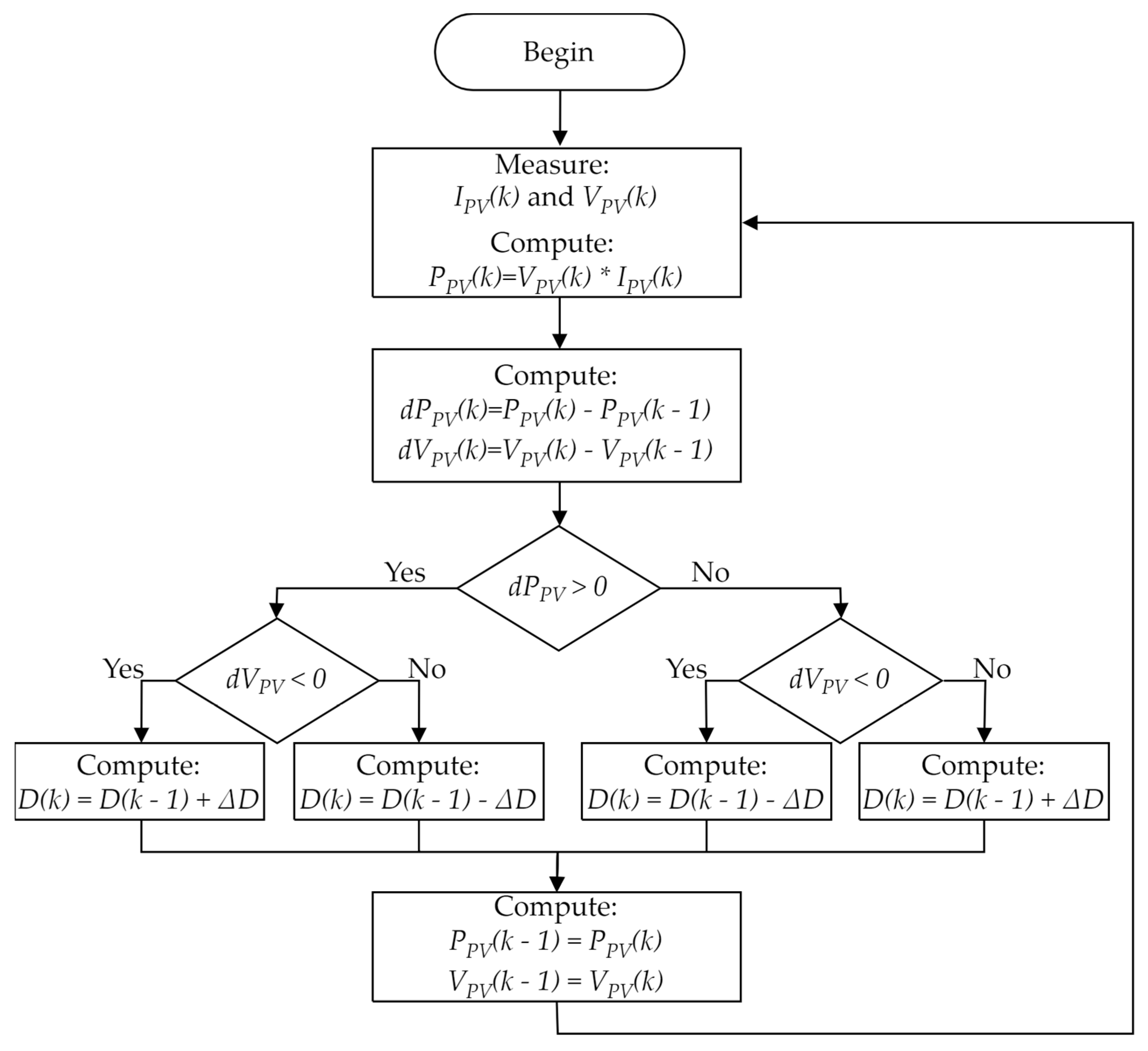
3. Incremental Conductance with Integral Compensator (IC-INC)
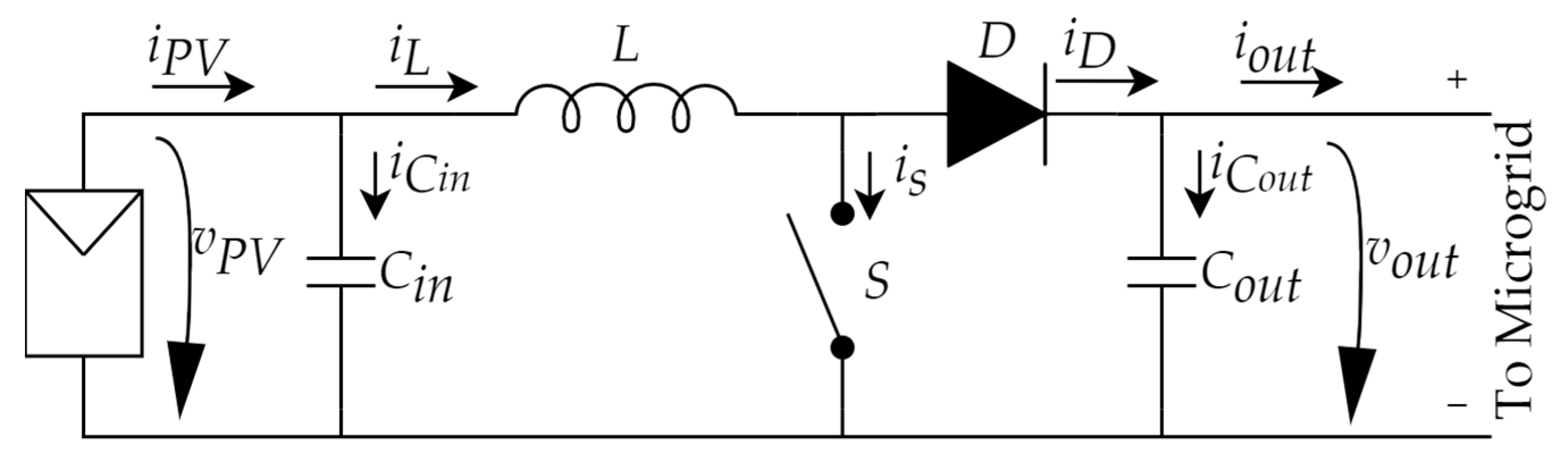
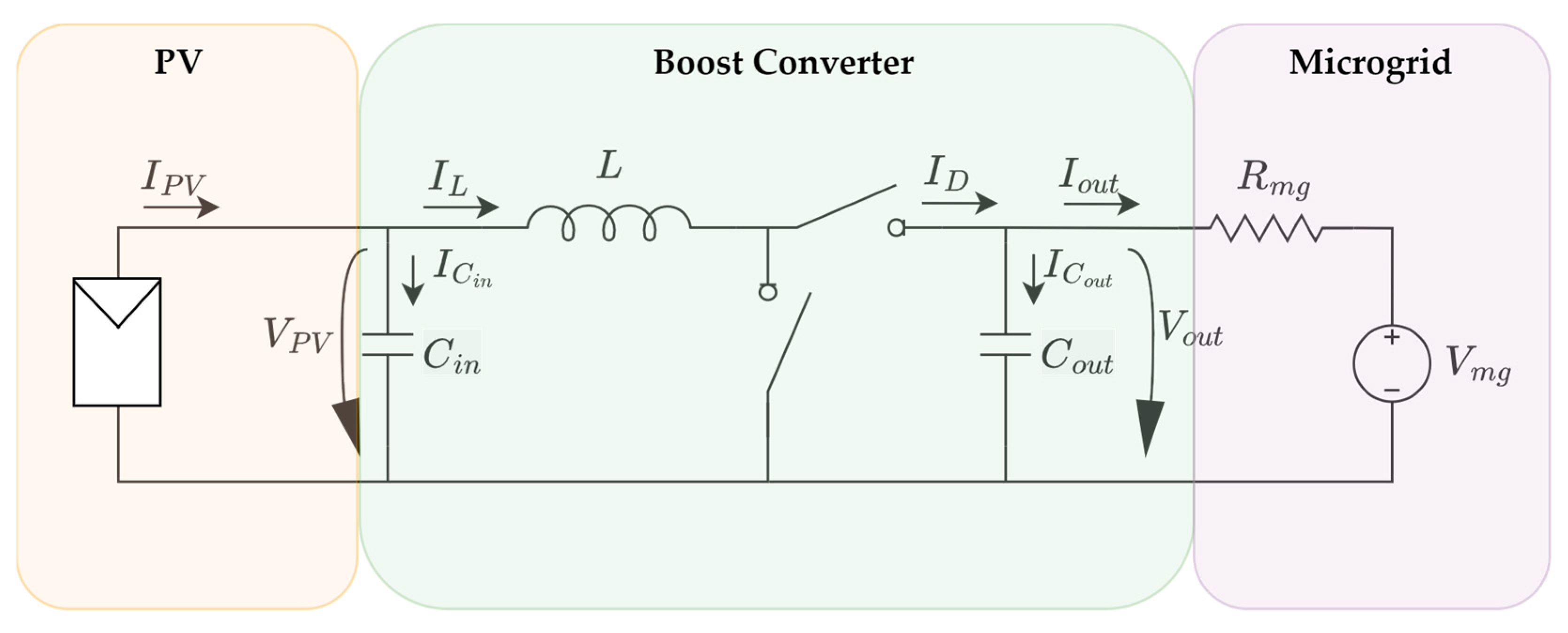
3.1. Converter Topology
3.2. IC-INC Method and Algorithm
3.3. Using the IC-INC Method to Train a Neural Network
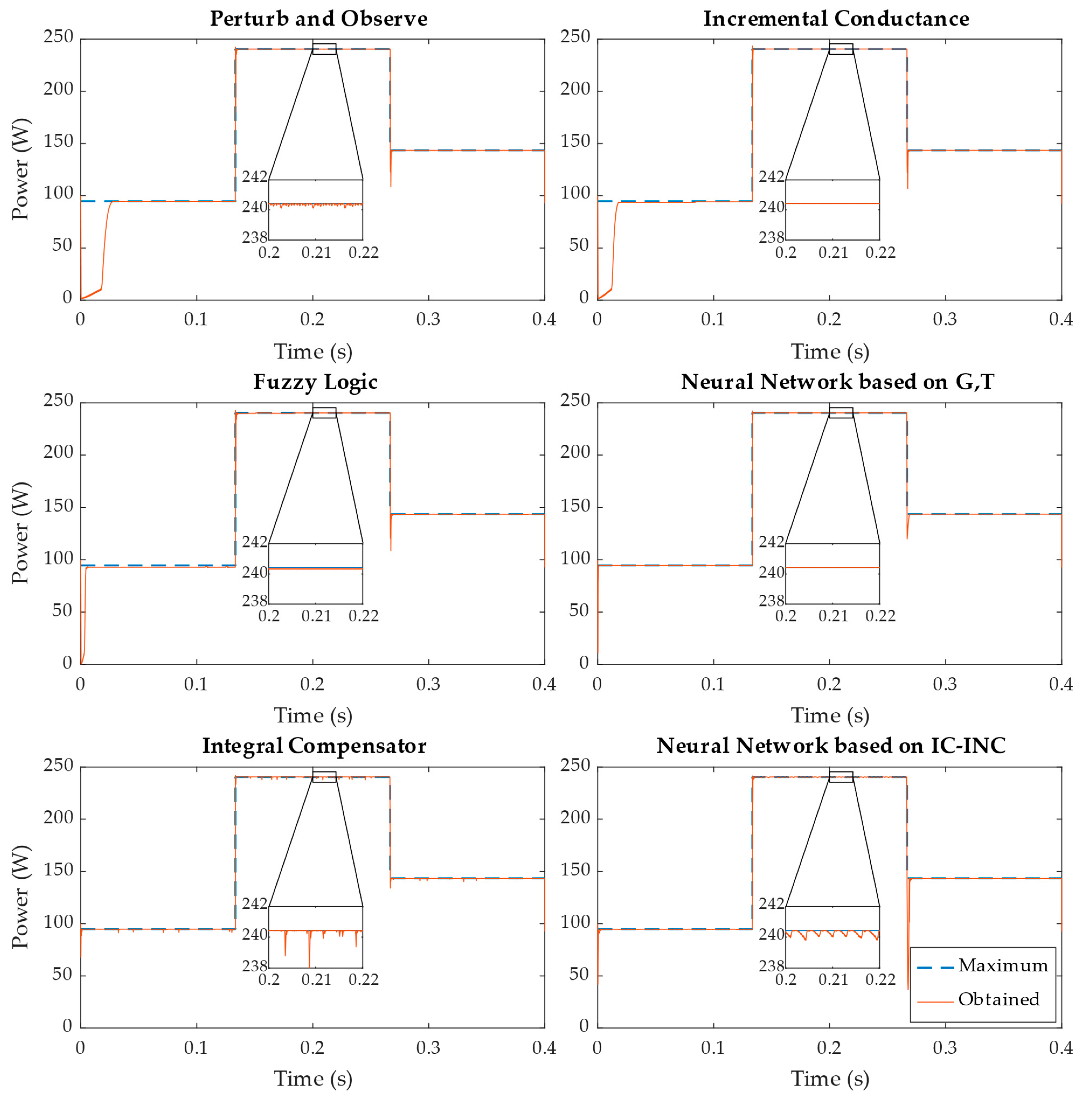
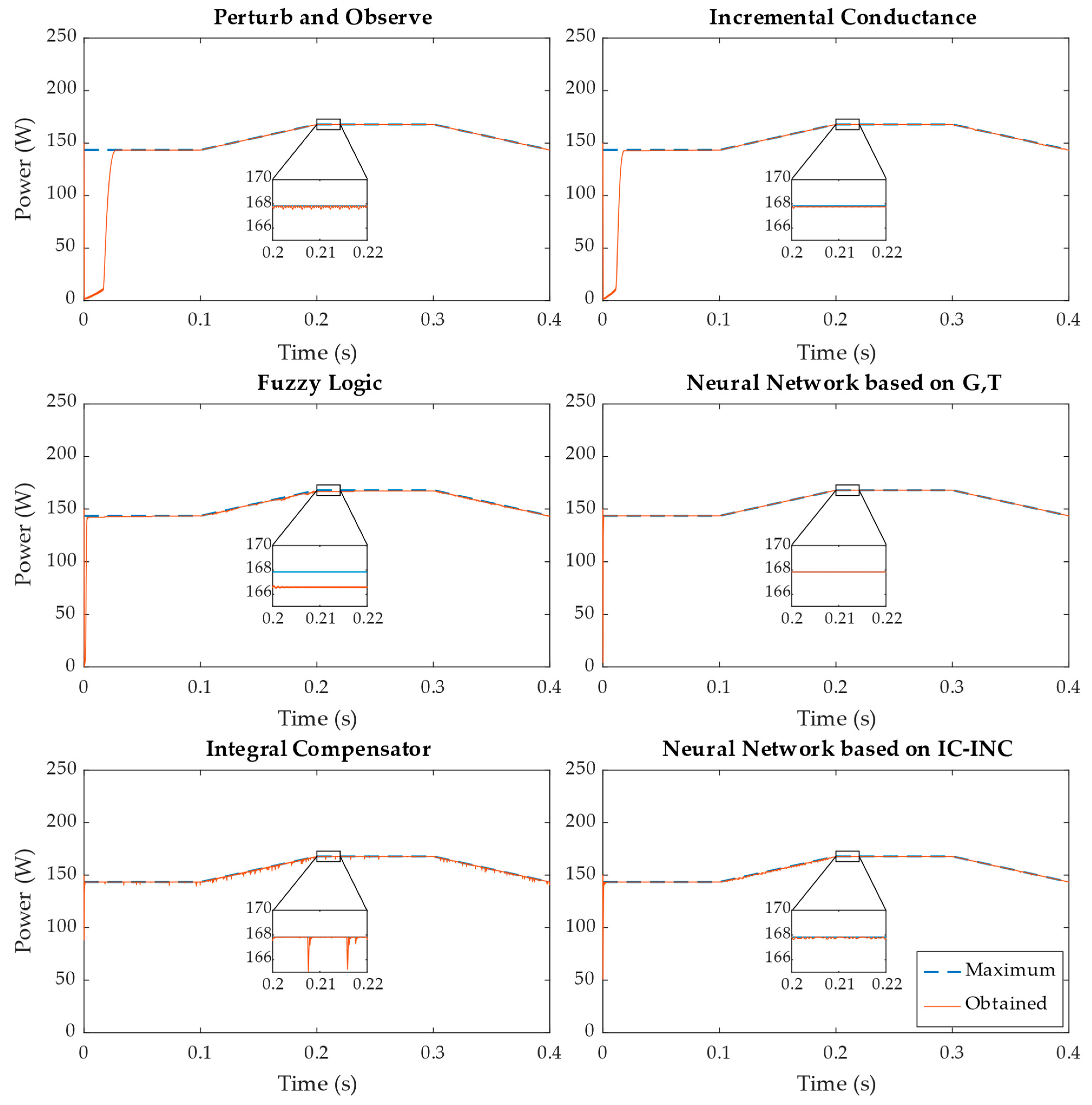
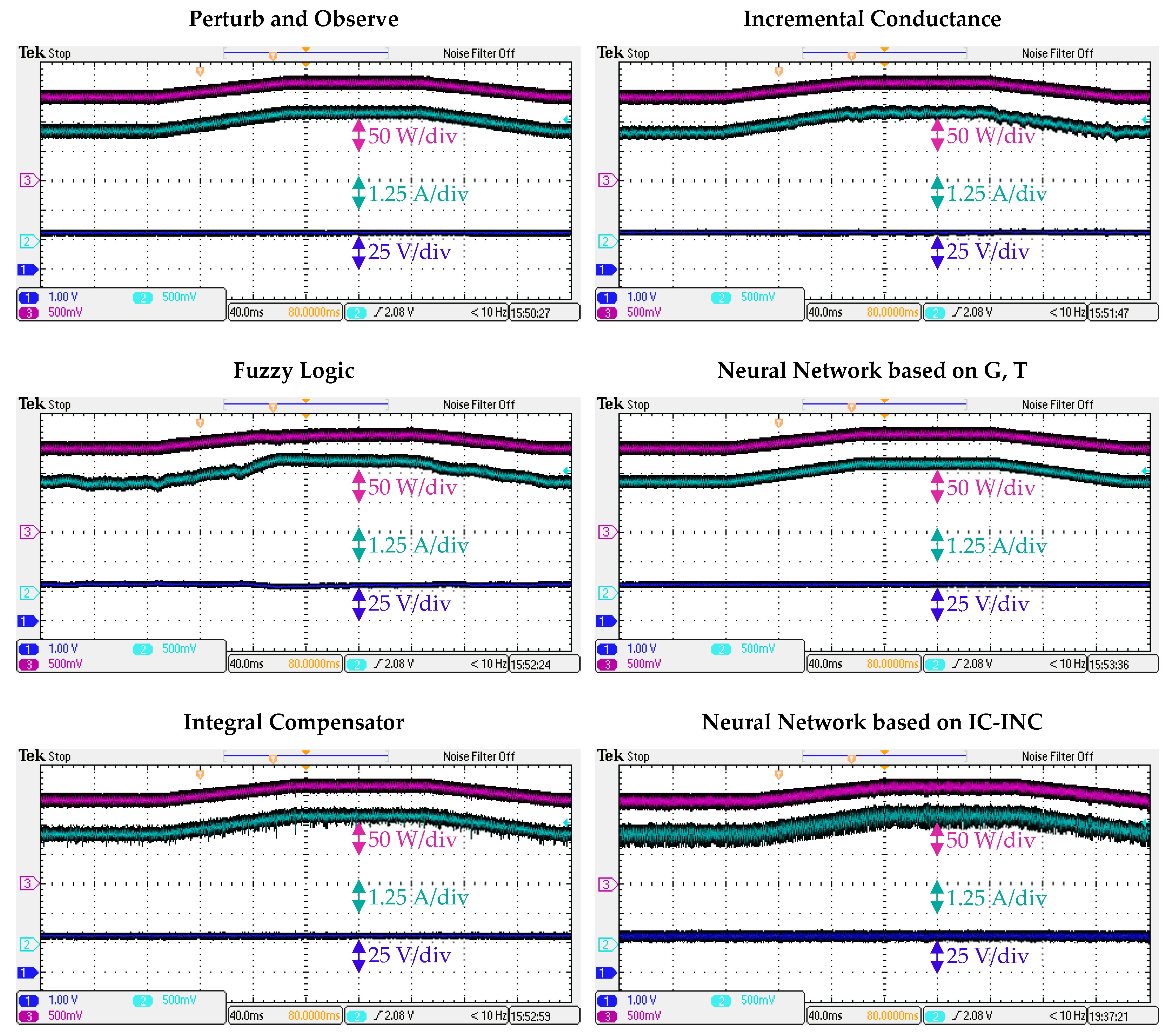
4. Results
4.1. Laboratory Setup
4.2. Test Results
4.3. Required Hardware Resources
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heidari, M. Improving Efficiency of Photovoltaic System by Using Neural Network MPPT and Predictive Control of Converter. Int. J. Renew. Energy Res. 2016, 6, 1524–1529. [Google Scholar]
- Ivanqui, J.; Voltolini, H.; Carlson, R.; Watanabe, E.H. “Pq Theory” Control Applied to Wind Turbine Trapezoidal PMSG under Symmetrical Fault. In Proceedings of the 2013 IEEE International Electric Machines and Drives Conference, IEMDC 2013, Chichago, IL, USA, 12–15 May 2013; pp. 534–540. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Y.; Yin, Y. Reliability of Wide Band Gap Power Electronic Semiconductor and Packaging: A Review. Energies 2022, 15, 6670. [Google Scholar] [CrossRef]
- Sun, F.; Wang, H.; Fu, F.; Li, X. Survey of FPGA Low Power Design. In Proceedings of the Proceedings of 2010 International Conference on Intelligent Control and Information Processing, ICICIP 2010, Dalian, China, 13–15 August 2010; pp. 547–550. [Google Scholar]
- Shiau, J.K.; Wei, Y.C.; Chen, B.C. A Study on the Fuzzy-Logic-Based Solar Power MPPT Algorithms Using Different Fuzzy Input Variables. Algorithms 2015, 8, 100–127. [Google Scholar] [CrossRef]
- Hassani, M.; Mekhilef, S.; Patrick Hu, A.; Watson, N.R. A Novel MPPT Algorithm for Load Protection Based on Output Sensing Control. In Proceedings of the International Conference on Power Electronics and Drive Systems, Singapore, 5–8 December 2011; pp. 1120–1124. [Google Scholar] [CrossRef]
- Derbeli, M.; Napole, C.; Barambones, O.; Sanchez, J.; Calvo, I.; Fernández-Bustamante, P. Maximum Power Point Tracking Techniques for Photovoltaic Panel: A Review and Experimental Applications. Energies 2021, 14, 7806. [Google Scholar] [CrossRef]
- Hanzaei, S.H.; Gorji, S.A.; Ektesabi, M. A Scheme-Based Review of MPPT Techniques with Respect to Input Variables Including Solar Irradiance and PV Arrays’ Temperature. IEEE Access 2020, 8, 182229–182239. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. Modified Perturb and Observe MPPT Algorithm for Drift Avoidance in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An Improved Perturb and Observe (P&O) Maximum Power Point Tracking (MPPT) Algorithm for Higher Efficiency. Appl. Energy 2015, 150, 97–108. [Google Scholar] [CrossRef]
- Kamran, M.; Mudassar, M.; Fazal, M.R.; Asghar, M.U.; Bilal, M.; Asghar, R. Implementation of Improved Perturb & Observe MPPT Technique with Confined Search Space for Standalone Photovoltaic System. J. King Saud Univ. Eng. Sci. 2020, 32, 432–441. [Google Scholar] [CrossRef]
- Nedumgatt, J.J.; Jayakrishnan, K.B.; Umashankar, S.; Vijayakumar, D.; Kothari, D.P. Perturb and Observe MPPT Algorithm for Solar PV Systems-Modeling and Simulation. In Proceedings of the 2011 Annual IEEE India Conference: Engineering Sustainable Solutions, INDICON-2011, Hyderabad, India, 16–18 December 2011. [Google Scholar] [CrossRef]
- Femia, N.; Granozio, D.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Predictive & Adaptive MPPT Perturb and Observe Method. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 934–950. [Google Scholar] [CrossRef]
- Putri, R.I.; Wibowo, S.; Rifa’i, M. Maximum Power Point Tracking for Photovoltaic Using Incremental Conductance Method. Energy Procedia 2015, 68, 22–30. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified Incremental Conductance MPPT Algorithm to Mitigate Inaccurate Responses under Fast-Changing Solar Irradiation Level. Solar Energy 2014, 101, 333–342. [Google Scholar] [CrossRef]
- Owusu-Nyarko, I.; Elgenedy, M.A.; Abdelsalam, I.; Ahmed, K.H.; Grandi, G.; Matas, J.; Ugalde-Loo, C.E. Modified Variable Step-Size Incremental Conductance MPPT for Photovoltaic Systems. Electronics 2021, 10, 2331. [Google Scholar] [CrossRef]
- Algarín, C.R.; Giraldo, J.T.; Álvarez, O.R. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. IC-Based Variable Step Size Neuro-Fuzzy MPPT Improving PV System Performances. Energy Procedia 2019, 157, 362–374. [Google Scholar] [CrossRef]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial Neural Network-Based Photovoltaic Maximum Power Point Tracking Techniques: A Survey. IET Renew. Power Gener. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Lopez-Guede, J.M.; Ramos-Hernanz, J.; Altın, N.; Ozdemir, S.; Kurt, E.; Azkune, G. Neural Modeling of Fuzzy Controllers for Maximum Power Point Tracking in Photovoltaic Energy Systems. J. Electron. Mater. 2018, 47, 4519–4532. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.G.; Loukriz, A.E. A New Neural Networks MPPT Controller for PV Systems. In Proceedings of the 2015 6th International Renewable Energy Congress, IREC 2015, Sousse, Tunisia, 24–26 March 2015. [Google Scholar] [CrossRef]
- Jyothy, L.P.N.; Sindhu, M.R. An Artificial Neural Network Based MPPT Algorithm for Solar PV System. In Proceedings of the 4th International Conference on Electrical Energy Systems, ICEES 2018, Chennai, India, 7–9 February 2018; pp. 375–380. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.C.; Lin, C.E. A Deep Reinforcement Learning-Based MPPT Control for PV Systems under Partial Shading Condition. Sensors 2020, 20, 3039. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Allam, D.; Ramachandaramurthy, V.K.; Etiba, M.B. A Novel Chaotic Flower Pollination Algorithm for Global Maximum Power Point Tracking for Photovoltaic System under Partial Shading Conditions. IEEE Access 2019, 7, 121432–121445. [Google Scholar] [CrossRef]
- Ram, J.P.; Pillai, D.S.; Jayan, V.; Shabunko, V.; Kim, Y.J.; Blaabjerg, F. A New Minimal Relocation Framework for Shade Mitigation in Photovoltaic Installations Using Flower Pollination Algorithm. IEEE J. Photovolt. 2022, 12, 888–897. [Google Scholar] [CrossRef]
- Sudhakar Babu, T.; Sangeetha, K.; Rajasekar, N. Voltage Band Based Improved Particle Swarm Optimization Technique for Maximum Power Point Tracking in Solar Photovoltaic System. J. Renew. Sustain. Energy 2016, 8, 013106. [Google Scholar] [CrossRef]
- Sangeetha, K.; Sudhakar Babu, T.; Rajasekar, N. Fireworks Algorithm-Based Maximum Power Point Tracking for Uniform Irradiation as Well as under Partial Shading Condition. In Proceedings of the Advances in Intelligent Systems and Computing; Springer Verlag: Berlin/Heidelberg, Germany, 2016; Volume 394, pp. 79–88. [Google Scholar]
- Ram, J.P.; Pillai, D.S.; Jang, Y.E.; Kim, Y.J. Reconfigured Photovoltaic Model to Facilitate Maximum Power Point Tracking for Micro and Nano-Grid Systems. Energies 2022, 15, 8860. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A.; Lozito, G.M.; Mancilla-David, F. Implementation of a Neural MPPT Algorithm on a Low-Cost 8-Bit Microcontroller. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2014, Ischia, Italy, 18–20 June 2014; pp. 977–981. [Google Scholar] [CrossRef]
- Messai, A.; Mellit, A.; Massi, P.A.; Guessoum, A.; Mekki, H. FPGA-Based Implementation of a Fuzzy Controller (MPPT) for Photovoltaic Module. Energy Convers. Manag. 2011, 52, 2695–2704. [Google Scholar] [CrossRef]
- Mellit, A.; Rezzouk, H.; Messai, A.; Medjahed, B. FPGA-Based Real Time Implementation of MPPT-Controller for Photovoltaic Systems. Renew Energy 2011, 36, 1652–1661. [Google Scholar] [CrossRef]
- Khaehintung, N.; Wiangtong, T.; Sirisuk, P. FPGA Implementation of MPPT Using Variable Step-Size P & O Algorithm for PV Applications. In Proceedings of the 2006 International Symposium on Communications and Information Technologies, ISCIT, Bangkok, Thailand, 18–20 October 2006; pp. 212–215. [Google Scholar]
- Bastos, J.L.; Figueroa, H.P.; Monti, A. FPGA Implementation of Neural Network-Based Controllers for Power Electronics Applications. In Proceedings of the Conference Proceedings—IEEE Applied Power Electronics Conference and Exposition—APEC, Dallas, TX, USA, 19–23 March 2006; Volume 2006, pp. 1443–1448. [Google Scholar]
- Hejri, M.; Mokhtari, H. On the Comprehensive Parametrization of the Photovoltaic (PV) Cells and Modules. IEEE J. Photovolt. 2017, 7, 250–258. [Google Scholar] [CrossRef]
- Implement PV Array Modules—Simulink. Available online: https://www.mathworks.com/help/sps/powersys/ref/pvarray.html (accessed on 23 February 2023).
- SolarHub—PV Module Details: A10J-M60-240—By A10Green Technology. Available online: http://www.solarhub.com/product-catalog/pv-modules/3320-A10J-M60-240-A10Green-Technology (accessed on 22 February 2023).
- Shongwe, S.; Hanif, M. Comparative Analysis of Different Single-Diode PV Modeling Methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Dadkhah, J.; Niroomand, M. Optimization Methods of MPPT Parameters for PV Systems: Review, Classification, and Comparison. J. Mod. Power Syst. Clean Energy 2021, 9, 225–236. [Google Scholar] [CrossRef]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the Perturb-and-Observe and Incremental Conductance Mppt Methods for PV Systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Kumar, M.; Kapoor, S.R.; Nagar, R.; Verma, A. Comparison between IC and Fuzzy Logic MPPT Algorithm Based Solar PV System Using Boost Converter. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2015, 4, 4927–4939. [Google Scholar] [CrossRef]
- Zečevič, Ž.; Rolevski, M. Neural Network Approach to MPPT Control and Irradiance Estimation. Appl. Sci. 2020, 10, 5051. [Google Scholar] [CrossRef]
- Nunes, I.; Danilo, S.; Spatti, H.; Andrade, R.; Luisa, F.; Liboni, H.B.; Franco, S.; Alves, R. Artificial Neural Networks A Practical Course; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
- Irmak, E.; Güler, N. A Model Predictive Control-Based Hybrid MPPT Method for Boost Converters. Int. J. Electron. 2020, 107, 1–16. [Google Scholar] [CrossRef]
- Sabry, A.H.; Shallal, A.H.; Hameed, H.S.; Ker, P.J. Compatibility of Household Appliances with DC Microgrid for PV Systems. Heliyon 2020, 6, e05699. [Google Scholar] [CrossRef] [PubMed]
- Generate HDL Code from Simscape Models in Simscape FPGA HIL Workflows—MATLAB & Simulink. Available online: https://www.mathworks.com/help/simscape/ug/generate-hdl-code-using-the-simscape-hdl-workflow-advisor.html (accessed on 22 February 2023).










| Fuzzy Rule | S(k) | |||||
|---|---|---|---|---|---|---|
| NB | NS | ZE | PS | PB | ||
| ΔS(k) | NB | ZE | PB | PS | ZE | NB |
| NS | PB | PS | ZE | ZE | NB | |
| ZE | PB | PS | ZE | NS | NB | |
| PS | PB | ZE | ZE | NS | NB | |
| PB | PB | ZE | NS | NB | ZE | |
| Parameter | Value |
|---|---|
| Voc (PV open circuit voltage) | 36.84 V |
| Isc (PV short circuit current) | 8.32 A |
| VMPP (PV MPP voltage) | 30.72 V |
| IMPP (PV MPP current) | 7.83 A |
| PMPP (PV MPP power) | 240.54 W |
| L (inductor) | 300 µH |
| Cin (input capacitor) | 150 µF |
| Cout (output capacitor) | 150 µF |
| fsw (switching frequency) | 50 kHz |
| Vmg (microgrid voltage) | 48 V |
| Rmg (microgrid resistance) | 50 mΩ |
| Algorithm | Step Variation | Fast Variation | Slow Variation | Steady State * |
|---|---|---|---|---|
| P&O | 97.03% | 97.14% | 95.58% | 99.98% |
| INC | 97.85% | 98.01% | 96.96% | 99.91% |
| FL | 99.03% | 99.08% | 99.20% | 99.87% |
| ANN (G, T) | 99.94% | 100.00% | 99.96% | 100.00% |
| IC-INC | 99.95% | 99.67% | 99.89% | 99.97% |
| ANN (IC-INC) | 99.67% | 98.50% | 99.86% | 99.94% |
| Algorithm | Step Variation | Fast Variation | Slow Variation | Steady State |
|---|---|---|---|---|
| P&O | 98.36% | 98.94% | 99.11% | 99.04% |
| INC | 99.21% | 98.98% | 99.04% | 99.17% |
| FL | 99.14% | 98.81% | 98.64% | 99.12% |
| ANN (G, T) | 97.88% | 98.55% | 99.06% | 97.95% |
| IC-INC | 98.54% | 98.92% | 99.10% | 99.23% |
| ANN (IC-INC) | 97.86% | 98.66% | 99.36% | 99.12% |
| Algorithm | LUTs (218,600) | F7 Muxes (109,300) | F8 Muxes (54,650) | DSPs (900) |
|---|---|---|---|---|
| P&O | 1.08% | 0.01% | 0.00% | 0.22% |
| INC | 2.48% | 0.01% | 0.00% | 0.00% |
| FL | 5.92% | 2.02% | 1.67% | 0.89% |
| ANN (G, T) | 28.38% | 0.08% | 0.02% | 11.78% |
| IC-INC | 2.53% | 0.00% | 0.00% | 0.44% |
| ANN (IC-INC) | 63.76% | 0.08% | 0.02% | 30.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
André, S.; Silva, F.; Pinto, S.; Miguens, P. Novel Incremental Conductance Feedback Method with Integral Compensator for Maximum Power Point Tracking: A Comparison Using Hardware in the Loop. Appl. Sci. 2023, 13, 4082. https://doi.org/10.3390/app13074082
André S, Silva F, Pinto S, Miguens P. Novel Incremental Conductance Feedback Method with Integral Compensator for Maximum Power Point Tracking: A Comparison Using Hardware in the Loop. Applied Sciences. 2023; 13(7):4082. https://doi.org/10.3390/app13074082
Chicago/Turabian StyleAndré, Sérgio, Fernando Silva, Sónia Pinto, and Pedro Miguens. 2023. "Novel Incremental Conductance Feedback Method with Integral Compensator for Maximum Power Point Tracking: A Comparison Using Hardware in the Loop" Applied Sciences 13, no. 7: 4082. https://doi.org/10.3390/app13074082
APA StyleAndré, S., Silva, F., Pinto, S., & Miguens, P. (2023). Novel Incremental Conductance Feedback Method with Integral Compensator for Maximum Power Point Tracking: A Comparison Using Hardware in the Loop. Applied Sciences, 13(7), 4082. https://doi.org/10.3390/app13074082






