Failure Modelling of CP800 Using Acoustic Emission Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Flow Behaviour
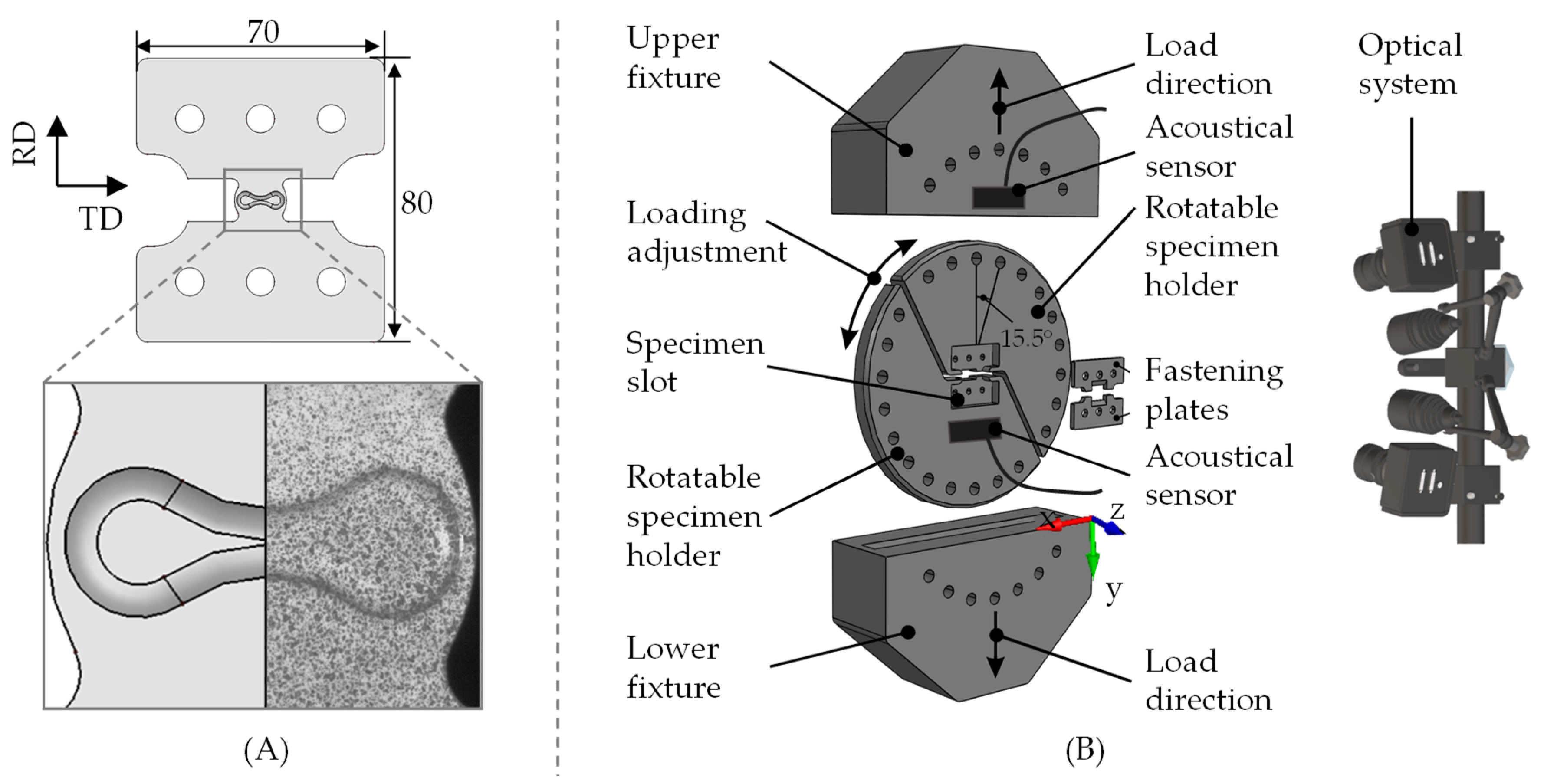
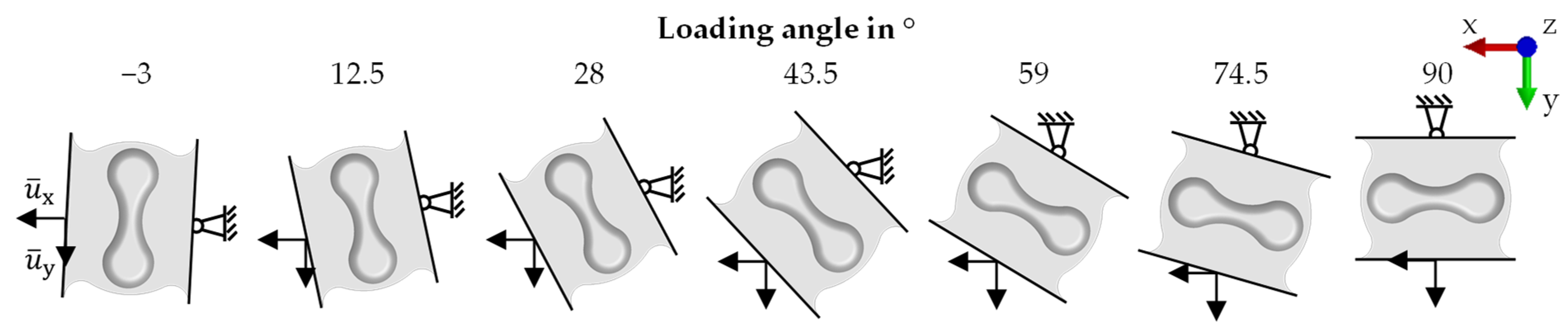
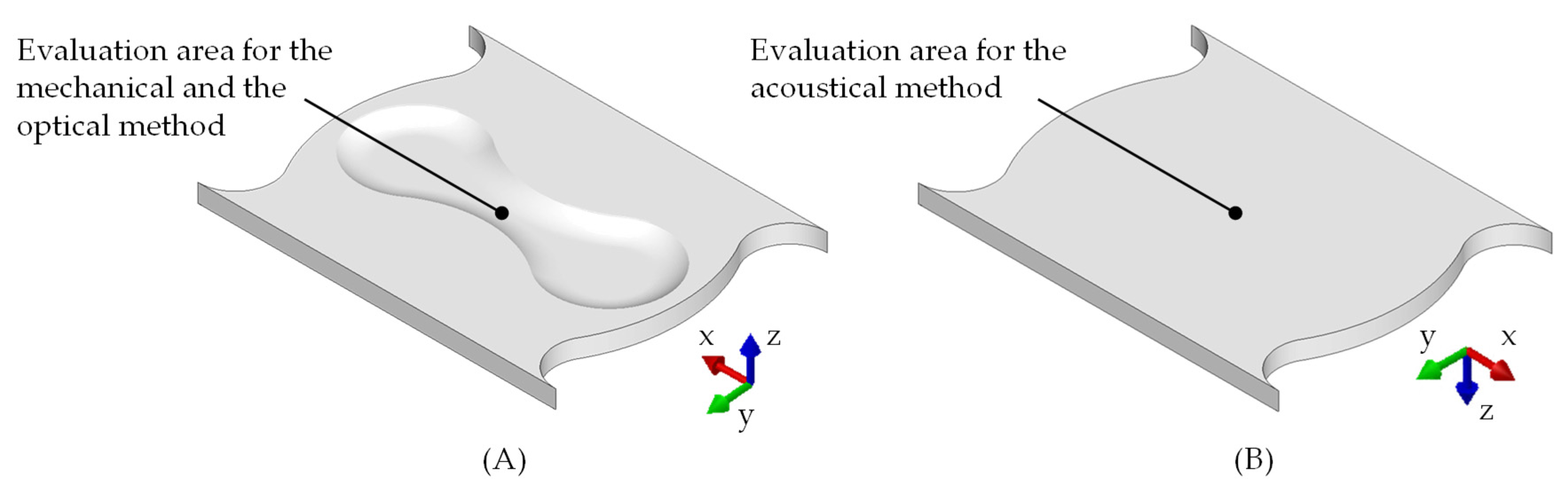
2.2. Failure Behaviour
3. Results and Discussion
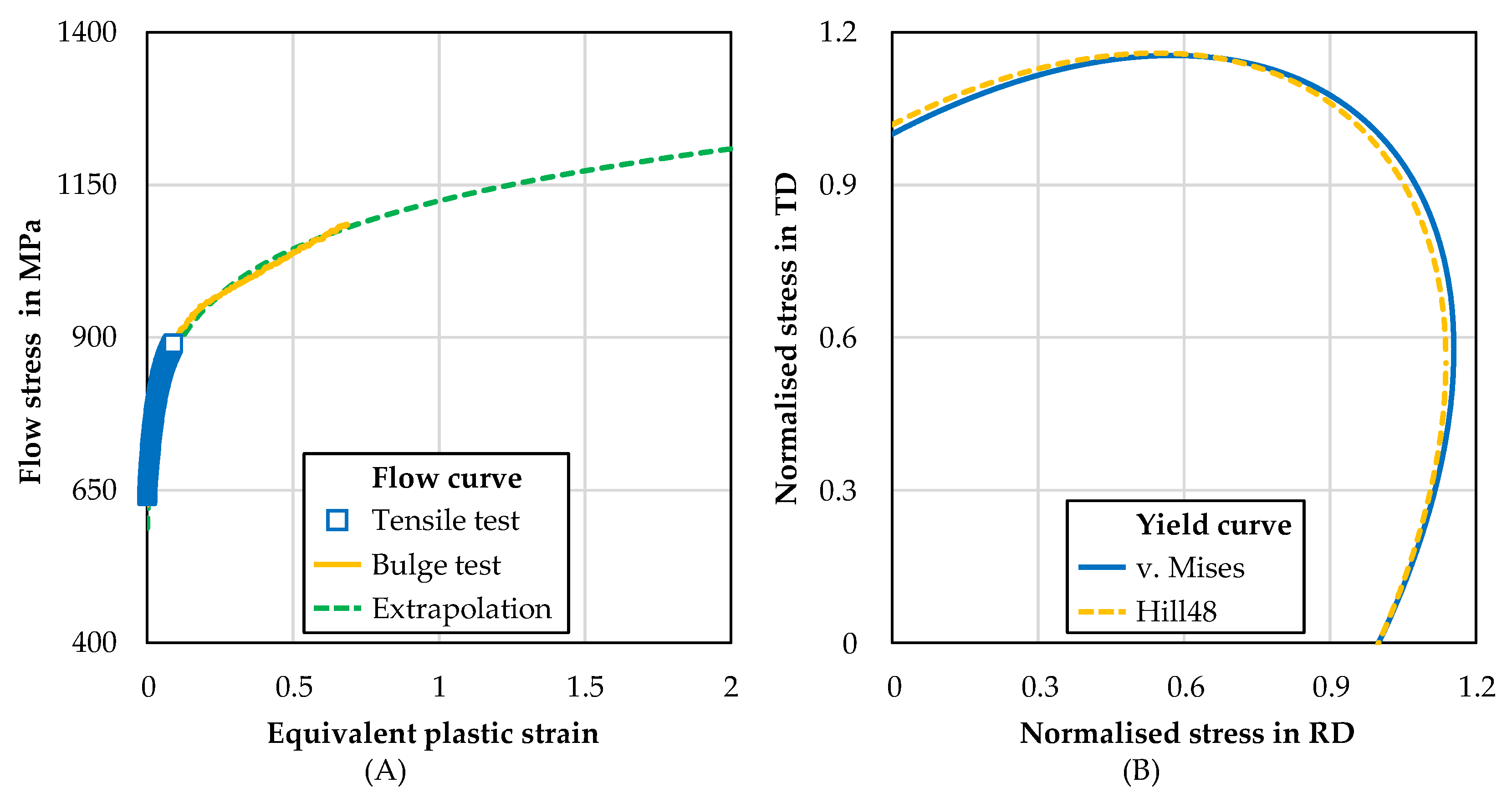
3.1. Flow Behaviour
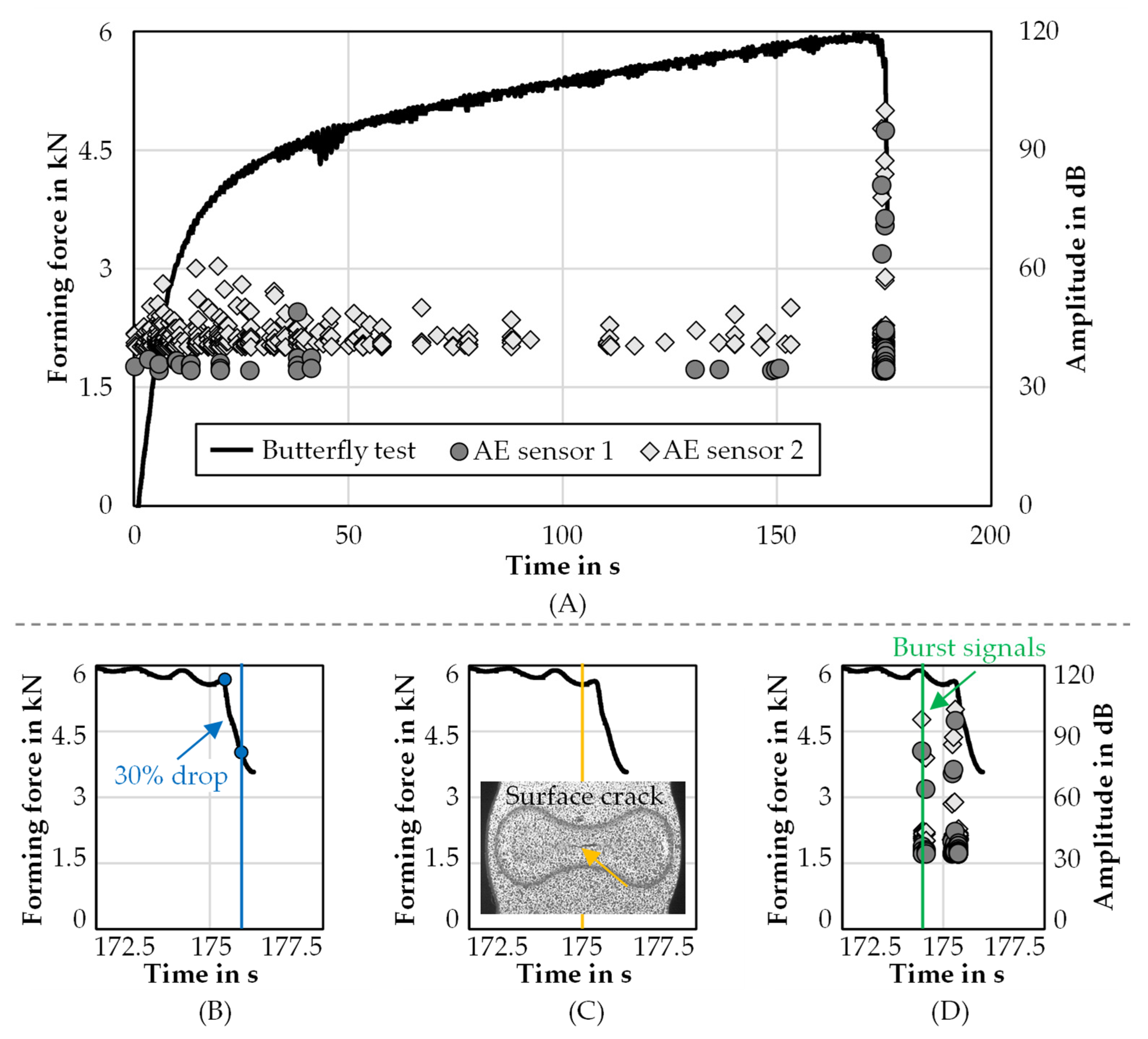
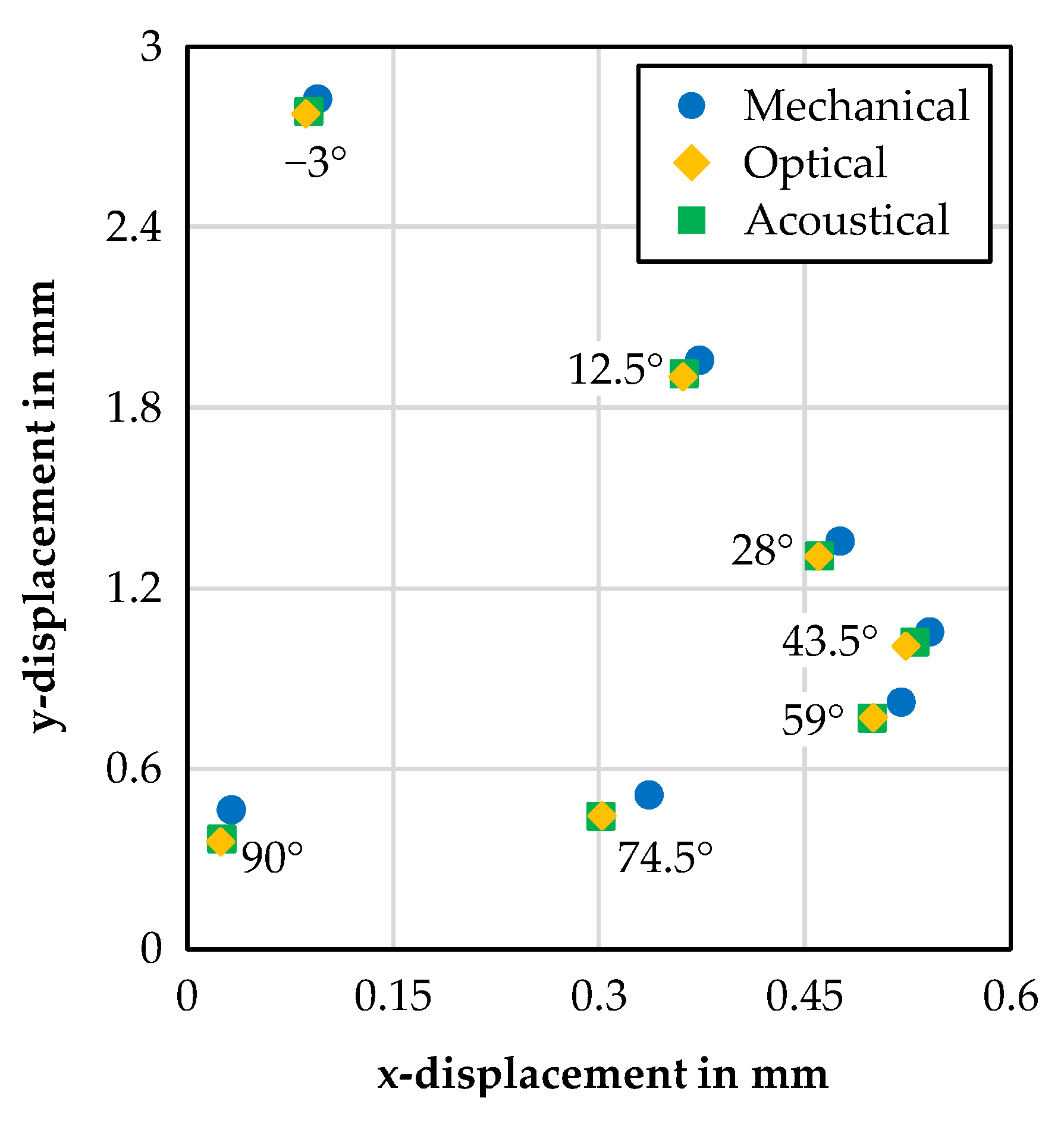
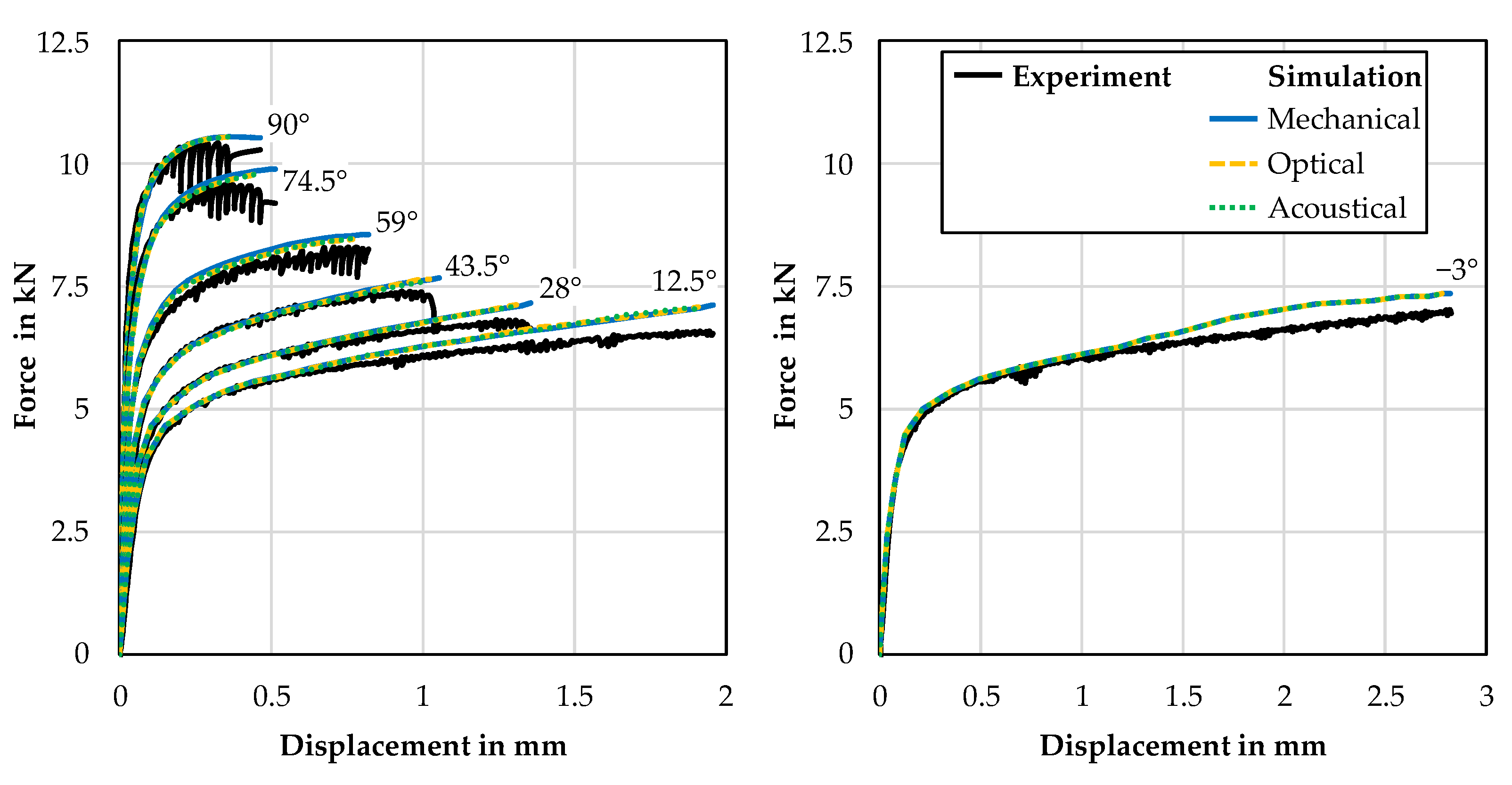
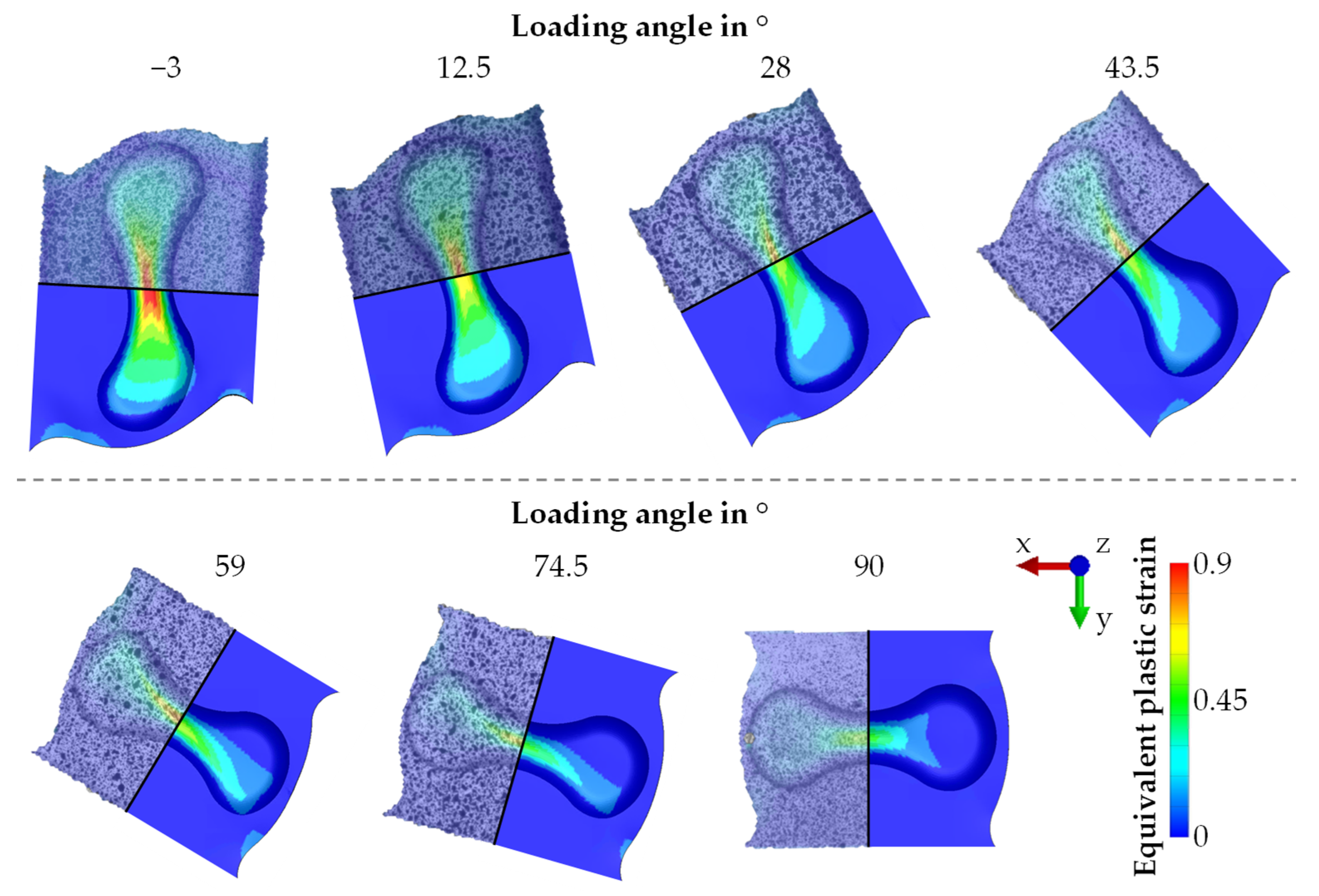
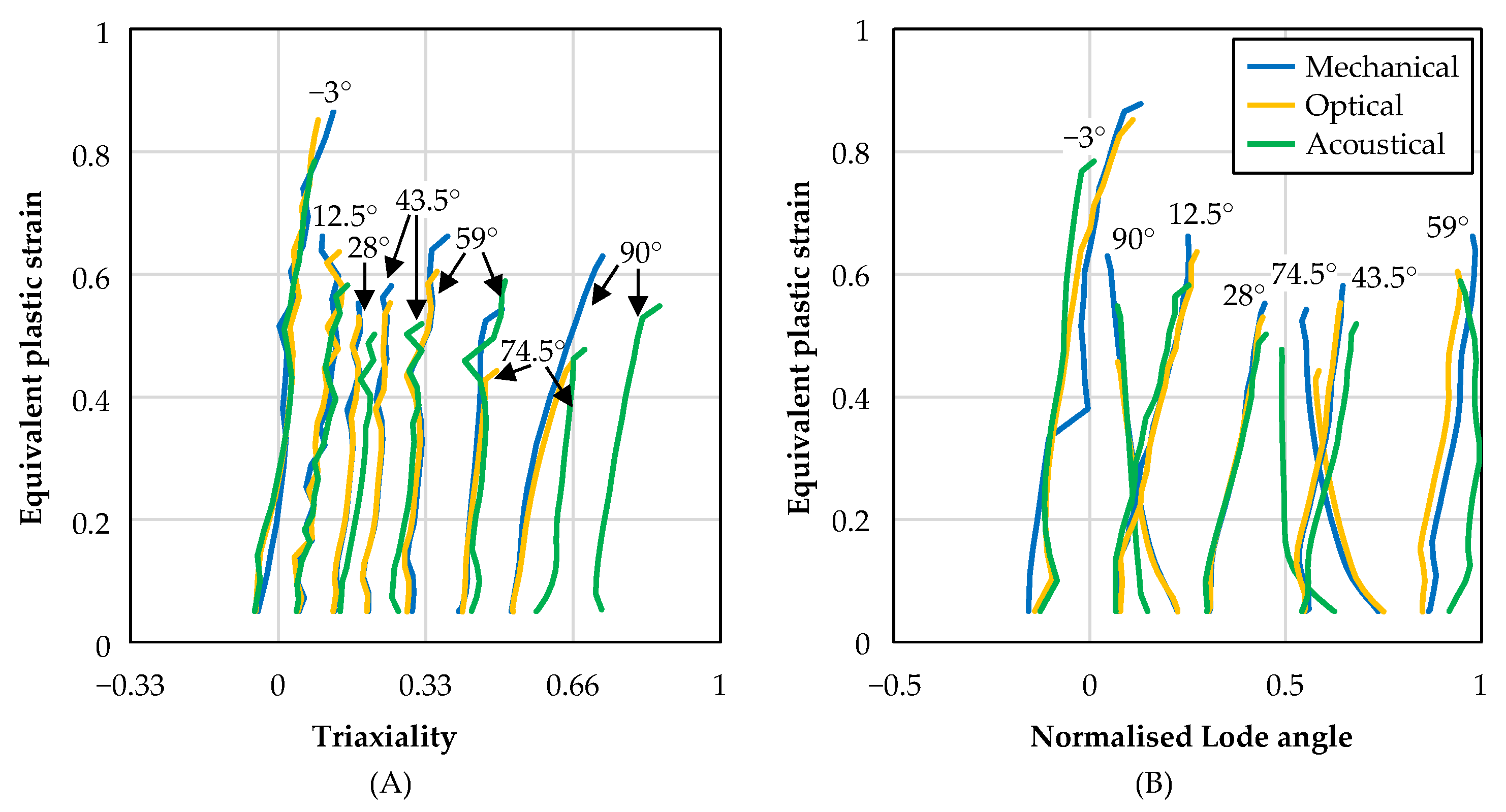
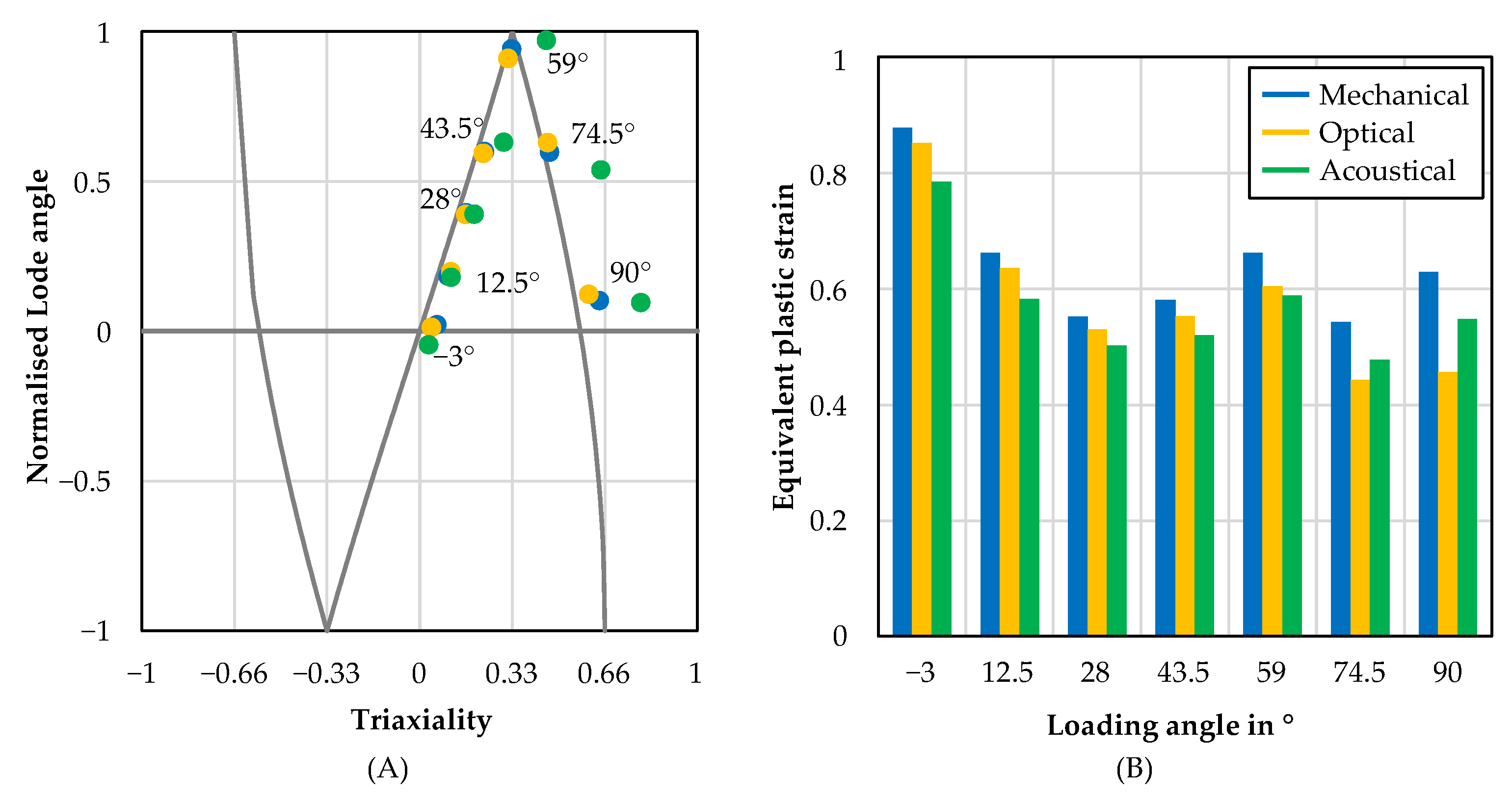
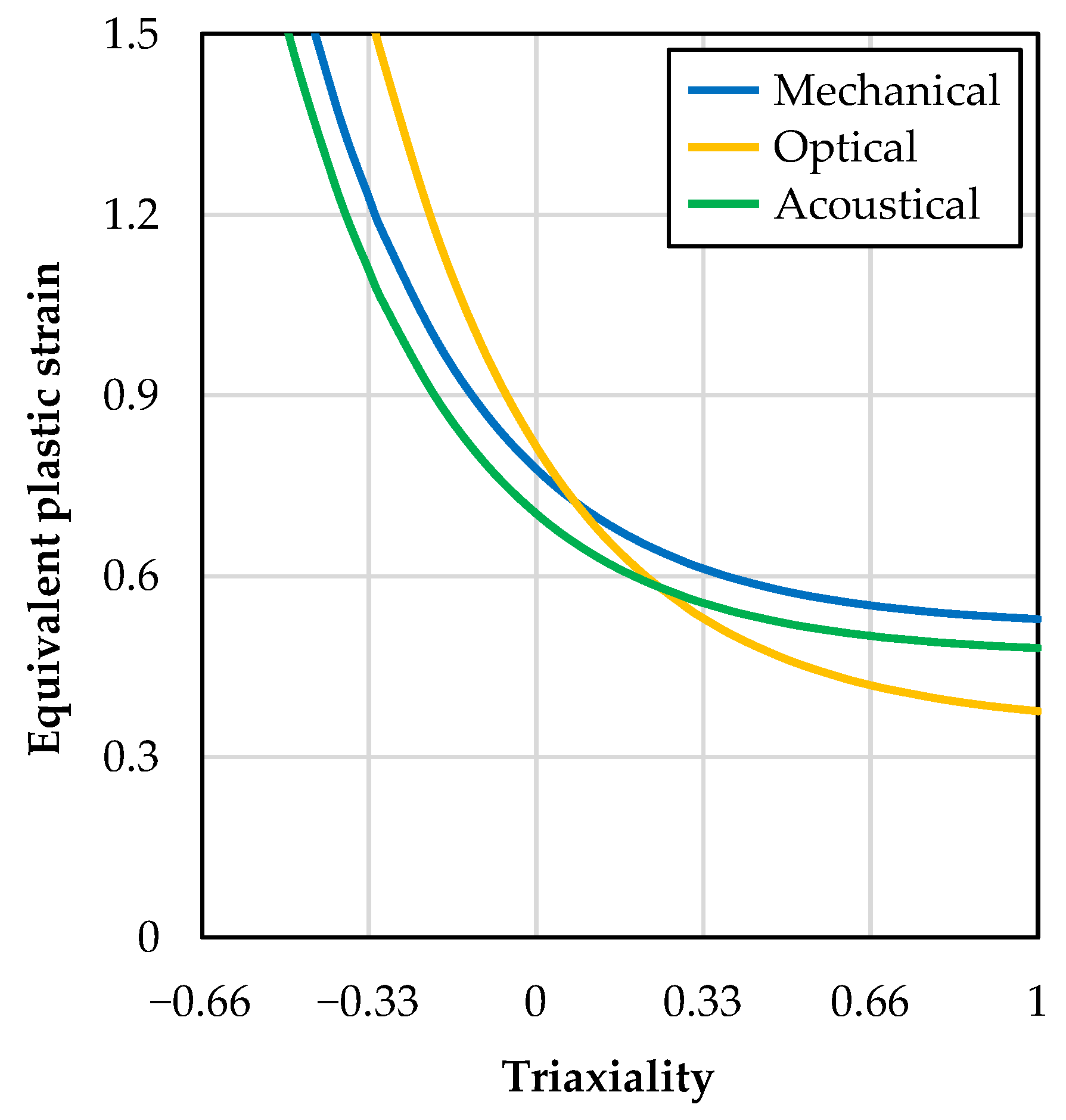
3.2. Failure Behaviour
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | Description |
| AHHS | Advanced high-strength steels |
| B | Bainite |
| CP | Complex phase steel |
| F | Ferrite |
| JC | Johnson–Cook failure model |
| M | Martensite |
| ND | Normal direction |
| RD | Rolling direction |
| TD | Transverse direction |
| Parameters | Description |
| Material parameters of the Swift extrapolation approach | |
| Material parameters of the JC failure model | |
| Hill48 parameters | |
| Equivalent plastic strain at failure | |
| Equivalent plastic strain | |
| Triaxiality | |
| Flow stress of the Swift extrapolation approach | |
| Anisotropy coefficients | |
| Tensile yield stresses | |
| Shear yield stresses | |
| Failure displacements in x-direction | |
| Failure displacements in y-direction |
References
- Fonstein, N. Dual-phase steels. In Automotive Steels—Design, Metallurgy, Processing and Applications; Elsevier: Amsterdam, The Netherlands, 2017; pp. 169–216. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Uhe, J.; Wester, H.; Stockburger, E. Hot forming limit Curves for numerical Press Hardening Simulation of AISI 420C. In Proceedings of the 29th International Conference on Metallurgy and Materials, Brno, Czech Republic, 20–22 May 2020; pp. 350–355. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Wilson-Heid, A.E.; Furton, E.T.; Beese, A.M. Contrasting the Role of Pores on the Stress State Dependent Fracture Behavior of Additively Manufactured Low and High Ductility Metals. Materials 2021, 14, 3657. [Google Scholar] [CrossRef] [PubMed]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Erice, B.; Roth, C.C.; Mohr, D. Stress-state and strain-rate dependent ductile fracture of dual and complex phase steel. Mech. Mater. 2018, 116, 11–32. [Google Scholar] [CrossRef]
- Hong, T.; Ding, F.; Chen, F.; Zhang, H.; Zeng, Q.; Wang, J. Study on the Fracture Behaviour of 6061 Aluminum Alloy Extruded Tube during Different Stress Conditions. Crystals 2023, 13, 489. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of three Metals subjected to various Strains, Strain Rates, Temperatures, and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Wang, H.; Sui, X.; Guan, Y. Prediction of Hot Formability of AA7075 Aluminum Alloy Sheet. Metals 2023, 13, 231. [Google Scholar] [CrossRef]
- Xu, T.; Li, F.; Wang, X.; Zhang, G. Characterization of Anisotropic Fracture Behavior of 7075-T6 Aluminum Alloy Sheet under Various Stress States. J. Materi. Eng. Perform. 2022. [Google Scholar] [CrossRef]
- Lou, Y.S.; Yoon, J.W. A User-friendly Anisotropic Ductile Fracture Criterion for Sheet Metal under Proportional Loading. Int. J. Solids Struct. 2021, 217, 48–59. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Sol. 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Chuluunbat, T.; Lu, C.; Kostryzhev, A.; Tieu, K. Investigation of X70 line pipe steel fracture during single edge-notched tensile testing using acoustic emission monitoring. Mater. Sci. Eng. A 2015, 640, 471–479. [Google Scholar] [CrossRef]
- Voestalpine Steel Division. Data Sheet Complex Phase Steels, 10/2022. Available online: https://www.voestalpine.com/ultralights/en/content/download/4638/file/Complex-phase-high-ductility-steels-voestalpine-EN-14102021.pdf (accessed on 7 February 2023).
- DIN EN ISO 10275:2020; Metallic Materials—Sheet and Strip—Determination of Tensile Strain Hardening Exponent. Beuth: Berlin, Germany, 2020. [CrossRef]
- DIN EN ISO 12004-2:2021; Metallic Materials—Determination of Forming-Limit Curves for Sheet and Strip. Beuth: Berlin, Germany, 2021. [CrossRef]
- Pelleg, J. Mechanical Testing of Materials. In Mechanical Properties of Materials; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–84. [Google Scholar] [CrossRef]
- DIN EN ISO 16808:2022-08; Metallic Materials—Sheet and Strip—Determination of Biaxial Stress-Strain Curve by Means of Bulge Test with Optical Measuring Systems. Beuth: Berlin, Germany, 2022.
- Sigvant, M.; Mattiasson, K.; Vegter, H.; Thilderkvist, H. A viscous pressure bulge test for the determination of a plastic hardening curve and equibiaxial material data. Int. J. Mater. Form. 2009, 2, 235–242. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Rosenbusch, D.; Wester, H.; Stockburger, E. Material Characterization and Modeling for Finite Element Simulation of Press Hardening with AISI 420C. J. Mater. Eng. Perform. 2022, 31, 825–832. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- DIN EN ISO 10113:2020; Metallic Materials—Sheet and Strip—Determination of Plastic Strain Ratio. Beuth: Berlin, Germany, 2021. [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. A 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Stockburger, E.; Vogt, H.; Wester, H.; Hübner, S.; Behrens, B.-A. Evaluating Material Failure of AHSS Using Acoustic Emission Analysis. Mater. Res. Proc. 2023, 25, 379–386. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Dröder, K.; Hürkamp, A.; Droß, M.; Wester, H.; Stockburger, E. Finite Element and Finite Volume Modelling of Friction Drilling HSLA Steel under Experimental Comparison. Materials 2021, 14, 5997. [Google Scholar] [CrossRef] [PubMed]
- Pathak, N.; Butcher, C.; Worswick, M.J.; Bellhouse, E.; Gao, J. Damage Evolution in Complex-Phase and Dual-Phase Steels during Edge Stretching. Materials 2017, 10, 346. [Google Scholar] [CrossRef] [PubMed]
- Behrens, B.-A.; Jüttner, S.; Brunotte, K.; Özkaya, F.; Wohner, M.; Stockburger, E. Extension of the Conventional Press Hardening Process by Local Material Influence to Improve Joining Ability. Procedia Manuf. 2020, 47, 1345–1352. [Google Scholar] [CrossRef]

| Element | C | Si | Mn | P | S | Al | Cr + Mo | Ti + Nb | B | V |
|---|---|---|---|---|---|---|---|---|---|---|
| Amount in mass-% | 0.18 | 1 | 2.5 | 0.05 | 0.01 | 0.5 | 0.74 | 0.07 | 0.001 | 0.1 |
| Coefficient | A | B | C | |||
| Value | 1123.7 MPa | 0.0022 | 0.1057 | |||
| Coefficient | F | G | H | L | M | N |
| Value | 0.495 | 0.531 | 0.469 | 1.5 | 1.5 | 1.634 |
| Coefficient | D1 | D2 | D3 |
|---|---|---|---|
| Mechanical | 0.5158 | 0.2617 | −3.02 |
| Optical | 0.3485 | 0.4664 | −3.03 |
| Acoustical | 0.4691 | 0.2345 | −2.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stockburger, E.; Wester, H.; Behrens, B.-A. Failure Modelling of CP800 Using Acoustic Emission Analysis. Appl. Sci. 2023, 13, 4067. https://doi.org/10.3390/app13064067
Stockburger E, Wester H, Behrens B-A. Failure Modelling of CP800 Using Acoustic Emission Analysis. Applied Sciences. 2023; 13(6):4067. https://doi.org/10.3390/app13064067
Chicago/Turabian StyleStockburger, Eugen, Hendrik Wester, and Bernd-Arno Behrens. 2023. "Failure Modelling of CP800 Using Acoustic Emission Analysis" Applied Sciences 13, no. 6: 4067. https://doi.org/10.3390/app13064067
APA StyleStockburger, E., Wester, H., & Behrens, B.-A. (2023). Failure Modelling of CP800 Using Acoustic Emission Analysis. Applied Sciences, 13(6), 4067. https://doi.org/10.3390/app13064067







