Research on Transmission Task Static Allocation Based on Intelligence Algorithm
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions
- Establishing a mathematical model suitable for intelligent algorithm calculation;
- Selecting an appropriate intelligent algorithm based on the characteristics of the problem;
- Making targeted improvements to the algorithm to improve its success rate and efficiency.
- According to the characteristics of TTSA, a mathematical model suitable for the application of intelligent algorithms is built, a matrix of evaluation values of the effect is constructed, and the input data, output data, and fitness function of the algorithm are defined;
- Based on GA, an improved crossover operator based on cyclic substitution grouping is proposed to avoid the loss of excellent chromosome genes due to conflict processing and to improve the execution efficiency of IGA;
- Based on GA and PSO, two hybrid intelligent algorithms are proposed to provide more intelligent algorithm ideas for solving TTSA;
- A DPSO is proposed. Based on TTSA, the position and direction of the particles are described again, the probability selection model is used to update the particle position, and the random disturbance strategy is added to improve the particle inertia retention.
2. Preliminaries
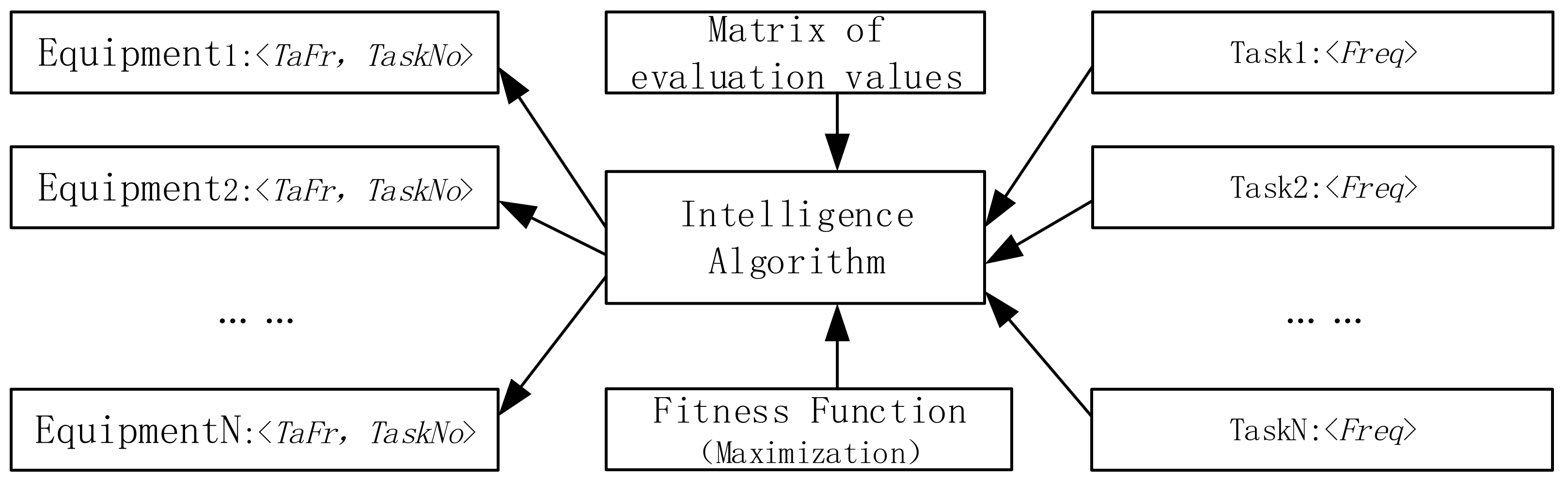
2.1. Model of TTSA
2.1.1. Input Data
2.1.2. Output Data
2.1.3. Fitness Function
2.2. GA
2.3. PSO
3. Methodologies
3.1. IGA
- The selection operator (SO) adopts the elitist retention strategy and increases the parameter of selection factor. When selecting the population, it retains a certain proportion of excellent parents, and enters the selection range together with the offspring, so as to achieve the optimal individual survival rate in the process of genetic evolution. In order to ensure the diversity of the population, the algorithm replaces the duplicate individuals in the new population during the execution of the selection operator in each iteration.
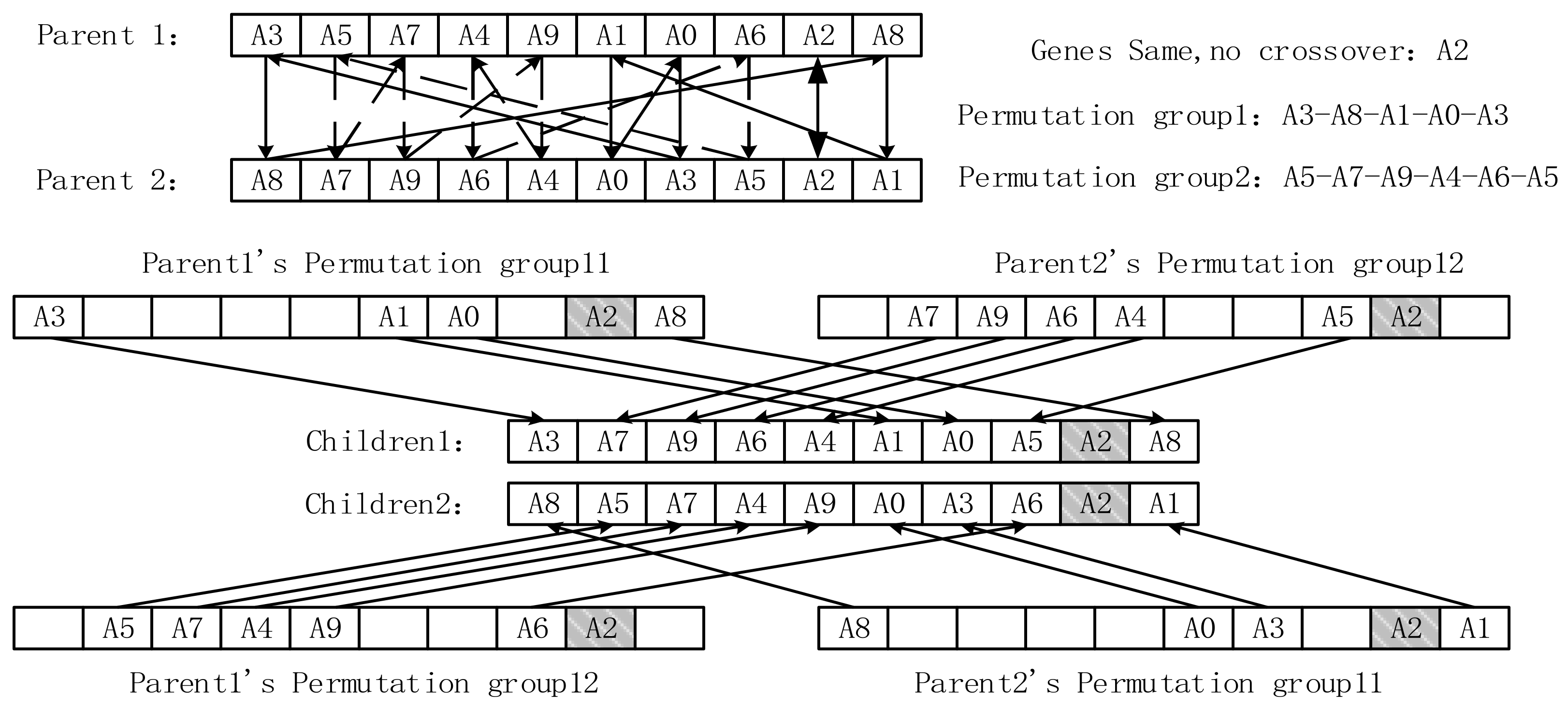
- The improved crossover operator (ICO) adopts the traditional genetic crossover processing according to the arrangement sequence that each individual is assigned to the equipment based on the task. Usually, the crossover point is determined, the sequence before the crossover point is reserved, and the sequence after the intersection point of two individuals is exchanged to generate new individuals. However, for two permutation sequences, there is a high probability of conflict after cross-processing, which is reflected in the issue of TTSA; that is, one task is assigned to two equipment items or two tasks are assigned to one equipment item. This paper proposes a method of the cyclic exchange of packets. The two sequences are divided into multiple packets according to the cyclic exchange calculation between two parents using a tracking calculation, and then one or more packets whose size is close to half of the length of the individual sequence are selected as the reservation or exchange reason, thus avoiding the occurrence of node gene conflict after the crossover operation and achieving the purpose of preserving all excellent genes. The specific operation is shown in the example provided in Figure 2.
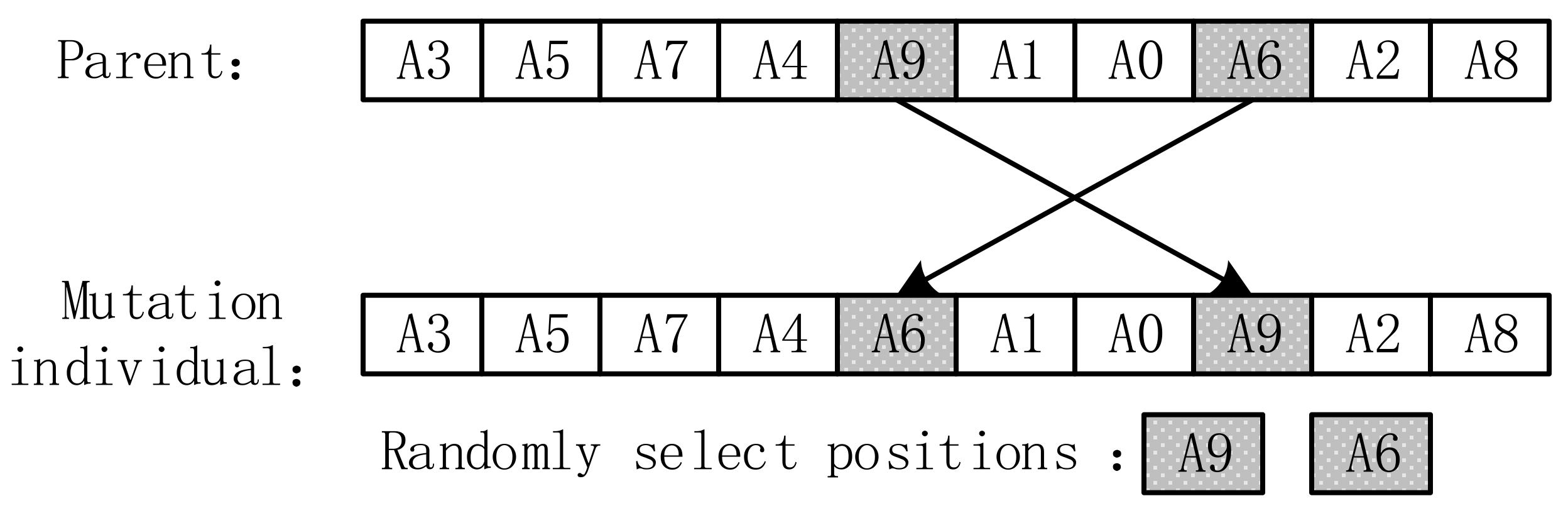
- The improved mutation operator (IMO): In order to ensure the diversity of the population and avoid falling into the local optimal trap, the mutation operator uses the random selection of two positions in the sequence to exchange the transmission tasks performed by the two positions of the transmission equipment to generate new mutation individuals. The specific operation is shown in the example provided in Figure 3.
3.2. PSO-GA Hybrid Algorithm
- Selection operator: PSO is adopted to formulate a genetic selection strategy and establish the PSO population. The update operation of each particle selects global best, particle best, and particle position for the crossover operator.
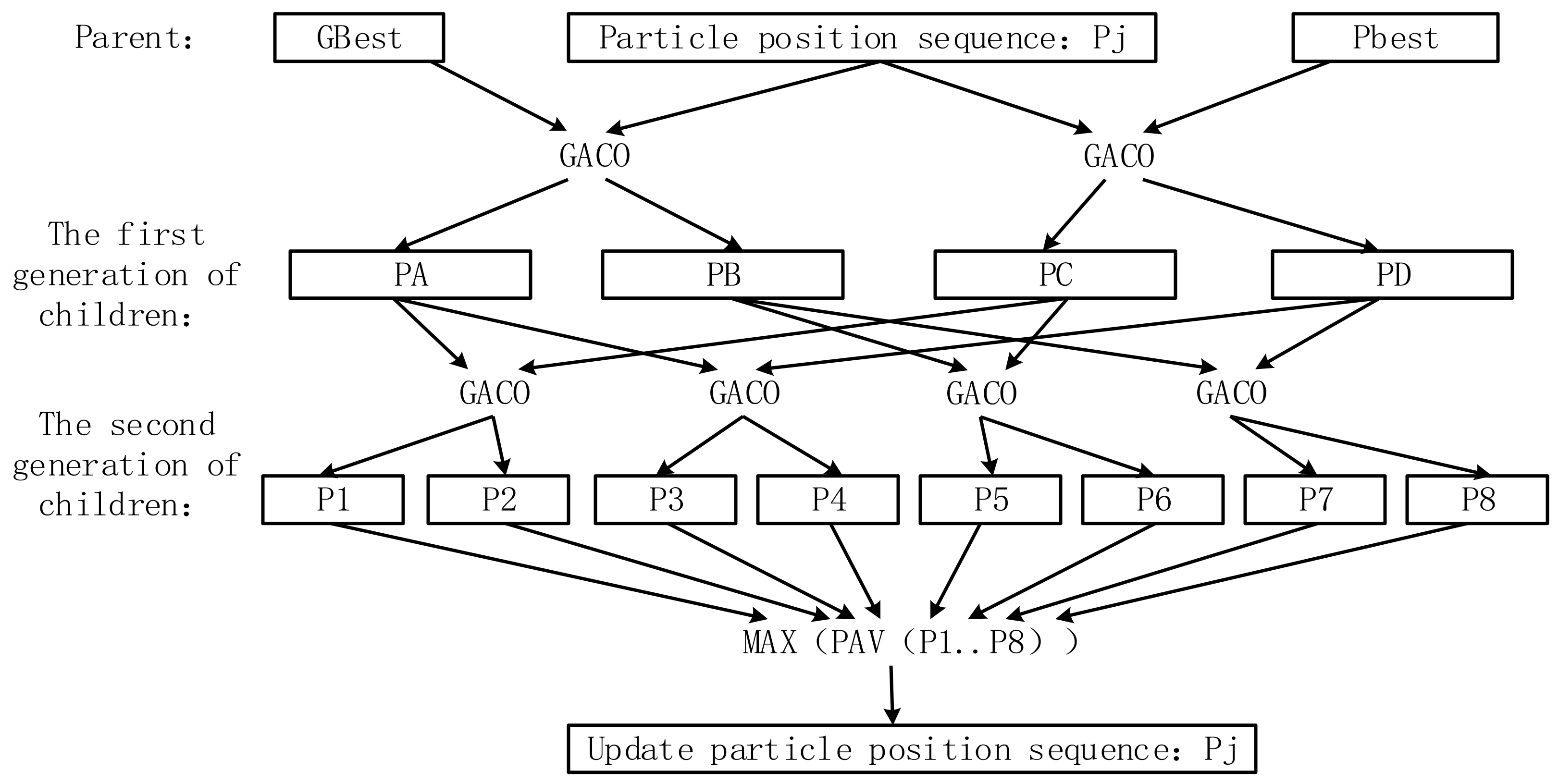
- Crossover operator: The ICO operator above is used for the crossover operation, and the idea of multi-agent inheritance is introduced. Three gene sequences are selected based on the selection operator, and the particle position is crossed with the global extreme and individual extreme, respectively, to generate four generations. Then, the four children are divided into two groups. The two children with a global best gene and the two children with a particle best gene cross over each other to generate eight children. The children with the largest evaluation value are selected from the eight children as the result of the crossover calculation to replace the particle position and complete the iteration. The specific operation is shown in Figure 4.
- Mutation operator: In order to ensure the diversity of the population and avoid falling into the local optimal trap, the IMO above performs a mutation operation on the particle position. The mutation factor is set, and the particle position of the population is calculated according to the factor proportion according to the gene mutation operation.
3.3. GA-SPO Hybrid Algorithm
3.3.1. Probability Selection Model and Random Disturbance
3.3.2. GA-PSO Operation
- Definition of particle position: According to the characteristics of TTSA solution space of the transmission task, the particle swarm coding is represented by the preceding text; that is, the “position” of the particle is represented by an orderly task sequence number. When the algorithm is started, a random sequence is used to initialize the particles. The goal of the algorithm is to continuously update the particle’s position, so that the task allocation sequence represented by the position information can obtain the maximum comprehensive effect evaluation value through Formula (10)—that is, continuously optimize the sequence, and obtain the optimization result of the particle swarm optimization, which is recorded as:The definition of particle best and global best is the same as the definition of particle position, which is recorded as:
- Particle update operation based on probability selection and ICO: When the particle branch direction is calculated according to the parameters, and inertia operation is performed according to the parameters, some particles move to global best, and some particles move to particle best. In order to avoid the problem whereby the motion direction and speed cannot be defined by a vector, the ICO is used to replace the particle motion operation for the move toward global best and particle best. One of the two generations is selected with a better evaluation value to replace the particle position to realize particle iteration. This achieves the goal of simplifying the PSO. The particles performing inertia operations adopt MO to increase the diversity of the particles.
- Algorithm termination: When the defined number of iterations is reached, the algorithm terminates, and the global best is the output of the algorithm’s optimal solution, ending the algorithm calculation.
3.4. DSPO
3.4.1. Particle Motion Direction and Target Definition
- 1.
- Definition of particle motion direction: According to the description of the PSO, the particle motion speed is calculated by the position vector, which contains the direction and displacement information. In TTSA, due to the discrete characteristics, the decomposition speed is divided into two items: direction and displacement. Each node of the task sequence is defined as the particle motion direction. The particle motion direction suitable for the problem in this paper is , defined as:
- 2.
- Definition of particle motion target: According to the discrete characteristics of TTSA, the velocity displacement is defined as the number of transmission tasks to be replaced by the node representing the particle motion direction. Referring to the PSO Formula (12), the particle motion target suitable for the problem in this paper is defined as:
3.4.2. Particle Position Update Calculation
4. Experiments
4.1. Simulation Experiment Environment
4.2. Comparison Algorithms
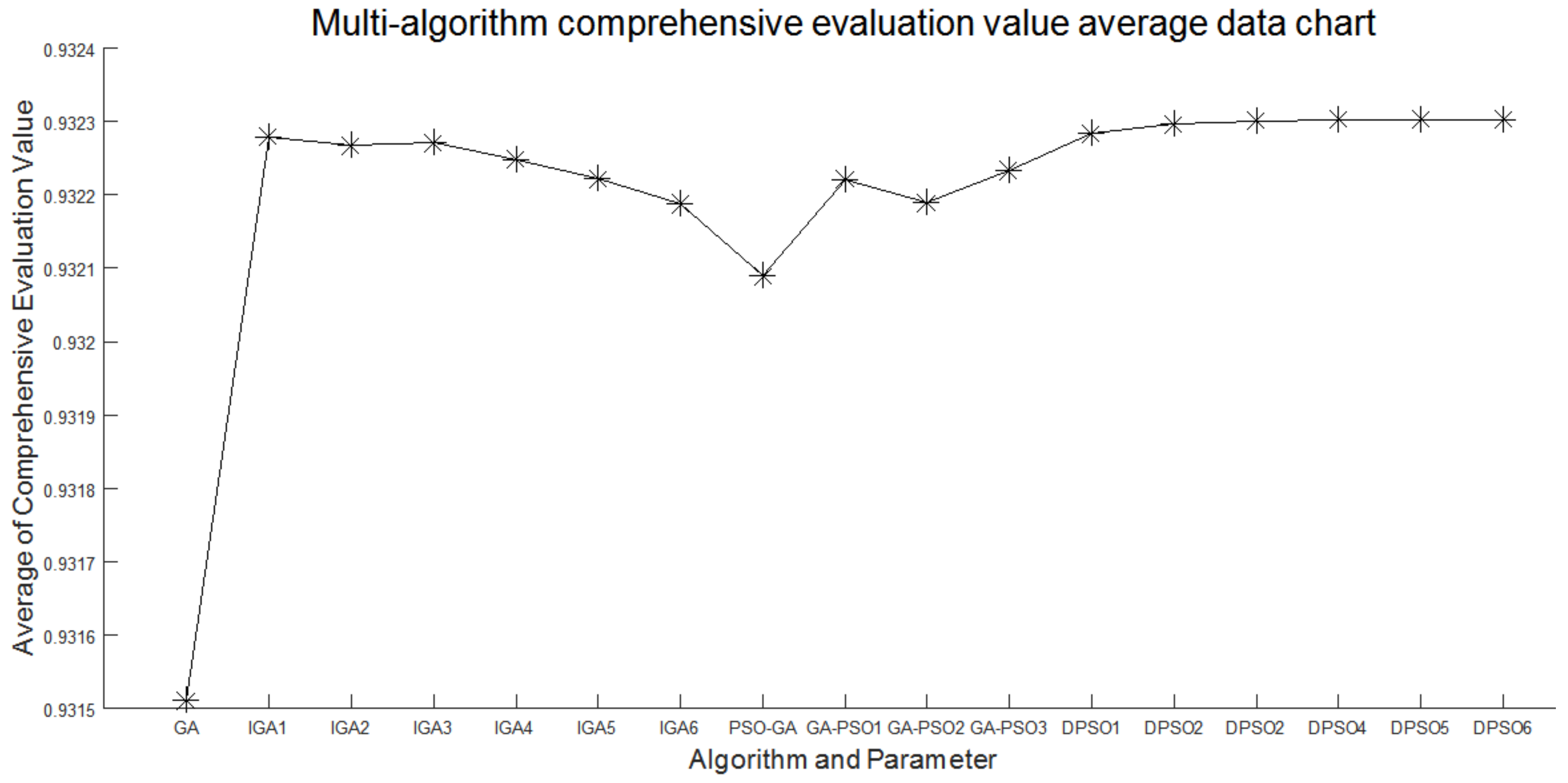
4.3. Algorithm Parameter Test
4.4. Algorithm Experiments
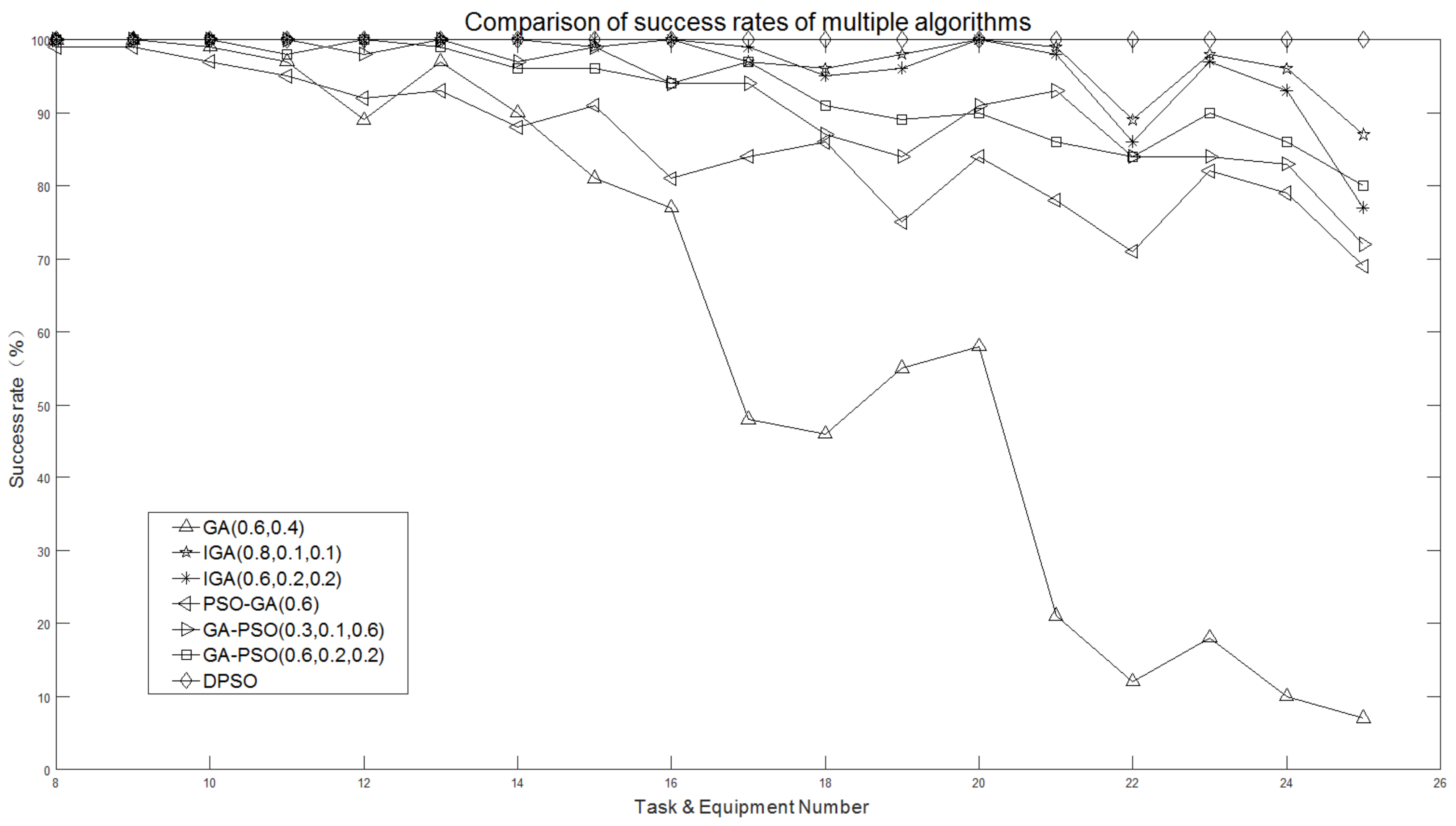
- Except for DPSO, the success rate of all algorithms decreases gradually with the number of tasks.
- Compared with other algorithms, the GA calculation results are the worst. The IGA, PSO-GA, and GA-PSO calculation results are equivalent, but with the increase in the number of tasks, the gap between the GA and DPSO calculation results is wide. It shows that the ICO can effectively improve the calculation success rate of the intelligent algorithm.
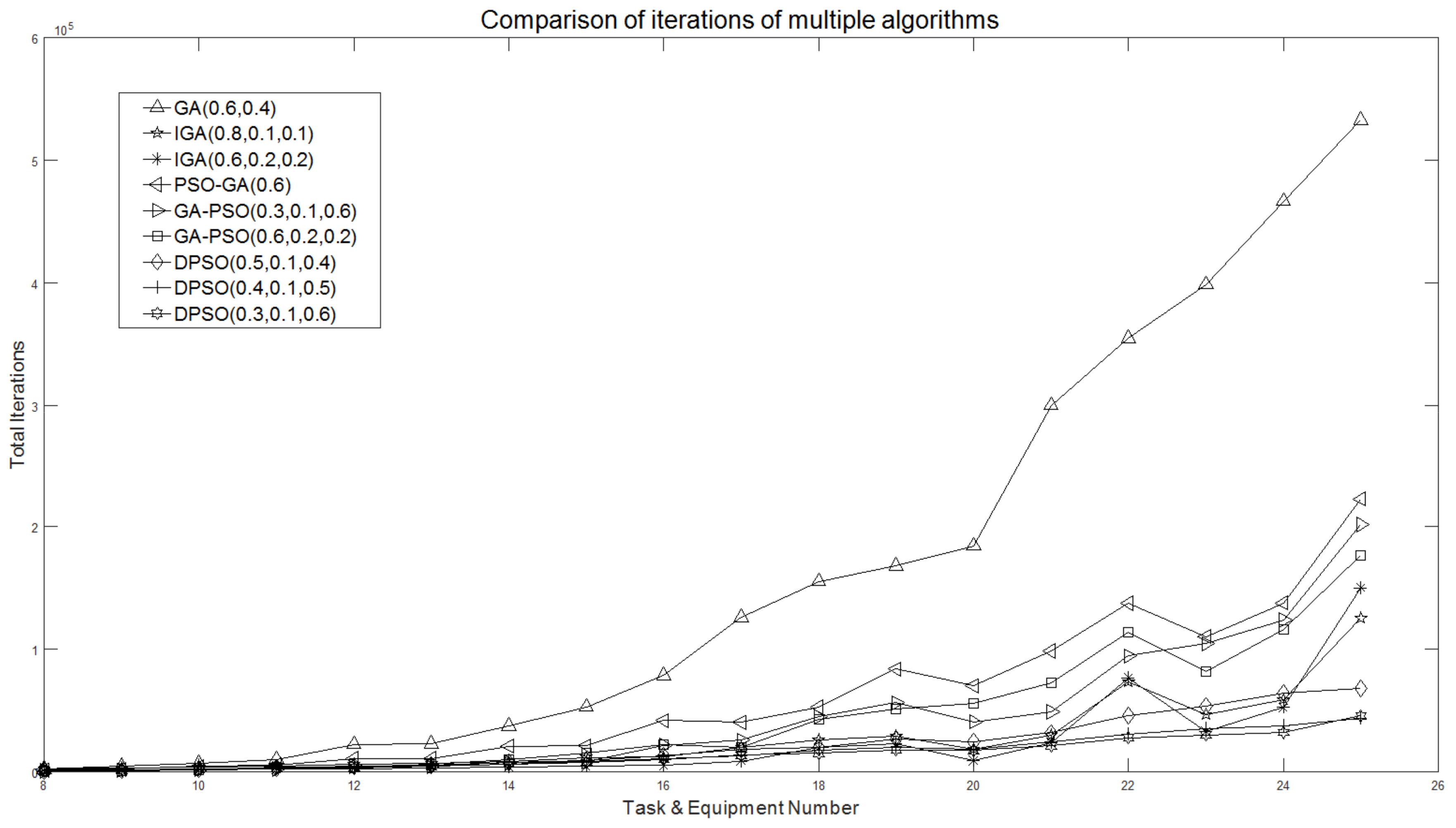
- The number of iterations of all algorithms increases gradually with the number of tasks.
- The number of iterations of the GA calculation increases rapidly because of the low success rate. In the experiment, it is almost impossible to obtain the optimal solution using the set number of iterations. The number of iterations of PSO-GA and GA-PSO is equal, which shows that both hybrid strategies can effectively improve the convergence of intelligent algorithms. The IGA calculation results are superior to those of the hybrid algorithms. The advantage of the number of iterations of the DPSO calculation is obvious, which proves that the convergence of DPSO is the highest.
4.5. Discussion of Experiments
- The mathematical model and intelligent algorithm built can solve the TTSA of radio and television transmission.
- Through the enumeration algorithm verification, when the number of tasks is small, the intelligent algorithm can calculate the global optimal solution, indicating that the intelligent approximation algorithm can achieve the same calculation results as the accurate algorithm. However, the limitation is that not all intelligent algorithms can achieve the same results as accurate algorithms. Comparing different intelligent algorithms is a contribution of this paper.
- A large number of attempts of the algorithms can find the optimal approximate calculation scheme for specific problems. The parameter selection of the algorithm is the key to achieving optimal results. This paper directly uses the results of parameter testing in previous studies. It is recommended that when using this algorithm to solve other similar problems, the algorithm parameter selection test ought to be conducted again.
- In order to obtain better results, the algorithm should be adapted to specific problems, for example, the improved crossover operator and probability selection model in this paper.
- The hybrid algorithm can achieve good results in a certain range, but it may not completely inherit the advantages of the original algorithm. Although the computational results of the PSO-GA and GA-PSO in this paper are better than GA, there is no advantage in comparing the results of IGA and DPSO.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, W.; Huang, X.; Luo, H.; Soo, V.; Lee, Y. Auction-Based Consensus of Autonomous Vehicles for Multi-Target Dynamic Task Allocation and Path Planning in an Unknown Obstacle Environment. Appl. Sci. 2021, 11, 5057. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, M.; Xing, L. Deep intelligent Ant Colony Optimization for Solving Travelling Salesman Problem. J. Comput. Res. Dev. 2021, 58, 1586–1598. [Google Scholar]
- Kenneth, N.; Frank, R.; John, A. Job—Shop scheduling theory: What is relevant? Interfaces 1988, 18, 84–90. [Google Scholar]
- Lawler, E.; Leenstra, J.; Kan, A. Sequencing and Scheduling: Algorithms and Complexity//Handbooks in Operations Research and Management Science, Volume 4: Logistics of Production and Inventory; Elsevier: Amsterdam, The Netherlands, 1993; pp. 455–522. [Google Scholar]
- Park, J.; Ng, H.; Chua, T.; Ng, Y.; Kim, J. Unified Genetic Algorithm Approach for Solving Flexible Job-Shop Scheduling Problem. Appl. Sci. 2021, 11, 6454. [Google Scholar] [CrossRef]
- Zhang, J.; Chong, X.; Wei, Y.; Bi, Z.; Yu, Q. Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm. Appl. Sci. 2022, 12, 5279. [Google Scholar] [CrossRef]
- Escamilla-Serna, N.; Seck-Tuoh-Mora, J.; Medina-Marin, J.; Barragan-Vite, I.; Corona-Armenta, J. A Hybrid Search Using Genetic Algorithms and Random-Restart Hill-Climbing for Flexible Job Shop Scheduling Instances with High Flexibility. Appl. Sci. 2022, 12, 8050. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, G.; Liu, Y.; Zhou, Y. Virtual network function deployment strategy based on improved genetic simulated annealing algorithm in MEC. J. Commun. 2020, 41, 70–80. [Google Scholar]
- Fan, H.; Xu, Z.; Li, Y.; Liu, W.; Geng, J. Hybrid Genetic Algorithm for Solving Multi-Depot Joint Distribution Routing Problem. J. Shanghai Jiaotong Univ. 2019, 53, 1000–1009. [Google Scholar]
- Belhadj, I.; Trigui, M.; Benamara, A. Subassembly generation algorithm from a CAD model. Int. J. Adv. Manuf. Technol. 2016, 87, 2829–2840. [Google Scholar] [CrossRef]
- Tseng, H.; Chang, C.; Lee, S. A block-based genetic algorithm for disassembly sequence planning. Expert Syst. Appl. 2018, 96, 492–505. [Google Scholar] [CrossRef]
- Song, H.; Yi, S.; Wu, C.; Zhang, S.; Deng, G.; Liu, P.; Wei, X. Research on group scheduling of optimal setup uncorrelated parallel machine based on GATS hybrid algorithm. J. Chongqing Univ. 2020, 1, 53–63. [Google Scholar]
- Jiao, Y.; Xu, T.; Liu, B.; Yu, G. Hybrid genetic algorithm-based planning method for virutal assembly operation. Chin. J. Constr. Mach. 2017, 4, 342–347. [Google Scholar]
- Li, M.; Wu, H.; Xi, J.; Cai, J. An optimal routing generation method for MANET based on genetic algorithm. Appl. Electron. Tech. 2017, 43, 19–122. [Google Scholar]
- Tian, G.; Ke, H.; Chen, X. Fuzzy cost-profit tradeoff model for locating a vehicle inspection station considering regional constraints. J. Zhejiang Univ. Sci. C 2014, 15, 1138–1146. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W. Comprehensive Learning Particle Swarm Optimization Algorithm with Local Search for Multimodal Functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L. A Review on Swarm Intelligence and Evolutionary Algorithms for Solving Flexible Job Shop Scheduling Problems. IEEE/CAA J. Autom. Sin. 2019, 4, 904–916. [Google Scholar] [CrossRef]
- Han, J.; Liu, Y.; Luo, L. Integrated production planning and scheduling under uncertainty: A fuzzy bi-level decision-making approach. Knowl. Based Syst. 2020, 201, 106056. [Google Scholar] [CrossRef]
- Jamrus, T.; Chien, C.F.; Gen, M. Hybrid Particle Swarm Optimization Combined With Genetic Operators for Flexible Job-Shop Scheduling Under Uncertain Processing Time for Semiconductor Manufacturing. IEEE Trans. Semicond. Manuf. 2018, 31, 32–41. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, Z.; Huang, Z. A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route. Appl. Sci. 2021, 11, 5078. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Chen, R.; Wang, X.; Zhang, M. Class Integration Testing Order Determination Method Based on Particle Swarm Optimization Algorithm. Chin. J. Comput. 2018, 41, 631–645. [Google Scholar]
- Zhou, Y.; Wang, J.; Huang, C. Estimation of Distribution-Discrete Particle Swarm Optimization Algorithm for Permutation-Based Problems. Acta Electron. Sin. 2014, 42, 561–571. [Google Scholar]
- Ma, D.; Zhuang, L.; Lan, J. Discrete particle swarm optimization based multi-objective service path constructing algorithm. J. Commun. 2017, 2, 94–105. [Google Scholar]
- Li, H.; Yin, Y.; Li, Y.; Zhao, Y.; Wang, G. Large-Scale Dynamic Network Community Detection by Multi—Objective Evolutionary Clustering. J. Comput. Res. Dev. 2019, 56, 281–292. [Google Scholar]
- Huang, L.; Qi, J.; Tan, Y.; Yang, B. A Genetic-Discrete Particle Swarm Optimization Algorithm for Rectangular Packing. Acta Electron. Sin. 2012, 6, 1103–1107. [Google Scholar]
- Tian, G.; Zhang, C.; Zhang, X.; Feng, Y.; Yuan, G.; Peng, T.; Pham, D.T. Multi-Objective Evolutionary Algorithm with Machine Learning and Local Search for an Energy-Efficient Disassembly Line Balancing Problem in Remanufacturing. J. Manuf. Sci. Eng. 2023, 145, 051002. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, Z.; Xu, W.; Tang, Q.; Zhou, Z.; Pham, D.T. Human-robot collaboration in disassembly for sustainable manufacturing. Int. J. Prod. Res. 2019, 57, 4027–4044. [Google Scholar] [CrossRef]
- Xu, W.; Tang, Q.; Liu, J.; Liu, Z.; Zhou, Z.; Pham, D.T. Disassembly sequence planning using discrete Bees algorithm for human-robot collaboration in remanufacturing. Robot. Comput.-Integr. Manuf. 2020, 62, 101860. [Google Scholar] [CrossRef]
- Hao, W. Application of Artificial Intelligence in Radio and Television Monitoring and Supervision. Radio TV Broadcast Eng. 2019, 46, 126–128. [Google Scholar]
- Zhou, D.; Song, J.; Lin, C.; Wang, X. Research on Transmission Selection Optimized Evaluation Algorithm of Multi-frequency Transmitter. In 2015 International Conference on Automation, Mechanical Control and Computational Engineering; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 323–326. [Google Scholar]
- GY/T 280-2014; Specifications of Interface Data for Transmitting Station Operation Management System, State Administration of Press, Publication, Radio, Film and Television. National Radio and Television Administration: Beijing, China, 2014.
- GY/T 290-2015; Specification of Code for Data Communication Interface of Radio and Television Transmitter, State Administration of Press, Publication, Radio, Film and Television. National Radio and Television Administration: Beijing, China, 2015.
| Parameter | Explanation |
|---|---|
| Transmission frequency value of the task | |
| Input data and transmission task sequence | |
| Evaluation value of the transmission effect of the ith transmission equipment operating in the jth frequency band | |
| Transmission effect evaluation value matrix | |
| Description of the ith transmitting equipment, including | |
| Output results, consisting n of ordered sequences |
| Parameter | Explanation |
|---|---|
| Particle evaluation value sequence: the evaluation value sequence taken from the task allocation sequence represented by the ith particle | |
| Particle best evaluation value sequence: the evaluation value sequence obtained from the task allocation sequence recorded by the ith particle best | |
| Global best evaluation value sequence: the evaluation value sequence obtained from the task allocation sequence of the global best record | |
| In the probability selection model, the inertia maintains part of the probability value. According to the DPSO, this part is the random disturbance probability value | |
| In the probability selection model, particle best partial probability value | |
| In the probability selection model, global best partial probability value |
| Algorithm | Explanation | Parameter Representation | Parameter Description |
|---|---|---|---|
| GA | Selection: roulette strategy, Crossover: direct crossover and then conflict processing strategy, Mutation: random mutation and then conflict processing strategy [8,11,12,13] | GA (CF, MF) | New individuals are generated in the new population according to the ratio of crossover factor (CF) and mutation factor (MF) |
| IGA | Selection: the elitist retention strategy, Crossover: replace the group crossover with the crossover cycle, Mutation: use the random exchange | IGA (SF, CF, MF) | In the new population, excellent individuals of the parent generation are retained according to the selection factor (SF), and new individuals are generated according to the ratio of crossover factor (CF) and mutation factor (MF) |
| PSO-GA | Establish a selection mechanism based on PSO, establish a multi-agent genetic mechanism based on particle itself, particle best, and global best, and use ICO and MO of IGA | PSO-GA (MF) | After the particle update operation, some particles are changed according to the proportion of the mutation factor (MF) |
| GA-PSO | Initialize the population based on PSO, according to the probability selection model, replace the particle position update with ICO, and perform the MO when maintaining inertia | GA-PSO (IRF, PBF, GBF) | According to the probability model, determine the proportion of particles in the population updated according to three parameters: inertia retention factor (IRF), particle best factor (PBF), global best factor (GBF) |
| DPSO | Initialize the population based on PSO, according to the probability selection model, and complete the position update operation. When the selected direction and target remain unchanged, add random disturbance | DPSO (IRF, PBF, GBF) | According to the probability model, determine the proportion of particles in the population updated according to three parameters: inertia retention factor (IRF), particle best factor (PBF), global best factor (GBF) |
| Algorithm and Parameter | Number of Equipment Items and Tasks | Average | ||||
|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | ||
| GA (0.6,0.4) | 100% | 99% | 100% | 100% | 88% | 97.4% |
| IGA (0.8,0.1,0.1) | 100% | 100% | 100% | 100% | 100% | 100% |
| IGA (0.7,0.2,0.1) | 100% | 100% | 100% | 100% | 100% | 100% |
| IGA (0.6,0.2,0.2) | 100% | 100% | 100% | 100% | 100% | 100% |
| IGA (0.5,0.3,0.2) | 100% | 100% | 100% | 100% | 100% | 100% |
| IGA (0.4,0.3,0.3) | 100% | 100% | 100% | 100% | 100% | 100% |
| IGA (0.3,0.3,0.4) | 100% | 100% | 100% | 100% | 100% | 100% |
| PSO-GA (0.6) | 100% | 99% | 97% | 94% | 95% | 97% |
| GA-PSO (0.3,0.1,0.6) | 100% | 100% | 100% | 100% | 100% | 100% |
| GA-PSO (0.1,0.2,0.7) | 100% | 99% | 100% | 100% | 99% | 99.6% |
| GA-PSO (0.6,0.2,0.2) | 100% | 100% | 100% | 99% | 99% | 99.6% |
| DPSO (0.2,0.3,0.5) | 100% | 100% | 100% | 100% | 100% | 100% |
| DPSO (0.3,0.2,0.5) | 100% | 100% | 100% | 100% | 100% | 100% |
| DPSO (0.1,0.2,0.7) | 100% | 100% | 100% | 100% | 100% | 100% |
| DPSO (0.5,0.1,0.4) | 100% | 100% | 100% | 100% | 100% | 100% |
| DPSO (0.4,0.1,0.5) | 100% | 100% | 100% | 100% | 100% | 100% |
| DPSO (0.3,0.1,0.6) | 100% | 100% | 100% | 100% | 100% | 100% |
| Algorithm and Parameter | Number of Equipment Items and Tasks | Total | ||||
|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | ||
| GA (0.6,0.4) | 1666 | 3932 | 6101 | 10,239 | 24,789 | 46,727 |
| IGA (0.8,0.1,0.1) | 2391 | 3079 | 4455 | 4821 | 5936 | 20,682 |
| IGA (0.7,0.2,0.1) | 1503 | 1926 | 2419 | 3216 | 4234 | 13,298 |
| IGA (0.6,0.2,0.2) | 1100 | 1397 | 1848 | 2193 | 2944 | 9482 |
| IGA (0.5,0.3,0.2) | 840 | 1053 | 1413 | 1652 | 2089 | 7047 |
| IGA (0.4,0.3,0.3) | 653 | 843 | 1192 | 1390 | 1742 | 5820 |
| IGA (0.3,0.3,0.4) | 576 | 699 | 923 | 1123 | 1418 | 4739 |
| PSO-GA (0.6) | 1188 | 1974 | 4049 | 8285 | 7990 | 23,486 |
| GA-PSO (0.3,0.1,0.6) | 894 | 1131 | 2153 | 2357 | 4913 | 11,448 |
| GA-PSO (0.1,0.2,0.7) | 625 | 1212 | 1676 | 2185 | 3463 | 9161 |
| GA-PSO (0.6,0.2,0.2) | 666 | 1236 | 2140 | 2935 | 5261 | 12,238 |
| DPSO (0.2,0.3,0.5) | 432 | 767 | 1136 | 1528 | 2123 | 5986 |
| DPSO (0.3,0.2,0.5) | 495 | 1071 | 1291 | 2070 | 2330 | 7257 |
| DPSO (0.1,0.2,0.7) | 515 | 1047 | 1364 | 1972 | 2398 | 7296 |
| DPSO (0.5,0.1,0.4) | 582 | 1362 | 2089 | 2856 | 3996 | 10,885 |
| DPSO (0.4,0.1,0.5) | 628 | 1354 | 1844 | 2747 | 3974 | 10,547 |
| DPSO (0.3,0.1,0.6) | 540 | 1464 | 1763 | 2623 | 3754 | 10,144 |
| Algorithm and Parameter | Number of Equipment Items and Tasks | |||||
|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | 13 | |
| GA (0.6,0.4) | 0.905917 | 0.910875 | 0.901094 | 0.937174 | 0.937185 | 0.936331 |
| IGA (0.8,0.1,0.1) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| IGA (0.7,0.2,0.1) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| IGA (0.6,0.2,0.2) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| IGA (0.5,0.3,0.2) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| IGA (0.4,0.3,0.3) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| IGA (0.3,0.3,0.4) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| PSO-GA (0.6) | 0.905898 | 0.910849 | 0.901045 | 0.936897 | 0.937376 | 0.936174 |
| GA-PSO (0.3,0.1,0.6) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937458 | 0.936362 |
| GA-PSO (0.1,0.2,0.7) | 0.905917 | 0.910875 | 0.901097 | 0.93715 | 0.937458 | 0.936349 |
| GA-PSO (0.6,0.2,0.2) | 0.905917 | 0.910875 | 0.901097 | 0.937178 | 0.937478 | 0.936349 |
| DPSO (0.2,0.3,0.5) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937444 | 0.936354 |
| DPSO (0.3,0.2,0.5) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937386 | 0.936362 |
| DPSO (0.1,0.2,0.7) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937466 | 0.936362 |
| DPSO (0.5,0.1,0.4) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| DPSO (0.4,0.1,0.5) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| DPSO (0.3,0.1,0.6) | 0.905917 | 0.910875 | 0.901097 | 0.937207 | 0.937478 | 0.936362 |
| Algorithm and Parameter | Number of Equipment Items and Tasks | |||||
| 14 | 15 | 16 | 17 | 18 | 19 | |
| GA (0.6,0.4) | 0.920982 | 0.927141 | 0.935498 | 0.937482 | 0.949289 | 0.925388 |
| IGA (0.8,0.1,0.1) | 0.921115 | 0.927263 | 0.936067 | 0.938276 | 0.949914 | 0.925894 |
| IGA (0.7,0.2,0.1) | 0.921115 | 0.927266 | 0.936067 | 0.938287 | 0.949892 | 0.925843 |
| IGA (0.6,0.2,0.2) | 0.921115 | 0.927269 | 0.936067 | 0.938286 | 0.949935 | 0.925872 |
| IGA (0.5,0.3,0.2) | 0.921115 | 0.927269 | 0.936067 | 0.938267 | 0.949858 | 0.92572 |
| IGA (0.4,0.3,0.3) | 0.921115 | 0.927266 | 0.936046 | 0.938245 | 0.949771 | 0.925716 |
| IGA (0.3,0.3,0.4) | 0.921078 | 0.927269 | 0.936063 | 0.938189 | 0.949753 | 0.925521 |
| PSO-GA (0.6) | 0.920734 | 0.92711 | 0.935687 | 0.938034 | 0.949794 | 0.925663 |
| GA-PSO (0.3,0.1,0.6) | 0.921099 | 0.92726 | 0.935907 | 0.938218 | 0.949846 | 0.925759 |
| GA-PSO (0.1,0.2,0.7) | 0.921094 | 0.927193 | 0.935904 | 0.938224 | 0.949888 | 0.925741 |
| GA-PSO (0.6,0.2,0.2) | 0.921027 | 0.927247 | 0.936019 | 0.93824 | 0.949925 | 0.92585 |
| DPSO (0.2,0.3,0.5) | 0.92102 | 0.927258 | 0.936053 | 0.938287 | 0.949983 | 0.925886 |
| DPSO (0.3,0.2,0.5) | 0.921103 | 0.927269 | 0.936067 | 0.938287 | 0.949983 | 0.925906 |
| DPSO (0.1,0.2,0.7) | 0.921115 | 0.927268 | 0.936067 | 0.938287 | 0.949978 | 0.925906 |
| DPSO (0.5,0.1,0.4) | 0.921115 | 0.927269 | 0.936067 | 0.938287 | 0.949983 | 0.925906 |
| DPSO (0.4,0.1,0.5) | 0.921115 | 0.927269 | 0.936067 | 0.938287 | 0.949983 | 0.925906 |
| DPSO (0.3,0.1,0.6) | 0.921115 | 0.927269 | 0.936067 | 0.938287 | 0.949983 | 0.925906 |
| Algorithm and Parameter | Number of Equipment Items and Tasks | |||||
| 20 | 21 | 22 | 23 | 24 | 25 | |
| GA (0.6,0.4) | 0.924698 | 0.93266 | 0.948151 | 0.945635 | 0.937196 | 0.932849 |
| IGA (0.8,0.1,0.1) | 0.942251 | 0.940722 | 0.940895 | 0.948123 | 0.936434 | 0.945138 |
| IGA (0.7,0.2,0.1) | 0.942251 | 0.940707 | 0.940848 | 0.948091 | 0.936418 | 0.945083 |
| IGA (0.6,0.2,0.2) | 0.942251 | 0.940727 | 0.94086 | 0.948109 | 0.936401 | 0.945047 |
| IGA (0.5,0.3,0.2) | 0.942251 | 0.940711 | 0.9408 | 0.948031 | 0.936405 | 0.945035 |
| IGA (0.4,0.3,0.3) | 0.942249 | 0.940695 | 0.940781 | 0.948053 | 0.936265 | 0.944858 |
| IGA (0.3,0.3,0.4) | 0.942251 | 0.940613 | 0.940735 | 0.947955 | 0.936355 | 0.94466 |
| PSO-GA (0.6) | 0.942028 | 0.940462 | 0.940715 | 0.948021 | 0.936212 | 0.944911 |
| GA-PSO (0.3,0.1,0.6) | 0.942157 | 0.940702 | 0.940873 | 0.94802 | 0.936288 | 0.94493 |
| GA-PSO (0.1,0.2,0.7) | 0.942062 | 0.940581 | 0.940739 | 0.947989 | 0.936225 | 0.944912 |
| GA-PSO (0.6,0.2,0.2) | 0.942084 | 0.940555 | 0.94081 | 0.948079 | 0.936324 | 0.945145 |
| DPSO (0.2,0.3,0.5) | 0.94223 | 0.94071 | 0.940962 | 0.9481 | 0.936462 | 0.945255 |
| DPSO (0.3,0.2,0.5) | 0.942249 | 0.940732 | 0.941009 | 0.948124 | 0.936484 | 0.945267 |
| DPSO (0.1,0.2,0.7) | 0.942242 | 0.940732 | 0.941009 | 0.948129 | 0.936482 | 0.945276 |
| DPSO (0.5,0.1,0.4) | 0.942251 | 0.940732 | 0.941009 | 0.948129 | 0.936485 | 0.945276 |
| DPSO (0.4,0.1,0.5) | 0.942251 | 0.940732 | 0.941009 | 0.948129 | 0.936485 | 0.945276 |
| DPSO (0.3,0.1,0.6) | 0.942251 | 0.940732 | 0.941009 | 0.948129 | 0.936485 | 0.945276 |
| Algorithm and Parameter | Number of Equipment Items and Tasks | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| GA (0.6,0.4) | 100% | 100% | 99% | 97% | 89% | 97% | 90% | 81% | 77% |
| IGA (0.8,0.1,0.1) | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 99% | 100% |
| IGA (0.6,0.2,0.2) | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| PSO-GA (0.6) | 99% | 99% | 97% | 95% | 92% | 93% | 88% | 91% | 81% |
| GA-PSO (0.3,0.1,0.6) | 100% | 100% | 100% | 100% | 98% | 100% | 97% | 99% | 94% |
| GA-PSO (0.6,0.2,0.2) | 100% | 100% | 100% | 98% | 100% | 99% | 96% | 96% | 94% |
| DPSO | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Algorithm and Parameter | Number of Equipment Items and Tasks | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| GA (0.6,0.4) | 48% | 46% | 55% | 58% | 21% | 12% | 18% | 10% | 7% |
| IGA (0.8,0.1,0.1) | 97% | 96% | 98% | 100% | 99% | 89% | 98% | 96% | 87% |
| IGA (0.6,0.2,0.2) | 99% | 95% | 96% | 100% | 98% | 86% | 97% | 93% | 77% |
| PSO-GA (0.6) | 84% | 86% | 75% | 84% | 78% | 71% | 82% | 79% | 69% |
| GA-PSO (0.3,0.1,0.6) | 94% | 87% | 84% | 91% | 93% | 84% | 84% | 83% | 72% |
| GA-PSO (0.6,0.2,0.2) | 97% | 91% | 89% | 90% | 86% | 84% | 90% | 86% | 80% |
| DPSO | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Algorithm and Parameter | Number of Equipment Items and Tasks | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| GA (0.6,0.4) | 2226 | 4544 | 7299 | 10,334 | 22,411 | 22,703 | 37,218 | 52,963 | 78,680 |
| IGA (0.8,0.1,0.1) | 2152 | 3206 | 3829 | 4906 | 5998 | 6733 | 8202 | 11,879 | 12,107 |
| IGA (0.6,0.2,0.2) | 1016 | 1397 | 1767 | 2390 | 2519 | 3247 | 3910 | 4570 | 5502 |
| PSO-GA (0.6) | 1407 | 2054 | 4339 | 5549 | 11,127 | 11,115 | 20,909 | 21,067 | 41,885 |
| GA-PSO (0.3,0.1,0.6) | 682 | 1282 | 1892 | 2424 | 4489 | 4743 | 7662 | 8182 | 21,488 |
| GA-PSO (0.6,0.2,0.2) | 639 | 984 | 1559 | 3582 | 3776 | 6524 | 9717 | 15,660 | 22,344 |
| DPSO (0.5,0.1,0.4) | 699 | 1226 | 2072 | 2967 | 4438 | 5397 | 7962 | 9579 | 12,810 |
| DPSO (0.4,0.1,0.5) | 622 | 1303 | 1910 | 2879 | 3651 | 4895 | 6265 | 8283 | 10,733 |
| DPSO (0.3,0.1,0.6) | 644 | 1237 | 1874 | 2613 | 3310 | 4407 | 6222 | 7747 | 10,097 |
| Algorithm and Parameter | Number of Equipment Items and Tasks | ||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| GA (0.6,0.4) | 125,956 | 155,587 | 168,004 | 184,432 | 299,930 | 354,558 | 398,367 | 466,670 | 532,595 |
| IGA (0.8,0.1,0.1) | 20,016 | 26,127 | 29,061 | 18,695 | 29,897 | 73,513 | 46,724 | 59,135 | 125,374 |
| IGA (0.6,0.2,0.2) | 8712 | 19,732 | 22,638 | 9329 | 23,594 | 76,462 | 33,057 | 52,605 | 150,233 |
| PSO-GA (0.6) | 40,362 | 52,858 | 83,780 | 70,156 | 98,626 | 137,713 | 110,321 | 137,800 | 222,637 |
| GA-PSO (0.3,0.1,0.6) | 25,750 | 44,814 | 56,354 | 40,915 | 48,824 | 94,523 | 104,378 | 123,837 | 201,774 |
| GA-PSO (0.6,0.2,0.2) | 19,774 | 43,101 | 51,090 | 56,063 | 73,014 | 114,275 | 81,685 | 116,186 | 176,458 |
| DPSO (0.5,0.1,0.4) | 18,052 | 20,118 | 26,519 | 24,658 | 31,859 | 45,711 | 53,620 | 64,200 | 67,979 |
| DPSO (0.4,0.1,0.5) | 12,995 | 17,680 | 19,686 | 18,324 | 24,852 | 30,707 | 35,037 | 37,732 | 43,879 |
| DPSO (0.3,0.1,0.6) | 13,612 | 14,993 | 17,979 | 17,297 | 21,105 | 27,875 | 30,236 | 32,038 | 45,693 |
| Algorithm | Parameter | Success Rate | Astringency | Accuracy | Comprehensive |
|---|---|---|---|---|---|
| GA | Middle | Low | Low | Low | Low |
| IGA | Middle | Middle | High | High | high |
| PSO-GA | Low | Low | Middle | Middle | Middle |
| GA-PSO | High | Middle | Middle | Middle | Middle |
| DPSO | High | High | Highest | Highest | Highest |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yao, W. Research on Transmission Task Static Allocation Based on Intelligence Algorithm. Appl. Sci. 2023, 13, 4058. https://doi.org/10.3390/app13064058
Wang X, Yao W. Research on Transmission Task Static Allocation Based on Intelligence Algorithm. Applied Sciences. 2023; 13(6):4058. https://doi.org/10.3390/app13064058
Chicago/Turabian StyleWang, Xinzhe, and Wenbin Yao. 2023. "Research on Transmission Task Static Allocation Based on Intelligence Algorithm" Applied Sciences 13, no. 6: 4058. https://doi.org/10.3390/app13064058
APA StyleWang, X., & Yao, W. (2023). Research on Transmission Task Static Allocation Based on Intelligence Algorithm. Applied Sciences, 13(6), 4058. https://doi.org/10.3390/app13064058





