Global Mechanical Response Sensing of Corrugated Compensators Based on Digital Twins
Abstract
1. Introduction
2. Method
2.1. Design of Experiments (DoE)
2.2. Gaussian Process Regression Model
2.3. Performance Criterion
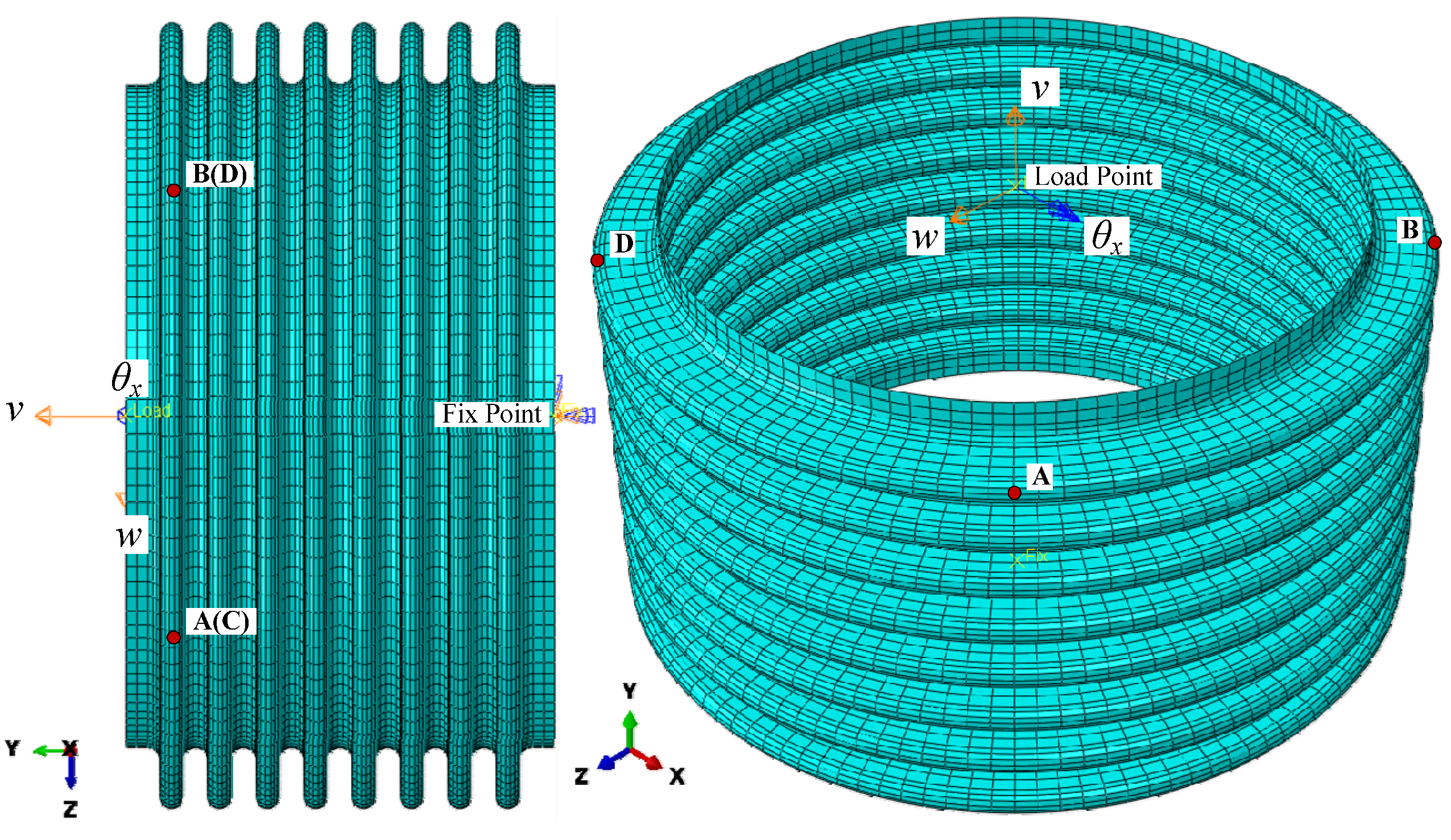
2.4. Finite Element Model
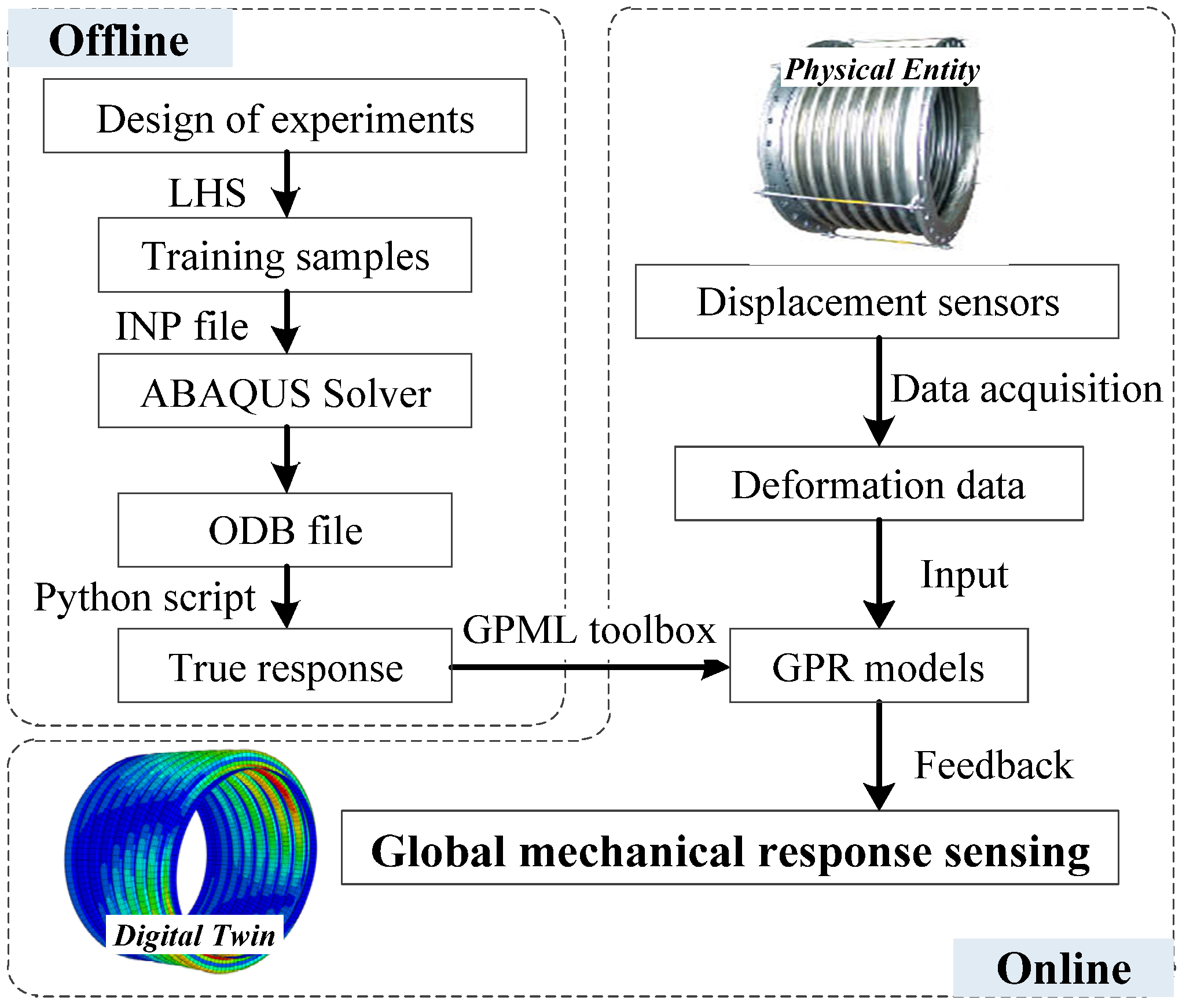
2.5. Construction Process of Digital Twin
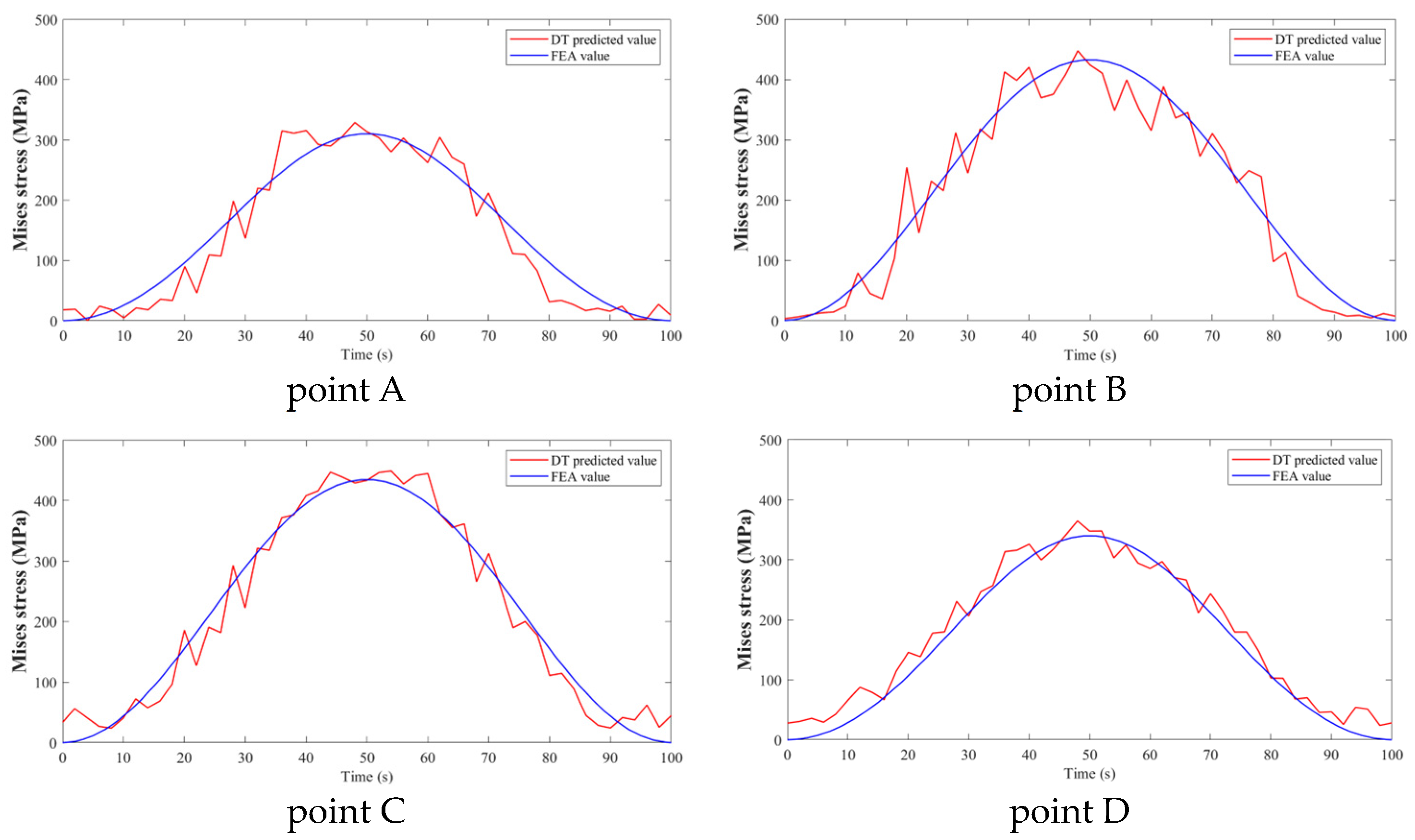
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, L. Optimization Design Research on Expansion Joint Bellows. Master’s Thesis, Southwest University, Chongqing, China, 2003. (In Chinese). [Google Scholar]
- Wang, W.; Yang, Y.; Yan, S.; Li, Z. Research on fatigue life of non-reinforced U-shaped bellows under displacement load. Press. Vessel. Technol. 2022, 39, 63–68. (In Chinese) [Google Scholar]
- Tsukimori, K.; Yamashita, T.; Kikuchi, M.; Iwata, K.; Imazu, A. Fatigue and Creep-Fatigue Life Evaluation of U-Shaped Bellows. J. Press. Vessel. Technol. 1992, 114, 280–291. [Google Scholar] [CrossRef]
- Liu, R. The Design and Implemention System of the Diagnosis and Maintain of Industry Equipment Based on IOT. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2013. (In Chinese). [Google Scholar]
- Yang, H.; Li, Y.; Jiao, S.; Xu, S.; Zhang, J.; Luan, N. Measurement of expansion deformation at an expansion joint in a heating network based on information from distributed temperature sensing. Meas. Sci. Technol. 2019, 30, 45011. [Google Scholar] [CrossRef]
- Pagar, N.S.; Gawande, S.H. Experimental Investigations on Meridional and Circumferential Stresses of Bellows due to Internal Pressure. In Proceedings of the ASME 2019 Gas Turbine India Conference, Chennai, India, 5–6 December 2019. [Google Scholar]
- Pagar, N.; Sanap, S. Investigations on Structural Integrity of Piping Compensators Under Angular Rotational Deformation. In Proceedings of the ASME 2021 Gas Turbine India Conference, Virtual, 2–3 December 2021. [Google Scholar]
- Liu, H.D.; Wang, W.Q.; Liu, Y. Failure Analysis of a Bellows Expansion Joint of Inconel625 Alloy. Adv. Mater. Res. 2012, 500, 580–585. [Google Scholar] [CrossRef]
- Song, X.; Lai, X.; He, X.; Yang, L.; Sun, W.; Guo, D. Key Technologies of Shape-Performance Integrated Digital Twin for Major Equipment. J. Mech. Eng. 2022, 58, 298–325. (In Chinese) [Google Scholar]
- Zheng, Y.; Yang, S.; Cheng, H. An application framework of digital twin and its case study. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 1141–1153. [Google Scholar] [CrossRef]
- Dong, L.T.; Zhou, X.; Zhao, F.B.; He, S.; Lu, Z.Y.; Feng, J.M. Key technologies for modeling and simulation of airframe digital twin. Acta Aeronaut. Astronaut. Sin. 2021, 42, 107–135. (In Chinese) [Google Scholar]
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering Aircraft Structural Life Prediction Using a Digital Twin. Int. J. Aerosp. Eng. 2011, 2011, 154798. [Google Scholar] [CrossRef]
- Zakrajsek, A.J.; Mall, S. The Development and Use of a Digital Twin Model for Tire Touchdown Health Monitoring; American Institute of Aeronautics and Astronautics: Grapevine, TX, USA, 2017. [Google Scholar]
- Haag, S.; Anderl, R. Digital twin—Proof of concept. Manuf. Lett. 2018, 15, 64–66. [Google Scholar] [CrossRef]
- Moi, T.; Cibicik, A.; Rølvåg, T. Digital twin based condition monitoring of a knuckle boom crane: An experimental study. Eng. Fail. Anal. 2020, 112, 104517. [Google Scholar] [CrossRef]
- Wang, S.; Lai, X.; He, X.; Qiu, Y.; Song, X. Building a Trustworthy Product-level Shape-performance Integrated Digital Twin with Multi-fidelity Surrogate Model. J. Mech. Des. 2022, 144, 3. [Google Scholar] [CrossRef]
- Lai, X.; Wang, S.; Guo, Z.; Zhang, C.; Sun, W.; Song, X. Designing a Shape—Performance Integrated Digital Twin Based on Multiple Models and Dynamic Data: A Boom Crane Example. J. Mech. Des. 2021, 143, 7. [Google Scholar] [CrossRef]
- He, X.; Qiu, Y.; Lai, X.; Li, Z.; Shu, L.; Sun, W.; Song, X. Towards a shape-performance integrated digital twin for lumbar spine analysis. Digit. Twin 2022, 8, 1–17. [Google Scholar] [CrossRef]
- Song, X.; He, X.; Li, K.; Lai, X.; Li, Z. Construction Method and Application of Human Skeleton Digital Twin. J. Mech. Eng. 2022, 1–11. (In Chinese) [Google Scholar]
- He, Z.; Liu, G.; Zhao, X.; Wang, M. Overview of Gaussian Process Regression. Control. Decis. 2013, 28, 1121–1129. (In Chinese) [Google Scholar]
- Görtler, J.; Kehlbeck, R.; Deussen, O. A Visual Exploration of Gaussian Processes. Distill 2019, 4, e17. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Guo, Z.; Song, L.; Park, C.; Li, J.; Haftka, R.T. Analysis of dataset selection for multi-fidelity surrogates for a turbine problem. Struct. Multidiscip. Optim. 2018, 57, 2127–2142. [Google Scholar] [CrossRef]
- Loeppky, J.L.; Sacks, J.; Welch, W.J. Choosing the Sample Size of a Computer Experiment: A Practical Guide. Technometrics 2009, 51, 366–376. [Google Scholar] [CrossRef]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Nascimbene, R. Penalty partial reduced selective integration: A new method to solve locking phenomena in thin shell steel and concrete structures. Curved Layer. Struct. 2022, 9, 352–364. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Gu, B.; Liu, Y.; Duan, M. The Finite Element Analysis to the U-shape Bellows by the ANSYS Program. Press. Vessel. Technol. 2000, 17, 34–36. (In Chinese) [Google Scholar]
- Rasmussen, C.E.; Nickisch, H. Gaussian Processes for Machine Learning (GPML) Toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Chen, Z.; Wang, B. How priors of initial hyperparameters affect Gaussian process regression models. Neurocomputing 2018, 275, 1702–1710. [Google Scholar] [CrossRef]



| Outer Diameter (mm) | Inner Diameter (mm) | Number of Layers | |
|---|---|---|---|
| Geometric Parameters | 363 | 295 | 1 |
| Wall thickness (mm) | Wave height (mm) | Effective length (mm) | |
| 1.2 | 34 | 352.8 | |
| Wave distance (mm) | Wave crest (valley) radius (mm) | Number of waves | |
| 44 | 10.4 | 8 | |
| Material properties | Material Type | Elastic modulus (MPa) | Poisson’s ratio |
| 304 Stainless Steel | 1.95 × 105 | 0.3 |
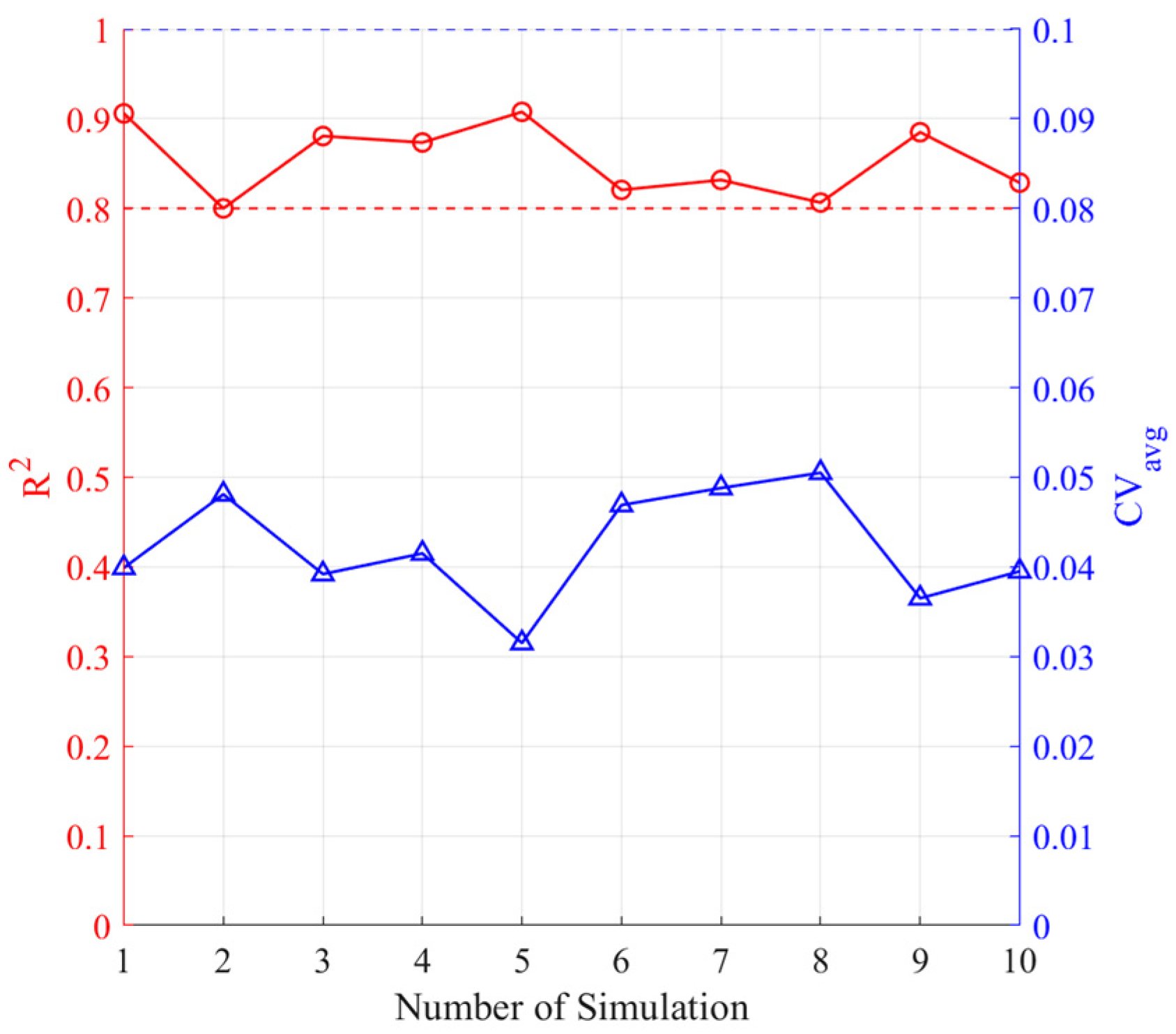
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.9060 | 0.8000 | 0.8807 | 0.8735 | 0.9077 | 0.8206 | 0.8317 | 0.8065 | 0.8850 | 0.8287 | 0.8540 ± 0.0409 |
| CVavg | 0.0399 | 0.0481 | 0.0392 | 0.0415 | 0.0315 | 0.0469 | 0.0488 | 0.0505 | 0.0365 | 0.0395 | 0.0422 ± 0.0061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Jiang, J.; Qin, J.; Du, N.; Shi, H.; Wang, Y. Global Mechanical Response Sensing of Corrugated Compensators Based on Digital Twins. Appl. Sci. 2023, 13, 4048. https://doi.org/10.3390/app13064048
Zhou R, Jiang J, Qin J, Du N, Shi H, Wang Y. Global Mechanical Response Sensing of Corrugated Compensators Based on Digital Twins. Applied Sciences. 2023; 13(6):4048. https://doi.org/10.3390/app13064048
Chicago/Turabian StyleZhou, Run, Jingyan Jiang, Jianhua Qin, Ning Du, Haoran Shi, and Ying Wang. 2023. "Global Mechanical Response Sensing of Corrugated Compensators Based on Digital Twins" Applied Sciences 13, no. 6: 4048. https://doi.org/10.3390/app13064048
APA StyleZhou, R., Jiang, J., Qin, J., Du, N., Shi, H., & Wang, Y. (2023). Global Mechanical Response Sensing of Corrugated Compensators Based on Digital Twins. Applied Sciences, 13(6), 4048. https://doi.org/10.3390/app13064048





