Abstract
The Radon transform constitutes the conventional tool for tomosynthesis, i.e., the composition of cross-sections of an object from its projections. It is actually a version of the Fourier Transform, which is accompanied by the appropriate digital high pass filters for correct distribution of energy among the reconstructed frequency components. The Radon transform and its inverse are employed in their 2D and 3D versions, respectively, and the whole procedure is verified by the a priori known cross-sections to be reconstructed (known fandom). Usually, 3D medical image cubes, which are to be reconstructed, require powerful computational tools since the 2D projections are of high-resolution containing millions of pixels. Although the 3D FFT is very fast, the large number of projections will result in a 3D spectrum of very large dimensions. Inverting this spectrum with the inverse 3D FFT is extremely time consuming. In this work, the implementation of the 2D Radon transform using the 2D Quantum Fourier Transform is analytically presented. Simultaneously, its inverse version is realized by means of the Quantum inverse 3D FFT. For this purpose, a review of the necessary quantum computational units is presented for the implementation of the quantum 3D FFT and simultaneously simple examples of tomosynthesis are given by means of the quantum version of the 2D Radon transform and its inverse 3D counterpart. The whole procedure of the quantum tomosynthesis is analytically described.
1. Introduction
The Fast Fourier Transform (FFT) gives the means for frequency analysis and filtering avoiding the operation of convolution. The Quantum version of the Fourier Transform (QFT) provides the opportunity to obtain very fast the results derived by the FFT. The use of the QFT has been investigated for various applications. Accordingly, in [1], it is proved that a quantum version for the filtering operation can be achieved, even though the quantum convolution of two sequences is physically impossible [2]. There are important differences between the classical and the quantum implementations for image filtering. These differences are analyzed in [1], and it is shown that the major advantage of the quantum approach lies in the exploitation of the efficient implementation of the QFT. In [3], a survey is provided with some topics on the properties of quantum gates and their assembly into interesting quantum circuits.
The application of the QFT within the field of quantum computation has been extensively presented in [4]. Shor’s algorithm, phase estimation and computing discrete logarithms are some classic examples of its use. These special properties of quantum algorithms have resulted in novel solutions to problems difficult to be solved on a classical computer. The QFT has been used in several applications [5,6,7]. Since QFT is the core to a lot of quantum algorithms, current research is mainly focused to its effective realization [7,8,9,10,11,12,13].
A review on quantum image processing is presented in [14], revealing the possibilities for intensive image processing procedures due to the powerful parallel computing capabilities of quantum computers. In [15], a quantum implementation of the FFT algorithm composed of a combination of quantum gates is proposed. A QFT has been implemented in [16] on a three-qubit nuclear magnetic resonance quantum computer to extract the periodicity of an input state. A fast quantum image component labeling algorithm was proposed in [17], which is the quantum counterpart of classical local operator technique. A quantum color image encryption algorithm was designed in [18] based on geometric transformation and intensity channel diffusion. A framework of quantum image filtering in the spatial domain was proposed in [19]. A quantum image median filtering approach is proposed, and its corresponding quantum circuit is designed in [20]. The main idea of the approach is that the classical image is converted into a quantum version based on the novel enhanced quantum representation of digital images, and then a unique quantum module is designed to realize the median calculation of neighborhood pixels for each pixel point in the image. In [21], the authors considered QFT-based color image filtering operations and their applications in image smoothing, sharpening, and selective filtering using quantum frequency domain filters. The proposed quantum filters use the principle of the quantum Oracle to implement the filter function.
The stroboscopic approach to quantum tomography originated in 1983 when A. Jamiolkowski published a theorem on the minimal number of distinct observables required for tomography of systems evolving according to the von Neumann equation [22]. The approach was developed in subsequent articles and applied to open quantum systems with evolution given by the Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) generators [23,24,25]. Among others, a general formula was proved for the minimal number of distinct observables for quantum tomography of systems with evolution given by the GKSL generator [26]. Quantum state tomography plays an important role in the field of quantum information. It can determine the mathematical representation of an unknown quantum system by measuring a large number of replicated quantum states to estimate them in real time [27]. Experimentally, there have been numerous proposals on the preparation of high dimensional probes on the physical architectures, such as superconducting circuits, color center spins nuclear magnetic resonance, nitrogen vacancy center, Rydberg atoms, and trapped ions [28,29,30,31,32]. A new numerical algorithm for the inversion of the Radon transform based on Chebyshev polynomials of the first kind is presented in [33]. By employing first-kind Chebyshev polynomial approximation, the computation of the derivative of the Hilbert transform of the sinogram is significantly simplified. Finally, in [34], an optical line scanning imaging technique is proposed by rotating a single cylindrical lens perpendicular to the optical axis. A two-step Radon transform was designed to obtain accurate rotation status of the cylindrical lens with diffraction patterns at the focal plane.
In the present work, the way that the basic quantum circuits are combined to build up the QFT structure is extensively presented. This structure is applied in the very well-known separable procedure in order to implement the 2D QFT and its 3D counterpart to implement the 2D Radon transform and its 3D back projection procedure, respectively. Reconstruction tomographic results are given to show off the applicability of the procedure.
The paper is organized in the following way. In Section 2, the quantum circuitry for supporting the QFT is presented. In Section 3, the basics in computed tomography are given in some detail. In Section 4, the use of the QFT for implementing the 2D Radon transform and the 3D back projection procedure is analyzed. Experimental results are presented in Section 5. Finally, the conclusions are drawn in the last section.
2. Quantum Computational Units
2.1. Quantum Fourier Transform Theory
The Fourier transform occurs in many different versions in all areas from signal processing to complexity theory and data compression [35,36,37]. The QFT is the classical discrete Fourier transform applied to the vector of amplitudes of a quantum state, where we usually consider vectors of length .
The discrete Fourier transform acts on a vector and maps it to the vector , according to the formula:
where and is an j-th root of unity.
Similarly, the QFT acts on a quantum state and maps it to a quantum state , according to the formula:
Since is a rotation, the Inverse Quantum Fourier Transform (IQFT) acts similarly:
In case that is a basis state, the QFT can also be expressed as the map:
Equivalently, the QFT can be viewed as a unitary matrix (or quantum gate) acting on quantum state vectors, where the unitary matrix is given by
where .
Most of the properties of the QFT follow from the fact that it is a unitary transformation. This can be checked by performing matrix multiplication and ensuring that the relation holds, where is the Hermitian adjoint of . Alternately, one can check that orthogonal vectors of norm 1 are mapped to orthogonal vectors of norm 1.
From the unitary property, it follows that the inverse of the QFT is the Hermitian adjoint of the Fourier matrix, thus . Since there is an efficient quantum circuit implementing the QFT, the circuit can be run in reverse to perform the IQFT. Thus, both transforms can be efficiently performed on a quantum computer.
The QFT transforms between two bases, the Fourier basis and the computational basis (Z). The H-gate is the single-qubit QFT, and it transforms between the Z-basis states and to the X-basis states and . In the same way, all multi-qubit states in the computational basis have corresponding states in the Fourier basis. The QFT is simply the tool that transforms between these bases.
2.2. Circuitry for Implementing QFT
The circuit implementation of QFT makes use of two gates. The one of them is the single-qubit Hadamard gate , and the other one is the phase gate .
Consider how the QFT operates on a single-qubit state (1-qubit QFT) Where , , and .
And
Thus, the final result is the state
This operation is exactly the result of applying the Hadamard gate on the qubit. If we apply the Hadamard gate to the state , we obtain a new state:
The Hadamard gate H for n-qubit is given
where is the Kronecker product, i.e., for , we have the Hadamard gate
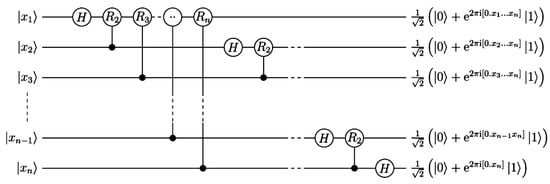
Figure 1.
The circuit implementation of n-qubit QFT using the Hadamard gate and the phase gate .
The basis states that enumerate all the possible states of the n-qubits is
where indicates that qubit is the state , with being either 1 or 0. The basis state index is the binary number encoded by with being the most significant bit. Thus, we can write the QFT as
After rearranging the sum and the products and expanding the action of the QFT can be expressed by:
i.e., for 3-qubit QFT
In a similar way, one can extend to n-qubit QFT.
3. Theory of Tomography
3.1. Radon Transform
The Radon transform, which is the basis of analytical reconstruction methods, relates a two-dimensional function to the set of curvilinear integrals of this function. Emission (such as PET and SPECT) or transmission (such as CT) imaging systems take measurements that look similar to fuzzy curvilinear integrals; thus, the above transform model is an idealization of such systems [14]. Applying the Radon transform to an image cube (human body) for a given set of angles can be thought of as computing the projection of the image cube along those angles. The resulting projection, in a 2D representation (Figure 2), is the sum of the pixel luminances in each direction, i.e., a contour integral. The result is a new image . This can be written mathematically by defining
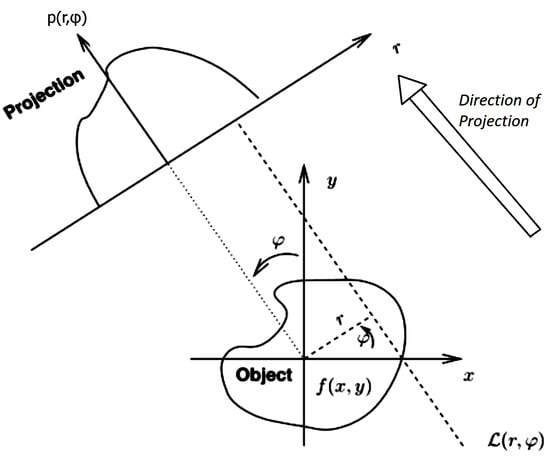
Figure 2.
Schematic representation of projection in two dimensions (2D) when performing the Radon transform.
Thus, we can write the Radon transform as:
where is the known unit impulse.
There are other ways of symbolizing this contour integral, each of which may be needed for different purposes. In its most idealized form, the image reconstruction problem is to recover from the projections , i.e., to apply the inverse Radon transform. To do this, we need to somehow return from the “projection field” (i.e., the Radon transform) to the “object field” (i.e., the image).
3.2. Back Projection
The back projection process is an attempt to reverse the Radon transform process. The problem here is that we have no specific information about the density variations, except its average for each projection, i.e., essentially measuring the attenuation along a line. One approach to receive the original object given the Radon transform of the object is to take all the values of the sinogram and try to spread them back into the image field, as shown in Figure 3 in 2D representation. The result we receive will be the original image but blurred. We can deal with this problem with various inversion methods of the Radon transform, as it is explained in the following.
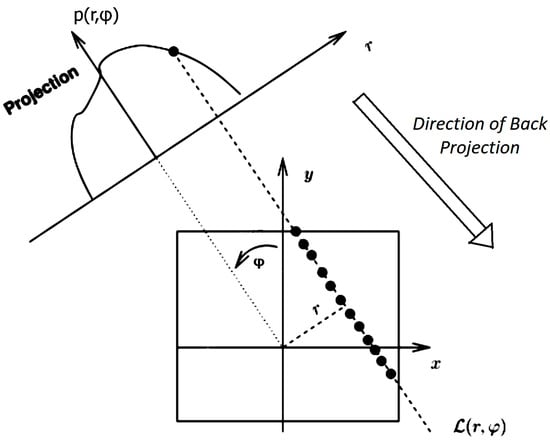
Figure 3.
Back projection. The information of the sinogram is spread back to the position of the initial image.
Some of the properties of the Radon transform are the following:
Linearity
If then,
Displacement
Rotation
Circular Symmetry
Magnification
Inversion
Projection integral theorem
For a scalar function h: R→R:
3.3. Sinogram and Fourier Section or Central Section Theorem
A sinogram is a way of displaying the data resulting from applying the Radon transform to the object . By having the function and setting the distance r on the horizontal axis and the angle on the vertical axis, we receive an image, such as the one in Figure 4. The named sinogram is because if we plot the projection function of an image consisting of only one point, we will receive the graph of a sinusoidal function.
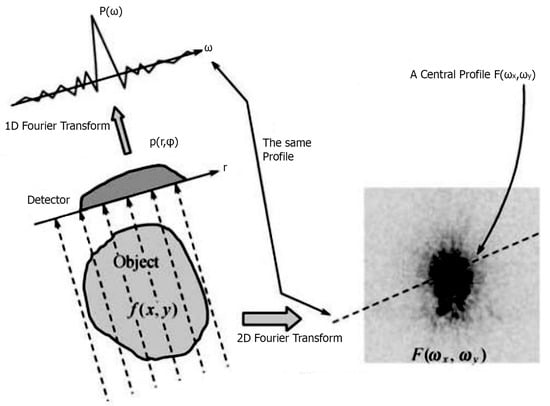
Figure 4.
Central section theorem in two dimensions.
The Fourier section or central section theorem is the foundation of tomographic imaging. The central intersection theorem in two dimensions states that the 1D Fourier transform P(ω) of the projection of a 2D function is equal to an intersection through the origin of the axes of the 2D Fourier transform of this function and is parallel to this projection (Figure 4).
If we project our object over a range of at least 180 degrees, the corresponding central intersection of the 2D Fourier transform will be rotated simultaneously and cover the entire 2D Fourier space. In other words, we can measure the entire 2D Fourier transform of the image, thus now we can take the inverse 2D Fourier transform to receive the image (Figure 5).
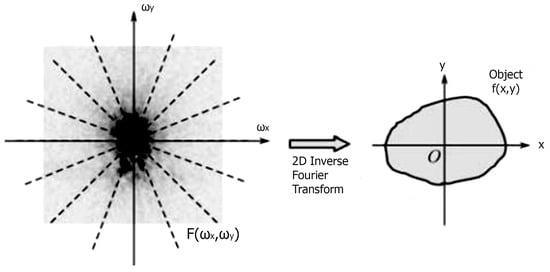
Figure 5.
Image reconstruction using the Fourier intersection theorem.
If we simply fill in the 2D Fourier space with its various intersections, the density grows closer to the origin of the axes. In short, the low frequencies outweigh the high frequencies, thus our image will be a blurry version of the original. Accordingly, what we will receive with this process will not be our original image, but we have a blurring created by the uneven distribution of low and high frequencies. This inequality of frequency density is proportional to the quantity
It is proportional to the distance from the origin of the axes. Thus, a simple way to restore equal frequency distribution is to multiply the reshaped 2D Fourier transform by . If we take the inverse transform after, then we will have the true original image .
3.4. Reconstruction Simulation
In the experiments we conducted, the 3D data cube (fandom), shown in Figure 6, was employed. The fandom contains a large sphere with the same intensity (no. 2), a truncated cone with increasing intensity downwards (no. 1), an inclined cylinder with increasing intensity upwards (no. 3), a white parallelepiped inside the sphere (no. 4), and four spheres with various intensities inside the cone (nos. 5–8).
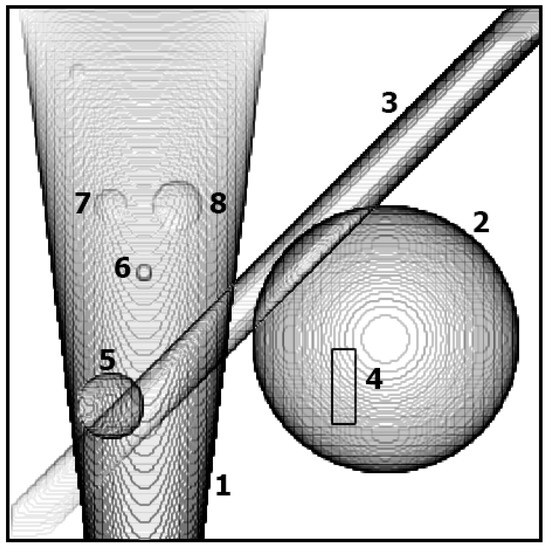
Figure 6.
A 3D fandom (data cube) containing a large sphere with the same intensity (no. 2), a truncated cone with increasing intensity downwards (no. 1), an inclined cylinder with increasing intensity upwards (no. 3), a white parallelepiped inside the sphere (no. 4), and four spheres with various intensities inside the cone (nos. 5–8).
The 2D projections of the 3D fandom were obtained every 0.7 degrees around it, covering 180 degrees so that a total of 256 projections are obtained. Projections that could be obtained from the rest aspects from the supplementary angles are not needed since they provide the same information as the initial 256 projections. Three of the projections are given in Figure 7. Specifically, the projections 1st, 110th, and 180th are presented, which correspond to rotation angles 0.7, 77, and 126 degrees.
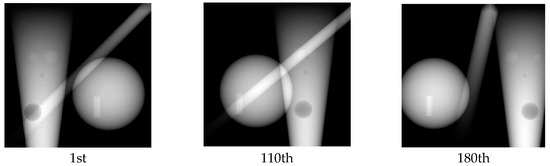
Figure 7.
Three of the projections of the 3D data cube of Figure 6. The projections 1st, 110th, and 180th corresponding to rotation angle 0.7, 77, and 126 degrees.
For each one of the 256 projections, the corresponding 2D spectrum is evaluated by means of the 2D QFT. In Figure 8, the amplitude of the 2D Fourier Transform for the 110th projection is given, i.e., the projection with a 77-degree angle. All of these 256 projections are combined in a radial arrangement, as shown in Figure 5 (left Figure, top view) to give a cube of spectra of the fandom in Figure 6. In actuality, this cube has the spectral content of the fandom in Figure 6 but with greater density in the center. Before inversely transforming by means of the inverse 3D QFT to the original fandom, the cube with the spectral content must be multiplied with the quantity

Figure 8.
The amplitude of the 2D QFT for the 110th projection, i.e., projection angle 77 degrees.
The whole procedure includes the following steps:
- Projections acquisition as those shown in Figure 7.
- Evaluation, using the 2D QFT, of the 2D spectra of the above projections.
- The derived 3D spectrum is filtered (multiplied) by a 3D filter of the type .
- On the new 3D spectrum, the inverse 3D QFT is applied in order to derive the 3D fandom.
In the next section, the Quantum 2D and 3D versions of the Fourier Transforms are applied in order to implement the above five-step procedure.
4. The Radon Transform and the Back Projection by Means of the Inverse 3D QFT
Based on the five-step procedure described previously, the implementation of the whole procedure requires, firstly, a 2D QFT stage to evaluate the spectrum of the projections, such as the one in Figure 8. A new filter block is used to radially distribute the spectra of the projections and multiply with the quantity in Equation (19). The output of this block is further fed to the Inverse 3D QFT procedure. Accordingly, the above stages are analyzed in the following subsections and are given in a block diagram at the end of this section.
4.1. The 2D Quantum Fourier Transform
The 2D QFT was analyzed in [1], hence it is not necessary to further elaborate on this issue. The quantum blocks to be used in the following are of the same operational performance as in [1].
4.2. The 3D Discreet Fourier Transform
The three-dimensional DFT is a separable procedure. This comes out from the fact that its expression
can be written as follows
Accordingly, a total of of complex operations are required. In another way, we must perform N-points FFTs along: all horizontal lines, all horizontal rows, and all vertical columns, regardless of the order they are going to be performed, as it is depicted in Figure 9 for N = 4. From this Figure and Equation (21), it is evident that the order of the implementation of the 1D transforms, i.e., the order of the summations in Equation (21), does not matter.
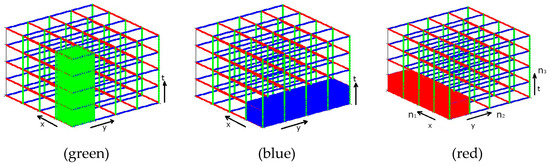
Figure 9.
A 3D image cube of 4 × 4 × 4 pixels. Since the 3D FFT is a separable procedure, it can be performed in 3 phases (green, blue, red). In each phase, the result from the previous phase is used as input. The obtained result of the 3D FFT procedure is irrelevant of the order that the 3 above phases are applied.
4.3. Quantum 3D Fourier Transform
A quantum cube can be represented by a quantum register Q constructed so that it encodes all required information, i.e., the position of a pixel in the data cube (x, y, z), as well as the intensity or color (c) of the pixel. We assume that we have 2n × 2n × 2n pixels in the data cube, and the color of each pixel requires m bits for its representation.
In this case, a register |P> having 3n qubits is adequate to hold all position information, while a register |C> with m qubits will represent 2m different colors or grayscale levels. The register |P> is separated into three sub-registers of n qubits each containing the row, column, and the level information in the form |y>|x>|z>. The quantum register Q, containing all the information of the quantum frame cube, can be expressed as:
In Equation (22) the coefficients aij sum up to one:
and are used to express the color of a pixel with position i by means of a superposition of all possible colors. For a given pixel i, the coefficients aij take the value 1 if the color of the pixel is j and 0 otherwise. This is illustrated in Figure 10 with a simple example of a 2 × 2 × 2 frame cube with eight colors (0–7), for which the values of the coefficients aij are given in the following in a form of a matrix:
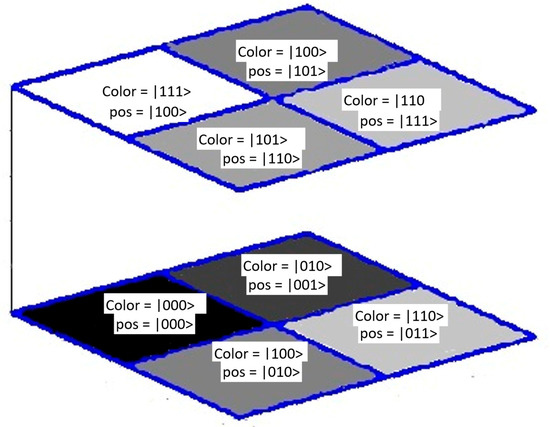
Figure 10.
This is an example of 2 × 2 × 2 quantum cube with eight different colors. Three qubits are used to represent color information and three-pixel position information.
The quantum register Q, expressed by Equation (22), is experimentally implemented by the circuit of Figure 11.
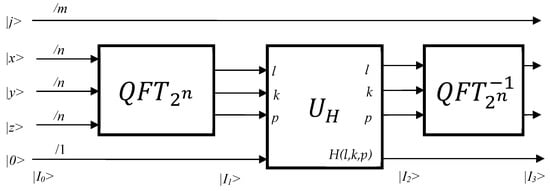
Figure 11.
Implementation of the quantum circuit for 3D filtering.
As shown in the block diagram of Figure 11, at the output of the quantum filtering circuit we actually find the input image cube. Additionally, by exploiting the quantum interference phenomenon, we can use an additional qubit initially in state to reinterpret the quantum image cube as a superposition of two image cubes. For example, for a high- or low-pass 3D filter, the output image is the sum of the image cube containing the high frequencies and the image cube containing the corresponding low frequencies. The additional qubit can be used to make the distinction between the two image cubes.
For implementing the Radon and the Inverse Radon transform as it was exposed in Section 3, the block diagram in Figure 11 is modified so that
- A 2D QFT is used in the input stage to provide the spectra of the 256 2D projections of the fandom taken as input.
- The projections spectra are radially placed to create the 3D spectrum of the initial data (fandom).
- This 3D spectrum is properly interpolated and normalized by multiplying with the function .
- The 3D inverse QFT is applied to provide the required fandom cube.
The whole procedure is depicted in Figure 12.
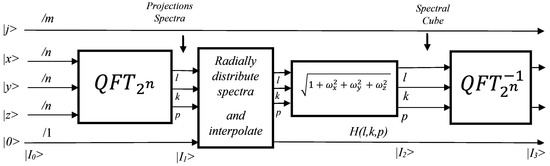
Figure 12.
The Radon and the inverse Radon transform using 2D QFT and 3D inverse QFT for image cube reconstruction.
In the following, we analyze this process and describe the state of the quantum reconstruction tomosynthesis filtering circuit at each step of the computation, as marked in Figure 12. The input state is represented by the input image cube and an additional qubit in state :
where holds the quantum image cube using the representation described previously.
The first block in Figure 12 evaluates, using the 2D QFT, the spectra of the projections of the image cube (fandom). The second block distributes the spectra of the projections radially and interpolates the values in the spectral cube. The third block normalizes the spectral content, multiplying it with the quantity . Finally, the 3D inverse QFT is applied to obtain the original image cube, from which the cross-sections are available.
5. Experimental Results
The experimental results were obtained by making use of the procedure given in Figure 12. The original fandom in Figure 6 was projected so that its projections and their spectra were obtained at the output of the first block of Figure 12. The inverse Radon transform was then applied based on the three blocks on the right of Figure 12. In Figure 13, the cross-sections at levels 90 and 170 of the fandoms are presented. On the left of the figure, the cross-sections appeared as they were designed. At the center of the figure, the corresponding cross-sections appeared as they were reconstructed by the tomosynthesis method using the inverse 3D QFT. At the right, no filtering was used to normalize frequencies in the spectral cube before applying the inverse 3D QFT.

Figure 13.
On the left, the cross-sections appear as they were designed. At the center, the corresponding cross-sections appear as they were reconstructed by the tomosynthesis method using the inverse 3D QFT. At the right, no filtering was used to normalize frequencies in the spectral cube before applying the inverse 3D QFT.
In Figure 14, details of the reconstructed 90th cross-section are provided in comparison with its initial shape. The same procedure was applied in other data cubes as well, and the obtained results were satisfactory as well. The derived cross sections are almost of the same quality as the original cross sections of the image cube.

Figure 14.
Details of the reconstructed 90th cross-section (right) in comparison with its initial shape (left).
6. Conclusions
The whole procedure for tomosynthesis reconstruction from projections was carried out by means of the 2D and 3D QFT, implementing the quantum version of the 2D Radon transform and the inverse 3D Radon transform, respectively. The whole procedure contains three distinctive stages:
- Evaluating the projections of the original fandom and computing their 2D QFT transform, so that their spectra are available (2D radon transform).
- Evaluating the 3D spectrum of the initial data cube by radially placing the spectra of the projections and simultaneously properly normalizing (filtering), so that high frequencies are amplified.
- Inverting the 3D spectrum by means of the inverse 3D QFT, so that the required data cube is obtained. Cross sections are now available from the reconstructed data cube.
The experimental results proved the efficiency of the proposed quantum approach and the high quality of the obtained cross-sections. Improvements of the 2nd and 3rd blocks in Figure 12 were currently investigated in order to optimize their performance and perfectly match their operation in the whole procedure.
Experimental results were carried out in this work simulating the QFT and its inverse based on the equations in Section 2 and Section 4 with MATLAB. For this purpose, software was developed in order to implement the Hadamard and the Controlled Phase gates. In a Quantum Computer, a 3D quantum object with a coherent wavefunction would be a reality.
Author Contributions
All authors have contributed to this work almost equally in all aspects of its conceptualization, realization, and presentation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There are no data sets related to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Caraiman, S.; Manta, V.I. Quantum Image Filtering in the Frequency Domain. Adv. Electr. Comput. Eng. 2013, 13, 77–84. [Google Scholar] [CrossRef]
- Lomont, C. Quantum Convolution and Quantum Correlation Algorithms Are Physically Impossible. arXiv 2003. [Google Scholar] [CrossRef]
- Divincenzo, D.P. Quantum Gates and Circuits. arXiv 1998. [Google Scholar] [CrossRef]
- Sakk, E. Chapter of Real Perspective of Fourier Transforms and Current Developments in Superconductivity. In Quantum Fourier Operators and Their Application; IntechOpen: London, UK, 2021; pp. 1–15. [Google Scholar]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Josza, R. Quantum Algorithms and the Fourier Transform. Proc. R. Soc. Lond. A 1998, 454, 323–337. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Barenco, A.; Ekert, A.; Suominen, K.A.; Torma, P. Approximate quantum Fourier transform and decoherence. Phys. Rev. A 1996, 54, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Fowler, A.; Hollenberg, L.C.L. Scalability of Shor’s algorithm with a limited set of rotation gate. Phys. Rev. A 2004, 70, 032329. [Google Scholar] [CrossRef]
- Pavlidis, A.; Gizopoulos, D. Fast Quantum Modular Exponentiation Architecture for Shor’s Factorization Algorithm. arXiv 2014, arXiv:1207.0511. [Google Scholar] [CrossRef]
- Prokopenya, A.N. Approximate Quantum Fourier Transform and Quantum Algorithm for Phase Estimation. In International Workshop on Computer Algebra in Scientific Computing; Springer: Cham, Switzerland, 2015; pp. 391–405. [Google Scholar]
- Ruiz-Perez, L.; Garcia-Escartin, J.C. Quantum arithmetic with the quantum Fourier transform. Quantum Inf. Process. 2017, 16, 152. [Google Scholar]
- Nam, Y.; Su, Y.; Maslov, D. Approximate quantum Fourier transform with O(n log(n)) T gates. NPJ Quantum Inf. 2020, 6, 26. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, M.; Zhang, Y. Review of Quantum Image Processing. Arch. Comput. Methods Eng. 2022, 29, 737–761. [Google Scholar] [CrossRef]
- Asaka, R.; Sakai, K.; Yahagi, R. Quantum circuit for the fast Fourier transform. Quantum. Inf. Process. 2020, 19, 277–296. [Google Scholar] [CrossRef]
- Weinstein, Y.S.; Pravia, M.A.; Fortunato, E.M.; Lloyd, S.; Cory, D.G. Implementation of the Quantum Fourier Transform. Phys. Rev. Lett. 2001, 86, 1889. [Google Scholar] [CrossRef]
- Li, Y.; Hao, D.; Xu, Y.; Lai, K. A Fast Quantum Image Component Labeling Algorithm. Mathematics 2022, 10, 2718. [Google Scholar] [CrossRef]
- Song, X.; Chen, G.; Abd El-Latif, A.A. Quantum Color Image Encryption Scheme Based on Geometric Transformation and Intensity Channel Diffusion. Mathematics 2022, 10, 3038. [Google Scholar] [CrossRef]
- Yuan, S.; Mao, X.; Zhou, J.; Wang, X. Quantum Image Filtering in the Spatial Domain. Int. J. Theor. Phys. 2017, 56, 2495–2511. [Google Scholar] [CrossRef]
- Jiang, S.; Zhou, R.G.; Hu, W.; Li, Y. Improved Quantum Image Median Filtering in the Spatial Domain. Int. J. Theor. Phys. 2019, 58, 2115–2133. [Google Scholar] [CrossRef]
- Li, P.; Xiao, H. An Improved Filtering Method for Quantum Color Image in Frequency Domain. Int. J. Theor. Phys. 2018, 57, 258–278. [Google Scholar] [CrossRef]
- Jamiołkowski, A. The minimal Number of Operators for Observability of N-level Quantum Systems. Int. J. Theor. Phys. 1983, 22, 369–376. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely Positive Dynamical Semigroups of N-level Systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Manzano, D. A short introduction to the Lindblad master equation. AIP Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
- Jamiołkowski, A. On complete and incomplete sets of observables, the principle of maximum entropy–revisited. Rep. Math. Phys. 2000, 46, 469–482. [Google Scholar] [CrossRef]
- Paris, M.G.A.; Rehacek, J. (Eds.) Quantum-State Estimation; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted Photons: New Quantum Perspectives in High Dimensions. Light. Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef]
- Soltamov, V.; Kasper, C.; Poshakinskiy, A.; Anisimov, A.; Mokhov, E.; Sperlich, A.; Tarasenko, S.; Baranov, P.; Astakhov, G.; Dyakonov, V. Excitation and Coherent Control of Spin Qudit Modes in Silicon Carbide at Room Temperature. Nat. Commun. 2019, 10, 1678. [Google Scholar] [CrossRef]
- Klimov, A.B.; Guzmán, R.; Retamal, J.C.; Saavedra, C. Qutrit Quantum Computer with Trapped Ions. Phys. Rev. A 2003, 67, 062313. [Google Scholar] [CrossRef]
- Abobeih, M.; Randall, J.; Bradley, C.; Bartling, H.; Bakker, M.; Degen, M.; Markham, M.; Twitchen, D.; Taminiau, T. Atomic-Scale Imaging of a 27-Nuclear-Spin Cluster using a Quantum Sensor. Nature 2019, 576, 411–415. [Google Scholar] [CrossRef]
- Protonorios, N.E.; Fokas, A.S.; Vrachliotis, A.; Marinakis, V.; Dikaios, N.; Kastis, G.A. Reconstruction of preclinical PET images via Chebyshev polynomial approximation of the sinogram. Appl. Sci. 2022, 12, 3335. [Google Scholar] [CrossRef]
- Geng, Y.; Tan, J.; Guo, C.; Shen, C.; Ding, W.; Liu, S.; Liu, Z. Computational coherent imaging by rotating a cylindrical lens. Opt. Express 2018, 26, 22110–22122. [Google Scholar] [CrossRef]
- Coppersmith, D. An Approximate Fourier Transform Useful in Quantum Factoring. arXiv 1994. [Google Scholar] [CrossRef]
- Quantum Fourier Transform. Available online: https://en.wikipedia.org/wiki/Quantum_Fourier_transform (accessed on 19 March 2021).
- Preskill, J. Quantum Information and Computation. Lecture Notes for Physics 229: CIT; California Institute of Technology: Pasadena, CA, USA, 1998; pp. 1–321. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).