Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems
Abstract
:1. Introduction
2. Theoretical Models
2.1. Conductivity Analysis of Coupled System Substructures
2.2. Solving for the Conductance Function of a Thin Underwater Cylindrical Shell
2.3. Level Drop, Transmitted Power Flow, Sound Pressure at the Hydroacoustic Field and Total Radiated Sound Power of the Coupled System
3. Analysis of Acoustic Vibration Transfer Characteristics of Coupled Systems
3.1. Structural Parameters of the Coupling System
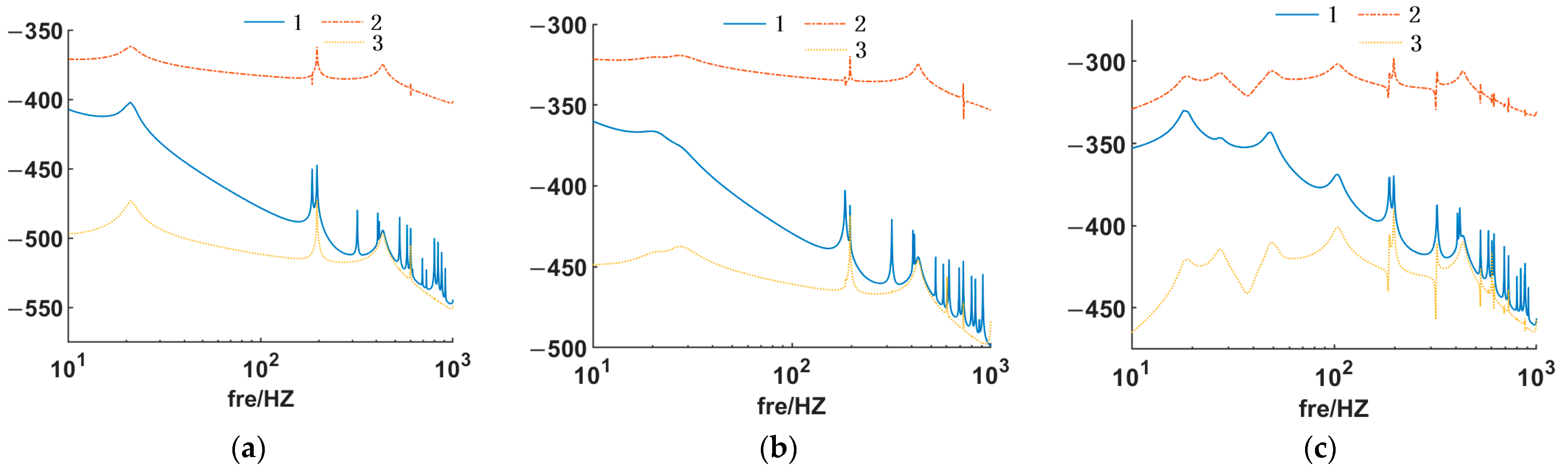
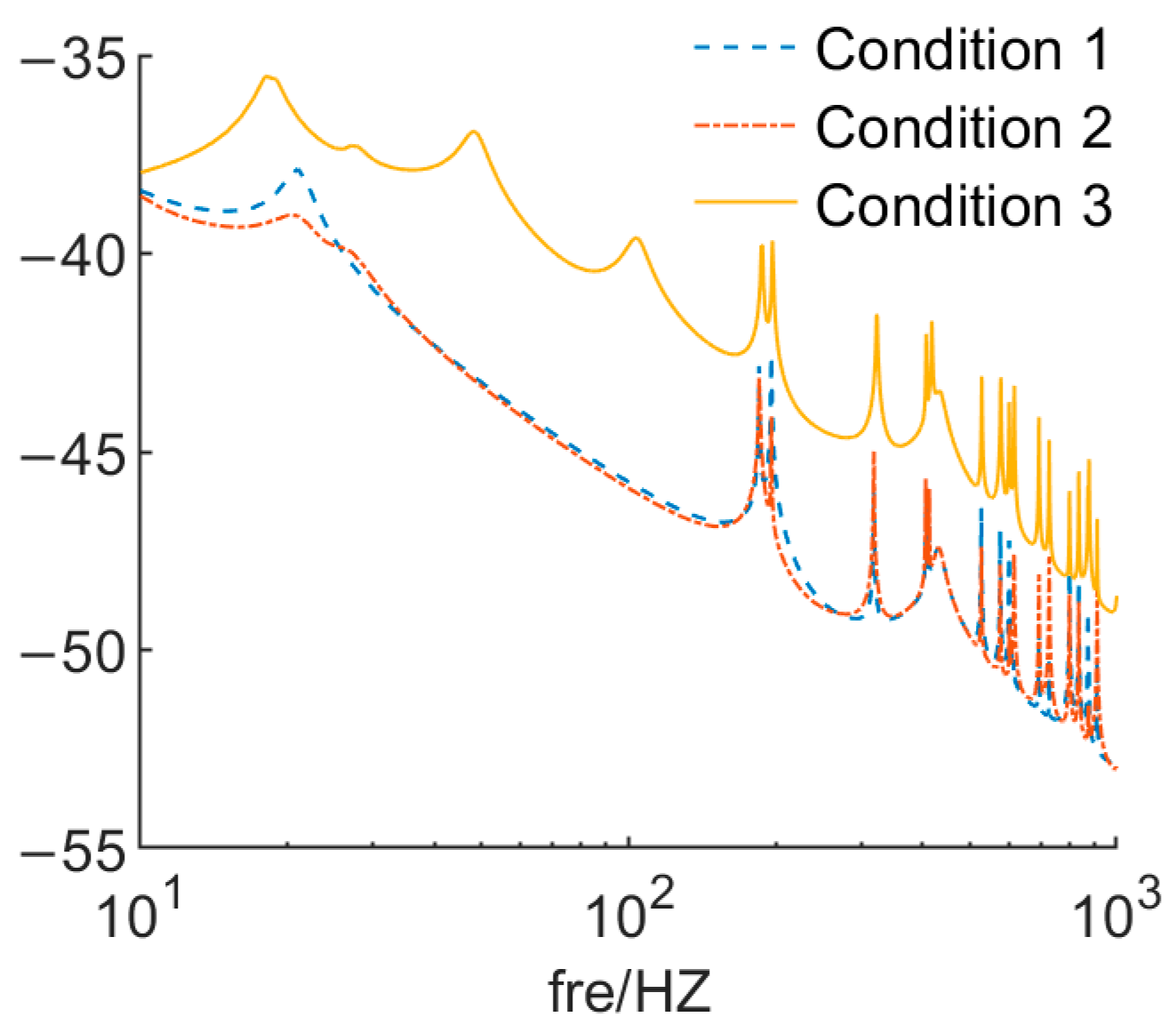
3.2. Patterns of Sound Pressure Distribution
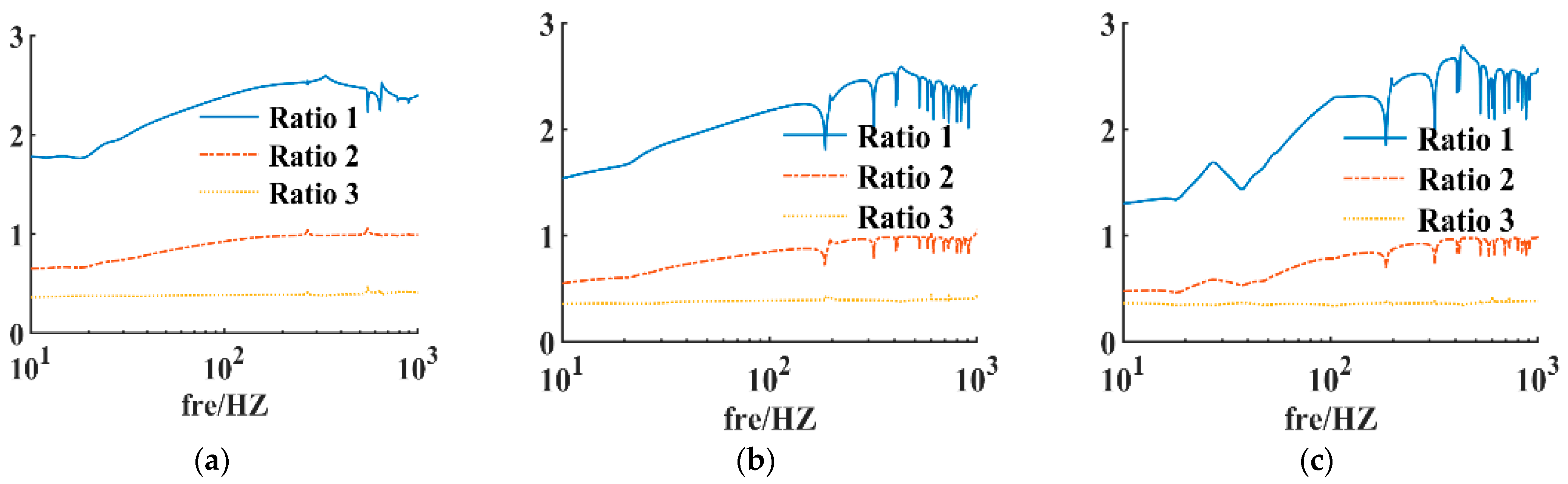
3.3. Analysis of the Numerical Correspondence between Vibration Isolation Performance Indicators and Sound Radiation Characteristics Indicators
4. Global Sensitivity Analysis and Optimisation for Structural Parameters of Coupled Systems
4.1. Sensitivity Theory
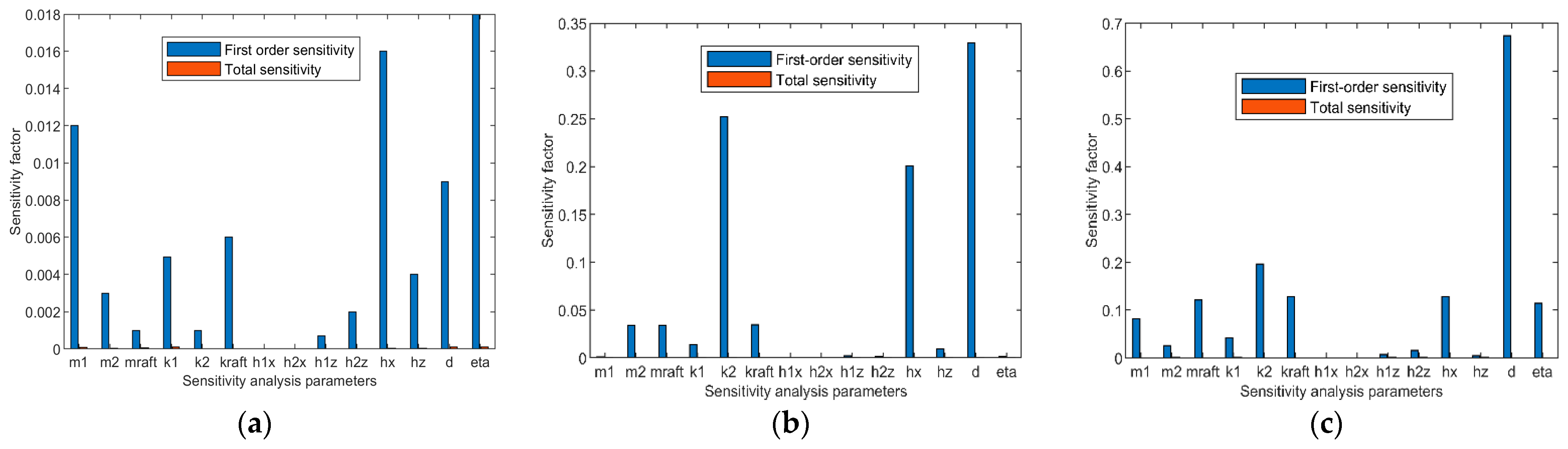
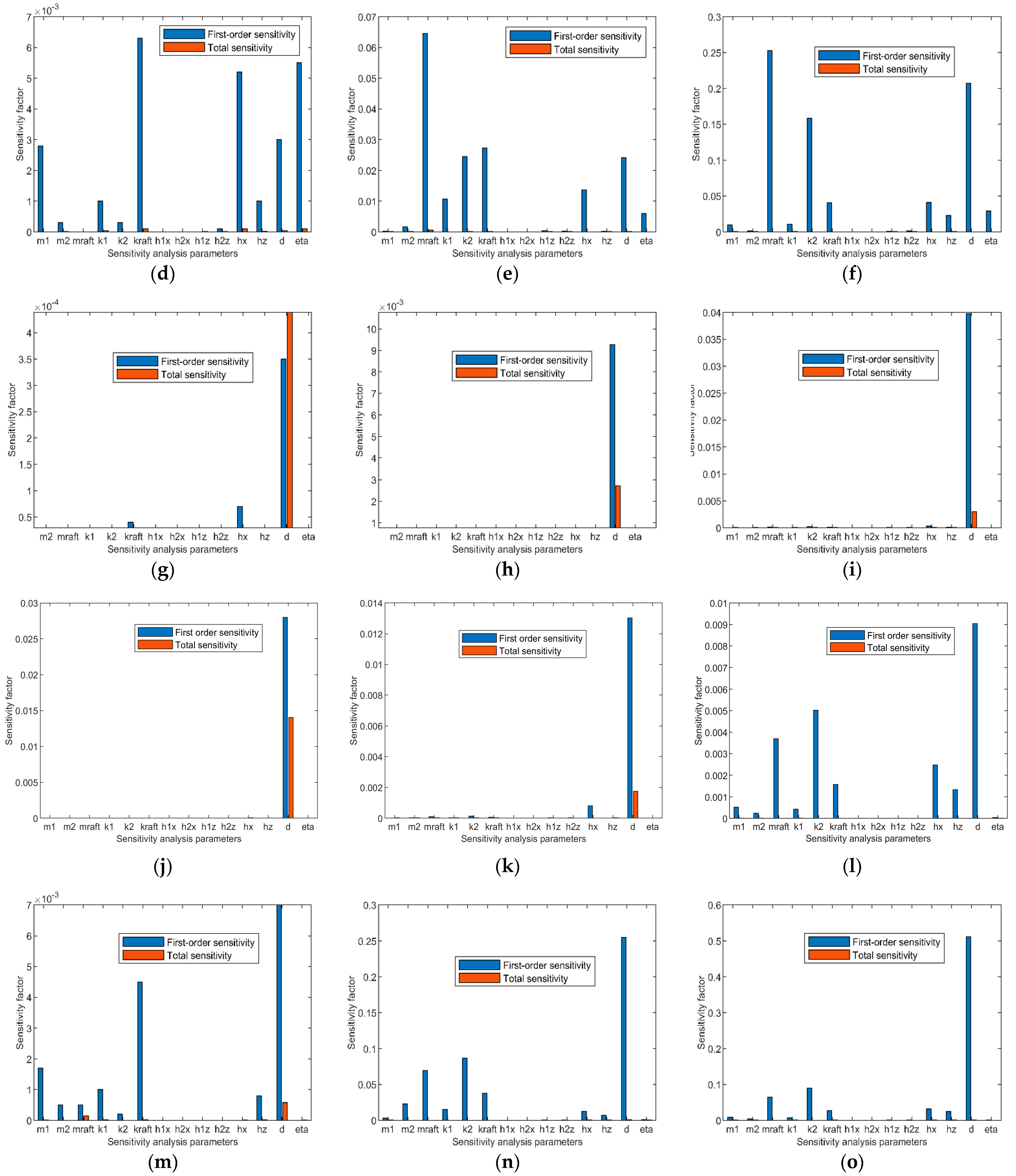
4.2. Global Sensitivity Analysis of Coupled Systems
4.3. Optimisation of Structural Parameters of Coupled Systems Based on Sensitivity Analysis
5. Conclusions
- (1)
- The radiation sound field distribution of the coupled system, including sound pressure directivity and main flap amplitude, shows a more complex variation pattern with frequency, which is related to the vibration mode of the coupled system, among which in the low frequency band where the sound pressure amplitude is large, the main flap of sound pressure mainly appears in the direction of excitation force action as well as the direction perpendicular to the excitation force.
- (2)
- On the whole, the ratio curve between the transmitted power flow and the vibration level dropout (difference in decibels) has a relatively regular linear or nearly linear nature, and the ratio between the acoustic radiated power and the transmitted power flow (ratio of decibels) grows approximately linearly in the lower frequency band and tends to 1 in the higher frequency band. However, it must be noted that in the resonance region of the coupled system, the above ratio will show large fluctuations.
- (3)
- The sensitivity analysis of the parameters with greater and lesser influence on the vibroacoustic transmission shows that the parameters of the vibration isolator and the impedance characteristics of the receptor have a significant influence in the low frequency range, while in the higher frequency range, the impedance characteristics of the receptor become the main influencing factor; the variation of the impedance characteristics of the receptor may also make the installation layout of certain vibration isolators on the receptor structure have an important influence on the vibroacoustic transmission characteristics. In addition, this paper also shows that the sensitivity calculation results of the vibration level dropout and the acoustic radiated power seem to have a high similarity.
- (4)
- Use the transferred power flow and the vibration level dropout as objective functions can effectively optimise the acoustic radiation index of the coupled system. At the same time, the ranking of the acoustic radiation optimisation effect is greater when the transferred power flow and the level drop are used as the same objective function than when the transferred power flow is used as the objective function than when the level drop is used as the objective function.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Li, B.; Yang, Z.C.; Lu, Y.D. Research on coupling noise source identification and spatial acoustic field localization of an underwater cylindrical cabin model. J. Ship Mech. 2021, 25, 238–245. [Google Scholar]
- Peng, C.G.; Zhang, S.Y.; Zhang, G.J. Study on acoustic vibration similarity law of complex stiffened cone-cylinder combined shell. J. Ship Res. 2022, 17, 165–172. [Google Scholar]
- Li, K.; Yu, M.S. Vibro-acoustic coupling analysis of deepsubmerged spherical shells. J. Ship Mech. 2022, 26, 584–594. [Google Scholar]
- Meyer, V.; Maxit, L.; Guyader, J.L.; Leissing, T. Prediction of the vibroacoustic behavior of a submerged shell with non-axisymmetric internal substructures by a condensed transfer function method. J. Sound Vib. 2016, 360, 260–276. [Google Scholar] [CrossRef] [Green Version]
- Meyer, V. Development of a Substructuring Approach to Model the Vibroacoustic Behavior of Submerged Stiffened Cylindrical Shells Coupled to Non-Axisymmetric Internal Frames. Ph.D. Thesis, Université de Lyon, Lyon, France, 2016. [Google Scholar]
- Cao, X.T. Acoustic radiation from stiffened double concentric large cylindrical shells: Part I Circumferential harmonic waves. J. Vib. Acoust. 2023, 145, 1–44. [Google Scholar] [CrossRef]
- Li, C.H. Prediction of Ship Equipment Vibration Transmission and Study on Vibration Isolation Effect of Floating Raft. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Sun, H.L. Simplified performance indicators and active control force of vibration isolation systems with elastic base. Acta Acust. 2016, 41, 227–235. [Google Scholar]
- Zheng, Q.; Lv, Z.Q.; Shuai, C.G.; Li, Y. Research on transmission characteristics of power flow in single stage vibration isolation system on flexible base. Ship Sci. Technol. 2017, 39, 64–68. [Google Scholar]
- Sun, Y.; Yang, T.J.; Liang, W.L.; Chen, B.; Huang, D. Vibration and sound radiation from a flexible base excited by a complex vibration isolation structure. J. Vib. Eng. Technol. 2015, 28, 902–909. [Google Scholar]
- Sun, Y. Research on Sound Radiation from the Flexible Base of a Vibration Isolation System and Its Active Control. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar]
- Ma, Y.Z. Power Flow Transmission Analysis of Nonlinear Isolation System Based on Flexible Foundation. Master’s Thesis, Shandong University, Jinan, China, 2008. [Google Scholar]
- Randin, D.; Abakumov, A.; Goryachkin, A. Research of a Nonlinear Vibration Isolation System with a Controlled Magnetorheological Damper. In Proceedings of the 7th International Conference on Industrial Engineering London, London, UK, 7–9 July 2021. [Google Scholar]
- Park, Y.H.; Kwon, S.C.; Koo, K.R.; Oh, H.U. High damping passive launch vibration isolation system using superelastic SMA with multilayered viscous lamina. Aerospace 2021, 8, 201. [Google Scholar] [CrossRef]
- Nazeer, A.; Nair, R.P.; Ebenezer, D.D. Numerical Analysis of a Vibration Isolator under Shock Load. In Recent Advances in Applied Mechanics: Proceedings of Virtual Seminar on Applied Mechanics; Springer: Singapore, 2022. [Google Scholar]
- Dalela, S.; Balaji, P.S.; Jena, D.P. Design of a metastructure for vibration isolation with quasi-zero-stiffness characteristics using bistable curved beam. Nonlinear Dyn. 2022, 108, 1931–1971. [Google Scholar] [CrossRef]
- Saffari, P.R.; Sirimontree, S.; Thongchom, C.; Jearsiripongkul, T.; Saffari, P.R.; Keawsawasvong, S. Effect of uniform and nonuniform temperature distributions on sound transmission loss of double-walled porous functionally graded magneto-electro-elastic sandwich plates with subsonic external flow. Int. J. Thermofluids 2023, 17, 100311. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathe2matical model. Appl. Math. Comput. 1993, 55, 407–414. [Google Scholar]
- Sobol’, I.M. On quasi-Monte Carlo integrations. Math. Comput. Simul. 1998, 47, 103–112. [Google Scholar] [CrossRef]
- Sobol’, I.M.; Levitan, Y.L. On the use of variance reducing multipliers in Monte Carlo computations of a global sensitivity index. Comput. Phys. Commun. 1999, 117, 52–61. [Google Scholar] [CrossRef]
- Cai, Q. Research on the Optimization Method of Mixed-Mode Magnetorheological Suspension Structure Based on the Whole Vehicle Model. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar]
- Yang, Q.H. Multi-Mode Magnetorheological Suspension Structure Multi-Objective Optimization Based on Whole Vehicle Vibration Control. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2020. [Google Scholar]
- Du, H.Y.; Li, H.G.; Meng, G.; Fu, X.H. Modeling analysis and structural optimization of horizontal sliding table for ultra-large electromagnetic vibration test equipment. J. Vib. Shock. 2021, 40, 305–312. [Google Scholar]
- Li, R. Study on the Application of Sobol’ Sensitivity Analysis Method in the Analysis of Dynamic Properties of Structures. Master’s Thesis, Hunan University, Changsha, China, 2003. [Google Scholar]
- He, Z.Y. Structural Vibration and Sound Radiation, 1st ed.; Harbin University of Engineering Press: Harbin, China, 2001; pp. 117–122. [Google Scholar]
- Ma, D.Y. Foundations of Modern Acoustic Theory, 1st ed.; Science Press: Beijing, China, 2004; pp. 95–96. [Google Scholar]
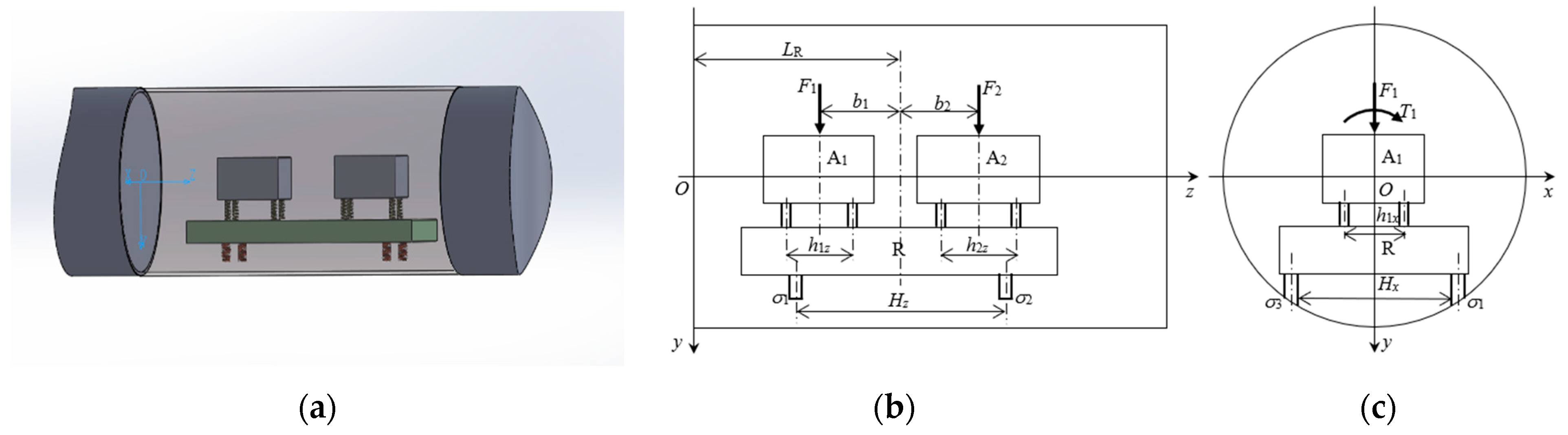

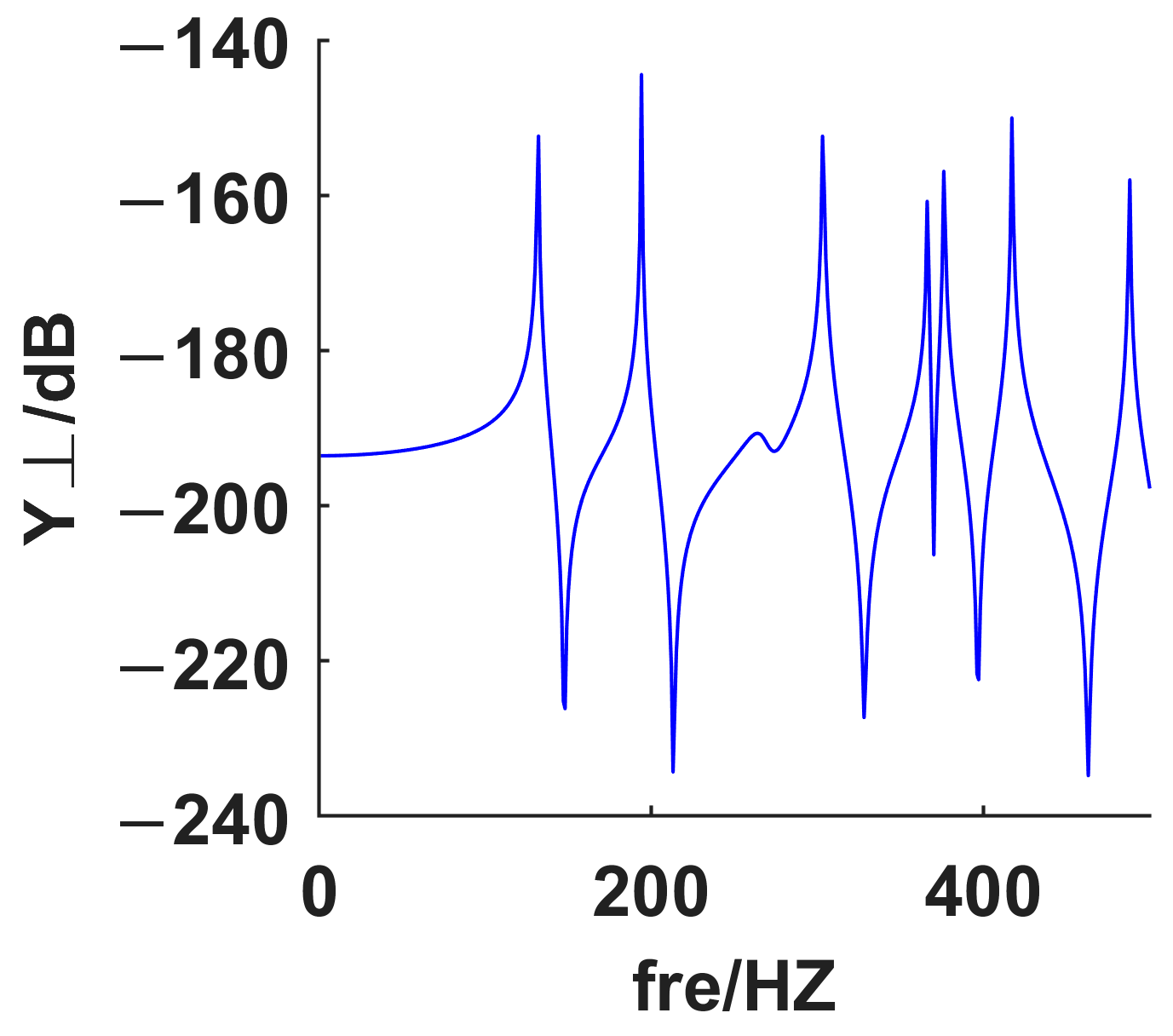
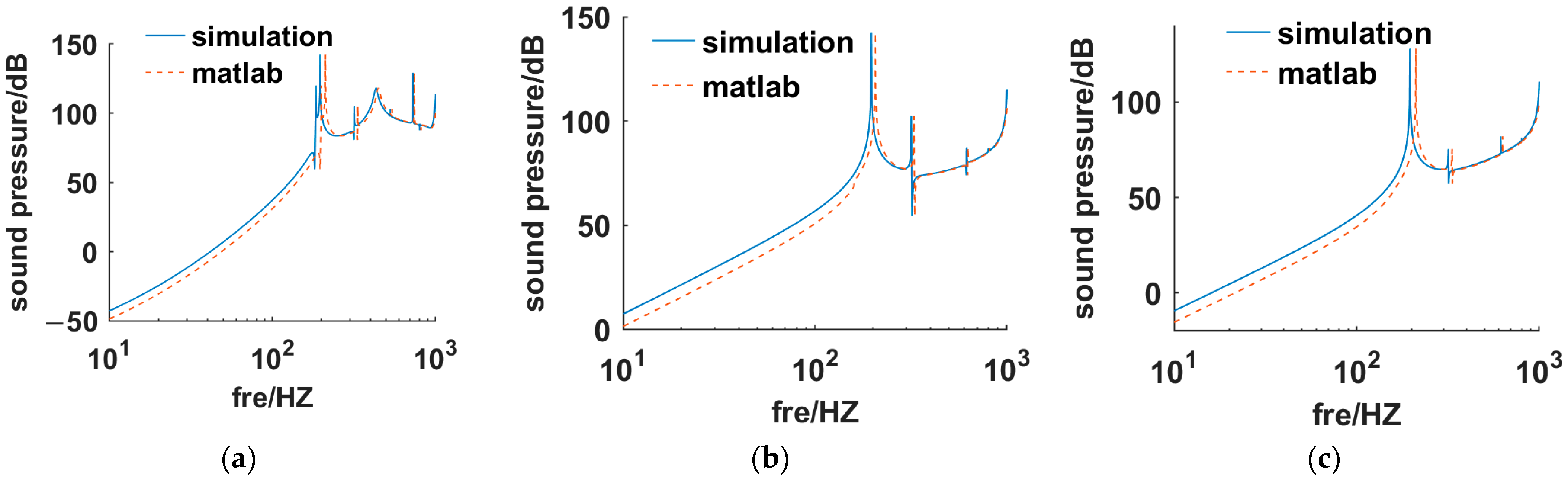
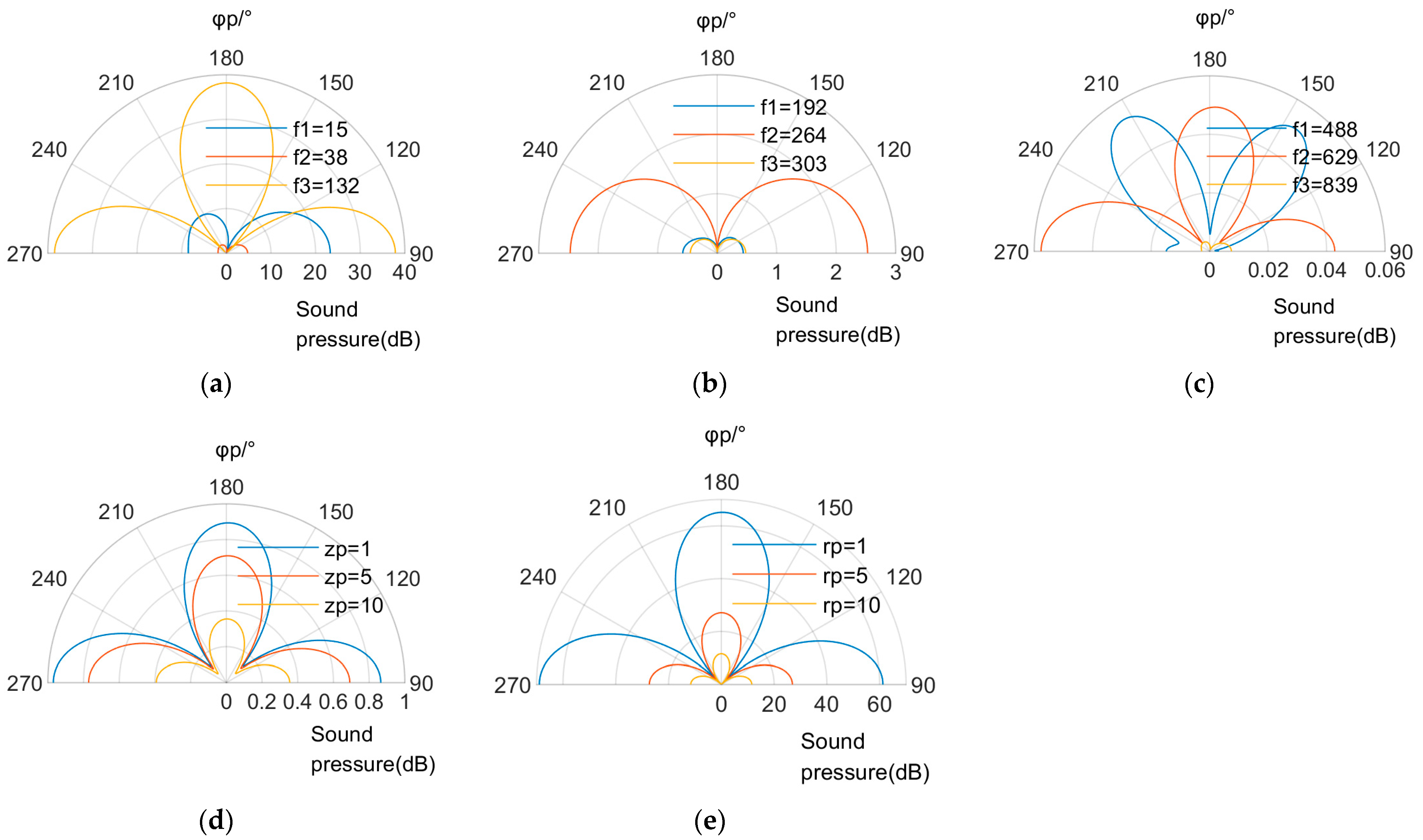


| Parameters | Unit | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|---|
| Unit quality m1, m2 | kg | 50, 70 | 100, 140 | 150, 210 |
| Upper vibration isolator re-stiffening k1, k2 | N/m2 | 10 × 105 × (1 + 0.1j) 1 × 105 × (1 + 0.1) | 2 × 105 × (1 + 0.2j) 2 × 105 × (1 + 0.2j) | 1.3 × 106 × (1 + 0.15j) 1.3 × 106 × (1 + 0.15j) |
| Upper vibration isolator spacing h1x, h1z, h2x, h2z | m | 0.06, 0.1, 0.06, 0.1 | 0.1, 0.15, 0.1, 0.15 | 0.2, 0.3, 0.2, 0.3 |
| Lower vibration isolator stiffness kR | N/m2 | 1 × 105 × (1 + 0.1j) | 2 × 105 × (1 + 0.2j) | 2.6 × 106 × (1 + 0.15j) |
| Lower vibration isolator spacing Hx, Hz | m | 0.18, 0.35 | 0.36, 0.7 | 0.5, 1.05 |
| Raft frame quality mR | kg | 100 | 200 | 300 |
| Rotational inertia of unit 1 Jx | Kg·m2 | 1 | 1 | 1 |
| Rotational inertia of unit 2 Jz | Kg·m2 | 1 | 1 | 1 |
| Inertia of raft frame rotation JRx | Kg·m2 | 1 | 1 | 1 |
| Inertia of raft frame rotation JRz | Kg·m2 | 1 | 1 | 1 |
| Names and Symbols | Mean Value of Parameters (μ) | Variance (σ) | Range of Variations |
|---|---|---|---|
| Unit quality m1 | 46 | 0.46 | μ ± 3σ |
| Unit quality m2 | 70 | 0.7 | μ ± 3σ |
| Raft frame quality mR | 100 | 1 | μ ± 3σ |
| Upper vibration isolator stiffness k1 | 2× 105 × (1 + 0.1j) | (1 + 0.1j) × 103 | μ ± 3σ |
| Upper vibration isolator stiffness k2 | 2.7× 105 × (1 + 0.1j) | (1 + 0.1 j) × 103 | μ ± 3σ |
| Lower vibration isolator stiffness kR | 8.6× 105 × (1 + 0.1j) | (1 + 0.1 j) × 103 | μ ± 3σ |
| Upper vibration isolator spacing h1x | 0.2 | 0.002 | μ ± 3σ |
| Upper vibration isolator spacing h1z | 0.2 | 0.002 | μ ± 3σ |
| Upper vibration isolator spacing h2x | 0.3 | 0.003 | μ ± 3σ |
| Upper vibration isolator spacing h2z | 0.3 | 0.003 | μ ± 3σ |
| Lower vibration isolator spacing Hx | 0.35 | 0.0035 | μ ± 3σ |
| Lower vibration isolator spacing Hz | 0.7 | 0.007 | μ ± 3σ |
| Cylindrical thin shell thickness d | 0.02 | 0.0002 | μ ± 3σ |
| Vibration isolator loss factor η | 0.1 | 0.001 | μ ± 3σ |
| Method 1 | Method 2 | Method 3 | |
|---|---|---|---|
| Objective functions | |||
| Binding conditions |
| Names and Symbols | Mean Value of Parameters | Variance | Range of Variations |
|---|---|---|---|
| Mass of upper unit m1 | 46 | 0.46 | μ ± 30σ |
| Raft frame quality mR | 100 | 1 | μ ± 30σ |
| Stiffness of upper vibration isolators k2 | 2.7 × 105 × (1 + 0.1j) | 2.7 × 103 × (1 + 0.1j) | μ ± 30σ |
| Stiffness of the lower vibration isolator kR | 8.6 × 105 × (1 + 0.1j) | 8.6 × 103 × (1 + 0.1j) | μ ± 30σ |
| Spacing of lower vibration isolators Hx | 0.35 | 0.0035 | μ ± 30σ |
| Thickness of cylindrical thin shells d | 0.02 | 0.0002 | μ ± 30σ |
| Loss factor for vibration isolators η | 0.1 | 0.001 | μ ± 30σ |
| Names and Symbols | Values before Optimisation | Optimisation (Method 1) | Optimisation (Method 2) | Optimisation (Method 3) |
|---|---|---|---|---|
| Mass of upper unit m1 | 46.0 | 47.32 | \ | 47.32 |
| Raft frame quality mR | 100 | \ | 127 | 127 |
| Stiffness of upper vibration isolators k2 | 2.70 × 105 × (1 + 0.1j) | \ | 2.84 × 105 × (1 + 0.1j) | 1.80 × 105 × (1 + 0.0996j) |
| Stiffness of the lower vibration isolator kR | 8.60 × 105 × (1 + 0.1j) | 8.32 × 105 (1 + 0.0992j) | \ | 8.32 × 105 × (1 + 0.0996j) |
| Spacing of lower vibration isolators Hx | 0.35 | 0.295 | 0.299 | 0.254 |
| Thickness of cylindrical thin shells d | 0.02 | 0.0254 | 0.0254 | 0.0254 |
| Loss factor for vibration isolators η | 0.10 | 0.0992 | \ | 0.0996 |
| Names and Symbols | Values before Optimisation | Optimisation (Method 1) | Optimisation (Method 2) | Optimisation (Method 3) |
|---|---|---|---|---|
| transmitted power flow (RMS) | 1.41 × 10−9 | 8.13 × 10−10 | 1.25 × 10−9 | 9.68 × 10−10 |
| vibration level dropout (RMS) | 1.45 × 10−4 | 1.75 × 10−5 | 1.18 × 10−5 | 1.77 × 10−5 |
| acoustic radiated power (RMS) | 9.68 × 10−13 | 2.95 × 10−13 | 4.72 × 10−13 | 1.10 × 10−13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Huo, R.; Wang, L. Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems. Appl. Sci. 2023, 13, 3994. https://doi.org/10.3390/app13063994
Liu S, Huo R, Wang L. Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems. Applied Sciences. 2023; 13(6):3994. https://doi.org/10.3390/app13063994
Chicago/Turabian StyleLiu, Shuqing, Rui Huo, and Likang Wang. 2023. "Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems" Applied Sciences 13, no. 6: 3994. https://doi.org/10.3390/app13063994
APA StyleLiu, S., Huo, R., & Wang, L. (2023). Vibroacoustic Transfer Characteristics of Underwater Cylindrical Shells Containing Complex Internal Elastic Coupled Systems. Applied Sciences, 13(6), 3994. https://doi.org/10.3390/app13063994







