Abstract
This work presents a three-dimensional (3D) surface-to-surface contact algorithm for SPH method and its application to the simulation of material failure during high velocity impact of a projectile on a ceramic plate. In the present contact algorithm, surfaces of 3D objects represented by SPH particles are reconstructed. Based on the reconstructed surfaces, a box test followed by a crossover test is employed to detect contacts between different objects, and a penalty method is employed to enforce contact conditions between contact pairs identified by contact detection. Validation examples are presented to demonstrate the accuracy and capability of the algorithm. The calculated results show that the present contact algorithm can achieve high accuracy and it is capable of handling various contact problems, including frictionless and frictional problems as well as small and significant deformation problems. The algorithm is then used to simulate the high velocity impact of a projectile on a ceramic plate. The material failure of the projectile and the ceramic plate is reproduced, and the residual velocity of the projectile is well predicted.
1. Introduction
Contact phenomenon extensively exists in engineering problems, such as the connection of components in the machine industry and projectile–target interaction in the weapon industry. Contact modeling is one of the most complex aspects in the dynamic stress, deformation and failure analysis of engineering components and structures with numerical methods using explicit time integration schemes. It generally involves contact detection and enforcement of contact conditions, including a non-penetration condition and, sometimes, a friction condition. The finite element method (FEM), as a well-developed numerical method, has been widely used in the modeling of contact problems. In the FEM, piecewise object surfaces (consisting of edges in two-dimensional (2D) space and triangular or quadrilateral faces in three-dimensional (3D) space) can be easily obtained by using the mesh information, so penetration between contact objects and normal vectors at surfaces can be conveniently and accurately determined. This produces convenience and high accuracy for the FEM in contact modeling. However, the FEM suffers mesh distortion when treating contact problems related to extremely large deformation. It may produce poor prediction results for impact failure of brittle materials such as ceramic, since an erosion technique is required to avoid mesh distortion and leads to formation of material loss and contact discontinuity [1]. The smoothed particle hydrodynamics (SPH) [2,3] method is a meshless particle method. It is free of mesh distortion and has advantages over the FEM in dealing with problems involving very large deformation and material failure. It has been successfully applied to many engineering fields, such as fluid flow, explosion and high-velocity impact. However, in the SPH method, object surfaces are denoted by discrete boundary particles (points) without connectivity, and explicit surfaces cannot be obtained as such using the FEM. Therefore, the determination of penetration between contact objects and normal vectors at surfaces is not as convenient and accurate as that in the FEM. This creates difficulties preventing accurate contact modeling using the SPH method. Currently, the SPH method is mainly limited to large deformation contact problems in contact modeling and is not competitive for small and moderate deformation contact problems due to the lack of rigorous contact algorithms. Thus, it is of interest to develop accurate contact algorithms for the SPH method which can versatilely model both frictional and frictionless contact cases and contact cases with deformation from small to extremely large or even material failure. This will be helpful for promoting the application scope of the SPH method.
During the development of the SPH method, various contact algorithms have been proposed to treat contacts. The early algorithm for the contact treatment is based on particle approximation. This algorithm takes all its particles from different objects in the calculation of particle approximation of the momentum conservation equation to deal with contact conditions. In this algorithm, contact detection is completed along with neighboring particle search. This algorithm is usually used to solve problems where materials behave as fluids, such as hypervelocity impact problems. Some researchers explored particle-to-particle contact algorithms [4,5,6]. These algorithms take particles as circles or spheres of a certain size and detect contacts between different objects based on distances between particles and sizes of particles. They employed the penalty method to enforce the contact conditions. They can eliminate the deficiency of virtual tensile and shear stresses of the particle approximation algorithm and can be used to simulate impact contact problems involving large deformation and material failure [7,8]. However, particle-to-particle contact algorithms may encounter non-physical penetrations between contact objects in some cases, such as the penetration process with all contact objects suffering very intense deformations [9]. Additionally, the accuracy of such contact algorithms is affected by the determination of particle size, and they usually require relatively high particle resolution to obtain satisfactory accuracy and do not allow large inconsistency of particle spacing for different contact objects [10]. Vignjevic et al. [11] proposed a contact algorithm which uses a contact potential to impose contact conditions. The algorithm was implemented in the SPH method and applied to the simulation of various problems, including fluid sloshing and hypervelocity impact. It can preserve the meshless feature of the SPH well. However, it did not consider the friction effect. Meanwhile, it may produce contact force according to the contact potential when objects are sufficiently close, even if they are not actually in contact. Wang et al. [12] developed a frictional contact algorithm to simulate the interaction between soils and rigid or deformable structures. Zhan et al. [13] presented a hybrid contact method to simulate frictionless and frictional contacts between soil and a rigid body and contacts between rigid bodies. The above two algorithms can be considered particle-to-surface contact algorithm. They both used the penalty method to enforce contact conditions. They defined surfaces for partial objects (generally rigid or small deformation objects) with boundary particles in the initial discretization, but without considering a possible change of topology of surfaces during the deformation process. Thus, they are mainly suitable for problems where at least one of the two contact objects is undeformable or does not experience very large deformation and material failure. In addition to this, they need to assume the offset from boundary particles (essentially particle size) to locate the actual surface positions. Therefore, their accuracy has an effect of the determination of the offset. Zhou et al. [14] presented a mortar segment-to-segment contact algorithm for frictionless contact problems and implemented it for two-dimensional (2D) problems. In this algorithm, surfaces are defined and located in a similar way in [12] for all objects, and the contact conditions are imposed by using the perturbed Lagrange method. This algorithm can provide accurate results for small and moderately large deformation problems. However, it is implemented in the total-Lagrangian SPH method and does not address significant surface changes, such as surface fragmentation, which may invalidate the surfaces initially defined. Thus, it is not applicable to problems with extremely large deformation and material failure. Gissler et al. [15] presented an algorithm with the artificial density concept. The algorithm was designed for the treatment of rigid-rigid contacts. Furthermore, a series of algorithms [16,17,18] was proposed for the SPH method to treat fluid–rigid/flexible body interactions. These algorithms are not suitable for treating contacts between solids, especially when solid surfaces have intense deformations.
In our previous work [10], a versatile penalty-based surface-to-surface contact algorithm was presented. It can treat both frictionless and frictional problems and deal with problems with arbitrary deformation, from small deformations to extremely large deformations. It can reach higher accuracy and better stability than the particle-to-particle contact algorithm. The algorithm reconstructs surfaces automatically instead of predefining surfaces with connectivity between boundary particles in the initial phase of simulation and, therefore, preserves the advantages of the SPH in modeling large deformations. However, the algorithm presented in the previous work is limited to 2D problems. It is not satisfactory for many practical applications, since few practical problems can be simplified as 2D problems. In this work, following the key ideas presented in the previous work, we present an approach to reconstruct 3D surfaces of SPH objects represented by particles, derive the contact formulation oriented at 3D problems and develop a 3D surface-to-surface contact algorithm for the SPH method. The accuracy and capability of the algorithm are firstly examined by two numerical validation examples, and the algorithm is then used to simulate a practical high-velocity impact problem that involves a ceramic plate impact by a projectile.
The rest of the paper is organized as follows: Section 2 briefly introduces the SPH formulation; Section 3 describes the 3D surface reconstruction of SPH objects and the contact formulation in detail; Section 4 presents two validation examples to demonstrate the accuracy and capability of the present algorithm and provides a practical application in high-velocity impact simulation; The last section draws the main conclusion of this paper.
2. SPH Formulation
In the SPH method, particle approximation is employed to discretize governing equations (mass, momentum and energy conservation equations) and yield SPH equations. With different discretization procedures, various SPH equations can be derived. The SPH equations for mass, momentum and energy conservation used in this work are given as follows:
where is the time, is the density, is the mass, is the coordinate, is the velocity, is the stress, is the internal energy per unit mass, is the gravitational acceleration, the superscripts and are tensor indices (ranging from 1 to 3 in 3D space), for which Einstein summation convention holds. The subscripts i and j denote particle number, is the Kronecker delta function, is the kernel function, and is the artificial viscosity. One can refer to the reference [19] for a detailed derivation of Equations (1)–(3) in the absence of artificial viscosity. To solve Equations (1)–(3) for the density, the velocity and the internal energy per unit mass of particles, the Leap-Frog algorithm is adopted to carry out the time integration of these equations, and a fixed time step is used. The time step is subject to the Courant-Friedrichs-Levy condition for the stability of time integration. It is estimated as , where is the smoothing length, is the sound speed, and is a safety coefficient, generally no more than 1.0. The coefficient is problem dependent. It can be taken as values close to 1.0 for some problems, such as the problems in Section 4.1 and Section 4.2, when only considering the stability of time integration. However, conservative values are used in our practical calculations for better accuracy. The coefficient is in the range of 0.1 to 0.3 for the problems considered in this work.
For the kernel function, the commonly used B-spline smoothing function, which was originally presented by Monaghan and Lattanzio [20], is used, and the symmetrization of the kernel function is employed. Then, the value of the kernel function is calculated for each interaction particle pair. It is calculated as
where , is the distance between particles i and j, is the average smoothing length, and are the smoothing lengths of particles i and j, respectively, and is a constant, which is , for 3D problems considered in the present work. The smoothing length is an important parameter for SPH simulation. For large deformation problems, particle spacing generally changes significantly as deformation develops. If the smoothing length is kept constant, some particles may have few neighboring particles or even no neighboring particle in certain directions due to the large particle spacing formed in the deformation process. This can result in a numerical fracture. Thus, it is necessary to evolve smoothing length in time to ensure sufficient neighboring particles and suppress the numerical fracture. In the current work, the smoothing length is evolved by using the smoothing length updating method found in the reference [21], which is based on maximum local particle spacing and takes into account inhomogeneity of material deformation. The equation for updating the smoothing length is given as follows:
where is an index of deformation inhomogeneity at particle i, and are, respectively, the minimum principal strain and the maximum principal strain of particle i, is an estimate of the maximum local particle spacing at particle i, is the initial local particle spacing at particle i, is the smoothing length coefficient which is the same for all particles and is 1.25, and is a constant in the range of 0 to 1. is set to 0.8 in order to achieve a good compromise between stability and efficiency when deformation inhomogeneity is severe.
In order to improve the stability of SPH calculation, the artificial viscosity is introduced in the SPH momentum and energy equations (see Equations (2) and (3)). The artificial viscosity is of the following form [22]:
where , , , , and are problem-dependent constants. To regulate particle distribution and ease the problem of particle clumping due to numerical instability, the XSPH correction [23] is adopted. The XSPH correction introduces shifts to particle positions by taking into account velocities of neighboring particles. It makes a particle move with a velocity closer to the mean velocity of its neighboring particles. With the XSPH correction, particle positions are updated with the following equation:
where is the average density of an interaction particle pair, and is a constant which is 1.0 in this work.
3. 3D SPH Surface-to-Surface Contact Algorithm Using Surface Reconstruction
3.1. 3D Surface Reconstruction of SPH Objects
In SPH simulation, objects are discretized by particles without explicit connectivity as that defined for nodes in the FEM, so surfaces of objects are not directly available. To retrieve the surfaces of 3D objects for contact treatment, surface reconstruction is adopted. The general procedure of surface reconstruction is illustrated in Figure 1. Firstly, Delaunay triangulation is performed for the particles representing an object, and a series of tetrahedrons, which connect the particles, is obtained. Then, the circumradius for each tetrahedron is calculated, and the tetrahedrons with circumradius larger than a critical distance are identified and dropped. Finally, the four triangular faces of each remaining tetrahedron are checked to determine whether they are on the surfaces of the object. If a triangular face is shared by only one tetrahedron, then it is a boundary face and becomes a part of the object surfaces. All these triangular faces shared by only one tetrahedron compose the reconstructed surfaces of the object. Here, the Delaunay triangulation is used in surface reconstruction because of its distinct features and easy availability of its construction algorithm and program module. It is known that the Delaunay triangulation is unique for a point set of general position (no 4 points on the same plane and no 5 points on the same sphere in 3D space). Meanwhile, the regularity of tetrahedrons obtained with the Delaunay triangulation is generally good. Thanks to these features, reconstructed surfaces based on the Delaunay triangulation will be not significantly affected by the triangulation process. Rather, they will consist of triangular faces of good shapes. The Delaunay triangulation algorithms have been widely investigated, and some program modules are available for use. In this work, the “delaunayTriangulation” function in MATLAB [24] is embedded in the main program coded in Fortran to achieve a robust 3D Delaunay triangulation. The Delaunay triangulation can only produce the convex hull of a point set. It may contain tetrahedrons connecting points with large distances which are not part of the volume of an object. In the surface reconstruction, such tetrahedrons, along with some skinny tetrahedrons, are eliminated by checking that the circumradius of a tetrahedron is larger than a critical distance specified according to local particle spacing.
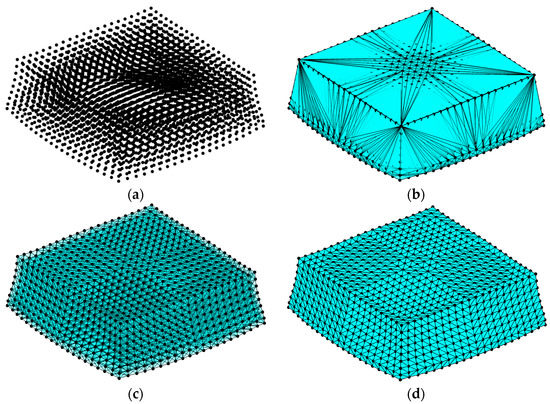
Figure 1.
Surface reconstruction for an 3D SPH object: (a) Particles representing the object; (b) Tetrahedrons obtained by Delaunay triangulation of particles; (c) Remaining tetrahedrons (including internal faces); (d) Reconstructed surface of the object (no internal faces).
When considering whether a tetrahedron is dropped during the surface reconstruction process, it is required to determine the circumradius of the tetrahedron and the critical distance. The circumradius of a tetrahedron I is calculated as
where , , , , , , and are the lengths of the edges of the tetrahedron, , , and denote the local numbers of particles at the four vertices of the tetrahedron, and is the volume of the tetrahedron which is calculated as
The critical distance is determined as , where α is a constant and is the local particle spacing. In this work, the constant α is 1.0, and the local particle spacing is estimated by the smoothing lengths of the four particles at the vertices of the tetrahedron as
It should be mentioned that care must be given when the circumradius is determined from Equation (8). For some extremely distorted tetrahedrons, the quantity under the root square sign in the expression of may be calculated as a very small minus value or zero due to the round-off error of numerical calculation. For this case, special treatment should be adopted to avoid numerical calculation difficulty and obtain reasonable results. In our implementation, the value is set to a very large positive value, then a large will be calculated from Equation (8) and the corresponding tetrahedron will be dropped. Similarly, the value of calculated with Equation (9) may be minus or zero. If it is zero, then is not calculated from Equation (8), but rather directly set to a very large positive value, so the corresponding tetrahedron will be dropped. If it is minus, then it is set to the absolute value and is still calculated from Equation (8).
In order to search the triangular faces on the boundaries of the remaining tetrahedrons and obtain the reconstructed surfaces of the object, an algorithm consisting of two stages (see Algorithm 1) is employed. The first stage is to determine the remaining tetrahedrons connected to each particle, and the second stage is to search the boundary faces of the remaining tetrahedrons using the information obtained in the first stage. The detailed search algorithm is given as follows:
| Algorithm 1: Searching of triangular faces on boundaries of remaining tetrahedrons |
| Stage 1 Determine remaining tetrahedrons connected to each particle 1.1. Initialize total number of remaining tetrahedrons connected each particle: nTetPar = 0 1.2. While i ≤ nT do 1.3. While j ≤ 4 do 1.4. Get number of particle at the jth vertice of tetrahedron i: k = Tet(i, j) 1.5. Update total number of tetrahedrons connected to particle k: nTetPar(k) = nTetPar(k) + 1 1.6. Record number of tetrahedron connected to particle k: TetPar(k, nTetPar(k)) = i 1.7. j = j + 1 1.8. i = i + 1 Stage 2 Search boundary faces of remaining tetrahedrons 2.1. Initialize total number of boundary faces and internal face flag: nBndFac = 0, IntFacFlag = False 2.2. While i ≤ nT do 2.3. While j ≤ 4 do 2.4. If IntFacFlag(i, j) is True, then the jth face of tetrahedron i is an internal face, go to step 2.17 2.5. Get numbers of the three particles on the jth face of tetrahedron i: p1, p2, p3 2.6. Get the total number of tetrahedrons connected to particle p1: num = nTetPar(p1) 2.7. While k ≤ num do 2.8. Get the number of the kth tetrahedron connected to particle p1: l = TetPar(p1, k) 2.9. If i = l, then skip tetrahedron l, and go to step 2.15 2.10. While m ≤ 4 do 2.11. Get numbers of the three particles on the mth face of tetrahedron l: q1, q2, q3 2.12. Compare p1, p2, p3 with q1, q2, q3. If they coincide, then go to Step 2.13, else go to 2.14 2.13. Set internal face flags: IntFacFlag(i, j) = True, IntFacFlag(l, m) = True; and go to step 2.17 2.14. m = m + 1 2.15. k = k + 1 2.16. Identify the jth face of tetrahedron i as a boundary face and record the face 2.17. j = j + 1 2.18. i = i + 1 * nT is the total number of remaining tetrahedrons; Loop variables are initialized to be 1 just before loops begin. |
The present surface reconstruction procedure is available for arbitrarily shaped 3D objects. It can produce 3D explicit surfaces which properly describe the shape of an object. It eliminates the need for predefining surfaces with connectivity between boundary particles in the initial phase of the SPH simulation. It enables us to develop surface-to-surface contact algorithms available for problems with arbitrary deformation, including material failure problems, where new surfaces may be generated during the deformation process. The frequency of surface reconstruction can be chosen according to the severity of the deformation. For small and moderate deformation problems, the surface reconstruction can be only performed at the first time step to save computational time, and the boundary particle connectivity defined by the reconstructed surfaces remains unchanged during the subsequent steps. For large deformation problems, where surfaces may be distorted or fractured, the surface reconstruction should be performed for each time step.
3.2. Detection of Contacts
Through the surface reconstruction procedure, reconstructed surfaces can be obtained individually for each object. To construct a general surface-to-surface contact algorithm, all the triangular faces on the reconstructed surfaces are collected for contact detection. Each triangular face is called a master segment. Meanwhile, all the particles on the reconstructed surfaces along with isolated particles (particles not connected to any remaining tetrahedrons), which possibly appear in extremely large deformation problems, are collected. Each of these particles is called a slave particle. With such a treatment, it is easy to deal with complex contact problems without troublesome identification and definition of possible contacts between different objects. However, this comes with a relatively expensive computational cost.
The task of contact detection is to identify all slave particle–master segment pairs in contact. To achieve this, the master segments are processed one by one, and, for each master segment, a strategy of a box test followed by a crossover test is used to search for slave particles in contact with the master segment. The search strategy used here is similar to that used for the finite element method [25].
For a given master segment, the box test is to find the slave particles possibly in contact with it from all the slave particles. Figure 2 shows a schematic diagram of the box test. A capture box is constructed by extending the minimum bounding box of the master segment outward for a distance de. The extending distance de is calculated as
where is the coefficient of extending distance, for which 1.2 is sufficient for most problems, is the time step, and is the maximum relative velocity of all particles which is defined as
where and are, respectively, the maximum and minimum velocities of all particles in x-direction, and , , , have the same meanings for y- and z-directions. To accelerate the box test process, the efficient point-in-box algorithm [26] is employed to identify the slave particles in the capture box. Those salve particles identified by the box test are contact candidates for the master segment.
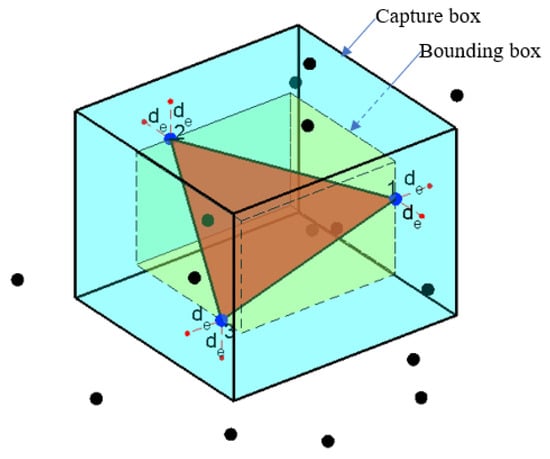
Figure 2.
Schematic diagram of box test (Blue dot: master particle; Black dot: slave particle).
The crossover test is to analyze whether the salve particle candidates found by the box test are actually in contact with the master segment. Figure 3 shows a schematic diagram of the crossover test. For a salve particle candidate, its penetration distance into the master segment and the position of its projection point to the master segment need to be determined. The penetration distance is calculated as
where is the unit outward normal vector of the master segment, and is the outward normal vector which can be calculated as
where , , , , and . The position vector of the projection point p can be determined as
A slave particle candidate is assumed to be actually in contact with master segment if the following conditions are satisfied:
Satisfying the above conditions, the slave particles are located in a triangular prism with the master segment as the bottom face and a height of de in the opposite direction of the outward normal vector, namely the shade region in blue in Figure 3. In the above expression, it is required to determine the projection point is in the triangle of the master segment. This can be achieved by checking the following inequalities:
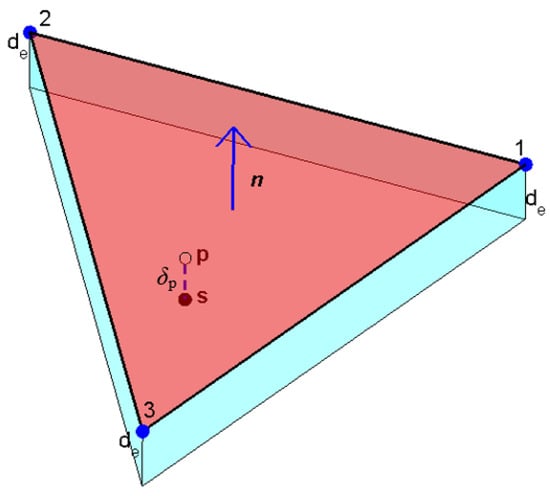
Figure 3.
Schematic diagram of crossover test.
Through the box test and the crossover test, salve particles in contact with each master segment are identified. These salve particles, along with their corresponding master segment, compose a series of contact pairs. It should be noted that a master segment may make contact with multiple slave particles and vice versa.
3.3. Enforcement of Contact Conditions
Contact conditions for slave particle–master segment contact pairs are enforced by a penalty method. The penalty method applies normal penalty forces to prevent the penetration between the contact pairs. It applies tangential friction forces to deal with the friction effect between them.
For a slave particle–master segment contact pair, the normal penalty force is derived by assuming that it removes the penetration between the contact pair in a time step. It is calculated as
where is a constant, which is about 0.5, is the mass of the slave particle, , and are the masses of the three master particles on the master segment, , and are the fractions of the normal penalty force transmitted to the three master particles, and is a correction to the penetration distance . The fractions , and are the area coordinates of the projection point of the slave particle in the master segment. is introduced to compensate the computational error of , since is calculated from Equation (13) with the coordinates of particles at the beginning of a time step, while the coordinates of particles will change at the end of the time step due to the motion of particles within it. is calculated as
where and are the predicted velocities of the slave particle and the projection point of the slave particle on the master segment, respectively, and their expressions are
respectively, where
Note that the accelerations , , and are those computed from Equation (2) in addition to the contributions of contact forces of other related contact pairs processed before the present contact pair.
The tangential friction force for a slave particle–master segment contact pair is determined based on the Coulomb’s Law of Friction. It is calculated as
where is the friction coefficient, is the magnitude of the normal penalty force, and is the magnitude of the predicted tangential friction force. The predicted tangential friction force is determined by assuming the slave particle and the master segment are in sticking state. It is calculated as
where is the tangential component of the relative velocity between the slave particle and the master segment, is the relative velocity between them, and is the normal component of the relative velocity between them. The magnitude of the predicted tangential friction force has an upper limit . When it does not exceed the limit, it is the actual magnitude of the friction force; otherwise, sliding between the slave particle and the master segment will occur and the tangential friction force predicted by Equation (23) becomes invalid, since the assumption of the sticking state conflicts with the actual contact state. Thus, the actual magnitude of the friction force is set to .
Simply adding the normal penalty force and the tangential friction force, we can obtain the contact force resulting from a slave particle–master segment contact pair as
for the slave particle. For the three master particles on the master segment, their contact forces resulting from the contact pair are obtained by distributing the contact force to the three master particles with fractions , and , but they are applied in the opposite direction of the contact force of the slave particle. Thus, the contact forces of the master particles are calculated as
4. Validation and Application
4.1. Validation Example 1: A Block Sliding along a Slope
This example considers an initially static block sliding along a slope with an incline angle of 30° due to gravitational force. The block is a cube with side length of 1 m. The slope is a plate with a length of 10 m, width of 1.6 m and thickness of 0.4 m. The block and the slope are both elastic and have the same elastic constants. The material parameters are set as density ρ = 7850 kg/m3, shear modulus G = 76.9 GPa and bulk modulus K = 166.7 GPa. The gravitational acceleration is set to 9.8 m/s2 for z-direction and zero for other directions. Uniform particles with a spacing of 0.2 m are used to discretize the block and the slope. There are 216 particles for the block and 1377 particles for the slope. Figure 4 shows the initial SPH calculation model for the present problem. In this example, the time step is set to 5 10−6 s, and the artificial viscosity constants and are 0.25 and 1.0, respectively. The total simulation time is set to 1.8 s. Since the problem is a small deformation problem, surface reconstruction is only performed at the first time step.
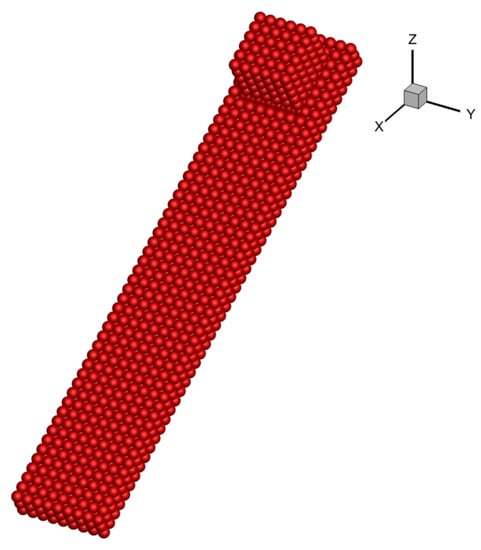
Figure 4.
Initial SPH calculation model for a block sliding along a slope.
Figure 5 shows the sliding processes of the block simulated by the present contact algorithm for both frictional and frictionless cases. In the figure, the triangular meshes represent the reconstructed surfaces of the block and the slope, and the small spheres are boundary particles. The same display method is used in the following sections to show deformed shapes of contact objects. The arrows in the figure indicate the velocity vectors of particles. It can be seen that the shapes of the block and the slope are well reconstructed. The deformations of the block and the slope are negligible, which means they can be considered as rigid bodies. The velocity vectors of all particles are uniform and parallel to the slope surface. This indicates that the block slides on the slope smoothly, and there is no significant numerical oscillation excited by the contact calculation.
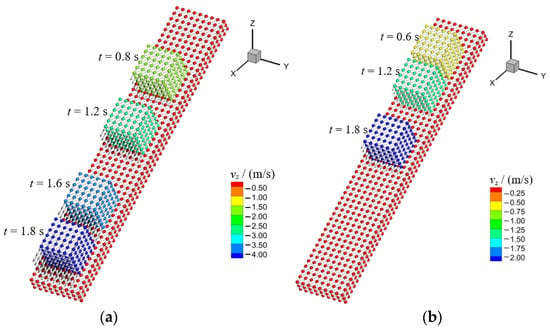
Figure 5.
Calculation results for a block sliding along a slope: (a) Friction coefficient ; (b) Friction coefficient .
By assuming the block and the slope are rigid bodies, analytical solutions to the displacements of the block can be easily obtained for a quantitative assessment of the accuracy of our numerical results. Figure 6 shows the displacements of the block in x- and z-directions. The displacements of the block are represented by the displacements of the particle closest to the center of the top face of the block. The results calculated with the present contact algorithm are in excellent agreement with the corresponding analytical solutions. This demonstrates that the present contact algorithm can achieve very good accuracy for such small deformation problems.
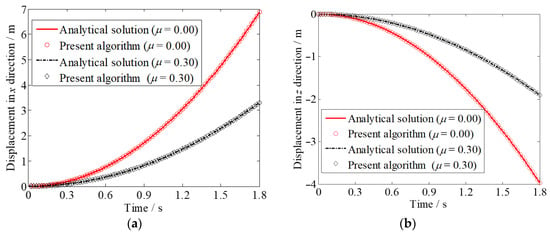
Figure 6.
Comparison of the displacements of the block calculated by the analytical method and the present algorithm: (a) Displacement in x-direction; (b) Displacement in z-direction.
For comparison, the particle-to-particle contact algorithm [6,8] is also used to calculate the present problem. The algorithm detects contacts between SPH objects by the following criterion
where and are the radii of particles i and j, respectively. It enforces the non-penetration contact condition with a penalty method. With this method, normal penalty forces are applied to particles in contact in order to prevent penetration between them. The penalty force is calculated as
where is a constant with the value 0.1, is the average normal vector of particles i and j, , and are the relative displacement between particles i and j along the average normal vector required for eliminating the penetration between them. is calculated as
Tangential friction forces are applied to handle the friction effect. The formulation of tangential friction force has the same form as Equation (22). However, the predicted tangential friction force is calculated as
where , and . For the calculation of the present problem with the particle-to-particle contact algorithm, a finer particle spacing of about 0.1 m is employed, since poor results are produced when the original spacing (0.2 m) is used. This leads to the total number of particles being 729 for the block and 4212 for the slope, respectively. The sliding processes of the block simulated by the particle-to-particle contact algorithm is shown in Figure 7. The displacements of the block calculated by the particle-to-particle contact algorithm are shown in Figure 8. Even though a finer spacing is used, the results of the particle-to-particle contact algorithm are less accurate than those of the present algorithm with the coarser particle spacing as shown in Figure 6. Figure 9 shows a comparison between the velocities of the block calculated by the present algorithm and the particle-to-particle contact algorithm. Velocity oscillation is excited by the particle-to-particle contact algorithm, while it is avoided by the present algorithm. The present algorithm produces more accurate velocity results than the particle-to-particle contact algorithm, as seen from the comparison with the analytical velocity results.
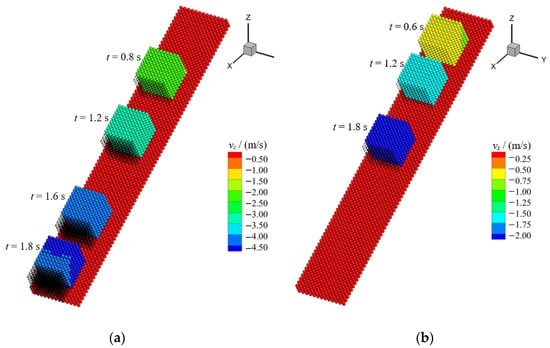
Figure 7.
Calculation results of the particle-to-particle contact algorithm: (a) Friction coefficient ; (b) Friction coefficient .
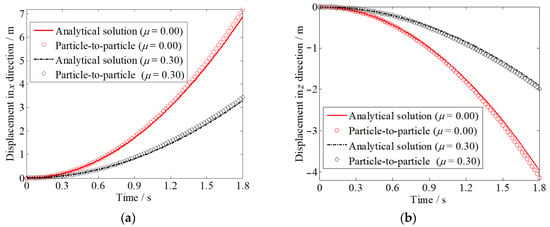
Figure 8.
Comparison of the displacements of the block calculated by the analytical method and the particle-to-particle contact algorithm: (a) Displacement in x-direction; (b) Displacement in z-direction.
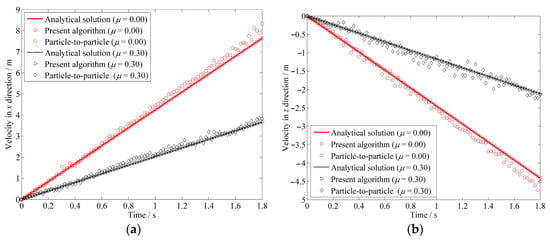
Figure 9.
Comparison of the velocities of the block calculated by the present algorithm and the particle-to-particle contact algorithm: (a) Velocity in x-direction; (b) Velocity in z-direction.
4.2. Validation Example 2: Impact between Two Elastic-Plastic Blocks
This example considers the impact of two blocks travelling with an initial velocity of 200 m/s in opposite directions. The two blocks are just in contact in the initial time. They have the same geometric dimensions, which are 10 mm in length and width and 4 mm in thickness. The materials of the blocks are the same and assumed to be elastic–perfectly plastic material. The material parameters are set as density ρ = 7850 kg/m3, shear modulus G = 76.9 GPa, bulk modulus K = 166.7 GPa and yield strength σ0 = 600 MPa. Uniform particles with a spacing of 0.5 mm are used to discretized the blocks. There are 3969 particles for each block. Figure 10 shows the initial SPH calculation model for the present problem. For this example, the time step is set to 2.5 10−8 s, the artificial viscosity constants are the same as those used in the previous example, and surface reconstruction is triggered in every time step.
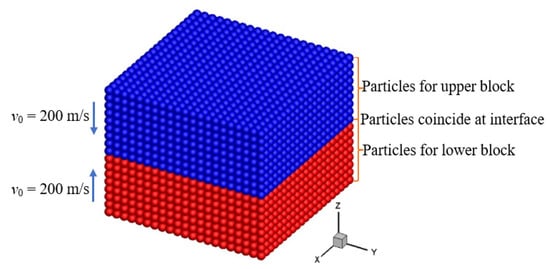
Figure 10.
Initial SPH calculation model for high-velocity impact of two blocks.
Figure 11 shows the deformed shapes of the blocks at two different time instants. The deformation results calculated with the present contact algorithm are compared with those obtained using the FEM in LS-DYNA [27]. In the FEM model, the element size is the same as the particle spacing used in the SPH model. The scale factor for the time step is 0.1, and the contacts between the blocks are treated by the algorithm defined by the keyword *CONTACT_AUTOMATIC_SURFACE_TO_SURFACE along with segments in contact regions of the two blocks specified as slave and master surfaces, so that an optimal result is obtained. From Figure 8, it can be seen that the complex shapes of the blocks are properly reproduced by the reconstruction approach employed in the present contact algorithm, and the shapes of the blocks calculated by SPH are in good agreement with those calculated by the FEM.
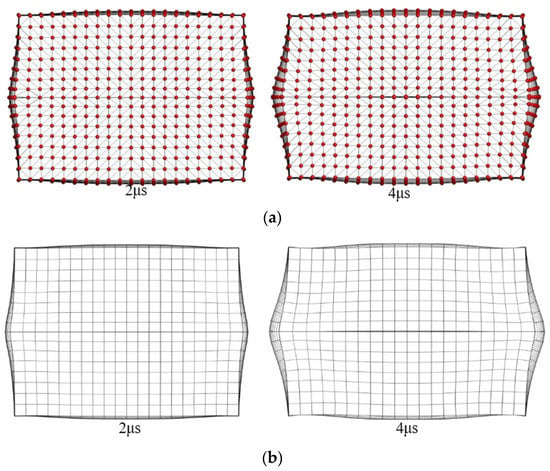
Figure 11.
Deformed shapes of the blocks calculated by different methods (Side view): (a) Present algorithm; (b) FEM.
Figure 12 gives a comparison of the deformed width and thickness of the upper block simulated by the SPH and the FEM. The width is measured as the distance between the midpoints of the opposite sides of the bottom surface, and the thickness is measured as the distance between the midpoints of the bottom and top surfaces. It can be seen that the variations of width and thickness calculated by SPH are in good agreement with those calculated using the FEM. The relative error is about 0.5% for the final width and 3.7% for the final thickness. Figure 13 gives a comparison for the global z-direction velocity histories of the two blocks simulated by the SPH and the FEM. Overall, the global z-direction velocity histories of SPH agree well with those of the FEM. Interestingly, the final velocities of the two blocks are in excellent agreement with those of the FEM.
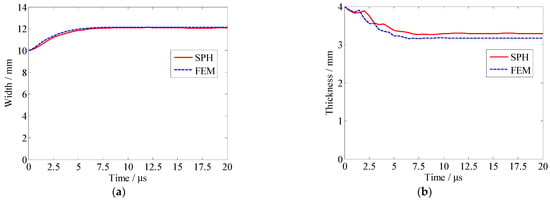
Figure 12.
Comparison of width and thickness of the upper block calculated by SPH and FEM: (a) Width; (b) Thickness.
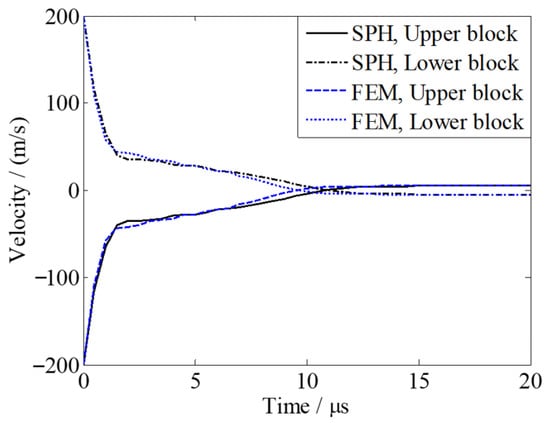
Figure 13.
Comparison of global z-direction velocity histories of the blocks calculated by SPH and FEM.
The results shown above demonstrate that the present contact algorithm is also applicable to impact contact problems with significant deformations and can achieve good accuracy for such problems.
With this example, the computational cost of the whole SPH simulation and the contact calculation with the present contact algorithm is examined. The computational cost is the consumed CPU time on a personal computer with Intel® Core™ i7-8750H CPUs (Operating frequency: 2.2 GHz) and 16 GB RAM. The computations are conducted in serial mode. The total computational cost includes nearly 5 s of CPU time spent on the output of result files. The contact calculation time is about 43 s, and it takes up about 26% of the total calculation time (about 168 s). The contact calculation consumes a considerable part of the total calculation time. With the use of the striped point-in-box search algorithm [28] instead of the tree search algorithm [19] for neighboring particle searching, the total calculation time can be reduced to 96 s, and the contact calculation time takes up about 45% and becomes a major part of the total calculation time. A rough comparison of computational cost is also made between the FEM simulation and the SPH simulation, although there are differences in the time-stepping algorithm, contact searching domain, output of result files and other aspects. The computational cost of the FEM simulation with the previously mentioned settings is about 6 s of CPU time. Compared with the FEM simulation, the SPH simulation is more computationally expensive for the current example. The main reasons for this include expensive neighboring particle searching and considerable particles required for the calculation of a particle of interest in the SPH method. Another reason is that the surface reconstruction required in the present contact algorithm brings significant extra computational costs. Thus, to save the computational cost of the present contact algorithm, and consequently of SPH simulation, it is of interest to develop intermittent and/or local surface reconstruction techniques.
4.3. Application: High-Velocity Impact of Projectile on Ceramic Plate
The SPH method with the present contact algorithm is now applied to the simulation of a practical problem originating from the reference [29]. The problem involves an alumina ceramic plate normally impacted by a blunt tungsten heavy alloy projectile with a high velocity. The ceramic plate has a square shape. Its side length is 101.6 mm and its thickness is 12.7 mm. The projectile is cylindrical. Its diameter is 6.14 mm and its length is 20.86 mm. It has an initial velocity of 903.9 m/s. Experiment results for the problem were reported by Nemat-Nasser et al. in the reference [29]. A more systematic study conducted by Nemat-Nasser and his co-workers [30] also provided experiment results for reference. The experimental results showed that extremely large deformation and material failure occur for both the projectile and the ceramic plate, so it is challenging for numerical simulation.
Figure 14 shows the SPH model established for the problem. The projectile is discretized by particles with a spacing of about 0.6 mm. The ceramic plate is discretized by uniform particles with a spacing of 1.0 mm. There is a total of about 140 thousand particles in the model. For the simulation of this problem, the time step is set to 2 10−8 s, the artificial viscosity constants and are 0.5 and 1.0, respectively, and surface reconstruction is performed in every time step.
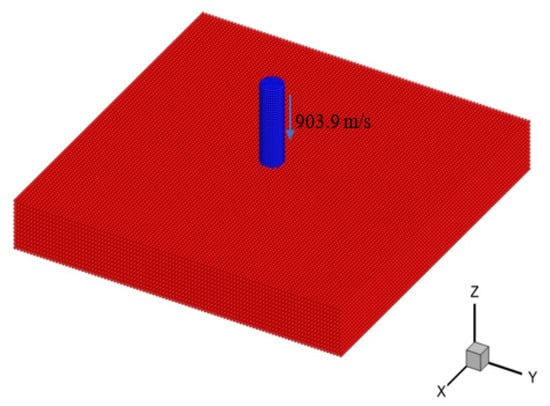
Figure 14.
SPH model for high velocity impact of ceramic plate impacted by projectile.
On the constitutive model, the JH-2 model [31] is implemented in our SPH program to model the dynamic behavior of the ceramic material. With the JH-2 model, the yield strength of the material is expressed in a normalized form as
where D is the damage variable between 0 and 1, is the normalized intact strength, and is the normalized fracture strength. , and are normalized by the stress at Hugoniot elastic limit (HEL), . The expressions for and are
and
respectively. In Equations (31) and (32), a1, n1, c1, b1 and m1 are material constants, P* = P/PHEL is the normalized pressure, P and PHEL are the actual pressure and the pressure at the HEL, respectively, is the normalized maximum tensile hydrostatic pressure (tensile strength), PT is the maximum tensile hydrostatic pressure that material can undergo, and where and are the actual strain rate and the reference strain rate, respectively. The damage D is defined as
where is the plastic strain increment in a time step, and is the failure strain which is defined as
where D1 and D2 are damage parameters. In the JH-2 model, the pressure for intact material (D = 0) is determined as
For damaged material (D > 0), the pressure of material under compression (μ ≥ 0) is modified as
and the pressure of material under tension (μ < 0) is calculated with P = K1μ. In Equations (35) and (36), K1, K2 and K3 are material constants, where ρ and ρ0 are, respectively, the current density and the initial density of the material, and ΔP is introduced for the consideration of conversion of elastic energy loss to potential hydrostatic energy. The Johnson-Cook (JC) constitutive model along with the Grüneisen equation of state (EOS) is implemented to model the dynamic behavior of the projectile material. With the JC model, the yield strength of material is expressed as
where a0, b0, n0, c0 and m0 are constants, εp is the plastic strain, and where T is the current temperature, is the room temperature and is the melt temperature. In this work, the temperature of material is determined based on the assumption that the internal energy increment converted into heat energy. It is calculated as
where T0 is the initial temperature which is assumed to be equal to the room temperature , where u and u0 are the current and initial internal energy per unit mass, respectively, and is the specific heat. Since u0 for the projectile material is zero, can be simplified as u. The Grüneisen EOS using cubic shock velocity (vs)-particle velocity (vp) relation [27] is used to calculate the pressure of the projectile material. When material is compressed (μ ≥ 0), the pressure is calculated as
When material is expanding (μ < 0), the pressure is calculated as
In Equations (39) and (40), is the intercept for the cubic vs-vp curve, , and are the coefficients for the slope of the curve, is the Grüneisen parameter, is the parameter for the correction to , and is the internal energy per initial volume. In our SPH calculation, is solved with . The damage model for the projectile material has the same form in Equation (33). However, the failure strain is defined as
where d1–d5 are damage parameters, and is the stress triaxiality where is the mean stress and is the von Mises equivalent stress. The material parameters for the projectile material and the ceramic material are the same as those in reference [9] and summarized in Table 1 and Table 2, respectively.

Table 1.
Material parameters for projectile material.

Table 2.
Material parameters for ceramic material.
Figure 15a shows the impact process simulated by the SPH method with the present contact algorithm. It can be seen that the ceramic material is ejected from the front face. The back-face of the ceramic plate begins to move at about 10 μs, and a slight smooth bulge is formed at this time. The bulge expands as the impact process progresses. The back-face motion of the ceramic plate in the experiment was clearly captured by Sarva et al. [30] with a high-speed camera. The back-face deformation motion reproduced by the simulation agrees well with the experimental observation (see Figure 15b). Figure 16 shows the projectile velocity history. The projectile velocity (absolute value of the velocity in z-direction) decreases monotonically with time and becomes stable at the time of 30 μs. The residual velocity of the projectile predicted by the simulation is about 683 m/s. It is in good agreement with the experimentally measured one (682 m/s) [29].
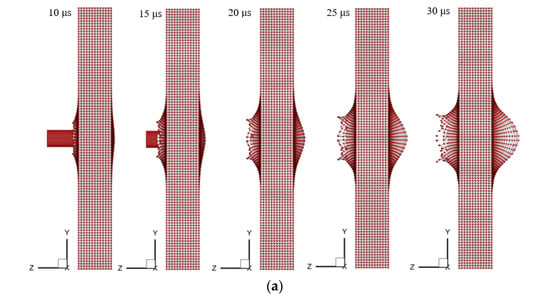

Figure 15.
Impact process simulated by SPH method with the present contact algorithm and observed by experiment [30]: (a) SPH simulation; (b) Experiment.
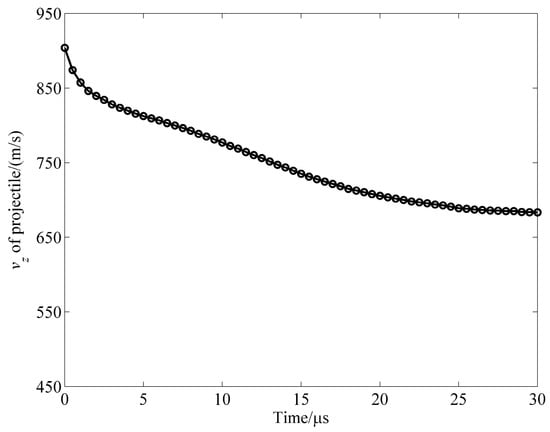
Figure 16.
Velocity history of the projectile.
Figure 17 shows the particle distributions and reconstructed surfaces of the ceramic plate and the projectile at different time instants with a section view. The particles of surfaces of the projectile and the ceramic plate are in different colors. Both the ceramic plate and the projectile experience very large deformation. Meanwhile, it can be clearly seen from this figure that the projectile forms a mushroom-shaped head under the resistance of the ceramic plate. Part of failed projectile material becomes fragments separating from the projectile and moves toward the opposite direction of the projectile motion. This indicates the mass loss of the projectile. Note that the mushrooming deformation and erosion of the projectile is also reported in the experimental results [29,30]. Figure 18 shows a comparison between the simulation result of the mushrooming deformation of the projectile at 8 μs and the corresponding experimental result. A good correlation between the simulated and experimental results is observed. Additionally, as seen from this figure, the interface between ceramic material and projectile material is kept clear under such a complex deformation condition. This proves that the present contact algorithm has the strong capability and good stability in dealing with large deformation.
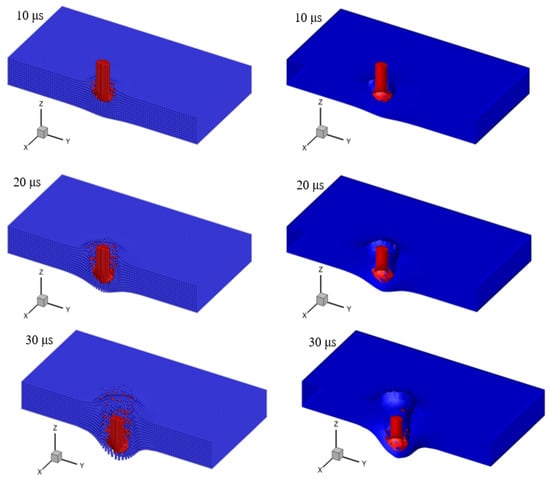
Figure 17.
Particle distributions (left) and surfaces (right) of the ceramic plate and the projectile at different time.

Figure 18.
A comparison between the simulated mushrooming deformation of the projectile at 8 μs and the corresponding experimental result: (a) SPH simulation; (b) Experiment result [30].
The present SPH simulation result is also compared with the simulation results of Bresciani et al. [1], as shown in Figure 19. Two different approaches were employed by Bresciani et al. to model the present problem with quarter models. One is the classical FEM with erosion technique, which deletes elements when the material fails. The other approach they proposed is to use a fragmentation model along with the conversion of FE elements to SPH particles (named “fragmentation approach” for short). In this approach, the projectile is divided into sub-parts that are discretized with FE elements, and the sub-parts are bonded by the tiebreak contact algorithm and allowed to separate from each other based on a failure criterion. The ceramic plate is initially modeled with FE elements, and FE elements are converted to SPH particles when a failure criterion is met. This approach can produce good results. However, it involves complex contacts, especially when the number of sub-parts of the projectile is large, and it causes complexity in the model establishment as well as the determination of extra parameters, such as the parameters in the failure criterion of bonding. As seen from Figure 19, the FEM with erosion technique cannot reproduce the front-face ejecta and back-face bulge of the ceramic plate as well as the fragmentation of the projectile well, while the present SPH method performs better than the FEM with the erosion technique in this aspect and produces results similar to those of the fragmentation approach. On the residual velocity of the projectile, the FEM with erosion technique predicts a result of 782 m/s, which is 100 m/s larger than the experimental value (682 m/s). The fragmentation approach predicts a residual velocity of 683 m/s [1]. The predicted result is very close to the experimental value, although it is affected by the number of sub-parts of the projectile. The present SPH method, with the current settings produces the same result as that of the fragmentation approach. It also performs better in the residual velocity prediction than the FEM with erosion technique. The above comparison confirms the reasonability of the simulation results of the present SPH method further, and demonstrates that it is a promising alternative for impact failure of ceramics or similar materials.
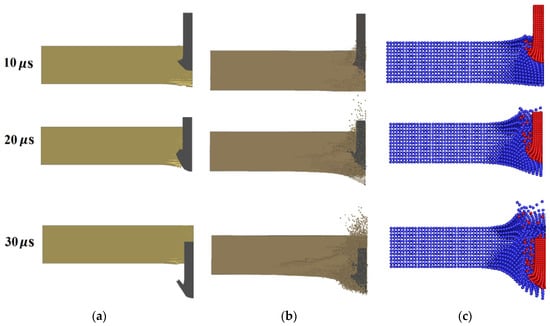
Figure 19.
Comparison between the present SPH simulation result and the simulation results of Bresciani et al. with two different approaches: (a) FEM with erosion technique [1]; (b) Fragmentation approach (7 radial sectors for projectile) [1]; (c) The present SPH method.
5. Conclusions
In this work, we presented a 3D surface-to-surface contact algorithm using a surface reconstruction technique. Validation examples of 3D contact problems were calculated to examine its accuracy and capability. The calculated results showed that the present contact algorithm can deal with both frictionless and frictional contact problems. It can provide a fine treatment for contact problems with small deformation and achieve high accuracy. It is also capable of handling impact contact problems with significant deformation. The algorithm was successfully applied to the simulation of material failure during projectile impact on a ceramic plate. The deformation modes of the projectile and the ceramic plate were correctly reproduced, and the predicted residual velocity was in good agreement with the experimental one.
The present contact algorithm preserves the advantages of the SPH method over Lagrangian mesh-based methods in simulating large deformation and material failure. It enables the SPH method to simulate a wide range of contact problems with an accurate way. As an extension of the previously proposed 2D algorithm [10], it allows us to model engineering problems in 3D space and consequently provides results agreeing better with the reality. Thus, it is promising in many engineering applications, such as contact stresses between mechanical components, impact resistance of protective structures and fluid-structure interaction.
Author Contributions
Conceptualization, Y.X.; methodology, Y.X.; software, Y.X.; validation, Y.X. and K.L.; formal analysis, Y.X.; investigation, Y.X. and K.L.; resources, Y.X.; data curation, Y.X.; writing—original draft preparation, Y.X.; writing—review and editing, K.L.; visualization, Y.X. and K.L.; supervision, Y.X.; project administration, Y.X.; funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (Grant No.: 11862005) and Natural Science Foundation of Jiangxi Province of China (Grant No.: 20181BAB211012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bresciani, L.M.; Manes, A.; Romano, T.A.; Iavarone, P.; Giglio, M. Numerical modelling to reproduce fragmentation of a tungsten heavy alloy projectile impacting a ceramic tile: Adaptive solid mesh to the SPH technique and the cohesive law. Int. J. Impact Eng. 2016, 87, 3–13. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astrophys. J. 1977, 8, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Campbell, J.; Vignjevic, R.; Libersky, L. A contact algorithm for smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 2000, 184, 49–65. [Google Scholar] [CrossRef]
- Seo, S.; Min, O. Axisymmetric SPH simulation of elasto-plastic contact in the low velocity impact. Comput. Phys. Commun. 2006, 175, 583–603. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Hu, D.A.; Han, X.; Yang, G.; Long, S.Y. Simulation of normal perforation of aluminum plates using axisymmetric smoothed particle hydrodynamics with contact algorithm. Int. J. Comput. Methods 2013, 10, 1350039. [Google Scholar] [CrossRef]
- Seo, S.; Min, O.; Lee, J. Application of an improved contact algorithm for penetration analysis in SPH. Int. J. Impact Eng. 2008, 35, 578–588. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Dong, H.H.; Zhou, J.M.; Wang, J.G. Studying normal perforation of monolithic and layered steel targets by conical projectiles with SPH simulation and analytical method. Eng. Anal. Bound. Elem. 2017, 75, 12–20. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Wu, H.C.; Ping, X.C. On the simulation of fragmentation during the process of ceramic tile impacted by blunt projectile with SPH method in LS-DYNA. Comput. Model. Eng. Sci. 2020, 122, 923–954. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Liu, K. Penalty-based surface-to-surface contact algorithm for SPH method. Appl. Math. Model. 2023, 107, 359–377. [Google Scholar] [CrossRef]
- Vignjevic, R.; Vuyst, T.D.; Campbell, J.C. A frictionless contact algorithm for meshless methods. Comput. Model. Eng. Sci. 2006, 13, 35–47. [Google Scholar]
- Wang, J.; Wu, H.; Gu, S.; Hua, H. Simulating frictional contact in smoothed particle hydrodynamics. Sci. China Technol. Sci. 2013, 56, 1779–1789. [Google Scholar] [CrossRef]
- Zhan, L.; Peng, C.; Zhang, B.; Wu, W. A SPH framework for dynamic interaction between soil and rigid body system with hybrid contact method. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1446–1471. [Google Scholar] [CrossRef]
- Zhou, M.; Fang, Q.; Peng, Q. A mortar segment-to-segment contact method for stabilized total-Lagrangian smoothed particle hydrodynamics. Appl. Math. Model. 2022, 107, 20–38. [Google Scholar] [CrossRef]
- Gissler, C.; Peer, A.; Band, S.; Bender, J.; Teschner, M. Interlinked SPH pressure solvers for strong fluid-rigid coupling. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Oger, G.; Doring, M.; Alessandrini, B.; Ferrant, P. Two-dimensional SPH simulations of wedge water entries. J. Comput. Phys. 2006, 213, 803–822. [Google Scholar] [CrossRef]
- Akinci, N.; Ihmsen, M.; Akinci, G.; Solenthaler, B.; Teschner, M. Versatile rigid-fluid coupling for incompressible SPH. ACM Trans. Graph. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Band, S.; Gissler, C.; Ihmsen, M.; Cornelis, J.; Peer, A.; Teschner, M. Pressure boundaries for implicit incompressible SPH. ACM Trans. Graph. 2018, 37, 1–11. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Xiao, Y.H.; Zou, W.B.; Liu, K. An effective smoothing length updating method for smoothed particle hydrodynamics. Int. J. Comput. Methods 2022, 19, 2250004. [Google Scholar] [CrossRef]
- Johnson, G.R.; Stryk, R.A.; Beissel, S.R. SPH for high velocity impact computations. Comput. Methods Appl. Mech. Eng. 1996, 139, 347–373. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- MATLAB Documentation; The MathWorks, Inc.: Natick, MA, USA, 2014.
- Johnson, G.R.; Stryk, R.A. Symmetric contact and sliding interface algorithms for intense impulsive loading computations. Comput. Methods Appl. Mech. Eng. 2001, 190, 4531–4549. [Google Scholar] [CrossRef]
- Swegle, J.W.; Attaway, S.W.; Heinstein, M.W.; Mello, F.J.; Hicks, D.L. An Analysis of Smoothed Particle Hydrodynamics; Report No. SAND93-2513; Sandia National Laboratories: Albuquerque, NM, USA, 1994.
- LS-DYNA Keywords User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2014.
- Hu, D.A.; Long, T.; Xiao, Y.H.; Han, X.; Gu, Y. Fluid-structure interaction analysis by coupled FE-SPH model based on a novel searching algorithm. Comput. Methods Appl. Mech. Eng. 2014, 276, 266–286. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Sarva, S.; Isaacs, J.B.; Lischer, D.W. Novel ideas in multi-functional ceramic armor design. Ceram. Trans. 2002, 134, 511–525. [Google Scholar]
- Sarva, S.; Nemat-Nasser, S.; Mcgee, J.; Isaacs, J. The effect of thin membrane restraint on the ballistic performance of armor grade ceramic tiles. Int. J. Impact Eng. 2007, 34, 277–302. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. An improved computational constitutive model for brittle materials. AIP Conf. Proc. 1994, 309, 981–984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).