Study on the Effect of Micro-Vessels on Ablation Effect in Laser Interstitial Brain Tissue Thermal Therapy Based on PID Temperature Control
Abstract
1. Introduction
2. Materials and Methods
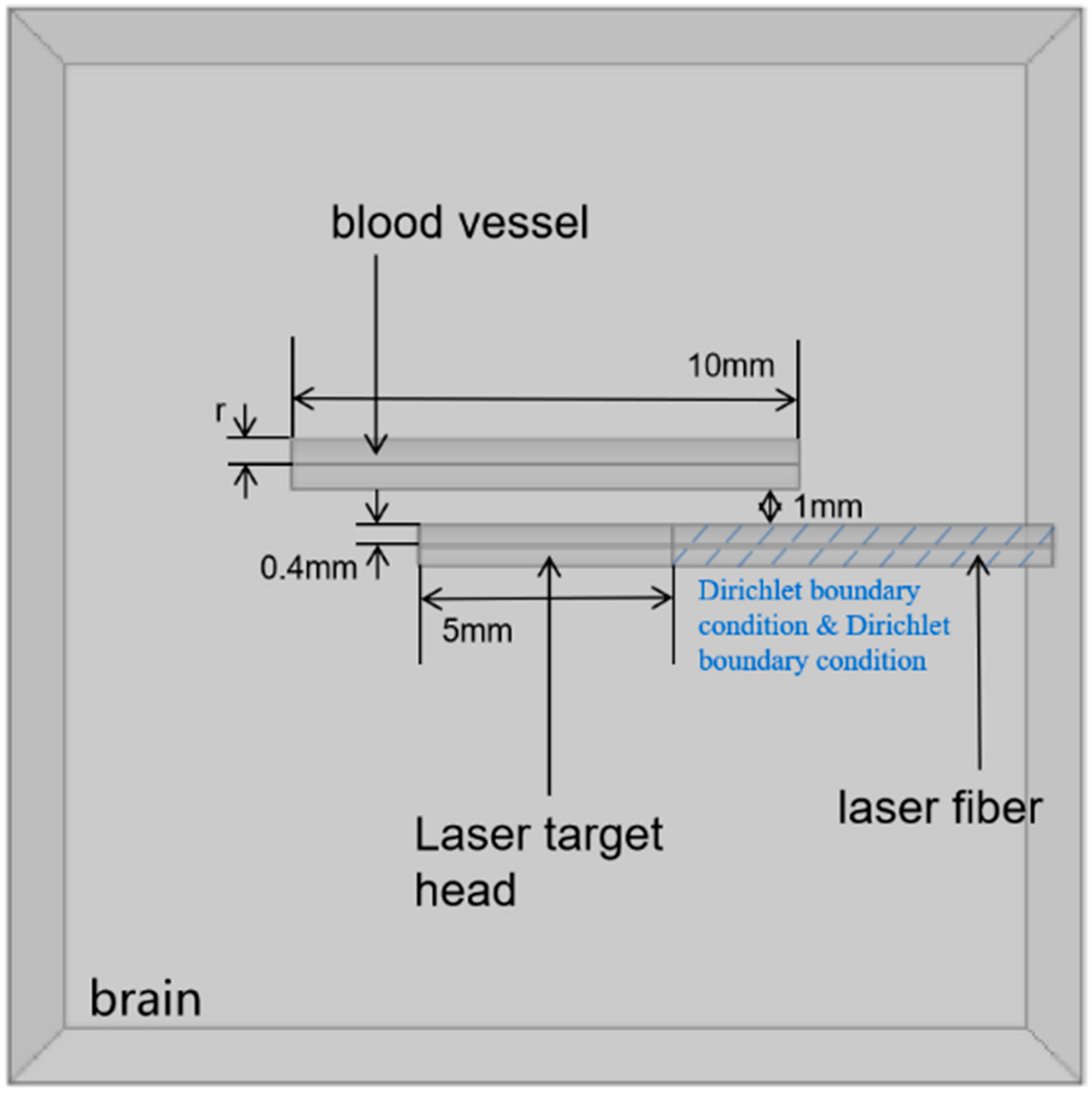
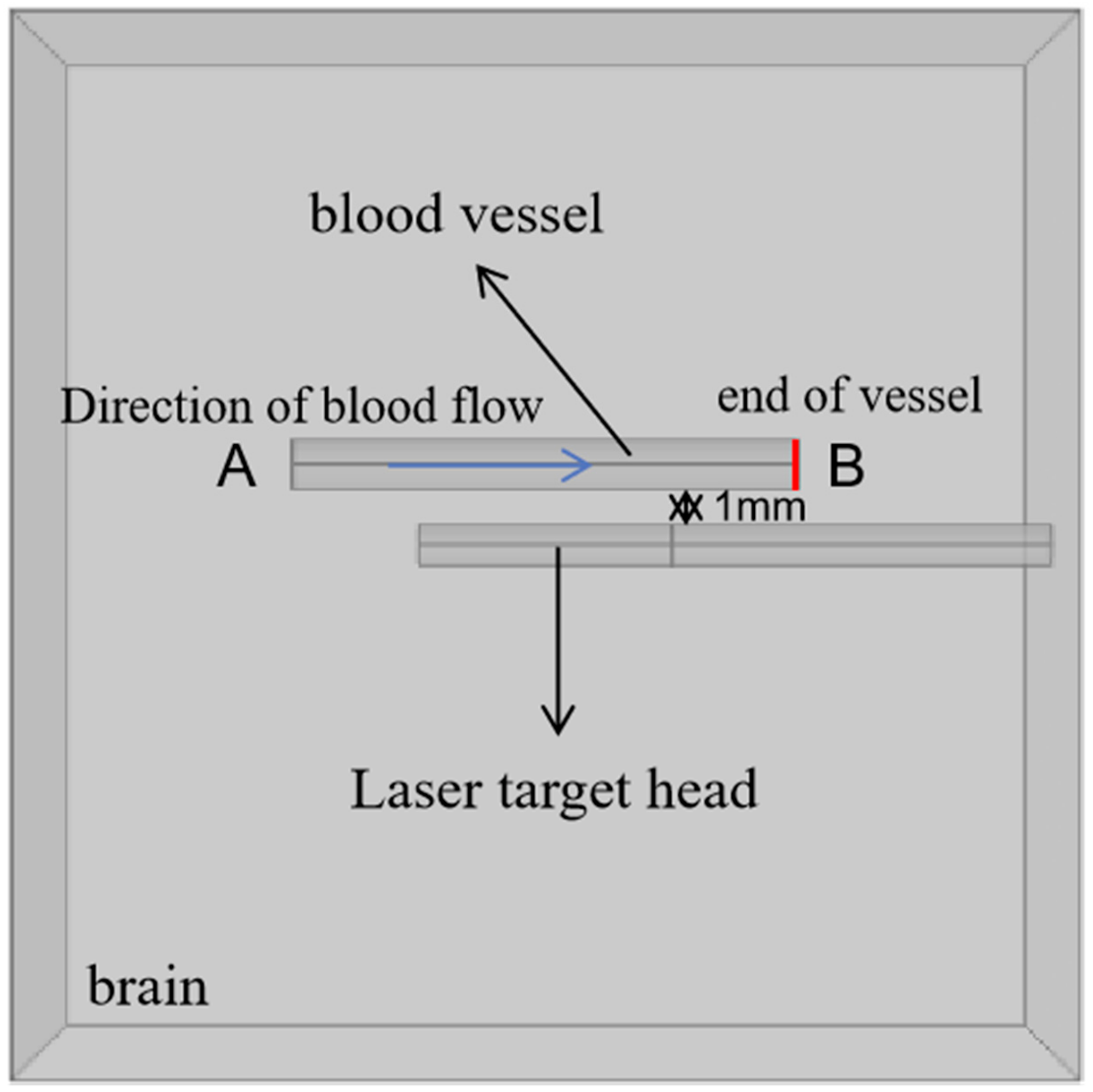
2.1. Model Geometry
2.2. Mathematical Models
- Laser irradiance
- Radial super-Gaussian distribution equation
- Axial Gaussian distribution equation
- Absorption coefficient
- Scattering coefficient
- Anisotropy factor
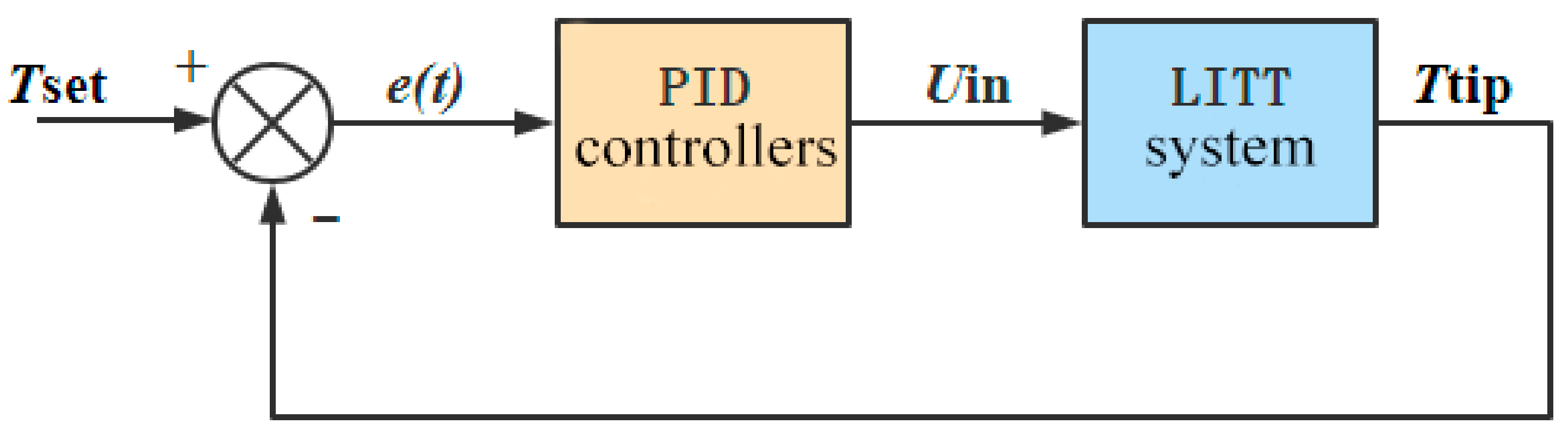
2.3. Boundary and Initial Conditions
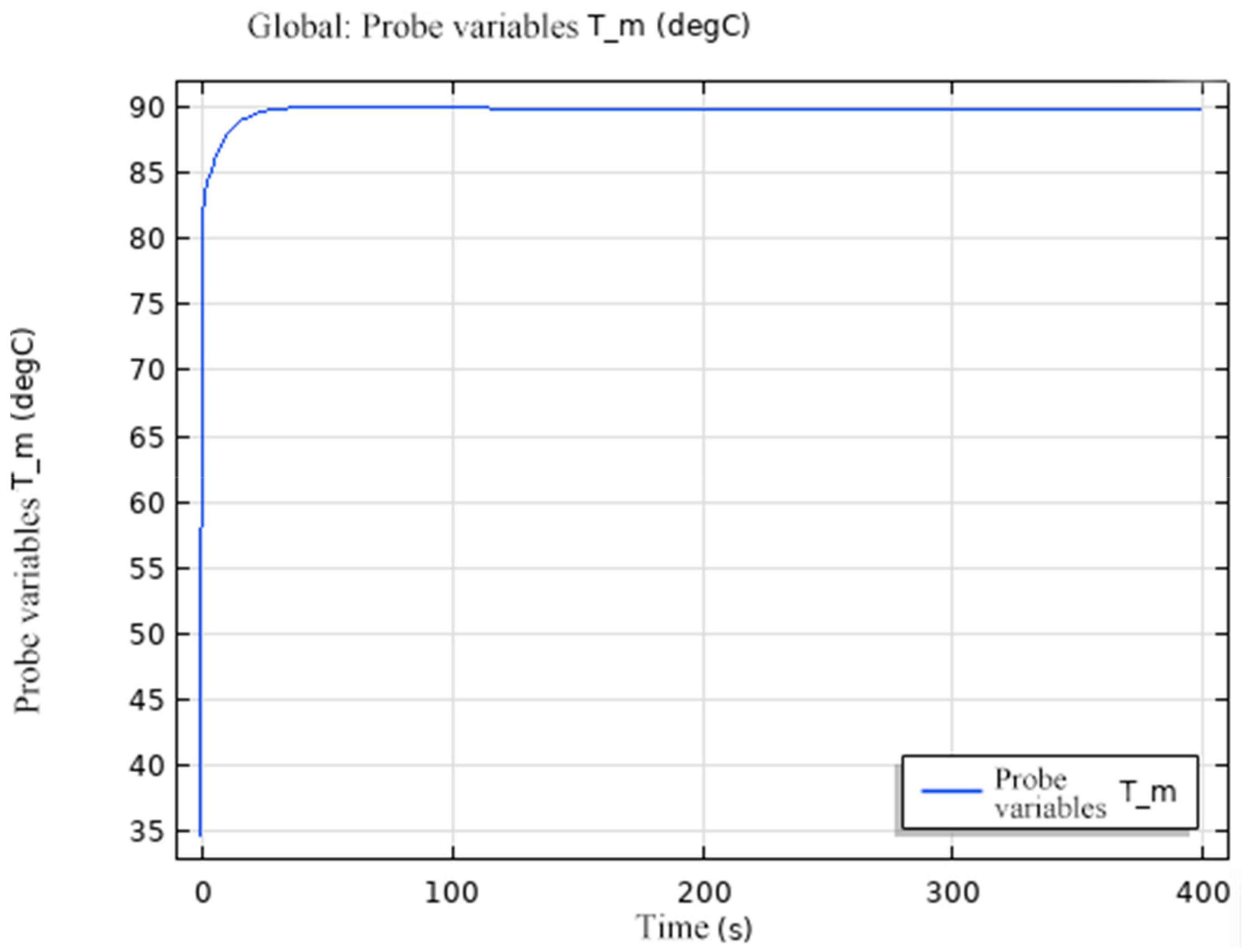
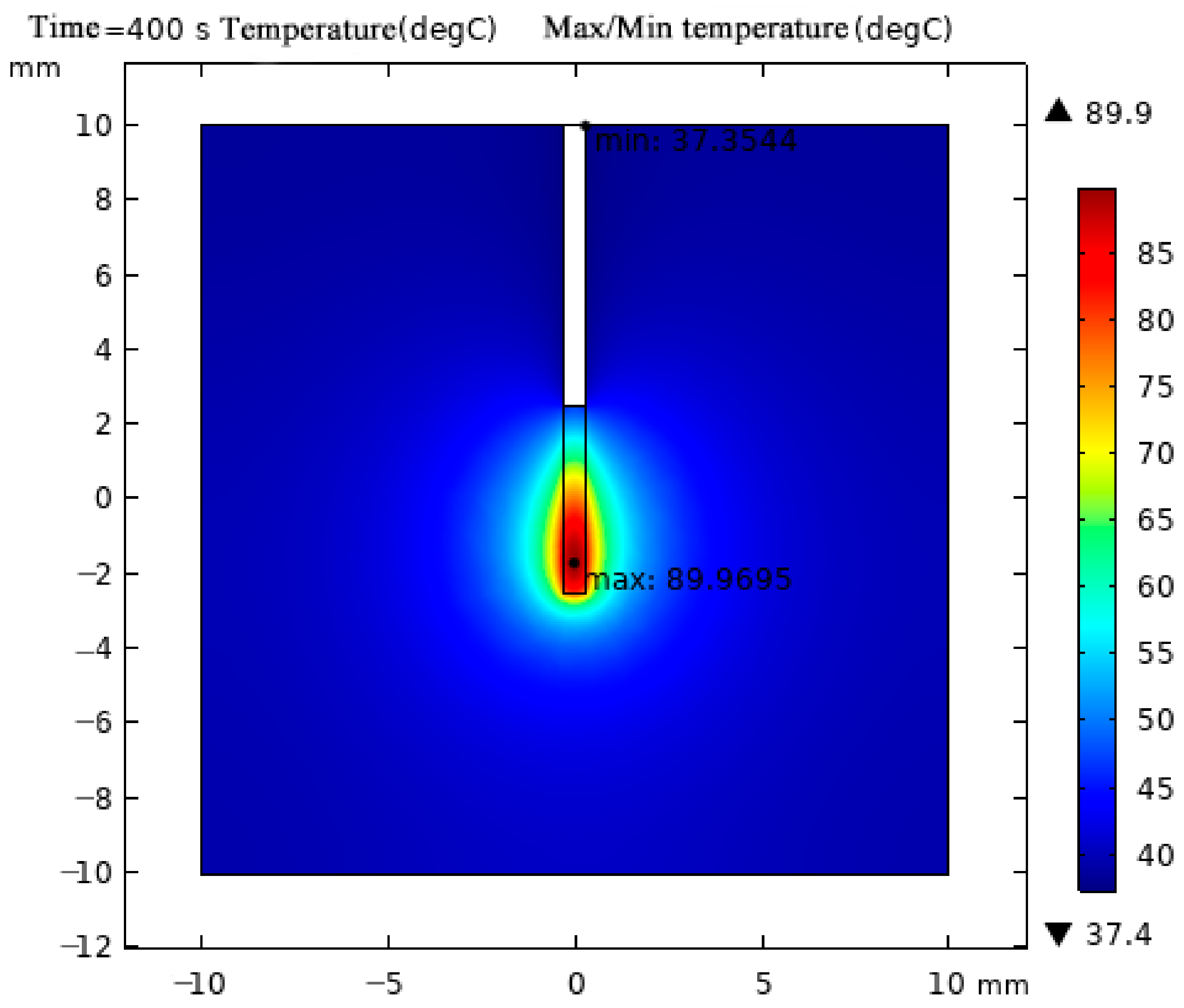
3. Result
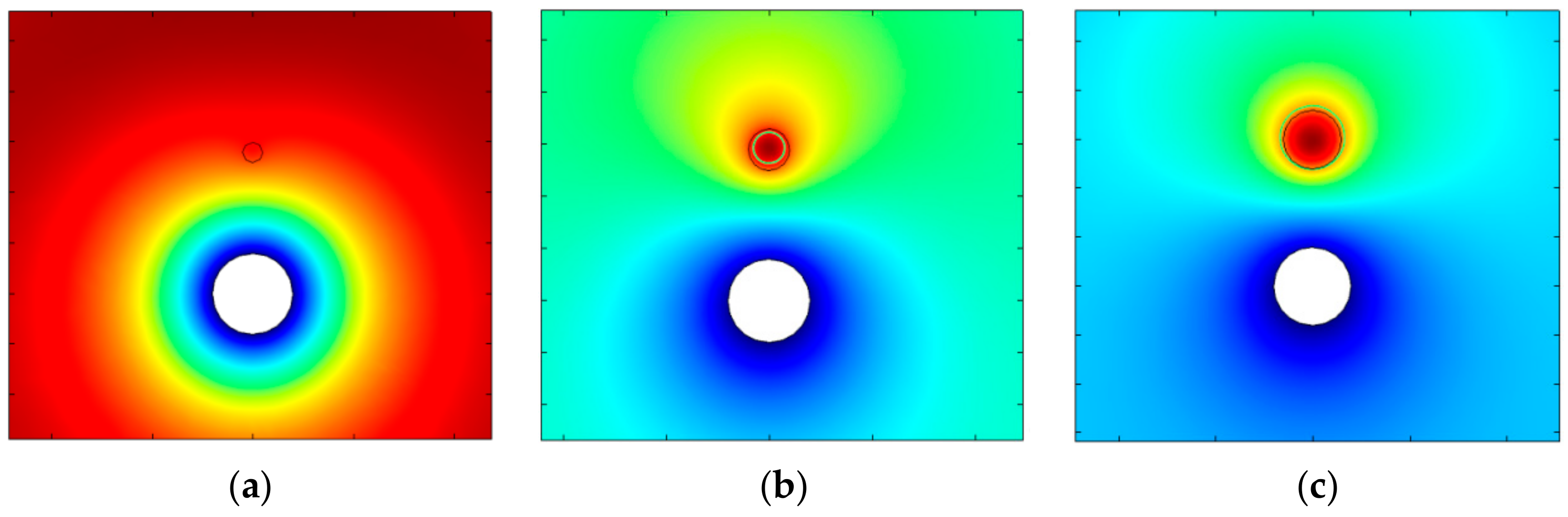
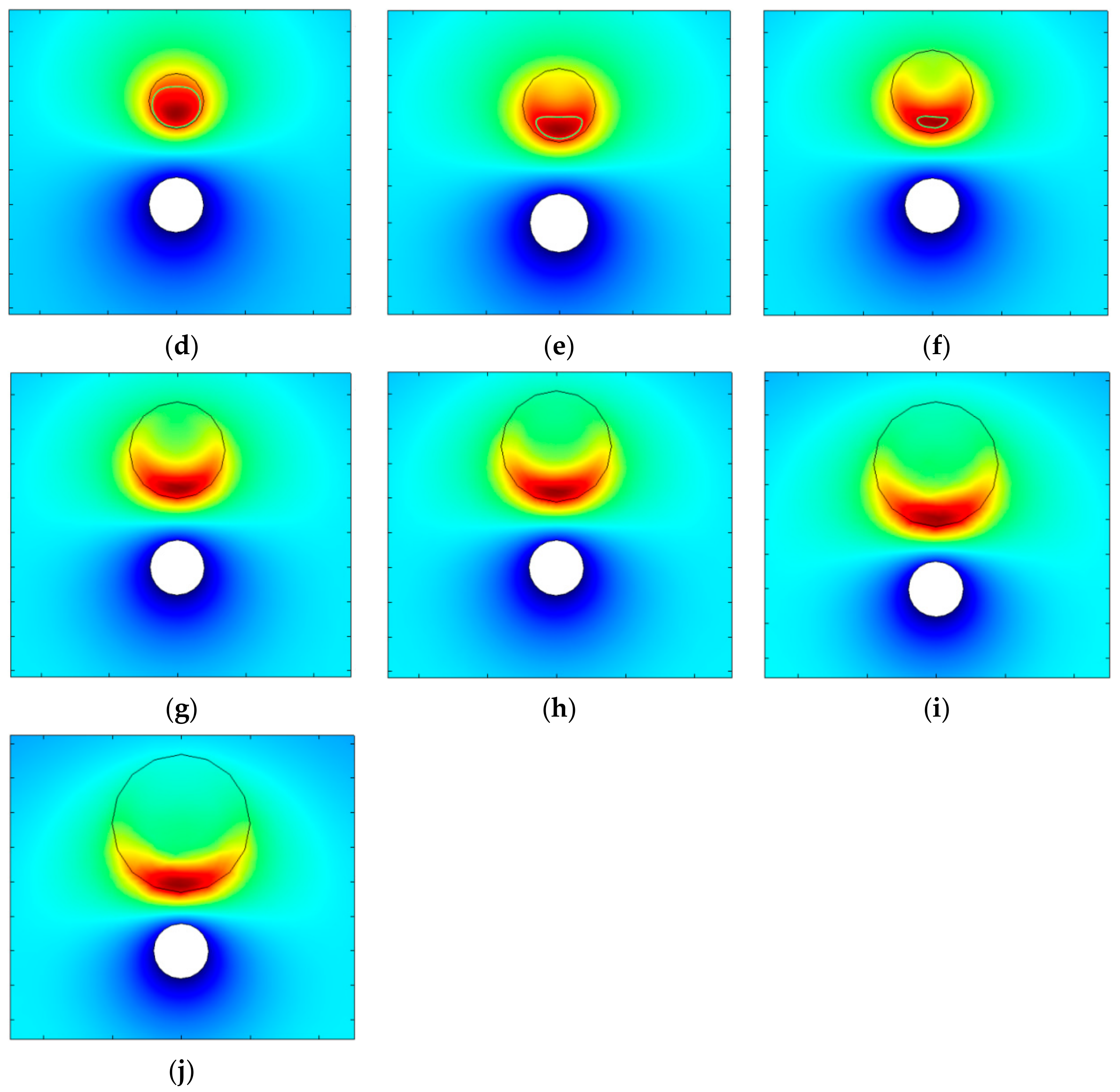
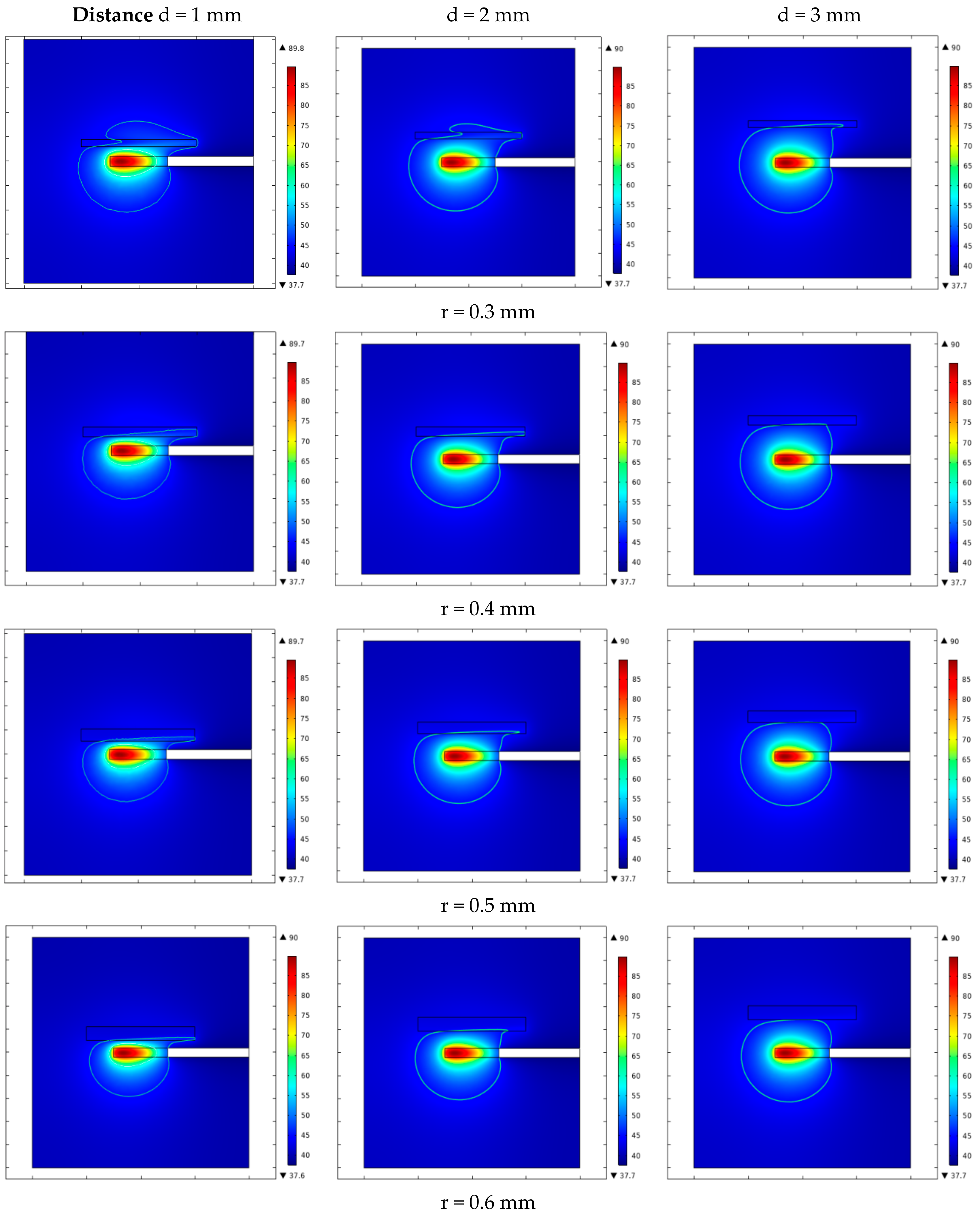
3.1. Temperature Field Variation at Different Vessel Radii
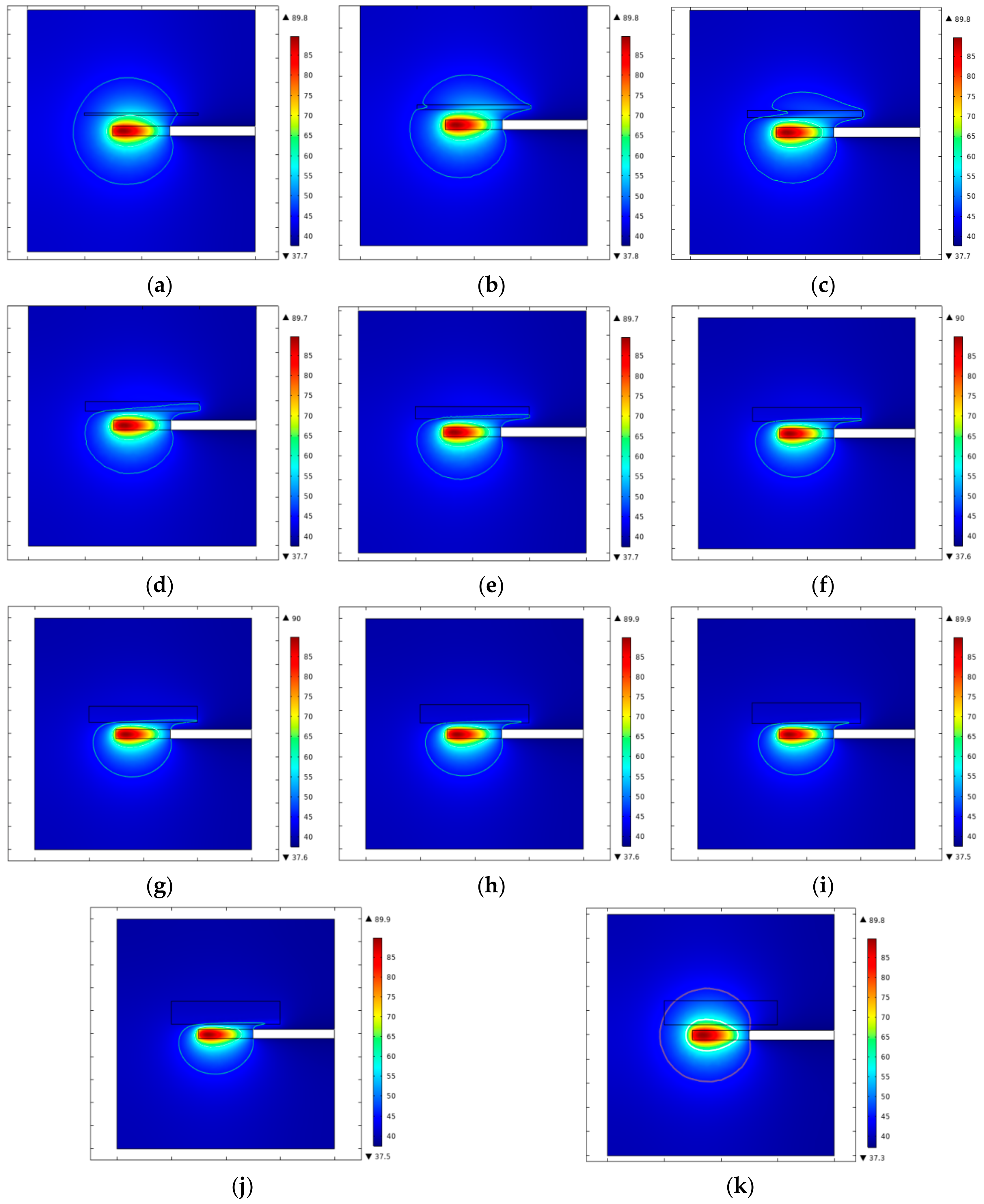
3.2. Temperature Field Variation for Different Fiber-to-Vessel Distances
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Davis, F.G.; Mccarthy, B.J. Epidemiology of brain tumors. Curr. Opin. Neurol. 2000, 13, 635–640. [Google Scholar] [CrossRef]
- Yan, J.F.; Liu, J. Cryosurgery and hyperthermia treatment on brain tumors and the thermal issues involved. Beijing Biomed. Eng. 2006, 25, 325–329. [Google Scholar]
- Franck, P.; Henderson, P.W.; Rothaus, K.O. Basics of lasers: History, physics, and clinical applications. Clin. Plast. Surg. 2016, 43, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Menovsky, T.; Beek, J.F.; Van Gemert, M.J.C.; Roux, F.X.; Bown, S.G. Interstitial laser thermotherapy in neurosurgery: A review. Acta Neurochir. 1996, 138, 1019–1026. [Google Scholar] [CrossRef]
- Ye, Y.Y. Experimental Study and Device Design of Thermal Damage by Laser Action on Biological Tissues; South China University of Technology: Guangzhou, China, 2020. [Google Scholar]
- Wang, X.R.; Gao, H.J.; Wu, S.C.; Bai, Y. Review of simulation techniques for radiofrequency ablation of liver tumor. Chin. Med. Devices 2018, 33, 108–114. [Google Scholar]
- Marqa, M.F.; Mordon, S.; Betrouni, N. Laser interstitial thermotherapy of small breast fibroadenomas: Numerical simulations. Lasers Surg. Med. 2012, 44, 832–839. [Google Scholar] [CrossRef] [PubMed]
- Nishii, T.; Kotoko, A.; Hori, Y.; Matsuzaki, Y.; Watanabe, Y.; Morita, Y.; Kono, A.K.; Matsuda, H.; Fukuda, T. Filtered back projection revisited in low-kilovolt computed tomography angiography: Sharp filter kernel enhances visualization of the artery of Adamkiewicz. Neuroradiology 2019, 61, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Sheu, T.W.H.; Solovchuk, M.A.; Chen, A.W.J.; Thiriet, M. On an acousticsthermal-fluid coupling model for the prediction of temperature elevation in liver tumor. Int. J. Heat Mass Transf. 2011, 54, 4117–4126. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. A novel local thermal non-equilibrium model for biological tissue applied to multipleantennas configurations for thermal ablation. Numer. Heat Transf. Part A Appl. 2021, 79, 111–121. [Google Scholar] [CrossRef]
- Hassanpour, S.; Saboonchi, A. Modeling of heat transfer in a vascular tissue-like medium during an interstitial hyperthermia process. J. Therm. Biol. 2016, 62, 150–158. [Google Scholar] [CrossRef]
- Huang, W.H. Influence of blood vessel on the thermal lesion formation during radiofrequency ablation for liver tumors. Med. Phys. 2013, 40, 073303. [Google Scholar] [CrossRef]
- Vaidya, N.; Baragona, M.; Lavezzo, V.; Maessen, R.; Veroy, K. Simulation study of the cooling effect of blood vessels and blood coagulation in hepatic radio frequency ablation. Int. J. Hyperth. 2021, 38, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.B. PID Control Temperature Feedback Photothermal Treatment System Based on Infrared Thermal Imager; Fujian Normal University: Fuzhou, China, 2019. [Google Scholar]
- Zhu, F.L. Simulation and Experimental Monitoring of Temperature Field in Laser Induced Interstitial Hyperthermia; Fujian Normal University: Fuzhou, China, 2018. [Google Scholar]
- Kerbage, Y.; Rouillès, J.; Vignion, A.S.; Delhem, N.; Thecua, E.; Deleporte, P.; Collinet, P.; Mordon, S. Laser interstitial thermotherapy (LITT) for breast cancer: Dosimetry optimization and numerical simulation. Lasers Med. Sci. 2022, 37, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.; Park, S.; Hlaing, K.K.; Kang, H.W. Temperature feedback-controlled photothermal treatment with diffusing applicator: Theoretical and experimental evaluations. Biomed. Opt. Express 2016, 7, 1932–1947. [Google Scholar] [CrossRef]
- Li, L.; Dong, W.W.; Shi, P.; Gan, A.; Xu, Q. Thermal effect of high power Yb: YAG microlaser. Laser Technol. 2010, 34, 8–12. [Google Scholar]
- Du, W.; Wang, L.T.; Wang, J.Y.; Zhang, X. Transverse intensity distribution of output beam of fiber coupled semiconductor laser based on super Gaussian function. Henan Sci. Technol. 2022, 41, 39–43. [Google Scholar]
- Miaskowski, A.; Gas, P. Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation. Materials 2022, 16, 223. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, G.M.; Kotte, A.N.; Raaymakers, B.W.; Lagendijk, J.J. Temperature simulations in tissue with a realistic computer- generated vessel network. Phys. Med. Biol. 2000, 45, 1035–1049. [Google Scholar] [CrossRef] [PubMed]
- Consiglieri, L.; Santos, I.D.; Haemmerich, D. Theoretical analysis of the heat convention coefficient in large vessels and the significance for thermal ablative therapies. Phys. Med. Biol. 2003, 48, 4125–4134. [Google Scholar] [CrossRef] [PubMed]
- Sutera, S.P.; Skalak, R. The history of poiseuille’s law. Annu. Rev. Fluid Mech. 1993, 25, 19. [Google Scholar] [CrossRef]
- Williams, H.R.; Trask, R.S.; Weaver, P.M.; Bond, I.P. Minimum mass vascular networks in multifunctional materials. J. R. Soc. Interface 2008, 5, 55–65. [Google Scholar] [CrossRef]
- Gas, P.; Kurgan, E. Evaluation of Thermal Damage of Hepatic Tissue During Thermotherapy based on the Arrhenius Model. In Proceedings of the Progress in Applied Electrical Engineering (PAEE), IEEE Conference, Koscielisko, Poland, 18–22 June 2018; pp. 1–4. [Google Scholar]
- Rossmanna, C.; Haemmerich, D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Crit. Rev. Biomed. Eng. 2014, 42, 467–492. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Yamada, Y.; Zaccanti, G. Analytical approximate solutions of the time-domain diffusion equation in layered slabs. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2002, 19, 71–80. [Google Scholar] [CrossRef]
- Jiang, S.C.; Zhang, J.Z.; Zhang, X.X. Parameter selection in laser-induced tumor interstitial hyperthermia based on a dynamic photothermal model. Acta Laser Biol. Sin. 2006, 15, 221–227. [Google Scholar]
- Kim, B.M.; Jacques, S.L.; Rastegar, S.; Thomsen, S.; Motamedi, M. Nonlinear finite-element analysis of the role of dynamic changes in blood perfusion and optical properties in laser coagulation of tissue. IEEE J. Sel. Top. Quantum Electron. 1997, 2, 922–933. [Google Scholar]
- Amini, S.; Ahmadikia, H. New approach of controlling the area affected in brain tumour treatment by LITT. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1221–1227. [Google Scholar] [CrossRef]
- Chen, R.; Xie, S.S.; Chen, Y.J.; Lin, A.; Li, D. Tissue optical parameters of Chinese blood. Optoelectron. Laser 2002, 92–93+97. [Google Scholar]
- Fasano, A.; Homberg, D.; Naumov, D. On a mathematical model for laser-induced thermotherapy. Appl. Math. Model. 2010, 34, 3831–3840. [Google Scholar] [CrossRef]
- Zhang, B.; Moser, M.A.J.; Zhang, E.M.; Luo, Y.; Liu, C.; Zhang, W. A review of radiofrequency ablation: Large target tissue necrosis and mathematical modelling. Phys. Med. 2016, 32, 961–971. [Google Scholar] [CrossRef] [PubMed]

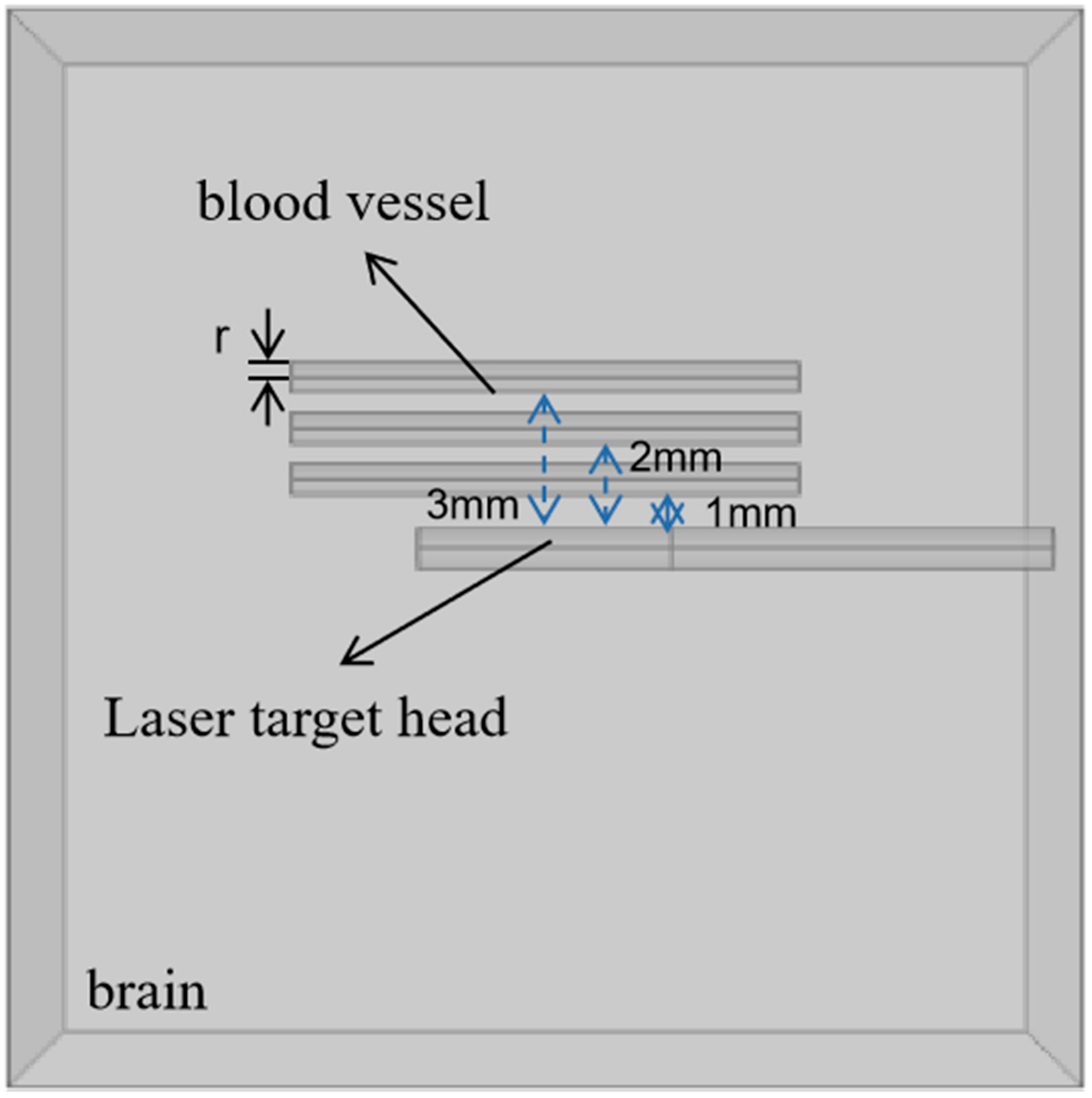
| Parameter | Brain | Blood | |
|---|---|---|---|
| Native | Denatured | ||
| Absorption coefficient, μa (1/m) | 50 | 62 | 883 |
| Scattering coefficient, μs (1/m) | 6700 | 7890 | 14,201 |
| Anisotropy factor, g | 0.96 | 0.93 | 0.98 |
| Density, ρ (kg/m3) | 1040 | 1050 | |
| Specific heat capacity, c (J/(kg·K)) | 3590 | 4180 | |
| Thermal conductivity, k (W/(m·K)) | 0.503 | 0.517 | |
| Dynamic viscosity, μ (Pa·s) | - | 0.00365 | |
| Parameter | Fiber Core | Thin Layer |
|---|---|---|
| Absorption coefficient, μa (1/m) | - | 266 |
| Scattering coefficient, μs (1/m) | - | 3000 |
| Anisotropy factor, g | - | 0.98 |
| Density, ρ (kg/m3) | 2203 | 2203 |
| Specific heat capacity, c (J/(kg·K)) | 703 | 703 |
| Thermal conductivity, k (W/(m·K)) | 1.38 | 1.38 |
| No. | Radius, r (mm) | No. | Radius, r (mm) |
|---|---|---|---|
| 1 | 0.1 | 6 | 0.6 |
| 2 | 0.2 | 7 | 0.7 |
| 3 | 0.3 | 8 | 0.8 |
| 4 | 0.4 | 9 | 0.9 |
| 5 | 0.5 | 10 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, S.; Liu, H.; Nan, Q.; Mai, X. Study on the Effect of Micro-Vessels on Ablation Effect in Laser Interstitial Brain Tissue Thermal Therapy Based on PID Temperature Control. Appl. Sci. 2023, 13, 3751. https://doi.org/10.3390/app13063751
Bi S, Liu H, Nan Q, Mai X. Study on the Effect of Micro-Vessels on Ablation Effect in Laser Interstitial Brain Tissue Thermal Therapy Based on PID Temperature Control. Applied Sciences. 2023; 13(6):3751. https://doi.org/10.3390/app13063751
Chicago/Turabian StyleBi, Sixin, Huihui Liu, Qun Nan, and Xin Mai. 2023. "Study on the Effect of Micro-Vessels on Ablation Effect in Laser Interstitial Brain Tissue Thermal Therapy Based on PID Temperature Control" Applied Sciences 13, no. 6: 3751. https://doi.org/10.3390/app13063751
APA StyleBi, S., Liu, H., Nan, Q., & Mai, X. (2023). Study on the Effect of Micro-Vessels on Ablation Effect in Laser Interstitial Brain Tissue Thermal Therapy Based on PID Temperature Control. Applied Sciences, 13(6), 3751. https://doi.org/10.3390/app13063751





