Torque Allocation of Hybrid Electric Trucks for Drivability and Transient Emissions Reduction
Abstract
1. Introduction
- propose a nonlinear dynamic model that considers the main vehicle nonlinearities, e.g., the elastic and damping behaviour of the torsional damper and the transient model of the tyres’ dynamics—thus representing a reference model for vehicle performance assessment and torque controller validation;
- show the benefits introduced by the proposed controller in terms of dynamic performance, driveline oscillations, and NOx emissions;
- test the controller’s robustness against the presence of unpredictable external inputs, e.g., a sudden road slope.
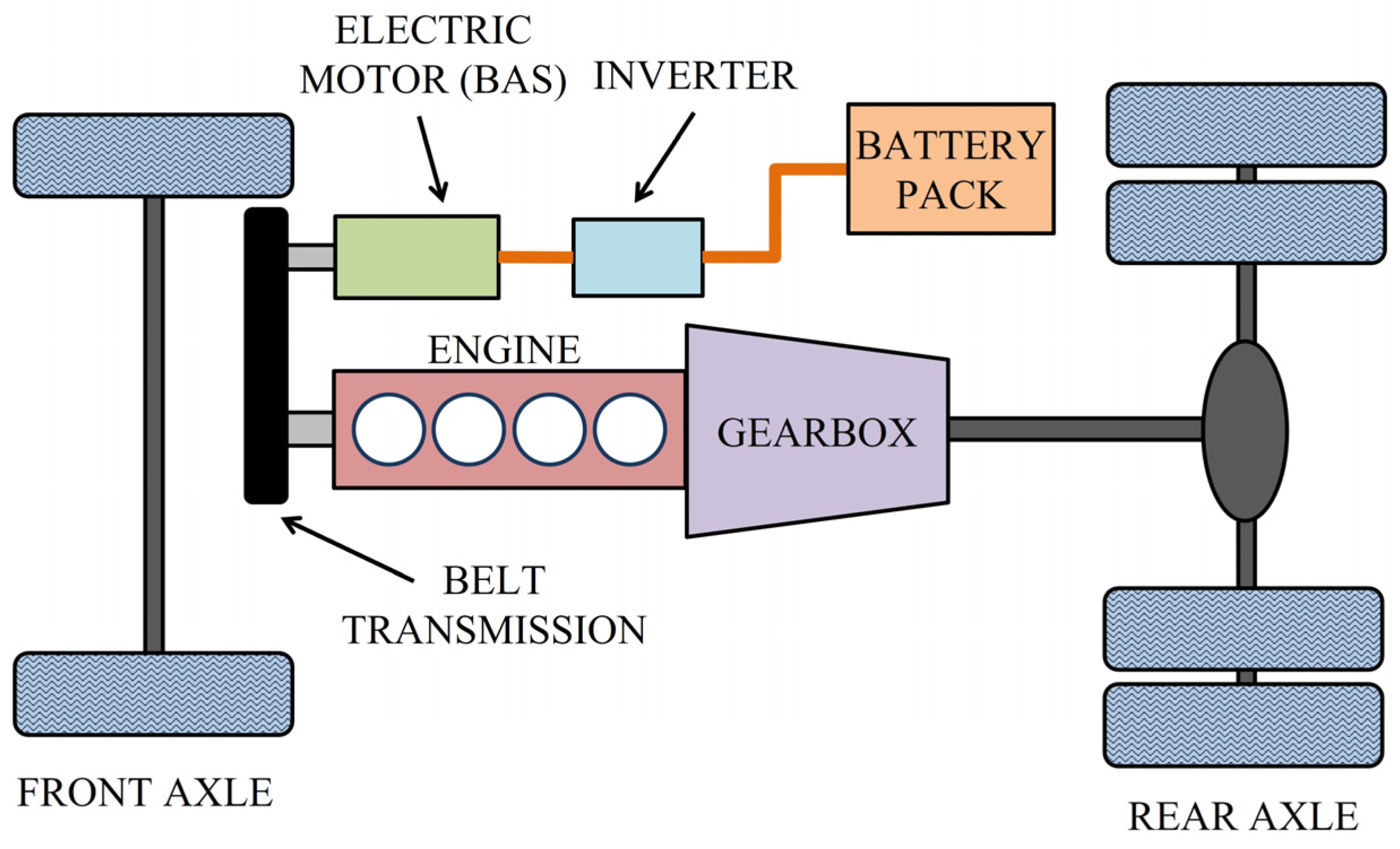
2. Hybrid Vehicle Powertrain Layout
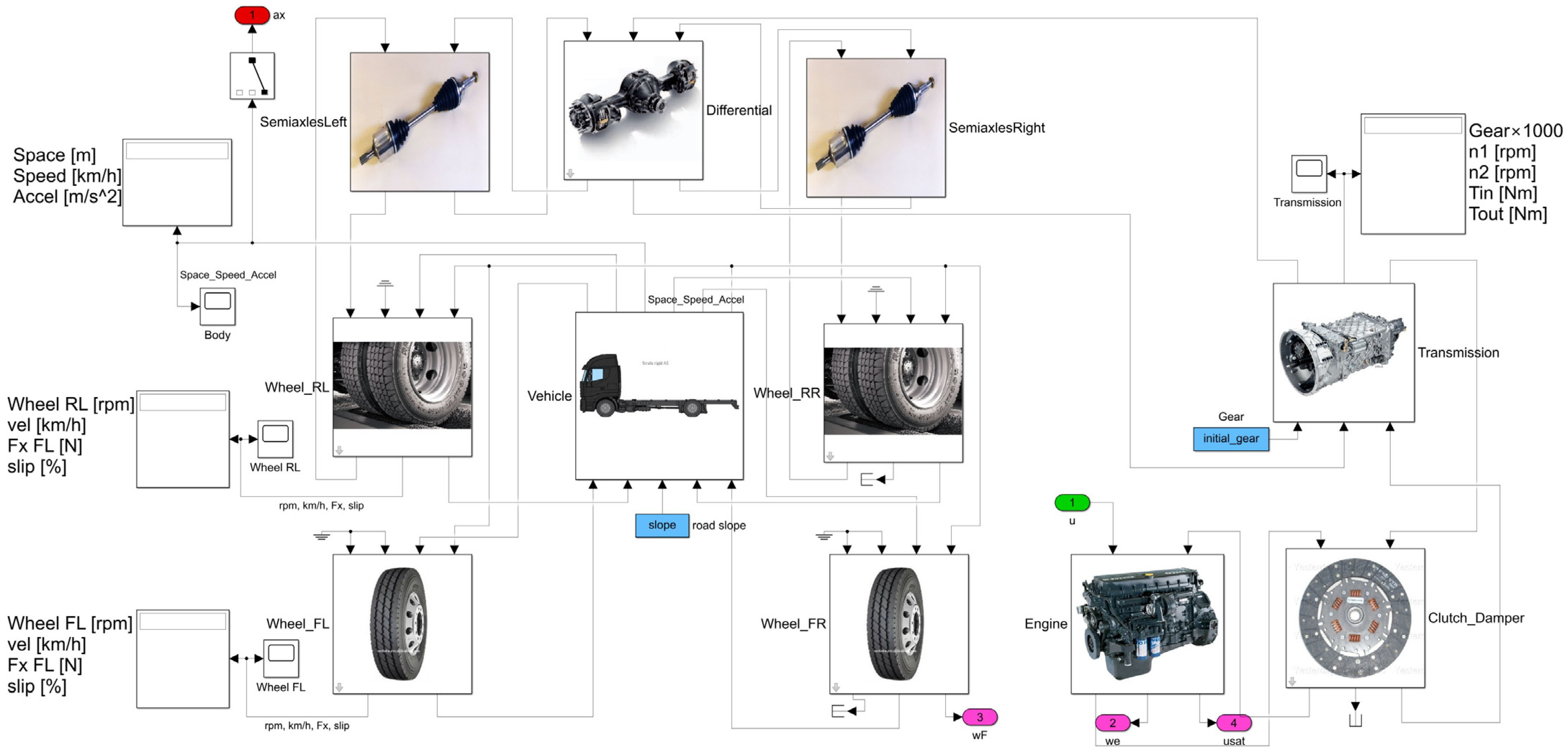
2.1. Matlab/Simulink Nonlinear Truck Model
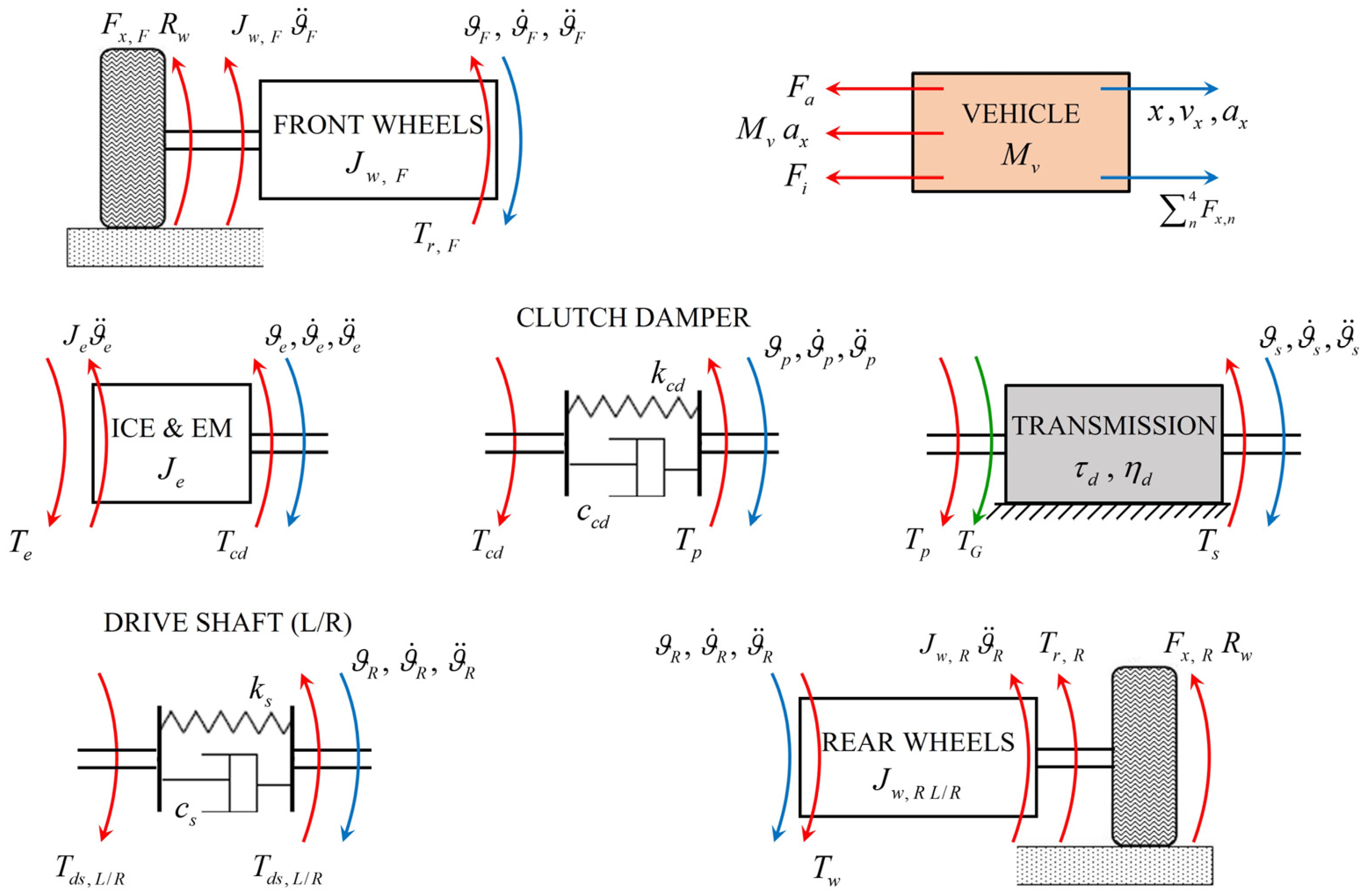
2.2. Dynamic Equations
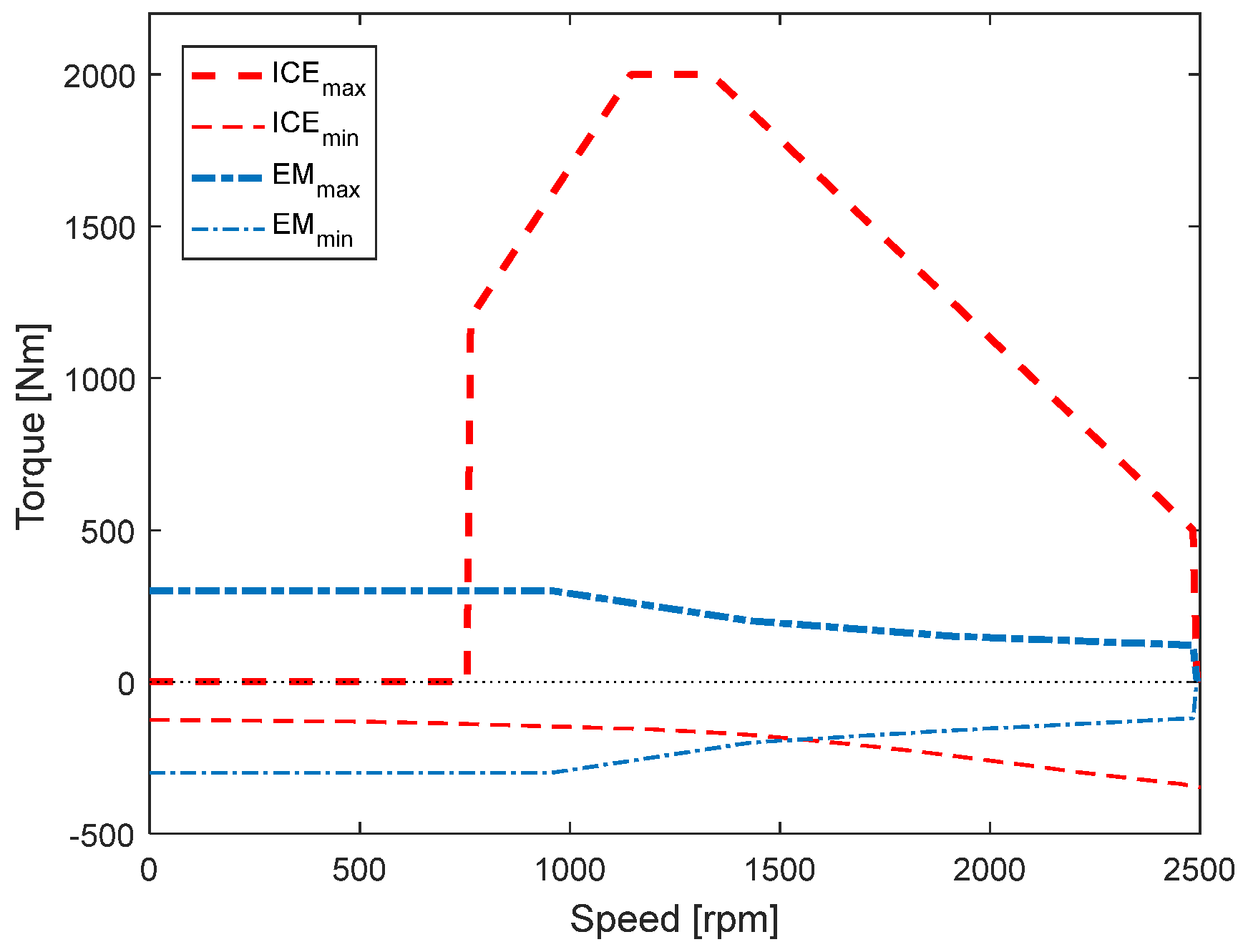
2.2.1. Power Source: ICE and EM
2.2.2. Transmission: From Clutch Damper to Differential
2.2.3. Vehicle and Wheels
2.2.4. NOx Modelling
3. Closed Loop Control System
3.1. High-Level Control Strategy
3.2. Control Allocation
4. Results
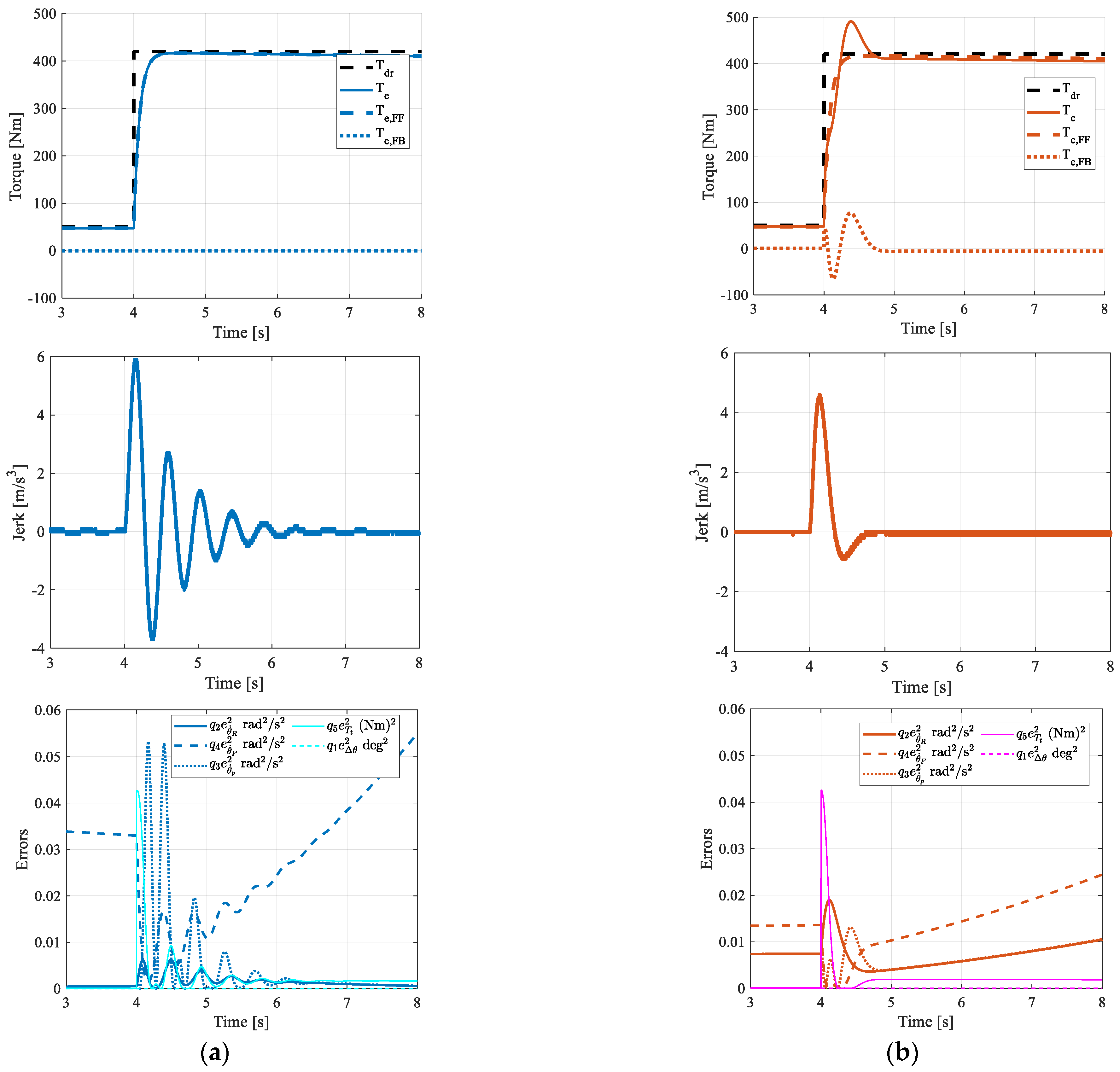
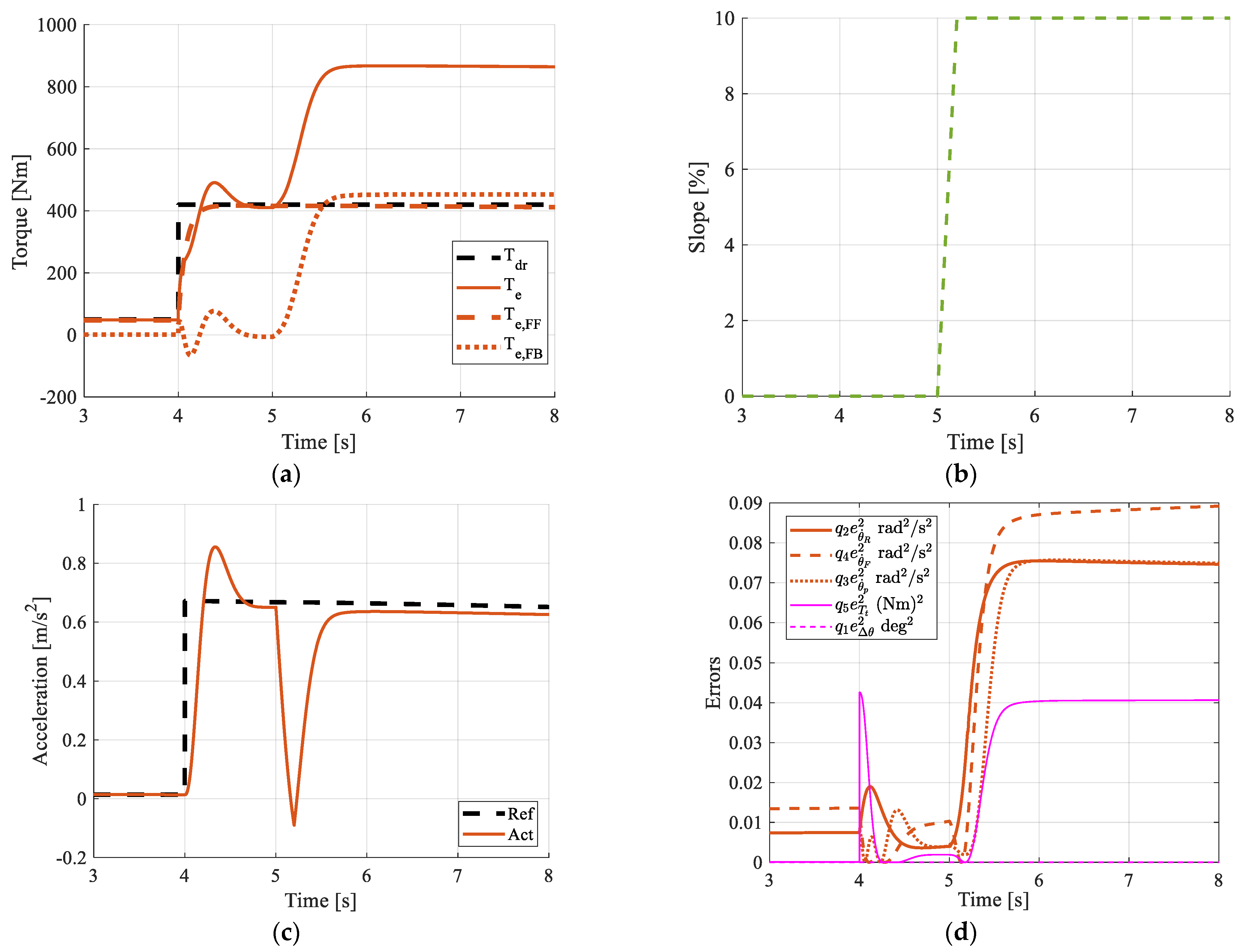
4.1. Reference Tracking Performance
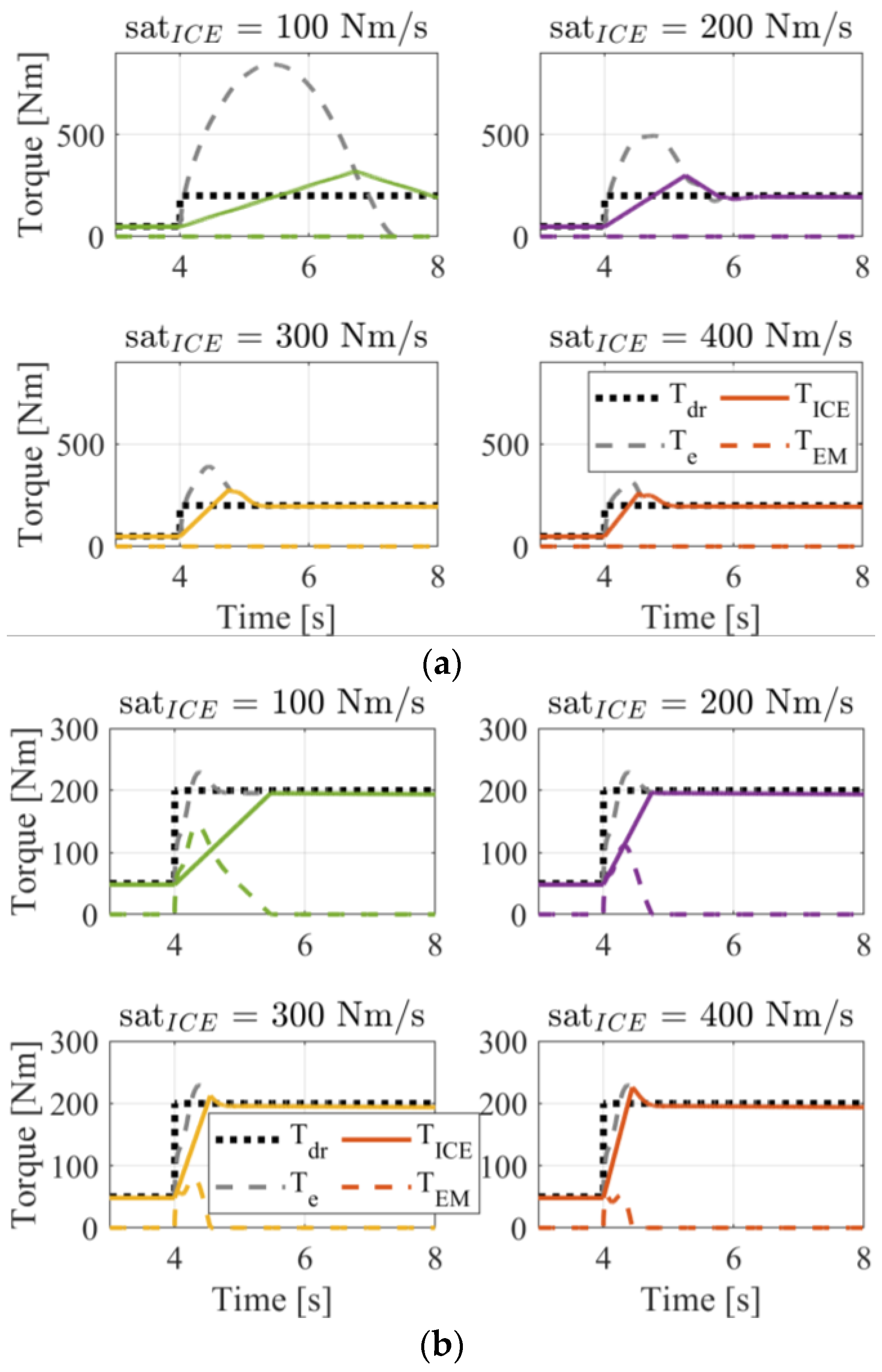
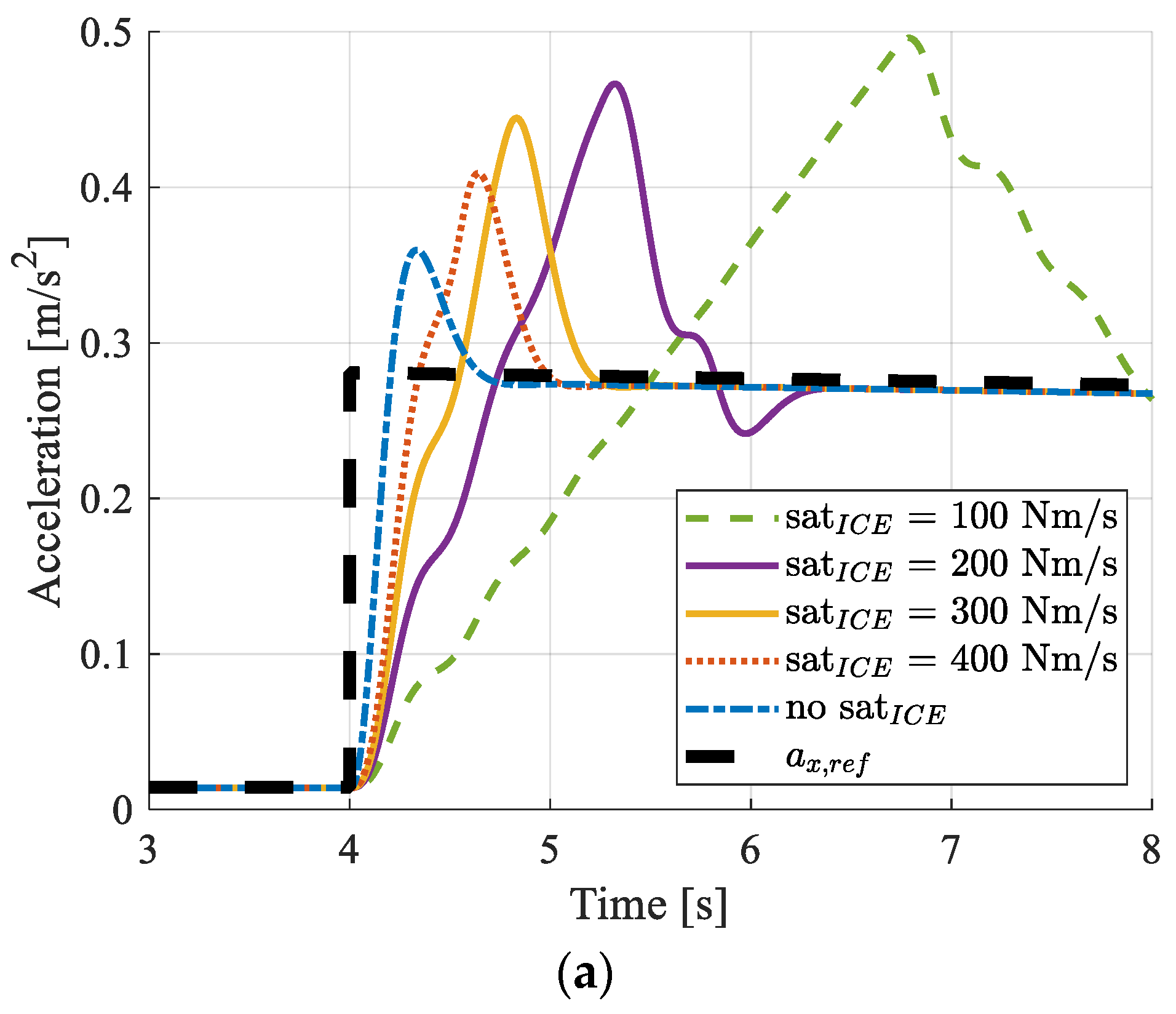
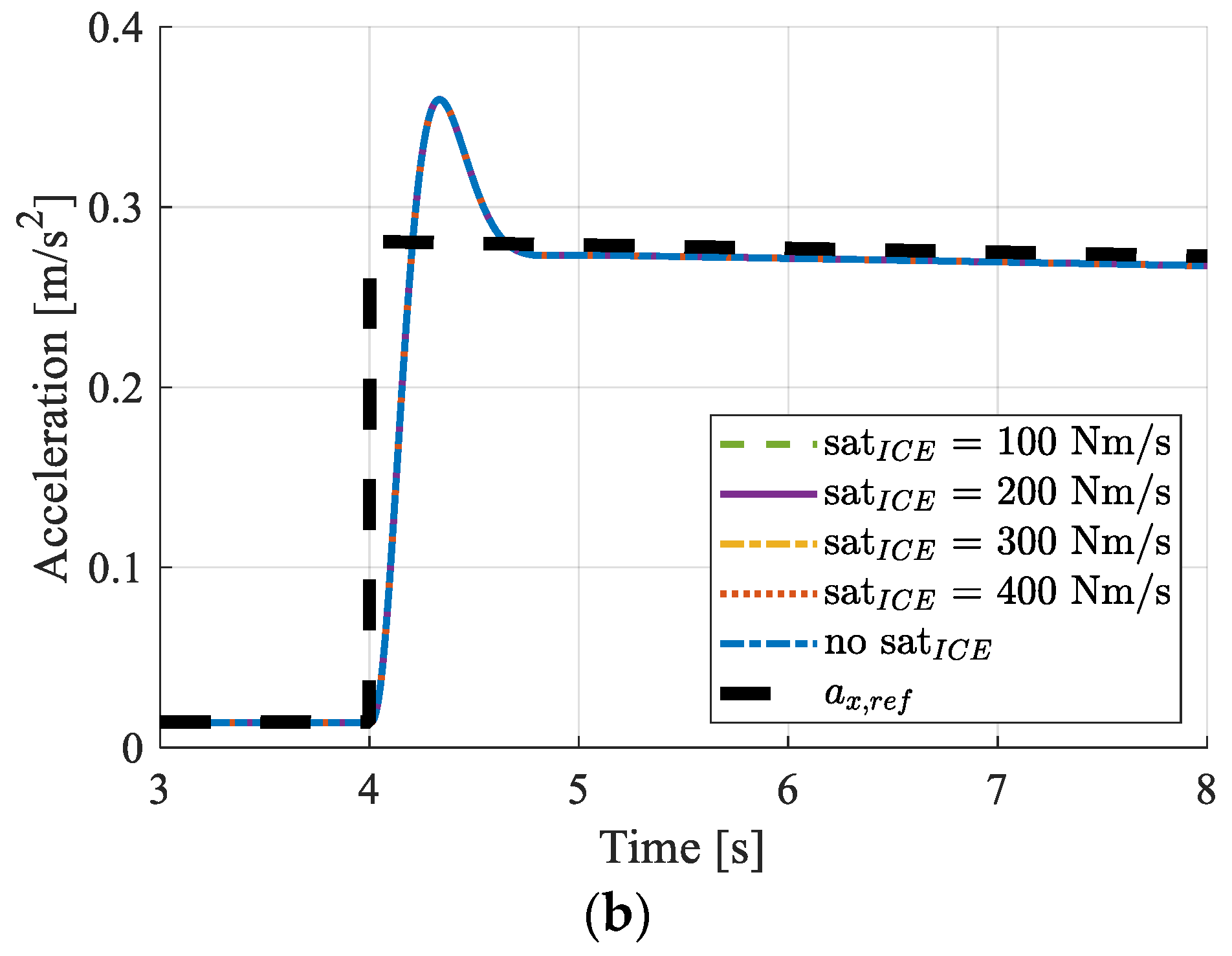
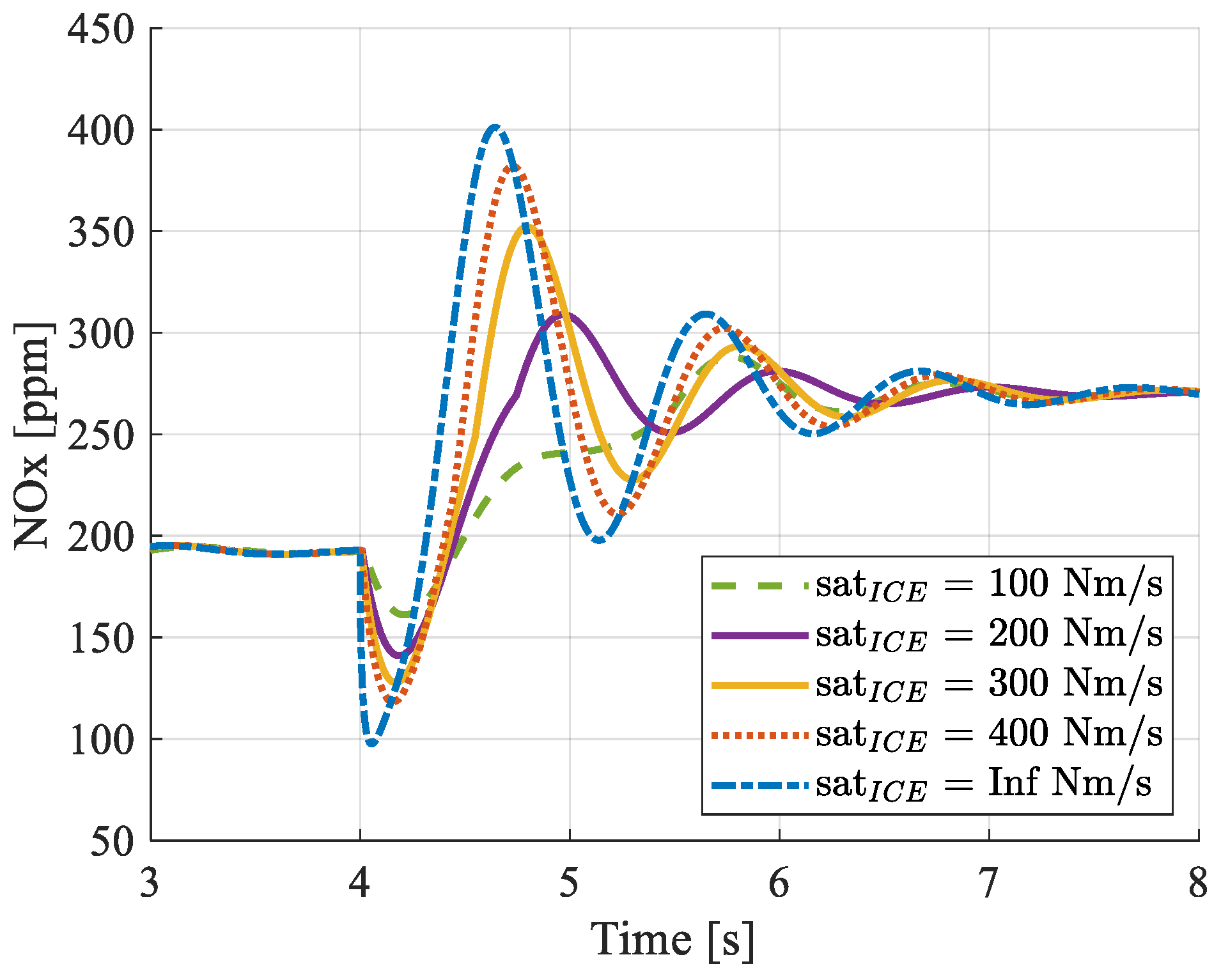
4.2. Control Allocation Evaluation
5. Conclusions
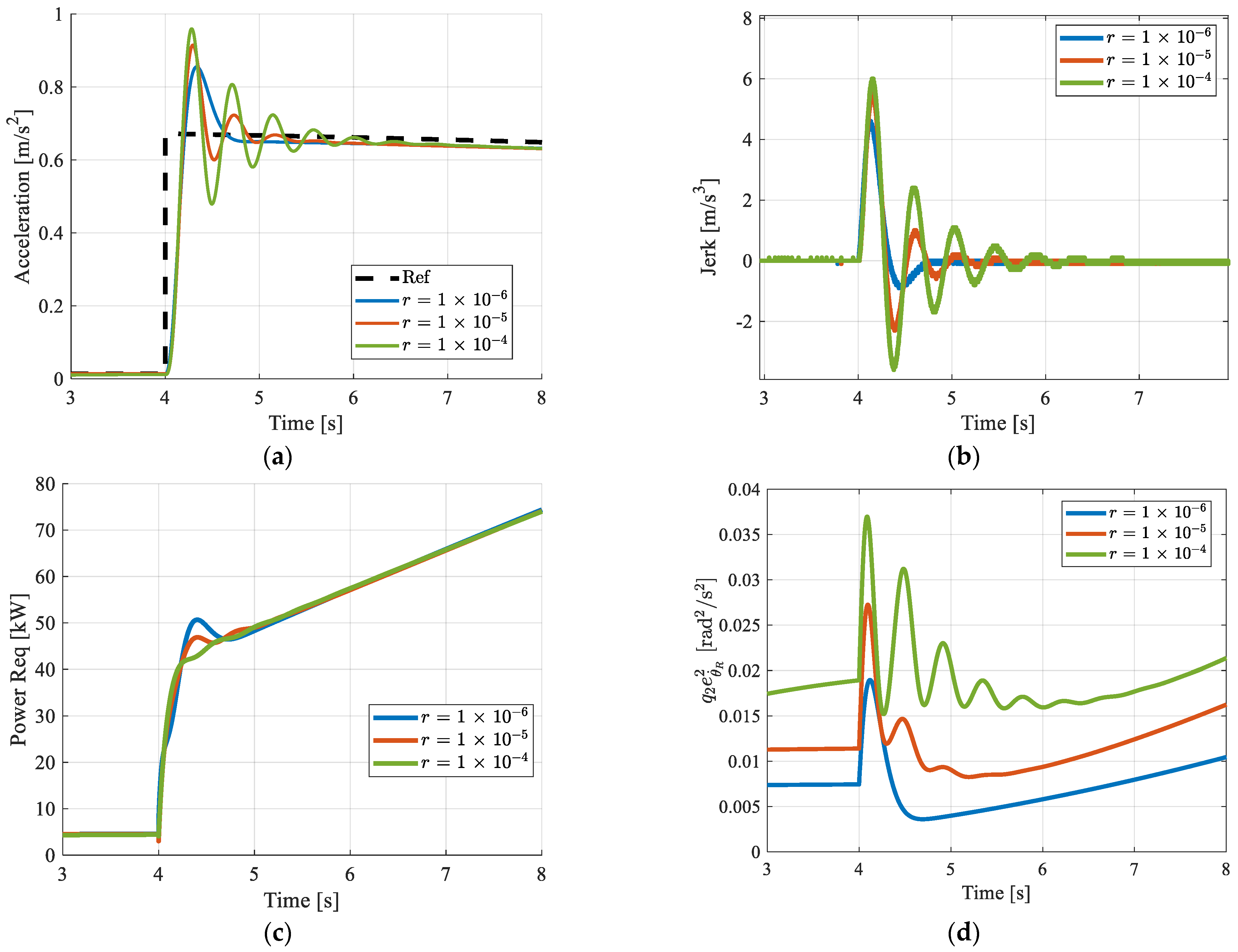
- The high level of the torque control logic generated a total torque demand that satisfied the performance requirements in terms of vehicle speed and acceleration. Both the FF and FB contributions were designed based on a simplified version of the more accurate non-linear model. The FB contribution was fundamental in improving the vehicle’s transient response, damping the acceleration and jerk oscillations. Differing calibrations of the FB gains can cope with different trade-offs between state error tracking performance and the power required to minimize errors;
- The paper also showed how the FB contribution was effective in rejecting external disturbances, e.g., the road slope, by compensating for the FF contribution with an additional contribution—thus satisfying the desired reference tracking performance;
- The control allocation strategy proved to produce a satisfactory vehicle drivability performance, even in the presence of tighter constraints in the ICE torque rate. The hybrid architecture showed outstanding robustness properties against variations in the ICE torque rate when compared to the ICE-only configuration. The redundancy offered by the fast dynamics of an electric machine represents an effective way of establishing the best combination between emissions and dynamic performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Awadallah, M.; Tawadros, P.; Walker, P.; Zhang, N. Comparative fuel economy, cost and emissions analysis of a novel mild hybrid and conventional vehicles. Proc. IMechE Part D J. Automob. Eng. 2018, 232, 1846–1862. [Google Scholar] [CrossRef]
- Emadi, A.; Rajashekara, K.; Williamson, S.S.; Lukic, S.M. Topological overview of hybrid electric and fuel cell vehicular power system architectures and configurations. IEEE Trans. Veh. Technol. 2005, 54, 763–770. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Barsali, S.; Miulli, C.; Possenti, A. A control strategy to minimize fuel consumption of series hybrid electric vehicles. IEEE Trans. Energy Convers. 2004, 19, 187–195. [Google Scholar] [CrossRef]
- Castellano, A.; Cammalleri, M. Power losses minimization for optimal operating maps in power-split HEVs: A case study on the Chevrolet Volt. Appl. Sci. 2021, 11, 7779. [Google Scholar] [CrossRef]
- Tota, A.; Galvagno, E.; Velardocchia, M. On the power-weighted efficiency of multimode powertrains: A case study on a two-mode hybrid system. In I4SDG 2021, Proceedings of the 1st Workshop IFToMM for Sustainable Development Goals, Mechanisms and Machine Science, Online, 25–26 November 2021; Quaglia, G., Gasparetto, A., Petuya, V., Carbone, G., Eds.; Springer: Cham, Switzerland, 2022; Volume 108, pp. 522–531. [Google Scholar] [CrossRef]
- Tota, A.; Galvagno, E.; Dimauro, L.; Vigliani, A.; Velardocchia, M. Energy management strategy for hybrid multimode powertrains: Influence of inertial properties and road inclination. Appl. Sci. 2021, 11, 11752. [Google Scholar] [CrossRef]
- Mantriota, G.; Reina, G.; Ugenti, A. Performance evaluation of a compound power-split CVT for hybrid powertrains. Appl. Sci. 2021, 11, 8749. [Google Scholar] [CrossRef]
- Cirimele, V.; Dimauro, L.; Repetto, M.; Bonisoli, E. Multi-objective optimisation of a magnetic gear for powertrain applications. Int. J. Appl. Electromagn. Mech. 2019, 60, S25–S34. [Google Scholar] [CrossRef]
- Nazari, S.; Siegel, J.; Stefanopoulou, A. Optimal energy management for a mild hybrid vehicle with electric and hybrid engine boosting systems. IEEE Trans. Veh. Technol. 2019, 68, 3386–3399. [Google Scholar] [CrossRef]
- Galvagno, E.; Velardocchia, M.; Vigliani, A. Drivability enhancement and transient emission reduction for a mild hybrid diesel-electric truck. Int. J. Powertrains 2013, 2, 262–291. [Google Scholar] [CrossRef]
- Parmar, V.; Di Rocco, D.; Sopouch, M.; Albertini, P. Multi-physics simulation model for noise and vibration effects in hybrid vehicle powertrain. SAE Tech. Pap. 2014, 2014-01-2093. [Google Scholar] [CrossRef]
- Chen, J.-S.; Hwang, H.-Y. Engine automatic start–stop dynamic analysis and vibration reduction for a two-mode hybrid vehicle. Proc. IMechE Part D J. Automob. Eng. 2013, 227, 1303–1312. [Google Scholar] [CrossRef]
- Hagena, J.R.; Filipi, Z.S.; Assanis, D.N. Transient diesel emissions: Analysis of engine operation during a tip-in. SAE Tech. Pap. 2006, 2006-01-1151. [Google Scholar] [CrossRef]
- Wüst, M.; Krüger, M.; Naber, D.; Cross, L.; Greis, A.; Lachenmaier, S.; Stotz, I. Operating strategy for optimized CO2 and NOx emissions of diesel-engine mild-hybrid vehicles. In Proceedings of the 15. Internationales Stuttgarter Symposium: Automobil- und Motorentechnik, Stuttgart, Germany, 17–18 March 2015; Springer: Wiesbaden, Germany, 2015. [Google Scholar] [CrossRef]
- Thibault, L.; Sciarretta, A.; Degeilh, P. Reduction of pollutant emissions of diesel mild hybrid vehicles with an innovative energy management strategy. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1274–1279. [Google Scholar] [CrossRef]
- Le Guen, D.; Weck, T.; Balihe, A.; Verbeke, B. Definition of gearshift pattern: Innovative optimization procedures using system simulation. SAE Int. J. Engines 2011, 4, 412–431. [Google Scholar] [CrossRef]
- Pramanik, S.; Anwar, S. Predictive optimal control of mild hybrid trucks. Vehicles 2022, 4, 71. [Google Scholar] [CrossRef]
- Guercioni, G.R.; Galvagno, E.; Tota, A.; Vigliani, A. Adaptive equivalent consumption minimization strategy with rule-based gear selection for the energy management of hybrid electric vehicles equipped with dual clutch transmissions. IEEE Access 2020, 8, 190017–190038. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Ebrahimi, M.; Bartlett, H. Hybrid modelling and simulation of the torsional vibration of vehicle driveline systems. Proc. IMechE Part D J. Automob. Eng. 2001, 215, 217–229. [Google Scholar] [CrossRef]
- Galvagno, E.; Dimauro, L.; Mari, G.; Velardocchia, M.; Vella, A.D. Dual Clutch Transmission vibrations during gear shift: A simulation-based approach for clunking noise assessment. SAE Tech. Pap. 2019, 2019-01-1553. [Google Scholar] [CrossRef]
- Galvagno, E.; Guercioni, G.R.; Vigliani, A. Sensitivity analysis of the design parameters of a Dual-Clutch Transmission focused on NVH performance. SAE Tech. Pap. 2016, 2016-01-1127. [Google Scholar] [CrossRef]
- Awadallah, M.; Tawadros, P.; Walker, P.; Zhang, N. Dynamic modelling and simulation of a manual transmission based mild hybrid vehicle. Mech. Mach. Theory 2017, 112, 218–239. [Google Scholar] [CrossRef]
- Guzzomi, A.L.; Sharman, A.; Stone, B.J. Some torsional stiffness and damping characteristics of a small pneumatic tyre and the implications for powertrain dynamics. Proc. IMechE Part D J. Automob. Eng. 2010, 224, 229–244. [Google Scholar] [CrossRef]
- Bartram, M.; Mavros, G.; Biggs, S. A study on the effect of road friction on driveline vibrations. Proc. IMechE Part K J. Multi-Body Dyn. 2010, 224, 321–340. [Google Scholar] [CrossRef]
- Rill, G. First order tyre dynamics. In Proceedings of the III European Conference on Computational Mechanics, Solids, Structures and Coupled Problems in Enginnering, Lisbon, Portugal, 5–8 June 2006. [Google Scholar] [CrossRef]
- Dolcini, P.J.; Canudas-de-Wit, C.; Béchart, H. Dry Clutch Control for Automotive Applications, 1st ed.; Springer: London, UK, 2010; pp. 1–144. [Google Scholar]
- Canudas-de-Wit, C.; Tsiotras, P.; Velenis, E.; Basset, M.; Gissinger, G. Dynamic Friction Models for Road/tyre Longitudinal Interaction. Veh. Syst. Dyn. 2003, 39, 189–226. [Google Scholar] [CrossRef]
- Rovarino, D.; Actis Comino, L.; Bonisoli, E.; Rosso, C.; Venturini, S.; Velardocchia, M.; Baecker, M.; Gallrein, A. Hardware and virtual test-rigs for automotive steel wheels design. SAE Int. J. Adv. Curr. Prac. Mobil. 2020, 2, 3481–3489. [Google Scholar] [CrossRef]
- Friedriksson, J. Improved driveability of a hybrid electric vehicle using powertrain control. Int. J. Altern. Propuls. 2006, 1, 97–111. [Google Scholar] [CrossRef]
- Ito, Y.; Tomura, S.; Moriya, K. Development of vibration reduction motor control for hybrid vehicles. In Proceedings of the IECON 2007—33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 516–521. [Google Scholar] [CrossRef]
- Baumann, J.; Torkzadeh, D.D.; Ramstein, A.; Kiencke, U.; Schlegl, T. Model-based predictive anti-jerk control. Control Eng. Pract. 2006, 14, 259–266. [Google Scholar] [CrossRef]
- Filippini, M.; Torchio, R.; Alotto, P.; Bonisoli, E.; Dimauro, L.; Repetto, M. A new class of devices: Magnetic gear differentials for vehicle drivetrains. IEEE Trans. Transp. Electrif. 2022. [Google Scholar] [CrossRef]
- Berriri, M.; Chevrel, P.; Lefebvre, D. Active damping of automotive powertrain oscillations by a partial torque compensator. Control Eng. Pract. 2008, 16, 874–883. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Control: Linear Quadratic Methods, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Ostertag, E. Mono- and Multivariable Control and Estimation: Linear, Quadratic and LMI Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Venturini, S.; Bonisoli, E. Design of a spherical pendulum didactic test rig. Int. J. Mech. Control 2018, 19, 69–76. [Google Scholar]
- Walters, J.E.; Krefta, R.J.; Gallegos-Lopes, G.; Fattic, G.T. Technology considerations for belt alternator starter systems. SAE Tech. Pap. 2004, 2004-01-0566. [Google Scholar] [CrossRef]
- Morra, E.; Spessa, E.; Ciaravino, C.; Vassallo, A. Analysis of various operating strategies for a parallel-hybrid diesel powertrain with a belt alternator starter. SAE Int. J. Altern. Powertrains 2012, 1, 231–239. [Google Scholar] [CrossRef]
- Auerbach, M.; Ruf, M.; Bargende, M.; Reuss, H.-C.; Van Doorn, R.; Wilhelm, F.; Kutschera, I. Potentials of phlegmatization in diesel hybrid electric vehicles. SAE Tech. Pap. 2011, 2011-37-0018. [Google Scholar] [CrossRef]
- Velardocchia, M.; D’Alfio, N.; Bonisoli, E.; Galvagno, E.; Amisano, F.; Sorniotti, A. Block-oriented models of torque gap filler devices for AMT transmissions. SAE Tech. Pap. 2008, 2008-01-0631. [Google Scholar] [CrossRef]
- Dimauro, L.; Bonisoli, E.; Repetto, M. Dynamic behaviour and magneto-mechanical efficiency of a contactless magnetic transmission. In Rotating Machinery, Optical Methods & Scanning LDV Methods, Proceedings of the 40th IMAC, Orlando, FL, USA, 7–10 February 2022; Di Maio, D., Baqersad, J., Eds.; Springer: Cham, Switzerland, 2023; Volume 6, pp. 129–138. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tyre and Vehicle Dynamics, 2nd ed.; Butterworth: Oxford, UK, 2005; pp. 1–621. [Google Scholar]
- Sorniotti, A.; Sampò, E.; Velardocchia, M.; Bonisoli, E.; Galvagno, E. Friction inside wheel hub bearings: Evaluation through analytical models and experimental methodologies. SAE 2007 Trans. J. Engines 2007, 116, 1665–1676. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimauro, L.; Tota, A.; Galvagno, E.; Velardocchia, M. Torque Allocation of Hybrid Electric Trucks for Drivability and Transient Emissions Reduction. Appl. Sci. 2023, 13, 3704. https://doi.org/10.3390/app13063704
Dimauro L, Tota A, Galvagno E, Velardocchia M. Torque Allocation of Hybrid Electric Trucks for Drivability and Transient Emissions Reduction. Applied Sciences. 2023; 13(6):3704. https://doi.org/10.3390/app13063704
Chicago/Turabian StyleDimauro, Luca, Antonio Tota, Enrico Galvagno, and Mauro Velardocchia. 2023. "Torque Allocation of Hybrid Electric Trucks for Drivability and Transient Emissions Reduction" Applied Sciences 13, no. 6: 3704. https://doi.org/10.3390/app13063704
APA StyleDimauro, L., Tota, A., Galvagno, E., & Velardocchia, M. (2023). Torque Allocation of Hybrid Electric Trucks for Drivability and Transient Emissions Reduction. Applied Sciences, 13(6), 3704. https://doi.org/10.3390/app13063704









