Featured Application
Method introduced in this article may be used for comparing musical pieces (both different arrangements of some piece and entirely different tracks as well). In particular, it may be used for automated plagiarism control and evaluation of arrangements created upon a certain original track.
Abstract
This paper describes methods and techniques of measuring similarity of musical pieces. This topic is crucial in plagiarism control and arrangement evaluation as these processes depend in particular on a previous experience and subjective aesthetical feelings of a researcher. Although there are some common frameworks for comparing musical pieces (i.e., some characteristics of compared pieces and details to consider), having a set of comprehensive metrics would allow to make such comparisons more unbiased. We show that such a comparison can be made using a network representation of a track. Tracks are compared using a structural and quantitative similarity between matrices corresponding to these musical pieces. In this article, we describe network representations of music. We introduce a set of specific methods of calculating this similarity and study their characteristics. We also evaluate them on the set of test pieces and provide results. We show that this method can be especially used for detecting instances of plagiarism between pieces and evaluating similarity of created arrangements, thus measuring their “innovativeness”.
1. Introduction
The last few years have witnessed a considerable increase in interest in computer-generated music and automatic analysis of music pieces. The development of information technology renders it possible to increase the computational capabilities of the devices used, and thus to boost the aesthetic values of the composed pieces. The development of digital models of soundtracks additionally allows for automated analyzing of pieces, in particular extracting their features, discovering dependencies, and comparing tracks with each other.
Nevertheless, methods of automatic music generation have existed for hundreds of years and predate computer science. The first compositions enabling the semi-automatic generation of pieces based on pre-composed samples date back to the second half of the 18th century. The most renowned piece representing this style in music is the composition attributed to Wolfgang Amadeus Mozart “Musikalisches Würfelspiel” (“Musical Dice Game”), which allows the creation of almost 800 trillion sixteen-bar pieces, which was analyzed in [1]. As the authors of these pieces themselves note (C. P. E. Bach—a piece entitled “Einfall, einen doppelten Contrapunct in der Octave von sechs Tacten zu machen, ohne die Regeln davon zu wissen”—”A Method of Creating Six-Bar Pieces with Double Counterpoint in an Octave, Requiring no Knowledge of the Rules”), music systems constructed in this way do not require knowledge of music theory, and this allows automated devices to compose pieces.
Nowadays, there are other, much more complex methods of automatically generating music in use, employing advanced mathematical models and IT tools. One can mention methods utilizing neural networks: especially generative adversarial networks [2,3], convolutional neural networks [4,5], recurrent neural networks [6] and others (many of the remaining neural networks-based methods are described in [7]). These methods perform especially well when creating new arrangements or orchestrating existing soundtracks—it is worthwhile to note that the generated pieces are usually characterized by a good listenability. Other approaches include models based on genetic algorithms [8], score reduction [9], Bayesian networks (e.g., [10]), statistics (as proposed in [11]) and non-musical inspiration sources [12]. These models are specialized to serve other purposes such as chord prediction for a monophonic track, rhythm generation or harmonization of the musical piece.
Most of the abovementioned methods use a given corpus of original pieces and create their arrangements (namely generate completely new soundtracks based on them) or harmonize a given soundtrack (namely create tracks of other instruments/voices “matching” the theme introduced by the user) while maintaining a style similar to their prototypes. What is worthwhile to note is the fact that some of these methods make it possible to generate polyphonic tracks characterized by high aesthetic values. On the other hand, all of these methods are generally focused on some aspects of automated music composition and therefore it is not possible to easily reuse them for other purposes such as comparing different musical tracks.
One of such concepts that enables the creation of compositions based on original song tracks is the use of graph and network theory to represent the relationship between the notes used in the track. Analyzing the coexistence of notes and their cardinality helps draw conclusions about the original piece as well as generate arrangements containing similar musical themes (this procedure is thoroughly described in [13]). Contrary to the methods described above, the graph-based representation of music allows both to create new arrangements (i.e., a soundtrack similar to the piece represented by the graph) and to calculate the similarity of different pieces by comparing graph structures corresponding to them (and not by comparing the musical content itself).
At the same time, the issue of comparing pieces on the basis of their graph representation has not been widely discussed so far. Unfortunately, none of the previously existing publications described calculating the similarity of the pieces, thus making it impossible to decide whether the considered music (e.g., generated arrangement) is innovative enough to be considered a separate piece, distinguishable from the original. In particular, no metrics have been defined to measure the distance of musical pieces based on their graph and network representation. Notwithstanding generating musical arrangements and attempts to compare them with the original pieces on the basis of their graph representation (e.g., [13,14,15]), no studies have been conducted dealing with this subject systematically. Using a critical analysis method, we point out why the current approach is insufficient. Therefore, we propose a new method of comparing musical pieces and analyze it quantitatively: by providing a series of experiments in order to verify its effectiveness.
The aim of the article is to introduce a formal description and to study the operation of a new method for comparing musical pieces on the basis of their graph and network representation. The authors examine the results obtained for various scenarios of using the described method—it can be used to compare different musical pieces, classify them to a potential genre, compare different musical arrangements, and detect plagiarism. In particular, in the case of the latter two applications, the method achieves very good results, and this implies that it can be successfully used in the work of arrangers and anti-plagiarism control systems.
The article introduces a novel and comprehensive method of checking if the compared pieces are similar to each other and to what extent they share the structure of connections between notes. In addition, by providing a single, numeric value of this similarity, this method remains untainted by the previous experience and “musical proficiency” of the human operator. Therefore, it may be used in a variety of applications: from purely musical (checking if the arrangement being created is still similar to the original piece) to legal (validating if the plagiarism was committed).
The article comprises six sections. Section 1 is this introduction. In Section 2, the authors outline the background of the studies—they describe the field and the hitherto known approaches to solving the described issues. Section 3 contains a description of the authors’ method of comparing graphs and networks and adapting it to the examined application. In Section 4, the authors describe the results obtained in a series of experiments. Section 5 summarizes the results obtained with the described method in the context of previous studies and potential applications. Section 6 sets out the final conclusions from the studies carried out.
2. Background
2.1. Prerequisites
The examined musical pieces involve monophonic tracks recorded on the score or in MIDI format. Most of the graph methods of song representation existing today operate on monophonic soundtracks. Accordingly, the graph represents, for example, the theme of the piece or the part of the leading (solo) instrument or voice. Although there are graph methods rendering it feasible to generate polyphonic arrangements (e.g., [16]), the method of notation used in them, in turn, rules out the possibility of extracting the theme, which is the most important part of the piece in regard to the value of the musical work and its recognizability.
The terms and definitions introduced in this subsection will be used further in this article. Let us examine a piece of music as the following set defined in [17]:
where a single note of the piece is defined as follows (as in [17]):
where
- —the frequency of the i-th note (, where −1 is used as a rest representation),
- —the duration of the i-th note (e.g., in seconds or the length of a note: whole note, half note, quarter note, etc.),
- —the point in the piece where the i-th note starts (number of seconds since the piece started or a measure number).
We shall additionally assume the following definition of a graph according to [18]:
where —set of vertices, —set of edges.
We shall also assume the following definition of a network (a.k.a. a weighted graph) according to [19]:
where G—directed graph defined as in (3) and (where —number of vertex functions) and (where —number of edge functions).
In the further part of the paper, the terms “network” and “weighted graph” are used interchangeably in a description of the graph structure along with “labels” of vertices and edges.
The above definitions are used in the further part of the paper to formally describe the method of comparing musical works.
2.2. Graph and Network Representation of Music
There are several ways to map a piece to its graph representation. The individual issues that should be considered and the available possibilities of the graph and network representation of notes have been described in more detail in [17], hence only those aspects that are used for the purpose of graph similarity study are mentioned below.
The first aspect of the graph representation of a piece is the way in which the notes are mapped to the vertices of the graph. Formally speaking, the issue concerns defining the function:
The following function is adopted in this paper (similar to that proposed in [20] but limited to keys from a piano keyboard and distinguishing only note names instead of names with octaves):
Such a definition means that all notes are transformed to vertices corresponding to their names (e.g., 0—note C, 1—note C#, 2—note D, etc.), while all rests are represented by a separate vertex of the graph. There are 12 semitones in a single octave, hence the resulting graph has a maximum of 13 vertices. Information about the octave number comprising the note in the piece is not stored—when notes have the same name but originate from different octaves (namely the frequency of one of them is 2i times the frequency of the other), they are represented by the same vertex. In the described method, the graph always contains all possible vertices (even when some of them are not present in the piece), and this is due to the need to generate an adjacency matrix with a size of 13 × 13 vertices. Vertices representing notes that are not present in the piece are called isolated vertices—their addition is a technical operation and is responsible for the “standardization” of the resulting matrix (whereas the algorithms for generating the arrangement take into account only vertices with a positive degree).
The next aspect of note representation consists in the mapping of the relationship between notes in the form of directed or undirected edges. For this purpose, the so-called note precedence relationship has been defined. This relationship takes the following form as described in [17]:
The relationship defined in this way is a relationship that introduces a linear order on the set of notes of a musical piece, and this was described in more detail in [17]. Particularly important are pairs of notes that occur immediately after each other, namely those constituting pairs of an immediate precedence relationship:
Pairs of this relationship are used to build the graph of a piece of music. In the method described in this article, directed edges (directing from the predecessor to the successor of the ordered pair) are added between all pairs of notes belonging to this relationship. This renders it possible to model the relationship between the notes in the piece, “flow” and “movement” between them.
The third aspect of note representation characteristic for the network is the weights (labels) of vertices and edges. Therefore, we may define the following vertex weight function reflecting the cardinality of occurrence of the corresponding note in the piece:
In other words, if note C occurred five times in the original piece (regardless of the octave and the length of the notes in each of its occurrences), then the vertex with index 0 corresponding to this note shall have a label equal to 5.
The weights on the edges are determined in a similar way—we may define them as the cardinality of the connection between the notes represented by vertices incident with this edge; this may be formally expressed as
taking into account all three aspects of mapping a piece to a graph/network results in a structure similar to the one presented in Figure 1 below. It has evident vertices representing the individual notes of the piece and the edges between them. The weights on the vertices describe the multiplicity of the note’s occurrence in the piece, hence the weight of the vertex representing note C is 3 (because note C occurs three times in the piece, in two different octaves). The weights on the edges, on the other hand, describe the multiplicity of the sequence between the notes, hence the directed edge from vertex D to vertex C has a weight of 2 (because such a sequence occurs twice: once between notes D and C and once between notes D and C1). Differences in note metric values are ignored in this representation.

Figure 1.
Sample piece and its representation. A simplified representation of notes (hence the difference in octaves and note lengths does not affect the number of vertices) and a directed network (arrows determine the direction of note precedence relationships; there are weights on vertices and directed edges) were used.
Such a method of representation, apart from the simplest cases, rules out the reconstruction of the original piece on the basis of its graphic representation. Nevertheless, this is not the purpose of such a conversion of the piece. Leaving aside the details (irrelevant from the point of view of examining the similarity of songs), we are able to more easily detect the relationships between individual notes of the compared pieces, and thus between the entire pieces. Further, the fact of using small graphs exerts a positive impact on the execution time of the algorithms used. With a problem defined this way (maximum 13 vertices in the graph), it would even be possible to use algorithms with exponential complexity as well as brute-force algorithms.
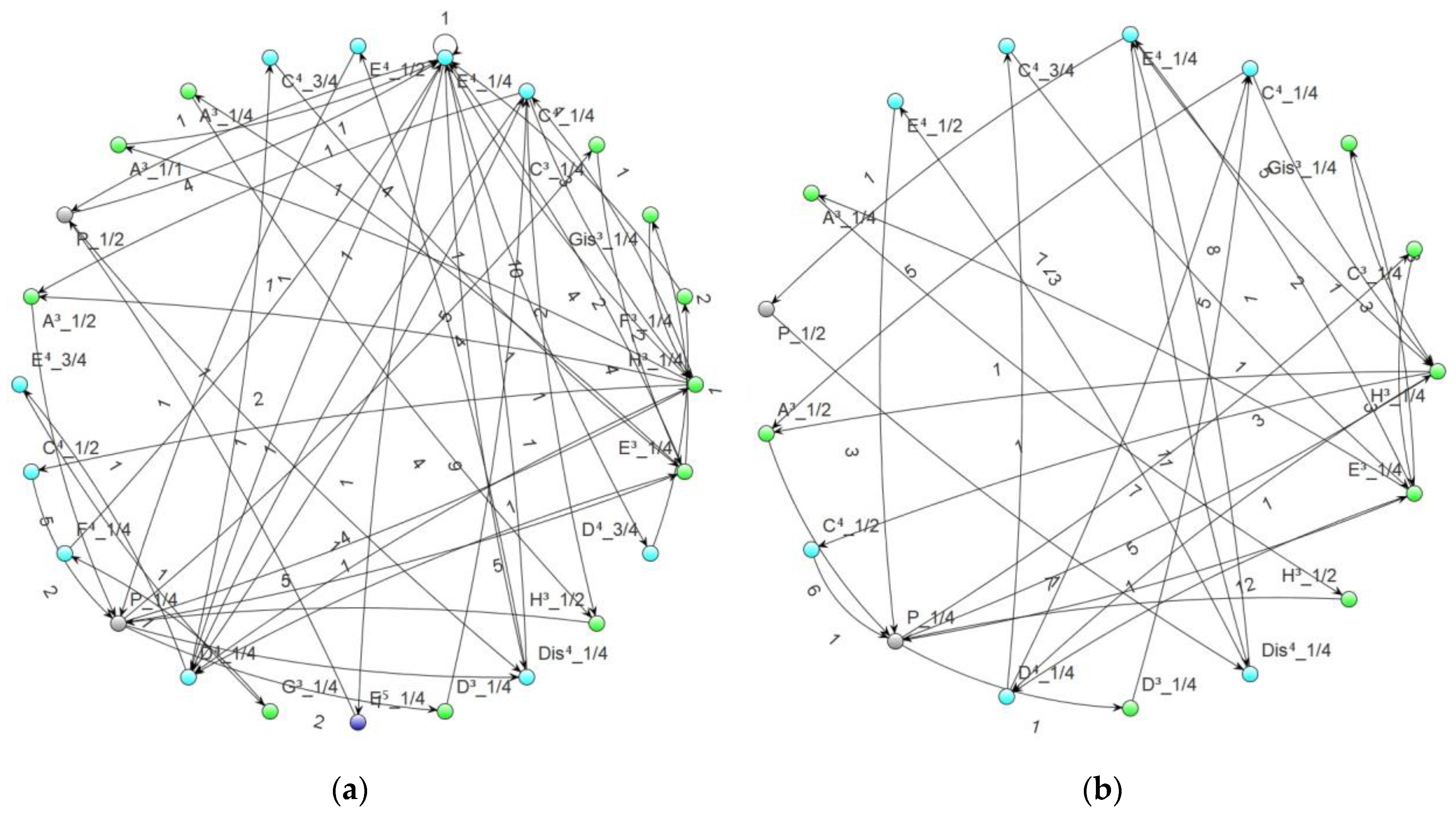
It is also worthwhile to mention that other, more elaborate methods work better in the task that involves generating musical arrangements. The pieces are generated on the basis of the so-called controlled random walk on the graph/network. If this is the case, it would be good, for a change, to reflect the original piece as accurately as possible, in the form of a network representation (singling out notes from different octaves and having different metrical values)—more extensively elaborated graphs make it feasible to generate arrangements that better imitate the sound of the original piece. An example of such a pair of pieces is shown in Figure 2 below. Their intuitively comprehended similarity is evident, both in terms of visual (similar number of vertices and the “distribution” of edges) and quantitative features (vertex degrees or edge labels are usually similar for corresponding vertices in both graphs). The use of a simplified way of representing notes would make the random walk less inspired by the original piece, and this, accordingly, would result in lower stylistic fidelity of the arrangement.
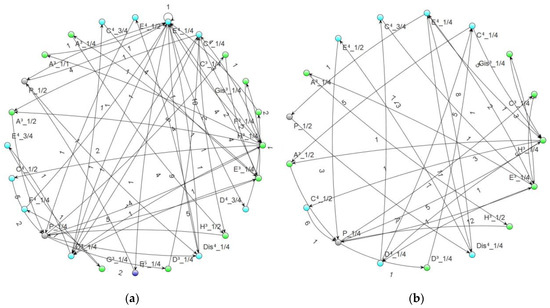
Figure 2.
Representation of (a) the opening measures of Für Elise and (b) the arrangement based on it. The structure of both networks is similar; however, not all notes of the original piece were used in the arrangement (e.g., the quarter note E5 visualized in dark blue at the bottom of the graph representing the original piece is not present in the arrangement).
The results of this part of the work were published in [17]. This part of the studies, however, emphasizes the quantitative analysis of the pieces in terms of examining their similarity, and not the fidelity of representation and the ability to generate aesthetically sounding arrangements.
2.3. Musical Piece Network Representation Similarity—Current State-of-the-Art
The hitherto literature has not widely discussed the issue of comparing pieces using their graph and network representation. Although there are studies in which musical tracks were compared with each other (this applies both to the comparison of completely different pieces and the original pieces and generated arrangements), the methods of comparison proposed in them are neither precise nor unambiguous.
In particular, in [20], the comparison of pieces is based on graph/network characteristic vectors representing these musical tracks. This allows for a basic comparison of these structures; however, the individual values of the examined vectors are compared one by one. No metric has been introduced to determine the distance between pieces expressed as a single numerical value.
Similarly, in [21], the author analyzes a few selected pieces relying upon the theory of complex networks. She carries out extensive studies on polyphonic pieces, inter alia, through the prism of the characteristics of the graphs that represent them. These studies are a testimony to certain properties of networks representing pieces belonging to classical music (including but not limited to the scale-free property); however, the subject matter of the study in this paper does not involve comparing pieces with each other.
Nor does [15] introduce a single measure of the distance between the pieces. Individual characteristics of the examined graphs are used to compare solos from selected pieces. They also form the grounds for general reflections on various musical styles (blues solos are usually characterized by a high clustering coefficient and a small average distance between vertices, rock solos—just the opposite, while “melodious” solos usually are of a much simpler structure). However, this paper compares also the pieces through the prism of individual characteristics; nonetheless, a single, scalar method of measuring the distance between the pieces has not been proposed.
Similarly, none of the methods described in papers [2,3,4,5,6,7,8,9,10,11,12] allow to calculate the similarity of musical pieces. They all are designed to harmonize the existing soundtracks or create new ones, but without any possibility to validate whether the outcomes are novel and innovative or highly influenced by some previous works.
3. Materials and Methods
3.1. Metrics for Calculating Music Similarity
In previous studies, the authors of this paper proposed a number of measures that can be used to determine the distance between pieces. In particular, one can quote [17], which describes the note equivalents of “text” measures—Hamming and Levenshtein. The metrics originally used to compare text patterns have been adapted to the musical domain, so as to determine the distance between the compared pieces.
The Hamming note measure allows for counting the number of positions that differ between two pieces with the same number of notes. For two pieces (marked as a and b), it is determined as
where square brackets mark the Iverson bracket. Accordingly, the metric determines the number of changes that have to be introduced to one piece in order to obtain the second of the pieces subjected to comparison. A significant constraint of this method rests with the requirement that the compared pieces must be equinumerous. In practice, this means that only simple samples of musical material, with no more than a few bars, can be compared in this way—not entire pieces.
A similar way of comparing works, yet free of this constraint, is the Levenshtein distance. In addition to the note-editing operation, it also introduces note deletion and note addition operations. The value of the distance between two pieces a and b is calculated recursively by the following formula:
Such a definition of the metric renders it possible to compare entire pieces of music, regardless of their length. The calculated distance value describes the number of operations of all types (adding, deleting, note editing) that must be performed to transform one piece into another.
The above measures based on text metrics are characterized by the simplicity of the idea and relatively quick execution time. The algorithm calculating the value of the Hamming distance is characterized by a linear computational complexity in relation to the length of the pieces. In turn, the calculation of the Levenshtein distance for pieces a, b requires performing operations; however, there are optimizations of this algorithm ([22,23]) that require performing operations and , respectively (where —the distance between the compared strings).
The downside of the methods described above is their relative ease of “deceiving” them when used for anti-plagiarism control. Introducing minor changes to the piece in terms of sonority, namely changes in key and/or changes in the length of notes, result in a failure to detect plagiarism. Examples of such pieces are described in [17]. Although a procedure to improve the operation of these algorithms so that plagiarism is correctly detected has been described, the postulated additional steps make these methods complicated and worsen their computational complexity. An additional problem may rest with the fact that the metrics defined in this way are not normalized. This hinders their usage, namely the interpretation of whether the calculated value is “high”, i.e., whether the pieces differ significantly from each other. In turn, normalization causes the calculated value ceases to be a metric (because the triangle inequality property is not satisfied).
Another method proposed in [19] is the structural and quantitative method of network comparison. Its fundamental assumptions, properties, and adaptation to the musical domain are described in the following subsections of this article.
3.2. Structural and Quantitative Metric of Network Similarity
A method differing from those described in the previous section involves measuring the similarity of pieces by examining the features of the adjacency matrix and the values of vertex and edge labels in a network representing a musical track. This way of calculating the distance between pieces accounts for both the structure (namely the graph of connections between the notes used in the piece) and the quantitative characteristics of the said connections (multiplicities: the occurrence of individual sounds and sequences between notes in the piece).
The proposed method is an iterative method and extends the concept originally described in [24]. The idea is based on the observation asserting that two graph vertices are as similar to each other as their “neighbors” are. Thus, by iterating over all graph vertices, one can determine the similarity of entire structures. The method described in [19] introduces the measurement of three types of similarity between graphs: structural similarity (calculated as described in [24]), quantitative similarity of vertices, and quantitative similarity of edges.
The structural similarity of graphs and characterized by transition matrices marked A and B, respectively, is calculated according to the following method. In the first place, the following matrix sequence should be calculated iteratively:
where matrix (matrix with all elements having the value 1), —transposition of matrix , —Euclidean norm of matrix (, where —number of columns of the matrix, i.e., number of vertices of the graph , —number of rows of the matrix, i.e., the number of vertices of the graph).
The matrix element describes the similarity between the i-th vertex of the graph and the j-th vertex of the graph . The higher the value, the greater the similarity between these vertices. On this basis, we can calculate the structural similarity matrix of the form:
With this matrix, the problem of the optimal assignment of vertices from one matrix to another matrix can be defined to maximize the similarity of both structures. The optimal assignment problem can therefore be defined as follows:
with the following constraints:
The aforementioned assignment problem can be solved by any algorithm (e.g., Hungarian algorithm allowing to solve the problem in polynomial time). The value of calculated in this way is a structural similarity of the graphs and .
The quantitative similarity of vertices of graphs is calculated on the basis of vertex functions (and thus weight values of individual vertices). In the first place, the matrix vector should be calculated:
where a single matrix describes the similarity of the vertices of both graphs from the perspective of the vertex function with index k defined on both graphs. The values are calculated as follows:
and describe the similarity (“distance”) of single compared vertices from the perspective of the vertex function ,. A norm with parameter p may be used as a norm in this formula:
where , describe the r-th component of the vector—functions ,, respectively. Subsequently, for each function ,, matrices of normalized values should be determined: , where . Doing so makes the values in the matrix satisfy the property . Having applied this procedure, it is feasible to calculate the value of the quantitative similarity of the vertices of both graphs, namely for the i-th vertex in the graph and the j-th vertex in the graph, using the following formula:
The value of can be calculated on the basis of the above matrix—the vertex quantitative similarity of both graphs. The optimization problem is the same as in the process of calculating structural similarity—with two changes: the values should be changed to values (hence values lower in terms of modulus mean greater similarity) and the value into .
A similar method is used to calculate the value of the quantitative similarity of graphs from the perspective of the functions defined on the edges. A matrix vector is built in the first place (where and ,—the number of edges in graphs and , respectively). The values of this matrix are calculated for individual functions defined on the edges: . Then, the whole process is normalized: , and the similarity for individual edges of both graphs can be calculated as follows:
The last step involves solving the assignment problem defined as before with the following changes: the value should be substituted with and the value should be replaced with . Doing so allows for calculating the value of the edge quantitative similarity of the graphs.
It is also worth mentioning that it is possible to calculate a single value of quantitative similarity of both graphs. To that end, one may use the method of transforming a weighted graph (with weights on vertices and edges) into a substitute graph with functions defined only on vertices. This method has been described in [19].
Since the result of the method described above is three criteria values ( value describing structural similarity, describing vertex quantitative similarity, describing edge quantitative similarity), in the problem to be solved, it is crucial to propose a way to select the graph representing the musical arrangement most similar to the given pattern. This is equivalent to the issue of solving the MWGSP multi-objective problem defined as follows:
where
Indeed, the simplest option would be to choose a Pareto-dominant solution. However, such a solution in actual examples will be relatively rare. Accordingly, a different method of solving this problem in the general case should be proposed.
3.3. Methods of Comparison by Solving a Multi-Objective Optimization Problem
The problem formulated in the previous subsection should be solved using the methods of solving multi-objective optimization problems.
The simplest method to reduce a multi-criteria problem to a single-criteria problem involves scalarization of the criteria by using a weighted average. In this way, instead of several original criteria, a single maximized substitute criterion is formulated:
where —normalized i-th criterion function and, additionally, the weights meet the following conditions:
and the problem can be solved using methods of classical single-criterion optimization (with minimization of the meta-criterion formulated in this way). In particular, providing equal weights for all criteria makes each of them equally important in regard to the impact on the value of the objective function.
Another way to solve the problem is goal programming. This approach does not involve calculating the extreme value (minimum/maximum of the objective function on the set of admissible solutions) but instead finding a solution that minimizes the distance of the function from the given vector of values constituting the objectives for individual criteria or the given value of the meta-criterion calculated as in (24). This problem is therefore designed to seek the assignment of the vertices of one graph to another, so that the similarity between them is as close as possible to this set of “reference” values or to the given value of the meta-criterion, respectively. Formally speaking, the problem in the first variant (minimization of deviations from —the vector of the given values) can be described as follows:
with constraints as before—i.e., — normalized i-th criterion function; —vector of goals set by the decision-maker; and with the following constraints:
or, alternatively, in the second variant (minimizing the deviation from —given single meta-criterion value),
with constraints
If vector values are selected appropriately, this can be used to select an assignment that results in a relatively high similarity between the graphs, but at the same time renders it impossible to detect “plagiarism” in the musical arrangement built on the basis of the graph representation of the piece.
The third method of reducing the problem to a single-criterion problem involves the use of threshold criteria. In this approach, we choose one leading criterion (and single-criteria optimization will be performed against it), whereas for the remaining criteria, we define the so-called satisfaction thresholds (namely, we add constraints). Doing so narrows the space of solutions and makes the problem solved by single-criterion methods. At the same time, the solution selected in this way is acceptable to the decision-maker because exceeding the threshold values of all other criteria means that the selected solution can be considered “good enough” in relation to them.
One should note, however, that the above methods are not an exhaustive list. In some applications, other methods of solving a such problem may also prove effective, e.g., lexicographic (hierarchical) optimization or the ideal point method.
3.4. Application of the Structural and Quantitative Metric of Network Similarity to Music Comparison
The method described in the above subsection can be used to measure the similarity of graphs representing musical pieces. Nevertheless, given the specificity of this field, it should be additionally noted that:
- The analyzed graphs always have 13 vertices. In European classical musical harmony, an octave is built of 12 semitones + there is a separate vertex for rests in the graph. Vertices representing notes that are not present in the piece are isolated vertices (i.e., they are not interlinked to other vertices—they have degree 0). As far as graph visualization and arrangement generation are concerned, they could be removed from the structure; however, in the problem of examining similarity, their presence is dictated by the desire to ensure the stability of the graph mapping into the adjacency matrix. This makes the matrix have a constant size of 13 × 13, and using Formula (6), one can always specify that the first row is for note C, the tenth for note A, and the thirteenth for the rest.
- In the problem under examination, only one vertex function (describing the frequency of the note represented by this vertex occurring in the piece) and exactly one edge function is used (describing the frequency of the sequence of the note represented by the directed edge’s antecedent occurring in the piece before the note represented by the consequent). This slightly simplifies the method, because the matrix vectors are always single-element.
- The vertex and edge functions described in the graph representation of a piece of music are logically interlinked. They both describe the multiplicity of selected “phenomena in the piece” (respectively, the occurrence of a specific note, the occurrence of a specific sequence of notes). Specifically, the value of the vertex label is equal to the sum of the weights of the labels entering it, i.e., (where —the set of directed edges entering vertex v or undirected edges incident with vertex v). It can therefore be assumed that their values are intercorrelated, and, consequently, the calculated similarity is similar for both measures of quantitative similarity. The only difference may occur in the vertex corresponding to the first note of the piece (the value of the vertex label will be 1 point greater than the sum of the label values of the directed edges entering that vertex). In regard to the large pieces of music analyzed in this article, this is a negligible difference, as shown in Section 4.
It is worthwhile to note that depending on the parameters assumed, the method will reach values in the range of . For the parameters corresponding to the structural analysis of the graph, the set of achieved values is , where 1 stands for pieces identical in terms of the structure and 0 denotes pieces dissimilar to each other. On the other hand, the construction of the objective function causes achieving negative values (range ) for the assumed parameters or , where −1—pieces divergent in the quantitative sense, 0—pieces identical in terms of quantity.
When using the meta-criterion in the form of a weighted sum for any parameter values, the objective function is a linear combination of the values of individual partial criteria and the weights assigned to them. Thus, for example, for parameters , the achieved function values originate from the range , where —pieces that are, to the maximum extent, similar to each other in terms of structure and quantity, —pieces that are completely dissimilar to each other. In this case, the objective function values can be regarded as an answer to the question of whether the structural similarity of the examined networks is greater than their “divergence” (“dissimilarity”) in terms of quantity. By calculating this value, we may easily verify whether the compared pieces are similar to one another. On the contrary, previous research either did not involve comparison of the generated pieces at all or required comparing subsequent vector’s coordinates on a one-by-one basis, thus reducing the precision of such a comparison.
4. Results
4.1. Dataset
A corpus consisting of 21 pieces representing various musical styles and from various eras was prepared for the study. The pieces have been broken down into the music genre they represent.
Classical music:
- J. S. Bach—Toccata and Fugue in D Minor (BWV 565);
- J. Pachelbel—Canon in D;
- M. Leontovych—Shchedryk (a.k.a. P. Wilhousky—Carol of the Bells);
- F. Chopin—Nocturne Op. 9 No. 2;
- L. van Beethoven—Für Elise (WoO 59);
- L. van Beethoven—4-th movement of IX Symphony Op. 125 (Ode to Joy).
Movie music:
- N. Rota—The Godfather;
- J. Williams—Harry Potter (Hedwig’s Theme);
- C. Mansell—Requiem for a Dream (Lux Aeterna);
- H. Shore—The Hobbit (Far over the Misty Mountains Cold).
Popular music:
- F. Sinatra—My Way;
- Adele—Rolling in the Deep;
- E. Sheeran—Thinking out Loud;
- T. Britten—UEFA Champions League theme (violin part);
- T. Britten—UEFA Champions League theme (vocal part);
- The Beatles—Yellow Submarine;
- The Beatles—Yesterday.
Rock music:
- Europe—The Final Countdown;
- Metallica—Nothing Else Matters;
- Linkin Park—Numb;
- Queen—We Will Rock You.
Moreover, in order to increase the data set, musical arrangements were generated on the basis of most of the abovementioned pieces. The method of generating arrangements based on original pieces has been described in [17]. To generate the arrangement, the full representation of the notes, as well as the so-called controlled random walk on the directed network described in the article above, have been used. The graph network characteristics of the compared music pieces are described in Table 1.

Table 1.
Graph characteristics of the compared pieces.
All the abovementioned musical pieces (sheet music and MIDI files) used in the experiments, along with the source codes and spreadsheets with calculated distance values are provided in Supplementary Materials.
4.2. Obtained Results—General Comparison of Tracks and Genres
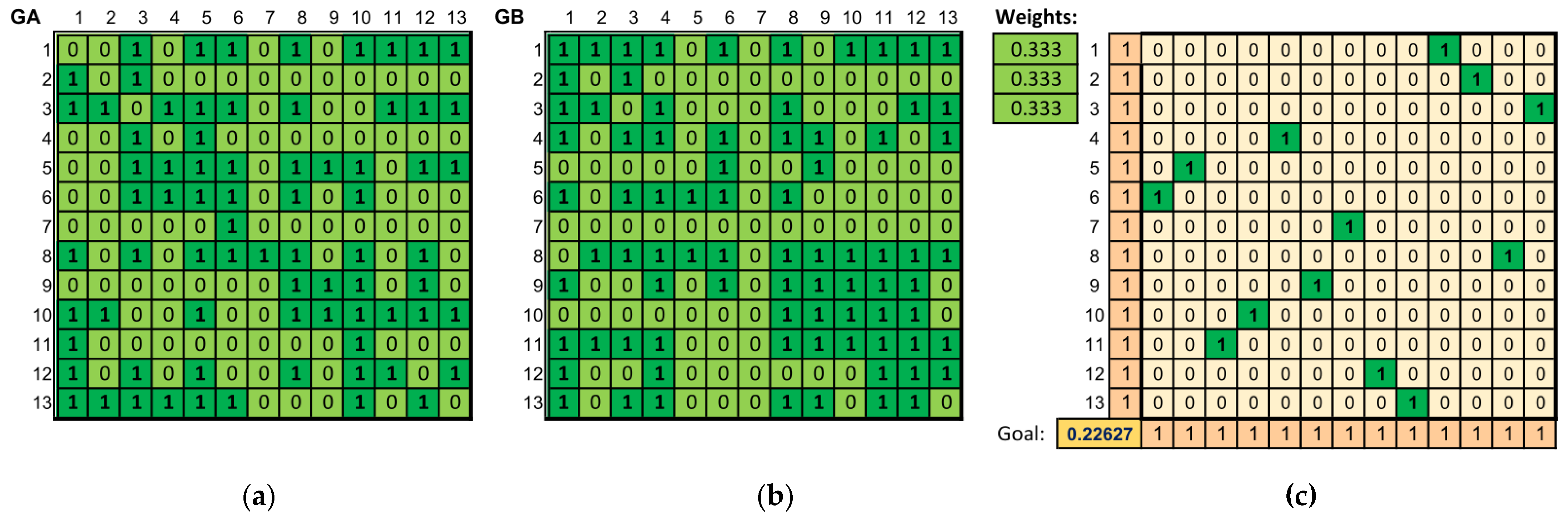
Network representations were calculated for each compared pair of pieces. Then, in each case, a vertex adjacency matrix, a matrix describing the weights on the edges existing between individual vertices, as well as the vertex weight vectors of both networks were calculated. For structures compared in this way, the values described in Section 3.2 were calculated, and subsequently the matrix of the optimal assignment of vertices from one structure to another was calculated using the meta-criterion. For the assignment calculated in this way, the value of the objective function is also calculated—a measure of the similarity of pieces. An example result is presented in Figure 3.
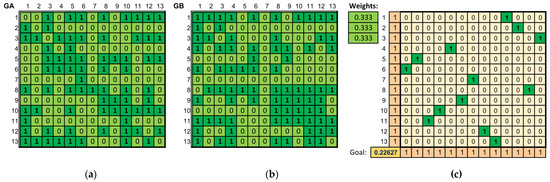
Figure 3.
Comparison of L. van Beethoven’s Für Elise and Nocturne Op. 9 by F. Chopin. (a) The adjacency matrix of the graph representing the first piece. (b) The adjacency matrix of the graph representing the second piece. (c) The optimal assignment matrix of vertices from one graph to another (maximizing graph similarity) together with the value of the objective function.
The obtained results were sorted by the genres of the pieces. The original pieces and their arrangements were also compared separately. In Table 2, Table 3, Table 4, Table 5 and Table 6, four comparison values are presented in each of the cells, respectively:
- the value obtained using the arithmetic mean of the criteria (scalarization using the meta-criterion in the form of a weighted average of criteria with equal weights of 0.333),
- structural similarity value,
- vertex quantitative similarity value,
- edge similarity value.
To increase the readability, Table 2, Table 3, Table 4, Table 5 and Table 6 ignore the comparison of the piece with itself (each piece is, by definition, maximally similar to itself), and only the lower triangular matrix is supplemented (distances meet the relation , hence every matrix is symmetric). The adopted domain and the interpretation of the values of individual criteria are described in Section 3.4.

Table 2.
Comparison of pieces from the classical music genre.
Table 2.
Comparison of pieces from the classical music genre.
| Compared Piece Similarity | Toccata and Fugue | Canon in D | Shchedryk | Nocturne op. 9 | Für Elise | Ode to Joy |
|---|---|---|---|---|---|---|
| Toccata and Fugue | ||||||
| Canon in D | 0.01 | |||||
| 0.89 | ||||||
| −0.44 | ||||||
| −0.44 | ||||||
| Shchedryk | −0.01 | 0.24 | ||||
| 0.86 | 0.98 | |||||
| −0.46 | −0.13 | |||||
| −0.46 | −0.13 | |||||
| Nocturne op. 9 | −0.01 | 0.12 | 0.13 | |||
| 0.99 | 0.94 | 0.92 | ||||
| −0.52 | −0.29 | −0.26 | ||||
| −0.52 | −0.30 | −0.26 | ||||
| Für Elise | 0.02 | 0.18 | 0.20 | 0.22 | ||
| 0.99 | 0.96 | 0.93 | 1.00 | |||
| −0.47 | −0.19 | −0.16 | −0.16 | |||
| −0.47 | −0.19 | −0.16 | −0.16 | |||
| Ode to Joy | −0.17 | −0.07 | −0.02 | −0.13 | −0.11 | |
| 0.73 | 0.87 | 0.94 | 0.79 | 0.79 | ||
| −0.64 | −0.56 | −0.51 | −0.60 | −0.58 | ||
| −0.64 | −0.56 | −0.51 | −0.60 | −0.58 |
Meta-criteria statistics: 0.04 ± 0.13; median: 0.01.
Table 2 presents the results of measurements of the distance between pieces representing classical music. It is worthwhile to note that the piece Toccata and Fugue is characterized by very low similarity values in relation to all other pieces. This is due to its far more extended structure compared to other compositions. As shown in Table 1, this piece consists of almost 2000 notes, and this is 2–3 times longer than the others. Furthermore, this piece uses all the notes in the octave and almost all possible connections between them—the graph density is very high as for the graphs of musical pieces and amounts to 0.7. This means that the calculated values of similarity of this piece to the other are very low. Similarly, the piece Ode to Joy is much shorter than all the other pieces, and is characterized by an extremely simple structure, which also means that the measured similarity to the other pieces takes only negative values.
Shchedryk and Canon in D (the substitute criterion is 0.24), as well as Für Elise and Nocturne, Op. 9 (value 0.22), feature the highest similarity among the compared pieces. As far as both compared pairs are concerned, it can also be observed that solving the problem in relation to individual partial criteria also produces results close to optimum: 0.98 and 1, respectively, for the structural criterion (maximum value is 1) and −0.13 and −0.16 for both quantitative criteria (maximum value is 0). In particular, in the case of pieces by F. Chopin and L. van Beethoven, the high value of similarity may be due to the same musical style represented by both composers (romanticism). In the case of works by M. Leontovych and J. Pachelbel, the reason for the similarity may be seen in the similar structure of both pieces (both of them consist of approximately 650 notes and their graph representations have a similar number of edges and non-isolated vertices).
Further, it can be noticed that the values of both quantitative criteria for all pieces are either the same or differ only in the second decimal place. This is due to the fact indicated above in Section 3.4: the values of the function described on the vertices depend on the value of the function described on the undirected edges incident with this vertex or directed edges entering it. The only discrepancies between these functions may rest with the vertex representing the first note of the piece, and this results in a slight difference in the values of the solutions in the case of comparing Nocturne op. 9 and Canon in D.
The set of film music pieces described in Table 3 has a smaller dispersion of measures—it lacks such large similarity values as those present in the set of classical music (the greatest similarity is 0.15; for comparison, in classical pieces, it was 0.24) as well as relatively small values (the smallest is 0.01, while in classical pieces it is −0.17). The foregoing might be due to the fact that these pieces are movie soundtracks of various genres, but all of them were created over the last 50 years.

Table 3.
Comparison of pieces from the film music genre.
Table 3.
Comparison of pieces from the film music genre.
| Compared Piece Similarity | The Godfather | Harry Potter | Requiem for a Dream | The Hobbit |
|---|---|---|---|---|
| The Godfather | ||||
| Harry Potter | 0.01 | |||
| 0.99 | ||||
| −0.47 | ||||
| −0.47 | ||||
| Requiem for a Dream | 0.15 | 0.06 | ||
| 0.88 | 0.96 | |||
| −0.22 | −0.40 | |||
| −0.22 | −0.40 | |||
| The Hobbit | 0.09 | 0.08 | 0.11 | |
| 0.93 | 0.97 | 0.95 | ||
| −0.33 | −0.38 | −0.33 | ||
| −0.33 | −0.39 | −0.33 |
Meta-criteria statistics: 0.08 ± 0.04; median: 0.08.
At the same time, all the meta-criterion statistics under analysis imply that the studied film music pieces are, in general, more similar to each other than classical music pieces. This is evidenced by the higher mean value of the calculated meta-criterion, a smaller dispersion around this value, and a larger median. This might be due to the fact the analyzed set described in Table 3 lacks pieces that significantly differ from the others (as opposed to classical music and the pieces Toccata and Fugue and Ode to Joy).
The set of pop music pieces described in Table 4 features pieces with a fairly significant similarity value. In particular, the pair Yellow Submarine and Thinking out Loud (value 0.26) as well as Rolling in the Deep and Thinking out Loud (value 0.21) are highly similar. As in the case of pieces representing classical music, both pairs here are also additionally characterized by the values of the remaining similarity measures close to the maximum values. One may also notice that the pieces that differ most from each other are the UEFA Champions League theme and F. Sinatra’s My Way. Indeed, this is due to differences in musical style and the different “purpose” of both compositions.

Table 4.
Comparison of tracks from the popular music genre.
Table 4.
Comparison of tracks from the popular music genre.
| Compared Pieces Similarity | My Way | Rolling in the Deep | Thinking out Loud | UEFA CL (Vocal) | Yellow Submarine | Yesterday |
|---|---|---|---|---|---|---|
| My Way | ||||||
| Rolling in the Deep | 0.10 | |||||
| 0.96 | ||||||
| −0.34 | ||||||
| −0.34 | ||||||
| Thinking out Loud | 0.16 | 0.21 | ||||
| 0.96 | 0.99 | |||||
| −0.25 | −0.19 | |||||
| −0.25 | −0.19 | |||||
| UEFA Champions League theme (vocal) | −0.07 | 0.00 | −0.02 | |||
| 0.88 | 0.96 | 0.96 | ||||
| −0.56 | −0.50 | −0.52 | ||||
| −0.57 | −0.50 | −0.52 | ||||
| Yellow Submarine | 0.18 | 0.17 | 0.26 | 0.01 | ||
| 0.97 | 0.99 | 0.99 | 0.96 | |||
| −0.21 | −0.24 | −0.11 | −0.47 | |||
| −0.22 | −0.24 | −0.12 | −0.47 | |||
| Yesterday | 0.18 | 0.08 | 0.12 | −0.01 | 0.18 | |
| 0.96 | 0.99 | 0.99 | 0.96 | 0.99 | ||
| −0.17 | −0.38 | −0.32 | −0.51 | −0.24 | ||
| −0.17 | −0.38 | −0.32 | −0.51 | −0.24 |
Meta-criteria statistics: 0.10 ± 0.10; median: 0.12.
It is also worth noting that two songs by The Beatles, Yesterday and Yellow Submarine, are characterized by an above-average similarity value—this may imply that both songs are actually the result of the musical sensitivity of the same authors. Nevertheless, this value is quite far from the maximum; the reasons for this may rest in the fact that they represent two different musical styles (Yellow Submarine is modeled on shanties, and Yesterday is a melodic soft rock piece) or in the time distance between the creation of these two pieces (the musical workshop of the artists changed over 10 years).
Again, it can be noticed that while the values of structural similarity in most cases are close to the maximum value, the values of quantitative similarities significantly differ from the maximum values for these quantities. The analyzed pieces are, in general, more similar to each other in comparison to the two genres analyzed above (the meta-criterion has a mean value of 0.10 and the median is 0.12—more than in Table 2 and Table 3), but the dispersion of values is more than twice as large as in the case of film music.
The set of rock music pieces described in Table 5 features pieces with a noticeable degree of similarity value. In particular, the pair of pieces Nothing Else Matters and The Final Countdown, as well as the pair We Will Rock You and Numb, are very similar to each other (in both cases the similarity value is 0.22 and the partial measures are close to their maximum values).

Table 5.
Comparison of tracks from the rock music genre.
Table 5.
Comparison of tracks from the rock music genre.
| Compared Pieces Similarity | The Final Countdown | Nothing Else Matters | Numb | We Will Rock You |
|---|---|---|---|---|
| The Final Countdown | ||||
| Nothing Else Matters | 0.22 | |||
| 1.00 | ||||
| −0.16 | ||||
| −0.16 | ||||
| Numb | 0.17 | 0.17 | ||
| 1.00 | 1.00 | |||
| −0.25 | −0.26 | |||
| 0.25 | −0.26 | |||
| We Will Rock You | 0.07 | 0.09 | 0.22 | |
| 0.96 | 0.96 | 0.98 | ||
| −0.39 | −0.36 | −0.16 | ||
| −0.39 | −0.36 | −0.17 |
Meta-criteria statistics: 0.15 ± 0.06; median: 0.17.
All pairs under comparison have a positive similarity value—film music is one of the two musical genres featuring such a situation. Furthermore, it is worth noting that the piece Numb is above-average in similarity to all pieces in the genre—the similarity has values in the range of [0.17, 0.22]. Among the compared music genres, rock music is characterized by far the highest mean value and the median of the meta-criterion. This might be due to the fact that the pieces represent a fairly similar musical style and, additionally, the tested sound material is quite similar in terms of the number of notes and graph and network characteristics described in Table 1.
Again, it is evident that the measure of structural similarity is close to the maximum in all comparisons; the reoccurrence of this situation renders it possible to claim that the mere structural similarity proposed in [24] would not work in this domain. The structure of graph representations of musical pieces always happens to be quite similar, regardless of the actual similarity between the pieces themselves.
A separate type of experiment was the comparison of pieces from various musical genres. The results of this part of the experiment are described in Table 6. For this comparison, one representative from each of the compared genres, as well as both tracks of the UEFA Champions League theme, were selected.

Table 6.
Comparison of pieces between genres.
Table 6.
Comparison of pieces between genres.
| Compared Pieces Similarity | Für Elise | Harry Potter | Thinking Out Loud | UEFA CL (Violin) | UEFA CL (Vocal) | We Will Rock You |
|---|---|---|---|---|---|---|
| Für Elise | ||||||
| Harry Potter | −0.06 | |||||
| 0.94 | ||||||
| −0.58 | ||||||
| −0.58 | ||||||
| Thinking Out Loud | 0.18 | −0.01 | ||||
| 0.92 | 0.98 | |||||
| −0.20 | −0.51 | |||||
| −0.20 | −0.51 | |||||
| UEFA Champions League theme (violin) | 0.04 | 0.06 | −0.02 | |||
| 0.98 | 0.98 | 0.96 | ||||
| −0.44 | −0.41 | −0.52 | ||||
| −0.44 | −0.41 | −0.52 | ||||
| UEFA Champions League theme (vocal) | −0.11 | 0.18 | 0.12 | (covered in Section 4.4) | ||
| 0.85 | 0.98 | 0.95 | ||||
| −0.60 | −0.22 | −0.30 | ||||
| −0.60 | −0.23 | −0.30 | ||||
| We Will Rock You | 0.05 | 0.08 | 0.19 | 0.17 | 0.07 | |
| 0.89 | 0.97 | 0.98 | 0.93 | 0.97 | ||
| −0.38 | −0.37 | −0.22 | −0.22 | −0.40 | ||
| −0.38 | −0.38 | −0.22 | −0.22 | −0.40 |
Meta-criteria statistics: 0.06 ± 0.09; median: 0.07.
It is evident that the comparison of pieces across genres provides far lower similarity values than when comparing works across all genres except classical music. This implies that the described method could be used to classify a piece into a musical style/genre, in particular after building a larger corpus of musical themes.
4.3. Obtained Results—Comparison of Pieces and Their Arrangements
The described method was also used to compare the pieces with the arrangements obtained on their basis. For this purpose, the first step involved building a graph representation of the original pieces. Then, based on that, musical arrangements were generated and their graph representation was calculated. Finally, both structures were compared using the measures described in this article, as was the case in previous subsections.
The results presented in Table 7 show that the method detects musical arrangements exceptionally well. In each of the comparisons, the similarity value is at least 0.27, and in half of the cases, the values are close to the maximum. The mean value and the median of the meta-criterion are also close to the maximum possible value. Such values did not occur in any case of comparing different pieces of music (Section 4.2); the proposed method thus allows detecting pieces with a common structure, a kind of “musical core”—the themes and sound progressions used. This means that it can be used to detect arrangements, covers, committed plagiarism, or broadly understood borrowings of a musical theme.

Table 7.
Comparison of tracks and their arrangements.
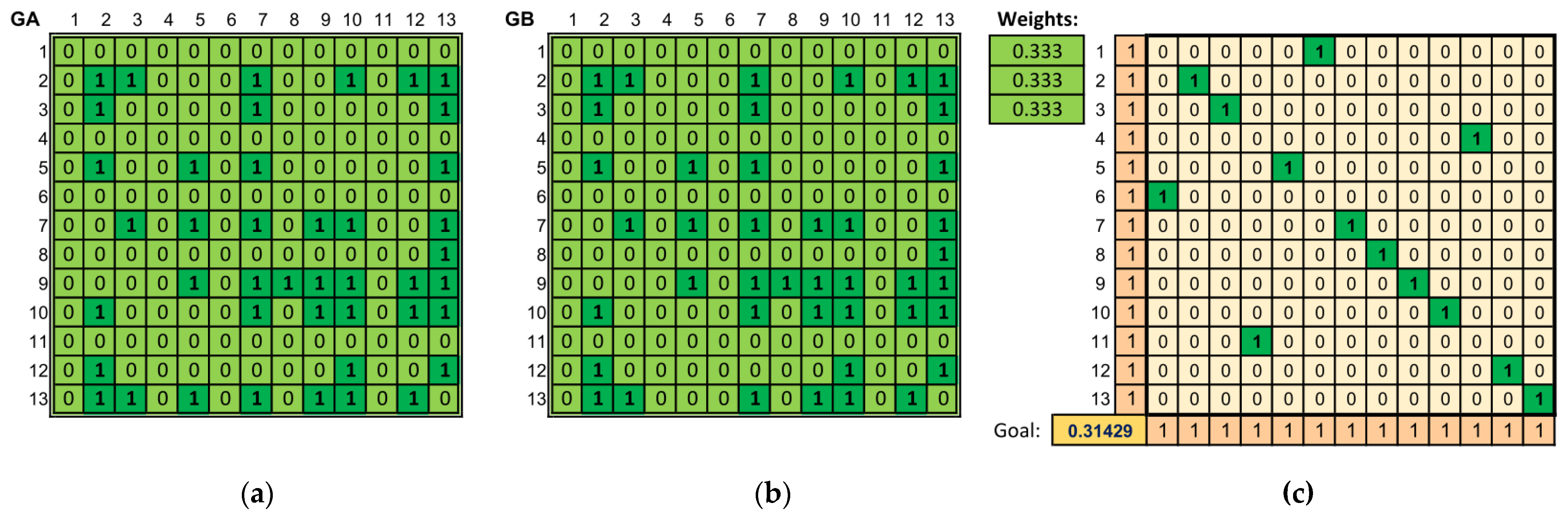
Figure 4 shows that the compared pieces (original and arrangement) are of almost identical structure. Although the pieces differ in the values of the vertex and edge labels (which are not shown in the illustration), the similarity calculated between them is close to the maximum value. Furthermore, one may notice that the calculated assignment matrix is close to the identity matrix in terms of its visual features, and this means that in the optimal assignment, almost all notes are transformed “into themselves”. On the other hand, the remaining notes (from lines 1, 4, 6, and 11, i.e., those that are transformed into other notes of the piece) do not appear in both pieces, so the assignment calculated for these notes is irrelevant from the musical point of view and that of the value of the objective function.
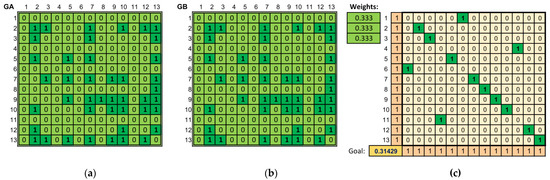
Figure 4.
Comparison of The Final Countdown in the original version and the arrangement generated on its basis. (a) The adjacency matrix of the graph representing the original piece. (b) The adjacency matrix of the graph representing the arrangement. (c) The calculated assignment matrix of vertices from one graph to another (maximizing graph similarity) together with the value of the objective function.
4.4. Obtained Results—Specific Cases
For a more complete reflection, the method was also used to test the similarity of two cases significantly different than those described above. The comparisons were drawn in the same way as before, yet they concerned specifically selected pieces of music. This part of the experiment is described in Table 8.

Table 8.
Comparison of tracks in different variants.
The first part of the experiment compares two musical tracks from the same piece—the vocal phrase and the violin part of the UEFA Champions League musical theme. It can be seen that the similarity of these phrases is relatively low in comparison to other pieces under analysis. Similar values of the meta-criterion and partial criteria were obtained when comparing works that were dissimilar in terms of their musical features (e.g., comparison of Toccata and Fugue and Shchedryk in Table 2).
Despite the fact that both tracks originate from the same piece (so they can be considered “complementary”, matching each other), the method returns values that imply a rather faint similarity between the two. Regardless of the fact that the aesthetic values of such a combination are good, the measure renders it impossible to detect the correctness of their consonance. This is because the described structural and quantitative method is based on a graph representation of both musical tracks. In this case, they are significantly different (the vocal theme differs from the accompaniment in terms of dynamics, melody, length of musical phrases, and their ambitus), and this translates into differences in the graphs representing them, whereas the method only assesses the similarity of these graph representations.
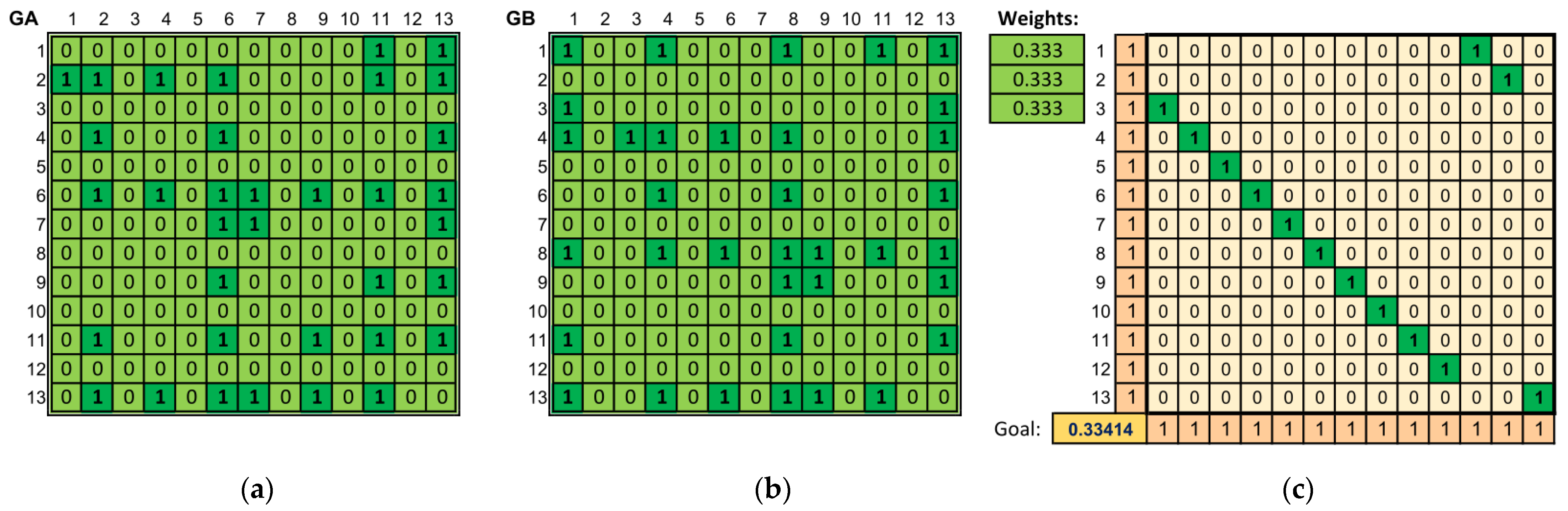
Yet another specific case under study is the comparison of the piece Rolling in the Deep—a piece in the original key with a transposed piece. The original is written in the key of G Minor, while the “arrangement” is an identical piece written in the key of F Minor. The comparison with the calculated similarity value is presented in Figure 5.
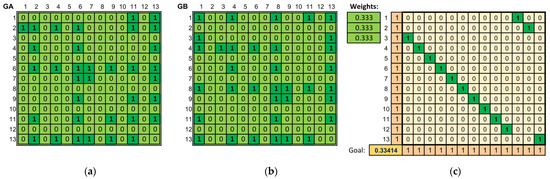
Figure 5.
Comparison of Rolling in the Deep in the original and transposed versions. (a) The adjacency matrix of the graph representing the original piece. (b) The adjacency matrix of the graph representing the transposed work. (c) The calculated optimal assignment matrix of vertices from one graph to another (maximizing graph similarity) together with the value of the objective function.
In this way, in the case of the piece Rolling in the Deep, an attempt to deceive the anti-plagiarism system by transposing the piece to a different octave was simulated. As described in the Hamming and Levenshtein metrics (Section 3.1), plagiarism would not be detected if these “text” metrics were used. After transposition, the successive notes of the compared pieces differ in frequency (and thus also in note name), and this makes the calculated distance between them significant.
The structural and quantitative method is resistant to the manipulation described above. Figure 5 shows that for the abovementioned comparison, the method calculated the optimal assignment resulting in a similarity value approximately equal to the maximum possible value (0.334) for such parameters.
Moreover, the optimal assignment itself also implies that we are dealing with plagiarism. Visually, it can be seen that the values in the matrix in rows 3–12 form a “ribbon” under the diagonal, and the values in rows 1–2 (i.e., values “1”) appear in cells , where c—column number. The above observation applies to all elements of the matrix except for the last one (which also has a musical justification: the last row and column of the matrix represent rests that are not transposed), thus the rest is correctly transformed into itself.
In other words, the obtained result indicates that the optimal value of similarity between the pieces can be obtained by replacing note C of the arrangement with note D of the original song, C# note—with note D#, and so on, until note B is transformed into C#. In fact, the arrangement was created by lowering the key by two semitones, so by raising each note by two semitones, the original piece will be obtained.
4.5. Other Methods for Solving the Multi-Objective Problem
As described in Section 3.3, there are other ways to solve the multi-criteria problem. In particular, one of the ways to find a solution that will satisfy the decision-maker is to select such an assignment of notes from one graph to another that the similarity value is as close as possible to the value set by the user, according to the formula given in (28).
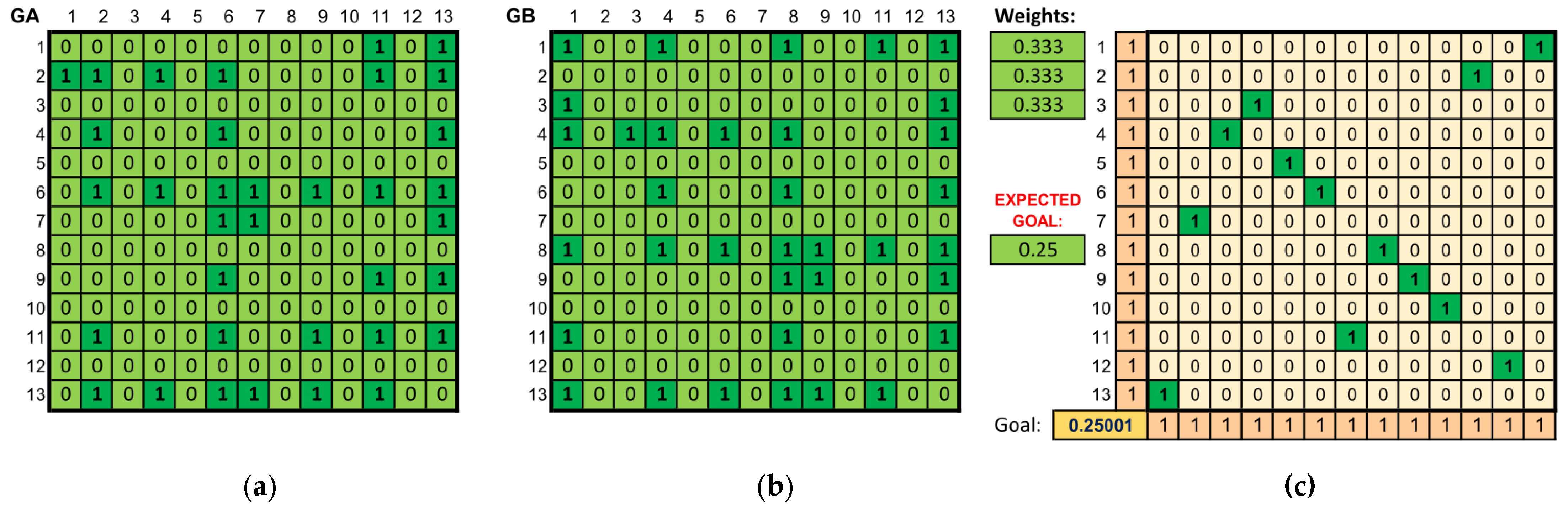
In the course of work on this publication, a tool was developed to calculate this assignment. For example, in the case of the piece Für Elise (original and arrangement), a similarity value of 0.25 was set. After running the problem of calculating the assignment matrix that meets the given objective, the result shown in Figure 6 was obtained, and thus the assignment was calculated for which the value of the objective function (0.25001) is approximately the same as the set objective (0.25).
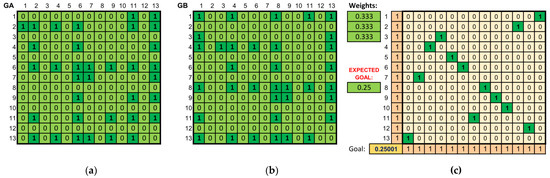
Figure 6.
Comparison of Für Elise in the original version and the arrangement generated on its basis. (a) The adjacency matrix of the graph representing the original piece. (b) The adjacency matrix of the graph representing the arrangement. (c) The calculated assignment matrix of vertices from one graph to another (maximizing graph similarity) together with the value of the objective function.
This method of solving the problem is justified, in particular, in the case of creating musical arrangements. The task of the composer in this case involves creating a new piece that will sound quite similar to the original, but in such a way that the piece is not plagiarism. The above method renders it possible to “control the similarity” of the resulting work, and thus to achieve the objective set in this way.
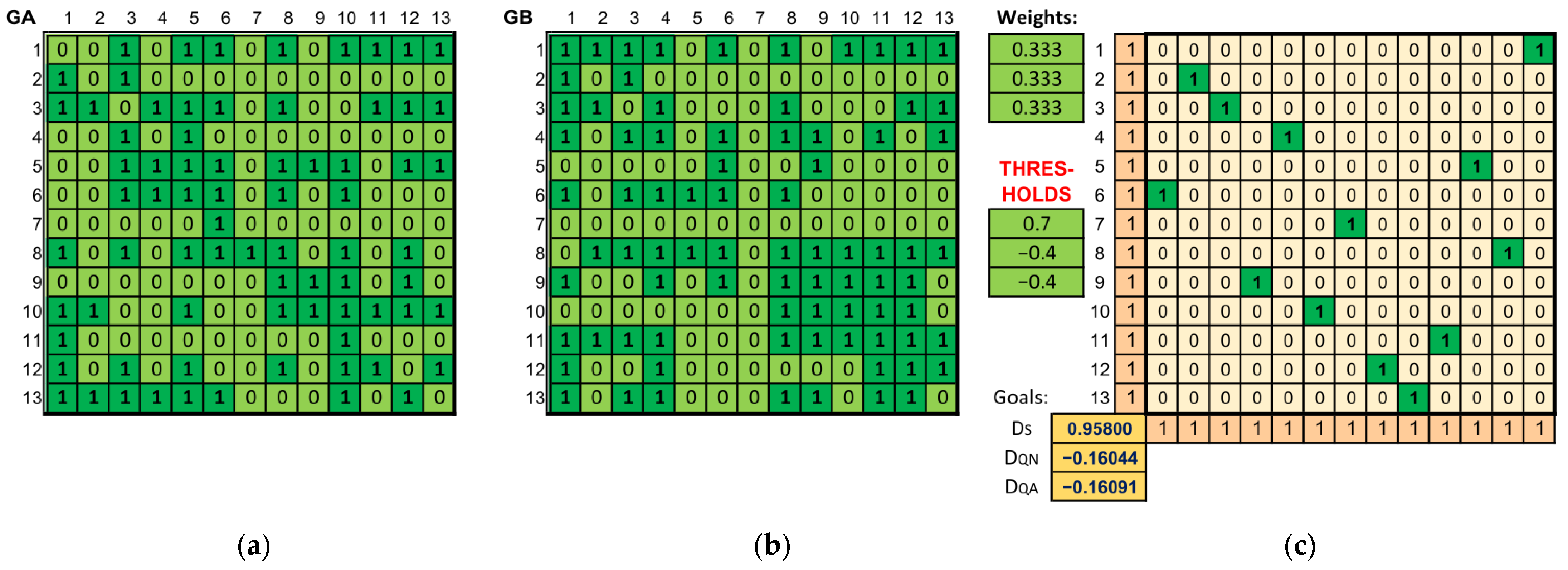
An alternative way to solve the problem is to use threshold optimization. This solves the single-criteria optimization problem, while the fact of exceeding the thresholds for the remaining criteria is achieved by adding additional constraints. Alternatively, one can find a solution that meets the imposed constraints, but without optimization in relation to the indicated criterion. The developed tool allows solving the problem defined in this way.
Figure 7 shows the threshold solution discovered for Für Elise and Nocturne Op. 9. Having defined the thresholds that are correct in terms of the values of individual criteria (structural criterion—positive value, quantitative criteria—negative values) and having solved the problem, one can read the assignment that meets all the imposed constraints, namely the values of the solution found are greater than the set thresholds.
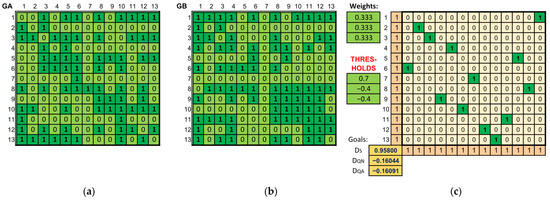
Figure 7.
Comparison of L. van Beethoven’s Für Elise and Nocturne Op. 9 by F. Chopin. (a) The adjacency matrix of the graph representing the first piece. (b) The adjacency matrix of the graph representing the second piece. (c) The calculated assignment matrix of vertices from one graph to another (meeting the given threshold criteria) together with the value of individual partial objective functions.
The ways of solving the problem formulated this way may constitute an additional added value in the context of generating pieces with specific musical values. At the same time, emphasis should be placed on the fact that these are not the only ways to solve the multi-criteria problem, and methods not listed here may work well in other specific applications.
5. Discussion
In this article, the authors proposed a new method of measuring the similarity of musical pieces based on their graph and network representation. The method based on the study of the structural and quantitative similarity of the network allows for disregarding the details of the piece that are irrelevant from the point of view of the examined application.
As shown in the article, this method works particularly well in the search for plagiarism, arrangement, or more generally pieces that are similar to each other. By examining both the structure similarity (connection between notes) and quantitative similarity (multiple occurrences of specific notes and their sequences in a piece), the method allows for detecting a common “musical core” present in pieces under analysis. Detection of such situations allows the use of this method in anti-plagiarism systems and in all applications where this issue is crucial (e.g., proceedings in court cases related to copyright infringement or competitions, scholarships, and artistic grants).
It should also be emphasized that the above method is the first attempt to systematically solve the problem of examining the similarity of musical pieces by examining the similarity of their graph and network representation. Although there were earlier studies analyzing such representation on the basis of graph and network characteristics, they did not describe the methods of calculating a single similarity value. This paper introduces a definition of such a measure, and this enables to measure the similarity of pieces in an objective way.
This publication shows that the method in its current version is insufficient to assess whether the compared music tracks harmonize well with each other. The issue of interpretation of the obtained similarity value may also be problematic; depending on the selected parameter values (criterion weights), the range of achieved values is different. Addressing the above inconveniences should be the goal of future studies developing the described method of examining the similarity of musical tracks.
The method described in this article does not render it possible to detect whether the analyzed music track is a vocal or instrumental track. As far as the graph and network structure is concerned, this information is redundant; however, in potential specific applications (such as clustering of music pieces), the above information may be an additional factor relevant to the obtained result.
The described method would also be worth developing from the point of view of the readability of the obtained result. Currently, a qualitative assessment of similarity (i.e., answering the question “does the value of 0.2 mean a high similarity of pieces”, fundamental in practical terms) is not possible without knowing the values of the parameters. Nevertheless, having provided constant parameter values, the introduced measure enables the analysis of pieces and the comparison of the obtained results, which is the most important issue from the point of view of the conducted studies.
6. Conclusions
In conclusion, the studies showed that the described method (originally regarding other applications) can be used in the field of comparing musical pieces. In particular, the applied approach works particularly well in detecting similarities in relation to entire pieces, both desirable (arrangements, covers) and generally considered inappropriate (plagiarism).
The paper describes a novel approach to comparing musical pieces. First of all, in this article, we propose to compare soundtracks by comparing not their music representation (either sheet music or audio samples) but graphs that reflect the notes’ precedence relationship. Second, we describe a new method to calculate the similarity of musical pieces. This method results in retrieving a single number quite clearly describing whether the pieces are similar or not.
The above observations lead to the conclusion that the described method should be implemented, in particular in anti-plagiarism control tools (used in legal proceedings and to control works created at art schools) and in CAC (computer-aided composition) systems used by composers and arrangers (for examining whether the piece of work is similar to the preceeding musical works).
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app13063567/s1. All the materials created along with this article (music scores, MIDI files, spreadsheets, source codes etc.).
Author Contributions
Z.T. has conceptualized the idea behind this research, authored the original methodology of network comparison, implemented the tool to measure network similarity, provided formal analysis and investigation, reviewed the draft and supervised the project. S.M. has adjusted the abovementioned method for this specific application, formalized methods of creating graph representation of music, implemented the software for music visualization and test automation, performed experiments (collected test data, adjusted and converted to a format required by the project), collected the results and drafted the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and supplementary material.
Acknowledgments
Compared tracks have been obtained from Free Midi Database (FreeMidi.org) as well as Musescore Sheet Music Database (Musescore.com/sheetmusic/public-domain) and pre-processed to monophonic samples using Musescore software (Musescore.org). Calculations have been made with OpenSolver extension for Excel (opensolver.org). Source code uses JUNG (jung.sourceforge.net) and jMusic (Explodingart.com/jmusic) libraries.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zbikowski, L.M. Conceptualizing Music: Cognitive Structure, Theory, and Analysis; Oxford University Press: Oxford, UK, 2002; ISBN 9780195140231. [Google Scholar] [CrossRef]
- Liu, H.; Yang, Y. Lead Sheet Generation and Arrangement by Conditional Generative Adversarial Network. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 722–727. [Google Scholar] [CrossRef]
- Lee, S.G.; Hwang, U.; Min, S.; Yoon, S. Polyphonic Music Generation with Sequence Generative Adversarial Networks. arXiv 2017, arXiv:1710.11418. [Google Scholar]
- Huang, A. Deep Learning for Music Composition: Generation, Recommendation and Control. Doctoral Dissertation, Harvard University, Harvard, UK, 2019. Available online: https://dash.harvard.edu/bitstream/handle/1/42029468/HUANG-DISSERTATION-2019.pdf (accessed on 5 March 2023).
- Huang, C.Z.; Hawthorne, C.; Roberts, A.; Dinculescu, M.; Wexler, J.; Hong, L.; Howcroft, J. The Bach Doodle: Approachable Music Composition with Machine Learning at Scale. In Proceedings of the 20th International Society for Music Information Retrieval Conference, Delft, The Netherlands, 4–8 November 2019; pp. 793–800, ISBN 978-1-7327299-1-9. [Google Scholar]
- Xie, J. A Novel Method of Music Generation Based on Three Different Recurrent Neural Networks. J. Phys. Conf. Ser. 2020, 1549, 042034. [Google Scholar] [CrossRef]
- Briot, J.-P. From Artificial Neural Networks to Deep Learning for Music Generation—History, Concepts and Trends. Neural Comput. Appl. 2021, 33, 39–65. [Google Scholar] [CrossRef]
- Daylamani Zad, D.; Araabi, B.N.; Lucas, C. A Novel Approach to Automatic Music Composing: Using Genetic Algorithm. Int. Comput. Music. Conf. Proc. 2006, 2006, 551–555. [Google Scholar]
- Huang, J.L.; Chiu, S.C.; Shan, M.K. Towards an automatic music arrangement framework using score reduction. ACM Trans. Multimed.Comput. Commun. Appl. (TOMM) 2012, 8, 1–23. [Google Scholar] [CrossRef]
- Kitahara, T. Music Generation Using Bayesian Networks. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2017, Skopje, Macedonia, 18–22 September 2017; pp. 368–372. [Google Scholar] [CrossRef]
- Goienetxea, I.; Mendialdua, I.; Rodríguez, I.; Sierra, B. Statistics-Based Music Generation Approach Considering Both Rhythm and Melody Coherence. IEEE Access 2019, 7, 183365–183382. [Google Scholar] [CrossRef]
- Smith, R.; Dennis, A.W.; Ventura, D. Automatic Composition from Non-musical Inspiration Sources. In Proceedings of the 3rd International Conference on Computational Creativity (ICCC), Dublin, Ireland, 30 May–1 June 2012; pp. 160–164. [Google Scholar]
- Yang, C.; Tse, C.K.; Liu, X. Analyzing and Composing Music from Network Motifs. In Proceedings of the International Symposium on Nonlinear Theory and Its Applications (NOLTA), Sapporo, Japan, 19–21 October 2009; pp. 407–410. [Google Scholar]
- Liu, X.; Tse, C.K.; Small, M. Composing music with complex networks. In Proceedings of the International Conference on Complex Networks and Their Applications (COMPLEX), Shanghai, China, 23–25 February 2009; pp. 2196–2205. [Google Scholar]
- Ferretti, S. On the Modeling of Musical Solos as Complex Networks. Inf. Sci. 2016, 375, 271–295. [Google Scholar] [CrossRef]
- Chen, W.A.; Lin, J.H.; Jeng, S.K. Harmony Graph, a Social-Network-Like Structure, and Its Applications to Music Corpus Visualization, Distinguishing and Music Generation. Int. J. Comput. Linguist. Chin. Lang. Process. 2010, 15, 1–19. [Google Scholar]
- Muszynski, S. Novel Graph-Based Approach for Creating and Comparing Music Arrangements. In Proceedings of the 36th International Business Information Management Association (IBIMA), Granada, Spain, 4–5 November 2020; pp. 13266–13279, ISBN 978-0-9998551-5-7. [Google Scholar]
- Wilson, R.J. Wprowadzenie do Teorii Grafów, 2nd ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2012. [Google Scholar]
- Tarapata, Z. Multicriteria weighted graphs similarity and its application for decision situation pattern matching problem. In Proceedings of the 13th IEEE/IFAC International Conference on Methods and Models in Automation and Robotics (MMAR), Szczecin, Poland, 27–30 August 2007; pp. 1149–1155, ISBN 978-83-751803-3-6. [Google Scholar]
- Liu, X.F.; Tse, C.K.; Small, M. Complex network structure of musical compositions: Algorithmic generation of appealing music. Phys. A Stat. Mech. Appl. 2010, 389, 126–132. [Google Scholar] [CrossRef]
- Ren, I.Y. Complexity of Musical Patterns, University of Warwick. Available online: https://warwick.ac.uk/fac/cross_fac/complexity/study/emmcs/outcomes/studentprojects/ren_m1.pdf (accessed on 19 January 2023).
- Ukkonen, E. Approximate string-matching with q-grams and maximal matches. Theor. Comput. Sci. 1992, 92, 191–211. [Google Scholar] [CrossRef]
- Berghel, H.; Roach, D. An Extension of Ukkonen’s Enhanced Dynamic Programming ASM Algorithm. ACM Trans. Inf. Syst. (TOIS) 1996, 14, 94–106. [Google Scholar] [CrossRef]
- Blondel, V.D.; Gajardo, A.; Heymans, M.; Senellart, P.; Van Dooren, P. A Measure of Similarity between Graph Vertices: Applications to Synonym Extraction and Web Searching. SIAM Rev. 2004, 46, 647–666. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).