A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco
Abstract
Featured Application
Abstract
1. Introduction
1.1. State of the Art
1.2. Justification and Objectives
2. Materials and Methods
2.1. Methodology
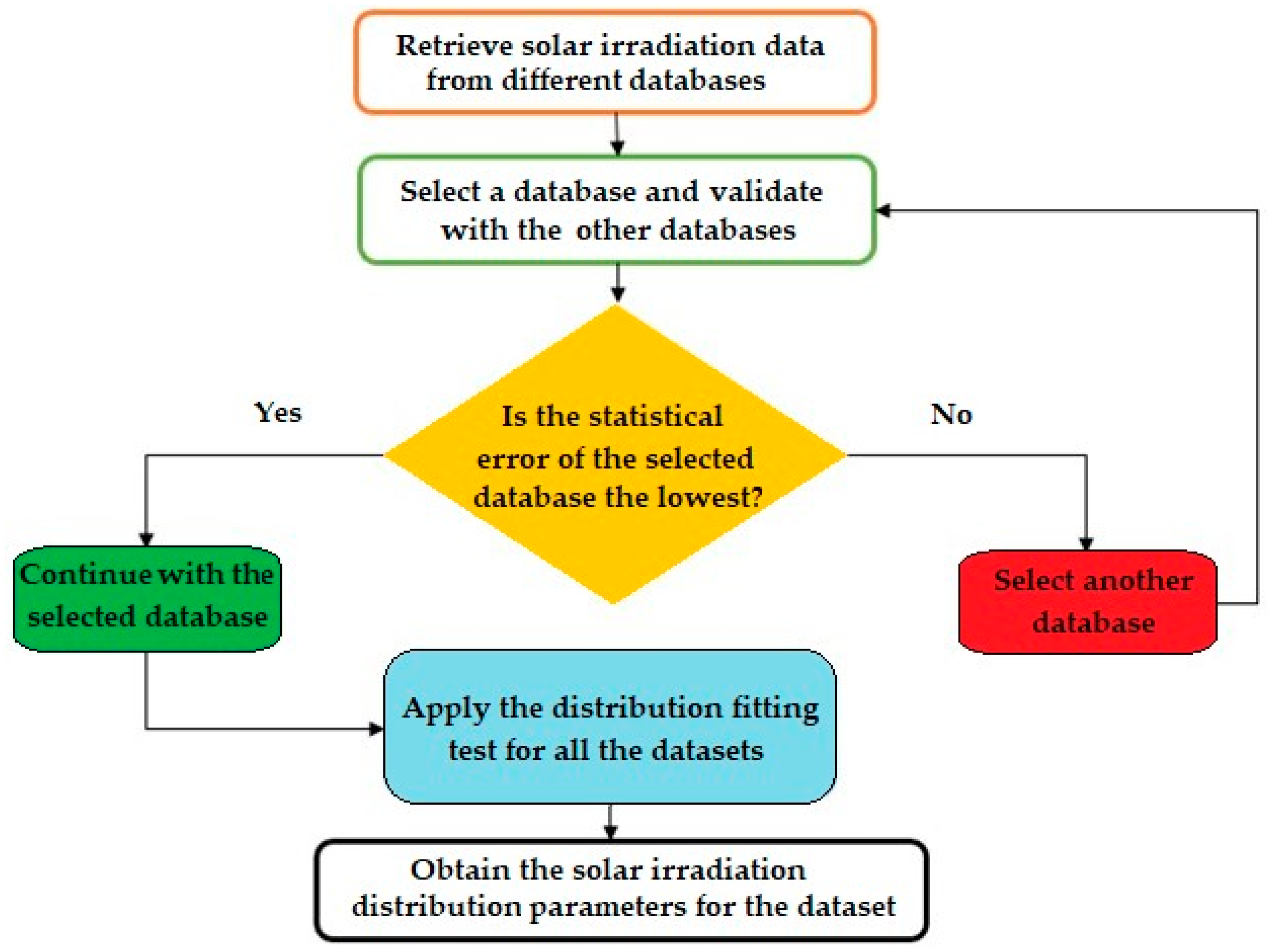
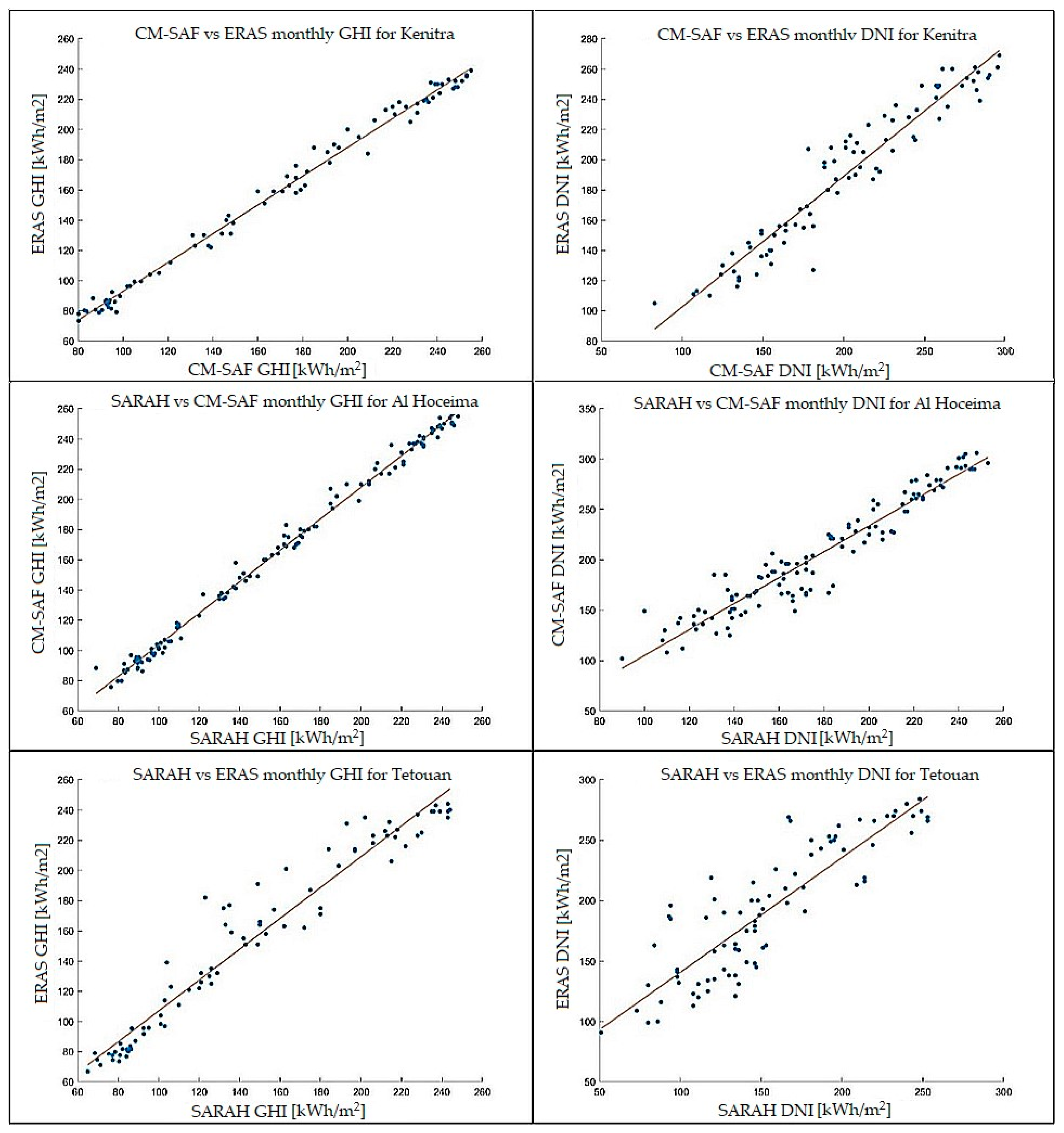
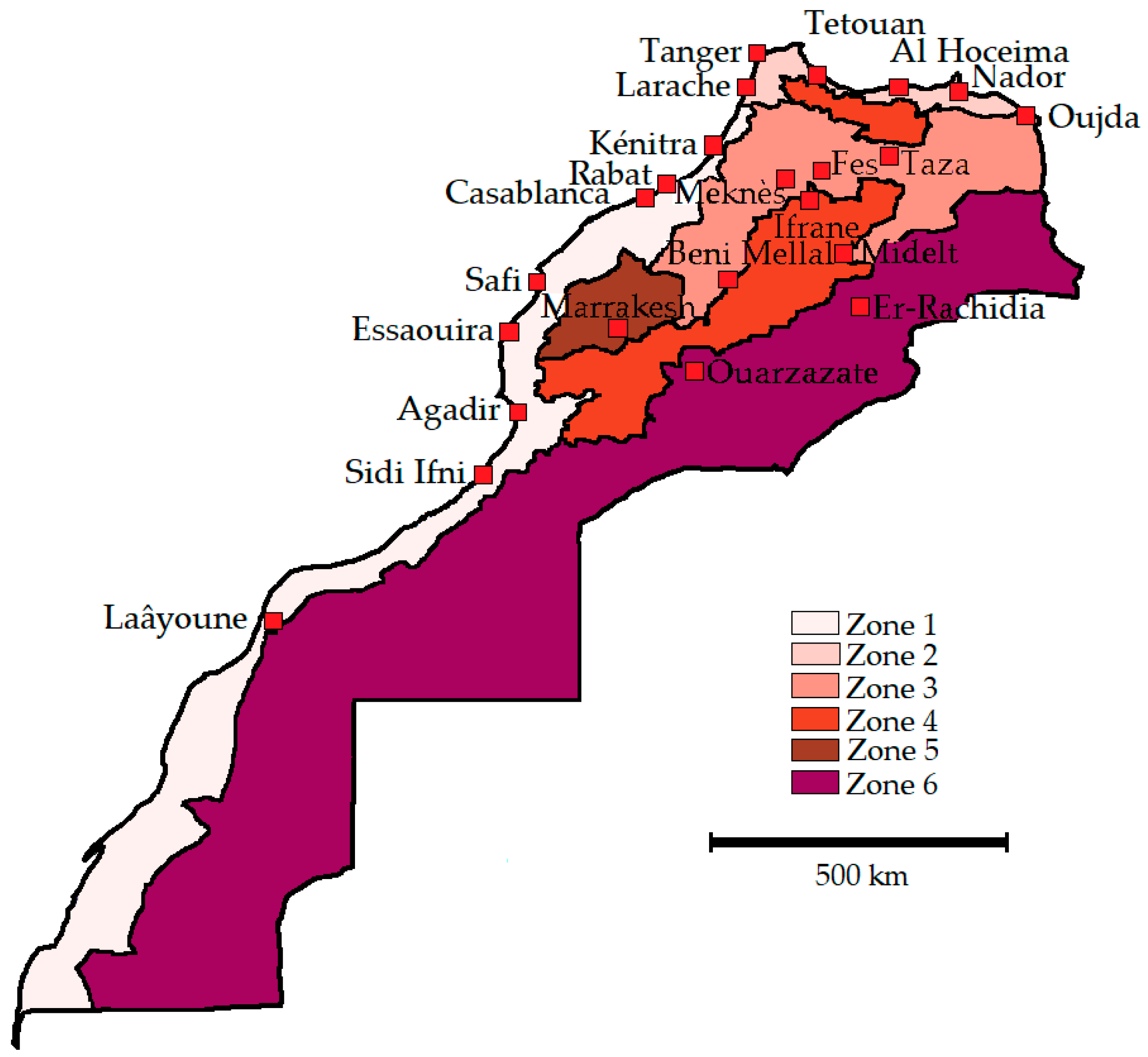
2.2. Case Study Definition and Data Collection and Validation

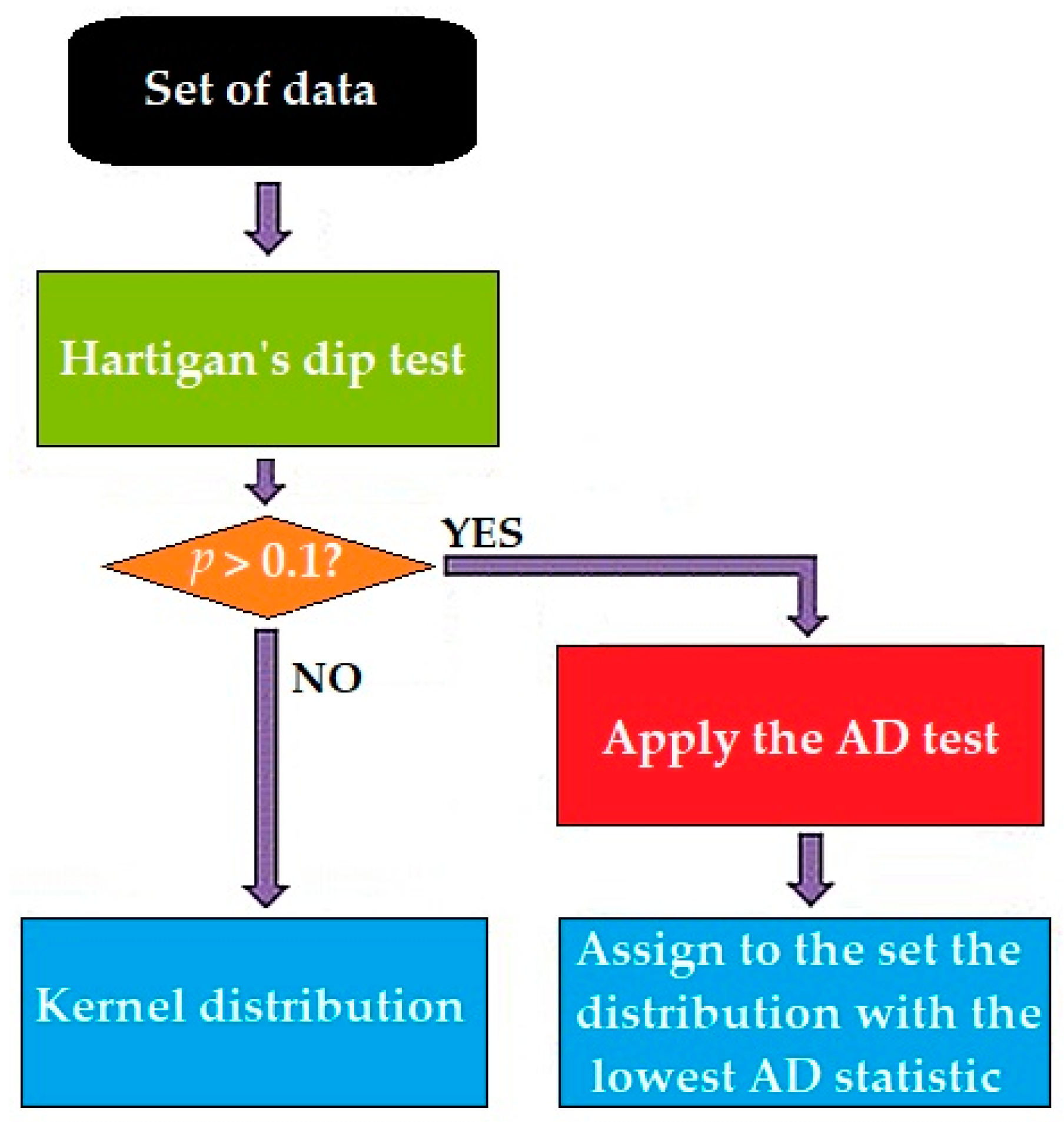
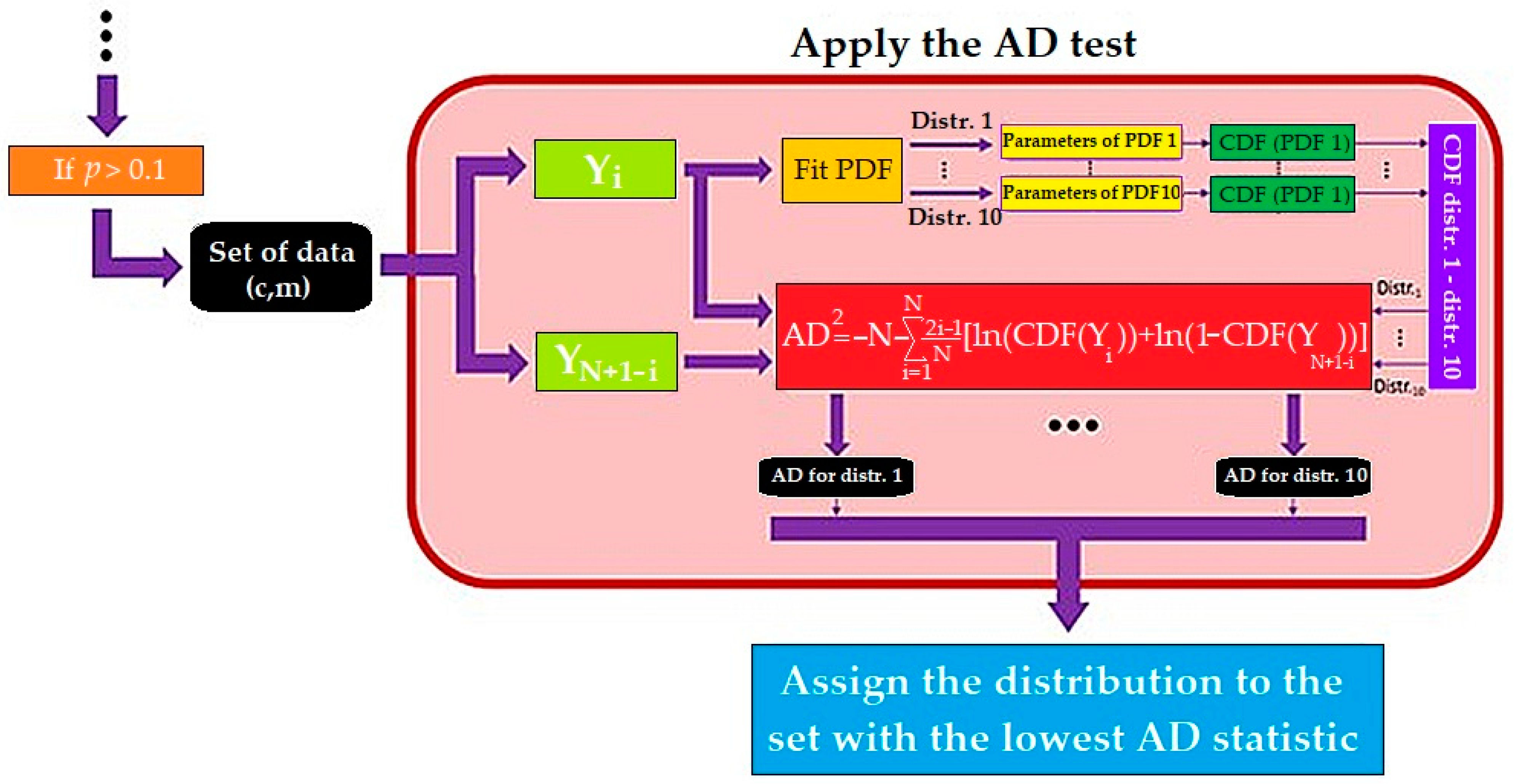
2.3. Probability Distribution Function Fitting
3. Results and Discussion
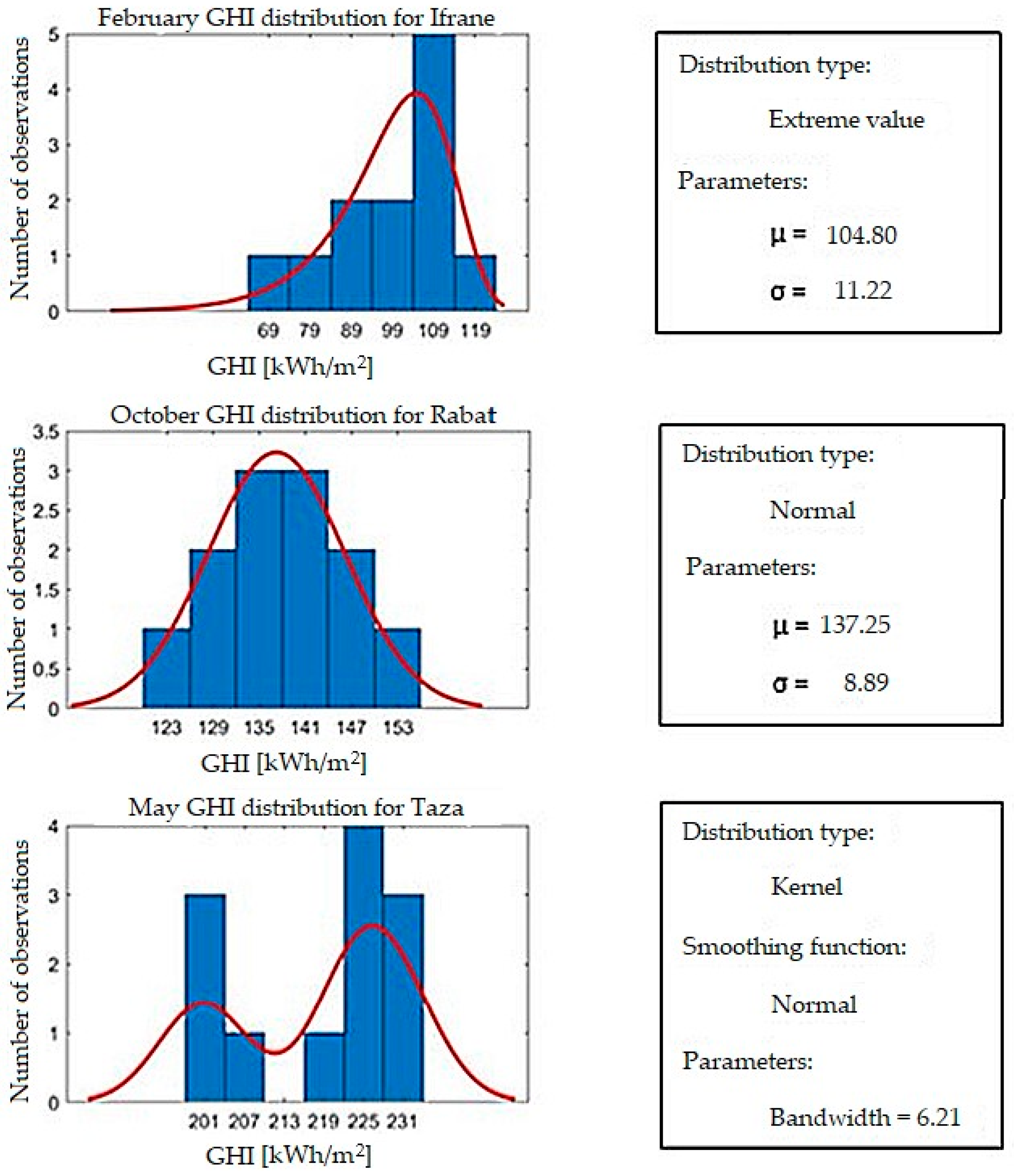
3.1. Obtained Results
| Zone | City | Month | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov. | Dec. | ||
| 1 | Agadir | Log | ExV | ExV | ExV | Nor | Nor | ExV | Log | ExV | Nor | Log | Web |
| Casablanca | ExV | Web | ExV | ExV | Log | Nor | ExV | Web | ExV | Nor | Krn | ExV | |
| Essaouira | Krn | ExV | Nor | Nor | ExV | ExV | Nor | ExV | ExV | ExV | ExV | Log | |
| Kenitra | ExV | Web | ExV | Log | Nor | Nor | ExV | Nor | ExV | Web | Gmm | Nor | |
| Laayoune | ExV | Nor | Log | ExV | ExV | Log | Nor | Web | ExV | Web | Log | Log | |
| Rabat | ExV | Web | Krn | Nor | Nor | Nor | Nor | Nor | Nor | ExV | Log | Nor | |
| Safi | Log | Web | ExV | Nor | ExV | Nor | Nor | ExV | ExV | Log | Nor | Log | |
| Sidi Ifni | Log | Log | ExV | Nor | ExV | Nor | Nor | ExV | ExV | ExV | ExV | Log | |
| 2 | Al Hoceima | ExV | Nor | Nor | Nor | ExV | Log | Log | Log | Log | Web | Log | ExV |
| Larache | Log | Log | ExV | ExV | Log | Nor | Nor | Nor | Log | Nor | ExV | ExV | |
| Nador | ExV | ExV | Nor | Krn | ExV | ExV | Log | ExV | Nor | ExV | Nor | Nor | |
| Tanger | ExV | ExV | ExV | Log | Nor | Nor | Nor | Krn | Web | ExV | Log | ExV | |
| Tetouan | ExV | Nor | Krn | Nor | ExV | Web | Log | Log | Nor | Nor | Log | Nor | |
| 3 | Beni Mellal | Krn | ExV | ExV | Nor | ExV | Log | Log | ExV | Nor | Log | Nor | ExV |
| Fes | Nor | ExV | ExV | Web | Log | Log | Log | ExV | Nor | ExV | Log | ExV | |
| Meknes | Nor | Web | ExV | ExV | Log | Krn | Nor | ExV | Web | Nor | Log | ExV | |
| Oujda | ExV | ExV | Nor | ExV | ExV | Web | Web | ExV | ExV | Nor | Nor | Log | |
| Taza | Nor | Log | ExV | ExV | ExV | Log | Web | Web | ExV | Web | Log | Log | |
| 4 | Ifrane | ExV | ExV | ExV | Nor | Nor | Log | Web | Log | ExV | Nor | Log | Nor |
| Midelt | Log | ExV | Log | ExV | ExV | Log | Nor | ExV | Log | Log | ExV | Log | |
| 5 | Marrakech | Nor | Krn | ExV | Nor | ExV | ExV | Log | Log | Log | Log | Krn | Log |
| 6 | Er-Rachidia | Log | ExV | Log | ExV | ExV | ExV | Log | ExV | Log | Log | ExV | Log |
| Ouarzazate | Nor | ExV | Log | Web | ExV | ExV | Web | Nor | Krn | Nor | Web | Log | |
| Zone | City | Month | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov. | Dec. | ||
| 1 | Agadir | ExV | Web | Web | Nor | Web | Web | Krn | Log | ExV | Web | Web | Log |
| Casablanca | Nor | Gmm | Web | Nor | Nor | Web | ExV | Nor | Web | ExV | Nor | Web | |
| Essaouira | Log | Gmm | ExV | Log | ExV | Log | ExV | ExV | Web | ExV | Log | Log | |
| Kenitra | Nor | Log | Web | Log | Log | Web | ExV | ExV | Nor | Nor | Nor | Krn | |
| Laayoune | ExV | Web | Nor | ExV | ExV | Log | ExV | Web | Web | Log | Log | Krn | |
| Rabat | Log | Log | Web | Log | Nor | Log | ExV | Krn | Log | Nor | Log | Krn | |
| Safi | Log | Log | ExV | Krn | ExV | Log | ExV | ExV | Nor | Nor | Log | Log | |
| Sidi Ifni | Nor | Log | Log | Log | Nor | Nor | ExV | ExV | Nor | ExV | Web | Log | |
| 2 | Al Hoceima | Log | Log | Krn | Nor | ExV | Nor | Nor | Log | Log | Web | Log | Web |
| Larache | Log | Log | Web | Log | Nor | Nor | Nor | Web | Nor | Nor | Log | ExV | |
| Nador | Nor | Krn | Krn | Nor | ExV | Nor | Log | Nor | Log | Web | Web | Nor | |
| Tanger | Log | Gmm | Web | Log | Web | Krn | Log | ExV | Nor | Web | Log | ExV | |
| Tetouan | Log | Web | Web | ExV | ExV | ExV | Krn | Log | Log | ExV | Nor | ExV | |
| 3 | Beni Mellal | Nor | ExV | Log | Web | ExV | Web | Web | ExV | Web | Log | Nor | ExV |
| Fes | Log | Nor | ExV | Log | Log | Web | Nor | Nor | ExV | Nor | Nor | ExV | |
| Meknes | Log | Nor | ExV | Log | Log | ExV | Nor | ExV | ExV | Krn | Nor | ExV | |
| Oujda | Nor | ExV | Log | ExV | ExV | Log | Web | Web | Nor | Web | Web | Log | |
| Taza | Log | Log | Log | ExV | Krn | Log | Web | Nor | ExV | Web | Log | ExV | |
| 4 | Ifrane | ExV | ExV | ExV | ExV | Log | Log | Nor | Log | ExV | Nor | Nor | ExV |
| Midelt | ExV | Nor | Log | Krn | ExV | Log | ExV | Nor | ExV | Log | Log | ExV | |
| 5 | Marrakech | Nor | Nor | Log | ExV | ExV | ExV | Log | Web | Web | Gmm | Log | Nor |
| 6 | Er-Rachidia | Gmm | Log | Log | Nor | Nor | Web | Nor | ExV | Log | Krn | Web | ExV |
| Ouarzazate | Nor | Log | Nor | Web | ExV | ExV | ExV | Nor | Nor | Web | ExV | ExV | |
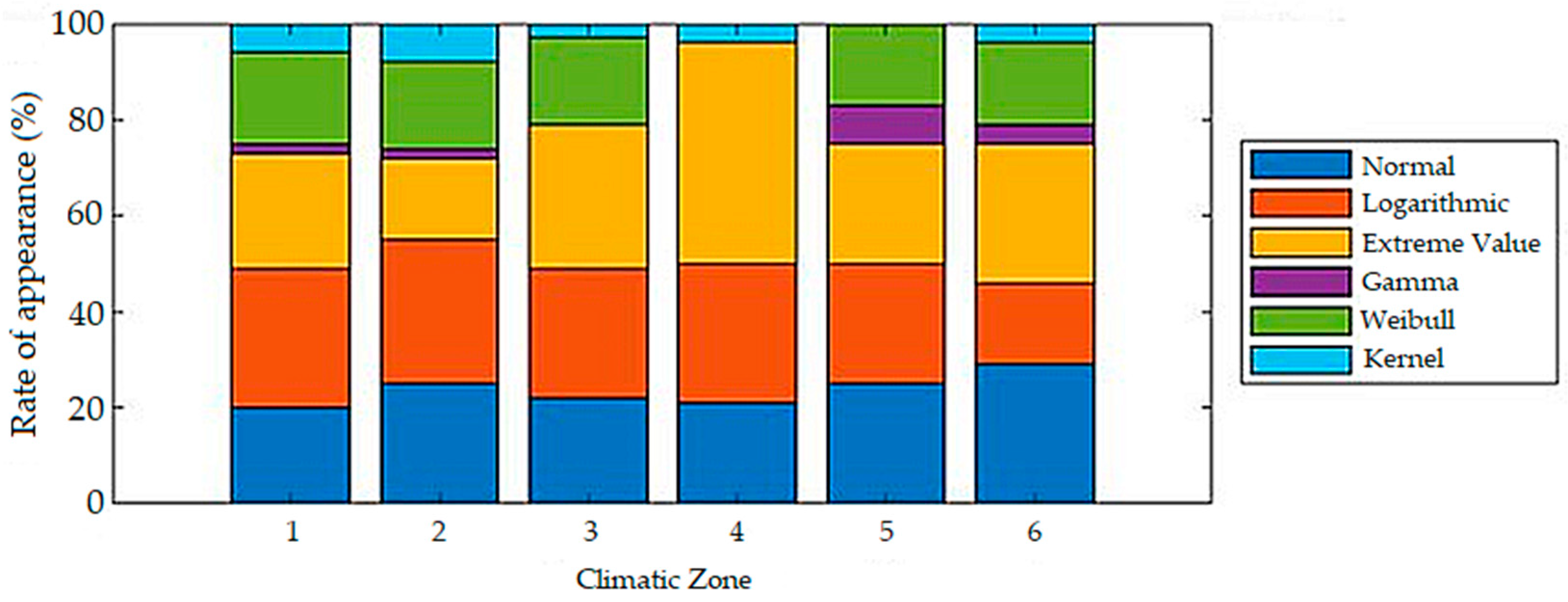
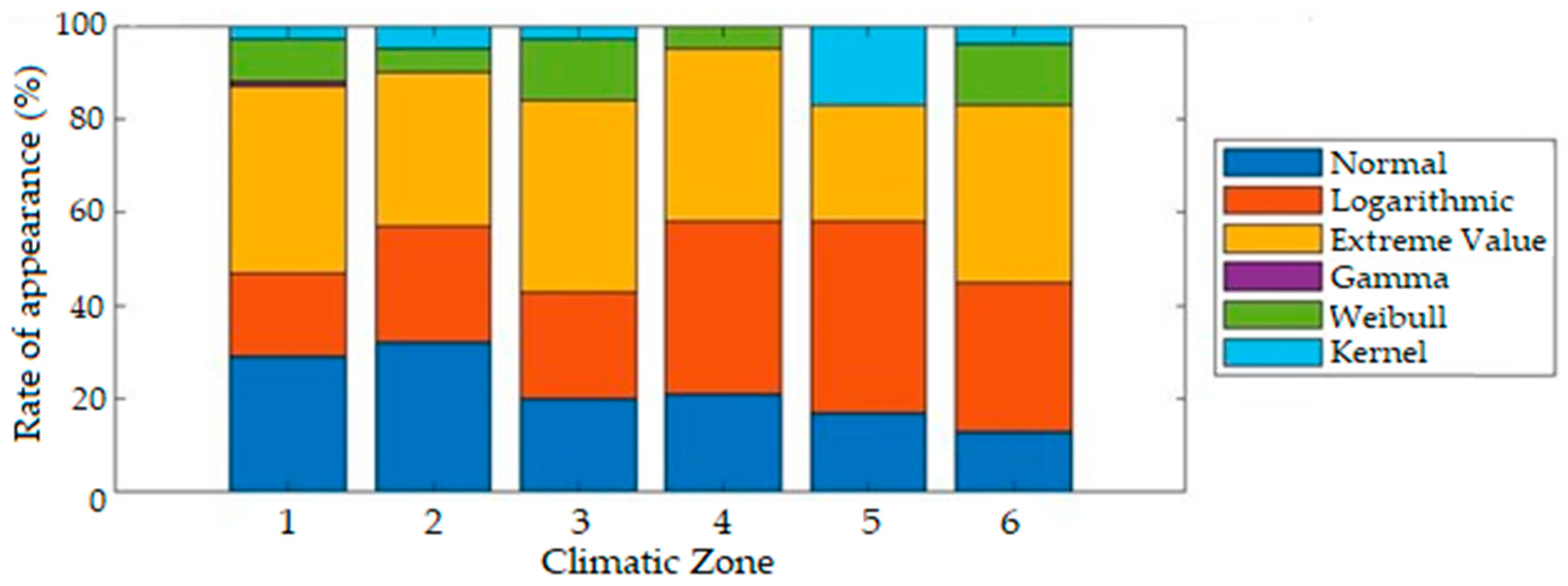
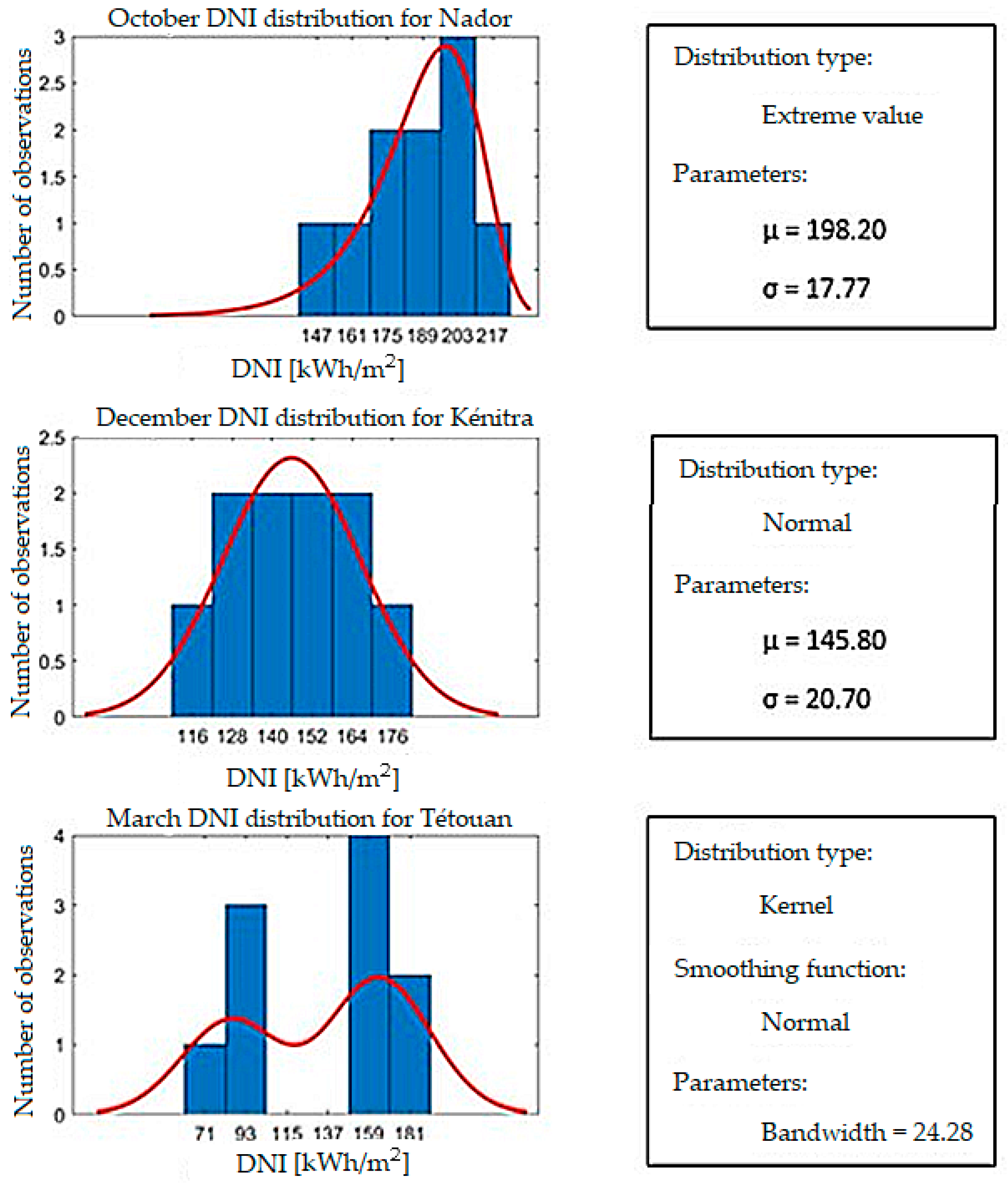
3.2. Analysis and Discussion of Results


4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- PV Magazine. Solar Is Gaining Traction in MENA Region—But Plenty of Obstacles Remain. 2020. Available online: https://www.pv-magazine.com/2020/01/17/mesia-outlines-past-progress-future-promise-in-sweeping-look-at-solar-across-middle-east-and-north-africa/ (accessed on 29 September 2022).
- EcoMENA. Countries Driving Solar Surge in MENA. 2019. Available online: https://www.ecomena.org/solar-surge-in-mena/ (accessed on 29 September 2022).
- NREL Transforming Energy. Concentrating Solar Power Projects. Available online: https://solarpaces.nrel.gov/concentrating-solar-power-projects-country (accessed on 29 September 2022).
- Masen|L’Agence Marocaine Pour l’Energie Durable. Available online: http://www.masen.ma (accessed on 29 September 2022).
- Royaume du Maroc—Ministère de l’Energie, des Mines et de l’Environnement. Available online: https://www.mem.gov.ma/Pages/secteur.aspx?e=2 (accessed on 29 September 2022).
- REN21—Building the Sustainable Energy Future with Renewable Energy. Available online: https://www.ren21.net (accessed on 29 September 2022).
- Blaga, R.; Sabadus, A.; Stefu, N.; Dughir, C.; Paulescu, M.; Badescu, V. A current perspective on the accuracy of incoming solar energy forecasting. Prog. Energy Combust. Sci. 2019, 70, 119–144. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Kumler, A.; Xie, Y.; Zhang, Y. A Physics-based Smart Persistence model for Intra-hour forecasting of solar radiation (PSPI) using GHI measurements and a cloud retrieval technique. Sol. Energy 2019, 177, 494–500. [Google Scholar] [CrossRef]
- Wang, P.; van Westrhenen, R.; Meirink, J.F.; van der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Kallio-Myers, V.; Riihelä, A.; Lahtinen, P.; Lindfors, A. Global horizontal irradiance forecast for Finland based on geostationary weather satellite data. Sol. Energy 2020, 198, 68–80. [Google Scholar] [CrossRef]
- Ohtake, H.; da Silva Fonseca, J.G., Jr.; Takashima, T.; Oozeki, T.; Shimose, K.-i.; Yamada, Y. Regional and seasonal characteristics of global horizontal irradiance forecasts obtained from the Japan Meteorological Agency mesoscale model. Sol. Energy 2015, 116, 83–99. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Gueymard, C.A. A multi-model benchmarking of direct and global clear-sky solar irradiance predictions at arid sites using a reference physical radiative transfer model. Sol. Energy 2018, 171, 447–465. [Google Scholar] [CrossRef]
- Zempila, M.-M.; Giannaros, T.M.; Bais, A.; Melas, D.; Kazantzidis, A. Evaluation of WRF shortwave radiation parameterizations in predicting Global Horizontal Irradiance in Greece. Renew. Energy 2016, 86, 831–840. [Google Scholar] [CrossRef]
- Fountoukis, C.; Martín-Pomares, L.; Perez-Astudillo, D.; Bachour, D.; Gladich, I. Simulating global horizontal irradiance in the Arabian Peninsula: Sensitivity to explicit treatment of aerosols. Sol. Energy 2018, 163, 347–355. [Google Scholar] [CrossRef]
- Yang, D.; Sharma, V.; Ye, Z.; Lim, L.I.; Zhao, L.; Aryaputera, A.W. Forecasting of global horizontal irradiance by exponential smoothing, using decompositions. Energy 2015, 81, 111–119. [Google Scholar] [CrossRef]
- Kim, C.K.; Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y.; Kim, S.Y. Probabilistic prediction of direct normal irradiance derived from global horizontal irradiance over the Korean Peninsula by using Monte-Carlo simulation. Sol. Energy 2019, 180, 63–74. [Google Scholar] [CrossRef]
- Zang, H.; Liu, L.; Sun, L.; Cheng, L.; Wei, Z.; Sun, G. Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations. Renew. Energy 2020, 160, 26–41. [Google Scholar] [CrossRef]
- Lopes, F.M.; Silva, H.G.; Salgado, R.; Cavaco, A.; Canhoto, P.; Collares-Pereira, M. Short-term forecasts of GHI and DNI for solar energy systems operation: Assessment of the ECMWF integrated forecasting system in southern Portugal. Sol. Energy 2018, 170, 14–30. [Google Scholar] [CrossRef]
- Huang, J.; Rikus, L.J.; Qin, Y.; Katzfey, J. Assessing model performance of daily solar irradiance forecasts over Australia. Sol. Energy 2018, 176, 615–626. [Google Scholar] [CrossRef]
- Pedro, H.T.; Coimbra, C.F.; David, M.; Lauret, P. Assessment of machine learning techniques for deterministic and probabilistic intra-hour solar forecasts. Renew. Energy 2018, 123, 191–203. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Aler, R.; Galván, I.M.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Pozo-Vazquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 2: Model blending approaches based on machine learning. Sol. Energy 2020, 195, 685–696. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Pereira, S.; Canhoto, P.; Salgado, R.; Costa, M.J. Development of an ANN based corrective algorithm of the operational ECMWF global horizontal irradiation forecasts. Sol. Energy 2019, 185, 387–405. [Google Scholar] [CrossRef]
- Aguiar, L.M.; Pereira, B.; Lauret, P.; Díaz, F.; David, M. Combining solar irradiance measurements, satellite-derived data and a numerical weather prediction model to improve intra-day solar forecasting. Renew. Energy 2016, 97, 599–610. [Google Scholar] [CrossRef]
- Mazorra Aguiar, L.; Pereira, B.; David, M.; Díaz, F.; Lauret, P. Use of satellite data to improve solar radiation forecasting with Bayesian Artificial Neural Networks. Sol. Energy 2015, 122, 1309–1324. [Google Scholar] [CrossRef]
- Hejase, H.A.; Al-Shamisi, M.H.; Assi, A. Modeling of global horizontal irradiance in the United Arab Emirates with artificial neural networks. Energy 2014, 77, 542–552. [Google Scholar] [CrossRef]
- Scolari, E.; Sossan, F.; Paolone, M. Irradiance prediction intervals for PV stochastic generation in microgrid applications. Sol. Energy 2016, 139, 116–129. [Google Scholar] [CrossRef]
- Pedro, H.T.; Coimbra, C.F. Nearest-neighbor methodology for prediction of intra-hour global horizontal and direct normal irradiances. Renew. Energy 2015, 80, 770–782. [Google Scholar] [CrossRef]
- Tolba, H.; Dkhili, N.; Nou, J.; Eynard, J.; Thil, S.; Grieu, S. GHI forecasting using Gaussian process regression: Kernel study. IFAC-PapersOnLine 2019, 52, 455–460. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; Akour, M.; Cotfas, D.T.; Cotfas, P.A.; El Bouardi, A. Long-Term Global Solar Radiation Prediction in 25 Cities in Morocco Using the FFNN-BP Method. Front. Energy Res. 2021, 9, 733842. [Google Scholar] [CrossRef]
- Bounoua, Z.; Chahidi, L.O.; Mechaqrane, A. Estimation of daily global solar radiation using empirical and machine-learning methods: A case study of five Moroccan locations. Sustain. Mater. Technol. 2021, 28, e00261. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; El Bouardi, A. A hybrid ARIMA–ANN method to forecast daily global solar radiation in three different cities in Morocco. Eur. Phys. J. Plus 2020, 135, 925. [Google Scholar] [CrossRef]
- El Mghouchi, Y.; Chham, E.; Zemmouri, E.; El Bouardi, A. Assessment of different combinations of meteorological parameters for predicting daily global solar radiation using artificial neural networks. Build. Environ. 2018, 149, 607–622. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; El Bouardi, A. One month-ahead forecasting of mean daily global solar radiation using time series models. Optik 2020, 219, 165207. [Google Scholar] [CrossRef]
- Stoffel, T.; Renne, D.; Myers, D.; Wilcox, S.; Sengupta, M.; George, R.; Turchi, C. Concentrating Solar Power: Best Practices Handbook for the Collection and Use of Solar Resource Data (CSP); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [CrossRef]
- HELIOSCSP. Steps for Solar Resource Assessment in Concentrated Solar Power Projects. 2018. Available online: http://helioscsp.com/steps-for-solar-resource-assessment-in-concentrated-solar-power-projects/ (accessed on 29 September 2022).
- Renne, D.; George, R.; Wilcox, S.; Stoffel, T.; Myers, D.; Heimiller, D. Solar Resource Assessment; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2008. [CrossRef]
- Mohandes, M.; Rehman, S.; Halawani, T. Estimation of global solar radiation using artificial neural networks. Renew. Energy 1998, 14, 179–184. [Google Scholar] [CrossRef]
- Mohandes, M.; Balghonaim, A.; Kassas, M.; Rehman, S.; Halawani, T. Use of radial basis functions for estimating monthly mean daily solar radiation. Sol. Energy 2000, 68, 161–168. [Google Scholar] [CrossRef]
- Mubiru, J.; Banda, E. Estimation of monthly average daily global solar irradiation using artificial neural networks. Sol. Energy 2008, 82, 181–187. [Google Scholar] [CrossRef]
- Marchand, M.; Ghennioui, A.; Wey, E.; Wald, L. Comparison of several satellite-derived databases of surface solar radiation against ground measurement in Morocco. Adv. Sci. Res. 2018, 15, 21–29. [Google Scholar] [CrossRef]
- Wahab, M.M.A.; El-Metwally, M.; Hassan, R.; Lefèvre, M.; Oumbe, A.; Wald, L. Assessing surface solar irradiance and its long-term variations in the northern Africa desert climate using Meteosat images. Int. J. Remote Sens. 2010, 31, 261–280. [Google Scholar] [CrossRef]
- Aguiar, L.M.; Polo, J.; Vindel, J.; Oliver, A. Analysis of satellite derived solar irradiance in islands with site adaptation techniques for improving the uncertainty. Renew. Energy 2019, 135, 98–107. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Huld, T.; Martinez-De-Pison, F.J.; Trentmann, J.; Lindfors, A.V.; Riihelä, A.; Sanz-Garcia, A. Quality control of global solar radiation data with satellite-based products. Sol. Energy 2017, 158, 49–62. [Google Scholar] [CrossRef]
- Schumann, K.; Beyer, H.G.; Meyer, R.; Chhatbar, K. Improving Satellite-Derived Solar Resource Analysis with Parallel Ground-Based Measurements. In Proceedings of the ISES Solar World Congress, Kassel, Germany, 28 August–2 September 2011. [Google Scholar]
- Meyer, R.; Butron, J.T.; Marquard, G.; Schwandt, M.; Geuder, N.; Hoyer-Klick, C.; Lorenz, E.; Hammer, A.; Beyer, H.G. Combining Solar Irradiance Measurements and Various Satellite-Derived Products to a Site-Specific Best Estimage. In Proceedings of the SolarPACES Symposium 2008, Las Vegas, NV, USA, 4–7 March 2008; Available online: https://elib.dlr.de/53849/ (accessed on 29 September 2022).
- Ineichen, P. Long Term Satellite Global, Beam and Diffuse Irradiance Validation. Energy Procedia 2014, 48, 1586–1596. [Google Scholar] [CrossRef]
- Kariuki, B.W.; Sato, T. Interannual and spatial variability of solar radiation energy potential in Kenya using Meteosat satellite. Renew. Energy 2018, 116, 88–96. [Google Scholar] [CrossRef]
- Plain, N.; Hingray, B.; Mathy, S. Accounting for low solar resource days to size 100% solar microgrids power systems in Africa. Renew. Energy 2019, 131, 448–458. [Google Scholar] [CrossRef]
- Müller, R.; Pfeifroth, U.; Träger-Chatterjee, C.; Trentmann, J.; Cremer, R. Digging the METEOSAT Treasure—3 Decades of Solar Surface Radiation. Remote Sens. 2015, 7, 8067–8101. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Palmer, D.; Koubli, E.; Cole, I.; Betts, T.; Gottschalg, R. Satellite or ground-based measurements for production of site specific hourly irradiance data: Which is most accurate and where? Sol. Energy 2018, 165, 240–255. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-De-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- El Mghouchi, Y.; El Bouardi, A.; Sadouk, A.; Fellak, I.; Ajzoul, T. Comparison of three solar radiation models and their validation under all sky conditions—Case study: Tetuan city in northern of Morocco. Renew. Sustain. Energy Rev. 2016, 58, 1432–1444. [Google Scholar] [CrossRef]
- El Mghouchi, Y.; Ajzoul, T.; El Bouardi, A. Prediction of daily solar radiation intensity by day of the year in twenty-four cities of Morocco. Renew. Sustain. Energy Rev. 2016, 53, 823–831. [Google Scholar] [CrossRef]
- AMEE | Adhérons à un Avenir Énergétique Durable. Available online: https://www.amee.ma/index.php?lang=en (accessed on 29 September 2022).
- Direction de la Météorologie Nationale|Ministère de l’Equipement, du Transport, de la Logistique et de l’Eau Département de l’Eau. Available online: http://www.marocmeteo.ma (accessed on 29 September 2022).
- Agence Nationale Pour le Développement des Energies Renouvelables et de l’Éfficacité Energétique. Règlement Thermique de Construction au Maroc (RTCM). Available online: https://www.amee.ma/sites/default/files/inline-files/Guide%20RTCM%20.pdf (accessed on 29 September 2022).
- Google Maps. Available online: https://www.google.com/maps/@29.3231834,-7.7723258,5.5z (accessed on 29 September 2022).
- PANGEA. BSRN Stations. Available online: https://www.pangaea.de/ddi?request=bsrn/BSRNEvent&format=html&title=BSRN+Stations (accessed on 29 September 2022).
- European Commission. Photovoltaic Geographical Information System (PVGIS). Available online: http://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 29 November 2018).
- Romero, S.M. CSP & Solar Resource Assessment. In: Bank TW. Washington DC, USA: Energy Sector Management Assistant Program. Available online: https://www.esmap.org/sites/default/files/esmap-files/ESMAP_IFC_RE_CSP_Training_World_Bank_Romero.pdf (accessed on 29 September 2022).
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]
- Freeman, J.B.; Dale, R. Assessing bimodality to detect the presence of a dual cognitive process. Behav. Res. Methods 2012, 45, 83–97. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Hartigan, P.M. The Dip Test of Unimodality. Ann. Stat. 1985, 13, 70–84. Available online: http://links.jstor.org/sici?sici=0090-5364%28198503%2913%3A1%3C70%3ATDTOU%3E2.0.CO%3B2-A (accessed on 29 September 2022). [CrossRef]
- Machine Learning Mastery. A Gentle Introduction to Probability Density Estimation. 2020. Available online: https://machinelearningmastery.com/probability-density-estimation/ (accessed on 29 September 2022).
- Kim, T.Y.; Park, B.U.; Moon, M.S.; Kim, C. Using bimodal kernel for inference in nonparametric regression with correlated errors. J. Multivar. Anal. 2009, 100, 1487–1497. [Google Scholar] [CrossRef]
- Engineering Statistics Handbook. 1.3.5.14. Anderson-Darling Test; National Institute of Standards and Testing (NIST): Gaithersburg, MD, USA, 2013. [CrossRef]
- Stephanie, G. Rayleigh Distribution: Definition, Uses, Mean, Variance. Statistics How to. 2014. Available online: https://www.statisticshowto.com/rayleigh-distribution/ (accessed on 29 September 2022).
- Weisstein, E.W. “Student’s t-Distribution”. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/Studentst-Distribution.html (accessed on 29 September 2022).
- Hernández, J.A.; Trujillo, C.L.; Vallejo, W.A. Modelamiento de la irradiancia y la temperatura ambiente utilizando funciones de probabilidad. Rev. Tecnura 2014, 18, 128–137. [Google Scholar] [CrossRef]


| Term of Solar Irradiance Forecasting | |
|---|---|
| Short-term irradiance forecasting [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] | [9] Intra-hour GHI cloud retrieval technique to develop a physics-based smart persistence model |
| [10] Intra-day GHI and DNI algorithm using cloud physical properties | |
| [11] A 15 min GHI forecasting model | |
| [12] Hourly-averaged GHI forecasts | |
| [13] Hourly GHI and DNI clear-sky irradiance vs. RRTMG physical radiative transfer model | |
| [14] Hourly and daily GHI from mesoscale atmospheric weather research forecasting model | |
| [15] Hourly GHI with a three-dimensional meteorology–chemistry model including a treatment of aerosols | |
| [16] Hourly GHI exponential smoothing model with decomposition methods | |
| [17] A 1 min DNI under a probabilistic approach | |
| [18] Short-term GHI with hybrid convolutional ANN model with spatiotemporal correlations | |
| [19] Short-term GHI and DNI forecasts of a global numerical weather model | |
| [20,21] A 5–30 min GHI and DNI with machine learning techniques | |
| [22] A 15 min GHI and DNI with machine learning techniques | |
| [23] Intra-day GHI with machine learning techniques | |
| [24] A 30 min GHI with ANN algorithm | |
| [25,26] Hourly GHI ANN models | |
| [27] Mean daily GHI with ANN models | |
| [28] A 500 ms–5 min GHI based on k-means algorithm | |
| [29] A 5–30 min GHI and DNI based on the k-nearest neighbours algorithm | |
| [30] A 30 min–5 h GHI Gaussian process regression method | |
| [31] Daily GHI with ANN models for for 25 Moroccan cities | |
| [32] Daily GHI with empirical and machine learning models for 5 Moroccan cities | |
| [33] Monthly mean daily GHI using time series models | |
| [34] Daily GHI with hybrid ARIMA–ANN model for 3 cities in Morocco | |
| [35] Daily GHI with ANN models for 35 Moroccan, Algerian, Spanish and Mauritian cities | |
| Monthly irradiance forecasting [36,37,38,39,40,41] | [36] Best Practices Handbook for the Collection and Use of Solar Resource Data, selection of potential sites |
| [37] Steps for solar resource assessment, selection of potential sites | |
| [38] Solar resource assessment, selection of potential sites | |
| [39] Monthly data, ANN models are used to estimate it in Saudi Arabia | |
| [40] ANN models are used to estimate it in Saudi Arabia | |
| [41] ANN models are used to estimate it in Uganda | |
| Use of satellite-based data for solar resource assessment | |
| Use of satellite-based data for solar resource assessment [42,43,44,45,46,47,48,49,50,51,52,53,54] | [42] Satellite data comparison with ground measurements in Morocco |
| [43] Satellite data comparison with ground measurements in North Africa | |
| [44] Satellite data comparison with ground measurements in the Canary Islands | |
| [45] Satellite data comparison with ground measurements for sites in Europe | |
| [46] Satellite data validation through statistical methods in Algeria | |
| [47] Satellite data validation through statistical methods in Spain | |
| [48] Satellite data comparison with ground measurements for European and Mediterranean sites | |
| [49,50,51] SARAH satellite database validation for several sites, especially for Africa | |
| [52] PVGIS satellite database validation for both Europe and Africa | |
| [53,54] Variability of irradiance values in areas with variable landforms | |
| Zone | City | Latitude [Degrees] | Longitude [Degrees] |
|---|---|---|---|
| 1 | Agadir | 30.383 | −9.567 |
| Casablanca | 33.567 | −7.667 | |
| Essaouira | 31.517 | −9.783 | |
| Kénitra | 34.300 | −6.600 | |
| Laâyoune | 27.160 | −13.210 | |
| Rabat | 34.050 | −6.767 | |
| Safi | 32.283 | −9.233 | |
| Sidi Ifni | 29.360 | −10.180 | |
| 2 | Al Hoceima | 35.180 | −3.850 |
| Larache | 35.180 | −6.130 | |
| Nador | 35.150 | −2.910 | |
| Tànger | 35.733 | −5.900 | |
| Tétouan | 35.580 | −5.330 | |
| 3 | Beni Mellal | 32.360 | −6.400 |
| Fes | 33.933 | −4.983 | |
| Meknes | 33.883 | −5.533 | |
| Oujda | 34.793 | −1.933 | |
| Taza | 34.217 | −4.000 | |
| 4 | Ifrane | 33.500 | −5.167 |
| Midelt | 32.683 | −4.733 | |
| 5 | Marrakech | 31.617 | −8.033 |
| 6 | Er-Rachidia | 31.930 | −4.400 |
| Ouarzazate | 30.933 | −6.900 |
| CM-SAF and ERA5 | SARAH and ERA5 | SARAH and CM-SAF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| City | MAD | MBD | RMSD | MAD | MBD | RMSD | MAD | MBD | RMSD |
| Agadir | 17.57 | −11.62 | 23.53 | 23.18 | −19.75 | 29.28 | 12.91 | −5.01 | 16.09 |
| Al Hoceima | 13.02 | 4.45 | 16.70 | 27.26 | −24.88 | 31.79 | 29.03 | −27.39 | 33.59 |
| Beni Mellal | 20.98 | −20.33 | 24.05 | 20.52 | −19.43 | 24.26 | 13.14 | 1.78 | 16.24 |
| Casablanca | 14.23 | −0.18 | 17.09 | 21.63 | −17.89 | 25.49 | 20.96 | −12.96 | 25.34 |
| Er−Rachidia | 39.11 | −39.11 | 41.09 | 19.48 | −15.24 | 21.83 | 26.33 | 25.13 | 30.61 |
| Essaouira | 17.98 | 17.71 | 21.04 | 18.80 | −17.32 | 22.90 | 33.18 | −32.71 | 36.88 |
| Fes | 23.23 | −21.11 | 27.88 | 17.14 | −11.45 | 20.28 | 24.40 | 11.62 | 30.82 |
| Ifrane | 23.82 | −23.01 | 26.82 | 26.35 | −25.51 | 29.89 | 13.02 | −1.68 | 16.97 |
| Kenitra | 15.15 | 11.13 | 18.76 | 19.15 | −16.30 | 22.22 | 24.58 | −23.50 | 29.05 |
| Laayoune | 14.55 | −12.71 | 17.80 | 11.92 | −8.08 | 15.02 | 12.38 | 6.21 | 15.81 |
| Larache | 13.17 | −5.86 | 16.85 | 19.19 | −16.93 | 21.95 | 16.74 | −14.04 | 20.66 |
| Marrakech | 10.61 | −7.06 | 13.47 | 14.30 | −8.06 | 16.70 | 12.88 | 0.02 | 15.75 |
| Meknes | 12.61 | −7.89 | 15.56 | 16.73 | −13.23 | 19.22 | 13.46 | −3.79 | 16.84 |
| Midelt | 24.60 | −24.36 | 27.14 | 25.74 | −23.79 | 30.58 | 15.78 | 1.58 | 19.79 |
| Nador | 16.93 | 4.57 | 21.47 | 25.88 | −24.26 | 30.56 | 27.78 | −25.55 | 33.88 |
| Ouarzazate | 21.79 | −21.71 | 24.18 | 15.92 | −9.87 | 21.35 | 19.81 | 14.58 | 24.82 |
| Oujda | 14.81 | −2.52 | 17.49 | 19.23 | −18.68 | 22.31 | 19.54 | −13.91 | 24.61 |
| Rabat | 15.24 | 8.14 | 17.83 | 21.76 | −19.38 | 24.95 | 25.31 | −22.44 | 29.88 |
| Safi | 14.83 | 12.33 | 17.52 | 15.50 | −11.98 | 19.71 | 24.73 | −22.82 | 29.06 |
| Sidi Ifni | 26.04 | −13.87 | 33.89 | 25.83 | −25.29 | 32.75 | 25.82 | −16.33 | 29.85 |
| Tanger | 14.23 | −3.23 | 17.78 | 17.67 | −15.10 | 21.62 | 18.20 | −10.85 | 21.76 |
| Taza | 10.98 | 0.43 | 13.66 | 15.42 | −10.35 | 18.40 | 15.78 | −8.96 | 19.57 |
| Tetouan | 36.69 | −36.10 | 44.23 | 38.43 | −37.95 | 46.31 | 13.97 | −1.22 | 18.15 |
| CM-SAF and ERA5 | SARAH and ERA5 | SARAH and CM-SAF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| City | MAD | MBD | RMSD | MAD | MBD | RMSD | MAD | MBD | RMSD |
| Agadir | 6.51 | 1.30 | 8.30 | 6.06 | 0.89 | 7.53 | 3.87 | 0.55 | 5.35 |
| Al Hoceima | 7.54 | 4.80 | 8.93 | 6.05 | −2.51 | 8.96 | 6.55 | −6.20 | 8.20 |
| Beni Mellal | 4.65 | −1.93 | 6.24 | 5.07 | −1.93 | 6.98 | 3.73 | 0.46 | 4.64 |
| Casablanca | 7.23 | 5.53 | 8.51 | 5.70 | 2.44 | 6.88 | 5.29 | −1.27 | 6.99 |
| Er-Rachidia | 11.00 | −11.00 | 12.24 | 4.38 | 1.77 | 6.05 | 14.16 | 13.81 | 15.11 |
| Essaouira | 12.07 | 12.07 | 13.07 | 5.19 | 2.61 | 6.60 | 8.19 | −8.10 | 10.05 |
| Fes | 4.97 | −1.24 | 6.23 | 5.62 | 3.88 | 6.86 | 6.91 | 5.90 | 8.40 |
| Ifrane | 7.36 | −6.10 | 8.77 | 6.15 | −3.61 | 7.97 | 5.10 | 3.05 | 6.44 |
| Kenitra | 10.45 | 10.34 | 11.96 | 5.49 | 3.73 | 6.57 | 5.54 | −4.89 | 7.55 |
| Laayoune | 4.89 | 2.75 | 6.29 | 7.00 | 5.36 | 8.03 | 6.33 | 3.79 | 7.76 |
| Larache | 3.95 | −0.55 | 5.17 | 4.59 | 2.38 | 5.51 | 3.30 | 2.33 | 4.21 |
| Marrakech | 4.86 | 3.03 | 5.73 | 5.36 | 3.76 | 6.52 | 3.31 | 1.14 | 4.22 |
| Meknes | 4.70 | 2.71 | 6.17 | 4.82 | 2.78 | 5.85 | 3.27 | 0.71 | 4.07 |
| Midelt | 8.79 | −8.62 | 10.60 | 7.50 | −5.91 | 10.34 | 6.95 | 3.59 | 8.93 |
| Nador | 7.50 | 2.81 | 9.61 | 5.75 | −1.49 | 8.63 | 5.12 | −2.92 | 6.61 |
| Ouarzazate | 3.88 | −2.00 | 4.82 | 6.85 | 2.23 | 9.33 | 8.53 | 5.77 | 10.05 |
| Oujda | 4.69 | 1.20 | 6.04 | 4.21 | 0.24 | 5.50 | 4.04 | 0.15 | 5.13 |
| Rabat | 9.91 | 9.56 | 11.46 | 4.98 | 1.80 | 6.02 | 6.67 | −5.50 | 8.94 |
| Safi | 9.06 | 8.88 | 10.20 | 5.09 | 3.03 | 6.38 | 5.75 | −4.79 | 7.78 |
| Sidi Ifni | 12.48 | 0.31 | 15.45 | 8.17 | −2.60 | 11.66 | 11.22 | −4.97 | 13.01 |
| Tanger | 5.61 | 3.63 | 6.86 | 5.26 | 3.00 | 6.31 | 3.89 | −0.30 | 4.68 |
| Taza | 6.70 | 5.77 | 8.36 | 5.97 | 4.04 | 7.26 | 4.13 | −0.55 | 5.85 |
| Tetouan | 13.08 | −12.41 | 18.69 | 10.75 | −7.97 | 16.04 | 5.42 | 4.87 | 7.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouhorma, N.; Martín, H.; de la Hoz, J.; Coronas, S. A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco. Appl. Sci. 2023, 13, 3365. https://doi.org/10.3390/app13053365
Bouhorma N, Martín H, de la Hoz J, Coronas S. A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco. Applied Sciences. 2023; 13(5):3365. https://doi.org/10.3390/app13053365
Chicago/Turabian StyleBouhorma, Naoufal, Helena Martín, Jordi de la Hoz, and Sergio Coronas. 2023. "A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco" Applied Sciences 13, no. 5: 3365. https://doi.org/10.3390/app13053365
APA StyleBouhorma, N., Martín, H., de la Hoz, J., & Coronas, S. (2023). A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco. Applied Sciences, 13(5), 3365. https://doi.org/10.3390/app13053365






